ABSTRACT
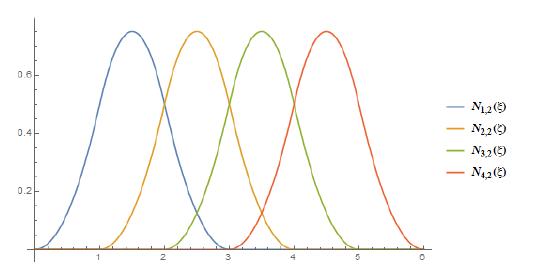
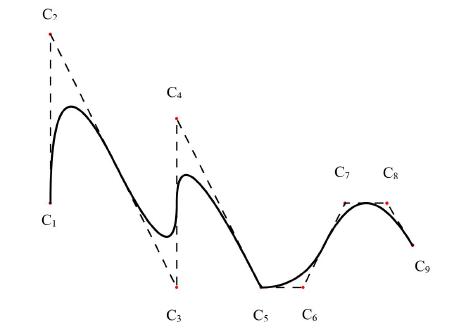
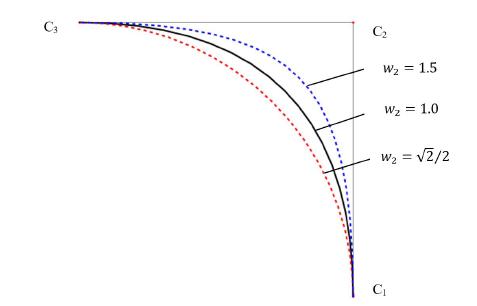
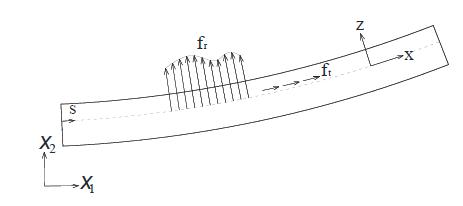
The isogeometric analysis (IGA) consists of using the same shape functions, usually employed on Computer-Aided Design (CAD) technologies, on both geometric modelling and approximation of the fields of physical models. One issue that concerns IGA is how to make the connection or apply general constraints in the connection of structures described by different curves and surfaces (multi-patch structures), particularly when the shape functions are not interpolatory at the selected point for the imposition of the constraint or the desired constraint is not related directly to degrees of freedom, which may be an issue on Kirchhoff-Love shells and Euler-Bernoulli beams, since usually no rotational degrees of freedom are employed. In this context, the present contribution presents an isogeometric 2D curved beam formulation based on Bernoulli-Euler assumptions. An approach about the implementation of multi-patch structures enforcing constraints, such as same displacement or same rotation among neighbor paths, is developed based on Penalty and Lagrange methods. The applicability of the methods is verified by examples of application.
Keywords:
Isogeometric analysis; curved beam; Lagrange method; Penalty method