Isogeometric analysis applied to 2D Bernoulli-Euler beam model: imposition of constraints by Lagrange and Penalty methods

ABSTRACT

The isogeometric analysis (IGA) consists of using the same shape functions, usually employed on Computer-Aided Design (CAD) technologies, on both geometric modelling and approximation of the fields of physical models. One issue that concerns IGA is how to make the connection or apply general constraints in the connection of structures described by different curves and surfaces (multi-patch structures), particularly when the shape functions are not interpolatory at the selected point for the imposition of the constraint or the desired constraint is not related directly to degrees of freedom, which may be an issue on Kirchhoff-Love shells and Euler-Bernoulli beams, since usually no rotational degrees of freedom are employed. In this context, the present contribution presents an isogeometric 2D curved beam formulation based on Bernoulli-Euler assumptions. An approach about the implementation of multi-patch structures enforcing constraints, such as same displacement or same rotation among neighbor paths, is developed based on Penalty and Lagrange methods. The applicability of the methods is verified by examples of application.

Keywords:
Isogeometric analysis; curved beam; Lagrange method; Penalty method

Graphical Abstract

2. INTRODUCTION

The isogeometric analysis (IGA) consists of using the same functions employed on the geometric modelling on the approximation of the independent variables of physical problems governed by differential equations, such as, solid and fluid mechanics. These functions are usually employed on Computer-Aided Design (CAD) technologies. As examples, one may mention B-Splines, NURBS and T-Splines. The isogeometric concept was proposed by [¹] with the motivation of bridging the gap between geometric modelling and structural analysis, reducing mesh generation and refinement costs of the traditional Finite Element Method (FEM) by adopting the exact geometry of design on the analysis.

IGA has much in common with the traditional FEM, the main difference is the use of functions from CAD technologies as shape functions. The functions that generates B-splines and NURBS curves and surfaces, known as B-spline and rational basis functions, respectively, are smooth and C^p-1 continuous, where p is the order of the basis functions. Traditional FEM approaches, however, usually provides only C⁰ continuity on an approximated field. Despite of the difference on the functions used to approximate independent variables in IGA and FEM, a isogeometric finite element structure data can be created, based on Bézier extraction of NURBS and T-splines ([²] and [³]), and easily incorporated into Finite Element existing codes, by only changing shape functions subroutines.

IGA uses the exact geometry of a solid or structure designed by CAD techniques, while traditional FEM models correspond to approximations of the desired geometry. It is such an advantage of IGA on the integration of modelling and analysis in a single software, since the geometry of design constructed using CAD techniques can be directly used on analysis. When the smoothness of the geometry must be considered on analysis, which is the case of fluid-structure interaction and contact applications, IGA is also more appropriate than FEM, since FEM models generally present sharp edges due to the approximation of curves and surfaces.

The IGA efficiency is closely related to numerical integration, and quadrature rules must take into account the smoothness of basis functions across element boundaries. A study about efficient quadrature rules for NURBS-based isogeometric analysis was presented in [⁴], leading to several rules of practical interest besides of a numerical procedure for determining efficient rules.

Beam elements can be employed on the modelling of a great sort of structures of engineering interest, such as bridges, footbridges, arches, rails, offshore risers for oil exploitation and buildings, and there are many contributions being made about the application of IGA to beam models. In [⁵]-[⁹], treatments of locking phenomena, such as shear and membrane locking, are studied through IGA approaches, beam vibrations are studied in [¹⁰]-[¹¹], a study about isogeometric sizing and shape optimization of beam structures is presented in [¹²], 2D and 3D isogeometric beam analysis are presented in [¹³]-[¹⁵] and [⁶] and [¹⁶], respectively.

B-Splines and NURBS curves and surfaces are created by linear combinations between control points and basis functions, which are generated by a set of coordinates (knots) from parametric space named knot vector. So, a structure described by a single curve or surface is called a single-patch structure. One issue that concerns IGA is how to make the connection or apply general constraints in the connection of structures described by different basis functions and knot vectors, that is, how to deal with multi-patch structures.

Particularly, in the context of IGA, when dealing with problems with constraints related to degrees of freedom directly, it is possible to employ interpolatory schemes of shape functions at selected points. However, when this is not convenient or when the desired constraints are not related directly to degrees of freedom, the remedy for employing patch connection is not that straightforward. For example, this may be an issue on Kirchhoff-Love shells and Euler-Bernoulli beams, since usually no rotational degrees of freedom are employed, but rotations are commonly required to be prescribed in a physical sense. In [¹⁷], an isogeometric formulation, based on Kirchhoff-Love shell theory, for rotation-free thin shell analysis of structures comprised of multiple patches is presented. Strips of fictitious material with unidirectional bending stiffness and zero membrane stiffness are added at patch interfaces in order to establish the connection among different surfaces. In [¹⁸], a multi-patch implicit G¹ formulation for the isogeometric analysis of Kirchhoff-Love space rod elements is introduced. Through this formulation, the end rotations can be introduced as degrees of freedom using a re-parametrization of the first and the last segments of the control polygon as a composition of a rigid rotation and a stretch (polar decomposition). Then, adopting a spatial description for the rigid motions of the end directors, an automatic G¹ assemblage for the global stiffness is obtained.

In the present contribution, IGA is applied to a 2D curved beam formulation based on Bernoulli-Euler assumptions. Both B-Spline and NURBS curves can be applied on the description of the geometry. Taking inspiration on the done for the meshless method in [¹⁹], a multi-patch structure can be implemented enforcing constraints, such as same displacement or same rotation among neighbor paths. This may be enforced by use of Penalty and Lagrange methods, in which the energy contribution of the constraints is added into the model potential. The applicability of the methods is verified by some examples of application.

The paper starts with a brief overview about B-Splines and NURBS, showing the main aspects of the CAD technologies and their relation with finite element related analysis. Then, the 2D isogeometric beam formulation is presented. Subsequently, the Penalty and Lagrange Methods approaches are developed. Finally, examples of application are presented.

B-SPLINES AND NURBS

This section presents briefly the main concepts for self-containing of herein developed contributions. Further information about NURBS and isogeometric analysis can be found on [²⁰] and [¹], respectively.

Knot vector is a set of non-decreasing ordinates of the parametric space from which B-Spline basis functions are generated. It is a vector of the form $\mathrm{\Xi }=\left\{{\xi }_1,{\xi }_2,\dots ,{\xi }_{n+p+1}\right\}$, where ${\xi }_i\in \mathbb{R}$ is the i-th knot, n is the number of basis functions, and p is the polynomial order of the B-spline basis.

When the knots are equally spaced, the knot vector is called uniform, otherwise, the knot vector is called non-uniform. The knots also may be repeated, and when the first and last knot appears $p+1$ times, the knot vector is said to be open.

An open knot vector generates B-spline basis functions that are interpolatory at ends of the parametric space interval $\left[{\xi }_1,{\xi }_{n+p+1}\right]$, that is, at the first end of the interval, ${\xi }_1$, $N_{1,p}$ is unitary while the other basis functions are null; and at the last end of the interval,${\xi }_{n+p+1}$, $N_{n,p}$ is unitary while the other basis functions are null. This feature makes the basis functions analogous to the Lagrange polynomials used in the traditional Finite Element Method, which are interpolatory at the ends of the element.

B-spline basis functions are generated recursively according to a knot vector, starting from piecewise constant polynomials:

$N_{i,0}=\left\{\begin{array}{cc}1& if{\xi }_i\le \xi \le {\xi }_{i+1}\\ 0& otherwise\end{array}\right.$ (1)

Then, basis functions of order $p\ge 1$ are given by a linear combination of two $(p-1)$-order basis functions:

$N_{i,p}\left(\xi \right)=\frac{\xi -{\xi }_i}{{\xi }_{i+p}-{\xi }_i}{N}_{i,p-1}\left(\xi \right)+\frac{{\xi }_{i+p+1}-\xi }{{\xi }_{i+p+1}-{\xi }_{i+1}}{N}_{i+1,p-1}\left(\xi \right)$ (2)

An interesting aspect about B-splines lies on the continuity of the basis functions. If there are no repeated knots, B-spline basis functions of order $p$ have $(p-1)$ continuous derivatives. If an internal knot appears $k$ times, the number of continuous derivatives at the knot is equal to $(p-k)$. When the multiplicity of an internal knot coincides with $p$, the basis functions are interpolatory at the knot.

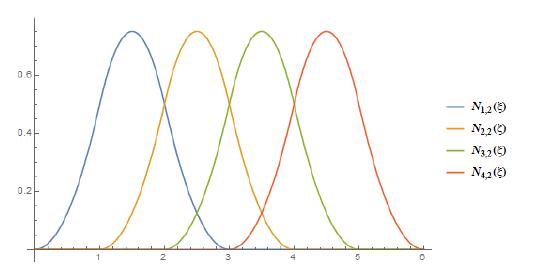
Figure 1 illustrates a second-order B-spline basis created by a uniform knot vector, ${\mathrm{\Xi }}_1=\left\{\mathrm{0,1},\mathrm{2,3},\mathrm{4,5},6\right\}$. Since there are no repeated knots, the basis functions have the first derivative continuum, which is indicated by the smoothness of their shapes. While Figure 2 exemplifies a second-order B-spline basis generated by an open knot vector, ${\mathrm{\Xi }}_2=\left\{\mathrm{0,0},\mathrm{0,1},\mathrm{2,3},\mathrm{3,4},\mathrm{5,6},\mathrm{6,6}\right\}$, which also is composed by an internal knot (3) with multiplicity equal to the polynomial order. So, Basis functions are interpolatory at ends of the parametric space, 1 and 6, and at the repeated knot 3.

Figure 1
Second order B-spline basis functions created by a uniform knot vector, ${\Xi }_1=\left\{\mathrm{0,1},\mathrm{2,3},\mathrm{4,5},6\right\}$

Figure 2
Second order B-spline basis functions created by an open knot vector, ${\Xi }_2=\left\{\mathrm{0,0},\mathrm{0,1},\mathrm{2,3},\mathrm{3,4},\mathrm{5,6},\mathrm{6,6}\right\}$

In addition, we summarize some other interesting features about B-spline basis functions, adapted from [²⁰]:

• 1) Piecewise polynomials: each basis function $\left(N_i\right)$ domain is contained in the parametric space interval $\left[{\xi }_i,{\xi }_{i+p+1}\right]$;

• 2) Partition of unity: $\sum _{i=1}^n{N}_{i,p}\left(\xi \right)=1,\forall \xi$;

• 3) Non-negativity: $N_{i,p}\ge 0,\forall \xi$.

B-spline curves, in turn, are generated by a linear combination of control points in ${\mathbb{R}}^2$ or ${\mathbb{R}}^3$ ($C_i)$ employing B-spline basis functions such that:

$S\left(\xi \right)=\sum _{i=1}^n{N}_{i,p}\left(\xi \right)C_i$ (3)

If there are no repeated knots or control points, the B-spline curve has $\left(p-1\right)$ continuous derivatives. If a knot or control point appears $k$ times, the number of continuous derivatives is equal to $\left(p-k\right)$.

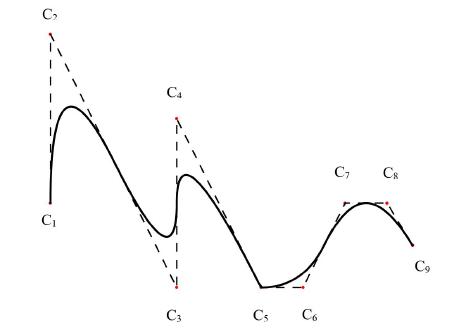
Figure 3 illustrates the B-spline curve obtained through the combination between the second order basis functions from Figure 2 and the set of control points $C=\left\{\left\{\mathrm{0,0}\right\},\left\{\mathrm{0,2}\right\},\left\{1.5,-1\right\},\left\{\mathrm{1.5,1}\right\},\left\{2.5,-1\right\},\left\{3,-1\right\},\left\{\mathrm{3.5,0}\right\},\left\{\mathrm{4,0}\right\},\{4.3,-0.5\}\right\}$. The dashed lines are called control polygon and correspond to the linear interpolation between the control points. Note that the curve first derivative is not continuous at control point $C_5$. This fact is due to the repetition of knot 3, whose multiplicity is responsible for the generation of the interpolatory basis functions at $\xi =3$ (see Figure 2).

Figure 3
B-Spline Curve obtained with the knot vector ${\Xi }_2=\left\{\mathrm{0,0},\mathrm{0,1},\mathrm{2,3},\mathrm{3,4},\mathrm{5,6},\mathrm{6,6}\right\}$ and the set of control points $C=\left\{\left\{\mathrm{0,0}\right\},\left\{\mathrm{0,2}\right\},\left\{1.5,-1\right\},\left\{\mathrm{1.5,1}\right\},\left\{2.5,-1\right\},\left\{3,-1\right\},\left\{\mathrm{3.5,0}\right\},\left\{\mathrm{4,0}\right\},\{4.3,-0.5\}\right\}$

A NURBS (Non-uniform rational B-spline) curve is given by a B-spline basis generated by an open knot vector $\left(N_{i,p}\right)$, a set control points $\left(C_i\right)$ and a set of coefficients named weights $\left(w_i\right)$, as follows:

$S\left(\xi \right)=\frac{\sum _{i=1}^n{N}_{i,p}\left(\xi \right)w_i{C}_i}{\sum _{i=1}^n{N}_{i,p}\left(\xi \right)w_i}$ (4)

The rational basis functions can be defined as:

$R_{i,p}\left(\xi \right)=\frac{N_{i,p}\left(\xi \right)w_i}{\sum _{j=1}^n{N}_{j,p}\left(\xi \right)w_j}$ (5)

So, the NURBS curve is also given by:

$S\left(\xi \right)=\sum _{i=1}^n{R}_{i,p}\left(\xi \right)C_i$ (6)

The rational basis functions have the same properties described above for the B-spline basis, such as, partition of unity, piecewise polynomials, non-negativity and continuity conditions related to the multiplicity of knots. Thus, if all of the weights are equal to unity$\left(w_i=1,1\le i\le n\right)$, the rational basis functions are equal to the B-spline basis functions. So, B-Splines are a particular case of NURBS.

One interesting aspect about NURBS, in detriment of B-splines, consists on the additional local shape control due to the weights. Both NURBS and B-splines can be shaped by changing the position of the control points, but NURBS also are composed by the weights, which control the proximity of the curve to the control points. It is important to state that any change in either a weight$\left(w_i\right)$ or a control point $\left(C_i\right)$ affects only the portion of the curve comprehended in the interval $\left[{\xi }_i,{\xi }_{i+p+1}\right]$, which is the support of the rational$\left(R_i\right)$ or B-spline basis function $\left(N_i\right)$ they are related to (see Eq. (3) and (4)).

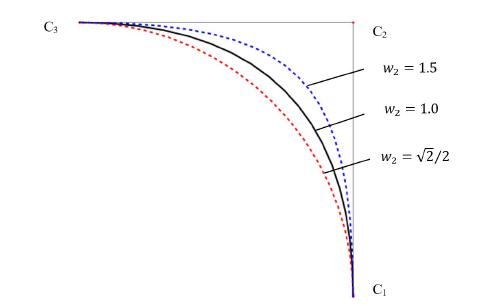
Figure 4 illustrates local shape control associated with the weight $w_2$. The second order NURBS curves are generated by the same open knot vector ${\mathrm{\Xi }}_3=\left\{\mathrm{0,0},\mathrm{0,1},\mathrm{1,1}\right\}$ and control points ${\mathrm{C}}_3=\left\{\left\{\mathrm{1,0}\right\},\left\{\mathrm{1,1}\right\},\left\{\mathrm{0,1}\right\}\right\}$, and the initial curve, which is shown in black, is created by a set of unitary weights $w=\left\{\mathrm{1,1},1\right\}$. So, the initial curve is also a B-spline curve. Decreasing the value of $w_2$ to $\sqrt{2}/2$, the NURBS curve gets far from control point $C_2$, matching a quarter circumference, represented by the red dashed curve. Increasing the value of $w_2$ to 1.5, the curve, drawn in dashed blue, approaches the control point $C_2$. So, one can observe that increasing the value of weight, the curve approaches the respective control point, and vice-versa.

Figure 4
Second order NURBS curves generated by the same open knot vector ${\Xi }_3=\left\{\mathrm{0,0},\mathrm{0,1},\mathrm{1,1}\right\}$ and control points $C_3=\left\{\left\{\mathrm{1,0}\right\},\left\{\mathrm{1,1}\right\},\left\{\mathrm{0,1}\right\}\right\}$: illustration of the shape control associated to one of the weights, $w_2$.

The aim of the isogeometric analysis is the approximation of the element displacements using the same basis functions employed on the construction of the geometry, that is, the rational or B-splines basis functions (in the present work). Sometimes, even when the basis functions are able to perfectly construct the geometry, they might be unsatisfactory to approximate displacements, yielding bad results. However, there are some kinds of refinements in which the basis functions can be enriched, without changing the curve geometrically or parametrically, and, so, the results for the displacements can be improved.

In isogeometric analysis, there are two types of refinements that are analogous to the traditional finite element method: h- and p-refinements. In h-refinement, knots are inserted into the knot vector. For each knot inserted into the knot vector, one basis function is created. So, inserting knots into the knot vector leads to a more numerous basis, which might conduct to a better approximation. In p-refinement, the order of the basis functions are elevated, the functions get more complex and the approximation is improved. There is one more refinement procedure that can be applied in isogeometric analysis that is called k-refinement, which consists of first order elevating the basis functions (p-refinement) and then inserting knots to the knot vector (h-refinement). The k-refinement takes advantage of the non-commutativity of order elevating and knot insertion to construct a higher continuity basis. Further information about refinements can be found at [¹] and [²⁰].

BERNOULLI-EULER CURVED BEAM MODEL

In this section, a curved beam model based on geometrically-linear Bernoulli-Euler kinematic assumptions is presented. The beam axis, which is described by a 2-D B-spline or NURBS curve, passes through the centroid of the successive constant cross sections. As established on Bernoulli-Euler kinematic assumptions, the cross sections remain plane and orthogonal to the deformed beam axis. So, kinematics assumptions leads to neglecting the shear strain energy.

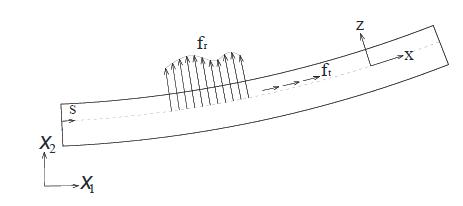
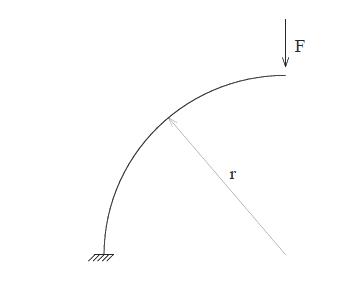
Figure 5 illustrates the curved beam model. Coordinate $s$ describes the beam axis,$x$ and $z$ corresponds to the tangent and transverse local axes, respectively, to the beam axis, $x_1$and $x_2$ are the global axes, $f_r$ and $f_t$ corresponds to the radial and tangential loads, respectively.

Figure 5
Curved beam model

Since the beam is curved, the longitudinal strain of the beam axis $\left({\epsilon }_{xx0}\right)$ is also function of the transverse displacement $\left(w\right)$ and the radius $\left(r\right)$, besides of the tangential displacement $\left(u\right)$. Based on Figure 6, it is possible to find the equation of the longitudinal strain of the beam axis, as follows:

Figure 6
Displacements on an infinitesimal piece of beam (ds)

${\epsilon }_{xx0}=\frac{{ds}^d-ds}{ds};$ (7)

${ds}^d=\left(r+w\right)d\theta +du;$ (8)

${\epsilon }_{xx0}=\frac{du}{ds}+\frac{w}{r}.$ (9)

Then, the longitudinal strain of a point at an arbitrary distance $z$ from the beam axis is related to the change of the beam curvature $\left(\chi \right)$, as follows:

${\epsilon }_{xx}={\epsilon }_{xx0}-z\chi .$ (10)

Adopting a linear elastic constitutive model, in which $E$ is the Young modulus, the longitudinal stress of the beam is given by:

${\sigma }_{xx}=E{\epsilon }_{xx}.$ (11)

As the beam axis is curved, the tangential displacement $u$ affects the rotation of the cross sections, which is represented in the Figure 7. So, the change of the beam curvature is given by:

$\chi =\frac{d}{ds}\left(\phi \right)=\frac{d}{ds}\left(\frac{dw}{ds}-\frac{u}{r}\right),$ (12)

where $\phi$ is the rotation of the cross sections.

Figure 7
Influence of the tangential displacement u on the rotation of the cross sections

The formulation of the isogeometric beam model starts from the Principle of Virtual Work (PVW):

${\delta W}_i={\delta W}_e,$ (13)

Where ${\delta W}_i$ and ${\delta W}_e$ are the internal and external virtual works, respectively. The symbol $\delta$ is used, in the present work, in front of variables to denote that they are virtual quantities.

The internal virtual work is given by:

${\delta W}_i={\int }_V^{}{\sigma }_{xx}{\delta \epsilon }_{xx}dV$ (14)

where V is beam volume. One may develop:

${\delta W}_i={\int }_V^{}E\left({\epsilon }_{xx0}-z\chi \right)\left({\delta \epsilon }_{xx0}-z\delta \chi \right)dV,$ (15)

${\delta W}_i={\int }_L^{}\left({\int }_A^{}E\left({\epsilon }_{xx0}{\delta \epsilon }_{xx0}-{\epsilon }_{xx0}z\delta \chi -z\chi {\delta \epsilon }_{xx0}+z^2\chi \delta \chi \right)dA\right)ds,$ (16)

where L is the beam length and A is the cross-sectional area. Since the beam axis passes through the centroid of cross sections:

${\int }_A^{}zdA=0,$ (17)

${\int }_A^{}{z}^{2}dA=I.$ (18)

So, Eq. (16) reduces to:

${\delta W}_i={\int }_L^{}\left(EA{\epsilon }_{xx0}{\delta \epsilon }_{xx0}+EI\chi \delta \chi \right)ds.$ (19)

Eq. (19) also can be written as the sum of two contributions, as follows:

${\delta W}_i={\delta W}_{i.N}+{\delta W}_{i,M},$ (20)

where:

${\delta W}_{i,N}={\int }_L^{}\left(EA{\epsilon }_{xx0}{\delta \epsilon }_{xx0}\right)ds={\int }_L^{}EA\left(\frac{du}{ds}+\frac{w}{r}\right)\left(\frac{d\delta u}{ds}+\frac{\delta w}{r}\right)ds,$ (21)

${\delta W}_{i,M}={\int }_L^{}\left(EI\chi \delta \chi \right)ds={\int }_L^{}EI\left(\frac{d^{2}w}{{ds}^2}-\frac{1}{r}\frac{du}{ds}\right)\left(\frac{d^2\delta w}{{ds}^2}-\frac{1}{r}\frac{d\delta u}{ds}\right)ds.$ (22)

The external virtual work, in turn, is given by the following equation:

${\delta W}_e={\int }_L^{}{f}_r\delta wds+{\int }_L^{}{f}_t\delta uds+F_r\left(s_0\right)\delta w\left(s_0\right)+F_t\left(s_0\right)\delta u\left(s_0\right)+M\left(s_0\right){\left.\left(\frac{d\delta w}{ds}-\frac{\delta u}{r}\right)\right|}_{s=s_0},$ (23)

where $f_r$ and $f_t$ are the radial and tangential loads distributed along the beam axis, respectively, $F_r$, $F_t$ and $M$ are the radial and tangential forces and the moment, respectively, applied at an arbitrary coordinate value $s_0$ of the beam axis.

As the geometry of beam axis is described, in this model, by a B-spline or a NURBS curve, transverse and tangential displacements are approximated by a linear combination between B-spline or rational basis functions, $\left\{N_1,\dots ,N_n\right\}$, and the unknown parameters, $\left\{u_1,\dots ,u_n\right\}$ and $\left\{w_1,\dots ,w_n\right\}$. Thus, Galerkin Theorem is applied, that is, the virtual displacements, $\delta w$ and $\delta u$, are approximated by the same functions used on the approximation of the real displacements, $\left\{N_1,\dots ,N_n\right\}$. The approximation for the transverse displacement is showed below, the other ones can be found analogously:

$w\left(\xi \right)=w_1{N}_1+w_2{N}_2+\dots +w_n{N}_n,$ (24)

Rearranging Eq. (24) using vectors, we have:

$w\left(\xi \right)=\mathit{N}\mathbf{}\mathit{w},$ (25)

Where:

$\mathit{N}=\left[N_1{N}_2\dots N_n\right],$ (26)

$\mathit{w}={\left[w_1{w}_2\dots w_n\right]}^T.$ (27)

Being $J$ the Jacobian of transformation between coordinates $s$ and $\xi$, we can find the following equations of the first and second derivatives of $w$ in relation to $s$:

$J=\frac{ds}{d\xi },$ (28)

$\frac{dw}{d\xi }=\frac{dw}{ds}\frac{ds}{d\xi },$ (29)

$\frac{dw}{ds}=\frac{1}{J}\frac{dw}{d\xi },$ (30)

$\frac{d^{2}w}{{ds}^2}=\frac{1}{J^2}\frac{d^{2}w}{{d\xi }^2}.$ (31)

Rewriting Eq. (30) and (31) using Eq. (26) and (27), we have:

$\frac{dw}{ds}=J^{-1}\mathit{N}\mathbf{\text{'}}\mathit{w},$ (32)

$\frac{d^{2}w}{{ds}^2}=J^{-2}{\mathit{N}}^{\mathbf{\text{'}}\mathbf{\text{'}}}\mathit{w},$ (33)

where:

$\mathit{N}\mathbf{\text{'}}=\left[{N\mathrm{\text{'}}}_1{N\mathrm{\text{'}}}_2\dots {N\mathrm{\text{'}}}_n\right],$ (34)

${\mathit{N}}^{\mathbf{\text{'}}\mathbf{\text{'}}}=\left[{N^{\mathrm{\text{'}}\mathrm{\text{'}}}}_1{N^{\mathrm{\text{'}}\mathrm{\text{'}}}}_2\dots {N^{\mathrm{\text{'}}\mathrm{\text{'}}}}_n\right],$ (35)

$\left(\right)\text{'}$ and $\left(\right)\text{'}\text{'}$ are the first and second derivatives with respect to $\xi$, respectively.

Then, substituting the approximations for the real and virtual displacements in Eq. (21), (22) and (23), we have:

$\mathit{K}\mathbf{}\mathit{a}=\mathit{F},$ (36)

where:

$\mathit{K}=\left({\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EA\left[\begin{array}{cc}{J}^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}{\mathit{N}}^{\mathbf{\text{'}}}& r^{-1}{\mathit{N}}^{\mathit{T}}{\mathit{N}}^{\mathbf{\text{'}}}\\ r^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}& r^{-2}J{\mathbf{}\mathit{N}}^{\mathit{T}}\mathit{N}\end{array}\right]d\xi +{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EI\left[\begin{array}{cc}{r}^{-2}{J}^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}& -r^{-1}{J}^{-2}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}\\ -r^{-1}{J}^{-2}{\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}& J^{-3}{\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}\end{array}\right]d\xi \right),$ (37)

$\mathit{F}=\left[\begin{array}{c}{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{t}J{\mathit{N}}^{\mathit{T}}d\xi +F_t{\mathit{N}}^{\mathit{T}}\left({\xi }_{c2}\right)-M{r}^{-1}{\mathit{N}}^{\mathit{T}}\left({\xi }_{c3}\right)\\ {\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{r}J{\mathit{N}}^{\mathit{T}}d\xi +F_r{\mathit{N}}^{\mathit{T}}\left({\xi }_{c1}\right)+M{J}^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\left({\xi }_{c3}\right)\end{array}\right],$ (38)

$\mathit{a}={\left[\begin{array}{cc}\mathit{u}& \mathit{w}\end{array}\right]}^T,$ (39)

and ${\xi }_{c1}$, ${\xi }_{c2}$ and ${\xi }_{c3}$ are the ordinates from the parametric space in which the radial and tangential concentrated forces and concentrated moment are applied, respectively. The suppressed calculations are detailed in section “Development of the equations of the Bernoulli-Euler beam model” of the ^{Appendix A}.

So, we find an analogous form to the traditional finite element method, since $\mathit{K}$ corresponds to the stiffness matrix, $\mathit{a}$ is the vector of the displacements and $\mathit{F}$ is the vector of external forces.

In addition, according to [¹⁴], the Jacobian of the transformation between coordinates $s$ and $\xi$, and the radius of curvature are given by:

$J=\frac{ds}{d\xi }=\sqrt{{\left(\frac{{dx}_1}{d\xi }\right)}^2+{\left(\frac{{dx}_2}{d\xi }\right)}^2},$ (40)

$r=\frac{J^3}{\left|\frac{{dx}_1}{d\xi }\frac{{d^{2}x}_2}{{d\xi }^2}-\frac{{d^{2}x}_1}{{d\xi }^2}\frac{{dx}_2}{d\xi }\right|},$ (41)

where $x_1$ and $x_2$ correspond to the projections of the curve $s$ on the axis $x_1$ and $x_2$, respectively.

3. CONSTRAINTS

When the independent variables of the isogeometric Bernoulli-Euler beam solution patch, from now on named “element”, $u$ and $w$, are approximated by a basis generated by an open knot vector, the basis functions are interpolatory at the ends of the element, and it is not a hard task to impose displacement constraints on $u$ and $w$ at the ends of the element. Since the rotation of the cross sections $\phi$ is not an independent variable in the isogeometric Bernoulli-Euler beam element, that is, $\phi$ is function of the derivative of the transverse displacement $w$ with respect to $s$ and the tangential displacement $u$, it is not so straightforward to impose the rotation-related constraints at the ends of the element. However, this problem can be solved by using the Penalty or the Lagrange method. In both methods, contributions are added into the equation of the PVW in order to impose the kinematic constraints, as follows:

${\delta W}_{int}-{\delta W}_{ext}+{\delta W}_c=0,$ (42)

where ${\delta W}_c$ is the contribution of the constraints to the model equations, which is calculated differently for each method: ${\delta W}_c=-{\delta W}_{Lag}$ for Lagrange method, and ${\delta W}_c={\delta W}_{Pen}$ for penalty method.

The approaches presented in this section may be used to impose displacement constraints on any point of the element (patch) and also establish the connection between different elements (patches).

For the development of the contributions to the model PVW of a given desired constraint, we assume a scenario involving two isogeometric Bernoulli-Euler beam elements, numbered 1 e 2, with the external constraints applied only to the element 1 and the internal constraints for the linking of both elements. Any other situation can be derived analogously.

According to Lagrange Method, the potential contribution $\left({{\mathrm{\Pi }}_{Lag}}^e\right)$ to enforce a desired constraint given by $\left({d_1}^e-d_p\right)=0$ may be written as follows:

${{\mathrm{\Pi }}_{Lag}}^e={\lambda }^e\left({d_1}^e-d_p\right),$ (43)

where ${\lambda }^e$ is a scalar Lagrange parameter (or Lagrange multiplier) and ${d_1}^e=d_p$ is the desired constraint we want to enforce, where ${d_1}^e$ is a given component of displacement for an element 1 and $d_p$ is the prescribed displacement.

The contribution of the constraint term to the model weak form (PVW) is obtained by the variation of Eq. (43):

${{\mathrm{\delta }\mathrm{W}}_{Lag}}^e={\delta \lambda }^e\left({d_1}^e-d_p\right)+{\lambda }^e{{\delta d}_1}^e,$ (44)

According to Lagrange Method, the potential contribution $\left({{\mathrm{\Pi }}_{Lag}}^i\right)$ to enforce a desired constraint given by $\left({d_1}^i-{d_2}^i\right)=0$ may be written as follows:

${{\mathrm{\Pi }}_{Lag}}^i={\lambda }^i\left({d_1}^i-{d_2}^i\right),$ (45)

where ${\lambda }^i$ is a scalar Lagrange parameter (or Lagrange multiplier) and ${d_1}^i={d_2}^i$ is the desired constraint we want to enforce, where ${d_1}^i$ is a given component of displacement for an element 1 and ${d_2}^i$ is a given component of displacement for an element 2.

The contribution to the model weak form (PVW) is obtained by variation of Eq. (45):

${{\mathrm{\delta }\mathrm{W}}_{Lag}}^i={\delta \lambda }^i\left({d_1}^i-{d_2}^i\right)+{\lambda }^i{{\delta d}_1}^i-{\lambda }^i{{\delta d}_2}^i$ (46)

The external constrained displacements can be written in terms of their approximations by B-splines or rational basis functions (see Eq. (25) and (30)), as follows:

${w_1}^e={\mathit{N}}_1\left({\xi }_{{w_1}^e}\right){\mathit{w}}_1,$ (47)

${u_1}^e={\mathit{N}}_1\left({\xi }_{{u_1}^e}\right){\mathit{u}}_1,$ (48)

${{\phi }_1}^e=\frac{1}{J_1}{\left.\frac{{dw}_1}{d\xi }\right|}_{\xi ={\xi }_{{{\phi }_1}^e}}-\frac{u_1\left({\xi }_{{{\phi }_1}^e}\right)}{r_1}={J_1}^{-1}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right){\mathit{w}}_1-{r_1}^{-1}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right){\mathit{u}}_1,$ (49)

where ${\xi }_{{w_1}^e}$, ${\xi }_{{u_1}^e}$ and ${\xi }_{{{\phi }_1}^e}$, are the coordinates from parametric space that generate the basis functions of element 1 in which the external constraints are applied on $w_1$, $u_1$ and ${\phi }_1$, respectively, ${\mathit{N}}_1$ is the vector that contains the basis functions of element 1, ${\mathit{u}}_1$ and ${\mathit{w}}_1$ are the vectors of the unknowns of element 1, $r_1$ and $J_1$ are the radius of curvature and the Jacobian of element 1, respectively.

Analogously, the internal constrained displacements can also be written in terms of their approximations by B-splines or rational basis functions, as follows:

${w_1}^i={\mathit{N}}_1\left({\xi }_{{w_1}^i}\right){\mathit{w}}_1,$ (50)

${u_1}^i={\mathit{N}}_1\left({\xi }_{{u_1}^i}\right){\mathit{u}}_1,$ (51)

${{\phi }_1}^i=\frac{1}{J_1}{\left.\frac{{dw}_1}{d\xi }\right|}_{\xi ={\xi }_{{{\phi }_1}^i}}-\frac{u_1\left({\xi }_{{{\phi }_1}^i}\right)}{r_1}={J_1}^{-1}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right){\mathit{w}}_1-{r_1}^{-1}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right){\mathit{u}}_1,$ (52)

${w_2}^i={\mathit{N}}_2\left({\xi }_{{w_2}^i}\right){\mathit{w}}_2,$ (53)

${u_2}^i={\mathit{N}}_2\left({\xi }_{{u_2}^i}\right){\mathit{u}}_2,$ (54)

${{\phi }_2}^i=\frac{1}{J_2}{\left.\frac{{dw}_2}{d\xi }\right|}_{\xi ={\xi }_{{{\phi }_2}^i}}-\frac{u_2\left({\xi }_{{{\phi }_2}^i}\right)}{r_2}={J_2}^{-1}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right){\mathit{w}}_2-{r_2}^{-1}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right){\mathit{u}}_2,$ (55)

where ${\xi }_{{w_1}^i}$, ${\xi }_{{u_1}^i}$ and ${\xi }_{{{\phi }_1}^i}$ are the coordinates from parametric space that generate the basis functions of element 1 in which the internal constraints are applied on $w_1$, $u_1$ and ${\phi }_1$, respectively; and ${\xi }_{{w_2}^i}$, ${\xi }_{{u_2}^i}$ and ${\xi }_{{{\phi }_2}^i}$ are the coordinates from parametric space that generate the basis functions of element 2 in which the internal constraints are applied on $w_2$, $u_2$ and ${\phi }_2$, respectively, ${\mathit{N}}_2$ is the vector that contains the basis functions of element 2, ${\mathit{u}}_2$ and ${\mathit{w}}_2$ are the vectors of the unknowns of element 2, $r_2$ and $J_2$ are the radius of curvature and the Jacobian of element 2, respectively.

Substituting Eq. (47) to (49) into Eq. (44) and Eq. (50) to (55) into (46) and remembering Eq. (37), (38) and (42), we have:

$\left[\begin{array}{cccccccccc}{\mathit{K}}_{11,1}& {\mathit{K}}_{12,1}& 0& 0& -{{\mathit{N}}_1\left({\xi }_{{u_1}^e}\right)}^{\mathit{T}}& 0& {r_1}^{-1}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}& -{{\mathit{N}}_1\left({\xi }_{{u_1}^i}\right)}^{\mathit{T}}& 0& {r_1}^{-1}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}\\ {\mathit{K}}_{21,1}& {\mathit{K}}_{22,1}& 0& 0& 0& {{-\mathit{N}}_1\left({\xi }_{{w_1}^e}\right)}^{\mathit{T}}& -{J_1}^{-1}{{{\mathit{N}}_1}^{\mathbf{\text{'}}}\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}& 0& -{{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)}^{\mathit{T}}& -{J_1}^{-1}{{{\mathit{N}}_1}^{\mathbf{\text{'}}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}\\ 0& 0& {\mathit{K}}_{11,2}& {\mathit{K}}_{12,2}& 0& 0& 0& {{\mathit{N}}_2\left({\xi }_{{u_2}^i}\right)}^{\mathit{T}}& 0& {{-r}_2}^{-1}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}\\ 0& 0& {\mathit{K}}_{21,2}& {\mathit{K}}_{22,2}& 0& 0& 0& 0& {{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)}^{\mathit{T}}& {J_2}^{-1}{{{\mathit{N}}_2}^{\mathbf{\text{'}}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}\\ {-\mathit{N}}_1\left({\xi }_{{u_1}^e}\right)& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& -{\mathit{N}}_1\left({\xi }_{{w_1}^e}\right)& 0& 0& 0& 0& 0& 0& 0& 0\\ {r_1}^{-1}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)& -{J_1}^{-1}{{\mathit{N}}_1}^{\mathbf{\text{'}}}\left({\xi }_{{{\phi }_1}^e}\right)& 0& 0& 0& 0& 0& 0& 0& 0\\ {-\mathit{N}}_1\left({\xi }_{{u_1}^i}\right)& 0& {\mathit{N}}_2\left({\xi }_{{u_2}^i}\right)& 0& 0& 0& 0& 0& 0& 0\\ 0& -{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)& 0& {\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)& 0& 0& 0& 0& 0& 0\\ {r_1}^{-1}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)& {-J_1}^{-1}{{\mathit{N}}_1}^{\mathbf{\text{'}}}\left({\xi }_{{{\phi }_1}^i}\right)& {{-r}_1}^{-1}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)& {J_2}^{-1}{{\mathit{N}}_2}^{\mathbf{\text{'}}}\left({\xi }_{{{\phi }_2}^i}\right)& 0& 0& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}{\mathit{u}}_1\\ {\mathit{w}}_1\\ {\mathit{u}}_2\\ {\mathit{w}}_2\\ {{\lambda }_{u_1}}^e\\ {{\lambda }_{w_1}}^e\\ {{\lambda }_{{\phi }_1}}^e\\ {{\lambda }_{u_{12}}}^i\\ {{\lambda }_{w_{12}}}^i\\ {{\lambda }_{{\phi }_{12}}}^i\end{array}\right]=\left[\begin{array}{c}{\mathit{F}}_{1,1}\\ {\mathit{F}}_{2,1}\\ {\mathit{F}}_{1,2}\\ {\mathit{F}}_{2,2}\\ -u_{1,p}\\ -w_{1,p}\\ -{\phi }_{1,p}\\ 0\\ 0\\ 0\end{array}\right]$ (56)

Where:

${\mathit{K}}_{\mathrm{11,1}}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}\left(E_1{A}_1{J_1}^{-1}{{{\mathit{N}}_1}^{\mathbf{\text{'}}}}^{\mathit{T}}{{\mathit{N}}_1}^{\mathbf{\text{'}}}+E_1{I}_1{r_1}^{-2}{J_1}^{-1}{{{\mathit{N}}_1}^{\mathbf{\text{'}}}}^{\mathit{T}}{{\mathit{N}}_1}^{\mathbf{\text{'}}}\right)d\xi ,$ (57)

${\mathit{K}}_{\mathrm{12,1}}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}\left(E_1{A}_1{r_1}^{-1}{{\mathit{N}}_1}^{\mathit{T}}{{\mathit{N}}_1}^{\mathbf{\text{'}}}-E_1{I}_1{r_1}^{-1}{J_1}^{-2}{{{\mathit{N}}_1}^{\mathbf{\text{'}}}}^{\mathit{T}}{{\mathit{N}}_1}^{\mathbf{\text{'}}\mathbf{\text{'}}}\right)d\xi ,$ (58)

${\mathit{K}}_{\mathrm{21,1}}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}\left(E_1{A}_1{r_1}^{-1}{{{\mathit{N}}_1}^{\mathbf{\text{'}}}}^{\mathit{T}}{\mathit{N}}_1-E_1{I}_1{r_1}^{-1}{J_1}^{-2}{{{\mathit{N}}_1}^{\mathbf{\text{'}}\mathbf{\text{'}}}}^{\mathit{T}}{{\mathit{N}}_1}^{\mathbf{\text{'}}}\right)d\xi ,$ (59)

${\mathit{K}}_{\mathrm{22,1}}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}\left(E_1{A}_1{r_1}^{-2}{J}_1{{\mathit{N}}_1}^{\mathit{T}}{\mathit{N}}_1+E_1{I}_1{J_1}^{-3}{{{\mathit{N}}_1}^{\mathbf{\text{'}}\mathbf{\text{'}}}}^{\mathit{T}}{{\mathit{N}}_1}^{\mathbf{\text{'}}\mathbf{\text{'}}}\right)d\xi ,$ (60)

${\mathit{F}}_{\mathrm{1,1}}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{t,1}{J}_1{{\mathit{N}}_1}^{\mathit{T}}d\xi +F_{t,1}{{\mathit{N}}_1}^{\mathit{T}}\left({\xi }_{c\mathrm{2,1}}\right)-M_1{r_1}^{-1}{{\mathit{N}}_1}^{\mathit{T}}\left({\xi }_{c\mathrm{3,1}}\right),$ (61)

${\mathit{F}}_{\mathrm{2,1}}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{r,1}{J}_1{{\mathit{N}}_1}^{\mathit{T}}d\xi +F_{r,1}{{\mathit{N}}_1}^{\mathit{T}}\left({\xi }_{c\mathrm{1,1}}\right)+M_1{J_1}^{-1}{{{\mathit{N}}_1}^{\mathbf{\text{'}}}}^{\mathit{T}}\left({\xi }_{c\mathrm{3,1}}\right),$ (62)

${\mathit{K}}_{\mathrm{11,2}}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}\left(E_2{A}_2{J_2}^{-1}{{{\mathit{N}}_2}^{\mathbf{\text{'}}}}^{\mathit{T}}{{\mathit{N}}_2}^{\mathbf{\text{'}}}+E_2{I}_2{r_2}^{-2}{J_2}^{-1}{{{\mathit{N}}_2}^{\mathbf{\text{'}}}}^{\mathit{T}}{{\mathit{N}}_2}^{\mathbf{\text{'}}}\right)d\xi ,$ (63)

${\mathit{K}}_{\mathrm{12,2}}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}\left(E_2{A}_2{r_2}^{-1}{{\mathit{N}}_2}^{\mathit{T}}{{\mathit{N}}_2}^{\mathbf{\text{'}}}-E_2{I}_2{r_2}^{-1}{J_2}^{-2}{{{\mathit{N}}_2}^{\mathbf{\text{'}}}}^{\mathit{T}}{{\mathit{N}}_2}^{\mathbf{\text{'}}\mathbf{\text{'}}}\right)d\xi ,$ (64)

${\mathit{K}}_{\mathrm{21,2}}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}\left(E_2{A}_2{r_2}^{-1}{{{\mathit{N}}_2}^{\mathbf{\text{'}}}}^{\mathit{T}}{\mathit{N}}_2-E_2{I}_2{r_2}^{-1}{J_2}^{-2}{{{\mathit{N}}_2}^{\mathbf{\text{'}}\mathbf{\text{'}}}}^{\mathit{T}}{{\mathit{N}}_2}^{\mathbf{\text{'}}}\right)d\xi ,$ (65)

${\mathit{K}}_{\mathrm{22,2}}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}\left(E_2{A}_2{r_2}^{-2}{J}_2{{\mathit{N}}_2}^{\mathit{T}}{\mathit{N}}_2+E_2{I}_2{J_2}^{-3}{{{\mathit{N}}_2}^{\mathbf{\text{'}}\mathbf{\text{'}}}}^{\mathit{T}}{{\mathit{N}}_2}^{\mathbf{\text{'}}\mathbf{\text{'}}}\right)d\xi ,$ (66)

${\mathit{F}}_{\mathrm{1,2}}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{t,2}{J}_2{{\mathit{N}}_2}^{\mathit{T}}d\xi +F_{t,2}{{\mathit{N}}_2}^{\mathit{T}}\left({\xi }_{c\mathrm{2,2}}\right)-M_1{r_1}^{-1}{{\mathit{N}}_1}^{\mathit{T}}\left({\xi }_{c\mathrm{3,2}}\right),$ (67)

${\mathit{F}}_{\mathrm{2,2}}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{r,2}{J}_2{{\mathit{N}}_2}^{\mathit{T}}d\xi +F_{r,2}{{\mathit{N}}_2}^{\mathit{T}}\left({\xi }_{c\mathrm{1,2}}\right)+M_2{J_2}^{-1}{{{\mathit{N}}_2}^{\mathbf{\text{'}}}}^{\mathit{T}}\left({\xi }_{c\mathrm{3,2}}\right).$ (68)

The suppressed calculations can be found in “Development of the equations of the Lagrange Method” of the Appendix B.

So, according to Eq. (56), the contributions of the internal and external constraints calculated through Lagrange method are added to the stiffness matrix of the structural model constructed with the isogeometric Bernoulli-Euler beam elements, and the structural analysis can be accomplished by solving the forthcoming linear system, already encompassing the original degrees of freedom, but now also containing the Lagrange multipliers as unknowns.

The approach for the Penalty method starts in the same way as done for Lagrange method, that is, it begins with the potentials of the constraints:

${{\mathrm{\Pi }}_{Pen}}^e=\frac{1}{2}{\beta }^e{\left({d_1}^e-d_p\right)}^2,$ (69)

${{\mathrm{\Pi }}_{Pen}}^i=\frac{1}{2}{\beta }^i{\left({d_1}^i-{d_2}^i\right)}^2,$ (70)

where ${{\mathrm{\Pi }}_{Pen}}^e$ is the potential of the external constraint, ${{\mathrm{\Pi }}_{Pen}}^i$ is the potential of the internal constraint, ${\beta }^e$ and ${\beta }^i$ are the penalty constants, which corresponds to real arbitrary values, usually taken as big as possible, in order to better impose the desired constraint.

The contribution to the model weak form (PVW) is obtained by variation of Eq. (69) and (70):

${{\mathrm{\delta }\mathrm{W}}_{Pen}}^e={\beta }^e{{\delta d}_1}^e\left({d_1}^e-d_p\right),$ (71)

${{\mathrm{\delta }\mathrm{W}}_{Pen}}^i={\beta }^e\left({\delta d_1}^i-{{\delta d}_2}^i\right)\left({d_1}^i-{d_2}^i\right),$ (72)

where ${{\mathrm{\delta }\mathrm{W}}_{Pen}}^e$ and ${{\mathrm{\delta }\mathrm{W}}_{Pen}}^i$ are the virtual works of the external and internal constraints, respectively.

Substituting the approximations for the external constrained displacements, Eq. (47) to (49), into Eq. (71) leads to:

${{\mathrm{\delta }\mathrm{W}}_{Pen,w_1}}^e={\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{w}}_1}}^{\mathit{e}}\mathit{a}-{\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{w}}_1}}^{\mathit{e}},$ (73)

${{\mathrm{\delta }\mathrm{W}}_{Pen,u_1}}^e={\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{u}}_1}}^{\mathit{e}}\mathit{a}-{\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{u}}_1}}^{\mathit{e}},$ (74)

${{\mathrm{\delta }\mathrm{W}}_{Pen,{\phi }_1}}^e={\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{\phi }}_1}}^{\mathit{e}}\mathit{a}-{\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{\phi }}_1}}^{\mathit{e}},$ (75)

Where:

${{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{w}}_1}}^{\mathit{e}}={\beta }^e\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& {{\mathit{N}}_1\left({\xi }_{{w_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{w_1}^e}\right)& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],$ (76)

${{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathbf{}\mathit{w}}_1}}^{\mathit{e}}={\beta }^e\left[\begin{array}{c}0\\ w_{1,p}{{\mathit{N}}_1\left({\xi }_{{w_1}^e}\right)}^{\mathit{T}}\\ 0\\ 0\end{array}\right],$ (77)

${{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{u}}_1}}^{\mathit{e}}={\beta }^e\left[\begin{array}{cccc}{{\mathit{N}}_1\left({\xi }_{{u_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{u_1}^e}\right)& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],$ (78)

${{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathbf{}\mathit{u}}_1}}^{\mathit{e}}={\beta }^e\left[\begin{array}{c}{u}_{1,p}{{\mathit{N}}_1\left({\xi }_{{u_1}^e}\right)}^{\mathit{T}}\\ 0\\ 0\\ 0\end{array}\right],$ (79)

${{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathbf{}\mathit{\phi }}_1}}^{\mathit{e}}={\beta }^e\left[\begin{array}{cccc}{r_1}^{-2}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)& -{J_1}^{-1}{r_1}^{-1}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)& 0& 0\\ -{J_1}^{-1}{r_1}^{-1}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)& {J_1}^{-2}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],$ (80)

${{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathbf{}\mathit{\phi }}_1}}^{\mathit{e}}={\beta }^e\left[\begin{array}{c}-{r_1}^{-1}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}\\ {J_1}^{-1}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}\\ 0\\ 0\end{array}\right],$ (81)

The suppressed calculations can be found in “Development of the equations of the Penalty Method” of the Appendix C.

Analogously, the approximations for the internal constrained displacements, Eq. (50) to (55), are substituted into Eq. (72), as follows:

${{\mathrm{\delta }\mathrm{W}}_{Pen,w_{12}}}^i={\beta }^i{\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{w}}_{12}}}^{\mathit{i}}\mathit{a},$ (82)

${{\mathrm{\delta }\mathrm{W}}_{Pen,u_{12}}}^i={\beta }^i{\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{u}}_{12}}}^{\mathit{i}}\mathit{a},$ (83)

${{\mathrm{\delta }\mathrm{W}}_{Pen,{\phi }_{12}}}^i=\mathbf{}{\beta }^i{\mathit{\delta }\mathit{a}}^{\mathit{T}}\mathbf{}{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{\phi }}_{12}}}^{\mathit{i}}\mathbf{}\mathit{a},$ (84)

Where:

${{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathbf{}\mathit{w}}_{12}}}^{\mathit{i}}={\beta }^i\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& {{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)& 0& -{{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)\\ 0& 0& 0& 0\\ 0& -{{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)& 0& {{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)\end{array}\right],$ (85)

${{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathbf{}\mathit{u}}_{12}}}^{\mathit{i}}={\beta }^i\left[\begin{array}{cccc}{{\mathit{N}}_1\left({\xi }_{{u_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{u_1}^i}\right)& 0& -{{\mathit{N}}_1\left({\xi }_{{u_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{u_2}^i}\right)& 0\\ 0& 0& 0& 0\\ -{{\mathit{N}}_2\left({\xi }_{{u_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{u_1}^i}\right){\mathit{u}}_1& 0& {{\mathit{N}}_2\left({\xi }_{{u_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{u_2}^i}\right)& 0\\ 0& 0& 0& 0\end{array}\right],$ (86)

${{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathbf{}\mathit{\phi }}_{12}}}^{\mathit{i}}={\beta }^i\left[\begin{array}{cccc}{r_1}^{-2}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)& -{r_1}^{-1}{J_1}^{-1}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)& -{r_1}^{-1}{r_2}^{-1}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)& {r_1}^{-1}{J_2}^{-1}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)\\ -{r_1}^{-1}{J_1}^{-1}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)& {J_1}^{-2}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)& {J_1}^{-1}{r_2}^{-1}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)& -{J_1}^{-1}{J_2}^{-1}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)\\ -{r_1}^{-1}{r_2}^{-1}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)& {J_1}^{-1}{r_2}^{-1}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)& {r_2}^{-2}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)& -{r_2}^{-1}{J_2}^{-1}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)\\ {r_1}^{-1}{J_2}^{-1}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)& -{J_1}^{-1}{J_2}^{-1}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)& -{r_2}^{-1}{J_2}^{-1}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)& {J_2}^{-2}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)\end{array}\right].$ (87)

The suppressed calculations can be found in “Development of the equations of the Penalty Method” of the Appendix C.

Remembering Eq. (37), (38) and (42), Eq. (73) to (87) can be organized to compose the following global system:

$\left({\mathbf{K}}_{1,2}+{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n}}\right)\mathit{a}={\mathbf{F}}_{1,2}+{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n}},$ (88)

Where:

${\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n}}={{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{w}}_1}}^{\mathit{e}}+{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{u}}_1}}^{\mathit{e}}+{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{\phi }}_1}}^{\mathit{e}}+{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{w}}_{12}}}^{\mathit{i}}+{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{u}}_{12}}}^{\mathit{i}}+{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{\phi }}_{12}}}^{\mathit{i}},$ (89)

${\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n}}={{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{w}}_1}}^{\mathit{e}}+{{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{u}}_1}}^{\mathit{e}}+{{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{\phi }}_1}}^{\mathit{e}},$ (90)

${\mathit{K}}_{1,2}=\left[\begin{array}{cccc}{\mathit{K}}_{11,1}& {\mathit{K}}_{12,1}& 0& 0\\ {\mathit{K}}_{21,1}& {\mathit{K}}_{22,1}& 0& 0\\ 0& 0& {\mathit{K}}_{11,2}& {\mathit{K}}_{12,2}\\ 0& 0& {\mathit{K}}_{21,2}& {\mathit{K}}_{22,2}\end{array}\right],$ (91)

${\mathit{F}}_{1,2}=\left[\begin{array}{c}{\mathit{F}}_{1,1}\\ {\mathit{F}}_{2,1}\\ {\mathit{F}}_{1,2}\\ {\mathit{F}}_{2,2}\end{array}\right],$ (92)

So, through the approaches based on the Penalty and the Lagrange method presented in this section, constraints can be imposed to the isogeometric Bernoulli-Euler beam elements in order to compose a great sort of scenarios involving 2-D curved beams.

NUMERICAL EXAMPLES

In this section, we show examples to demonstrate the proposed isogeometric beam formulation and the imposition of the constraints using the Penalty and the Lagrange methods. All the numerical results here shown were obtained by an implementation using Mathematica™.

In the numerical examples, the integrations were made using the standard Mathematica´s numerical integration function, which usually uses adaptive algorithms that recursively subdivide the integration region as needed. The method and rule options were set to “automatic”. The block of zeros in the stiffness matrix produced by the Lagrange Method (for cases with constraint imposition), by its turn, was handled by a linear solver standard function from Mathematica´s library, which can work even with sparse matrices.

1. Quarter circumference arch

The first example consists of a cantilever quarter circumference arch with a vertical force applied at the free end (Figure 8). The problem data are listed on Table 1.

Figure 8
Cantilever quarter circumference arch with a vertical force applied at the free end

Table 1
Numerical example 1 data

Beam cross sections (rectangular)	0.2 m x 0.5 m
Curvature radius (r)	5.00 m
Young modulus (E)	24 GPa
Vertical force (F)	10 kN
Moment of inertia (I)	2.083 x 10-3 m4
Cross section area (A)	0.01 m2

The geometry is described by a fourth order NURBS curve, whose knot vector is open and corresponds to $\left\{\mathrm{0,0},\mathrm{0,0},\mathrm{0,0.2,0.4,0.6,0.8,1},\mathrm{1,1},\mathrm{1,1}\right\}$, and the weights and control points are organized on Table 2.

Table 2
Control points and weights used to construct the quarter circumference arch

C. P.	x1	x2	Weight
C1	0.00000	0.00000	1.00000
C2	0.00000	0.36422	0.97071
C3	0.07247	1.12295	0.91994
C4	0.42281	2.27098	0.86722
C5	1.38265	3.61735	0.84379
C6	2.72902	4.57719	0.86722
C7	3.87705	4.92753	0.91994
C8	4.63578	5.00000	0.97071
C9	5.00000	5.00000	1.00000

As the problem is simple, the external constraints can be imposed exploring rational basis functions properties on the following equations:

$w\left(0\right)=\mathit{N}\left(0\right)\mathit{w}=0,$ (93)

$u\left(0\right)=\mathit{N}\left(0\right)\mathit{u}=0,$ (94)

$\phi \left(0\right)=J^{-1}{\mathit{N}}^{\mathbf{\text{'}}}\left(0\right)\mathit{w}-r^{-1}\mathit{N}\left(0\right)\mathit{u}=0.$ (95)

Since the knot vector is open, basis functions are interpolatory at the ends of the parametric space, and Eq. (93) and (94) can be simplified as:

$N_1\left(0\right)w_1=0\Rightarrow w_1=0,$ (96)

$N_1\left(0\right)u_1=0\Rightarrow u_1=0,$ (97)

Another feature of the basis functions generated by the open knot vector is that, at $\xi =0$, only $N_1\text{'}$ and $N_2\text{'}$ are non-null. Thus, Eq. (95) is simplified as:

$J^{-1}\left(N_1\mathrm{\text{'}}\left(0\right)w_1+N_2\mathrm{\text{'}}\left(0\right)w_2\right)-r^{-1}{N}_1\left(0\right)u_1=0,$ (98)

$N_2\mathrm{\text{'}}\left(0\right)w_2=0\Rightarrow w_2=0.$ (99)

So, the external constraints of this problem can be applied by only making $w_1$, $w_2$ and $u_1$ equal to zero.

Then, the obtained linear system is solved, and the result for the transverse displacement at the free end is given by:

$w\left(1\right)=-0.019899m.$ (100)

According to [²¹], the analytical solution for this problem is given by:

$w=\frac{Fr}{2E}\left(\frac{r^2}{I}+\frac{1}{A}\right)\frac{\pi }{2},$ (101)

$w=-\frac{\mathrm{10,000}\times 5.00}{2\times 2.4\times {10}^{10}}\left(\frac{{5.00}^2}{\mathrm{2,083}\times {10}^{-3}}+\frac{1}{0.01}\right)\frac{\pi }{2}=-0.019802m.$ (102)

Comparing the results obtained through Mathematica and the analytical solution:

$e=\left|\frac{-0.019899+0.019802}{-0.019802}\right|=0.004898,$ (103)

A 0.49% error is verified. So, we conclude that the problem is well represented by the isogeometric Bernoulli-Euler beam element and the approximations for the displacements by means of nine rational functions, that is, nine degrees of freedom, are satisfactory for engineering purposes.

2. Tudor arch

The second example corresponds to a structure named Tudor arch, which is composed, geometrically, by two circular arches and two straight lines. Figure 9 illustrates the geometry and the loads applied on the structure, and the problem data are listed on Table 3.

Figure 9
Geometry and loads applied on Tudor arch (a) Dimensions of the structure (b) Transverse loads applied on the structure.

Table 3
Numerical example 2 data

Beam cross sections (rectangular)	0.2 m x 0.5 m
Young modulus (E)	24 GPa
Transverse load (p)	100 kN/m
Moment of inertia (I)	2.083 x 10-3 m4
Cross section area (A)	0.01 m2

The structure’s computational model is composed by four isogeometric elements: two circular arches and two straight bars. At the ends of the arches, there are two external constraints, one on w and the other one on u, for each arch. The arches are linked to the straight bars by three internal constraints, on $u$, $w$ and $\phi$. The straight bars, in turn, are connected only by translational displacements $\phi$ and $w$, the continuity of the rotations are not imposed between them.

The geometry of the arches are given by fourth order NURBS curves, whose knot vector is open and corresponds to $\left\{\mathrm{0,0},\mathrm{0,0},\mathrm{0,0.2,0.4,0.6,0.8,1},\mathrm{1,1},\mathrm{1,1}\right\}$, and the weights and control points are listed on Table 4.

For the approximation of the displacements of the straight beams, it was used a fourth order B-spline basis generated by the open knot vector $\left\{\mathrm{0,0},\mathrm{0,0},\mathrm{0,0.5,1},\mathrm{1,1},\mathrm{1,1}\right\}$. As they are straight beams, their curvature radii are infinite, which simplifies some of terms in the model equations. For instance, for straight beams, Eq. (37) and (38) are simplified to:

$\mathit{K}=\left({\int }_{{\xi }_1}^{{\xi }_{n+p+1}}\left[\begin{array}{cc}EA{J}^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}{\mathit{N}}^{\mathbf{\text{'}}}& 0\\ 0& EI{J}^{-3}{\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}\end{array}\right]d\xi \right),$ (104)

$\mathrm{a}\mathrm{n}\mathrm{d}\mathbf{}\mathit{F}=\left[\begin{array}{c}{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{t}J{\mathit{N}}^{\mathit{T}}d\xi +F_t{\mathit{N}}^{\mathit{T}}\left({\mathit{\xi }}_{\mathit{c}2}\right)\\ {\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{r}J{\mathit{N}}^{\mathit{T}}d\xi +F_r{\mathit{N}}^{\mathit{T}}\left({\mathit{\xi }}_{\mathit{c}1}\right)+M{J}^{-1}{\mathit{N}\mathbf{\text{'}}}^{\mathit{T}}\left({\mathit{\xi }}_{\mathit{c}3}\right)\end{array}\right].$ (105)

Table 4
Control points and weights used to construct the circular arches

C. P.	x1	x2	Weight
C1	0.00000	0.00000	1.00000
C2	0.00000	0.05704	0.98281
C3	0.00879	0.17378	0.95300
C4	0.04999	0.34947	0.92205
C5	0.16148	0.56769	0.90830
C6	0.32269	0.75226	0.92205
C7	0.47051	0.85578	0.95300
C8	0.57564	0.90731	0.98281
C9	0.62860	0.92850	1.00000
C1’	3.37140	0.92850	1.00000
C2’	3.42436	0.90731	0.98281
C3’	3.52949	0.85578	0.95300
C4’	3.67731	0.75226	0.92205
C5’	3.83852	0.56769	0.90830
C6’	3.95001	0.34947	0.92205
C7’	3.99121	0.17378	0.95300
C8’	4.00000	0.05704	0.98281
C9’	4.00000	0.00000	1.00000

Firstly, the problem was solved using Lagrange method, and the resultant Lagrange multipliers are listed on Table 5. Then, the results obtained for the displacements were used to calibrate Penalty parameters. Table 6 shows a comparison between the resultant displacement $\left(d=\sqrt{{d_{x_1}}^2+{d_{x_2}}^2}\right)$ at the top of the structure obtained with the Lagrange $\left(d_{lag}=4.1372\times {10}^{-4}m\right)$ and Penalty Method, varying penalty parameters in a range comprehended between 10¹² to 10¹⁸. One can observe that for ${10}^{15}\le \beta \le {10}^{16}$, the solutions obtained through Penalty method are practically the same as the solution obtained using Lagrange method, considering four digits of precision.

Table 5
Numerical example 2 Lagrange multipliers

λe u,1	160724.74850
λe w,1	-7407.38617
λi u,12	-131261.15452
λi w,12	-53899.71335
λi ϕ,12	29466.57338
λi u,23	-131261.15452
λi w,23	93800.28665
λi u,34	-159741.09597
λi w,34	51249.85131
λi ϕ,34	-21157.80539
λe u,4	-138585.42987
λe w,4	-84630.58198

Table 6
Comparison between the resultant displacement at the top of the structure obtained with the Lagrange and Penalty Method, varying the penalty parameter.

β	dpen (m)	dpen/dlag
1.0 x 1012	4.1326 x 10-4	9.9891 x 10-1
1.0 x 1013	4.1367 x 10-4	9.9989 x 10-1
1.0 x 1014	4.1371 x 10-4	9.9999 x 10-1
1.0 x 1015	4.1372 x 10-4	1.0000
1.0 x 1016	4.1372 x 10-4	1.0000

The Lagrange multiplier can be also used as a hint about the magnitude of the penalty parameter to be employed. For instance, λ^e _u,1 is the Lagrange multiplier associated to the external constraint on the axial displacement u of the left arch, and it is also the axial force on the end of the arch. Based on the Lagrange multiplier and an expected violation on the constraint $∆d$, an estimative of the penalty parameter is given by:

$\beta =\frac{\lambda }{\mathrm{ﾄ}d}.$ (106)

In fact, the violation on the external constraint above mentioned using 1.0E+12 as the penalty parameter is about 1.6E-07, and the Lagrange multiplier is about 1.6E+05, so:

$\beta =\frac{1.6\times {10}^5}{1.6\times {10}^{-7}}=1.0\times {10}^{12}.$ (107)

Finally, based on the solutions obtained with the Lagrange and the Penalty methods for ${10}^{15}\le \beta \le {10}^{16}$, we show the deformed configuration of the structure and the bending moment and axial force diagrams on Figure 10.

Figure 10
Example 2 solutions (a) Bending moment diagram (b) Axial force diagram (c) Deformed configuration

The Lagrange multiplier may be understood as the force or moment required to impose a constraint, and, comparing the Lagrange multipliers from Table 6 with the diagrams from Figure 10, this fact is exemplified. For instance, ${{\lambda }^e}_{u,1}$ and ${{\lambda }^e}_{u,4}$ correspond to the axial forces on the ends of the arches (160.7 kN and 138.6 kN, respectively), and ${{\lambda }^i}_{\varphi ,12}$ and ${{\lambda }^i}_{\varphi ,34}$ are the bending moment on the linkage of the arches with the straight bars (29.5 kNm and 21.2 kNm, respectively), and so on.

3. Bridge application

The last example corresponds to a 2D beam structure inspired on an arch bridge, which is composed, geometrically, by a circular arch and a straight line. Figure 11 illustrates the geometry and the loads applied on the structure, and the problem data are listed on Table 7.

Figure 11
Geometry and loads applied on the numerical example 3 structure (a) Dimensions of the structure (b) Transverse loads applied on the structure.

Table 7
Numerical example 3 data

Beam cross sections (rectangular)	0.2 m x 0.5 m
Young modulus (E)	24 GPa
Transverse load (p)	10 kN/m
Moment of inertia (I)	2.083 x 10-3 m4
Cross section area (A)	0.01 m2

The structure’s computational model is composed by four isogeometric elements: two circular arches and two straight bars. At the ends of the arches, there are three external constraints, on $u$, $w$ and $\phi$, for each arch. The arches are joined themselves by three internal constraints, on $u$, $w$ and $\phi$. At the ends of the straight bars, there are two external constraints, on $u$ and $w$, for each bar. The straight bars are joined themselves by three internal constraints, on $u$, $w$and$\phi$. The arches are linked to the straight bars only by translational displacements, $u$ and $w$, the continuity of the rotations are not imposed among them.

The geometry of the arches are given by fourth order NURBS curves, whose knot vector is open and corresponds to $\left\{\mathrm{0,0},\mathrm{0,0},\mathrm{0,0.2,0.4,0.6,0.8,1},\mathrm{1,1},\mathrm{1,1}\right\}$, and the weights and control points are listed on Table 8. For the approximation of the displacements of the straight beams, it was used a fourth order B-spline basis generated by the open knot vector $\left\{\mathrm{0,0},\mathrm{0,0},\mathrm{0,0.5,1},\mathrm{1,1},\mathrm{1,1}\right\}$.

Table 8
Control points and weights used to construct the circular arches

C. P.	x1	x2	Weight
C1	0.00000	0.00000	1.00000
C2	0.09819	0.09352	0.99285
C3	0.30578	0.27244	0.98045
C4	0.64624	0.51081	0.96758
C5	1.14703	0.75741	0.96185
C6	1.67975	0.92421	0.96758
C7	2.09068	0.98640	0.98045
C8	2.36440	1.00000	0.99285
C9	2.50000	1.00000	1.00000
C1’	2.50000	1.00000	1.00000
C2’	2.63560	1.00000	0.99285
C3’	2.90932	0.98640	0.98045
C4’	3.32025	0.92421	0.96758
C5’	3.85297	0.75741	0.96185
C6’	4.35376	0.51081	0.96758
C7’	4.69422	0.27244	0.98045
C8’	4.90181	0.09352	0.99285
C9’	5.00000	0.00000	1.00000

Firstly, the problem was solved using Lagrange method, and the resultant Lagrange multipliers are listed on Table 9. Then, the results obtained for the displacements were used to calibrate Penalty parameters. Table 10 shows a comparison between the resultant displacement $\left(d=\sqrt{{d_{x_1}}^2+{d_{x_2}}^2}\right)$ at the top of the arch obtained with the Lagrange $\left(d_{lag}=3.5402\times {10}^{-4}m\right)$ and Penalty Method, varying penalty parameters in a range comprehended from 10¹¹ to 10¹⁶. One can observe that for ${10}^{15}\le \beta \le {10}^{16}$, the solutions obtained through Penalty method are practically the same as the solution obtained using Lagrange method, considering four digits of precision.

Table 9
Numerical example 3 Lagrange multipliers

λe u,1	-89341.306
λe w,1	25074.220
λe ϕ,1	2792.629
λe u,2	89341.306
λe w,2	25074.220
λe ϕ,2	-2792.629
λe u,3	0.000
λe w,3	-56523.562
λe u,4	0.000
λe w,4	-6523.562
λi u,12	82173.146
λi w,12	-43480.975
λi ϕ,12	-28893.944
λi u,34	0.000
λi w,34	18476.438
λi ϕ,34	14941.096
λi u,1234	0.000
λi w,1234	86952.877

Table 10
Comparison between the resultant displacement at the top of the arch obtained with the Lagrange and Penalty Method, varying the penalty parameter.

β	dpen (m)	dpen/dlag
1.0 x 1011	3.5014 x 10-4	9.9891 x 10-1
1.0 x 1012	3.5363 x 10-4	9.9890 x 10-1
1.0 x 1013	3.5397 x 10-4	9.9986 x 10-1
1.0 x 1014	3.5401 x 10-4	9,9997 x 10-1
1.0 x 1015	3.5402 x 10-4	1.0000
1.0 x 1016	3.5402 x 10-4	1.0000

Finally, based on the solutions obtained with the Lagrange and the Penalty methods for ${10}^{15}\le \beta \le {10}^{16}$, we show the deformed configuration of the structure and the bending moment and axial force diagrams on Figure 12.

Figure 12
Example 3 solutions (a) Bending moment diagram (b) Axial force diagram (c) Structure deformed configuration

The Lagrange multiplier may be understood as the force or moment required to impose a constraint, and, comparing the Lagrange multipliers from Table 9 with the diagrams from Figure 12, this fact is exemplified. For instance, ${{\lambda }^e}_{u,1}$ and ${{\lambda }^e}_{u,2}$ correspond to the axial forces on the ends of the arches (89.3 kN), and ${{\lambda }^i}_{\varphi ,12}$ and ${{\lambda }^i}_{\varphi ,34}$ are the bending moment on the linkage of the arches and the straight bars (28.9 kNm and 14.9 kNm, respectively), and so on.

4. CONCLUSION

In the present paper, a 2D isogeometric curved beam element based on Bernoulli-Euler assumption is presented. In order to establish connections and aiming the continuity of rotation between elements, two different approaches, according to Lagrange and Penalty methods, of imposing constraints on the beam elements are developed.

Three examples of application are presented. The first one corresponds to a single patch example and is dedicated to verify the concordance of the isogeometric curved beam element with analytical solution. The other ones are multi-patch and they are solved by using the Penalty and Lagrange methods to impose the displacements constraints. The results are compared with each other and the calibrating of the penalty parameters is discussed.

Attention should be given to some features about Lagrange and Penalty methods in order to not compromise the problems solutions. The Lagrange method brings new unknowns to the problem, which are the Lagrange multipliers, and also blocks of zeros to the structure global stiffness matrix. These blocks of zeros may be carefully handled, since the resulting linear system of equations may not be solved by a simple algorithm. The Penalty method, in turn, does not introduce unknows to the problem, but the precision of the solution is highly dependent of the arbitrary parameter β. Despite of all, the methods can be applied in order to compose a great amount of scenarios involving isogeometric elements.

As future perspectives, the Penalty and Lagrange methods could be applied on the imposition of constraints on more complex isogeometric multi-patch structures, such as 3D beams and shells in the context of IGA analysis.

5. ACKNOWLEDGEMENTS

The second author acknowledges CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) under the grant 304680/2018-4.

6. REFERENCES

• ^[1]
  T. J. R. Hughes, J. A. Cottrell, Y. Bazilevs, Isogeometric Analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement, Comput. Methods Appl. Mech. Engrg., 194 (2005), 4135-4195. https://doi.org/10.1016/j.cma.2004.10.008
• ^[2]
  M. J. Borden, M. A. Scott, J. A. Evans, T. J. R. Hughes, Isogeometric finite element data structures based on Bézier extraction of NURBS, Int. J. Numer. Meth. Engng., 87 (2011), 15-47. https://doi.org/10.1002/nme.2968
  » https://doi.org/10.1002/nme.2968
• ^[3]
  M. A. Scott, M. J. Borden, C. V. Verhoosel, T. W. Sederberg, T. J. R. Hughes, Isogeometric finite element data structures based on Bézier extraction of T-Splines, Int. J. Numer. Meth. Engng., 88 (2011), 126-156. https://doi.org/10.1002/nme.3167
  » https://doi.org/10.1002/nme.3167
• ^[4]
  T. J. R. Hughes, A. Reali, G. Sangalli, Efficient quadrature for NURBS-based isogeometric analysis, Comput. Methods Appl. Mech. Engrg., 199 (2010), 301-313. https://doi.org/10.1016/j.cma.2008.12.004
  » https://doi.org/10.1016/j.cma.2008.12.004
• ^[5]
  L. B. Veiga, C. Lovadina, A. Reali, Avoiding shear locking for the Timoshenko beam problem via isogeometric collocation methods, Comput. Methods Appl. Mech. Engrg. 241-244 (2012), 38-51. https://doi.org/10.1016/j.cma.2012.05.020
  » https://doi.org/10.1016/j.cma.2012.05.020
• ^[6]
  F. Auricchio. L. B. Veiga, J. Kiendl, C. Lovadina, A. Reali, Isogeometric collocation methods for spatial Timoshenko rods, Comput. Methods Appl. Mech. Engrg., 263 (2013), 113-126. https://doi.org/10.1016/j.cma.2013.03.009
  » https://doi.org/10.1016/j.cma.2013.03.009
• ^[7]
  R. Bouclier, T. Elguerdj, A. Combescure, Locking free isogeometric formulations of curved thick beams, Comput. Methods Appl. Mech. Engrg., 245-246 (2012), 144-162. https://doi.org/10.1016/j.cma.2012.06.008
  » https://doi.org/10.1016/j.cma.2012.06.008
• ^[8]
  L. Greco, M. Cuomo, L. Contrafatto, S. Gazzo, An efficient blended mixed B-spline formulation for removing membrane locking in plane curved Kirchhoff rods, Comput. Methods Appl. Mech. Engrg., 324 (2017), 478-511. https://doi.org/10.1016/j.cma.2017.06.032
  » https://doi.org/10.1016/j.cma.2017.06.032
• ^[9]
  E. Marino, Locking-free isogeometric collocation formulation for three-dimensional geometrically exact shear-deformable beams with arbitraty initial curvature, Comput. Methods Appl. Mech. Engrg., 324 (2017), 546-572. https://doi.org/10.1016/j.cma.2017.06.031
  » https://doi.org/10.1016/j.cma.2017.06.031
• ^[10]
  O. Weeger, U. Wever, B. Simeon, Isogeometric analysis of nonlinear Euler-Bernoulli beam vibrations, Nonlinear Dyn., 72 (2013), 813-835. https://doi.org/10.1007/s11071-013-0755-5
  » https://doi.org/10.1007/s11071-013-0755-5
• ^[11]
  S. J. Lee, K. S. Park, Vibrations of Timoshenko beams with isogeometric approach, Applied Mathematical Modelling, 37 (2013), 9174-9190. https://doi.org/10.1016/j.apm.2013.04.034
  » https://doi.org/10.1016/j.apm.2013.04.034
• ^[12]
  A. P. Nagy, M. M. Abdalla, Z. Gürdal, Isogeometric sizing and shape optimisation of beam structures, Comput. Methods Appl. Mech. Engrg., 199 (2010), 1216-1230. https://doi.org/10.1016/j.cma.2009.12.010
  » https://doi.org/10.1016/j.cma.2009.12.010
• ^[13]
  A. Cazzani, M. Malagù & E. Turco. “Isogeometric analysis of plane-curved beams”. Mathematics and Mechanics of Solids., V. 21, I. 5, 1-16, 2016.
• ^[14]
  A. Cazzani, M. Malagù, E. Turco, Constitutive models for strongly curved beams in the frame of isogeometric analysis, Mathematics and Mechanics of Solids, 21 (2016), 182-209. https://doi.org/10.1177/1081286515577043
  » https://doi.org/10.1177/1081286515577043
• ^[15]
  J. Kiendl, F. Auricchio, T. J. R. Hughes, A. Reali, Single-variable formulations and isogeometric discretizations for shear deformable beams, Comput. Methods Appl. Mech. Engrg., 284 (2015), 988-1004. https://doi.org/10.1016/j.cma.2014.11.011
  » https://doi.org/10.1016/j.cma.2014.11.011
• ^[16]
  L. Greco, M. Cuomo, B-Spline interpolation of Kirchhoff-Love space rods, Comput. Methods Appl. Mech. Engrg., 256 (2013), 251-269. https://doi.org/10.1016/j.cma.2012.11.017
  » https://doi.org/10.1016/j.cma.2012.11.017
• ^[17]
  J. Kiendl, Y. Basilevs, M.-C. Hsu, R. Wüchner, K.-U. Bletzinger, The bending strip method for isogeometric analysis of Kirchhoff-Love shell structures, Comput. Methods Appl. Mech. Engrg. 199 (2010), 2403-2416. https://doi.org/10.1016/j.cma.2010.03.029
  » https://doi.org/10.1016/j.cma.2010.03.029
• ^[18]
  L. Greco, M. Cuomo, An implicit G1 multi patch B-spline interpolation for Kirchhoff-Love space rod, Comput. Methods Appl. Mech. Engrg., 269 (2014), 173-197. https://doi.org/10.1016/j.cma.2013.09.018
  » https://doi.org/10.1016/j.cma.2013.09.018
• ^[19]
  J. Costa, P. Pimenta, P. Wriggers, Meshless analysis of shear deformable shells: boundary and interface constraints, Comput. Mech., 57 (2016), 679-700. https://doi.org/10.1007/s00466-015-1253-z
  » https://doi.org/10.1007/s00466-015-1253-z
• ^[20]
  L. Piegl, W. Tiller, The NURBS book (Monographs in Visual Communication), Second ed., Springer-Verlag, New York, 1997.
• ^[21]
  M. L. Bucalem, K. J. Bathe, The mechanics of solids and structures - Hierarchical modeling and the Finite Element Solution, First ed., Springer-Verlag, New York, 2011.

APPENDIX A: DEVELOPMENT OF THE EQUATIONS OF THE BERNOULLI-EULER CURVED BEAM MODEL

The development of the equations of the Bernoulli-Euler curved beam model is detailed in this appendix. Substituting the approximations for the real and virtual displacements (see Eq. (24) to (35)) in Eq. (21), we have:

${\delta W}_{i,N}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EA\left(J^{-1}{\mathit{N}}^{\mathbf{\text{'}}}\mathit{u}+r^{-1}\mathit{N}\mathit{w}\right)\left(J^{-1}{\mathit{N}}^{\mathbf{\text{'}}}\mathit{\delta }\mathit{u}+r^{-1}\mathit{N}\mathit{\delta }\mathit{w}\right)Jd\xi ,$ (A.1)

${\delta W}_{i,N}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EA\left(J^{-1}{\mathit{\delta }\mathit{u}}^{\mathit{T}}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}{\mathit{N}}^{\mathbf{\text{'}}}\mathit{u}+r^{-1}{\mathit{\delta }\mathit{w}}^{\mathit{T}}{\mathit{N}}^{\mathit{T}}{\mathit{N}}^{\mathbf{\text{'}}}\mathit{u}\right)d\xi +{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EA\left(r^{-1}{\mathit{\delta }\mathit{u}}^{\mathit{T}}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}\mathit{w}+r^{-2}J{\mathit{\delta }\mathit{w}}^{\mathit{T}}{\mathit{N}}^{\mathit{T}}\mathit{N}\mathit{w}\right)d\xi ,$ (A.2)

Substituting the approximations for the real and virtual displacements in Eq. (22), we have:

${\delta W}_{i,M}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EI\left(J^{-2}{\mathit{N}}^{\mathbf{\text{'}}\mathbf{\text{'}}}\mathit{w}-r^{-1}{J}^{-1}\mathit{N}\mathbf{\text{'}}\mathit{u}\right)\left(J^{-2}{\mathit{N}}^{\mathbf{\text{'}}\mathbf{\text{'}}}\mathit{\delta }\mathit{w}-r^{-1}{J}^{-1}\mathit{N}\mathbf{\text{'}}\mathit{\delta }\mathit{u}\right)Jd\xi ,$ (A.3)

${\delta W}_{i,M}={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EI\left(J^{-3}{\mathit{\delta }\mathit{w}}^{\mathit{T}}{\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}\mathit{w}-r^{-1}{J}^{-2}{\mathit{\delta }\mathit{u}}^{\mathit{T}}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}\mathit{w}\right)d\xi +{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EI\left(-r^{-1}{J}^{-2}{\mathit{\delta }\mathit{w}}^{\mathit{T}}{{\mathit{N}}^{\mathbf{\text{'}}\mathbf{\text{'}}}}^{\mathit{T}}{\mathit{N}}^{\mathbf{\text{'}}}\mathit{u}+r^{-2}{J}^{-1}{\mathit{\delta }\mathit{u}}^{\mathit{T}}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\mathit{u}\right)d\xi ,$ (A.4)

Finally, the approximations are introduced in Eq. (23), of the external virtual work:

${\delta W}_e={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_r\mathit{N}\mathit{\delta }\mathit{w}Jd\xi +{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_t\mathit{N}\mathit{\delta }\mathit{u}Jd\xi +F_r\mathit{N}\left({\xi }_{c1}\right)\mathit{\delta }\mathit{w}+F_t\mathit{N}\left({\xi }_{c2}\right)\mathit{\delta }\mathit{u}+M\left(J^{-1}\mathit{N}\mathbf{\text{'}}\left({\xi }_{c3}\right)\mathit{\delta }\mathit{w}-r^{-1}\mathit{N}\left({\xi }_{c3}\right)\mathit{\delta }\mathit{u}\right),$ (A.5)

${\delta W}_e={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_r\mathit{N}\mathit{\delta }\mathit{w}Jd\xi +{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_t\mathit{N}\mathit{\delta }\mathit{u}Jd\xi +F_r\mathit{N}\left({\xi }_{c1}\right)\mathit{\delta }\mathit{w}+F_t\mathit{N}\left({\xi }_{c2}\right)\mathit{\delta }\mathit{u}+M\left(J^{-1}\mathit{N}\mathbf{\text{'}}\left({\xi }_{c3}\right)\mathit{\delta }\mathit{w}-r^{-1}\mathit{N}\left({\xi }_{c3}\right)\mathit{\delta }\mathit{u}\right),$ (A.6)

where ${\xi }_{c1}$, ${\xi }_{c2}$ and ${\xi }_{c3}$ are the ordinates from the parametric space in which the radial and tangential concentrated forces and concentrated moment are applied, respectively.

Creating the vectors:

${\delta W}_e={\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_r\mathit{N}\mathit{\delta }\mathit{w}Jd\xi +{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_t\mathit{N}\mathit{\delta }\mathit{u}Jd\xi +F_r\mathit{N}\left({\xi }_{c1}\right)\mathit{\delta }\mathit{w}+F_t\mathit{N}\left({\xi }_{c2}\right)\mathit{\delta }\mathit{u}+M\left(J^{-1}\mathit{N}\mathbf{\text{'}}\left({\xi }_{c3}\right)\mathit{\delta }\mathit{w}-r^{-1}\mathit{N}\left({\xi }_{c3}\right)\mathit{\delta }\mathit{u}\right),$ (A.7)

$\mathit{\delta }\mathit{a}={\left[\begin{array}{cc}\mathit{\delta }\mathit{u}& \mathit{\delta }\mathit{w}\end{array}\right]}^T,$ (A.8)

and substituting in Eq. (A.2), (A.4) and (A.6), it leads to:

${\delta W}_{i,N}={\mathit{\delta }\mathit{a}}^T\left({\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EA\left[\begin{array}{cc}{J}^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}{\mathit{N}}^{\mathbf{\text{'}}}& r^{-1}{\mathit{N}}^{\mathit{T}}{\mathit{N}}^{\mathbf{\text{'}}}\\ r^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}& r^{-2}J{\mathbf{}\mathit{N}}^{\mathit{T}}\mathit{N}\end{array}\right]d\xi \right)\mathit{a},$ (A.9)

${\delta W}_{i,M}={\mathit{\delta }\mathit{a}}^T\left({\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EI\left[\begin{array}{cc}{r}^{-2}{J}^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}& -r^{-1}{J}^{-2}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}\\ -r^{-1}{J}^{-2}{\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}& J^{-3}{\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}\end{array}\right]d\xi \right)\mathit{a},$ (A.10)

${\delta W}_e={\mathit{\delta }\mathit{a}}^T\left[\begin{array}{c}{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{t}J{\mathit{N}}^{\mathit{T}}d\xi +F_t{\mathit{N}}^{\mathit{T}}\left({\xi }_{c2}\right)-M{r}^{-1}{\mathit{N}}^{\mathit{T}}\left({\xi }_{c3}\right)\\ {\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{r}J{\mathit{N}}^{\mathit{T}}d\xi +F_r{\mathit{N}}^{\mathit{T}}\left({\xi }_{c1}\right)+M{J}^{-1}{\mathit{N}\mathbf{\text{'}}}^{\mathit{T}}\left({\xi }_{c3}\right)\end{array}\right].$ (A.11)

Then, substituting Eq. (A.9) to (A.11) in Eq. (13), we have:

${\mathit{\delta }\mathit{a}}^T\left({\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EA\left[\begin{array}{cc}{J}^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}{\mathit{N}}^{\mathbf{\text{'}}}& r^{-1}{\mathit{N}}^{\mathit{T}}{\mathit{N}}^{\mathbf{\text{'}}}\\ r^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}& r^{-2}J{\mathbf{}\mathit{N}}^{\mathit{T}}\mathit{N}\end{array}\right]d\xi +{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EI\left[\begin{array}{cc}{r}^{-2}{J}^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}{\mathit{N}}^{\mathbf{\text{'}}}& -r^{-1}{J}^{-2}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}\\ -r^{-1}{J}^{-2}{{\mathit{N}}^{\mathbf{\text{'}}\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}& J^{-3}{\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}\end{array}\right]d\xi \right)\mathit{a}={\mathit{\delta }\mathit{a}}^T\left[\begin{array}{c}{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{t}J{\mathit{N}}^{\mathit{T}}d\xi +F_t{\mathit{N}}^{\mathit{T}}\left({\xi }_{c2}\right)-M{r}^{-1}{\mathit{N}}^{\mathit{T}}\left({\xi }_{c3}\right)\\ {\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{r}J{\mathit{N}}^{\mathit{T}}d\xi +F_r{\mathit{N}}^{\mathit{T}}\left({\xi }_{c1}\right)+M{J}^{-1}{\mathit{N}\mathbf{\text{'}}}^{\mathit{T}}\left({\xi }_{c3}\right)\end{array}\right],$ (A.12)

$\left({\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EA\left[\begin{array}{cc}{J}^{-1}{{\mathit{N}}^{\mathbf{\text{'}}\mathbf{\text{'}}}}^{\mathit{T}}{\mathit{N}}^{\mathbf{\text{'}}}& r^{-1}{\mathit{N}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\\ r^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}& r^{-2}J{\mathbf{}\mathit{N}}^{\mathit{T}}\mathit{N}\end{array}\right]d\xi +{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EI\left[\begin{array}{cc}{r}^{-2}{J}^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}& -r^{-1}{J}^{-2}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}\\ -r^{-1}{J}^{-2}{{\mathit{N}}^{\mathbf{\text{'}}\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}& J^{-3}{\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}\end{array}\right]d\xi \right)\mathit{a}=\left[\begin{array}{c}{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{t}J{\mathit{N}}^{\mathit{T}}d\xi +F_t{\mathit{N}}^{\mathit{T}}\left({\xi }_{c2}\right)-M{r}^{-1}{\mathit{N}}^{\mathit{T}}\left({\xi }_{c3}\right)\\ {\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{r}J{\mathit{N}}^{\mathit{T}}d\xi +F_r{\mathit{N}}^{\mathit{T}}\left({\xi }_{c1}\right)+M{J}^{-1}{\mathit{N}\mathbf{\text{'}}}^{\mathit{T}}\left({\xi }_{c3}\right)\end{array}\right].$ (A.13)

Making:

$\mathit{K}=\left({\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EA\left[\begin{array}{cc}{J}^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}{\mathit{N}}^{\mathbf{\text{'}}}& r^{-1}{\mathit{N}}^{\mathit{T}}{\mathit{N}}^{\mathbf{\text{'}}}\\ r^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}& r^{-2}J{\mathbf{}\mathit{N}}^{\mathit{T}}\mathit{N}\end{array}\right]d\xi +{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}EI\left[\begin{array}{cc}{r}^{-2}{J}^{-1}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}& -r^{-1}{J}^{-2}{{\mathit{N}}^{\mathbf{\text{'}}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}\\ -r^{-1}{J}^{-2}{\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}& J^{-3}{\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}}^{\mathit{T}}\mathit{N}\mathbf{\text{'}}\mathbf{\text{'}}\end{array}\right]d\xi \right),$ (A.14)

$\mathrm{a}\mathrm{n}\mathrm{d}\mathbf{}\mathit{F}=\left[\begin{array}{c}{\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{t}J{\mathit{N}}^{\mathit{T}}d\xi +F_t{\mathit{N}}^{\mathit{T}}\left({\xi }_{c2}\right)-M{r}^{-1}{\mathit{N}}^{\mathit{T}}\left({\xi }_{c3}\right)\\ {\int }_{{\xi }_1}^{{\xi }_{n+p+1}}{f}_{r}J{\mathit{N}}^{\mathit{T}}d\xi +F_r{\mathit{N}}^{\mathit{T}}\left({\xi }_{c1}\right)+M{J}^{-1}{\mathit{N}\mathbf{\text{'}}}^{\mathit{T}}\left({\xi }_{c3}\right)\end{array}\right],$ (A.15)

we find an analogous form to the traditional finite element method, since $\mathit{K}$ corresponds to the stiffness matrix, $\mathit{a}$ is the vector of the displacements and $\mathit{F}$ is the vector of external forces.

APPENDIX B: DEVELOPMENT OF THE EQUATIONS OF THE LAGRANGE METHOD

The development of the equations of the Lagrange method is detailed in this appendix.

Substituting Eq. (47), (48) and (49) into Eq. (44), we have:

${{\mathrm{\delta }\mathrm{W}}_{Lag,w_1}}^e={{\delta \lambda }_{w_1}}^e\left({\mathit{N}}_1\left({\xi }_{{w_1}^e}\right){\mathit{w}}_1-w_{1,p}\right)+{{\lambda }_{w_1}}^e{{\mathit{\delta }\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{w_1}^e}\right)}^{\mathit{T}},$ (B.1)

${{\mathrm{\delta }\mathrm{W}}_{Lag,u_1}}^e={{\delta \lambda }_{u_1}}^e\left({\mathit{N}}_1\left({\xi }_{{u_1}^e}\right){\mathit{u}}_1-u_{1,p}\right)+{{\lambda }_{u_1}}^e{{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{u_1}^e}\right)}^{\mathit{T}},$ (B.2)

${{\mathrm{\delta }\mathrm{W}}_{Lag,{\phi }_1}}^e={{\delta \lambda }_{{\phi }_1}}^e\left({J_1}^{-1}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right){\mathit{w}}_1-{r_1}^{-1}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right){\mathit{u}}_1-{\phi }_{1,p}\right)+{{\lambda }_{{\phi }_1}}^e\left({J_1}^{-1}{\mathit{\delta }{\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}-{r_1}^{-1}{{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}\right),$ (B.3)

Then, substituting Eq. (50) to (55) in Eq. (46), we have:

${{\mathrm{\delta }\mathrm{W}}_{Lag,w_{12}}}^i={{\delta \lambda }_{w_{12}}}^i\left({\mathit{N}}_1\left({\xi }_{{w_1}^i}\right){\mathit{w}}_1-{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right){\mathit{w}}_2\right)+{{\lambda }_{w_{12}}}^i\left({{\mathit{\delta }\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)}^{\mathit{T}}-{{\mathit{\delta }\mathit{w}}_2}^{\mathit{T}}{{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)}^{\mathit{T}}\right),$ (B.4)

${{\mathrm{\delta }\mathrm{W}}_{Lag,u_{12}}}^i={{\delta \lambda }_{u_{12}}}^i\left({\mathit{N}}_1\left({\xi }_{{u_1}^i}\right){\mathit{u}}_1-{\mathit{N}}_2\left({\xi }_{{u_2}^i}\right){\mathit{u}}_2\right)+{{\lambda }_{u_{12}}}^i\left({{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{u_1}^i}\right)}^{\mathit{T}}-{{\mathit{\delta }\mathit{u}}_2}^{\mathit{T}}{{\mathit{N}}_2\left({\xi }_{{u_2}^i}\right)}^{\mathit{T}}\right),$ (B.5)

${{\mathrm{\delta }\mathrm{W}}_{Lag,{\phi }_{12}}}^i={{\delta \lambda }_{{\phi }_{12}}}^i\left({J_1}^{-1}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right){\mathit{w}}_1-{r_1}^{-1}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right){\mathit{u}}_1-{J_2}^{-1}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right){\mathit{w}}_2+{r_2}^{-1}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right){\mathit{u}}_2\right)+{{\lambda }_{{\phi }_{12}}}^i\left({J_1}^{-1}{\mathit{\delta }{\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}-{r_1}^{-1}{{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}-{J_2}^{-1}{\mathit{\delta }{\mathit{w}}_2}^{\mathit{T}}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}+{r_2}^{-1}{{\mathit{\delta }\mathit{u}}_2}^{\mathit{T}}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}\right).$ (B.6)

Remembering Eq. (37), (38), (39) and (42), Eq. (B.1) to (B.6) can be organized in matrix form, as follows:

$\left[\begin{array}{cccccccccc}{\mathit{K}}_{11,1}& {\mathit{K}}_{12,1}& 0& 0& -{{\mathit{N}}_1\left({\xi }_{{u_1}^e}\right)}^{\mathit{T}}& 0& {r_1}^{-1}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}& -{{\mathit{N}}_1\left({\xi }_{{u_1}^i}\right)}^{\mathit{T}}& 0& {r_1}^{-1}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}\\ {\mathit{K}}_{21,1}& {\mathit{K}}_{22,1}& 0& 0& 0& {{-\mathit{N}}_1\left({\xi }_{{w_1}^e}\right)}^{\mathit{T}}& -{J_1}^{-1}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}& 0& -{{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)}^{\mathit{T}}& -{J_1}^{-1}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}\\ 0& 0& {\mathit{K}}_{11,2}& {\mathit{K}}_{12,2}& 0& 0& 0& {{\mathit{N}}_2\left({\xi }_{{u_2}^i}\right)}^{\mathit{T}}& 0& {{-r}_2}^{-1}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}\\ 0& 0& {\mathit{K}}_{21,2}& {\mathit{K}}_{22,2}& 0& 0& 0& 0& {{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)}^{\mathit{T}}& {J_2}^{-1}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}\\ {-\mathit{N}}_1\left({\xi }_{{u_1}^e}\right)& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& -{\mathit{N}}_1\left({\xi }_{{w_1}^e}\right)& 0& 0& 0& 0& 0& 0& 0& 0\\ {r_1}^{-1}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)& -{J_1}^{-1}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)& 0& 0& 0& 0& 0& 0& 0& 0\\ {-\mathit{N}}_1\left({\xi }_{{u_1}^i}\right)& 0& {\mathit{N}}_2\left({\xi }_{{u_2}^i}\right)& 0& 0& 0& 0& 0& 0& 0\\ 0& -{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)& 0& {\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)& 0& 0& 0& 0& 0& 0\\ {r_1}^{-1}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)& {-J_1}^{-1}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)& {{-r}_1}^{-1}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)& {J_2}^{-1}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)& 0& 0& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}{\mathit{u}}_1\\ {\mathit{w}}_1\\ {\mathit{u}}_2\\ {\mathit{w}}_2\\ {{\lambda }_{u_1}}^e\\ {{\lambda }_{w_1}}^e\\ {{\lambda }_{{\phi }_1}}^e\\ {{\lambda }_{u_{12}}}^i\\ {{\lambda }_{w_{12}}}^i\\ {{\lambda }_{{\phi }_{12}}}^i\end{array}\right]=\left[\begin{array}{c}{\mathit{F}}_{1,1}\\ {\mathit{F}}_{2,1}\\ {\mathit{F}}_{1,2}\\ {\mathit{F}}_{2,2}\\ -u_{1,p}\\ -w_{1,p}\\ -{\phi }_{1,p}\\ 0\\ 0\\ 0\end{array}\right]$ (B.7)

APPENDIX C: DEVELOPMENT OF THE EQUATIONS OF THE PENALTY METHOD

The development of the equations of the Penalty method is detailed in this appendix.

Substituting the approximations for the external constrained displacements, Eq. (47) to (49), into Eq. (72) leads to:

${{\mathrm{\delta }\mathrm{W}}_{Pen,w_1}}^e={\beta }^e{{\mathit{\delta }\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{w_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{w_1}^e}\right){\mathit{w}}_1-{\beta }^e{w}_{1,p}{{\mathit{\delta }\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{w_1}^e}\right)}^{\mathit{T}},$ (C.1)

${{\mathrm{\delta }\mathrm{W}}_{Pen,u_1}}^e={\beta }^e{{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{u_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{u_1}^e}\right){\mathit{u}}_1-{\beta }^e{u}_{1,p}{{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{u_1}^e}\right)}^{\mathit{T}},$ (C.2)

${{\mathrm{\delta }\mathrm{W}}_{Pen,{\phi }_1}}^e={\beta }^e\left({J_1}^{-2}{\mathit{\delta }{\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right){\mathit{w}}_1-{J_1}^{-1}{r_1}^{-1}{\mathit{\delta }{\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right){\mathit{u}}_1-{J_1}^{-1}{r_1}^{-1}{{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right){\mathit{w}}_1+{r_1}^{-2}{{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right){\mathit{u}}_1\right)-{\beta }^e{\phi }_{1,p}\left({J_1}^{-1}{\mathit{\delta }{\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}-{r_1}^{-1}{{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}\right).$ (C.3)

Analogously, the approximations for the internal constrained displacements, Eq. (50) to (55), are substituted into Eq. (72), as follows:

${{\mathrm{\delta }\mathrm{W}}_{Pen,w_{12}}}^i={\beta }^i\left({{\mathit{\delta }\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right){\mathit{w}}_1-{{\mathit{\delta }\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right){\mathit{w}}_2-{{\mathit{\delta }\mathit{w}}_2}^{\mathit{T}}{{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right){\mathit{w}}_1+{{\mathit{\delta }\mathit{w}}_2}^{\mathit{T}}{{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right){\mathit{w}}_2\right),$ (C.4)

${{\mathrm{\delta }\mathrm{W}}_{Pen,u_{12}}}^i={\beta }^i\left({{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{u_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{u_1}^i}\right){\mathit{u}}_1-{{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{u_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{u_2}^i}\right){\mathit{u}}_2-{{\mathit{\delta }\mathit{u}}_2}^{\mathit{T}}{{\mathit{N}}_2\left({\xi }_{{u_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{u_1}^i}\right){\mathit{u}}_1+{{\mathit{\delta }\mathit{u}}_2}^{\mathit{T}}{{\mathit{N}}_2\left({\xi }_{{u_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{u_2}^i}\right){\mathit{u}}_2\right),$ (C.5)

${{\mathrm{\delta }\mathrm{W}}_{Pen,{\phi }_{12}}}^i={\beta }^i\left({J_1}^{-1}{\mathit{\delta }{\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}-{r_1}^{-1}{{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}-{J_2}^{-1}{\mathit{\delta }{\mathit{w}}_2}^{\mathit{T}}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}+{r_2}^{-1}{{\mathit{\delta }\mathit{u}}_2}^{\mathit{T}}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}\right)\left({J_1}^{-1}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right){\mathit{w}}_1-{r_1}^{-1}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right){\mathit{u}}_1-{J_2}^{-1}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right){\mathit{w}}_2+{r_2}^{-1}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right){\mathit{u}}_2\right),$ (C.6)

${{\mathrm{\delta }\mathrm{W}}_{Pen,{\phi }_{12}}}^i={\beta }^i\left({J_1}^{-2}{\mathit{\delta }{\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right){\mathit{w}}_1-{r_1}^{-1}{J_1}^{-1}{\mathit{\delta }{\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right){\mathit{u}}_1-{J_1}^{-1}{J_2}^{-1}{\mathit{\delta }{\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right){\mathit{w}}_2+{J_1}^{-1}{r_2}^{-1}{\mathit{\delta }{\mathit{w}}_1}^{\mathit{T}}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right){\mathit{u}}_2\right)+{\beta }^i\left(-{r_1}^{-1}{J_1}^{-1}{{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right){\mathit{w}}_1+{r_1}^{-2}{{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right){\mathit{u}}_1+{r_1}^{-1}{J_2}^{-1}{{\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right){\mathit{w}}_2-{r_1}^{-1}{{{r_2}^{-1}\mathit{\delta }\mathit{u}}_1}^{\mathit{T}}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right){\mathit{u}}_2\right)+{\beta }^i\left(-{J_1}^{-1}{J_2}^{-1}{\mathit{\delta }{\mathit{w}}_2}^{\mathit{T}}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right){\mathit{w}}_1+{r_1}^{-1}{J_2}^{-1}{\mathit{\delta }{\mathit{w}}_2}^{\mathit{T}}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right){\mathit{u}}_1+{J_2}^{-2}{\mathit{\delta }{\mathit{w}}_2}^{\mathit{T}}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right){\mathit{w}}_2-{r_2}^{-1}{J_2}^{-1}{\mathit{\delta }{\mathit{w}}_2}^{\mathit{T}}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right){\mathit{u}}_2\right)+{\beta }^i\left({J_1}^{-1}{r_2}^{-1}{{\mathit{\delta }\mathit{u}}_2}^{\mathit{T}}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right){\mathit{w}}_1-{r_1}^{-1}{r_2}^{-1}{{\mathit{\delta }\mathit{u}}_2}^{\mathit{T}}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right){\mathit{u}}_1-{r_2}^{-1}{J_2}^{-1}{{\mathit{\delta }\mathit{u}}_2}^{\mathit{T}}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right){\mathit{w}}_2+{r_2}^{-2}{{\mathit{\delta }\mathit{u}}_2}^{\mathit{T}}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right){\mathit{u}}_2\right).$ (C.7)

The works of the external constraints, Eq. (C.1) to (C.3), can be rewritten using matrices and vectors, as follows:

${{\mathrm{\delta }\mathrm{W}}_{Pen,w_1}}^e={\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{w}}_1}}^{\mathit{e}}\mathit{a}-{\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{w}}_1}}^{\mathit{e}},$ (C.8)

${{\mathrm{\delta }\mathrm{W}}_{Pen,u_1}}^e={\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{u}}_1}}^{\mathit{e}}\mathit{a}-{\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{u}}_1}}^{\mathit{e}},$ (C.9)

${{\mathrm{\delta }\mathrm{W}}_{Pen,{\phi }_1}}^e={\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{\phi }}_1}}^{\mathit{e}}\mathit{a}-{\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{\phi }}_1}}^{\mathit{e}},$ (C.10)

Where:

${{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{w}}_1}}^{\mathit{e}}={\beta }^e\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& {{\mathit{N}}_1\left({\xi }_{{w_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{w_1}^e}\right)& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],$ (C.11)

${{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathbf{}\mathit{w}}_1}}^{\mathit{e}}={\beta }^e\left[\begin{array}{c}0\\ w_{1,p}{{\mathit{N}}_1\left({\xi }_{{w_1}^e}\right)}^{\mathit{T}}\\ 0\\ 0\end{array}\right],$ (C.12)

${{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{u}}_1}}^{\mathit{e}}={\beta }^e\left[\begin{array}{cccc}{{\mathit{N}}_1\left({\xi }_{{u_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{u_1}^e}\right)& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],$ (C.13)

${{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathbf{}\mathit{u}}_1}}^{\mathit{e}}={\beta }^e\left[\begin{array}{c}{u}_{1,p}{{\mathit{N}}_1\left({\xi }_{{u_1}^e}\right)}^{\mathit{T}}\\ 0\\ 0\\ 0\end{array}\right],$ (C.14)

${{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathbf{}\mathit{\phi }}_1}}^{\mathit{e}}={\beta }^e\left[\begin{array}{cccc}{r_1}^{-2}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)& -{J_1}^{-1}{r_1}^{-1}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)& 0& 0\\ -{J_1}^{-1}{r_1}^{-1}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)& {J_1}^{-2}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],$ (C.15)

${{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathbf{}\mathit{\phi }}_1}}^{\mathit{e}}={\beta }^e\left[\begin{array}{c}-{r_1}^{-1}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}\\ {J_1}^{-1}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^e}\right)}^{\mathit{T}}\\ 0\\ 0\end{array}\right],$ (C.16)

The works of the internal constraints, in turn, Eq. (C.4) to (C.7), can also be rewritten using matrices and vectors, as follows:

${{\mathrm{\delta }\mathrm{W}}_{Pen,w_{12}}}^i={\beta }^i{\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{w}}_{12}}}^{\mathit{i}}\mathit{a},$ (C.17)

${{\mathrm{\delta }\mathrm{W}}_{Pen,u_{12}}}^i={\beta }^i{\mathit{\delta }\mathit{a}}^{\mathit{T}}{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{u}}_{12}}}^{\mathit{i}}\mathit{a},$ (C.18)

${{\mathrm{\delta }\mathrm{W}}_{Pen,{\phi }_{12}}}^i=\mathbf{}{\beta }^i{\mathit{\delta }\mathit{a}}^{\mathit{T}}\mathbf{}{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{\phi }}_{12}}}^{\mathit{i}}\mathbf{}\mathit{a},$ (C.19)

Where:

${{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathbf{}\mathit{w}}_{12}}}^{\mathit{i}}={\beta }^i\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& {{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)& 0& -{{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)\\ 0& 0& 0& 0\\ 0& -{{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)& 0& {{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)\end{array}\right],$ (C.20)

${{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathbf{}\mathit{w}}_{12}}}^{\mathit{i}}={\beta }^i\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& {{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)& 0& -{{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)\\ 0& 0& 0& 0\\ 0& -{{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{w_1}^i}\right)& 0& {{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{w_2}^i}\right)\end{array}\right],$ (C.21)

${{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathbf{}\mathit{\phi }}_{12}}}^{\mathit{i}}={\beta }^i\left[\begin{array}{cccc}{r_1}^{-2}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)& -{r_1}^{-1}{J_1}^{-1}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)& -{r_1}^{-1}{r_2}^{-1}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)& {r_1}^{-1}{J_2}^{-1}{{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)\\ -{r_1}^{-1}{J_1}^{-1}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)& {J_1}^{-2}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)& {J_1}^{-1}{r_2}^{-1}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)& -{J_1}^{-1}{J_2}^{-1}{{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)\\ -{r_1}^{-1}{r_2}^{-1}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)& {J_1}^{-1}{r_2}^{-1}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)& {r_2}^{-2}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)& -{r_2}^{-1}{J_2}^{-1}{{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)\\ {r_1}^{-1}{J_2}^{-1}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\left({\xi }_{{{\phi }_1}^i}\right)& -{J_1}^{-1}{J_2}^{-1}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_1\mathrm{\text{'}}\left({\xi }_{{{\phi }_1}^i}\right)& -{r_2}^{-1}{J_2}^{-1}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\left({\xi }_{{{\phi }_2}^i}\right)& {J_2}^{-2}{{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)}^{\mathit{T}}{\mathit{N}}_2\mathrm{\text{'}}\left({\xi }_{{{\phi }_2}^i}\right)\end{array}\right].$ (C.22)

Remembering Eq. (37), (38) and (42), Eq. (C.8) to (C.22) can be organized to compose the following global system:

$\left({\mathbf{K}}_{1,2}-{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n}}\right)\mathit{a}={\mathbf{F}}_{1,2}-{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n}},$ (C.23)

Where:

${\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n}}={{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{w}}_1}}^{\mathit{e}}+{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{u}}_1}}^{\mathit{e}}+{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{\phi }}_1}}^{\mathit{e}}+{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{w}}_{12}}}^{\mathit{i}}+{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{u}}_{12}}}^{\mathit{i}}+{{\mathbf{K}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{\phi }}_{12}}}^{\mathit{i}},$ (C.24)

${\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n}}={{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{w}}_1}}^{\mathit{e}}+{{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{u}}_1}}^{\mathit{e}}+{{\mathbf{q}}_{\mathit{P}\mathit{e}\mathit{n},{\mathit{\phi }}_1}}^{\mathit{e}},$ (C.25)

${\mathit{K}}_{1,2}=\left[\begin{array}{cccc}{\mathit{K}}_{11,1}& {\mathit{K}}_{12,1}& 0& 0\\ {\mathit{K}}_{21,1}& {\mathit{K}}_{22,1}& 0& 0\\ 0& 0& {\mathit{K}}_{11,2}& {\mathit{K}}_{12,2}\\ 0& 0& {\mathit{K}}_{21,2}& {\mathit{K}}_{22,2}\end{array}\right],$ (C.26)

${\mathit{F}}_{1,2}=\left[\begin{array}{c}{\mathbf{F}}_{1,1}\\ {\mathbf{F}}_{2,1}\\ {\mathbf{F}}_{1,2}\\ {\mathbf{F}}_{2,2}\end{array}\right],$ (C.27)

Edited by

Editor:

Marco L. Bittencourt.

Publication Dates

• Publication in this collection
  03 Feb 2020
• Date of issue
  2020

History

• Received
  04 Apr 2019
• Reviewed
  20 Nov 2019
• Accepted
  16 Dec 2019
• Published
  08 Jan 2020