Dynamic Analysis of Elastically Supported Cracked Beam Subjected to a Concentrated Moving Load

Abstract

This study deals with the dynamic behavior of a cracked beam subjected to a concentrated force traveling at a constant velocity. Dynamic analyses for a hinged-hinged cracked beam resting on elastic supports under the action of a moving load are carried out by the finite element method. For the beam having rectangular cross-section, element formulation for crack element is developed by using the principles of fracture mechanics. In the numerical analysis, Newmark integration method is employed in order to calculate the dynamic response of the beam. The effects of crack depth, crack location, elastic support and load velocity on the dynamic displacements calculated for different locations on the beam are investigated. The results related to the dynamic response of the beam are presented in 3D graphs.

Keywords:
Cracked beam; Finite element analysis; Newmark integration; Moving load; Elastic support

1 INTRODUCTION

Recently, the dynamic analysis of the engineering structures subjected to moving loads has gained great importance. The engineering structures with moving loads often come out in buildings, bridges, railways and cranes. Moreover, the cracks can be seen in engineering structures due to reasons like erosion, corrosion, fatigue or accidents. The presence of a crack can not only cause a local variation in the stiffness, but many also affect the dynamic behavior of the entire structure to a considerable extent. In this context, dynamic behavior of an engineering structure subjected to moving loads is affected with the presence of a crack.

Many investigations on the dynamic behaviour of the different isotropic structures subjected to moving loads have been carried out. Olsson (1991) has presented the fundamentals of the moving load problem for an isotropic beam. Rao (2000) has studied the dynamic response of multi-span Euler-Bernoulli beam to moving loads. Wang (1997) has investigated the forced vibration of multi-span Timoshenko beams. The effects of span number, rotary inertia, and shear deformation on the maximum moment, maximum deflection, and critical load velocity were investigated in this study. The moving force identification for a Timoshenko beam model has been given and the results, which obtained for an Euler-Bernoulli beam model, have been compared by Law and Zhu (2000). Esmailzadeh and Ghorashi (1997) have analyzed the effects of shear deformation, rotary inertia and the length of load distribution on the vibration of the Timoshenko beam subjected to a traveling mass. Hino et al. (1985) has investigated the vibration of a beam subjected to a moving load by using the Galerkin finite element formulation.

The deterministic and random vibration analyses of a nonlinear beam resting on an elastic foundation subjected to a moving load have been performed by Chang and Liu (1996). Thambiratnam and Zhuge (1996) have developed a simple procedure based on the finite element method for treating the dynamic analysis of beams on an elastic foundation subjected to moving point load, where the foundation was modelled by springs of variable stiffness. A method for the dynamic analysis of elastic beams subjected to dynamic loads induced by the arbitrary movement of a spring-mass-damper system has been presented by Lin and Trethewey (1990). In this study, the governing equations have solved with a Runge-Kutta integration scheme to obtain the dynamic response for both the supporting beam and the moving system. Kidarsa et al. (2008) have proposed a new numerical integration scheme in force-based elements, which enables to computing the internal force history at any location along a structural member under the effect of moving load. Gören (Kıral and Kıral 2009, 2008) and Kıral (2009)have studied the dynamic response of a symmetric laminated composite beam subjected to a concentrated moving load with constant velocity considering the effect of different boundary conditions, foundation stiffness and damping.

As seen from the aforementioned references, all studies on the moving load problem are related to the intact beams. Because of the practical importance of the subject, effects of cracks on the dynamic behaviors of beams have been the subject of many investigations. Unfortunately, literature research reveals that much less study investigating the dynamic behavior of cracked beam subjected to a moving load and elastic foundation is present in the published literature. A surface crack on a beam section has introduced a local flexibility to the structural member in the study which has been carried out by Gounaris and Dimarogonas (1988). In this study, a finite element model for a cracked prismatic beam has been developed. Ostachowicz and Krawczuk (1990) have studied the forced vibrations of the beam and the effects of the crack locations and sizes on the vibrational behavior of the structure were discussed. Karaagac, Ozturk and Sabuncu (2009) have investigated the effects of crack ratios and positions on the fundamental frequencies and buckling loads of slender cantilever Euler beams with a single-edge crack both experimentally and numerically using the finite element method, based on energy approach. Zheng and Kessissoglou (2004) have studied the natural frequencies and mode shapes of a cracked beam using the finite element method. In this study, an "overall additional flexibility matrix", instead of the "local additional flexibility matrix", has been added to the flexibility matrix of the corresponding intact beam element to obtain the total flexibility matrix, and therefore the stiffness matrix. Yokoyama and Chen (1998) have investigated the vibration characteristics of a uniform Bernoulli-Euler beam with a single edge crack using a modified line-spring model.Law and Zhu (2006) have studied the dynamic behavior of a beam with a breathing crack subject to moving loads. For dynamic analysis, the equations of motion in matrix form for a cracked beam subjected to a moving load with constant velocity have been formulated using Hamilton's principle and the assumed mode method by Lee and Ng (1994). In this study, the beam has modeled as two separate beams divided by the crack. Mahmoud and Abou Zaid (2002) have developed an iterative modal analysis approach to determine the effect of transverse cracks on the dynamic behavior of simply supported undamped Bernoulli-Euler beams subject to a moving mass. Lin and Chang (2006) have developed an analytical method to present the dynamic response of a cracked cantilever beam subject to a concentrated moving load. The cracked beam system has modeled as a two-span beam and each span of the continuous beam is assumed to obey Euler-Bernoulli beam theory. Yang et al. (2008) have investigated the free and forced vibration of slender functionally graded material (FGM) beams with open edge cracks under a combined action of an axial compression and a concentrated transverse moving load. Kargarnovin et al. (2012) have presented dynamic response of a delaminated composite beam under the action of moving oscillatory mass with the Poisson's effect, shear deformation and rotary inertia. Esen (2015)has presented a combined plate element for the analysis of transverse and longitudinal vibrations of a thin plate which carries a load moving along an arbitrary trajectory with variable velocity.

In this study, the dynamic behavior of a cracked beam subjected to a concentrated force traveling at a constant velocity is investigated by using the finite element method. The end conditions of the beam are assumed to be hinged-hinged. The effect of the elastic support is included in the study by using the linear springs distributed to the nodes of the beam. For the rectangular cross-section beam, a crack element is modeled by using the principles of fracture mechanics. The Newmark integration method, which is frequently used in the structural dynamic analyses, is employed in order to calculate the dynamic response of the beam. The effects of crack depth, crack location, elastic support and load velocity on the dynamic displacements of the beam are investigated. The results are presented in 3D graphs.

2 CALCULATION OF THE LOCAL FLEXIBILITY

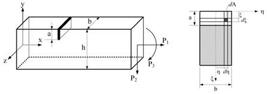
A crack on a beam introduces considerable local flexibility due to the strain energy concentration in the vicinity of the crack tip under load. The idea of an equivalent spring i.e. a local compliance is used to quantify, in a macroscopic way, the relation between the applied load and the strain concentration around the tip of the crack (Karaagac et al., 2009). A beam element of rectangular cross-section has an edge crack with a tip line parallel to thez-axis, i.e. with a uniform depth. A generalized loading is indicated by three general forces: an axial force P₁, shear force P₂ and bending momentP₃ as seen in Figure 1 (a).

Figure 1:
Schematic view of a cracked beam under generalized loading conditions.

In this work, the cross section of the beam is assumed to be rectangular. The additional strain energy due to the existence of a crack can be expressed as (Karaagac et al., 2009; Zheng and Kessissoglou, 2004):

Where G is the strain energy release rate function andA_c is the effective cracked area. The strain energy release rate function G can be expressed as (Zheng and Kessissoglou, 2004)

In this expression, E' = E for plane stress problem and E' = E/(1-ν²⁾ for plane strain problem (Karaagac et al., 2009;Zheng and Kessissoglou, 2004), whereE denotes the modulus of elasticity and denotes the poissons's ratio. K_In and K_IIn(n=1,2,3) are the stress intensity factors of the two modes of fracture (opening and sliding types) corresponding to generalized loading P_n, respectively. The stress intensity factor K_I2 is ignored due to the Euler beam theory and K_I1 is given as (Ibrahim et al., 2013; Shen and Pierre, 1994).

where

Fn(s=(/h) represents the correction function which takes into account the finite dimensions of the beam and takes particular forms for different geometry and loading modes. It is worth noting that a is the final crack depth while ( is the crack depth during the process of penetration from zero to the final depth.

The elements of the overall additional flexibility matrixc_ij can be expressed as (Karaagac et al., 2009; Zheng and Kessissoglou, 2004).

Substituting Eq. (3- 6) in Eqn 7 yields the general equation for the local compliances as follows (considering that all K's are independent of (; (: see Figure 1 (b) ):

where c_ijis the local flexibility matrix:

3 CRACKED BEAM MODEL AND ENERGY EQUATIONS

In this study, a finite element model is constituted to represent a cracked beam element of length d and the crack is located at a distance d₁ from the left end of the element as shown in Figure 2. The element is then considered to be split into two segments by the crack. The left and right segments are represented by non-cracked sub elements. The crack represents net ligament effect created by loadings. This effect can be related to the deformation of the net ligament through the compliance expressions (c_ij) by replacing the net ligament with a fictitious spring connecting both faces of the crack (Yokoyama and Chen, 1998; Ibrahim et al., 2013).

Figure 2:
Crack locations in crack element.

The spring effects are introduced to the system by using the local flexibility matrix given by Eq. (9). The cracked element has two nodes with two degrees of freedom in each node. They are denoted as lateral bending displacements (v₁,v₂) and slopes (v'₁,v'₂),

For 0 ≤ x ≤ d₁

For d₁ ≤ x ≤ d

The coefficients a of the polynomials can be expressed uniquely in terms of the boundary conditions and the local flexibility concept at the crack location. Eventually, the following expressions are obtained for a cracked element:

For lateral bending,

At the crack location d₁, the flexibility concept requires:

For lateral bending:

Continuity of the vertical displacement,

Discontinuity of the cross-sectional rotation (slope),

Where andI denotes the area moment of inertia of the beam cross section.

Continuity of bending moment,

Continuity of shear force,

By considering Eq. (10) which describes the displacement for the left and right parts of the element and rearranging Eqs. (11) and (12), the nodal displacement can be expressed in matrix forms as

where

The generalized displacement vector according to local reference coordinates can be expressed as:

Energy equations should be expressed separately from the crack element and intact elements on the left side of the crack element.

The elastic potential energy U:

For intact elements on the left side of the cracked element,

For the cracked element,

For intact element on the right side of the cracked element,

Similarly, the kinetic energy T of an element of lengthd in an Euler beam is given as follows for the intact elements on the left side of the cracked element,

For the cracked element,

For intact element on the right side of the cracked element,

4 PROCEDURE FOR DYNAMIC ANALYSIS

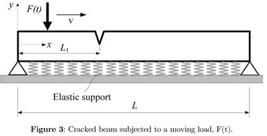
For a hinged-hinged cracked beam with elastic supports under the action of a moving load shown in Figure 3, the overall mass and stiffness matrices are obtained by assembling the element matrices. The number of elements used in the finite element vibration analysis is 30.

Figure 3:
Cracked beam subjected to a moving load, F(t).

The dynamic response of the cracked beam is calculated by using the procedure described in the Newmark integration method which is widely used in structural dynamics. By using the overall mass [M ], damping [C ] and stiffness [K ] matrices for the beam, the governing equations of the system are written in the matrix form as

Where {}_t, {}_t and {q}_t are the nodal acceleration, velocity and displacement vectors at time t, respectively. {F}_t is the global external excitation vector subjected to the beam at time t. The nodal external excitation vector at time t is constructed using the linear variation assumption of the force when it travels between two adjacent nodes as described byEq. (18).

where F₀ denotes the magnitude of the moving load,t_node denotes the time interval to travel between two nodes and t_υ is the local time, which has the value between 0 and t_node. If the force is on the i^th node, t_υ equals to zero, and if the force is on one of the adjacent nodes, t_υ equals tot_node. In the Newmark method, the integration constants are defined as follows (Clough and Penzien, 1993),

where (t is the time increment used in the numeric analysis and taken as (t=T₁₀/20 andT₁₀ is the 10^th natural period of the beam. The integration parameters ( and ( are selected as 1/4 and 1/2, respectively, in order to obtain a stable solution. The effective stiffness matrix is calculated to perform the dynamic analyses as

The effective load vector F_ef is calculated for each time step as

The nodal displacement, acceleration and velocity responses at time t+(t can be obtained by using the following equations

In this study, the effect of damping on the dynamic response of the beam is not taken into consideration and the damping matrix [C] is taken as zero. Moreover, the elastic support is modeled using the linear translation springs located on each node as seen in Figure 3. The linear springs have the effect on the vertical translational degree of freedom and the stiffness of each spring is added to the diagonal terms of the global elastic stiffness matrix. The elastic foundation parameter is used as the ratio between the equivalent spring coefficient of the elastic support and the hinged-hinged beam.

5 NUMERIC ANALYSIS AND RESULTS

In this study, a computer code developed using the MATLAB 6.5 (Dabney and Harman, 1999) is used to calculate the dynamic response of a hinged-hinged cracked beam with elastic supports under the action of a concentrated moving load as shown in Figure 3. The effects of crack depth, crack location, elastic foundation parameter and load velocity on the dynamic response of the beam are presented in 3D graphs. The dimensions and material properties of the beam are given in Table 1.

Table 1:
Properties of the beam.

Properties			Quantity
Modulus of elasticity,E			69 GPa
Mass density, ρ			2700 kg/m3
Cross-section	h	5 mm
	b	20 mm
Beam length, L			500 mm

Figures from 4 to 6 show the effect of crack ratio (a/h) and crack location (L₁/L) on the first three natural frequencies of the cracked beam with different elastic foundation parameters. As can be seen from these figures, as the crack ratio (or depth) increases, the variations of the the natural frequencies become significant. When the crack ratio is between 0 and 0.3, there is no considerable effect of the crack depth and location on the first natural frequency. But, the effects of these parameters towards the higher natural frequencies become evident even in smaller crack ratios. Moreover, the crack does not affect the natural frequencies when it is located at the particular points (nodes in mode shapes) of the beam length, since stresses in these points are so small. The maximum reduction occurs in the first, second and third natural frequency values, respectively for unsupported case. These reductions are 8.85%, 8.23% and 7.75%.However, for supported case, the maximum reduction occurs in the second, third and first natural frequency values, respectively namely as 7.72%, 7.65% and 4.28%.

Figure 4:
The effect of crack ratio and location on the first natural frequency of cracked beam with elastic support.

Figure 5:
The effect of crack ratio and location on the second natural frequency of cracked beam with elastic support.

The maximum decreases in the natural frequencies occur when the crack location at the mid-point of the beam (L₁/L=0.5) for the first natural frequency, at theL₁/L=0.24 andL₁/L=0.75 for the second natural frequency and at the L₁/L=0.138,L₁/L=0.5 andL₁/L=0.86 for the third natural frequency. It is observed that the crack location is more effective at the higher natural frequencies while the crack ratio increases. As known fact is that when an elastic support or spring is added to the hinged-hinged beam, the natural frequencies increase. As seen in Figures 4,5 and 6, while the first natural frequency increases significantly with increasing the elastic foundation parameter, this increment is greatly reduced towards the higher natural frequencies. The effects of the crack ratio and location on the natural frequencies are similar to unsupported case.

In this study, the dynamic response of the cracked beam is presented with respect to the nondimensional load velocity α which is defined as:

where T₁ is the first natural period of the beam, andτ is the total time in which the moving load completes its movement on the beam. The moving load velocity increases as the nondimensional load velocity α increase. In the numerical analyses, the cracked beam is discretized with 30 finite elements resulting in 31 nodes. The concentrated load is moved from 1^st node to 31^nd node with a constant velocity.

Figure 6:
The effect of crack ratio and location on the third natural frequency of cracked beam with elastic support.

Figures 7-11 present the effects of the elastic foundation parameter, crack ratio and crack location on the maximum displacement values calculated at the nodes of the cracked beam for different nondimensional load velocities. The dynamic displacement has the maximum value around the mid-point of the beam without being dependent on the nondimensional load velocity, crack ratio and crack location. When the nondimensional load velocity is 2, the maximum displacement is observed at the locations 0.5L and 0.66L for supported case.

Figure 7:
The effects of elastic foundation parameter, crack ratio and crack location on the maximum displacement at the nodes of the cracked beam for nondimensional load velocity α=0.25.

The displacement decreases as expected when the elastic foundation parameter increases. As the crack ratio increases, considerable increment in the dynamic displacements appear as shown in figures, but this increment is more noticeable when the crack ratio is larger than the value of 0.3 and the crack location is betweenL₁/L=0.2 andL₁/L=0.8 . Similar to the natural frequency analysis, there is no strong influence of the crack location on the dynamic displacements until a certain crack depth. When the crack ratio is 0.5, the pattern of the maximum displacement values of the beam changes significantly with respect to the crack location as seen in figures from 7(c) to 11(c).

Figure 8:
The effects of elastic foundation parameter, crack ratio and crack location on the maximum displacement at the nodes of the cracked beam for nondimensional load velocity α=0.5.

Figure 9:
The effects of elastic foundation parameter, crack ratio and crack location on the maximum displacement at the nodes of the cracked beam for nondimensional load velocity α=1.

Figure 10:
The effects of elastic foundation parameter, crack ratio and crack location on the maximum displacement at the nodes of the cracked beam for nondimensional load velocity α=1.5.

Figure 11:
The effects of elastic foundation parameter, crack ratio and crack location on the maximum displacement at the nodes of the cracked beam for nondimensional load velocity α=2.

As can be seen from Figures 7-11, it is observed that the dynamic displacement of the beam increases with nondimensional load velocity value approaching to 1. However, it decreases after nondimensional load velocity value of 1.5. This case can be distinctly observed when the crack ratio and elastic foundation parameter are equal to 0. Besides, Kiral (2009) have found that the critical nondimensional load velocity, at which the maximum mid-point displacements occur, is 1.2 for a hinged-hinged beam. As seen from Figures 7-11, the maximum displacements along the beam occur symmetrically with respect to the mid-point of the beam until a crack ratio value of 0.3. After this value, this symmetric variation does not appear. As the elastic foundation parameter increases, the pattern of the maximum displacement values shows a difference according to the case without an elastic foundation due to the change in the structural stiffness. This situation can be seen more clearly in Figures 10 (c) and 11 (c) in which the nondimensional load velocity is 1.5 and 2.

The time-varying maximum displacements of the cracked beam calculated for the beam mid-point are given in 3D graphics in Figures from 12 to 16. Figure 12 shows the dynamic displacements of the beam obtained at α=0.25 for different sizes and locations of the crack. The time axis is normalized by dividing the elapsed time by the total load travel time for each case. It is seen from the Figures 12a, 12b and 12c that the dynamic displacements increase apparently as the crack depth increases. Similar to the maximum displacement of the beam analysis, the displacement changes with respect to the crack location (L₁/L). These situations are shown in Figures 14 to 16. At this low load velocity (α=0.25), the maximum mid-point displacements occur when the load is on the beam mid-point. In addition, Figure 12c shows that reduction in the mid-point displacements for the case that the crack is near to the mid-point of the beam, is bigger than those obtained when the crack is near to the end of the beam. The camel's hump-like displacement pattern shown in Figure 12c is the clear reflection of this result. Figure 12 also shows that the elastic support reduces the dynamic displacements as expected. Figure 13 shows the mid-point dynamic displacements of the cracked beam for the nondimensional load velocity α=0.5. For this load velocity, dynamic displacements increase and the time at which the maximum displacements are recorded shifts left. Effect of the crack location on the dynamic displacements is more apparent as seen in Figure 13c. But, the elastic support significantly suppresses the effect of the crack location on the dynamic displacements.

Figure 14 represents the mid-point dynamic displacements of the cracked beam for the nondimensional load velocityα=1. For this velocity, dynamic displacements get larger and the maximum displacements are recorded when the load past the mid-span of the beam.Figure 15 shows that, for the nondimensional load velocity α=1.5, the maximum displacements are still large and they are observed when the moving load is very close to the right end of the beam.Figure 16 presents the dynamic displacements for the nondimensional velocity α=2. At this load velocity, the maximum dynamic displacements are smaller than those obtained forα=1.5 and they occur when the moving load leaves the beam. The effects of the elastic support, crack size and crack location are still apparent.

Figure 12:
The mid-point dynamic displacements of the hinged-hinged cracked beam for nondimensional load velocity α=0.25.

Figure 13:
The mid-point dynamic displacements of the hinged-hinged cracked beam for nondimensional load velocity α=0.5.

Figure 14:
The mid-point dynamic displacements of the hinged-hinged cracked beam for nondimensional load velocity α=1.

Figure 15:
The mid-point dynamic displacements of the hinged-hinged cracked beam for nondimensional load velocity α=1.5.

Figure 16:
The mid-point dynamic displacements of the hinged-hinged cracked beam for nondimensional load velocity α=2.

6 CONCLUSIONS

In this study, dynamic displacements of a cracked beam subjected to a concentrated moving load with constant velocity are investigated by using the finite element method. The crack element and its local flexibility are obtained by using the fundamental knowledge of fracture mechanics. The depth and location of the crack and the moving load velocity are used as the parameters of the numerical analysis. Effect of the elastic support, which is modelled by linear springs, on the dynamic response of the cracked beam is also investigated. Based on the numerical results obtained in this study, the following conclusions are drawn,

• The natural frequencies of the cracked beam get smaller as the crack depth increases. Moreover, the crack does not affect the natural frequencies when it is located at the particular points (nodes in mode shapes) of the beam length.

• Reduction in the natural frequencies induced by the increasing crack size is more apparent at the lower natural modes without the elastic supports.

• Effect of the elastic support on the natural frequencies of the cracked beam reduces at the higher vibration modes.

• The crack, which is located near to the middle of the beam, has more influence on the increase in the dynamic displacement amplitudes.

• The amplitude of the dynamic displacements increases as the crack ratio increases for all load velocities. The elastic support helps to reduce the dynamic displacements of the beam.

• When the crack ratio is 0.5, the pattern of the maximum displacement values of the beam changes significantly with respect to the crack location.

• The maximum displacements along the beam occur symmetrically with respect to the mid-point of the beam until a crack ratio value of 0.3. After this value, this symmetric variation does not appear. As the elastic foundation parameter increases, the pattern of the maximum displacement values shows a difference according to the case without an elastic foundation.

• For with or without the elastic support case, the displacement pattern loses its symmetry as the load velocity increases.

• Velocity of the moving load has considerable influence on both the mid-point dynamic displacements and their occurrence time.

REFERENCES

• Chang, T.P., Liu, Y.N. (1996). Dynamic finite element analysis of a nonlinear beam subjected to a moving load. International Journal of Solids and Structures 33(12): 1673-1688.
• Clough, R.W., Penzien, J. (1993). Dynamics of Structures. New York: McGraw-Hill.
• Dabney, J., Harman, T.L. (1999). Advanced Engineering Mathematics with MATLAB. USA: Brooks/Cole Publishing Company.
• Esen, I. (2015). A new FEM procedure for transverse and longitudinal vibration analysis of thin rectangular plates subjected to a variable velocity moving load along an arbitrary trajectory. Latin American Journal of Solids and Structures 12:808-830.
• Esmailzadeh, E., Ghorashi, M. (1997). Vibration analysis of a Timoshenko beam subjected to a traveling mass. Journal of Sound and Vibration 199: 615-328.
• Goren Kıral, B., Kıral, Z. (2009). Effect of elastic foundation on the dynamic response of laminated composite beams to moving loads. Journal of Reinforced Plastics and Composites 28(8): 913-935.
• Gounaris, G., Dimarogonas, A. (1988). A finite element of a cracked prismatic beam for structural analysis. Computers & Structures 28(3): 309-313.
• Hino, J., Yoshimura, T., Ananthanarayana, N. (1985). Vibration analysis of non-linear beams subjected to a moving load using the finite element method. Journal of Sound and Vibration 100(4): 477-491.
• Ibrahim, A.M., Ozturk, H., Sabuncu, M. (2013). Vibration analysis of cracked frame structures. Structural Engineering and Mechanics 45(1): 33-52.
• Karaagac, C., Ozturk, H., Sabuncu, M. (2009). Free vibration and lateral buckling of a cantilever slender beam with an edge crack: Experimental and numerical studies. Journal of Sound and Vibration 326(1-2): 235-250.
• Kargarnovin, M.H., Ahmadian, M.T., Talookolaei, R.A.J. (2012). Dynamics of a delaminated timoshenko beam subjected to a moving oscillatory mass. Mechanics Based Design of Structures and Machines 40: 218-240.
• Kidarsa, A., Scott, M.H., Higgins, C.C. (2008). Analysis of moving loads using force-based finite elements. Finite Elements in Analysis and Design 44: 214-224.
• Kıral, Z. (2009). Damped response of symmetric laminated composite beams to moving load with different boundary conditions. Journal of Reinforced Plastics and Composites 28(20): 2511-2526.
• Kıral, Z., Gören Kıral, B. (2008). Dynamic analysis of a symmetric laminated composite beam subjected to a moving load with constant velocity. Journal of Reinforced Plastics and Composites 27(1): 19-32.
• Law, S.S., Zhu, X.Q. (2000). Study on different beam models in moving force identification. Journal of Sound and Vibration 234(4): 661-679.
• Law, S.S., Zhu, X.Q. (2006). Vibration of a beam with a breathing crack subject to moving mass, In: Liu, G.R., Tan, V.B.C., Han, X. (eds) Computational Methods. Netherlands: Springer, 1963-1968.
• Lee, H.P., Ng, T.Y. (1994). Dynamic response of a to a moving load cracked beam subject. Acta Mechanica 106: 221-230.
• Lin, H.P., Chang, S.C. (2006). Forced responses of cracked cantilever beams subjected to a concentrated moving load. International Journal of Mechanical Sciences 48: 1456-1463.
• Lin, Y.H., Trethewey, M.W. (1990). Finite element analysis of elastic beams subjected to moving dynamic loads. Journal of Sound and Vibration 136(2): 323-342.
• Mahmoud, M.A., Abou Zaid, M.A. (2002). Dynamic response of a beam with a crack subject to a moving mass. Journal of Sound and Vibration 256(4): 591-603.
• Olsson, M. (1991). On the fundamental moving load problem. Journal of Sound and Vibration 145(2): 299-307.
• Ostachowicz, W.M., Krawczuk, M. (1990). Vibration analysis of a cracked beam. Computers & Structures 36(2): 245-250.
• Rao, G.W. (2000). Linear dynamics of an elastic beam under moving loads. Journal of Vibration and Acoustics 122(3): 281-289.
• Shen, M.H.H., Pierre, C. (1994). Free vibrations of beams with a single-edge crack. Journal of Sound and Vibration 170(2): 237-259.
• Thambiratnam, D., Zhuge, Y. (1996). Dynamic analysis of beams on an elastic foundation subjected to moving loads. Journal of Sound and Vibration 198(2): 149-169.
• Wang, R.T. (1997). Vibration of multi-span Timoshenko beams to a moving force. Journal of Sound and Vibration 207(5): 731-742.
• Yang, J., Chen, Y., Xiang, Y., Jia, X.L. (2008). Free and forced vibration of cracked inhomogeneous beams under an axial force and a moving load. Journal of Sound and Vibration 312: 166-181.
• Yokoyama, T., Chen, M.C. (1998). Vibration analysis of edge-cracked beams using a line-spring model. Engineering Fracture Mechanics 59(3): 403-409.
• Zheng, D.Y., Kessissoglou, N.J. (2004). Free vibration analysis of a cracked beam by finite element method. Journal of Sound and Vibration 273: 457-475.

Publication Dates

• Publication in this collection
  Jan 2016

History

• Received
  03 June 2015
• Accepted
  05 Oct 2015