Numerical Study on Ultimate Behaviour of Bolted End-Plate Steel Connections

Abstract

Bolted end-plate steel connections have become more popular due to ease of fabrication. This paper presents a three dimension Finite Element Model (FEM), using the multi-purpose software ABAQUS, to study the effect of different geometrical parameters on the ultimate behavior of the connection. The proposed model takes into account material and geometrical non-linearities, initial imperfection, contact between adjacent surfaces and the pretension force in the bolts. The Finite Element results are calibrated with published experimental results ''briefly reviewed in this paper'' and verified that the numerical model can simulate and analyze the overall and detailed behavior of different types of bolted end-plate steel connections. Using verified FEM, parametric study is then carried out to study the ultimate behavior with variations in: bolt diameter, end-plate thickness, length of column stiffener, angle of rib stiffener. The results are examined with respect to the failure modes, the evolution of the resistance, the initial stiffness, and the rotation capacity. Finally, the ultimate behavior of the bolted end-plate steel connection is discussed in detail, and recommendations for the design purpose are made.

Keywords:
Beam to column connections; end-plate steel connection; ultimate behavior; rotation capacity, and Finite Element Modeling; bolted connection; bolt's pretension force

1 INTRODUCTION

Extended end-plate connections are widely used in steel structures as moment resistance connections and as an alternative to fully welded ones that has been considered for use in steel frames. These connections consist of end-plate welded to the end of beam and field bolted to the connecting column as illustrated in Figure 1. The behaviors of end-plate connections significantly influence the internal forces and overall deformations of the structures. The problem of connections flexibility and its effects on the behavior of steel structure has been an area of interest to engineers and scientists for more than 90 years. End-plate connections are commonly classified as semi-rigid joints, because the concept of perfect rigid or pinned is a pure theoretical point of view. These connections should be classified in terms of relationship between the moment transmitted by the connection and their rotation in the plane of connection. According to (Euro Code 3, 2003) and most researches; it can be classified by its rotational stiffness, strength and ductility.

Figure 1
Connection configuration.

Many researches were carried out analytically and experimentally on end-plate steel connections to determine an accurate method for predicting the connection rotational behavior under the monotonic and cyclic loadings. (Dabaon, 2010) presented a review article which described the classification of beam-to-column joints. In addition he reported experimental work on composite joints. (Dabaon et al., 2002) presented a simple formula based on (Euro Code 3, 2003) to predict the initial rotation stiffness of the semi-rigid joints. (Shi et al., 2007) presented a new theoretical model to evaluate the M-ϕ relation for stiffened and extended steel beam-column end-plate connection. In addition five specimens were tested under monotonic loads to verify the analytical model. (Mohamadi-Shoore and Mofid, 2011) developed a new exponential model to predict the standard M-ϕ curves of bolted end-plate connections. (Faella et al., 1977) investigated the relations between the parameters representing the rotational behavior of extended end- plate connections and their dependence on the geometrical details by a large number of numerical analysis. (Yun et al., 2007), developed a neural network based hysteretic models for steel beam-column connections. (Lemonis and Gantes, 2009) developed a component-based model for the mechanical representation of the beam-to-column connection.

Three-dimensional finite element models were analyzed by (Bursi and Jaspart, 1998), (Ju et al., 2004), (Maggi et al. 2005) and (Mohamadi-Shoore and Mofid, 2008, 2013), to evaluate the moment-rotation relation for bolted end-plate beam connections. (Dabaon et al., 2007) proposed a three dimensional Finite Element model utilizing ANSYS software for analytical investigation of the effect of loads in the minor direction on the behavior of semi-rigid joint in the major direction. (Shi et al., 1996) developed a new nominal model to evaluate the M-ϕ relation for stiffened and extended steel beam-column end-plate connections. (Dessouki et al., 2013) presented a finite element model to study the non-linear behavior of the extended end-plate moment connections. They used the presented model to conduct a parametric study on two end-plate configurations: four bolts and multiple row extended end plates. Their studied parameters are beam depth, end-plate thickness, bolts diameter, bolts inside and outside pitch, inner bolts pitch, bolts gage, and end-plate stiffener. During their study, the distribution of stresses in the end plates was monitored for different configurations, and yield line patterns were observed for each configuration. These yield line patterns were analyzed and new design equations were proposed. The proposed equations were then compared to their finite element analysis results and to the current design codes equations. (Shaker and Abd Elrahman, 2014) studied two types of steel connections; flushed end plate and extended end plate utilizing nonlinear finite element modeling techniques using ANSYS program, considering both geometric and material nonlinearities.

Based on a specific definition of rotation for the bolted end-plate connection, the end-plate connection is decomposed into several components, including the panel zone, bolt, end-plate and the column flange. (Mashaly et al., 2011) conducted a parametric analysis to investigate the effect of both material and geometric properties of four-bolt extended end-plate connections upon their behavior under lateral loading. Their parametric study took into account 12 parameters which were expected to affect the behavior of studied connection. Their Finite Element results were compared with those of experiments done by (Díaz et al., 2011), (Swanson et al., 2002) and (Kukreti and Zhou, 2006).

Different test setups covered a large number of connections were carried out by (Tsai et al., 1995), (Swanson and Leon, 2000), (Kim et al., 2002), (Dabaon et al., 2007), (Coelho and Bijlaard, 2007), (Coelho et al., 2004) and (Shi et al., 2010) to investigate their behavior under monotonic and cyclic load, the influences of each parameter on connection's behavior such as rotational stiffness, moment resistance, failure mode and ductility and develop a large data base to calibrate suitable simplified models for the design of such type of connection.

The first objective of this paper is to develop a reliable three dimension FEM for the analysis of bolted end-plate steel connection including bolt pretension force, initial imperfection, local buckling, and modeling of contact between different surfaces and compare the results with those of available published experiments. Due to a lack of sufficient information on the effect of stiffeners with different geometrical dimensions on the connection behavior, the second objective is to use the proposed FEM to carry out an extensive parametric study to investigate the effect of different parameters on the behavior of bolted end-plate connection.

2 THREE DIMENSION FINITE ELEMENT MODEL

The aim of this study is to develop a 3D FE model simulating stiffened and unstiffened end-plate connection. Modeling semi-rigid connections helps to predict the actual behavior of connections under monotonic loading and to study the characteristic of the connections, as well as the factors affecting their behavior.

2.1 Geometry of the connections

The general purpose finite element Software ABAQUS is used to develop a three dimension Finite Element Model (FEM) to simulate the behavior of bolted end-plate connections under monotonic load. In order to verify the proposed FEM, eight specimens of a cruciform end-plate steel connection, tested experimentally by Shi et al. (2010), are selected. Details of these specimens are shown in Table 1 and Figure 2. Beam and column dimensions of all specimens have the same dimensions and are listed in Table 2.

Table 1
Details of investigated end-plate connections.

Specimen number	Connection type	End-plate thickness (mm)	Bolt diameter (mm)	Number of bolts	Column stiffener	End-plate stiffener
SC01	Flush	20	20	6	Yes	No
SC02	Extended	20	20	8	Yes	Yes
SC03	Extended	20	20	8	Yes	No
SC04	Extended	20	20	8	No	Yes
SC05	Extended	25	20	8	Yes	Yes
SC06	Extended	20	24	8	Yes	Yes
SC07	Extended	25	24	8	Yes	Yes
SC08	Extended	16	20	8	Yes	Yes

Table 2
Sectional dimension of beam and column (unit:mm).

	Section depth	Web thickness	Flange width	Flange thickness
Beam	300	8	200	12
Column	300	8	250	12

Figure 2
Details of the connection (Dim. in mm), (Shi et al., 2010)

2.2 Finite Element Model

In the present FEM, all connected parts including the beam, column, plates, and bolts were modeled using the continuum three dimensional eight nodes solid element with reduced integration technique (C3D8R). Since this solid element has no rotational degree of freedom, the number of elements through the thickness of each component plate plays a critical role. A set of six elements across the end-plate thickness and four elements across the column/beam flanges was used at connecting region to simulate precisely the rotation of the considered plate. The structural steel components such as steel beam, steel column and bolt are modeled as an isotropic elastic-plastic material in both tension and compression. Yield and ultimate tensile strength of the steel beam as well as Young's modulus (E) are obtained from the test results carried by (Shi et al., 2010), and listed in Table 3. The Poisson's ratio of 0.3 is assumed.

Table 3
Material properties.

Material	Measured Yield Stress (MPa)	Measured Tensile Strength (MPa)	Measured Elastic Modulus (MPa)	Measured Bolt average Pretension Force (KN)
Steel (t ≤ 16mm)	391	559	190707	-
Steel (t > 16mm)	363	573	204228	-
Bolts (M20)	995	1160	204228	185
Bolts (M24)	975	1188	204288	251

The nominal stress - nominal strain relationship is determined using Equation1 proposed by (Gattesco, 1999).

in which σ_s and ε_s are the measured nominal stress and nominal strain values, respectively.f_sy is the yield stress. ε_sh is the strain at starting of strain hardening. f_su is the ultimate stress.E_sh is the strain hardening modulus. The true stress - true strain relationship is then obtained and tabulated for the use in ABAQUS (see ABAQUS manual, 2012).

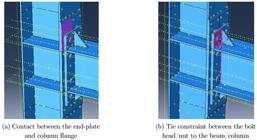
Modeling the contact between the different model parts is one of the most critical processes. If contact is improperly modeled, results of the analysis will not reflect the real behavior of the connection definitely. In the case of the contact between the end-plate and column flanges, two relevant properties were considered: the first one is tangential behavior and normal behavior of the contact surface interaction considering small sliding surface-to-surface contact. Tangential behavior is defined with a frictional coefficient of 0.3 using penalty stiffness formulation. Normal behavior is defined as "hard" contact. This property assumes that constraints related to contact can only occur, when the surfaces are touching no sticking between the contact surfaces. The second one is hard ''Tie'' constraint which is used for connecting the bolt head/nut to the beam/column as shown in Figure 3.

Figure 3
Contacts used in end-plate connection

Finite element analysis for such connection, using ABAQUS, requires two types of analyses. The first type is Eigenvalue buckling analysis which is used to estimates the first buckling mode. The second type is to perform inelastic geometrical nonlinear analysis in which the first buckling mode obtained from the buckling analysis is factored by a magnitude ofLu/1000, where Lu is the length between points of effective bracing, and is used as initial imperfection of the structure members to initiate the local buckling in the component plates. In order to prevent local yielding around the loading point, the concentrated load is simulated by a uniform pressure distributed above an elastic rigid solid element. The arc length method (Riks) with the aid of full Newton-Raphson iteration method is used to trace loading path till failure point is reached.

In both types of analysis, the boundary conditions of the model are prescribed according to those existing in test setup, as shown in Figure 4. In the inelastic nonlinear analysis, the bolt pretension force is simulated by applying compressive forces on the annular area of the bolt head/nut. The bolt load variation is chosen to produce the standardized preloads of 185 and 251 KN for 20 and 24 mm, respectively.

Figure 4
Boundary conditions of the connection.

One of the most important issues in the Finite Element Analysis is the element meshing used in the model, since the accuracy of the results largely depends on it. Different mesh sizes have been examined to determine a reasonable mesh that provides accurate results with less computational time. The optional solution is to use a fine mesh in regions of high stress and coarser mesh in the remaining regions, as shown in Figure 5.

Figure 5
Finite element mesh of bolted end-plate steel connection.

3 VALIDATION OF THE PROPOSED FINITE ELEMENT MODEL

Validation of the proposed finite element model is examined by comparing its numerical results with those of experiments conducted by (Shi et al., 2010), in terms of load-displacement characteristics, moment-rotation characteristics, and failure modes of the connections. The force at the loading point, shown in Figure 4, was identified and its peak value was taken as the loading capacity of each of the connection specimens. Moment resistance of the joint is calculated as the product of the applied load times the lever arm of 1200 mm. The lever arm is defined as the distance from the loading point to the column flange, as shown in Figure 4. Table 4 shows comparisons of the moment resistance, rotation capacities, and initial stiffness of all of these connections.

Table 4
Comparison of moment capacities and initial stiffness between FEM and tests.

Specimen Number	Test M [KN.m]	FEM.M [KN.m]	Test Sj.ini / [KN.m/rad]	FEM Sj.ini /[KN.m/rad]	Rot. capacity (rad) Test	Rot. Cap. (rad) FEM.
SC01	186.4	205.40	23544	20008	.043	.058
SC02	343.7	343.8	52276	51253	.07	.063
SC03	308.3	290.0	49093	45503	.067	.0522
SC04	307.9	283.2	51535	47352	.05	.085
SC05	322.1	382.9	46094	46090	.043	.067
SC06	390.3	391.9	46066	46061	.108	.096
SC07	410.8	375.0	47469	47462	.073	.052
SC08	355.4	343.2	41634	38819	.101	.093

The connection rotation is defined as the relative rotation of the centerlines of the top and bottom flanges at the beam end (Shi et al., 2010). It usually consists of two parts: the shearing rotation ϕ_s, contributed by the panel zone of the column, and the gap rotation ϕ_ep caused by the relative deformation between the end plate and the column flange. A good correlation ofM - ϕ curves obtained from the Finite Element model to that obtained from the tests for extended end-plate connection is found as shown in Figure 6. It can be seen that the experimental and Finite Element results match better in the starting part than in the ending part. The results of the Finite Element and those of experiment, in the nonlinear range of response, are very close for the case of extended end-plate with rib stiffener. While minor discrepancies are found in the case of flush type connection.

Figure 6
Comparison of moment-rotation curves for all connections.

Comparisons of the failure modes occurred in the experiments with those predicted by the Finite Element analysis for the eight specimens are shown in Figure 7, where the local deformations of the end-plate, the column flange, and the end-plate stiffener are clearly shown.

Figure 7
Comparison of ultimate failure modes for eight specimens.

Failure point of the connection is defined as a numerical converges in the nonlinear range, as it identifies some model instability. This nonlinear convergence depends on several variables, especially when contact elements are being used. As a matter of fact, the numerical divergence of the solution does not always indicate the actual failure point. Therefore, simple inspection procedures can be used to identify the criterion caused failure and ultimate state of the connection. The first criterion is to monitor the stress and strain states in the bolts. The second criteria is to control the deflection of connected beam which should not exceed 20 times of the allowable value of deflection, to emphasizes that sufficient rotation capacity exists in order to develop the plastic collapse mechanism as the plastic theory of partial strength connection design recommends, so that a plastic hinge tends to be formed in the connection. The third criterion is to observe the beam flange local buckling by exhibiting the contour of plastic strain with a magnification value equal to one.

4 SELECTIONS OF VARIABLE PARAMETERS FOR PARAMETRIC STUDY

Connection is mainly composed of two zones. The first zone is the panel zone, in which moment-rotation behavior doesn't depend on the connection component. The second zone is the connection, in which moment-rotation behavior depends on the connecting elements such as endplate, bolts, column flange, stiffeners, by EC3 (2003). To conduct the parametric study, the determination of the range of input variables is very important. Therefore, the geometric parameters are selected and varied within the comprehensive practical ranges of extended end-plate connections.

Based on common practical details, Table 5 andFigure 8 show the selected parameters for Finite Element Analysis. Figure 8 shows the variable parameters of the connection. Only one parameter was changed at one group so as to clarify its effect. They are considered to be the most influential factors for the considered connections. A total of 288 models are analyzed to study the behavior of the connection. However, due to limited space, some of the results are presented here.

Table 5
Different parameters selected for Finite Element Analysis.

Figure 8
Variable parameters of the connection.

5 ANALYSES OF RESULTS

5.1 Effect of Bolt Diameter

Figure 9 shows the effect of different bolt diameters on the initial stiffness, the ultimate moment, and the rotation capacity for the shown connection type with three values of end-plate thickness, 16, 20, and 25 mm. It can be noticed that increasing of both bolt diameter and thickness of end plate increases the initial stiffness, the ultimate moment, and the rotation.

Figure 9
Effect of bolt diameter on initial stiffness, ultimate moment, and rotation capacity.

The lowest initial stiffness, ultimate moment, and rotation capacity are found in the case when bolt diameter of 20 mm is used. In this case, the failure is due to bolt fracture, due to yielding of the bolt, which causes the brittle failure of the connections and causes loss of resistance in bending.

Precisely, for end-plate having moderate thickness of 20 mm, increasing the bolt diameter from 20 to 24 mm increases the initial stiffness, the ultimate moment, and the rotation capacity by about 8.7%, 14% and 63%, respectively. But increasing bolt diameter from 24 to 27 mm increases the initial stiffness, the ultimate moment and the rotation capacity by about 5.4%, 3.5% and 3.5%, respectively.

5.2 Effect of End-Plate Thickness

Figure 10 shows the effect of different end-plate thickness on the initial stiffness, the ultimate moment, and the rotation capacity for the shown connection type. Three values of end-plate thickness are considered, 16, 20, and 25 mm. The results are sown for bolt diameter equal to, 20, 24, and 27 mm.

Figure 10
Effect of end-plate thickness on initial stiffness, ultimate moment, and rotation capacity.

Generally, it can be observed that the initial stiffness significantly increases with the increase of end-plate thickness, while it slightly increases with the increase of bolt diameter. In addition, It can be observed that the bolt diameter and end-plate thickness have significant influence on the ultimate moment and rotation capacity. This could be due to that the increase of the end-plate thickness allows more tensile force in the bolts which increases the moment capacity, but the increase is not very significant and will cause brittle failure of the bolts with low rotation capacity of the connection. It is suggested that for the end-plate, it is necessary to limit the thickness of the end-plate in order to avoid brittle failure of the bolts and to obtain ductile connections by allowing the yielding to be occurred in end-plate. However, the end-plate should also have a proper thickness to avoid the brittle failure of the end-plate itself.

5.3 Effect of Column Tension Stiffener

To study the effect of column tension stiffener on behavior of the connection, four models with different values of column tension stiffener height, "without column stiffener, h_stiff = 1 / 2(h_t - 2t_f) h_stiff = 3 / 4(h_t - 2t_f) and h_stiff = (h_t - 2t_f) ", are analyzed. The connection without column tension stiffness represents the flush type of end-plate connection. The moment- rotation curves are plotted in Figure 11. It can be observed that using column stiffener increases the ultimate moment and rotation capacity by small values within the limits of 3%. Also it can be noticed that stiffening the column web slightly increases initial stiffness of the connection. Since the column without stiffener, its flange bends easily about the intersection of column web and flange.

Figure 11
Variation of M- curve for different length of column stiffener.

Presence of panel zone tension stiffeners minimizes the deformation in the panel zone of the connection, although it has no significant effect on ultimate moment and rotation capacity. For end-plate connections, their rotation consists of shearing deformation of the panel zone, and gab rotation of end-plate. This result also indicates that panel zone deformation is more important source of end-plate connection rotation for unstiffened panel zone than that for stiffened one. Only the shearing deformation of this panel zone can cause the end-plate connection to be a semi-rigid one.

5.4 Effect of Extended End-Plate and Angle of Rib Stiffener

The influence of the extended end-plate with rib stiffener on the behavior of the considered connection is studied in this section. Four models are analyzed. One model has no rib stiffener to represent the flush type of end-plate connection. Each of other three models has extended end-plate strengthened by rib stiffener. Three values of rib stiffener angle, 30^o, 45^o and 60^o, are considered. The Moment-rotation curves are plotted inFigure 12 for the case of bolt diameter equal to 20 mm and end-plate thickness of 16 mm. Compared with flush type of end-plate, the initial stiffness, ultimate moment and rotation capacity of extended end-plate connection are seen to be significantly higher and this indicates that the extended end-plate and its rib stiffener make a remarkable contribution to improve the behavior of end-plate connection. Using extended end-plate, instead of flush one, may increase the ultimate moment by 60^~ 90 %. Precisely, increasing the rib stiffener angle from 30^o to 45^o and from 45^o to 60^ocauses an increase of the ultimate moment by about 16% and 4 %, respectively.

Figure 12
Variation of M-ϕ curves for different connection type.

Deformed shapes with equivalent plastic strain contours are shown in Figure 13 for extended end-plate connections with different angle of rib stiffener. It can be noticed that the rotation of flush type of end-plate connection is mainly contributed by the relative deformation between the end-plate and the column flange. On the contrary for the extended end-plate connections, its rotation comes from the shearing deformation of the panel zone as illustrated in Figure 13. Also it can be observed that the gap between the end-plate and the column flange is affected by the rib stiffener angle. Further, increasing the rib stiffener angle decreases the gab deformation. This can be attributed to that increasing of the dimension of rib stiffener increases the stiffness of the extension of end-plate which may postpone reaching the yield and ultimate moments.

Figure 13
Failure Modes for connections with different angles of end-plate rib stiffener.

The rib stiffener has remarkable influence on the behavior of the extended end-plate connection and the above results indicates that the stiffened connections have higher ultimate moment because the stiffeners can change the mechanism of load transition and ameliorate the restrained condition. In addition, the brittle failure of connection can be avoided when the rib stiffener has large angle γ_stiff.

Figure 14 shows the effect of end-plate rib stiffener angle on initial stiffness, ultimate moment, and rotation capacity of the connection, shown in the figure, with different values of bolt diameter. The results are shown for the cases of end plate thickness equal to 16 mm. Generally, it can be observed that the ultimate moment increases with the increase of rib stiffener angle for all values of bolt diameter. Further, the rotation capacity increases with the increase of rib stiffener angle in case of bolt diameter equal to 20 mm, but it decreases in cases of bolt diameter greater or equal to 24 mm. Precisely, the use of extended end-plate with rib stiffener may increase the ultimate moment by 60 ^~ 90% and initial stiffness by about 115^~140% more than those of flush type connection. Further, increasing the rib stiffener angle from 30^o to 60^oincreases the initial stiffness and the ultimate moment by about 9^~12 % and 8^~19%, respectively.

Figure 14
Effect of end-plate stiffener angle on initial stiffness, ultimate moment, and rotation capacity.

6 CONCLUSIONS

This study presents three-dimension finite element model, for the analysis of end-plate steel connections subjected to monotonic loading with different types and details, and to study the effect of various parameter on connection behavior. For the cases considered in the present study, the following findings are summarized:

1. The proposed Finite Element model allows considering the actual inelastic nonlinear behavior of end-plate steel connection. The pretension force in the bolt and the contact between the end-plate and the column is simulated well. The eigenvalue analysis is first carried out to obtain the first buckling mode which is used after proper scale as an initial imperfection in the nonlinear analysis.

2. The comparisons between the experimental results and those obtained by the present Finite Element Model indicate that the present numerical model is able to simulate and predict, with relatively good accuracy, the behavior of bolted end-plate. The comparisons include the moment-rotation curve and the mode of failure.

3. For the flush type connection with column tension stiffener and having moderate end-plate thickness, increasing the bolt diameter from 20 to 24 mm increases the ultimate moment and rotation capacity by about 14% and 63%, respectively. While, increasing bolt diameter from 24 to 27 mm increases the ultimate moment and rotation capacity by about 3.5% and 3.5%, respectively.

4. For the extended end-plate with rib stiffener, the initial stiffness significantly increases with the increase of end-plate thickness, while it slightly increases with the increase of bolt diameter. In addition, It can be observed that the bolt diameter and end-plate thickness have significant influence on the ultimate moment and rotation capacity.

5. Presence of column tension stiffeners slightly increases the ultimate moment but decreases the rotation capacity.

6. The use of extended end-plate with rib stiffener may increase the ultimate moment by 60 ^~ 90% and initial stiffness by about 140% more than those of flush type connection.

7. Increasing the rib stiffener angle from 30^o to 60^oincreases the initial stiffness and the ultimate moment by about 9^~12 % and 8^~19%, respectively.

References

• Hibbitt, Karlsson and Sorensen, Inc., (2014). ABAQUS Standard User's Manual. Version 6.14., Rhode Island, USA.
• Ana M. Girao Coelhoa, Frans S.K. Bijlaard, (2007). Experimental behavior of high strength steel end-plate connections, Journal of Constructional Steel Research, 63(9), 1228-1240.
• Bursi, O. S. and Jaspart, J. P., (1998). Basic issues in the finite element simulation of extended end plate connections, Computers & Structures, 69, 361-382.
• Coelho, A. M. G., and Bijlaard, F. S. K. and da Silva, L. S., (2004). Experimental assessment of the ductility of extended end plate connections, Engineering Structures, 26(01), 1185-1206.
• Dabaon, M. A., El-Boghdadi, M. H., El-Kasaby, E. A. And Gerges, N. N., (2002). Early prediction of initial stiffness of composite joints, Regional Conference on Civil Engineering Technology & International Symposium on Enviromental Hydrology. Cairo: Amrecan Society of Civil Engineers.
• Dabaon, M. A., El boghdadi, M. and Kharoob, O., (2007). Finite element modeling of extended end-plate connection subjected to static and cyclic loading, Twelfth International Colloquium Structural and Geotechnical Engineering, Ain Shams University, Cairo, Egypt, 42(2).
• Dabaon, M. A., El-Boghdady, M. H. and Kharoob, O. F., (2007). Semi-rigid joints in bare steel and composite frames subjected to loading in space part II: Finite element modeling, Twelfth International colloquium on structural and geotechnical engineering, Cairo, Egypt, December 10-12, STL010.
• Dabaon, M.A., (2010).Fundamental of steel design course and design tables, Tanta, Egypt: Tanta University, Second edition.
• Dessouki, A.K., Youssef, A.H. and Ibrahim, M.M., (2013). Behavior of I-beam bolted extended end-plate moment connections, Ain Shams Engineering Journal, 4 (4), 685-699, doi: 10.1016/j.asej.2013.03.004
  » https://doi.org/10.1016/j.asej.2013.03.004
• Díaz Concepción, Victoria Mariano, Martí, Pascual, Querin, Osvaldo M., (2011). FE model of beam-to-column extended end-plate joints, Journal of Constructional Steel Research, 67, 1578-1590.
• ENV 1993-1-8 Euro Code 3, (2003). Design of steel structure, Design of joints, CEN European Committee for Standardization.
• Faella C., Piluso V., and Rizzzano G., (1997). A new method to design extended end plate connections and semi rigid braced frames, Journal of Constructional Steel Research, 41, 61-91.
• Gattesco, N., (1999). Analytical modeling of nonlinear behavior of composite beams with deformable connection, Journal of Constructional Steel Research, 52, 195-218.
• Ju, S.-H., Fan, C.-Y. and Wu, G.H., (2004).Three-dimensional finite elements of steel bolted connections, Engineering Structures, Vol. 26, 403-413.
• Kim, T., Whittaker, A. S., Gilani, A. S. J., Bertero, V. V. and Takhirov, S. M., (2002). Experimental evaluation of plate-reinforced steel moment-resisting connections, Journal of Structural Engineering-ASCE, 128(4), 483 - 491.
• Kukreti A. R. and Zhou, F.-F., (2006). Eight-bolt endplate connection and its influence on frame behavior, Engineering Structures, 28(11), 1483-1493.
• Lemonis, M. E. and Gantes, C. J., (2009). Mechanical modeling of the nonlinear response of beam-to-column joints, Journal of Constructional Steel Research, 65(4), 879-890.
• Maggi, Y.I., Goncalves, R.M., Leon, R.T., and Ribeiro, L.F.L., (2005). Parametric analysis of steel bolted end plate connections using finite element modeling, Journal of Constructional Steel Research, 61(5), 689-708.
• Mashaly, E., El-Heweity, M., Abou-Elfath, H. and Osman, M., (2011). Behavior of four-bolt extended end-plate connection subjected to lateral loading, Alexandria Engineering Journal, Vol. 50, 79-90.
• Mohamadi-shoore, M.R. and Mofid, M., (2008). Parametric analyses on the initial stiffness of flush end-plate splice connections using FEM", Journal of Constructional Steel Research, 64, 1129-1141.
• Mohamadi-Shoore, M.R. and Mofid, M. (2011). New modeling for moment-rotation behavior of bolted endplate connections", Scientia Iranica, 18(4), 827-834.
• Mohamadi-shoore, M.R. and Mofid, M., (2013). Prediction of the yielding moment of flush endplate splice connections using finite element modeling", Scientia Iranica, 20 (2), 270-277.
• Shaker, F.M.F. and Abd Elrahman, W.M., (2014). Analytical Behavior of Steel Pre-tensioned Bolted Connections with Flushed and Extended End Plates under Bending, World Applied Sciences Journal, 30 (6): 673-684.
• Shi Y. J, Chan S.L. and Wong Y. L., (1996). Modeling for moment-rotation characteristics for end-plate connections, Journal of Structural Engineering-ASCE, 122(11), 1300-1306.
• Shi Y., Shi, G. and Wang, Y., (2007). Experimental and theoretical analysis of the moment-rotation behavior of stiffened extended end-plate connections, Journal of Constructional Steel Research., 63(9), 1279-1293.
• Shi, G., Shi, Y., Wang, Y. and Bijlaard. F.S.K., (2010). Monotonic loading tests on semi-rigid end-plate connections with welded I-shaped columns and beams, Advances in Structural Engineering, 13(2), 215-230.
• Tsai, K. C., Wu, S. and Popov, E. P., (1995). Cyclic performance of steel beam column moment joints, Engineering Structures, 17(8), 596-602.
• Swansonl, J. A. and Leon, R. T., (2000). Bolted steel connections: tests on t-stub components", Journal of Structural Engineering, 126, 50-56.
• Swanson, J. A., Kokan, D. S. and Leao, R. T., (2002). Advanced finite element modeling of bolted T-stub connection components, Journal of Constructional Steel Research, 58(5-8), 1015-1031.
• Yun G. J., Ghaboussi, J. and Elnashai, A. S., (2007). Development of neural network based hysteretic models for steel beam-column connections through self-learning simulation, Journal of Earthquake Engineering, 11, 453-467.

Publication Dates

• Publication in this collection
  Jan 2016

History

• Received
  11 Sept 2014
• Accepted
  09 Nov 2015