Abstract
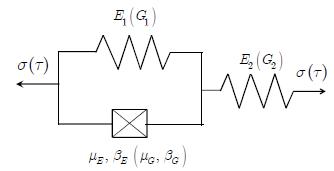
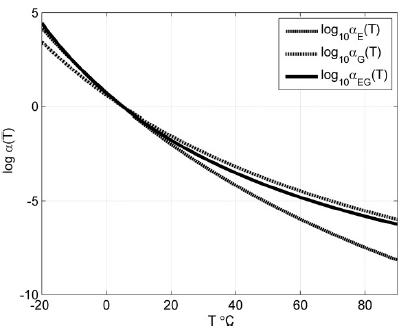
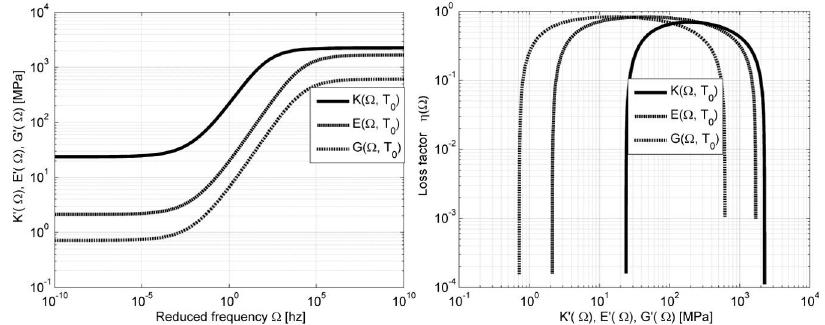
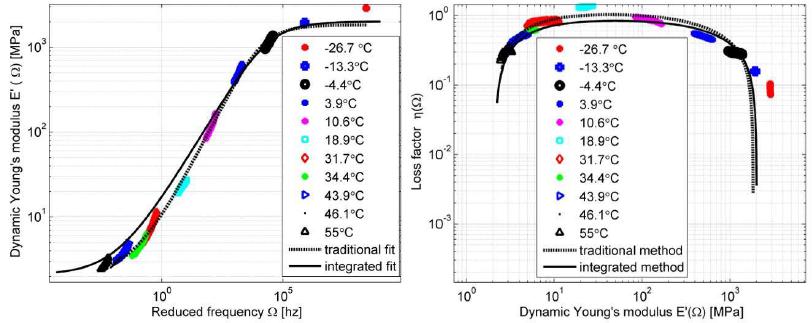
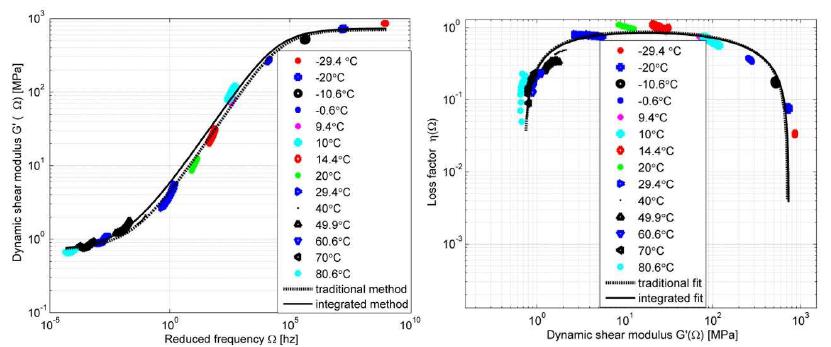
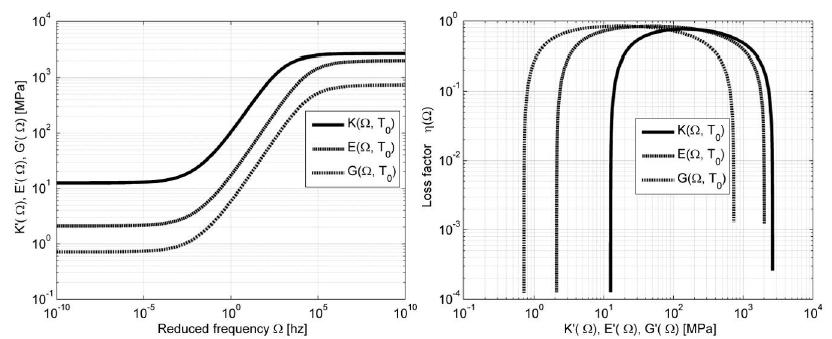
The use of viscoelastic materials (VEMs) has becoming more and more frequent both as vibration control in general or as parts of structural components. In all applications, the mechanical behavior of such materials can be predicted by the complex moduli (Young’s, shear or volumetric) and the complex Poisson’s ratio. Over recent decades, various methodologies have been presented aiming at characterizing complex moduli. On the other hand, the indirect identification of the Poisson’s ratio, in the frequency domain, proves to be underexplored. The present paper discusses two computational methodologies in order to obtain, indirectly, the complex Poisson’s ratio in linear and thermorheologically simple solid VEMs. The first of them uses a traditional methodology, which individually identifies the complex Young’s and the shear moduli and, from them, one obtains the complex Poisson’s ratio. The second methodology - proposed in the present paper and called ‘integrated’ - obtains the complex Poisson’s ratio through a simultaneous identification of those two complex moduli. Both methodologies start from a set of experimental points of the complex moduli in the frequency domain, carried out at different temperatures. From those points, a hybrid optimization technique is applied (Genetic Algorithms and Non-Linear Programming) in order to obtain the parameters of the constitutive models for the VEM under analysis. For the experiments described here, the integrated methodology proves to be very promising and with a great application potential.
Keywords
Viscoelastic behavior; Complex Poisson's ratio; Complex Young's modulus; Complex shear modulus; Hybrid optimization