Abstract
Currently, there are a lot of research activities dealing with gamma titanium aluminide (γ-TiAl) alloys as new materials for low pressure turbine (LPT) blades. Even though the scatter in mechanical properties of such intermetallic alloys is more distinctive as in conventional metallic alloys, stochastic investigations on γ -TiAl alloys are very rare. For this reason, we analyzed the scatter in static and dynamic mechanical properties of the cast alloy Ti-48Al-2Cr-2Nb. It was found that this alloy shows a size effect in strength which is less pronounced than the size effect of brittle materials. A weakest-link approach is enhanced for describing a scalable size effect under multiaxial stress states and implemented in a post processing tool for reliability analysis of real components. The presented approach is a first applicable reliability model for semi-brittle materials. The developed reliability tool was integrated into a multidisciplinary optimization of the geometry of a LPT blade. Some processes of the optimization were distributed in a wide area network, so that specialized tools for each discipline could be employed. The optimization results show that it is possible to increase the aerodynamic efficiency and the structural mechanics reliability at the same time, while ensuring the blade can be manufactured in an investment casting process.
Keywords:
Size effect; weakest link; investment casting
1 INTRODUCTION
The introduction of gamma titanium aluminide (γ-TiAl) alloys, as a material for low pressure turbine (LPT) blades, is one of the most promising attempts for saving weight and consequently fuel of aero engines like shown in (Appel, 2011Appel, F., Paul, J.D.H., Oehring, M. (2011). Gamma Titanium Aluminide Alloys, Wiley-VCH.). For this reason, there are a lot of activities in industrial and scientific research dealing with different γ-TiAl alloys and since some years first blades made of γ-TiAl alloys are used in real airplanes, see also the press releases of (MTU, 2015MTU (2015). Titanium aluminide - MTU Aero Engines develops new turbine blade material, www.pressebox.com.
www.pressebox.com...
), (Snecma, 2015Snecma (2015). A technological LEAP forward, www.snecma.com
www.snecma.com...
) and (GE, 2015GE Aviation (2015). The GEnx Commercial Aircraft Engine, www.geaviation.com
www.geaviation.com...
).
Due to the high specific modulus and strength, the weight of a LPT blade made of a γ-TiAl alloy would be approximately half of a conventional blade made of a nickel based alloy. This weight reduction also leads to much smaller centrifugal forces acting on the blades and consequently on the disc, which holds the blades. An additional re-design to decrease the weight of disc and other fixation components should be possible. Thus, not only the lightweight γ-TiAl blades, but also the effects on other engine parts could reduce the total engine weight and accordingly save a significant amount of fuel.
Most of current investigations are related to material characterization in a temperature range of 500°C - 900°C (Recina and Karlsson, 2000Recina, V. and Karlsson, B. (2000). High Temperature Low Cycle Fatigue Properties of Ti-48Al-2Cr-2Nb Gamma Titanium Aluminides Cast in Different Dimensions, Scripta Materialia 43: 609-615. / Henaff and Gloanec, 2005Henaff, G. and Gloanec, A.L. (2005). Fatigue properties of TiAl alloys, Intermetallics 13: 543-558. / Appel et al., 2010Appel, A., Heckel, T.H., Christ, H.J. (2010). Electron microscope characterization of low cycle fatigue in a high-strength multiphase titanium aluminide alloy, International Journal of Fatigue 32: 792-798.), micromechanical modeling (Chakraborty and Earthman, 1998Chakraborty, A. and Earthman, J.C. (1998). Finite Element Analysis of Cavitating Facet Interaction in a Fully Lamellar Titanium Aluminide Alloy under Creep Conditions, Metallurgical and Materials Transactions 29A: 957-964. / Kabir et al., 2010Kabir, M.R., Chernova, L., Bartsch, M. (2010). Numerical investigation of room-temperature deformation behavior of a duplex type γTiAl alloy using a multi-scale modeling approach, Acta Materialia 58: 5834-5847.), or classical component design processes based on deterministic approaches. However, probabilistic aspects should be considered when developing γ-TiAl turbine blades due to the quasi-brittle behavior of these alloys at room temperature. Classical stochastic approaches like Monte Carlo are inefficient and cannot be used to directly address failure probabilities of technical components smaller than 10-4, when the component loading needs to be calculated by time-consuming numerical methods like the finite element method. There are well-known probabilistic methods, see for example (Munz and Fett, 1999Munz, D. and Fett, T. (1999). Ceramics: Mechanical Properties, Failure Behaviour, Materials Selection, Springer.) or (Nemeth et al., 2005Nemeth, N. N., Jadaan, O. M., Gyekenyesi, J. P. (2005). Lifetime Reliability Prediction of Ceramic Structures Under Transient Thermomechanical Loads, NASA/TP 2005-212505.), for calculating the failure probability of brittle components based on the weakest link theory developed by (Weibull, 1951). Still, these methods cannot be directly applied for quasi-brittle materials like γ-TiAl. Therefore, in this work we present a modified weakest link approach representing the experimental findings of a commercially available cast γ-TiAl alloy and show its applicability for calculating the component failure probability.
When substituting a low pressure turbine blade made of a nickel alloy with one made of a γ-TiAl alloy, the original geometry of the blade needs to be modified due to the different material properties and specific manufacturing restrictions. For this purpose, it is necessary to consider the aerodynamic efficiency and the structural mechanics reliability as well as manufacturing limitations and expenses. Usually, aspects of aerodynamic performance and deterministic structural mechanics are treated by the original equipment manufacturer (OEM), while the manufacturability is in the hand of the component supplier and stochastic aspects are neglected so far. Since manufacturing aspects are assessed only at the end of such a design process, complete aerodynamic re-designs are often necessary, resulting in a time-consuming iterative design process. Thus, a blade design generated in this sequential way would probably not lead to an optimal geometry. Accordingly, we present a fully automated and multidisciplinary simulation process chain. This process chain is used in a geometry optimization of a low pressure turbine blade to demonstrate the feasibility to increase its aerodynamic efficiency and the structural mechanics reliability. At the same time it is ensured that the resulting geometry can be manufactured by an investment casting process as well.
2 STATIC AND FATIGUE STRENGTH OF CAST Ti-48Al-2Cr-2Nb
In this investigation we characterized the static and fatigue material behavior of the gamma titanium aluminide alloy Ti-48Al-2Cr-2Nb, which is already used for turbine blades in aircraft engines. The specimens were prepared by creating round bars with an investment casting process resulting in a duplex microstructure. After applying a hot isostatic pressing (HIP) process, the bars were lathed to the final geometry. The specimens used for the fatigue experiments were additionally polished before testing.
Three different specimen geometries were developed. All specimens are round tensile bars with a parallel section in the middle. The enlargement sections of the specimens were defined by a b-spline formulation instead of a classical radius to minimize the stress concentration without enlarging the specimens too much. The optimal spline definition was identified by finite element simulations for each specimen size. The parameters of the developed geometries are listed in Table 1. Tensile tests were performed using a 100 kN Instron spindle testing machine with a load cell scaled to 30 kN, while the strain was measured by a Fiedler laser extensometer. Different tensile test procedures were used for characterizing the elastic and the elasto-plastic material behavior. The Young's modulus is determined from an un- and reloading segment after reaching a nominal stress slightly over the initial yield stress. 20 samples with a diameter of D = 4 mm were used for this investigation. For characterizing the elasto-plastic behavior the nominal stresses and strains were determined while loading until fracture in a displacement controlled experiment. For each of the three geometries, 20 samples were used in this test series.
Geometry parameters of the specimens for tensile tests and fatigue experiments; sketch with colored stress levels and photograph of a specimen with a diameter in parallel section of D = 4mm.
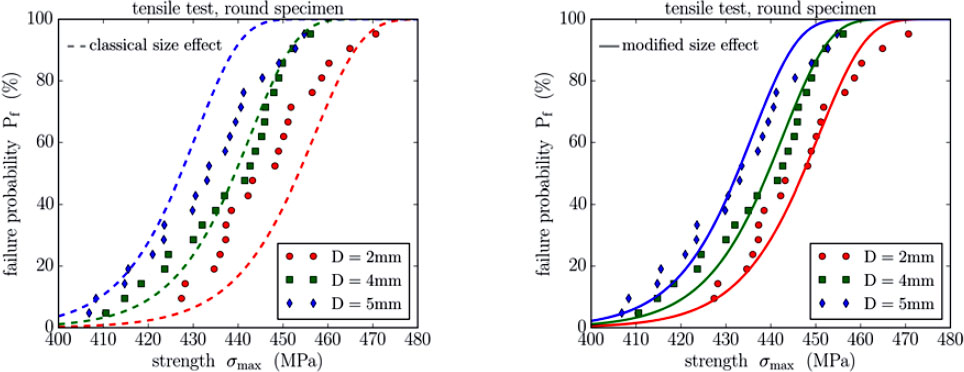
The experimentally determined Young's modulus is normal distributed with a mean value of 174 GPa and a standard deviation of 14 GPa. After an initial yield stress of 357 ± 16 MPa (mean value ± standard deviation) some amount of hardening occurs until the strength of 437 ± 13 MPa is reached. The maximum plastic strain is determined to be 0.94 ± 0.18 %. The fracture positions are uniformly distributed and not localized in the transition section between the parallel section and the fixation of the specimen. From this, it is concluded that the geometry optimization was successful. The probability plot of the tensile strength values in Figure 1 (left) shows a size effect indicating that the larger the loaded volume the smaller the measured strength value. Additionally, it is shown that the size effect is less pronounced than the classical size effect of brittle materials, which is implicitly included in Weibull's weakest link theory, as shown in (Munz and Fett, 1999Munz, D. and Fett, T. (1999). Ceramics: Mechanical Properties, Failure Behaviour, Materials Selection, Springer.). Here, the failure probability Pf is expressed by the applied stress σ, the material's characteristic strength σ0, the Weibull modulus m, the loaded volume V and the reference volume V0 as shown in the following equation:
Probability plot of the measured strength values for three different specimen sizes (D: 2 mm, 4 mm, 6 mm) in comparison with the classical size effect of brittle materials calculated from the mean sample size (left) and in comparison with the modified size effect following the Curtin model (right).
In Figure 1 (left) the expected strength distribution for the samples with D = 2 mm and D = 6 mm are calculated from the results of the samples with D = 4 mm assuming a classical size effect with the loaded volume being equal to the nominal volume of the sample. The fact that Ti-48Al-2Cr-2Nb shows a reduced size effect is not surprising, since this intermetallic compound behaves nearly brittle with a small amount of plastic deformation. A similar effect of a less pronounced size effect has already been shown by (Padgett et al., 1995Padgett, W.J., Durham, S.D., Mason, A.M. (1995). Weibull Analysis of the Strength of Carbon Fibers Using Linear and Power Law Models for the Length Effect, Journal of Composite Materials 29, 14: 1873-1884.) for carbon fibers and by (Curtin, 1999Curtin, W. A. (2000). Tensile Strength of Fiber-Reinforced Composites: III. Beyond the Traditional Weibull Model for Fiber Strengths, Journal of Composite Materials 34, 15: 1301-1332.) for fiber reinforced composites. Both groups introduced a scaling parameter on the size ratio, which is a length ratio for these fiber materials. Transferred to the case of volume related failure, as we expect for an intermetallic alloy, equation (1) is extended by a scaling parameter α, which has a range from zero to one:
Using this approach, it is possible to rebuild the experimental findings of a moderate size effect in strength, see Figure 1 (right). The determined parameters for this case are σ 0 = 443 MPa, m = 44, V0 = 125 mm3, α = 0.56. All values are listed in Table 2.
Identified model parameters from different experiments for a defined reference volume V0. Values in round brackets (...) are taken from the experiments listed the lines above.
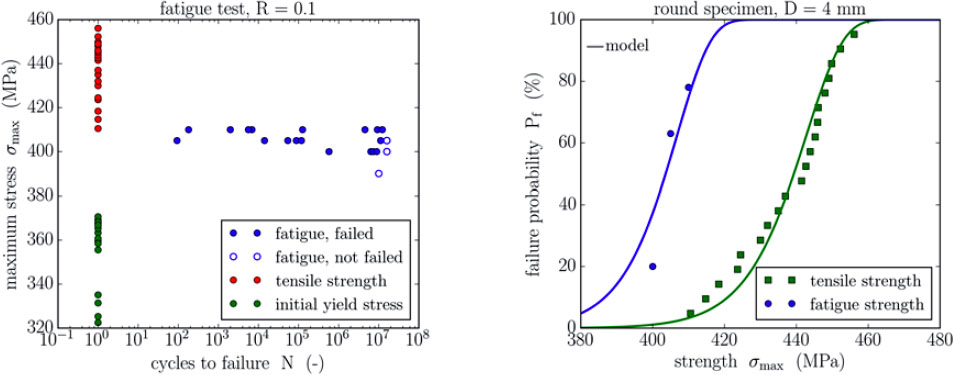
Additional load controlled fatigue tests with a stress ratio of R = σmin / σmax = 0.1 were performed using specimens with a diameter of D = 4 mm in a servo hydraulic testing machine at frequencies of 10 Hz and 30 Hz. In Figure 2 (left) the cycles to failure are plotted against the maximum applied stress for the fatigue experiments. The tensile strength data as well as the initial yield stress data are additionally represented for comparison. The fatigue data shows that the fatigue regime for this cast γ-TiAl alloy is very narrow and directly below the tensile strength regime. This leads to a great scatter in the fatigue behavior. When creating a probability plot of the fatigue strength data for a defined number of cycles to failure, it is possible to adopt the former described probabilistic strength model to rebuild this fatigue behavior. In Figure 2 (right) the estimated fatigue probability data for 6 million cycles to failure is in a good agreement with the scaled probabilistic strength model with σ0 = 407 MPa, when the other parameters are not changed.
Comparison of the fatigue data, the tensile strength data and the initial yield stress data (left); estimated probability plot of fatigue strength for 6 million cycles with R = 0.1 in comparison to the tensile strength.
3 A MODIFIED FAILURE CRITERION AND ITS IMPLEMENTATION IN A RELIABILITY TOOL
The former described model is able to rebuild the experimental findings of an assumed uniaxial experiment with a constant stress level in the tested volume. For applying it in a reliability assessment of a real technical component, it is necessary to enhance the model to deal with multiaxial stress states and non-uniform stresses. Furthermore, the model needs to be independent of the discretization, when the stress level is in a converged state. For this purpose, a post processing tool called HYPRA was developed. This reliability tool acts in principle like other tools such as CaresLife from NASA (Nemeth et al., 2005Nemeth, N. N., Jadaan, O. M., Gyekenyesi, J. P. (2005). Lifetime Reliability Prediction of Ceramic Structures Under Transient Thermomechanical Loads, NASA/TP 2005-212505.) or STAU from KIT (Roudi et al., 2005Roudi, S., Riesch-Oppermann, H., Kraft, O. (2005). Advanced probabilistic tools for the uncertainty assessment in failure and lifetime prediction of ceramic components, Mat.-wiss. u. Werkstofftech. 36: 171-176.).
Before performing the reliability assessment, stresses and strains within the component under load have to be calculated using the finite element method (FEM). The FEM results are then imported into the reliability tool, so that for each element of the FE model the local failure probability can be calculated. From the local failure probabilities the overall failure probability of the whole component is calculated and the local results are exported in a vtk-file format for visualization. In the developed code the element probability can be directly calculated based on the element stress results or calculated by integrating over the volume within each element based on the nodal results. When the stresses vary only gradually within an element, the results obtained from element solution and element integration are nearly the same. But for the case of significant differences between the element and nodal results, the more time-consuming approach of the element integration should be preferred.
To address a multiaxial stress state, two classical failure criteria for brittle materials were implemented: the 'principle of independent action' (PIA) model and the 'normal stress averaging' (NSA) method. Both models and their implementation are briefly described in the following section. For more details of the original models, the reader is referred to the paper of (Nemeth et al., 2005Nemeth, N. N., Jadaan, O. M., Gyekenyesi, J. P. (2005). Lifetime Reliability Prediction of Ceramic Structures Under Transient Thermomechanical Loads, NASA/TP 2005-212505.). The failure probability Pf,comp of a component under mechanical load can be calculated following Weibull's weakest link theory by solving the volume integral of the local stress function g(σ):
The PIA model assumes that the principle stresses (σ1, σ2, σ3) are independently contributing to the overall failure probability:
The angle brackets (<...>) denote a function which assigns a zero value to negative argument values. This effectively leads to taking only tensile stresses into account. Instead of independently considering the principle stresses, the NSA model uses an effective tensile stress acting normal to an arbitrarily orientated flaw. The stress function is then defined as:
With
Following equation (3), the failure probability of the component can be estimated by multiplying the element probabilities of survival ps,elem(i):
In case of using the element results, ps,elem can be directly calculated from the element stress tensor σelem and the element volume Velem:
A more accurate way of calculating the volume integral within the element ps,elem is using Gaussian quadrature rules. For hexahedron elements a degree of 4 with 64 integration points is used to approximate ps,elem:
Here, J is the Jacobian matrix of the node coordinates. For tetrahedron elements, the element probability of survival is calculated by multiplying the probabilities of survival at the integration points ps,int:
With
Here, an integration degree of 5 with 15 integration points or a degree of 7 with 84 integration is used (Williams et al., 2014Williams, D.M., Shunn, L., Jameson, A. (2014). Symmetric quadrature rules for simplexes based on sphere close packed lattice arrangements, Journal of Computational and Applied Mathematics 266: 18-38.). The stresses at the integration points σint are calculated from the nodal results by using the element shape functions, while the volumes associated to the integration points are calculated from the element volumes considering the weights of the integration points.
After verifying the implemented models, they were modified to describe a scalable size effect. As described before, the scaling factor α is introduced in the uniaxial model as an exponent on the volume fraction of the loaded volume and the reference volume, which only works for constant stresses. If there are different stress levels present in the investigated volume, this needs to be considered. The most promising way to realize this is to consider an effective volume Veff. By introducing α as the exponent of the fraction of Veff / V0 and normalizing it by a factor of 1 / Veff, it is ensured that the model rebuilds the classical size effect for α = 1:
Furthermore, for α = 0 the volume effect totally vanishes when the effective volume is calculated by a volume integral of the stress ratio, as it is usually defined for classical brittle materials (Munz and Fett, 1999Munz, D. and Fett, T. (1999). Ceramics: Mechanical Properties, Failure Behaviour, Materials Selection, Springer.):
In this case, the failure probability only depends on the maximum stress in the structure:
Consequently, the scalable size effect is implemented in the PIA model as presented in the following equation:
with
The modified stress function of the NSA model is realized as:
with
Due to the incorporation of the component measure Veff in the stress function g(σ), the local values of  corresponds to:
corresponds to: should not be treated as physical interpretations of the local probability of survival anymore, because they are now scaled values considering the modified size effect. However, the part in the equation considering the scalable size effect can be brought before the volume integral without changing the component probability of failure as can be seen from the following equations. For an easier understanding, a general formulation of the failure probability considering one effective volume is used and the stress function is modified by dividing it in a stress and a volume part:
should not be treated as physical interpretations of the local probability of survival anymore, because they are now scaled values considering the modified size effect. However, the part in the equation considering the scalable size effect can be brought before the volume integral without changing the component probability of failure as can be seen from the following equations. For an easier understanding, a general formulation of the failure probability considering one effective volume is used and the stress function is modified by dividing it in a stress and a volume part:  . Thus, the total scaled failure probability
. Thus, the total scaled failure probability
By rearranging this equation, it can be shown that the scaling factor indirectly acts as an exponent on the component probability of survival:
Even though it is possible to consider the scalable size effect only on component level, all following illustrations of the local failure probabilities are based on the local scaled values. This is expected to be the more realistic representation of the local material behavior.
4 IDENTIFICATION OF THE MODEL PARAMETERS
Since the developed method considers real stress distributions and multiaxial stresses, the tensile test results were re-evaluated with the developed reliability assessment tool to determine the correct material parameters. For this purpose, a parameter identification routine was set up with the software OptiSLang(r) (Dynardo, 2014Dynardo GmbH (2014). Methods for multi-disciplinary optimization and robustness analysis, documentation of OptiSLang 4.2. Weimar.) as described in the following. First, a parameterized three dimensional finite element model of the tensile tests was created using the FEM software ANSYS(r). The geometry of the tensile samples was rebuilt in a 1/8 model considering symmetry effects. The acting force was applied on a node of the fixation area, while the displacements of the other nodes of this area were coupled in loading direction. The model was used to simulate the tensile behavior of the three different geometries. Here, a maximum force higher than the maximum experimentally measured force was applied in a ramped manner by multiple load steps. The stress results of each load step were exported after the simulation. During the parameter identification process the failure probability is calculated for each load step and geometry. After analyzing all load steps, a calculated probability plot is created. As objective function, which has to be minimized, the total absolute failure sum between experimental and simulated stresses for equidistant probability levels between 0.1 and 0.9 of all three geometries is calculated. The adaptive response surface (ARS) method of the software OptiSLang(r) is used for the identification process (Dynardo, 2014Dynardo GmbH (2014). Methods for multi-disciplinary optimization and robustness analysis, documentation of OptiSLang 4.2. Weimar.).
The parameter identification converges relatively fast (best design achieved after 100 calculations) and results in a very good agreement between experiment and simulation, as can be seen from Figure 3. There is nearly no difference between the modified PIA and modified NSA model. The identified characteristic strength of σ0 = 453 MPa is slightly higher compared to the nominal evaluation, while the scatter is more pronounced (lower m) and the size effect less pronounced (lower α). All values are listed in Table 2. For comparison the results of a parameter identification using the classical PIA criterion are additionally plotted in Figure 3. As expected, the classical approach cannot represent the experimental findings in contrast to the new method that enables a scaled size effect.
Comparison of the experimental and calculated probability plot for the identified parameter set using the modified PIA criterion (left) and the classical PIA criterion (right).
The results of the fatigue experiments are also re-evaluated using the numerical model. Here, the characteristic fatigue strength for six million cycles is estimated to be σ0 = 413 MPa, when fixing the scatter parameter m and size effect parameter α.
5 CHARACTERIZING THE MANUFACTURING INFLUENCES ON THE STRENGTH OF CAST TIAl
It is now possible to calculate the failure probability of a component under load with the described model and identified material parameters. This approach should work as long as the defect distribution inside the component is similar to that of the tested tensile samples. To investigate a possible manufacturing influence, which could result in different failure distribution, samples with typical aspects of low pressure turbine blades were designed. These samples were flat geometries with high aspect ratios defined by a thickness of 2.3 mm, a typical length of 195 mm and a width of 36 mm. The samples were tested as cast, meaning that no additional sample machining was done. Therefore, the samples were not of ideal shape: In fact, they had some amount of bow and slightly different thicknesses. Additional notches with a radius of r = 6 mm and r = 10 mm were milled in some samples to investigate if the model is also valid for different stress states. The geometry of all samples was characterized by measuring bow, thickness, width and difference in notch position to ensure a correct evaluation of the experimental results after testing. Special clampings were designed to reduce possible bending moments during the experiment.
At first, the sensitivity of the parameter deviations on the expected results was investigated by a Monte Carlo simulation of the tensile experiments considering the measured geometry parameter distributions and their correlations. In this pre-investigation it was found that the geometry deviations would lead to great scatter in a force related probability plot, whereas the scatter in a probability plot related to the nominal stress (F/Amin) is small and can be neglected. From this it was decided to evaluate the experimental results based on the nominal stresses using the finite element results based on the mean geometry. The geometry of the samples was rebuilt in a 1/4 model also considering the bow of the samples. The acting force was applied on a node of the fixation area, while the displacements of the other nodes of this area were coupled in loading direction.
In total 43 flat samples (24 with r = 10 mm, 10 with r = 6 mm, 9 without a notch) were successfully tested under tensile load. In Figure 4 (left) can be seen, that the newly developed method could represent the experimental findings very well, when applying the same parameter identification process as described for the tensile experiments. Again, there is nearly no difference between the modified PIA and modified NSA model. Whereas a classical von-Mises criterion, assuming a normal distribution in strength, is not able to describe the relative differences between the different specimen geometries in a correct way, see Figure 4 (right). From this it is concluded that the method considering a scalable size effect can be used to describe the stochastic strength behavior of this cast intermetallic titanium aluminide alloy.
Comparison of the experimental and calculated probability plot for the cast flat specimen; using the modified NSA model (left) and a von Mises criterion assuming a normal distribution in strength (right).
Additionally, 12 flat samples with a notch radius of r = 10 mm were characterized in a fatigue experiment with a stress ratio of R = 0.1 at three different stress levels. Based on the estimated probability data for one million cycles, the fatigue strength is determined to be 331.5 MPa, when assuming m and α being constant. Consequently, the experimental findings that cast titanium aluminide alloy Ti-48Al-2Cr-2Nb has got a very high fatigue limit compared to the static strength as described in the former sections is confirmed by these results.
6 APPLICATION OF THE RELIABILITY MODEL IN A MULTIDISCIPLINARY OPTIMIZATION OF A LOW PRESSURE TURBINE BLADE
The original objective for developing the described reliability model is the consideration of scatter in materials strength during a geometry optimization process of a low pressure turbine blade made of cast γ-TiAl concerning the aerodynamic performance, structural durability and castability. For this purpose, a fully automated multidisciplinary process chain was developed, see Figure 5.
The DLR software RCE (Remote Component Environment) connects the different specialized simulation tools for realizing this process chain (Seider et al., 2013Seider, D., Basermann, A., Mischke, R., Siggel, M., Tröltzsch, A., Zur, S. (2013). Ad hoc Collaborative Design with Focus on Iterative Multidisciplinary Process Chain Development applied to Thermal Management of Spacecraft, 4th CEAS Air & Space Conference. / Zur and Tröltzsch, 2015Zur, S. and Tröltzsch, A. (2014). Optimization of the DLR Space Liner inside the integration environment RCE, in Engineering Optimization, CRC Press: pp. 757-761.). RCE is an integration framework, in which numerical tools of multiple disciplines can be coupled and then be started on different computers, which can be distributed in a wide area network. For this process chain, the tools were located at three different DLR sites. First, the generated blade geometry is tested for castability based on experimental and numerical investigations done by Access (Tiefers et al., 2014Tiefers, R., Aguilar, J., Dresbach, C., Buske, C. Schmidt, T. Zur, S. (2014). Titanium Aluminide Turbine Toolbox, A new tool for optimizing the design process for γ-TiAl low pressure turbine blades, EICF - 28th International Congress, Lugano.). The blade generation and test for castability is performed on a workstation in Cologne. If the geometry can be cast, the aerodynamic simulation is performed using the DLR in-house CFD code for turbomachines TRACE (Yang, 2005Yang, H., Kersken, H.-P., Nuernberger, D. (2005). Toward Excellence in Turbomachinery Computational Fluid Dynamics: A Hybrid Structured-Unstructured Reynolds-Averaged Navier-Stokes Solver. Journal of Turbomachinery 128: 390 - 402.) on a HPC cluster located in Braunschweig. RCE is responsible for connecting to the cluster, data transfer, job submission and retrieval of the results when the job is finished. Subsequently, the aerodynamic results are used as an input for the structural mechanics simulation using the FEM software PERMAS on a workstation in Stuttgart. At the end the calculated stresses are used for the reliability assessment with HYPRA again on the workstation in Cologne. The castability, aerodynamic efficiency, maximum equivalent stress and failure probability are used for the multi criterion objective function in a multidisciplinary optimization. The overall optimization process is realized by the DLR software AutoOpti (Voß et al., 2006Voß, C., Aulich, M., Kaplan, B., Nicke, E. (2006). Automated multiobjective optimization in axial compressor blade design. ASME Turbo Expo, Barcelona, Spain GT2006-90420.), which continuously creates new geometry parameter sets that define the blade, called optimization members.
155 free geometric design parameters are varied in total for a new blade, including among others the shapes of 5 profiles at different blade span positions, the circumferential shift of these profiles and the circumferential position of the shrouding band. For each optimization member a RCE instance is started, inside which the process chain is executed. Up to 15 RCE instances are started and executed in parallel by AutoOpti. After successful execution, the objectives are returned to AutoOpti, which evaluates each member by assigning a combined Pareto rank to it. Furthermore, all relevant physical properties of the process are stored in a database. Based on this database, AutoOpti uses an evolutionary strategy and a Kriging surrogate model to create new members. A surrogate model (Voss et al., 2014Voß C., Aulich M., Raitor T. (2014). Metamodel assisted aeromechanical optimization of a transonic centrifugal compressor, ISROMAC.) aims to describe the objective functions mathematically. In order to find promising new members, an optimization on the surrogate model is performed. Those surrogate optimized members are then passed by AutoOpti through the complete process chain to obtain reliable physical results. Surrogate models greatly accelerate the optimization process in finding improved blade geometries. However, the generation of the surrogate models requires a lot of computational resources and is time-intensive when the optimization database becomes large.
Besides the objective functions, the members were constrained with respect to the mass flow difference to the initial design. Thus, the mass flow through the optimized turbine should not differ more than 1 % of the original mass flow. The initial blade design is derived from a high-bypass ratio turbofan jet engine with a five stage low pressure turbine. The second to last stage was chosen as object of investigation in this work to represent common inflow and outflow conditions. The 4th LPT stage has 84 vanes and 126 shrouded rotor blades, rotating at 5000 rpm. Castability is ensured when the trailing edge thickness of the generated blade is not thinner than 1.25 mm and the parallelism range of suction and pressure side profile legs in the trailing edge region does not exceed 8 mm (Tiefers et al, 2014Tiefers, R., Aguilar, J., Dresbach, C., Buske, C. Schmidt, T. Zur, S. (2014). Titanium Aluminide Turbine Toolbox, A new tool for optimizing the design process for γ-TiAl low pressure turbine blades, EICF - 28th International Congress, Lugano.).
For the steady aerodynamic simulations one passage of the stator and one passage of the rotor including the cavities were meshed and simulated, see Figure 6 (left). The structured mesh consists of about 2.7 million elements. Conservative mixing planes are used between the rotating and the stationary blocks. At the hub and casing end walls the boundary layer is modeled with wall functions, whereas at the blade surfaces the boundary layer is directly resolved by a fine mesh with y+ values below 1. The k-ω turbulence model of (Wilcox, 1994Wilcox, D. A. (1994). Simulation of Transition with a Two-Equation Turbulence Model. AIAA Journal 32: 247-255.) was used in conjunction with the γ-Reθ transition model by (Menter et al., 2006Menter, F. R., Langtry, R. B., Likki, S. R., Suzen, Y. B., Huang, P. G. and Volker, S. A. (2004). Correlation-Based Transition Model Using Local Variables: Part I - Model Formulation. ASME Conf. Proc.: pp. 57-67.). Convergence of the aerodynamic simulation is reached, when the mass flow between inlet and outlet of the stage does not differ more than 1 g/s, the standard deviation of the aerodynamic loss and specific work is below 10-5 and the residuals drop by three orders of magnitude. If no convergence is achieved, the member is still processed by the following tools in the process chain, but its Pareto rank is decreased by a penalty factor. The stage characteristics are calculated in a postprocessing step, of which the stage efficiency is used as an objective function for AutoOpti.
Mach number and stream traces on a S2-plane through the stage (left), mesh of the structural mechanics simulation of the initial member design (right).
The blade surface pressure is extracted from the aerodynamic solution and transferred to the subsequent structural mechanics simulation process using the FE software PERMAS. Here, the blade is represented by 70,762 brick elements, see Figure 6 (right). Additionally, part of the disc is modelled for maintaining an approximately realistic fixation of the blade, without considering this part in the reliability assessment. By applying the determined surface pressure and the rotational speed, the stresses and strains are calculated. Furthermore, a hot to cold transformation is realized, to calculate the exact corresponding cast geometry.
The resulting stresses calculated by the finite element model are transferred to the reliability tool HYPRA. By using the fatigue parameters determined from the notched flat specimen, the total failure probability is calculated as described before.
A total of 5,147 configurations were successfully analyzed during the optimization. Using the described procedure it was possible to significantly increase the aerodynamic efficiency and the reliability of a low pressure turbine blade at the same time. For example, the geometry of the chosen Pareto front member in Figure 7 has a good aerodynamic efficiency, which increased from initially 89.90 % to 90.57 %. In addition, it is reliable from a mechanical point of view considering the scatter in the material fatigue strength, which is expressed in the significant reduction of the failure probability from 0.95 to 10-10.
Comparison of aerodynamic profile and local failure probability of the initial member (left) and a member of the optimization Pareto front (middle); superimposed blade geometries of the initial (gray) and the optimized (blue) design (right).
7 SUMMARY AND DISCUSSION
In this work, it is shown by tensile experiments with different geometries that the investigated cast gamma titanium aluminide alloy Ti-48Al-2Cr-2Nb shows a size effect in strength, which is less pronounced than the classical size effect of brittle materials. This experimental finding is additionally confirmed by experiments based on notched samples with high aspect ratios. The reduced size effect of the uniaxial tensile tests could be successfully represented by a modified weakest link model. This model is further enhanced to consider a scalable size effect also for multiaxial and non-constant stress states and implemented in a new developed reliability assessment tool called HYPRA. Here, the model is combined with a classical effective volume approach for two fast-fracture models for brittle failure (PIA, NSA). Both adapted models were able to rebuild the scalable size effect as found in tensile experiments and notched samples. The modified PIA and NSA models are in principle comparable and show only small differences in the failure probability of the tested cases. Additionally, it is shown that the manufacturing process can have a significant influence on the material strength. By using the presented approach it is now possible to describe the scatter in materials strength not only for brittle materials but also for semi-brittle materials with some amount of plastic deformation. Therefore, the developed model is the first attempted to develop a unified reliability theory for brittle and non-brittle materials.
The newly developed reliability tool is integrated in a fully automated multidisciplinary optimization process chain realized by the DLR software RCE. Using this process chain in a geometry optimization of a low pressure turbine blade shows that it is possible to increase the aerodynamic efficiency and the reliability of a turbine blade at the same time, while ensuring the castability of the blade.
The next step, which is required for dimensioning turbine blades applied in real aero engines, will be the expansion of the model to consider temperature dependencies.
ACKNOWLEDGEMENTS
The authors kindly thank Ms. S. Sabet and Mr. K. Wilkinghoff for supporting the model and software development as well as Mr. R. Nodeh-Farahani, Mr. U. Fuchs, Mr. D. Lütz and Mr. T. Merzouk for designing the testing equipment and performing the mechanical experiments. The study is funded by the German Federal Ministry of Economics and Technology embedded in the LuFo project TATT under the founding code 20T1112B.
REFERENCES
- Appel, A., Heckel, T.H., Christ, H.J. (2010). Electron microscope characterization of low cycle fatigue in a high-strength multiphase titanium aluminide alloy, International Journal of Fatigue 32: 792-798.
- Appel, F., Paul, J.D.H., Oehring, M. (2011). Gamma Titanium Aluminide Alloys, Wiley-VCH.
- Chakraborty, A. and Earthman, J.C. (1998). Finite Element Analysis of Cavitating Facet Interaction in a Fully Lamellar Titanium Aluminide Alloy under Creep Conditions, Metallurgical and Materials Transactions 29A: 957-964.
- Curtin, W. A. (2000). Tensile Strength of Fiber-Reinforced Composites: III. Beyond the Traditional Weibull Model for Fiber Strengths, Journal of Composite Materials 34, 15: 1301-1332.
- Dynardo GmbH (2014). Methods for multi-disciplinary optimization and robustness analysis, documentation of OptiSLang 4.2. Weimar.
- GE Aviation (2015). The GEnx Commercial Aircraft Engine, www.geaviation.com
» www.geaviation.com - Henaff, G. and Gloanec, A.L. (2005). Fatigue properties of TiAl alloys, Intermetallics 13: 543-558.
- Kabir, M.R., Chernova, L., Bartsch, M. (2010). Numerical investigation of room-temperature deformation behavior of a duplex type γTiAl alloy using a multi-scale modeling approach, Acta Materialia 58: 5834-5847.
- Menter, F. R., Langtry, R. B., Likki, S. R., Suzen, Y. B., Huang, P. G. and Volker, S. A. (2004). Correlation-Based Transition Model Using Local Variables: Part I - Model Formulation. ASME Conf. Proc.: pp. 57-67.
- MTU (2015). Titanium aluminide - MTU Aero Engines develops new turbine blade material, www.pressebox.com
» www.pressebox.com - Munz, D. and Fett, T. (1999). Ceramics: Mechanical Properties, Failure Behaviour, Materials Selection, Springer.
- Nemeth, N. N., Jadaan, O. M., Gyekenyesi, J. P. (2005). Lifetime Reliability Prediction of Ceramic Structures Under Transient Thermomechanical Loads, NASA/TP 2005-212505.
- Padgett, W.J., Durham, S.D., Mason, A.M. (1995). Weibull Analysis of the Strength of Carbon Fibers Using Linear and Power Law Models for the Length Effect, Journal of Composite Materials 29, 14: 1873-1884.
- Recina, V. and Karlsson, B. (2000). High Temperature Low Cycle Fatigue Properties of Ti-48Al-2Cr-2Nb Gamma Titanium Aluminides Cast in Different Dimensions, Scripta Materialia 43: 609-615.
- Roudi, S., Riesch-Oppermann, H., Kraft, O. (2005). Advanced probabilistic tools for the uncertainty assessment in failure and lifetime prediction of ceramic components, Mat.-wiss. u. Werkstofftech. 36: 171-176.
- Seider, D., Basermann, A., Mischke, R., Siggel, M., Tröltzsch, A., Zur, S. (2013). Ad hoc Collaborative Design with Focus on Iterative Multidisciplinary Process Chain Development applied to Thermal Management of Spacecraft, 4th CEAS Air & Space Conference.
- Snecma (2015). A technological LEAP forward, www.snecma.com
» www.snecma.com - Tiefers, R., Aguilar, J., Dresbach, C., Buske, C. Schmidt, T. Zur, S. (2014). Titanium Aluminide Turbine Toolbox, A new tool for optimizing the design process for γ-TiAl low pressure turbine blades, EICF - 28th International Congress, Lugano.
- Voß C., Aulich M., Raitor T. (2014). Metamodel assisted aeromechanical optimization of a transonic centrifugal compressor, ISROMAC.
- Voß, C., Aulich, M., Kaplan, B., Nicke, E. (2006). Automated multiobjective optimization in axial compressor blade design. ASME Turbo Expo, Barcelona, Spain GT2006-90420.
- Wilcox, D. A. (1994). Simulation of Transition with a Two-Equation Turbulence Model. AIAA Journal 32: 247-255.
- Williams, D.M., Shunn, L., Jameson, A. (2014). Symmetric quadrature rules for simplexes based on sphere close packed lattice arrangements, Journal of Computational and Applied Mathematics 266: 18-38.
- Yang, H., Kersken, H.-P., Nuernberger, D. (2005). Toward Excellence in Turbomachinery Computational Fluid Dynamics: A Hybrid Structured-Unstructured Reynolds-Averaged Navier-Stokes Solver. Journal of Turbomachinery 128: 390 - 402.
- Zur, S. and Tröltzsch, A. (2014). Optimization of the DLR Space Liner inside the integration environment RCE, in Engineering Optimization, CRC Press: pp. 757-761.
Publication Dates
-
Publication in this collection
Dec 2016
History
-
Received
09 Oct 2015 -
Reviewed
02 May 2016 -
Accepted
10 June 2016