Simulating Intermediate Crack Debonding on RC Beams Strengthened with Hybrid Methods

Abstract

The externally bonded (EB) and the near-surface mounted (NSM) are two well-known methods for strengthening reinforced concrete (RC) beams. Both methods are unfortunately prone to fail prematurely through debonding when the amount of strengthening reinforcement provided is high. In response to this, a hybrid method that combines the EB and NSM method was introduced. The method allows the amount of reinforcement needed for EB and NSM methods to be reduced; this, in theory, should lower the interfacial stresses, thus reducing the possibility of debonding failures. While debonding failure can be prevented, certain amounts of debonding would still occur through the interfacial crack (IC) debonding mechanism which can affect the strength and stiffness of hybrid strengthened beams even if it does not directly cause failure. This paper presents a method to simulate IC debonding of hybrid strengthened beams using the moment-rotation approach. The proposed method allows a better prediction of maximum load and stiffness of the beams. The method is also less dependent on empirical formulations compared to the commonly used moment-curvature approach; this allows the method to be applicable to all material and shape of hybrid strengthening reinforcement, assuming correct material models are used. The proposed method was then used to perform parametric studies; among the important findings is the length of IC debonding tend to increase when FRP sheet with higher elastic modulus is used, thus negating most of the benefit from the higher modulus.

Keywords
Externally bonded; fibre reinforced polymers; near-surface mounted; numerical analysis; partial-interaction; reinforced concrete

1 INTRODUCTION

There are generally two types of strengthening methods available for reinforced concrete (RC) structural members in flexure: the externally bonded (EB) method (Barros et al., 2017; Ceroni et al., 2008; Chen et al., 2016; Fabrics et al., 2003; Maalej, 2005; Pesic, 2005; Tam et al., 2016; Toutanji et al., 2006) and the near-surface mounted (NSM) method (Badawi and Soudki, 2009; Capozucca et al., 2016; Capozucca and Magagnini, 2016; Kreit et al., 2011; Pachalla and Prakash, 2017; Seo et al., 2016). The EB method uses either fibre reinforced polymer (FRP) plates or sheets that are attached on the soffit of RC beams using epoxy adhesive. The NSM method involves making a groove on the soffit of RC beams and inserting either FRP bars or strips into the grooves and filling them with epoxy adhesive.

Both of these methods are prone to one or more types of debonding failures. An EB strengthened RC beam can fail prematurely due to either critical diagonal crack (CDC) debonding, interfacial crack (IC) debonding or end debonding (Narayanamurthy et al., 2012). On the other hand, NSM strengthened RC beams tend to fail prematurely only from end debonding through concrete cover separation (Zhang and Teng, 2014). While the NSM method is less prone to IC and CDC debonding failures, the probability of concrete cover separation failure is significantly high and the failure occurs in nearly all experimental tests in the literature (Zhang and Teng, 2014). To reduce the possibility of concrete cover separation, several rules were introduced with regard to the use of NSM method. One of them is the requirement of sufficient clear spacing and edge clearance for the NSM reinforcements. This causes difficulty to apply the NSM method on beams with small widths.

In response to this, a new method was proposed. The method is a hybrid between the EB method and the NSM method. The main purpose of the hybrid method is to reduce the amount of strengthening reinforcement needed by EB and NSM method individually, thus reducing the thickness of the FRP sheet needed as well as reducing the number of NSM grooves needed. The theory is that the reduction of strengthening reinforcement reduces the interfacial stresses, thus reducing the possibility of concrete cover separation debonding failures for both EB and NSM strengthening used in the hybrid method.

There are at least two earlier research on the hybrid method. The first research by Rahman et al. (2015) introduced a hybrid strengthening method using EB steel plates and NSM steel bars. The use of steel instead of FRP was intended to increase the ductility of the strengthened beam, as steel is much more ductile than FRP. However, the increase in ductility was barely noticeable from the experimental results due to the concrete cover separation failure that occurred on all the tested strengthened beams. Furthermore, the concrete cover separation debonding failure that occurred shows that the proposed method was unable to give the supposed higher resistance against debonding failures. Due to the poor performance of steel bars and plates, Darain et al. (2016) used carbon FRP (CFRP) bars and sheets to apply hybrid strengthening on RC beams. The results show that the use of CFRP gives much better result compared to steel bars and plates as none of the beams tested failed due to concrete cover separation. Most of the beams failed due to fracture of FRP sheet, though one of the beams experienced end debonding at the epoxy-FRP interface; this type of failure is rare and can be prevented by proper application of epoxy adhesive (Narayanamurthy et al., 2012). As the hybrid method is very new, various aspects of it remain unknown, among them the effect of IC debonding. It is well known that IC debonding is particularly prevalent on EB strengthened beams and can result in loss of an EB strengthened beam’s strength even if it does not directly cause the beam’s failure.

Conducting further experimental works, while necessary, is costly and time consuming. As an alternative method of study, this paper intends to apply the moment-rotation (M/θ) approach to simulate and study the effect of IC debonding on hybrid strengthened RC beams. The M/θ approach (Darain et al., 2016; Knight et al., 2014b; Oehlers et al., 2012, 2013, 2015; Shukri et al., 2015, 2016; Shukri and Jumaat, 2016; Visintin et al., 2012a, 2012b; Visintin et al., 2013a, 2013b) is a relatively new simulation method, which applies the partial interaction theory (Gupta and Maestrini, 1990; Haskett et al., 2008; Muhamad et al., 2011) to simulate various mechanics of RC beams, such as the formation of flexural cracks, widening of flexural cracks, tension stiffening and concrete wedge formation. The advantage that the M/θ approach has over conventional moment-curvature approach is the fact that it can readily simulate these mechanics without resorting to empirical formulations, such as the use of Branson’s equation in the moment-curvature approach to simulate tension stiffening, although it should be noted that empirical formulations are still required in terms of material models, such as stress-strain relationships and bond stress-slip relationships. Apart from this, however, the M/θ approach presented in this paper should be applicable to any material type and shape of hybrid strengthening used as long as the correct material models are used.

In this paper, a new method for tension stiffening simulation for hybrid strengthened RC beams will be presented. The proposed method presents an improvement to the method used by Darain et al. (2016) as it allows for a better simulation of IC debonding, specifically the loss of strength that is caused by IC debonding of FRP sheets used in the hybrid strengthening method. The proposed method was validated against published experimental results. This is followed by a parametric study performed using the proposed method.

2 TENSION STIFFENING SIMULATION

For RC beams without any flexural cracks, there exists perfect bonding between the steel reinforcements and the concrete adjacent to them. Once flexural cracks occur, this perfect bonding no longer applies; causing the steel reinforcements to slip from the concrete. The partial interaction theory has been applied by many researchers as the basis to form a numerical simulation of the slip of steel reinforcement mentioned above (Gupta and Maestrini, 1990; Haskett et al., 2008; Muhamad et al., 2011; Shukri et al., 2015; Shukri and Jumaat, 2016; Visintin et al., 2012a, 2012b). It has also been shown that this tension stiffening simulation is also applicable to FRP reinforcements, such as NSM FRP bars (Darain et al., 2016; Shukri et al., 2015, 2016; Shukri and Jumaat, 2016) and FRP sheets (Darain et al., 2016; Oehlers et al., 2013, 2015).

The tension stiffening simulation has also been successfully applied on hybrid strengthened beams (Darain et al., 2016), where a tension stiffening simulation based on the multiple crack segmental analysis (Shukri et al., 2015; Visintin et al., 2012a) was applied on the steel bars, CFRP bars, and CFRP sheets respectively.

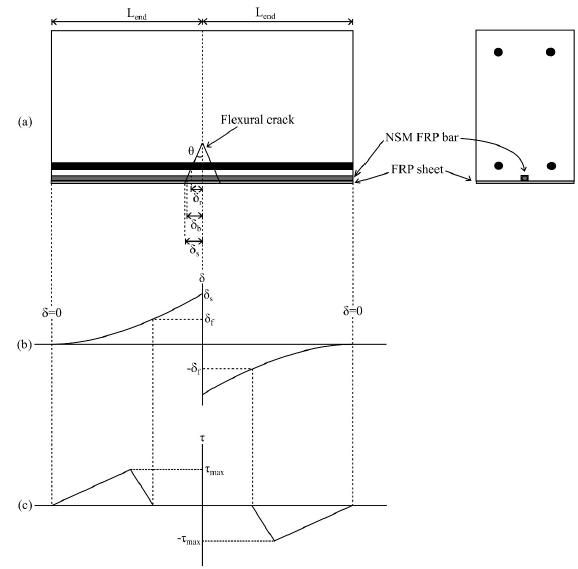
In the multiple crack segmental analysis, the length of primary crack is first determined, allowing the area of analysis to be reduced to half of the primary crack length, L_def as shown in Figure 1(a) due to the symmetry of forces where S_cr is the primary crack length. From Figure 1(a), the load applied to the beam segmental causes a rotation θ. The reinforcements slip by δ_r, δ_b and δ_s for the steel bar, FRP bar, and FRP sheet respectively. The slips are gradually reduced the further away from the crack face due to the transfer of load from the steel and FRP reinforcements to the adjacent concrete through bond stress. A numerical analysis is then performed to determine the value of loads P_r, P_b, and P_s that causes these slips by applying the boundary condition of slip being reduced to zero at the centre of the beam section, as shown in Figure 1(b). With regard to the FRP sheet, a bilinear bond stress-slip such as the one proposed by Lu et al. (2005) is usually applied. In the bilinear model, as shown in Figure 2, the bond stress is reduced to zero at δ_f. This loss of bond allows the multiple crack segmental analysis to simulate IC debonding (Darain et al., 2016). As shown in Figure 1(b) and Figure 1(c), when the slip for FRP sheet is increased higher than δ_f, the bond stress is reduced to zero and the area is considered to have debonded.

Figure 1
Multiple crack segmental analysis (a) RC beam segment; (b) Slip distribution for FRP sheet; (c) Bond stress distribution for FRP sheet.

Figure 2
Bond stress-slip model for FRP sheet.

The multiple crack segmental analysis allows for an accurate simulation of tension stiffening in hybrid strengthened RC beams. However, the resulting equilibrium of forces in the multiple crack segmental analysis does not limit the force in the FRP strengthening reinforcements (Oehlers et al., 2015). This greatly affects the accuracy of the simulation as the loss of strength due to IC debonding is not taken into account; this was reflected in the simulated results of Darain et al. (2016), where multiple crack analysis was applied and the simulated results overpredict most of the ultimate load. In response to this, in this paper, a single crack segmental analysis will be used to form a tension stiffening simulation for the FRP sheets and bars.

The single crack segmental analysis is focused on the flexural crack forming in the maximum moment region, as shown in Figure 3(a). The load applied to the beam causes a rotation θ which in turn causes slips δ_r, δ_b and δ_s for the steel bar, FRP bar, and FRP sheet respectively. Numerical analysis is then applied to determine the values of loads P_r, P_b, and P_s that causes these slips. The single crack segmental analysis does not limit the tension stiffening analysis to half-crack length L_def; the numerical analysis is continued until the slip is reduced to zero at L_end, which can be any distance from the crack face. When a slip of FRP sheet is higher than δ_f, the bond stress is reduced to zero, as shown in Figure 3(b) and Figure 3(c). Unlike in the multiple crack analysis, the equilibrium of forces in the single crack analysis causes the debonded section to occur while the applied load on the FRP sheet remains constant at P_IC, which is the load at which IC debonding starts occurring.

Figure 3
Single crack segmental analysis (a) RC beam segment; (b) Slip distribution for FRP sheet; (c) Bond stress distribution for FRP sheet.

The numerical procedure required for the single crack analysis is as shown below, along with a flowchart in Figure 4:

1. The beam geometry and material properties are determined:

   1. Area of EB/NSM/steel reinforcement, A_r.

   2. Area of concrete adjacent to the EB/NSM/steel reinforcement, A_c. More information on determining the A_c is available elsewhere (Darain et al., 2016; Shukri et al., 2015; Shukri and Jumaat, 2016).

   3. Perimeter of EB/NSM/steel reinforcement, L_per.

   4. Compressive strength of concrete, f_c.

   5. Elastic modulus of concrete, E_c.

   6. Yield strength of steel reinforcement, σ_y.

   7. Ultimate strength of EB/NSM/steel reinforcement, σ_f.

   8. Ultimate load of EB/NSM/steel reinforcement, P_{r_max}=A_rσ_f

   9. Elastic modulus of EB/NSM/steel reinforcement, E_y.

   10. Strain hardening modulus of steel reinforcement, E_h.

2. The beam is divided into small segments where the length, L_s=0.1mm. The analysis will start at the crack face, with the following boundary conditions:

   1. Slip of reinforcement, Δ_r = δ(1) = 0.01 mm.

   2. P_c(1) = 0

   3. The value of P_r(1) is assumed.

3. The rest of the procedure will determine the forces and strains acting on each beam segment; a dummy variable ‘i’ is introduced to identify the beam segment being solved.

4. The bond stress, τ(i) acting on the EB/NSM/steel reinforcement is determined.

5. The bond force is determined as B(i) = τ(i)L_sL_per. The strain of the EB/NSM/steel reinforcement is determined as ε_r = P_r(i)A_r/E_r. The change in slip for the reinforcement from this beam segment to the next segment is determined as ∆δ = (ε_r − ε_c)L_s. It should be noted that for the EB reinforcements, it is assumed that the area of concrete is thin enough to be negligible; the change in slip is thus ∆δ = ε_rL_s.

6. The values of boundary conditions for the next beam segment are determined. Note that the values of P_c(i + 1) and ε_c are only calculated for NSM/steel reinforcements:

   1. δ(i + 1) = δ(i) + ∆δ

   2. P_r(i + 1) = P_r(i) − B(i)

   3. P_c(i + 1) = P_c(i) + B(i)

   4. ε_c = P_c(i + 1)A_c/E_c

7. The condition δ(i + 1)/δ(1) < 0.01, which represents a 99% reduction from δ(1) is checked.

8. If the condition in procedure 7 is not met, another condition is checked, which is P_r(i + 1) < 0.

9. If the condition in procedure 8 is also not met, the analysis will move on to the next beam segment. The dummy variable i is updated by 1 and procedure 3-8 is repeated.

10. If the condition in procedure 8 is met, the assumed value of applied load P_r(1) is too low and the procedure 2-7 will be repeated with a higher value of assumed P_r(1).

11. If P_r(1)>P_{r_max}, the EB/NSM/steel reinforcement has fractured and failed.

12. If condition 11 is not met, the slip δ(1) and the corresponding P_r(1) is then recorded and a larger value of δ(1) is set. The analysis is then repeated starting from procedure 3.

13. If condition 11 is met, the analysis can be stopped and the load-slip (P_r(1)/δ(1)) relationship is recorded.

Figure 4
Single crack tension stiffening analysis procedure.

The numerical procedure for multiple crack analysis is not presented here, however the full procedure can be found in Shukri and Jumaat (2016).

3 MOMENT-ROTATION SIMULATION

The M/θ simulation is performed within the range of length L_def, which is determined using the tension stiffening simulation (Shukri and Jumaat, 2016). Consider Figure 4, where a beam section of length L_def is rotated by θ degree due to moment M. Prior to flexural cracking, the forces that cause deformation on the beam as shown in Figure 5(a) can be determined from the stress-strain relationships of each material. The depth of neutral axis d_na is then adjusted until equilibrium of forces is achieved; the actual value of moment M which causes rotation θ is then determined.

Figure 5
Moment-rotation analysis (a) Beam segment and deformation profile; (b) Strain profile; (c) Stress profile; (d) Force profile.

When flexural cracking occurs, a slip of reinforcements occurs such that the strains of reinforcement are no longer constant along length L_def. The forces acting on the steel and FRP reinforcements must then be determined using the load-slip (P_r/δ_r) relationship obtained from the tension stiffening simulation, where the slip is determined from the deformation profile in Figure 5(a). It should be noted that where more than one FRP sheet is used, the slip and the resulting load for each slip must be determined separately as shown in Figure 5(a) and Figure 5(d). The neutral axis d_na is then adjusted to obtain the equilibrium of forces and the actual value of is determined. The process is repeated for different values of θ in order to obtain an M/θ relationship. The moment-curvature can be obtained by dividing the values of θ with L_def. The load-deflection relationship of hybrid strengthened RC beams can then be determined using the commonly used double integration method.

4 VALIDATION OF PROPOSED METHOD

The proposed method was validated against the published experimental results of Darain et al. (2016). The experimental results are from four RC beams strengthened with the hybrid method made up of carbon FRP (CFRP) bars and CFRP sheets. A single CFRP bar was used for each beam, with a diameter of either 8mm or 10mm; the size of the NSM groove on the beam is twice the diameter of the bar used. The beams used either a single or two plies of CFRP sheets used had 0.17mm thickness. Further details on the beams and the materials used are given in Table 1 and Table 2.

Table 1
Beam details.

Beam Designation	EB reinforcement	NSM reinforcement
CBC8P1	One ply of CFRP sheet	One 8 mm CFRP bar
CBC8P2	Two ply of CFRP sheet	One 8 mm CFRP bar
CBC10P1	One ply of CFRP sheet	One 10 mm CFRP bar
CBC10P2	Two ply of CFRP sheet	One 10 mm CFRP bar

Table 2
Material properties.

Material	Property	Value (MPa)
Concrete	Compressive strength	50.1
	Tensile strength	5.5
	Elastic modulus	33260
Steel bar	Yield stress	529
	Ultimate strength	587
	Elastic modulus	200000
CFRP bar	Ultimate strength	2400
	Elastic modulus	165
CFRP sheet	Ultimate strength	4900
	Elastic modulus	230000

5 MATERIAL MODELS

Several material models were used in this paper, which will be mentioned only in brief to keep the paper short. Further details on the material models can be found in the reference given. The material models are only used as input for the tension stiffening and moment-rotation simulations; they can be replaced with other models if deemed appropriate (Knight et al., 2014a).

A bilinear stress-strain relationship with strain hardening was used for the steel reinforcements, while a linear stress-strain relationship was used for the CFRP bars. For the tension stiffening simulation, the bond-slip model by CEB-FIP (1993) was used for the steel reinforcement while the bond-slip model by De Lorenzis (2004) was used to determine the bond force of the NSM reinforcement. The maximum bond stress, τ_max was obtained using the bond strength model by Hassan and Rizkalla (2004). For the tension stiffening analysis of FRP sheet, the bilinear bond-slip model by Lu et al. (2005) was used. For concrete in compression, the stress-strain model by Popovics (1973) was used in conjunction with the size-dependent stress-strain method by Chen et al. (2014).

6 COMPARISONS OF SIMULATED AND EXPERIMENTAL RESULTS

A summary of the simulated results is given in Table 3. The proposed method was able to predict the maximum loads very well, where the deviation is found to be within 4% of the experimental value. The accuracy of the simulated deflection at maximum load is also good, apart from the simulated value for beam CBC8P2 which was found to be 20% higher than the experimental value. The simulated yield loads overpredict the experimental values, with a deviation between 12-16%. The use of the single crack analysis as the basis of the tension stiffening simulation may be the cause of this, as the single crack analysis is known to be less accurate at predicting tension stiffening effect compared to the multiple crack analysis. The simulated length of IC debonding is also given in Table 3, although its accuracy cannot be verified in this case. The length of IC debonding is affected by the amount of strengthening reinforcement provided. The use of two FRP sheets can be seen to give a shorter length of IC debonding compared to when only one FRP sheet is used. A similar effect can be seen when a larger size of NSM FRP bar is used, although the change to the length of IC debonding is negligible when compared to FRP sheets.

Table 3
Summary of simulated and experimental results

Beam	Results	Py (kN)	Pmax (kN)	∆max (mm)	LIC (mm)
CBC8P1	Simulated	59.40	69.80	41.75	483.60
	Experimental	52.51	70.66	39.50	-
	Simulated/Experimental	1.13	0.99	1.06	-
CBC8P2	Simulated	67.40	76.40	37.40	428.80
	Experimental	59.11	76.71	31.18	-
	Simulated/Experimental	1.14	1.00	1.20	-
CBC10P1	Simulated	64.40	78.00	46.34	469.00
	Experimental	57.64	81.66	42.96	-
	Simulated/Experimental	1.12	0.96	1.08	-
CBC10P2	Simulated	72.80	84.20	42.06	421.40
	Experimental	62.59	86.98	42.64	-
	Simulated/Experimental	1.16	0.97	0.99	-

• Note: P_y=yield load; P_max=maximum load; ∆_max=deflection at maximum load; L_IC=length of IC debonding.

A comparison between simulated and experimental load-deflection results are also given in Figure 6. The simulated load-deflection using the method proposed Darain et al. (2016) is also included in Figure 6; their simulated results were obtained using the multiple crack analysis and hence is incapable of simulating IC debonding. Its inclusion in Figure 6 is meant to show the benefit of simulating IC debonding as opposed to ignoring it. It can be seen that the method proposed in this paper is able to follow the general shape of the experimental load-deflection curve relatively well compared to the simulation using the method by Darain et al. (2016) which tends to overpredict the load-deflection capacity of hybrid strengthened RC beams, especially after steel yielding. However, the previous simulation method by Darain et al. (2016) was found to be better at predicting the pre-yield stiffness of the beams, which as mentioned before can be attributed to the multiple crack analysis being better at simulating tension stiffening (Oehlers et al., 2015). However, the new method proposed in this paper is better at predicting the failure load of the hybrid strengthened beams.

Figure 6
Comparison of load-deflection results (a) Beam CBC8P1; (b) Beam CBC8P2; (c) Beam CBC10P1; (d) Beam CBC10P2.

7 PARAMETRIC STUDY

The proposed simulation method was used to perform several parametric studies. The details of the simulated beams used for the parametric study is similar to beam CBC10P1, apart from the list of properties listed in Table 4. Four test groups were used for the parametric studies. Test groups n-e and s-e were used to study the effect of the elastic modulus of NSM FRP bars (E_r-nsm) and FRP sheets (E_r-sheet) respectively; test groups n-t and s-t, on the other hand, were used to determine the effect of the bond strength of NSM FRP bars (τ_max-nsm) and FRP sheets (τ_max-sheet) respectively.

Table 4
Properties of simulated hybrid strengthened RC beams.

Test Group	Beam	Er-nsm (GPa)	Er-sheet (GPa)	τmax-nsm (GPa)	τmax-sheet (GPa)
n-e	n-e-50	50	230	9.31	6.78
	n-e-100	100	230	9.31	6.78
	n-e-150	150	230	9.31	6.78
	n-e-200	200	230	9.31	6.78
s-e	s-e-50	165	50	9.31	6.78
	s-e-100	165	100	9.31	6.78
	s-e-150	165	150	9.31	6.78
	s-e-200	165	200	9.31	6.78
n-t	n-t-5	165	230	5	6.78
	n-t-10	165	230	10	6.78
	n-t-15	165	230	15	6.78
	n-t-20	165	230	20	6.78
s-t	s-t-5	165	230	9.31	5
	s-t-10	165	230	9.31	10
	s-t-15	165	230	9.31	15
	s-t-20	165	230	9.31	20

• Note: E_r-nsm=elastic modulus of NSM FRP bar; E_r-sheet=elastic modulus of FRP sheet; τ_max-nsm=bond strength of NSM FRP bar; τ_max-sheet=bond strength of FRP sheet.

The summary of the simulated results for test groups n-e and s-e is given in Table 5, while Figure 7 and Figure 8 shows the load-deflection results for test group n-e and s-e respectively. All the beams failed through concrete crushing, which in this paper is taken as the concrete strain of 0.003. The yield load (P_y) and maximum load (P_max) of the hybrid strengthened beams were found to increase as the values of E_r-nsm and E_r-sheet are increased.

Table 5
Summary of simulated results for test group n-e and s-e

Test group	Beam	Er (N/mm2)	Py (kN)	Pmax (kN)	∆max (mm)	LIC (mm)
n-e	n-e-50	Er-nsm=50	54.8	64.2	43.9	494.4
	n-e-100	100	59.8	70	42.6	439.8
	n-e-150	150	63.8	74.4	41.3	403
	n-e-200	200	66.8	77.8	40.5	377
s-e	s-e-50	Er-sheet=50	59.8	71.8	43.3	184.4
	s-e-100	100	62.2	73	42.4	262.8
	s-e-150	150	63.2	74	42.0	322.4
	s-e-200	200	63.8	74.6	41.1	368

• Note: E_r=Elastic modulus; E_r-nsm=elastic modulus of NSM FRP bar; E_r-sheet=elastic modulus of FRP sheet; P_y=yield load; P_max=maximum load; ∆_max=deflection at maximum load; L_IC=length of IC debonding.

Figure 7
Load-deflection results of test group n-e.

Figure 8
Load-deflection results of test group s-e.

In Figure 9, a plot of E_r against the length of IC debonding, L_IC is presented. It should be noted that the value of E_r for test group n-e and s-e refer to E_r-nsm and E_r-sheet respectively. The L_IC was found to decrease when higher E_r-nsm was used. On the other hand, as the E_r-sheet is increased, the L_IC also increases. This contrasting IC debonding behaviour inevitably affects the load-deflection relationships of the beams as well. As shown in Figure 7, since the L_IC decreases for higher E_r-nsm, a significant increase in the stiffness and maximum load for beams in test group n-e can be seen. However, for beams in test group s-e, as shown in Figure 8, since L_IC will also increase when higher E_r-sheet is used, the increase in stiffness and the maximum load becomes minimal.

Figure 9
Comparison of simulated IC debonding length for test group n-e and s-e.

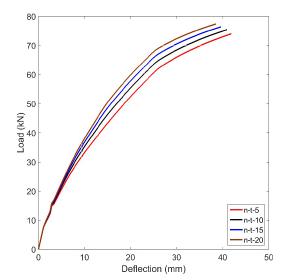
A summary of the results for test groups n-t and s-t is given in Table 6; the load-deflection results are shown in Figure 10 and Figure 11. Similar to before, all beams failed by concrete crushing. From Table 6, it can be seen that higher values of τ_max-nsm and τ_max-sheet causes the P_y and P_max to increase. However, the overall increase is much lower when compared to the increase seen in the parametric study of elastic modulus, which suggests that while τ_max-nsm and τ_max-sheet are important for tension stiffening, changes in their values does not impact the behaviour of hybrid strengthened beams to a significant degree.

Table 6
Summary of simulated results for test group n-t and s-t

Test group	Beam	τmax (N/mm2)	Py (kN)	Pmax (kN)	∆max (mm)	LIC (mm)
n-t	n-t-5	τmax-nsm=5	62.2	74	41.9	395.6
	n-t-10	10	64.6	75.4	41.0	395.6
	n-t-15	15	66.8	76.4	39.6	384.4
	n-t-20	20	68.8	77.4	38.5	377
s-t	s-t-5	τmax-sheet=5	65.4	75.2	41.3	376.6
	s-t-10	10	65.6	75.2	41.1	412.8
	s-t-15	15	66.2	76.2	40.4	346.6
	s-t-20	20	67.2	77.2	39.5	298.6

• Note: τ_max=bond strength; τ_max-nsm=bond strength of NSM FRP bar; τ_max-sheet=bond strength of FRP sheet; P_y=yield load; P_max=maximum load; ∆_max=deflection at maximum load; L_IC=length of IC debonding.

Figure 10
Load-deflection results of test group n-t.

Figure 11
Load-deflection results of test group s-t.

A plot of L_IC against τ_max for test group n-t and s-t is given in Figure 12. The L_IC was found to reduce for higher values of τ_max-nsm. The result of L_IC-τ_max-sheet curve shows a similar trend, apart from a slight increase in L_IC for beam s-t-10, which uses τ_max-sheet = 10 N/mm². This slight increase in L_IC is related to the bond stress and slip of the FRP sheet. Consider Figure 13(b) and Figure 13(c), which shows the slip and bond stress distribution of the FRP sheet for beams s-t-5, s-t-10 and s-t-15. At the same amount of initial slip δ₁, the beam with a higher τ_max-sheet such as beam s-t-15 will have a shorter hinge span (L_end) due to a quicker transfer of force from the FRP sheet to the concrete. However, the transfer of force for beam s-t-10 is not high enough; this causes beam s-t-5 and s-t-10 to have an almost similar L_end. As the L_end is the same, the summation of bond stresses τ_sum for both beams should be similar. However, beam s-t-10 have a higher τ_max-sheet than beam s-t-5. This results in beam s-t-10 having a longer L_IC in order to have the same τ_sum as beam s-t-5. This situation does not occur in beam s-t-15, which have a high enough τ_max-sheet to cause it to have a significantly shorter L_end compared to the other two beams. The L_IC for beam s-t-15 is also the shortest of the three beams. The most significant effect of a longer L_IC is the reduction of the strength and stiffness for beam s-t-10. This can be seen in Figure 11, where the load-deflection curve for s-t-5 and s-t-10 is almost identical despite beam s-t-10 having a higher τ_max-sheet.

Figure 12
Comparison of simulated IC debonding length for test group n-t and s-t.

Figure 13
Distribution of slip and bond stress of FRP sheet (a) Beam detail; (b) Bond stress distribution for FRP sheet; (c) Slip distribution for FRP sheet.

8 CONCLUSIONS

An improvement to the method presented by Darain et al. (2016) for simulating the behaviour of hybrid strengthened RC beams was proposed, which can correctly simulate the effect of IC debonding. Several conclusions were made based on the work done:

• The proposed method was able to simulate the behaviour of hybrid strengthened beams with good accuracy. The single crack analysis was found to be important in simulating the loss of stiffness due to IC debonding in hybrid strengthened RC beams.

• The simulated maximum load was found to be within 4% of the experimental value.

• On the other hand, the simulated maximum deflection was found to be less accurate with deviation from the experimental value from 1% to 20%.

• The simulated yield load was found to deviate from experimental values from 12-16% due to the use of the single crack analysis as the basis of the tension stiffening simulation, as the single crack analysis is known to be less accurate at predicting tension stiffening effect compared to the multiple crack analysis.

• Increasing the elastic modulus of NSM FRP bar increases the stiffness and maximum load of the hybrid strengthened beam while decreasing the length of IC debonding.

• Increasing the elastic modulus of FRP sheet, on the other hand, increases the length of IC debonding; as such while the stiffness and maximum load of the hybrid strengthened beam still increase, the amount is less significant compared to increasing the elastic modulus of NSM FRP bar.

• Increasing the bond strength of NSM FRP bar and FRP sheet slightly increases the stiffness and maximum load of hybrid strengthened beams.

While the proposed method is perhaps too complicated to be used in general design, it is hoped that it can be used to perform further studies on the hybrid strengthening method similar to the parametric study presented in this paper. The proposed method should be applicable to hybrid strengthened beams using any type of material and shape of FRP reinforcement, assuming the correct material models (in particular the bond stress-slip model) are used.

Acknowledgement

This study was funded by the University of Malaya, Grand Challenge - SUS (Sustainability Science) Grant, project number GC003A-15SUS.

References

• Badawi M and Soudki K (2009) Flexural strengthening of RC beams with prestressed NSM CFRP rods - Experimental and analytical investigation. Construction and Building Materials 23(10): 3292-3300.
• Barros JAO, Rezazadeh M, Laranjeira JPS, et al. (2017) Simultaneous flexural and punching strengthening of RC slabs according to a new hybrid technique using U-shape CFRP laminates. Composite Structures 159: 600-614.
• Capozucca R and Magagnini E (2016) Vibration of RC beams with NSM CFRP with unbonded/notched circular rod damage. Composite Structures 144: 108-130.
• Capozucca R, Domizi J and Magagnini E (2016) Damaged RC beams strengthened with NSM CFRP rectangular rods under vibration in different constrain conditions. Composite Structures 154: 660-683.
• CEB-FIP (1993) CEB-FIP model code 1990. London, UK: Thomas Telford Ltd.
• Ceroni F, Pecce M, Matthys S, et al. (2008) Debonding strength and anchorage devices for reinforced concrete elements strengthened with FRP sheets. Composites Part B: Engineering 39(3): 429-441.
• Chen GM, Zhang Z, Li YL, et al. (2016) T-section RC beams shear-strengthened with anchored CFRP U-strips. Composite Structures 144: 57-79.
• Chen Y, Visintin P, Oehlers D, et al. (2014) Size-Dependent Stress-Strain Model for Unconfined Concrete. Journal of Structural Engineering 140(4): 4013088.
• Darain KM ud, Jumaat M, Shukri AA, et al. (2016) Strengthening of RC Beams Using Externally Bonded Reinforcement Combined with Near-Surface Mounted Technique. Polymers 8(7): 261.
• De Lorenzis L (2004) Anchorage length of near-surface mounted fiber-reinforced polymer rods for concrete strengthening - Analytical modeling. ACI Structural Journal 101(3): 375-386.
• Fabrics H, Cedex V, Cedex R, et al. (2003) Experimental analysis of flexural behaviour of externally bonded CFRP reinforced concrete structures. 36(May): 238-241.
• Gupta AK and Maestrini SR (1990) Tension Stiffness Model for Reinforced Concrete Bars. Journal of Structural Engineering 116(3): 769-790.
• Haskett M, Oehlers DJ and Mohamed Ali MS (2008) Local and global bond characteristics of steel reinforcing bars. Engineering Structures 30(2): 376-383.
• Hassan TK and Rizkalla SH (2004) Bond mechanism of near-surface-mounted fiber-reinforced polymer bars for flexural strengthening of concrete structures. ACI Structural Journal 101(6): 830-839.
• Knight D, Visintin P, Oehlers DJ, et al. (2014a) Short-Term Partial-Interaction Behavior of RC Beams with Prestressed FRP and Steel. Journal of Composites for Construction 18(1): 4013029.
• Knight D, Visintin Phillip, Oehlers DJ, et al. (2014b) Simulating RC beams with unbonded FRP and steel prestressing tendons. Composites Part B: Engineering 60: 392-399.
• Kreit A, Al-Mahmoud F, Castel A, et al. (2011) Repairing corroded RC beam with near-surface mounted CFRP rods. Materials and Structures 44(7): 1205-1217.
• Lu XZ, Teng JG, Ye LP, et al. (2005) Bond-slip models for FRP sheets/plates bonded to concrete. Engineering Structures 27(6): 920-937.
• Maalej M (2005) Analysis and design of FRP externally-reinforced concrete beams against debonding-type failures. Materials and Structures 34(241): 418-425.
• Muhamad R, Mohamed Ali MS, Oehlers D, et al. (2011) Load-slip relationship of tension reinforcement in reinforced concrete members. Engineering Structures 33(4): 1098-1106.
• Narayanamurthy V, Chen JF, Cairns J, et al. (2012) Plate end debonding in the constant bending moment zone of plated beams. Composites Part B: Engineering 43(8): 3361-3373.
• Oehlers D, Visintin P, Zhang T, et al. (2012) Flexural rigidity of reinforced concrete members using a deformation based analysis. Concrete in Australia 38(4): 50-56.
• Oehlers DJ, Visintin P, Haskett M, et al. (2013) Flexural ductility fundamental mechanisms governing all RC members in particular FRP RC. Construction and Building Materials 49: 985-997.
• Oehlers DJ, Visintin P and Lucas W (2015) Flexural Strength and Ductility of FRP-Plated RC Beams: Fundamental Mechanics Incorporating Local and Global IC Debonding. Journal of Composites for Construction 20(2): 4015046.
• Pachalla SKS and Prakash SS (2017) Efficient near surface mounting CFRP strengthening of pretensioned hollowcore slabs with opening - An experimental study. Composite Structures, Elsevier Ltd 162: 28-38.
• Pesic N (2005) Flexural analysis and design of reinforced concrete beams with externally bonded FRP reinforcement. Materials and Structures 38(276): 183-192.
• Popovics S (1973) A numerical approach to the complete stress-strain curve of concrete. Cement and Concrete Research 3(5): 583-599.
• Rahman M, Jumaat MZ, Rahman MA, et al. (2015) Innovative hybrid bonding method for strengthening reinforced concrete beam in flexure. Construction and Building Materials, Elsevier Ltd 79: 370-378.
• Seo S, Sung M and Feo L (2016) Flexural analysis of RC beam strengthened by partially de-bonded NSM FRP strip. Composites Part B, Elsevier Ltd 101: 21-30.
• Shukri AA and Jumaat MZ (2016) Simulating concrete cover separation in RC beams strengthened with near-surface mounted reinforcements. Construction and Building Materials 122: 1-11.
• Shukri AA, Darain KM ud and Jumaat MZ (2015) The Tension-Stiffening Contribution of NSM CFRP to the Behavior of Strengthened RC Beams. Materials 8(7): 4131-4146.
• Shukri AA, Hosen MA, Muhamad R, et al. (2016) Behaviour of precracked RC beams strengthened using the side-NSM technique. Construction and Building Materials 123: 617-626.
• Tam B, Si A and Limam A (2016) Numerical modelling of reinforced concrete beams repaired by TRC composites. Composite Structures 152: 779-790.
• Toutanji H, Zhao L and Zhang Y (2006) Flexural behavior of reinforced concrete beams externally strengthened with CFRP sheets bonded with an inorganic matrix. Engineering Structures 28(4): 557-566.
• Visintin P, Oehlers DJ, Wu C., et al. (2012a) A mechanics solution for hinges in RC beams with multiple cracks. Engineering Structures 36: 61-69.
• Visintin P, Oehlers DJ, Wu Chengwing, et al. (2012b) The reinforcement contribution to the cyclic behaviour of reinforced concrete beam hinges. Earthquake Engineering & Structural Dynamics 41: 1591-1608.
• Visintin P, Oehlers DJ, Muhamad R, et al. (2013a) Partial-interaction short term serviceability deflection of RC beams. Engineering Structures 56: 993-1006.
• Visintin P, Oehlers D and Haskett M (2013b) Partial-interaction time dependent behaviour of reinforced concrete beams. Engineering Structures 49: 408-420.
• Zhang SS and Teng JG (2014) Finite element analysis of end cover separation in RC beams strengthened in flexure with FRP. Engineering Structures 75: 550-560.

• Available Online: June 05, 2018

Publication Dates

• Publication in this collection
  2018

History

• Received
  06 Mar 2018
• Reviewed
  11 Mar 2018
• Accepted
  31 May 2018