Effect of uncertainty of fastening systems properties on wheel/rail dynamic force

Abstract

In this paper, effect of uncertainty of fastening system properties on the wheel/rail dynamic force (WRDF) was investigated. For this purpose, two deterministic and epistemic models of vehicle/track interaction were developed, using the finite element method. Validity of the results obtained from the models was shown through comparison between the model results and those obtained from field tests. The effects of uncertainty of fastening system properties on the WRDF in different axle loads, vehicle speeds, rail irregularities and various track maintenance conditions were derived through probability and sensitivity analyses. Using the results obtained, some contours were developed to obtain the amplification of WRDF (due the uncertainty of fastening system properties) as a function of vehicle axle load, vehicle speed and track maintenance conditions.

Keywords:
Slab track; fastening system properties; uncertainty; probability analysis

Graphical Abstract

1 INTRODUCTION

Nowadays railway slab track systems are widely used in subways and high-speed lines[¹]. Wheel/Rail Dynamic Force (WRDF) is one of the most effective parameters in analysis, design and performance of railway slab tracks [²]. According to the literature, the greater the WRDF, the shorter lifecycle of railway tracks [³-⁵]. Effects of different track and rolling stock parameters on the WRDF have been widely investigated in the literature [⁶, ⁷]. In this regard, influence of rail irregularity and damping, track geometry parameters, nonlinearity of wheel/rail contact, vehicle properties, track stiffness, vehicle speed, and axle load on the WRDF have been investigated in previous studies [⁸-¹⁰].

Rhayma et al. showed that the properties of railway track components have uncertainty [¹¹]. As the level of track maintenance quality condition lessens, the uncertainty level of track component properties is increased [¹¹-¹⁴]. Salcher et al. emphasized that uncertainty of track geometry parameters has considerable effect on the WRDF [¹⁵]. For instance, Mehrali et al. showed the effect of railway track parameters on the WRDF thorough several probability analyses [¹⁶]. Fastening system is one of the most important track components, influencing the WRDF [⁴].

Properties of fastening system (such as rail-pad stiffness, rail-pad damping and magnitude of preload) change along the time [¹², ¹⁷]. In fact, properties of fastening system are dependent on several items such as track quality maintenance, operation conditions and environmental circumstances [¹⁸, ¹⁹]. Changes in the properties of a railway fastening system cause differences in the properties of consecutive fasteners[²⁰, ²¹]. It means that properties of fastening systems might vary from one fastener to another, causing none-uniformity of track stiffness along the track [²²]. It indicates uncertainty in consistency of the properties of fastening system [⁴, ¹⁴]. Zhu et al. proved that uncertainty level of fastening properties is greater than uncertainty level of other railway slab track components properties [¹⁷]. Kaewunruen carried out probability analysis of fastening systems and indicated that fastening system properties have a high level of uncertainty [¹⁴]. Mohammadzadeh et al. investigated the life-cycle of fastening systems based on the probability analysis and showed that reliability of the railway track is dependent on the fastening system conditions [²³]. Wei et al. developed a method to determine the uncertainty of fastening system properties during its operation [²²]. Yuan et al. indicated that fastening system properties are changed during the time [²⁴]. They presented a method to evaluate the fastening system properties deterioration during the railway operation. Yuan et al. investigated the effects of track geometry and heavy vehicle axle load on the uncertainty of fastening system properties and indicated that the track geometry conditions can cause defects in the fastening systems [²⁵].

There are several studies which investigate the effect of uncertainty of a specific parameter on the response of structures using a numerical model in conjunction with the probability analysis [²⁶-²⁸]. For instance Xin et al. developed a numerical model of train-ballasted track-bridge and evaluated the influence of uncertainty of superstructure and rail irregularities on the performance, using a probability analysis [²⁸]. They showed that the finite element method along with the probability analysis is a reliable way to investigate the effect of uncertainty of different parameters on the response of structures[²⁸].

Although the previous studies have indicated significant influences of the variation in fastening system properties (along the track) on the WRDF [⁴, ²⁹, ³⁰], effect of uncertainty of fastening system properties on the WRDF is omitted in the available literature. This research is aimed at to investigate the effects of uncertainty of fastening system properties on the WRDF.

In this regard, two deterministic and epistemic models were developed. The results obtained from the models were validated against the data measured from a field test carried out in this study. Through several sensitivity and probability analyses, effects of uncertainty of fastening system on the WRDF were investigated for different vehicle and track conditions.

2 METHODLOGY

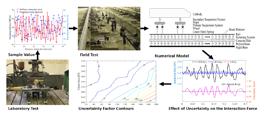
Figure (1) presents a flowchart of this study. In this flowchart the critical steps of the research are shown. As illustrated in Figure (1), the numerical models were developed in the first step of this research. In the second step, validity of the results obtained from the models was investigated through comparison of the results with those obtained from a field test. During the third step, the uncertainty of fastening properties was defined based on track maintenance level. In the next steps, the effect of uncertainty of fastening system properties on the WRDF was investigated for different axle loads, vehicle speeds, rail irregularities and track quality maintenance conditions through sensitivity and probability analyses. Finally, the results obtained were used to develop some contours which present the uncertainty factor for WRDF as a function of vehicle axle load, vehicle speed and level of track quality maintenance.

Figure 1
Methodology of this research

3 DEVELOPMENT OF NUMERICAL MODEL

This section presents the details of the numerical models. Two 2D numerical models of vehicle/slab track interaction were developed in this study [³¹]. In the first model (deterministic model), the stiffness and damping of fastening system were considered constant. In the second model (epistemic model), the stiffness and damping of each fastening system were variable. In other words, the properties of each fastening system are different from those of the adjacent fasteners in the epistemic model [³²].

The models were developed in MATLAB environment. A schematic view of the models is shown in Figure 2. The models comprise a slab track and a vehicle. The slab track was simulated as two-layered track system using the FEM [³³]. The slab track consists of two continuous layers (rail and concrete slab) [³⁴]. The rail and concrete slab layers were laid on fastening systems and an elastic layer, respectively. A rigid foundation was considered under the elastic layer. The rail and concrete slab layers were simulated using the Euler-Bernouli beam element. The mass and stiffness matrices of Euler-Bernouli beam element are presented in Equation (1) [³⁵].

$\begin{array}{l}\left[K_e\right]=\frac{2EI}{L_e{}^3}\left[\begin{array}{c}\begin{array}{ccc}6& 3L_e& \begin{array}{cc}-6& 3L_e\end{array}\\ 3L_e& 2L_e{}^2& \begin{array}{cc}-3L_e& L_e{}^2\end{array}\\ -6& -3L_e& \begin{array}{cc}6& -3L_e\end{array}\end{array}\\ \begin{array}{ccc}3L_e& L_e{}^2& \begin{array}{cc}-3L_e& 2L_e{}^2\end{array}\end{array}\end{array}\right]\\ \left[M_e\right]=\frac{M_e.L_e}{420}\left[\begin{array}{c}\begin{array}{ccc}156& 22L_e& \begin{array}{cc}54& -13L_e\end{array}\\ 22L_e& 4L_e{}^2& \begin{array}{cc}13L_e& -3L_e{}^2\end{array}\\ 54& 13L_e& \begin{array}{cc}2L^2& -22L_e\end{array}\end{array}\\ \begin{array}{ccc}-13L_e& -3L_e{}^2& \begin{array}{cc}-22L_e& 4L_e{}^2\end{array}\end{array}\end{array}\right]\end{array}$ (1)

In equation (1), EI is the flexural rigidity of the beam element, L_e stands for the length of element and M_e is the mass per length unit of the element. The damping matrix of Euler-Bernouli beam element $\left[C_e\right]$ was obtained based on the Rayleigh damping coefficients (Equation (2)) [³⁰].

$\left[C_e\right]=\alpha \left[M_e\right]+\beta \left[K_e\right]$ (2)

In Equation (2), $\alpha$ and $\beta$ are Rayleigh damping coefficients. The mass, stiffness and damping matrices of the rail and concrete slab ($\left[K_R\right]$, $\left[K_S\right]$, $\left[M_R\right]$, $\left[M_S\right]$, $\left[C_R\right]$ and $\left[C_S\right]$) were obtained based on the mass, stiffness and damping matrices of Euler-Bernouli beam element, respectively [³⁶]. The fastening system and elastic layer were modeled as the linear spring-dashpot element [³⁷]. The stiffness, mass and damping matrices of rail layer, concrete slab layer, fastening system and elastic layer were assembled to form stiffness ([KT]), mass ([MT]) and damping ([CT]) matrices of slab track[³⁸].

$\begin{array}{l}\left[K_T\right]=\left[\begin{array}{cc}\left[K_R\right]& \left[K_{R/S}\right]\\ \left[K_{S/R}\right]& \left[K_S\right]\end{array}\right]\\ \left[M_T\right]=diag\left(\left[M_R\right]\left[M_S\right]\right)\\ \left[C_T\right]=\left[\begin{array}{cc}\left[C_R\right]& \left[C_{R/S}\right]\\ \left[C_{S/R}\right]& \left[C_S\right]\end{array}\right]\end{array}$ (3)

In equation (3), subscripts of R, and S stand for the rail and slab degrees of freedom, respectively. Also, subscript of R/S stands for the rail/slab interaction components. Accordingly, the governing differential equation of the motion of slab track is presented in Equation (4) [³⁹].

$\left[K_T\right]\left\{d_T\right\}+\left[C_T\right]\left\{\dot{d_T}\right\}+\left[M_T\right]\left\{\ddot{d_T}\right\}=\left\{F_T\right\}$ (4)

In Equation (4), $\left\{F_T\right\}$, $\left\{d_T\right\}$, $\left\{{\dot{d}}_T\right\}$ and $\left\{{\ddot{d}}_T\right\}$ are the slab track force, displacement, velocity and acceleration vectors, respectively [³⁹].

Figure 2
Schematic view of new model

The vehicle was simulated as a wagon with ten Degrees of Freedom (DOF). As shown in Figure (2), the vehicle comprises one car body, secondary suspension system, two bogies, primary suspension system and four wheels. The stiffness ($\left[K_V\right]$), mass ($\left[M_V\right]$) and damping ($\left[C_V\right]$) matrices of the vehicle are available in the previous studies [⁴⁰]. For instance, Equation (5) presents the stiffness matrix of the vehicle [⁴⁰].

$\left[{\mathrm{K}}_V\right]=\left[\begin{array}{ccc}\begin{array}{c}2k_2\\ \\ \begin{array}{c}\\ \\ \begin{array}{c}\\ \\ \begin{array}{c}\\ \\ \begin{array}{c}\\ \end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}0\\ 2k_2{a}^2\\ \begin{array}{c}\\ \\ \begin{array}{c}\\ \\ \begin{array}{c}\\ \\ \begin{array}{c}\\ \end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{ccc}\begin{array}{c}{-k}_2\\ k_{2}a\\ \begin{array}{c}2k_1+k_2\\ \\ \begin{array}{c}\\ \\ \begin{array}{c}\\ Symm\\ \begin{array}{c}\\ \end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}{-k}_2\\ -k_{2}a\\ \begin{array}{c}0\\ 2k_1+k_2\\ \begin{array}{c}\\ \\ \begin{array}{c}\\ \\ \begin{array}{c}\\ \end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{ccc}\begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ 0\\ \begin{array}{c}2k_1{b}^2\\ \\ \begin{array}{c}\\ \\ \begin{array}{c}\\ \end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ 2k_1{b}^2\\ \begin{array}{c}\\ \\ \begin{array}{c}\\ \end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{ccc}\begin{array}{c}0\\ 0\\ \begin{array}{c}-k_1\\ 0\\ \begin{array}{c}{k}_{1}b\\ 0\\ \begin{array}{c}{k}_1\\ \\ \begin{array}{c}\\ \end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}-k_1\\ 0\\ \begin{array}{c}-k_{1}b\\ 0\\ \begin{array}{c}0\\ k_1\\ \begin{array}{c}\\ \end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ -k_1\\ \begin{array}{c}0\\ k_{1}b\\ \begin{array}{c}0\\ 0\\ \begin{array}{c}{k}_1\\ \end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ -k_1\\ \begin{array}{c}0\\ -k_{1}b\\ \begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ k_1\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]$ (5)

In equation (5), $k_1$ is the primary suspension stiffness, $k_2$ stands for the secondary suspension stiffness, a is the distance between bogies center and b is the distance between wheelsets center in the bogies. Subsequently, the governing differential equation of motion of the vehicle is presented in Equation (6) [³⁹].

$\left[K_V\right]\left\{d_V\right\}+\left[C_V\right]\left\{\dot{d_V}\right\}+\left[M_V\right]\left\{\ddot{d_V}\right\}=\left\{F_V\right\}$ (6)

In Equation (6), $\left\{F_V\right\}$, $\left\{d_V\right\}$, $\left\{{\dot{d}}_V\right\}$ and $\left\{{\ddot{d}}_V\right\}$ are vehicle force, displacement, velocity and acceleration vectors, respectively. The interaction between wheel and rail was simulated as nonlinear Hertz spring. The wheel/rail dynamic force was obtained using Equation (7) [³⁹, ⁴¹].

$F_H^{\mathrm{int}}=\{\begin{array}{c}\begin{array}{ccc}{C}_H{(Z_w-Z_r-Z_d)}^{3/2}& if& Z_w-Z_r-Z_d>0\end{array}\\ \begin{array}{ccc}0& if& Z_w-Z_r-Z_d<0\end{array}\end{array}$ (7)

In Equation (7), $C_H$ is the Hertz constant, $F_H^{\mathrm{int}}$ stands for the WRDF, $Z_w$ is the vertical displacement of wheel, $Z_r$ stands for the vertical displacement of rail and $Z_d$ is the magnitude of rail irregularity at the wheel/rail contact point. Equations (4) and (6) were assembled to obtain the governing differential equation of motion of whole model (Equation 8) [³⁹].

$\left[K_{Model}\right]\left\{d\right\}+\left[C_{Model}\right]\left\{\dot{d}\right\}+\left[M_{Model}\right]\left\{\ddot{d}\right\}=\left\{F^{ext}\right\}$ (8)

In equation (8), $\left\{F^{ext}\right\}$, $\left\{d\right\}$, $\left\{\dot{d}\right\}$ and $\left\{\ddot{d}\right\}$ are the external force, displacement, velocity and acceleration vectors of whole model, respectively. [K_Model], [M_Model] and [C_Model] are the stiffness, mass and damping matrices of whole model, respectively. Newmark-Beta integration method in conjunction with full Newton-Raphson iterative scheme were used to solve Equation (8) [⁴⁰, ⁴²].

4 VALIDATION OF MODELS

Validity of the results obtained from the models was evaluated by comparison of the results obtained from the model and those of the field tests. The tests were performed in Line 6 of Tehran subway which was a new line with the length of 32 kilometers, connecting south-east to north-west (Figure 3). As shown in Figure 3, the test location was between Park-Laleh (O6) and Kargar (P6) stations [⁴³]. The validation of the models was carried out in two steps. Accordingly, the field tests were made in two phases. In the first step of the validation, the results obtained from the deterministic model were compared with those obtained from the first phase of the field test. In the second step, the results of the epistemic model were compared with those measured from the second phase of the field test. The details are presented as follows.

4.1 First step/phase

The metro line, selected for the test, was newly constructed. It has not been under operation. In other word, the line has perfect quality condition and the properties of all the rail fasteners along the track were constant. The results obtained from the first phase of the field test were compared with those of the deterministic model.

Figure 3
A view of field test carried out in Tehran metro

Slab track in the field comprises rail, concrete slab and rigid foundation (tunnel lining). A Vosloh SK-14 fastening system connects rails and concrete slab. An elastic layer is placed between concrete slab and tunnel lining in order to reduce train-induced vibrations[⁴³]. Characteristics of slab track in Line 6 are presented in Table 1. A two-axle derezin was passed over the slab track during the tests. The derezin included one carbody and two wheelsets. The wheelbase, axle load, carbody and wheelset masses of the derezin were 4.5 m, 10 tons, 19.6 tons and 0.2 tons, respectively [⁴³].

Table 1
Characteristic of slab track in Line 6 of Tehran metro (adapted from [⁴³])

Value		Parameters
Rail	Mass of rail mr (kg/m)	60
	Modulus of elasticity Er (MPa)	2.1×10e-5
	Inertia Ir (m4)	3.217×10e-5
	Length of moving track element /(m)	0.5
Concrete slab	Mass of concrete slab mt (kg/m)	1275
	Modulus of elasticity Et (MPa)	3.9×10e4
	Inertia It (m4)	8.5×10e-5
Fastening system	Stiffness kr (MN/m)	60
	Damping cr (kN.s/m)	50
	Fastening space (m)	0.6
Elastic layer	Stiffness kt (MN/m)	900
	Damping ct (kN.s/m)	83

Based on Equation (7), rail displacement has a significant effect on the WRDF. Thus, the rail and concrete slab displacements were considered as criterions to evaluate the validity of the results obtained from the model. Linear Variable Displacement Transducers (LVDTs) produced by KANETEC company were used to measure/record displacements of rail and concrete slab[⁴⁴]. Views of LVDTs are shown in Figures (4-a) and (4-b). The derezin was passed over the track with speeds of 20 and 50 km/h and displacements of rail and concrete slab were measured/recorded by the LVDTs (Figure (4-c)). A view of derezin and laptop is shown in Figure (4-d-e). TMR-211 data-logger device (manufactured by Sokki Kenkyujo) was used to acquire the data measured by LVDTs[⁴⁵]. A view of Data-logger used in the field test is shown in Figure (4-f).

Figure 4
installation of LVDTs

Rail and concrete slab displacements were obtained from the model with consideration of characteristics of the slab track (as in Table 1) and the vehicle as the input parameters. The results obtained were compared with those recorded in the field test. They are presented in Figure (5). As illustrated in Figure (5), the trend of the model results is the same as that of the measurement. The maximum difference between the results is about 7 percent. This difference can be due to some minor differences between the model and the field (such as ambient temperature or possible small rail irregularities). The comparison of the results indicates that there is a good agreement between the results obtained from the field test and those of the model.

Figure 5
Comparison between results obtained from the model and those recorded in the field test

4.2. Second step/phase

In order to validate the results obtained from the epistemic model, a railway field in which the properties of fasteners along the track are changed from one to another was prepared. To this end, the properties of the fattening systems in the field (Line 6 of Tehran metro network, indicated in the first step) were changed manually such that the stiffness and damping of each fastener vary from one to another According to the literature, the stiffness and damping of a fastening system are changed as its preload is changed [²⁰]. Therefore, the preload of each fastening system in 50 m length of the line was changed. The preload of each fastening system was a value between 10 and 30 kN.

After preparation of the field, the wheel/rail dynamic force was measured. For this purpose, an accelerometer was installed on the wheelset (Figure (4-d)). The vehicle was passed over the 50 m length of test track and acceleration time history of wheelset was measured using the accelerometer (Figure (8-a)). The speed of the vehicle was 25 km/h. According to the D'Alembert's principle, the dynamic wheel/rail force was obtained using the acceleration time history of wheelset [⁴⁶]. The results are presented in Figure 8.

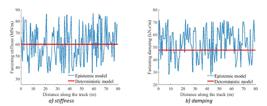
In order to drive the the WRDF from the model, damping and stiffness of the railway fasteners are needed. In this regard, several dynamic tests were performed in the laboratory to drive the dynamic stiffness and damping of each fastening system as a function of preload recorded in the field [²⁰]. A view of laboratory test is presented in Figure (6-a). The preload of fastening system was measured by a torque-meter (Figure (6-b)). It should be noted that the dynamic properties of fastening system were measured based on EN 13146-9 [⁴⁷]. The details of the dynamic test method are available in the literature [²⁰]. Figure (7) presents the results of laboratory tests which indicate dynamic stiffness and damping of each fastening system for 50 m length of the test track. The properties of the railway components as well as properties of the fasteners were imported into the epistemic model and consequently the dynamic wheel/rail force was derived.

Figure 6
Details of dynamic laboratory test of fastening system

Figure 7
Dynamic stiffness and damping of fastening system for the 50 m length of the test track

Figure (8-b) presents the comparison between the dynamic wheel/rail force obtained from the model and the test. As illustrated in this figure, the maximum difference between the results is about 8 percent which is insignificant.

Figure 8
Time histories of acceleration and wheel/rail forces

5 EFFECTS OF FASTENING SYSTEM UNCERTAINTY ON WRDF

In order to investigate the effects of uncertainty of fastening system properties on the WRDF, Uncertainty Factor (UF) was obtained using Equations (9) and (10).

$UF\left(t\right)=\frac{IFUI\left(t\right)}{IFCI\left(t\right)}$ (9)

$UF=Max\left(UF\left(t\right)\right)$ (10)

In Equations (9) and (10), IFUI(t) is the time history of interaction force between the wheel and the rail obtained from the epistemic model, IFCI(t) stands for the time history of the interaction force between the wheel and the rail obtained from the deterministic model, UF(t) is the time history of uncertainty factor and UF is the maximum of UF(t). UF is an index to determine the effect of uncertainty of damping and stiffness of fastening system on the WRDF. The methodology presented in Figure (9) was used in order to compute UF and consequently, evaluate the effect of uncertainty of damping and stiffness of fastening system on the WRDF.

Figure 9
Methodology of uncertainty factor calculation

As indicated in Figure (9), in the first step, the number of sampling is determined. Monte Carlo method with Latin Hypercube Sampling (LHS) was used to obtain the number of sampling (N) [¹⁷, ⁴⁸]. In this method, the required number of sampling (N) was obtained using Equation (11) [⁴⁹].

$N>\frac{-\ln (1-D)}{P_f}$ (11)

In Equation (11), D stands for the confidence level and $P_f$ is the level of vulnerability. Based on the literature, in order to obtain acceptable results, levels of confidence and vulnerability were considered 97% and 2%, respectively [⁴⁸]. As a result, N was considered 175.

The total numbers of track maintenance quality level, vehicle speed and vehicle axle load were obtained in the second to fourth steps, respectively. In order to perform probability analyses, four loops were defined for the numbers of sampling, track maintenance quality levels, vehicle speed, and vehicle axle load (Steps 5, 6, 8 and 9).

According to Figure (9), sample values of fastening system properties for the epistemic model were made based on the level of track maintenance quality (Step 7). A review of the literature indicates that the standard deviation of fastening system properties is dependent on the quality of track maintenance [¹⁷, ²⁴]. Figure (10) presents the variation in properties of fastening system along railway-tracks in three maintenance conditions [⁵⁰]. As shown in this figure, as the maintenance level of the track gets worse, the difference between the fastening properties increases. According to the literature, Coefficient of Variation (CoV) of fastening system properties is 10, 30 and 50 percent for good, medium and poor maintenance conditions, respectively [¹⁷, ²⁴]. Based on the data provided in the literature, Table 2 (dynamic properties of fastening system considered in epistemic and deterministic models) was prepared [²⁴].

Figure 10
Effect of track maintenance level on the uncertainty of fastening properties (adapted from [⁵⁰])

Table 2
Dynamic properties of fastening system considered in epistemic and deterministic models

Maintenance quality condition	Parameter	Mean	CoV (%)	Min.	Max.	Unit
Good	Stiffness	60	10	52.8	67.2	kN/mm
	Damping	50	10	44	56	kN.s/m
Medium	Stiffness	60	30	38.4	81.6	kN/mm
	Damping	50	30	32	68	kN.s/m
Poor	Stiffness	60	50	24	96	kN/mm
	Damping	50	50	20	80	kN.s/m

The truncated normal distribution was used to obtain sample values for fastening system properties in the epistemic model [¹⁷]. Using this method, the properties of each fastening system (stiffness and damping) are different from those of its adjacent fasteners in the epistemic model. In the deterministic model, the properties of all fastening systems were kept unchanged. Properties of fastening systems for the deterministic and epistemic models are presented in Figure (11). As shown in Figure (11), the slab track length was considered 80 m. In Figure (11), the damping and stiffness of fastening systems in the epistemic model were derived using the truncated normal distribution with damping mean value of 50 kN.s/m, stiffness mean value of 60 MN/m and CoV of 0.3 [¹⁷]. As shown in Figure (11), the properties of each fastening system in the epistemic model are different from those of other fasteners. The damping and stiffness of all fastening systems in the deterministic model are the damping mean value (50 kN.s/m) and the stiffness mean value (60 MN/m), respectively.

Figure 11
Fastening system properties along the track for epistemic and deterministic models

As illustrated in Figure (9), the uncertainty factor for each probability analysis is calculated (steps 10 to 11). In the last step, the maximum effect of damping and stiffness of fastening system on the uncertainty factor is obtained in the sensitivity analysis. The methodology presented in Figure (9) was performed for a slab track with and without rail irregularity.

5.1 Probability and sensitivity analyses

Probability and sensitivity analyses were performed in order to investigate the effects of uncertainty of fastening system properties on the WRDF for slab track with and without rail irregularity. In this regard, a vehicle with properties presented in Table (3) was passed over the slab track with characteristics presented in Table (3). The vehicle speed was considered 20, 50, 75, 100, 125, 150, 175 and 200 km/h. Axle load of vehicle was varied from 16 to 32 tons with intervals of 2 tons in the probability analyses (i.e., nine different magnitudes were considered for the vehicle axle load). The track length was considered 80 m which includes 134 fasteners. Thus, 134 sample values were assigned to the fastening systems in the epistemic model in each analysis (see Figure (11)). As presented in Table (3), sample values of dynamic properties of fasteners for the epistemic model were obtained based on damping mean value of 50 kN.s/m, stiffness mean value of 60 MN/m, and three levels of standard deviation [¹⁷]. The sensitivity analysis was performed in four parts. In the first and the second parts, the effect of uncertainty of fastener’s properties (damping and stiffness) on the WRDF were investigated in a smooth track (track without irregularities). In the third and fourth parts, the influences of uncertainty of damping and stiffness of fastening system on the WRDF was investigated for the track with irregularity. Also, the mean value of dynamic stiffness and damping of fastening system for the deterministic model were considered 60 kN/mm and 50 kN.s/m, respectively [¹⁷].

Table 3
Vehicle and Slab Track Properties (adopted from [³⁹, ⁴³])

Vehicle Properties			Slab Track Properties
Parameter	Value	Unit	Parameter	Value	Unit
Car body mass	40,000	Kg	Rail flexural rigidity	6.75e6	Nm2
Bogie mass	3,200	Kg	Rail mass per unit length	60	kg/m
Wheelset mass	2,400	Kg	Fastening space	0.6	M
Mass moment of inertia of the car body	547,000	Kg.m2	Railpad dynamic stiffness	60	MN/m
Mass moment of inertia of the bogie	6,800	Kg.m2	Railpad dynamic damping	47.7	kN.s/m
Primary suspension stiffness	2,080	kN/m	Slab flexural rigidity	3.31e6	Nm2
Primary suspension damping	100	kN.s/m	Slab mass per unit length	275	kg/m
Secondary suspension stiffness	800	kN/m	Elastic layer Stiffness	900	MN/m
Secondary suspension damping	120	kN.s/m	Elastic layer Damping	83	kN.s/m
Distance between bogie center	17.5	M
Distance between wheelset center in bogie	2.5	M
Hertz spring constant	702×10e8	N/m3/2

For eight different magnitudes of vehicle speed, nine different values of axle load, three levels of track maintenance quality, and 175 random samplings of fastening properties, 8925 probability analyses (3×9×175+3×8×175) were performed and consequently, UF was obtained for each analysis, using Equations (9) and (10). For instance, Figure (12) shows the time histories of interaction force between wheel and rail obtained from the epistemic and deterministic models (IFUI(t) and IFCI(t)) and UF(t) for the vehicle speed of 200 km/h, axle load of 240 kN and COV of 30% (for rail without irregularity). According to the results presented in Figure (12), the maximum values of UF(t) (UF) for uncertainty of fastening system stiffness and damping are 5% and 2.2%, respectively. The results obtained from probability analyses for slab track with and without rail irregularity are presented in the following sections.

Figure 12
Effect of uncertainty of fastening system properties on the wheel/rail force for slab track without irregularity

5.2 Slab track without irregularity

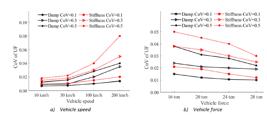
Sometimes, defective rail is replaced by a new one and its fastening systems are not changed/replaced in process of repair and maintenance. In this situation, while rail has no irregularity, the properties of fasteners might vary from one to another, making non-uniformity in the stiffness of rail supporting system along the track. A question which is raised, is how does the uncertainty of the uniformity of fasteners properties along the track might affects the WRDF. In response to this question, the effect of uncertainty of fastening system properties on the WRDF for slab track without irregularity was investigated. Figure (13) presents the effects of vehicle speed and axle load on UF for fastening properties uncertainty of 30%. As the number of sampling (N) is 175, 175 cloud curves are drawn in Figures (13-a) and (13-b). In other word, each cloud curve corresponds to each number of random sampling. Vehicle speed and axle load were considered 100 km/h and 24 tons in Figure (13-a) and (13-b), respectively. As shown in Figure (13-a), when the vehicle speed is lower than 100 km/h, the maximum value of UF is about 5% (which is negligible). On other hand, when the vehicle speed changes from 100 to 200 km/h, UF increases considerably (about 15%). As the vehicle speed increases from 20 to 200 km/h, the dispersion between curves increases.

Figure 13
Effects of variations of vehicle speed and axle load on UF for COV=0.3 (slab track without irregularity)

According to the results presented in Figure (13-b), as the axle load increases, UF decreases. When axle load is greater than 24 tons, the maximum value of UF reaches to about 5 percent which is negligible. As illustrated in Figure (13-b), uncertainty of fastening system properties has a significant effect on the WRDF for the axle load of lower than 24 tons.

In order to summarize the large amount of data presented in Figure 13, two indexes (dispersion of UF(β) and mean value of UF (Δ_UF)) were defined. Dispersion of UF(β) and mean value of UF (Δ_UF) are obtained by Equations (12) and (13), respectively [⁵¹].

${\Delta }_{UF}=mea{n}_j(U{F}_{}^j)$ (12)

$\beta =\sqrt{\frac{{\displaystyle {\sum }_{j=1}^N{(U{F}_{}^j-{\Delta }_{UF})}^2}}{N-1}}$ (13)

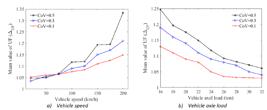
In Equations (12) and (13), j stands for the number of probability analysis, UFj is the maximum of UF _j (t) obtained from Equation 6, $me{d}_j$ stands for the mean function of UFj. The mean value of UF is a proper index to determine the effecting level of uncertainty of fastening system properties on the WRDF. Figure 10 presents the mean value of the UF for three levels of track maintenance quality (COV of 10, 30 and 50%). The vehicle axle load and vehicle speed were considered 200 km/h and 24 tons in Figures (14-a) and (14-b), respectively. As shown in Figure (14-a), when vehicle speed increases, the effect of uncertainty of fastening system properties increases. For instance, while the UF mean values for three maintenance quality levels are about 1.02 in vehicle speed of 20 km/h, the UF mean value of the good, medium and poor maintenance quality levels increases to 1.14, 1.11 and 1.08, respectively for the vehicle speed of 200 km/h.

As vehicle axle load increases, the effect of uncertainty of fastening system properties on UF decreases (Figure (14-b)). For instance, when axle load is increased from 16 to 32, the UF is decreased about 11% and 3% for COV of 30% and 10%, respectively. Figure (14) shows that the maximum effect of uncertainty of fastening system properties on the mean value of UF is about 15%.

Figure 14
Effects of variations of vehicle speed and axle load on UF mean value for three levels of maintenance quality for slab track without irregularity

Figure (15) presents the effects of variations of vehicle speed and axle load on dispersion of UF for different levels of track maintenance quality. As illustrated in Figure (15), the maximum dispersion reaches to about 0.045. This means that uncertainty of fastening system properties has not significant effect on the UF in slab track without irregularity.

Figure 15
Dispersion of UF for different levels of maintenance quality for slab track without irregularity

The uncertainties of stiffness and damping of fastening system were the same in the data presented in Figures 14 to 15. In other word, when COV of fastening system stiffness was 10, 30 and 50%, COV of fastening system damping was 10, 30 and 50%, respectively. Further random analyses (sensitivity analyses) were carried out to find out which one (uncertainty of stiffness or damping) has greater effect on the UF. In this regard, COVs of stiffness and damping of fastening system were varied independently during sensitivity analyses. Figure 16 shows the results obtained from sensitivity analyses. The axle load is considered 24 tons in Figure 16(a). Vehicle speed is considered 200 km/h in Figure 16(b).

As shown in Figure (16-a), when vehicle speed or COV of fastening properties increases, the COV of UF increases. Figure (16-a) shows that variation of COV of fastening system stiffness has a greater influence on the COV of UF compared with that of fastening system damping. As shown in Figure (16-b), as vehicle axle load increases or COV of fastening properties decreases, the COV of UF decreases.

Figure 16
Effect of COV of fastening system properties on the COV of UF for slab track without irregularity

5.3 Slab track with irregularity

According to the literature, the existence of rail irregularities considerably intensifies the effects of other parameters on the WRDF [⁵²-⁵⁴]. In order to investigate the effect of uncertainty of fastening system properties on the WRDF in presence of rail irregularities, a sinusoidal irregularity with wavelength of 3 m and amplitude of 7 mm (as mostly reported in the literature [³⁵]) was considered on the rail surface of the track studied in the previous section. All probability and sensitivity analyses performed in the previous section were carried out in this section with consideration of the sinusoidal irregularity on rail surface. The effects of uncertainty of fastening system properties on the UF in the presence of irregularity are shown in Figure 13 for different vehicle speeds and axle loads. The vehicle axle load and vehicle speed are 24 tons and 100 km/h in Figures (17-a) and (17-b), respectively. The trend of results presented in Figure 17 is the same as that of Figure 13. As shown in Figure 13, when vehicle speed increases from 10 to 100 km/h, the UF increases up to about 5% (which is same as that of slab track without irregularity). On other hand, as the vehicle speed increases from 100 to 200 km/h, the UF increases significantly (from 1.05% to 1.5%). A comparison between Figures 17 and 13 shows that rail irregularity increases the effects of uncertainty of fastening system properties on the UF. For instance, when vehicle speed increases 100 percent, the UF increases up to 40% and 15% for the slab tracks with and without irregularity, respectively.

Figure 17
Effects of variations of vehicle speed and axle load on UF for COV=0.3 in presence of irregularity

The mean values of UF for different levels of maintenance quality, vehicle speeds and vehicle axle loads are presented in Figure 18. According to Figure 14, the difference between the mean values of different levels of maintenance quality increases when the vehicle speed increases or the vehicle axle load decreases. The lower level of maintenance quality, the greater difference between mean values of UF. It means that probability methods with high reliability (such as Monte Carlo with LHS) should be used in order to investigate the effect of uncertainty of fastening system properties on the WRDF in presence of rail irregularity [¹⁵]. Results obtained shows that the difference between mean values of poor and good maintenance quality levels is about 4% for vehicle speed of 100 km/h (see Figure (18-a)). As vehicle speed increases from 100 to 200 km/h, the difference reaches to 14%. On other hand, the maximum difference between different levels of maintenance quality is limited to 5% for vehicle speeds lower than 100 km/h and axle loads greater than 24 tons. The results presented in Figure (18-a) indicate that the maximum effect of uncertainty of fastening system properties on the wheel/rail force reaches to about 35% for slab tracks with irregularity.

Figure 18
Effects of variations of vehicle speed and axle load on UF mean value for three levels of maintenance quality in presence of irregularity

Figure 19 shows the effects of variations of vehicle speed and axle load on dispersion of UF for different levels of track maintenance quality in presence of irregularity. As shown in Figure 19, the greater vehicle speed, the greater dispersion of UF. As illustrated in Figure (19), when vehicle speed is 200 km/h, the dispersion of UF for low quality maintenance condition reaches to a considerable value (0.06). When the vehicle axle load decreases, the dispersion of UF increases (Figure (19-b)). According to Figure (19), the maximum dispersion of UF is about 0.02 when vehicle speed is lower than 100 km/h or vehicle axle load is greater than 24 tons.

Figure 19
Dispersion of AF for different levels of maintenance quality in presence of irregularity

Figure (20-a) shows the effect of uncertainty of fastening system properties on the covariance (COV) of UF for axle load of 16, 20, 24 and 28 tons and vehicle speed of 100 km/h in the presence of rail irregularity. Figure (20-b) presents effect of uncertainty of fastening properties on the covariance (COV) of UF for vehicle speeds of 10, 50, 100 and 200 km/h and axle load of 24 tons in presence of irregularity. As shown in Figure (20-b), as vehicle speed or COV of fastening properties increases, the COV of UF increases. When the vehicle speed is 200 km/h, the maximum COV of UF is about 20% and 13% for uncertainty of stiffness and damping of fastening properties, respectively. As shown in Figure (20-a), variation of vehicle axle load has not significant effect on the COV of UF. For instance, when vehicle axle load increases 75%, the COV of UF increases 3% and 1.5% for uncertainties of stiffness and damping, respectively.

Figure 20
Effect of COV of fastening system properties on the COV of UF for slab track with irregularity

6 DEVELOPMENT UNCERTAINTY FACTOR FOR WRDF

In this research, it was shown that the amount of WRDF is considerably influenced by the uncertainty of fastening system properties. It was also shown that the variation in the WRDF due to uncertainty of fastener properties depends on the level of track maintenance quality, vehicle speed, vehicle axle load, and rail irregularity. To drive amplification of WRDF due the uncertainty of fastening system properties, probability analyses were performed for various vehicle speeds, vehicle axle loads and levels of real irregularity profile (i.e, track maintenance quality condition).

Federal Railroad Administration (FRA) Code presented real irregularity profile for different quality levels of track maintenance (six classes) [⁵¹, ⁵⁵-⁵⁷]. As the level of track maintenance quality decreases, the severity of irregularity profile increases. Based on the previous studies, irregularity classes 1, 4 and 6 of FRA were considered as irregularity profiles for the track with poor (COV=10), medium (COV=30) and good (COV=50) maintenance quality condition, respectively [⁵⁸, ⁵⁹]. Figure (21) presents three classes of irregularity profiles obtained from FRA.

Figure 21
Real irregularity profile (adapted from [⁵¹, ⁵⁵-⁵⁷])

Real profile irregularities presented in Figure 21 were considered on the rail surface of the track described in the previous section and 50400 probability analyses were performed for the slab track with the three irregularity profiles. For each probability analysis, the mean value of UF (${\Delta }_{UF}$) obtained from Equation 12 was considered as an index to show the variation of WRDF. The results obtained from the probability analyses are shown in Figure 22. Figures 22(a), 22(b) and 22(c) are related to good, medium and poor levels of maintenance quality, respectively.

Using Figure (22), one can derive ${\Delta }_{UF}$ based on level of track maintenance quality, vehicle speed and axle load. For instance, when vehicle axle load is 240 kN, vehicle speed is 140 km/h and the track is in good maintenance quality 1.1 is obtained for ${\Delta }_{UF}$ (Figure 22-a). According to Figure (22), the maximum variation of WRDF due to the uncertainty of fastening system properties is about 1.16, 1.3 and 1.5 for good, medium and pool level of track maintenance quality, respectively. The results obtained indicate that the uncertainty of fastening system properties causes a relatively significant increase in WRDF.

Figure 22
uncertainty factor contours

7 CONCLUSION

Although fastening system properties have uncertainty, the influence of uncertainty of fastening system properties on the Wheel/Rail Dynamic Force (WRDF) is omitted in the previous studies. In this regard, effects of uncertainty of fastening system properties on the WRDF were investigated in this research. To this end, two 2D models (deterministic and epistemic models) of vehicle/ slab track interaction were developed using finite element method and multi body system dynamics. The models include wagon, rail, fastening system, concrete slab, elastic layer, and subgrade. In the deterministic model, the stiffness and damping of fastening system were considered constant. The uncertainty of fastening system properties was considered in the epistemic model. The validity of the results obtained from the model was shown through a comparison between the results and those obtained from field test carried out in this study. A criterion named as Uncertainty Factor (UF) was defined in order to investigate the effects of uncertainty of fastening system on the WRDF. A large number of probability and sensitivity analyses were performed in different vehicle axle loads, vehicle speeds and different levels of track quality maintenance condition in order to calculate UF (Uncertainty Factor: the percent of increase/decrease on the WRDF due to uncertainty of fasteners properties). The analyses were carried out for slab track with and without irregularity.

The results obtained from the aleatory analyses show that uncertainty of fastening system properties has not significant effect on the WRDF in slab track without irregularity although when vehicle speed increases or vehicle axle load decreases, the effect of uncertainty of fastening system properties on the WRDF increases. The results obtained indicate that the maximum effect of uncertainty of fastening system properties on the mean value of UF is about 15% for slab track without irregularity. On the other hand, UF was dramatically influenced by the uncertainty of fastening system properties in a slab track with irregularity. For instance, when vehicle speed increases 100 percent, the UF increases up to 40% in the case of slab tracks with irregularity.

A large number of probability analyses were carried out for different vehicle speeds, vehicle axle loads, levels of track maintenance quality and real profile irregularities. Using the results obtained, the mean value of UF for the effect of uncertainty of fastening system properties on the WRDF was derived. Several counters were developed which provide the mean value of uncertainty factor (i.e., an amplification factor for the WRDF) as a function of vehicle axle load, vehicle speed and track quality maintenance conditions.

References

• ¹
  Yang, X., X. Ma, and J. Shen, Influence of railway track slab’s geometry and dynamic parameters on its sound radiation characteristics, in ICRT 2017: Railway Development, Operations, and Maintenance. 2018, American Society of Civil Engineers Reston, VA. p. 71-78.
• ²
  Sharma, S.K., et al., Challenges in rail vehicle-track modeling and simulation. International Journal of Vehicle Structures & Systems, 2015. 7(1): p. 1.
• ³
  Gao, J., W. Zhai, and Y. Guo, Wheel-rail dynamic interaction due to rail weld irregularity in high-speed railways. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2018. 232(1): p. 249-261.
• ⁴
  Fermér, M. and J.C. Nielsen, Vertical interaction between train and track with soft and stiff railpads-full-scale experiments and theory. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 1995. 209(1): p. 39-47.
• ⁵
  Baeza, L., A. Roda, and J.C.O. Nielsen, Railway vehicle/track interaction analysis using a modal substructuring approach. Journal of sound and vibration, 2006. 293(1-2): p. 112-124.
• ⁶
  Mandal, N.K., M. Dhanasekar, and Y.Q. Sun, Impact forces at dipped rail joints. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2016. 230(1): p. 271-282.
• ⁷
  Cremona, M.A., et al., Predicting railway wheel wear under uncertainty of wear coefficient, using universal kriging. Reliability Engineering & System Safety, 2016. 154: p. 49-59.
• ⁸
  Croft, B.E., C.J.C. Jones, and D.J. Thompson, Modelling the effect of rail dampers on wheel-rail interaction forces and rail roughness growth rates. Journal of Sound and Vibration, 2009. 323(1-2): p. 17-32.
• ⁹
  Yang, Z., et al., Numerical and experimental study of wheel-rail impact vibration and noise generated at an insulated rail joint. International Journal of Impact Engineering, 2018. 113: p. 29-39.
• ¹⁰
  Zhai, W., K. Wang, and C. Cai, Fundamentals of vehicle-track coupled dynamics. Vehicle System Dynamics, 2009. 47(11): p. 1349-1376.
• ¹¹
  Rhayma, N., et al., A probabilistic approach for estimating the behavior of railway tracks. Engineering Structures, 2011. 33(7): p. 2120-2133.
• ¹²
  Patra, A.P., P. Söderholm, and U. Kumar, Uncertainty estimation in railway track life-cycle cost: a case study from Swedish National Rail Administration. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2009. 223(3): p. 285-293.
• ¹³
  Macchi, M., et al., Maintenance management of railway infrastructures based on reliability analysis. Reliability Engineering & System Safety, 2012. 104: p. 71-83.
• ¹⁴
  Kaewunruen, S., M.H. Osman, and W. Hao Cheng Eric, Risk-Based Maintenance Planning for Rail Fastening Systems. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, 2019. 5(3): p. 04019007.
• ¹⁵
  Salcher, P., C. Adam, and A. Kuisle, A stochastic view on the effect of random rail irregularities on railway bridge vibrations. Structure and Infrastructure Engineering, 2019. 15(12): p. 1649-1664.
• ¹⁶
  Mehrali, M., et al., Investigating on Vehicle-Slab Track Interaction Considering Random track bed Stiffness. scientiairanica, 2014. 21(1): p. 82-90.
• ¹⁷
  Zhu, S., C. Cai, and W. Zhai, Interface damage assessment of railway slab track based on reliability techniques and vehicle-track interactions. Journal of Transportation Engineering, 2016. 142(10): p. 04016041.
• ¹⁸
  Feng, H., et al., Automatic fastener classification and defect detection in vision-based railway inspection systems. IEEE transactions on instrumentation and measurement, 2013. 63(4): p. 877-888.
• ¹⁹
  Kenjale, O., AUTOMATIC FASTENER CLASSIFICATION AND DEFECT DETECTION IN VISION-BASED RAILWAY INSPECTION SYSTEMS. International Journal Of Emerging Technology and Computer Science, 2016. 1(2).
• ²⁰
  Sadeghi, J., M. Seyedkazemi, and A. Khajehdezfuly, Nonlinear simulation of vertical behavior of railway fastening system. Engineering Structures, 2020. 209: p. 110340.
• ²¹
  Oregui, M., et al., Sensitivity analysis of railpad parameters on vertical railway track dynamics. Journal of Engineering Mechanics, 2017. 143(5): p. 04017011.
• ²²
  Wei, J., et al., Online condition monitoring of a rail fastening system on high-speed railways based on wavelet packet analysis. Sensors, 2017. 17(2): p. 318.
• ²³
  Mohammadzadeh, S., S. Ahadi, and M. Nouri, Stress-based fatigue reliability analysis ofthe rail fastening spring clipunder traffic loads. Latin American Journal of Solids and Structures, 2014. 11(6): p. 993-1011.
• ²⁴
  Yuan, Z., S. Zhu, and W. Zhai. Damage Detection of Rail Fastening System Through Deep Learning and Vehicle-Track Coupled Dynamics. in The IAVSD International Symposium on Dynamics of Vehicles on Roads and Tracks. 2019. Springer.
• ²⁵
  Yuan, X., et al. Reliability Analysis of Rail Fastening System When a Heavy Haul Locomotive Passing Through a Small Radius Curve. in The IAVSD International Symposium on Dynamics of Vehicles on Roads and Tracks. 2019. Springer.
• ²⁶
  Jiang, L., et al., Train-bridge system dynamics analysis with uncertain parameters based on new point estimate method. Engineering Structures, 2019. 199: p. 109454.
• ²⁷
  Nouri, M. and S. Mohammadzadeh, Probabilistic estimation of dynamic impact factor for masonry arch bridges using health monitoring data and new finite element method. Structural Control and Health Monitoring, 2020. 27(12): p. e2640.
• ²⁸
  Xin, L., et al., Uncertainty and sensitivity analysis for train-ballasted track-bridge system. Vehicle System Dynamics, 2020. 58(3): p. 453-471.
• ²⁹
  Khajehdezfuly, A., Effect of rail pad stiffness on the wheel/rail force intensity in a railway slab track with short-wave irregularity. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2019. 233(10): p. 1038-1049.
• ³⁰
  Xu, L., J. Gao, and W. Zhai, On effects of rail fastener failure on vehicle/track interactions. Structural Engineering and Mechanics, 2017. 63(5): p. 659-667.
• ³¹
  Sadeghi, J. and H. Askarinejad, Development of nonlinear railway track model applying modified plane strain technique. Journal of transportation engineering, 2010. 136(12): p. 1068-1074.
• ³²
  Rhayma, N., et al., Reliability analysis of maintenance operations for railway tracks. Reliability Engineering & System Safety, 2013. 114: p. 12-25.
• ³³
  Verachtert, R., et al., Changes of perceived unevenness caused by in-track vibration countermeasures in slab track. European Journal of Mechanics-A/Solids, 2017. 65: p. 40-58.
• ³⁴
  Costa, P.A., et al., Critical speed of railway tracks. Detailed and simplified approaches. Transportation Geotechnics, 2015. 2: p. 30-46.
• ³⁵
  Przemieniecki, J.S., Theory of Matrix Structural Analysis. Dover, New York, 1985.
• ³⁶
  Xu, L., et al., On effects of track random irregularities on random vibrations of vehicle-track interactions. Probabilistic Engineering Mechanics, 2017. 50: p. 25-35.
• ³⁷
  Luu, M., V. Zabel, and C. Könke, An optimization method of multi-resonant response of high-speed train bridges using TMDs. Finite Elements in Analysis and Design, 2012. 53: p. 13-23.
• ³⁸
  Chopra, A., Dynamics of structures, theory and applications to earthquake engineering. Englewood Cliffs, NJ: Prentice-Hall, 1995.
• ³⁹
  Sadeghi, J., et al., Dynamic interaction of vehicle and discontinuous slab track considering nonlinear Hertz contact model. Journal of Transportation Engineering, 2016. 142(4): p. 04016011.
• ⁴⁰
  Lei, X. and J. Wang, Dynamic analysis of the train and slab track coupling system with finite elements in a moving frame of reference. Journal of Vibration and Control, 2014. 20(9): p. 1301-1317.
• ⁴¹
  Salcher, P. and C. Adam, Estimating Exceedance Probabilities of Railway Bridge Vibrations in the Presence of Random Rail Irregularities. International Journal of Structural Stability and Dynamics, 2020: p. 2041005.
• ⁴²
  Sadeghi, J., et al., An efficient algorithm for nonlinear analysis of vehicle/track interaction problems. International Journal of Structural Stability and Dynamics, 2016. 16(08): p. 1550040.
• ⁴³
  Tehran-metro, Tehran metro line No.6 slab track design. 2010, Tehran urban & suburban railway operation Co: Iran-Tehran.
• ⁴⁴
  Esmaeili, M., K. Yousefian, and R. Nouri, Vertical load distribution in ballasted railway tracks with steel slag and limestone ballasts. International Journal of Pavement Engineering, 2019. 20(9): p. 1065-1072.
• ⁴⁵
  Alembagheri, M., M. Rashidi, and M. Seyedkazemi, Structural system identification of elevated steel water tank using ambient vibration test and calibration of numerical model. International Journal of Structural Stability and Dynamics, 2020. 20(10): p. 2071010.
• ⁴⁶
  Sadeghi, J., A. Masnabadi, and A. Mazraeh. Correlations among railway turnout geometry, safety and speeds. in Proceedings of the Institution of Civil Engineers-Transport. 2016. Thomas Telford Ltd.
• ⁴⁷
  Railway applications-track test methods for fastening systems-Part 9: Determination of stiffness. European committee for standardization. 2009, CEN (European Committee for Standardization): Brussels.
• ⁴⁸
  Alembagheri, M. and M. Seyedkazemi, Seismic performance sensitivity and uncertainty analysis of gravity dams. Earthquake Engineering & Structural Dynamics, 2015. 44(1): p. 41-58.
• ⁴⁹
  Broding, W.C., F.W. Diederich, and P.S. Parker, Structural optimization and design based on a reliability design criterion. Journal of Spacecraft and Rockets, 1964. 1(1): p. 56-61.
• ⁵⁰
  Sadeghi, J., Report on maintenance operations of Tehran metro lines. 2017: School of Railway Engineering, Iran University of Science and Technology.
• ⁵¹
  Mohammadzadeh, S., S.A. Mosayebi, and R. Moosapoor, Investigating on the effects of random irregularities of railway track by half-bogie model. Advances in Railway Engineering, An International Journal, 2013. 1(1): p. 61-75.
• ⁵²
  Steenbergen, M.J.M.M., Quantification of dynamic wheel-rail contact forces at short rail irregularities and application to measured rail welds. Journal of Sound and Vibration, 2008. 312(4-5): p. 606-629.
• ⁵³
  Remennikov, A.M. and S. Kaewunruen, A review of loading conditions for railway track structures due to train and track vertical interaction. Structural Control and Health Monitoring: The Official Journal of the International Association for Structural Control and Monitoring and of the European Association for the Control of Structures, 2008. 15(2): p. 207-234.
• ⁵⁴
  Perrin, G., et al., Track irregularities stochastic modeling. Probabilistic Engineering Mechanics, 2013. 34: p. 123-130.
• ⁵⁵
  Au, F., J. Wang, and Y. Cheung, Impact study of cable-stayed railway bridges with random rail irregularities. Engineering Structures, 2002. 24(5): p. 529-541.
• ⁵⁶
  Rezvani, M.A., M.M. Feizi, and M. Shadfar, An innovative method for stress analysis of Y25 bogie under oscillating loads due to tank wagon fluid sloshing. Journal of Theoretical and Applied Mechanics, 2014. 52(3): p. 745-755.
• ⁵⁷
  Xu, Q.-y., et al., Effects of track irregularities on environmental vibration caused by underground railway. European Journal of Mechanics-A/Solids, 2016. 59: p. 280-293.
• ⁵⁸
  Berggren, E., Railway track stiffness: dynamic measurements and evaluation for efficient maintenance. 2009.
• ⁵⁹
  Dahlberg, T., Railway track stiffness variations-consequences and countermeasures. International journal of civil engineering, 2010. 8(1): p. 1-12.

Edited by

Editor:

Marcílio Alves

Publication Dates

• Publication in this collection
  18 June 2021
• Date of issue
  2021

History

• Received
  24 Apr 2021
• Reviewed
  07 May 2021
• Accepted
  07 May 2021
• Published
  10 May 2021