Abstract
In the present paper, a new fifth-order shear and normal deformation theory (FOSNDT) is developed for the bi-directional bending analysis of laminated composite and sandwich plates subjected to transverse loads. This theory considered the effects of both transverse shear and normal deformations. In-plane displacements use a polynomial shape function expanded up to fifth-order in terms of the thickness coordinate to properly account the effect of transverse shear deformation. Transverse displacement is the function of x, y and z- coordinates to account the effect of transverse normal deformations i.e. thickness stretching. Hence, the present theory involves nine unknowns in the displacement field. The present theory does not require a problem dependent shear correction factor as it satisfies traction free boundary conditions at top and bottom surfaces of the plate. The governing differential equations and associated boundary conditions are obtained using the principle of virtual work. The plate is analysed for simply supported boundary conditions using Navier’s solution technique. To prove the efficiency of the present theory, the non-dimensional displacements and stresses obtained for laminated composite and sandwich plates are compared with existing exact elasticity solutions and other theories. It is observed from the comparision that the displacements and stresses obtained by the present theory are in excellent agreement with the results obtained by exact elasticity solutions compared to other higher-order plate theories available in the literature.
Keywords
2D analysis; fifth-order; shear deformation; normal deformation; shear correction factor; laminated; sandwich
1 INTRODUCTION
Due to attractive structural properties like high strength-to-weight and high stiffness-to-weight ratios, the demand of composite materials is increased in many engineering industries such as mechanical engineering, marine engineering, civil engineering, aerospace engineering, etc. Therefore, accurate prediction of bending behaviour of the structures made of advanced composite materials is an important part of the analysis. One of the important steps to develop accurate analysis of composite plates is to select a proper structural theory for the problem.
The analyses of laminated composite plates have been based on one of the following approaches. 1) Equivalent single layer (ESL) theories 2) Layer wise theories and 3) Three dimensional elasticity theories. The fundamental objective in the development of elasticity solution is to obtain accurate results of global and local quantities. These solutions are serving as benchmark solution for approximate theories. Pagano (1970Pagano, N. J. (1970). Exact solutions for bidirectional composites and sandwich plates. Journal of Composite Materials 4: 20-34.) and Zenkour (2007Zenkour, A. M. (2007). Three-dimensional elasticity solution for uniformly loaded cross-ply laminates and sandwich plates. Journal of Sandwich Structures and Materials 9: 213-238.) have developed exact elasticity solutions for rectangular bidirectional composites and sandwich plates. Since three dimensional elasticity theories and layer wise theories are computationally difficult, equivalent single layer theories are widely used for the modeling and analysis of laminated composite thick plates. The ESL theories are those in which a heterogeneous laminate plate is treated as a statically equivalent single layer having a complex constitutive behaviour, reducing the 3D continuum problem to a 2D problem.
The simplest ESL laminate theory is the classical laminated plate theory (CLPT) of Kirchhoff (1850Kirchhoff, G.R. (1850). Uber das gleichgewicht und die bewegung einer elastischen scheibe. Journal for Pure and Applied Mathematics (Crelle’s Journal) 40:51-88.). But, when CLPT is applied to the analysis of composite plates it underpredicts the deflections and stresses, and overpredicts natural frequencies and critical buckling loads. This is due to neglect of transverse shear deformation. Therefore, CLPT is suitable for thin plate only. To overcome this drawback of CLPT, Mindlin (1951Mindlin, R.D. (1951). Influence of rotary inertia and shear on flexural motions of isotropic, elastic plates. ASME Journal of Applied Mechanics 18: 31-38.) has developed first order shear deformation theory (FSDT) which considers the linear variation of transverse shear deformation across the thickness of the plate. The FSDT shows constant variation of transverse shear stress through the thickness of the plate and required shear correction factor to properly account the strain energy due to shear deformation. These limitations of CLPT and FSDT leads to the development of higher order refined plate theories.
Several higher order refined plate theories are developed by various researchers which uses polynomial and non-polynomial type shape functions to properly account the effect of shear deformation (Polynomial: Ambartsumian, 1958Ambartsumian, S.A. (1958). On the theory of bending plates. Izv Otd Tekh Nauk AN SSSR 5:69-77.; Reddy, 1984Reddy, J. N. (1984). A simple higher order theory for laminated composite plates. ASME Journal of Applied Mechanics 51:745-752.; Pandya and Kant, 1988Pandya, B.N., and Kant, T. (1988). Finite element stress analysis of laminated composite plates using higher-order displacement model. Composite Science and Technology 32:137-55.; etc. Non-polynomial: Levy, 1877Levy, M. (1877). Memoire sur la theorie des plaques elastique planes. Journal des Mathematiques Pures et Appliquees 30: 219-306.; Touratier, 1991Touratier, M. (1991). An efficient standard plate theory. Int J Eng Sci 29(8):901-16.; Soldatos, 1992Soldatos, K. P. (1992). A transverse shear deformation theory for homogeneous monoclinic plates. Acta Mechanica 94:195-200.; Karama et al., 2009Karama, M., Afaq, K.S., Mistou, S. (2009). A new theory for laminated composite plates. Proceedings of The Institution of Mechanical Engineers, Part L: Journals of Materials: Design and Applications 223:53-62.; Mantari et al., 2012Mantari, J. L., Oktem, A. S., Soares, C. G. (2012). A new trigonometric shear deformation theory for isotropic, laminated composite and sandwich plates. International Journal of Solids and Structures 49:43-53.; Grover et al., 2013Grover, N., Singh, B. N., Maiti, D. K. (2013). Analytical and finite element modeling of laminated composite and sandwich plates: an assessment of a new shear deformation theory for free vibration response. International Journal of Mechanical Science 67:89-99.; Sayyad and Ghugal, 2017aSayyad, A. S., and Ghugal, Y. M. (2017a). A unified shear deformation theory for the bending of isotropic, functionally graded, laminated and sandwich beams and plates. International Journal of Applied Mechanics 9(1):1-36. etc.). One can refer recently published review articles by Sayyad and Ghugal (2015aSayyad, A. S., and Ghugal, Y. M. (2015a). On the free vibration analysis of laminated composite and sandwich plates: A review of recent literature with some numerical results. Composite Structures 129: 177-201., 2017bSayyad, A. S., and Ghugal, Y. M. (2017b). Bending, buckling and free vibration of laminated composite and sandwich beams: A critical review of literature. Composite Structures 171:486-504.) for other refined beam and plate theories available in the literature. Chakrabarti and Sheikh (2005Chakrabarti, A., and Sheikh, A. H. (2005). Analysis of laminated sandwich plates based on interlaminar shear stress continuous plate theory. ASCE Journal of Engineering Mechanics 131(4): 377-384.) have studied the bending response of sandwich plates with stiff laminated face using six noded triangular element having seven degrees of freedom at each node. Zhen and Wanji (2007Zhen, W., and Wanji, C. (2007). A study of global-local higher order theories for laminated composite plates. Composite Structures 79:44-54.) have presented a study of global-local higher order theories for laminated composite plates. Thai et al. (2012Thai, C. H., Tran, L. V., Tran, D. T., Nguyen-Thoi, T., and Nguyen-Xuan, H. (2012). Analysis of laminated composite plates using higher order shear deformation plate theory and node based smoothed discrete shear gap method. Applied Mathematical Modeling 36:5657-5677.) have presented a novel finite element formulation for static, free vibration and buckling analyses of laminated composite plates. Thai and Choi (2013)Thai, H. T., and Choi, D. H. (2013). A simple first order shear deformation theory for laminated composite plates. Composite Structures 106:754-763. have developed a simple first order shear deformation theory for laminated composite plates, the theory contains only four unknowns and having similarities with the CPT and Navier’s solution approach is used to obtain solution. Sayyad and Ghugal (2015b)Sayyad, A. S., and Ghugal, Y. M. (2015b). A four variable plate theory for thermoelastic bending analysis of laminated composite plates. Journal of Thermal Stresses 38: 904-925. have presented a four-variable trigonometric plate theory for thermoelastic bending analysis of laminated composite plates subjected to thermal load liner across the thickness.
In all the aforementioned refined plate theories, the effect of transverse normal deformation i.e. thickness stretching is neglected to minimize the unknown variables. But, according to recommendations of Kant and Swaminathan (2002Kant, T. and Swaminathan, K. (2002). Analytical solutions for the static analysis of laminated composite and sandwich plates besed on a higher order refined theory. Composite Structures 56(4): 329-344.) and Carrera (2005Carrera, E., (2005). Transverse normal strain effects on thermal stress analysis of homogeneous and layered plates. AIAA Journal 43(10): 2232-2242.); the effects of both transverse shear and normal deformations plays important role to predict accurate structural behaviour of laminated composite thick plates. Few researchers have developed refined plate theories for the analysis of laminated composite plates considering both transverse shear and normal deformations such as Ghugal and Sayyad (2013Ghugal, Y. M., and Sayyad, A. S. (2013). Stress analysis of thick laminated plates using trigonometric shear deformation theory. International Journal of Applied Mechanics 5(1):1-23.), Sayyad and Ghugal (2013Sayyad, A. S., and Ghugal, Y. M. (2013). Effect of Stress Concentration on Laminated Plates. Journal of Mechanics 29(2):241-252., 2014aSayyad, A. S., and Ghugal, Y. M. (2014a). Flexure of cross-ply laminated plates using equivalent single layer trigonometric shear deformation theory. Structural Engineering and Mechanics 51(5): 867-891., bSayyad, A. S., and Ghugal, Y. M. (2014b). A new shear and normal deformation theory for isotropic, transversely isotropic, laminated composite and sandwich plates. International Journal of Mechanics and Material in Design 3: 247-267., cSayyad, A. S., and Ghugal, Y. M. (2014c). On the Buckling of Isotropic, Transversely Isotropic and Laminated Composite Rectangular Plates. International Journal of Structural Stability and Dynamics 14(6):1-32.), Neves et al. (2011Neves, A. M. A., Ferreira, A. J. M., Carrera, E., Roque, C. M. C., Cinefra, M., Jorge, R. M. N., Soares, C. M. M. (2011). Bending of FGM plates by a sinusoidal plate formulation and collocation with radial basis functions. Mechanics Research Communications 38:368-71., 2012Neves, A. M. A., Ferreira, A. J. M., Carrera, E., Roque, C. M. C., Cinefra, M., Jorge, R. M. N., Soares, C. M. M. (2012). A quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates. Composite Structure 94:1814-25.), Zenkour (2013Zenkour, A. M. (2013). A simple four-unknown refined theory for bending analysis of functionally graded plates. Applied Mathematical Modeling 37:9041-51.), Carrera (1999aCarrera, E. (1999a). Transverse normal stress effects in multilayered plates. ASME Journal of Applied Mechanics 66(4):1004-1012., 1999bCarrera, E. (1999b). A study of transverse normal stress effect on vibration of multilayered plates and shells. Journal of Sound and Vibration 225(5): 803-829., 2002Carrera, E. (2002). Theories and finite elements for multilayered anisotropic, composite plates and shells. Archives of Computational Methods in Engineering 9(2):87-140., 2003Carrera, E. (2003). Theories and finite elements for multilayered anisotropic, composite plates and shells: a unified compact formulation with numerical assessment and benchmarking. Archives of Computational Methods in Engineering 10(3):216-296.).
In this paper, a new quasi-3D polynomial type plate theory is developed for the bidirectional bending analysis of laminated composite and sandwich plates. The present theory does not require a problem dependent shear correction factor as it satisfies traction free boundary conditions at top and bottom surfaces of the plate. The governing differential equations and associated boundary conditions are obtained using the principle of virtual work. The plate is analysed for simply supported boundary conditions using Navier’s solution technique. To prove the efficiency of the present theory, the non-dimensional displacements and stresses obtained for laminated composite and sandwich plates and are compared with existing exact elasticity solutions and other theories. The important contributions in the present study are summarized as follows:
-
1) In the present study, a new higher-order shear and normal deformation theory is developed and applied for the bi-directional bending of laminated composite and sandwich plates subjected to transverse loadings.
-
2) Since the present theory is polynomial type, it is computationally simpler than non-polynomial type plate theories recently developed by many researchers.
-
3) The present theory different from the existing theories since, it considers the effects of transverse shear and normal deformations which are essential to avoid delamination type failures. Many theories available in the literature including theory of Reddy (1984Reddy, J. N. (1984). A simple higher order theory for laminated composite plates. ASME Journal of Applied Mechanics 51:745-752.) have neglected effect of transverse normal deformation i.e. thickness stretching.
-
4) The present theory is strongly recommended for the analysis of laminated composite and sandwich plates, because it yields accurate prediction of displacements and stresses compared to existing non-polynomial type theories.
-
5) The most important feature of the present theory is it predicts accurate interlaminar shear stresses as compared to any other refined plate theories available in the literature.
1.1 Modeling of the composite plate
For the present study, a cross-ply laminated composite plate made of orthotropic fibrous composite material having length ‘a’ in x direction, ‘b’ in y direction and thickness ‘h’ in z direction is considered (see Fig. 1). The plate is subjected to an out of plane load q (x, y) and the mid-plane is located at z=0.
2 FIFTH-ORDER SHEAR AND NORMAL DEFORMATION THEORY
A fifth-order shear and normal deformation theory is initially developed by authors for the cylindrical bending i.e. 1D analysis of laminated composite plates (Naik and Sayyad 2018Naik, N. S., and Sayyad, A. S. (2018). 1D analysis of laminated composite and sandwich plates using a new fifth-order plate theory. Latin American Journal of Solids and Structures 15:1-17.). In this study, it is extended for the bi-directional bending analysis of laminated composite and sandwich plates.
2.1 Kinematics of the present theory (FOSNDT)
The displacement field of the present theory (FOSNDT) can be expressed as
where u, v and w are the x, y and z-directional displacements respectively of any point on the plate; u 0, v 0 and w 0 are the displacements of mid-plane in x, y and z-directions respectively; are rotations of the normal to the mid-plane about y and x axes which account the effect of transverse shear deformation. repressent higher-order transverse cross-sectional deformation modes i.e. effect of transverse normal deformations. The normal and shear strains are obtained within the framework of linear theory of elasticity as follows.
where
The 3D constitutive equations for the k th lamina of laminated plate under bending can be written as
whereare the reduced elastic constants, () are the stress components and () are the strain components. The following relationships between the reduced elastic constants and the engineering elastic constants are used for the present study.
where E 1, E 2 and E 3 are the Young’s moduli; G12, G13 and G23 are the shear moduli and are Poisson’s ratios; the subscripts 1, 2, 3 correspond to x, y, z directions of Cartesian coordinate systems, respectively.
2.2 Governing equations and boundary conditions
The nine variationally consistent governing differential equations associated with the present theory are obtained using the principle of virtual work. The analytical form of the principle of virtual work stated in Eq. (6)
where is the variational operator. After introducing stress resultants, the Eq. (6) can be written in following form
where are the resultant in-plane forces, are the moment resultants analogus to classical plate theory; are the moment resultants due to transverse shear deformation effects; are the transverse shear and transverse normal stress resultants.
The governing differential equations and associated boundary conditions for the present theory can be obtained by integrating Eq. (7) by parts; collecting the coefficients of and equating them equal to zero, the following equations can be obtained
The boundary conditions along edges are of the following form:
Along the edges x =0 and x =a,
Along the edges y =0 and y =b,
The extension, bending, bending-extension, bending-twisting stiffnesses used in the governing equations (9)-(17) can be obtained as
2.4 Analytical solutions
Here, the analytical solutions of Eqs. (9)- (17) for laminated composite and sandwich plates are considered. Assuming that the plate is simply supported in such a way that tangential displacement is not admisible while the normal displacement is admisible. Following are the boundary conditions which will be satisfied the Navier’s solution.
Following Navier’s solution procedure, the solution to the displacement variables to satisfy the above boundary conditions can be expressesd in the following forms.
where
and the loading term q (x,y) is expanded as
where are the unknowns to be determined. is the coefficient of Fourier series expansion and; m and n are the positive integers. For sinusoidal load, and m=n=1. Substitution of Eqs. (22)- (24) into governing Eqs. (9)-(17) leads to the following equation.
where the elements of stiffness matrix [K ij] can be defined as below
After knowing the values of unknown displacement variablesfrom Eq. (22), all the displacement and stress components within the laminated composite plate under consideration can be calculated using Eqs. (1) through (5). The evaluation of transverse shear stresses from the constitutive relations leads to the discontinuity at the inter face of two adjacent layers of a laminate and thus violates the equilibrium conditions. Hence, transverse shear stresses can be obtained by using equilibrium equations of theory of elasticity neglecting body forces stated in Eq. (27).
The in-plane normal and shear stresses calculated from constitutive relations are substituted in Eq. (27). The transverse stress stresses () are evaluated by integrating Eq. (27) layerwise through the thickness coordinate (z).
3.0 NUMERICAL RESULTS AND DISCUSSION
In this section, various numerical examples solved are described and discussed for the bending analysis of laminated composite and sandwich plates using the present theory. In the present study, different configurations of the laminates are used and a simply supported plate subjected to transverse sinusoidal loading is considerd. Results are obtained using the present FOSNDT in closed form using Navier’s solution technique for above geometry and loading. The accuracy of the solution is checked by comparing results obtained using the present theory (FOSNDT) with the other theories and the exact elasticity solution wherever available in the literature. The following sets of material properties are used in obtaining numerical results for the present study.
a) Isotropic
b) Transversely Isotropic
c) Fibrous Composite (Graphite-Epoxy)
For the validity of the present theory, following examples are solved for the numerical study.
-
Bi-directional bending analysis of isotropic square plate under sinusoidal loading.
-
Bi-directional bending of two-layer (00/900) antisymmetric cross-ply laminated composite plates under sinusoidal loading.
-
Bi-directional bending of three-layer (00/900/00) symmetric cross-ply laminated composite plates under sinusoidal loading.
-
Bi-directional bending of three-layer (00/core/00) symmetric sandwich plates under sinusoidal loading.
Displacements and stresses for isotropic, laminated composite and sandwich plates under bi-directional bending obtained by using the present theory (FOSNDT) are presented in Tables 1-4 and compared with those obtained by using the CLPT, the FSDT of Mindlin (1951Mindlin, R.D. (1951). Influence of rotary inertia and shear on flexural motions of isotropic, elastic plates. ASME Journal of Applied Mechanics 18: 31-38.), HSDT of Reddy (1984Reddy, J. N. (1984). A simple higher order theory for laminated composite plates. ASME Journal of Applied Mechanics 51:745-752.), SSNPT of Sayyad and Ghugal (2014bSayyad, A. S., and Ghugal, Y. M. (2014b). A new shear and normal deformation theory for isotropic, transversely isotropic, laminated composite and sandwich plates. International Journal of Mechanics and Material in Design 3: 247-267.) and exact elasticity solution of Zenkour (2007Zenkour, A. M. (2007). Three-dimensional elasticity solution for uniformly loaded cross-ply laminates and sandwich plates. Journal of Sandwich Structures and Materials 9: 213-238.). The displacements and stresses are calculated at typical important locations using the following non-dimensional form.
where S=a/h and E 3 is the elastic modulus of the middle layer.
Example 1: In this example bi-directional bending analysis of isotropic square plate under sinusoidal loading is carried out. Material properties defined by Eq. (28) are used for the numerical study. Displacements and stresses obtained using the present theory are presented in non-dimensional form defined by Eq. (31). Results obtained by using the present theory are compared with exact elasticity solution given by Zenkour (2007Zenkour, A. M. (2007). Three-dimensional elasticity solution for uniformly loaded cross-ply laminates and sandwich plates. Journal of Sandwich Structures and Materials 9: 213-238.) and sinusoidal shear and normal plate theory (SSNPT) of Sayyad and Ghugal (2014bSayyad, A. S., and Ghugal, Y. M. (2014b). A new shear and normal deformation theory for isotropic, transversely isotropic, laminated composite and sandwich plates. International Journal of Mechanics and Material in Design 3: 247-267.). The results shown in Table 1 reveals that, the present theory accurately predicts the displacements and in-plane normal stresses for thin, moderately thick and thick plates, whereas exact results for in-plane shear stresses are not available in the literature. Transverse shear stresses predicted by the present theory are in excellent agreement with those obtained by using exact elasticity solution.
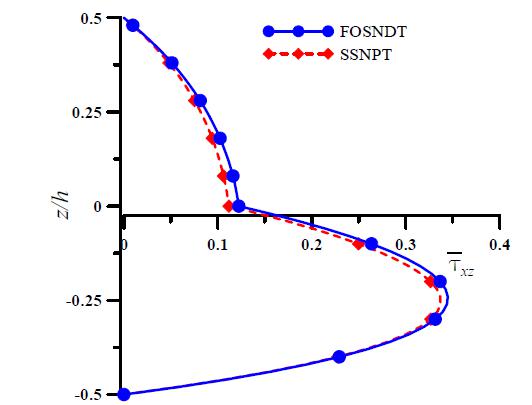
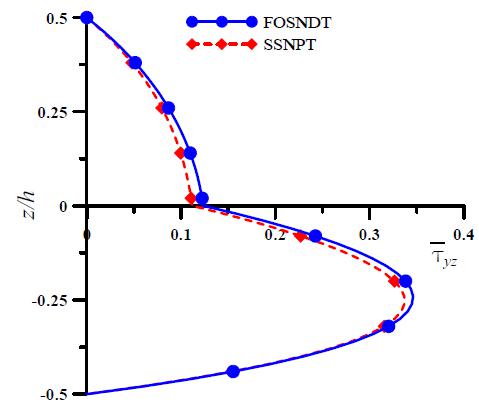
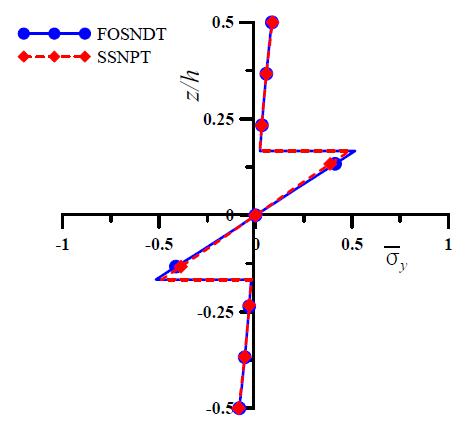
Example 2: In this example, the present theory is applied for the bending analysis of two-layer (00/900) anti-symmetric laminated composite plates subjected to sinusoidal load. The plate is made up of fibrous composite material defined in Eq. (30). The layers are of equal thickness i.e. h/2. The non-dimensional displacements and stresses obtained using the present theory are presented in Table 2 and are compared with classical laminated plate theory (CLPT) of Kirchhoff, first order shear deformation theory (FSDT) of Mindlin (1951Mindlin, R.D. (1951). Influence of rotary inertia and shear on flexural motions of isotropic, elastic plates. ASME Journal of Applied Mechanics 18: 31-38.), SSNPT of Sayyad and Ghugal (2014bSayyad, A. S., and Ghugal, Y. M. (2014b). A new shear and normal deformation theory for isotropic, transversely isotropic, laminated composite and sandwich plates. International Journal of Mechanics and Material in Design 3: 247-267.), HSDT of Reddy (1984Reddy, J. N. (1984). A simple higher order theory for laminated composite plates. ASME Journal of Applied Mechanics 51:745-752.), and exact elasticity solution given by Zenkour (2007Zenkour, A. M. (2007). Three-dimensional elasticity solution for uniformly loaded cross-ply laminates and sandwich plates. Journal of Sandwich Structures and Materials 9: 213-238.). The examination of Table 2 shows that the transverse displacements obtained by using the present theory are in excellent agreement with exact solution compared to HSDT and SSNPT. This is in fact due to inclusion of transverse normal deformation along with fourth-order variation of transverse displacement. The in-plane normal stress () predicted by the present theory is also in excellent agreement with exact solution. The present theory yields accurate transverse shear stresses compared to HSDT and SSNPT. This can be considered as a major contribution of the present theory over existing theories. This accuracy of transverse shear stresses is not achieved by other theories such as HSDT of Reddy (1984) and SSNPT of Sayyad and Ghugal (2014b). FSDT and CLPT underestimate the numerical results due to negelect of transverse shear and normal stresses. Through-the-thickness distributions of in-plane displacement, in-plane normal stresses and transverse shear stresses for 00/900 laminated composite plates subjected to sinusoidal load are shown in Figs. 2 through 6. The variation of transverse displacement with respect to aspect ratio is shown in Fig. 7.
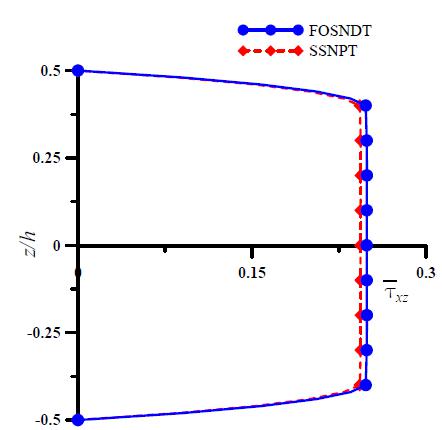
Example 3: In this example, an efficiency of the present theory is checked for the symmetric laminated laminated composite plates. Three layered (00/900/00) symmetric laminated composite plate made up of fibrous composite material subjected to sinusoidal load is considered for the numerical study. Material properites are mentioned in Eq. (30). The layers are of equal thickness i.e. h/3. Non-dimensional displacements and stresses are tabulated in Table 3 and the through thickness distributions of in-plane displacement at support, normal stress at mid span and transverse shear stress at boundary edges under the sinusoidal loading are plotted in Figs. 8 through 12. Variation of transverse displacement with respect to aspect ratio is plotted in Fig. 13. The present results are compared with exact solution, CLPT, FSDT, HSDT and SSNPT. It is pointed out from the Table 3 that the transverse displacements and shear stresses obtained by using the present theory are in excellent agreement with exact elasticity solutions. In-plane normal stresses are slightly on higher side compared to other theories available in the literature. FSDT and CLPT underestimate the results.
Example 4: Composite sandwich plates are basically a special form of fibre reinforced composite plates composed of two thin strong, stiff layers (face sheets) which resist bending bonded to a relatively thicker, less dense layer (core) to resist shear force. The validity of the present theory is also checked for the bending analysis of symmetric sandwich plate. A three layered (00/core/900) sandwich plate having face sheets of thickness 0.1h each and soft core of thickness 0.8h is considered for the analysis. The material properties of the face sheets are given by Eq. (30) while those for core are given by Eq. (29). Table 4 shows the non-dimensional displacements and stresses. The numerical results obtained by using the present theory are compared with those obtained by SSNPT and exact solution. It is observed that the results obtained by using the present theory are in good agreement with the exact elasticity solution and SSNPT. The through thickness distributions of in-plane displacement, in-plane normal stresses and transverse shear stresses are plotted in Figs. 14 through 18. It is pointed from the distribution that the normal stresses in the core (middle layer) are very less compared to those in face sheets. This is in fact due to high face sheet stiffness to core stiffness ratio. Variation of transverse displacement with aspect ratio is shown in Fig. 19.
Through thickness variation of in-plane displacement () for two-layer (00/900) antisymmetric laminated composite plate subjected to sinusoidal load. (s=4)
Through thickness variation of in-plane normal stress () for two-layer (00/900) antisymmetric laminated composite plate subjected to sinusoidal load. (s=4)
Through thickness variation of in-plane normal stress () for two-layer (00/900) antisymmetric laminated composite plate subjected to sinusoidal load. (s=4)
Through thickness variation of transverse shear stress () for two-layer (00/900) antisymmetric laminated composite plate subjected to sinusoidal load. (s=4)
Through thickness variation of transverse shear stress () for two-layer (00/900) antisymmetric laminated composite plate subjected to sinusoidal load. (s=4)
Variation of transverse displacement () with respect to aspect ratio for two-layer (00/900) antisymmetric laminated composite plate subjected to sinusoidal load.
Through thickness variation of in-plane displacement () for three-layer (00/900/00) symmetric laminated composite plate subjected to sinusoidal load. (s=4)
Through thickness variation of in-plane normal stress () for three-layer (00/900/00) symmetric laminated composite plate subjected to sinusoidal load. (s=4)
Through thickness variation of in-plane normal stress () for three-layer (00/900/00) symmetric laminated composite plate subjected to sinusoidal load. (s=4)
Through thickness variation of transverse shear stress () for three-layer (00/900/00) symmetric laminated composite plate subjected to sinusoidal load. (s=4)
Through thickness variation of transverse shear stress () for three-layer (00/900/00) symmetric laminated composite plate subjected to sinusoidal load. (s=4)
Variation of transverse displacement () with respect to aspect ratio for three-layer (00/900/00) symmetric laminated composite plate subjected to sinusoidal load.
Through thickness variation of in-plane displacement () for three-layer (00/core/00) symmetric sandwich plate subjected to sinusoidal load. (s=4)
Through thickness variation of in-plane normal stress () for three- layer (00/core/00) symmetric sandwich plate subjected to sinusoidal load. (s=4)
Through thickness variation of in-plane normal stress () for three- layer (00/core/00) symmetric sandwich plate subjected to sinusoidal load. (s=4)
Through thickness variation of transverse shear stress () for three-layer (00/core/00) symmetric sandwich plate subjected to sinusoidal load. (s=4)
Through thickness variation of transverse shear stress () for three-layer (00/core/00) symmetric sandwich plate subjected to sinusoidal load. (s=4)
Variation of transverse displacement () with respect to aspect ratio for three-layer (00/core/900) symmetric sandwich plate subjected to sinusoidal load.
4.0 CONCLUSIONS
A new fifth-order shear and normal deformation theory is developed for the bi-directional bending analysis of laminated composite and sandwich plates subjected to transverse loads. This theory considered the effects of both transverse shear and normal deformations. In-plane and transverse displacements uses a polynomial shape function expanded up to fifth-order in terms of the thickness coordinate to properly account the effects of transverse shear and normal deformations. The present theory does not require a problem dependent shear correction factor as it satisfies traction free boundary conditions at top and bottom surfaces of the plate using constitutive relations. The plate is analysed for simply supported boundary conditions using Navier’s solution technique. From the numerical study and discussion of results it is concluded that the present theory yields accurate prediction of displacements and stresses for all types of laminate configurations compared to other lower and higher order plate theories available in the iterature. The most important contribution of the present theory over existing theories is, it estimates accurate transverse shear stresses for laminated composite and sandwich plates. This accuracy is achieved by including fifth-order variation of displacements and transverse normal deformation. Therefore, it is strongly recommended that, for the accurate analysis of laminated composite and sandwich thick plates, effects of both transverse shear and normal deformations are essential.
References
- Ambartsumian, S.A. (1958). On the theory of bending plates. Izv Otd Tekh Nauk AN SSSR 5:69-77.
- Carrera, E. (1999a). Transverse normal stress effects in multilayered plates. ASME Journal of Applied Mechanics 66(4):1004-1012.
- Carrera, E. (1999b). A study of transverse normal stress effect on vibration of multilayered plates and shells. Journal of Sound and Vibration 225(5): 803-829.
- Carrera, E. (2002). Theories and finite elements for multilayered anisotropic, composite plates and shells. Archives of Computational Methods in Engineering 9(2):87-140.
- Carrera, E. (2003). Theories and finite elements for multilayered anisotropic, composite plates and shells: a unified compact formulation with numerical assessment and benchmarking. Archives of Computational Methods in Engineering 10(3):216-296.
- Carrera, E., (2005). Transverse normal strain effects on thermal stress analysis of homogeneous and layered plates. AIAA Journal 43(10): 2232-2242.
- Chakrabarti, A., and Sheikh, A. H. (2005). Analysis of laminated sandwich plates based on interlaminar shear stress continuous plate theory. ASCE Journal of Engineering Mechanics 131(4): 377-384.
- Ghugal, Y. M., and Sayyad, A. S. (2013). Stress analysis of thick laminated plates using trigonometric shear deformation theory. International Journal of Applied Mechanics 5(1):1-23.
- Grover, N., Singh, B. N., Maiti, D. K. (2013). Analytical and finite element modeling of laminated composite and sandwich plates: an assessment of a new shear deformation theory for free vibration response. International Journal of Mechanical Science 67:89-99.
- Kant, T. and Swaminathan, K. (2002). Analytical solutions for the static analysis of laminated composite and sandwich plates besed on a higher order refined theory. Composite Structures 56(4): 329-344.
- Karama, M., Afaq, K.S., Mistou, S. (2009). A new theory for laminated composite plates. Proceedings of The Institution of Mechanical Engineers, Part L: Journals of Materials: Design and Applications 223:53-62.
- Kirchhoff, G.R. (1850). Uber das gleichgewicht und die bewegung einer elastischen scheibe. Journal for Pure and Applied Mathematics (Crelle’s Journal) 40:51-88.
- Levy, M. (1877). Memoire sur la theorie des plaques elastique planes. Journal des Mathematiques Pures et Appliquees 30: 219-306.
- Mantari, J. L., Oktem, A. S., Soares, C. G. (2012). A new trigonometric shear deformation theory for isotropic, laminated composite and sandwich plates. International Journal of Solids and Structures 49:43-53.
- Mindlin, R.D. (1951). Influence of rotary inertia and shear on flexural motions of isotropic, elastic plates. ASME Journal of Applied Mechanics 18: 31-38.
- Naik, N. S., and Sayyad, A. S. (2018). 1D analysis of laminated composite and sandwich plates using a new fifth-order plate theory. Latin American Journal of Solids and Structures 15:1-17.
- Neves, A. M. A., Ferreira, A. J. M., Carrera, E., Roque, C. M. C., Cinefra, M., Jorge, R. M. N., Soares, C. M. M. (2011). Bending of FGM plates by a sinusoidal plate formulation and collocation with radial basis functions. Mechanics Research Communications 38:368-71.
- Neves, A. M. A., Ferreira, A. J. M., Carrera, E., Roque, C. M. C., Cinefra, M., Jorge, R. M. N., Soares, C. M. M. (2012). A quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates. Composite Structure 94:1814-25.
- Pagano, N. J. (1970). Exact solutions for bidirectional composites and sandwich plates. Journal of Composite Materials 4: 20-34.
- Pandya, B.N., and Kant, T. (1988). Finite element stress analysis of laminated composite plates using higher-order displacement model. Composite Science and Technology 32:137-55.
- Reddy, J. N. (1984). A simple higher order theory for laminated composite plates. ASME Journal of Applied Mechanics 51:745-752.
- Sayyad, A. S., and Ghugal, Y. M. (2013). Effect of Stress Concentration on Laminated Plates. Journal of Mechanics 29(2):241-252.
- Sayyad, A. S., and Ghugal, Y. M. (2014a). Flexure of cross-ply laminated plates using equivalent single layer trigonometric shear deformation theory. Structural Engineering and Mechanics 51(5): 867-891.
- Sayyad, A. S., and Ghugal, Y. M. (2014b). A new shear and normal deformation theory for isotropic, transversely isotropic, laminated composite and sandwich plates. International Journal of Mechanics and Material in Design 3: 247-267.
- Sayyad, A. S., and Ghugal, Y. M. (2014c). On the Buckling of Isotropic, Transversely Isotropic and Laminated Composite Rectangular Plates. International Journal of Structural Stability and Dynamics 14(6):1-32.
- Sayyad, A. S., and Ghugal, Y. M. (2015a). On the free vibration analysis of laminated composite and sandwich plates: A review of recent literature with some numerical results. Composite Structures 129: 177-201.
- Sayyad, A. S., and Ghugal, Y. M. (2015b). A four variable plate theory for thermoelastic bending analysis of laminated composite plates. Journal of Thermal Stresses 38: 904-925.
- Sayyad, A. S., and Ghugal, Y. M. (2017a). A unified shear deformation theory for the bending of isotropic, functionally graded, laminated and sandwich beams and plates. International Journal of Applied Mechanics 9(1):1-36.
- Sayyad, A. S., and Ghugal, Y. M. (2017b). Bending, buckling and free vibration of laminated composite and sandwich beams: A critical review of literature. Composite Structures 171:486-504.
- Soldatos, K. P. (1992). A transverse shear deformation theory for homogeneous monoclinic plates. Acta Mechanica 94:195-200.
- Thai, C. H., Tran, L. V., Tran, D. T., Nguyen-Thoi, T., and Nguyen-Xuan, H. (2012). Analysis of laminated composite plates using higher order shear deformation plate theory and node based smoothed discrete shear gap method. Applied Mathematical Modeling 36:5657-5677.
- Thai, H. T., and Choi, D. H. (2013). A simple first order shear deformation theory for laminated composite plates. Composite Structures 106:754-763.
- Touratier, M. (1991). An efficient standard plate theory. Int J Eng Sci 29(8):901-16.
- Zenkour, A. M. (2013). A simple four-unknown refined theory for bending analysis of functionally graded plates. Applied Mathematical Modeling 37:9041-51.
- Zenkour, A. M. (2007). Three-dimensional elasticity solution for uniformly loaded cross-ply laminates and sandwich plates. Journal of Sandwich Structures and Materials 9: 213-238.
- Zhen, W., and Wanji, C. (2007). A study of global-local higher order theories for laminated composite plates. Composite Structures 79:44-54.
-
Available Online: August 01, 2018
Publication Dates
-
Publication in this collection
2018
History
-
Received
18 Jan 2018 -
Reviewed
22 June 2018 -
Accepted
31 July 2018