Improved friction model applied to plane sliding connections by a large deformation FEM formulation

Abstract

Friction is an important source of dissipation in dynamical systems. Properly considering it in the numerical model is fundamental to obtain stable and representative responses in structures and mechanisms. This is especially significant for the well-known Coulomb model due to discontinuity in force when stick-slip transition occurs. In this work an improved friction force model is proposed to smooth the force transition at null velocity, with an additional parameter obtained from the own system state. The improved model is employed in sliding connections of plane frames finite elements. A total Lagrangian Finite Element Method (FEM) formulation based on a positional description of the motion is employed. Using a variational principle, frictional dissipation is added to the total mechanical energy to develop the equations of motion. The resulting nonlinear equations are solved by the Newton-Raphson method accounting for the friction force update in the iterative process. Examples are presented to show the formulation effectiveness and possibilities in simulating dynamical systems that present the stick-slip effect.

Keywords
Friction model; Sliding connection; Nonlinear dynamics; Lagrange multiplier; Stick-slip effect

Graphical Abstract

1 INTRODUCTION

In the analysis of structures and mechanisms their dynamical systems are frequently assumed conservative, while, in reality, systems present dissipation due to several sources. The frictional dissipative effect, in particular, is important to be considered when relative motion between parts of the body exists. This is the case of sliding connections, such as prismatic and cylindrical joints, that, by introducing translational movement among body members, allow friction forces to develop at their contact regions.

Mathematical models try to describe some of the many characteristics of friction complex nature. For instance, evolving from the classical one-parameter Coulomb friction model, values of the friction force at rest (static friction) and in motion (kinetic friction) can be distinguished. The continuous decrease of friction values for increasing, but low, velocities, referred as the Stribeck effect (Rabinowicz, 1951), or the adhesion between contacting surfaces before sliding, resulting in local pre-sliding deformation (Hsieh and Pan, 2000), may be important and included in some models. The effect of lubricant layers between the surfaces (Armstrong-Hélouvry et al., 1994) and the ‘frictional lag’, a delay in the change of the force with change in velocity (Hess and Soom, 1990), among other aspects, may be also encountered in current friction models. Comprehensive surveys (Olsson et al., 1998; Andersson et al., 2007; Marques et al., 2016) present in-depth discussions on the characteristics of friction dissipation and several available models.

Friction models can be broadly classified in ‘dynamic’ or ‘static’ (Marques et al., 2016). Dynamical models, also referred as state-variable models, aim to capture more characteristics of the physically observed friction response by including additional degrees of freedom in the system, and usually demanding more parameters. Common state-variable friction models are referred as Dahl (Dahl, 1976), LuGre (Canudas de Wit et al., 1995), Elasto-Plastic (Dupont et al., 2002), Gonthier (Gonthier et al., 2004), only to list a few.

Models referred as static, as opposed to dynamical models, dismiss the introduction of state variables to the problem, rendering a direct description of the force expression. In those models, however, the discontinuity of the friction force at null speed is a major drawback in the numerical solution. Some models (Kikuuwe et al., 2005; Threlfall, 1978; Armstrong-Hélouvry et al., 1994; Ambrósio, 2003) try to circumvent this problem suggesting null friction at a defined null speed interval. This assumption is not a good approximation when relative motion is intermittent, such as the sticking and slipping of sliding surfaces, known as the stick-slip effect (Rabinowicz, 1958), as it disregards the influence of the resultant force acting on the bodies in contact. Other models (Karnopp, 1985; Leine et al., 1998; Cha et al., 2011; Awrejcewicz et al., 2008) consider the resultant force requiring additional parameters, related to a null speed interval, for the transition between motion and rest states, which may be problem dependent and difficult to establish.

It is important to stress that, although several studies developed formulations to capture some of friction characteristics, no model is general (Pennestrì et al., 2016) and simpler force models are largely employed for design and are present in commercial software. Still, stability of the numerical solution for the formulation comprising the friction model is always desired.

In this study, we propose a modification on a static friction model and employ it in sliding connections of plane frames in a large deformation finite element context. The improved model is based on Coulomb friction considering the Stribeck curve for the static and kinetic forces transition and viscous effect. Its numerical solution is improved by reducing the abrupt transition between rest and motion states of the joints by an interpolation between the static friction value and the resultant force in a quasi-null relative speed interval. Differently from other friction models, that define a constant value for a null speed interval, here we propose an expression to automatically calculate the referred quasi-null interval from the system state. Thus, no additional non-physical parameter needs to be informed. The resultant force expression at the sliding connection is achieved for any generic finite element system with multiple degrees of freedom. With the proposed improved friction model, stable responses for the stick-slip effect are captured, which is important for the correct motion reproduction in structures and mechanisms.

The framework employed to model the dynamical system (Coda and Paccola, 2014; Siqueira and Coda, 2016; 2017; 2019) is a fully nonlinear finite element approach for large deformations based on a total Lagrangian description of solids. As the formulation uses positions as the main degrees of freedom, instead of displacements, the adopted approach is referred as positional. Sliding connections, as prismatic and cylindrical joints, are introduced in the system by means of Lagrange multipliers. In the sliding connection formulation, the friction force is associated with a curvilinear displacement variable introduced in the system by the joints. This formulation is also capable of representing roughness on the sliding surface, making it possible to be combined with the introduced friction dissipation to simulate, for instance, vehicle-bridge interaction as show in the examples. The Saint-Venant-Kirchhoff constitutive model is adopted to define the plane frame elastic strain energy using the Green-Lagrange strain and the second Piola-Kirchhoff stress tensor. The Principle of Stationary Total Energy is used to find the equations of motion, comprising the frictional effect, which is discretized along time using the generalized-α method. The resulting nonlinear system is solved by the Newton-Raphson method accounting for the friction force update in the iterative process.

This study is organized as follows. Section 2 briefly presents necessary aspects of the employed nonlinear plane frame element followed by the sliding connections kinematical constraints in Section 3. The dynamical equilibrium is obtained in Sections, 4 and 5. Known the system parameters, the friction force is introduced in its variational form in Section 6 and the improved model is presented in detail by Section 7. Time integration (Section 8) and system solution (Section 9) are presented next. In Section 10, examples verify the proposed improved friction model and show the possibilities of the developed formulation in the analysis of dynamical systems.

Dyadic notation is preferred throughout this text due its brevity; however, index notation is also used to clarify particular aspects when necessary.

2 NONLINEAR PLANE FRAME KINEMATICS

The employed plane frame finite element is presented thoroughly in Coda and Paccola (2014) and Siqueira and Coda (2017), however, to develop the present formulation some aspects need to be briefly stated. As the finite element behavior is represented by a total Lagrangian description, its strain field needs to be written as a function of the initial and current configurations of the solid, restricted to a finite number of degrees of freedom.

In the positional approach of the FEM, instead of nodal displacements, the parameters of the discretized plane frame are its positions (coordinates) and the cross section angle (Fig. 1). The deformation function, $\overrightarrow{f}$, depicted in Fig. 2, can be written indirectly as function of the non-dimensional space and nodal parameters by mappings from the non-dimensional space to the initial configuration, ${\overrightarrow{f}}^0$, as

$$\begin{array}{l}{f}_1^0=x_1={\varphi }_{\mathcal{l}}(\xi )X_1^{\mathcal{l}}+\frac{h_0}{2}\eta \text{cos}\left[{\varphi }_{\mathcal{l}}(\xi ){\theta }_{\mathcal{l}}^0\right]\\ f_2^0=x_2={\varphi }_{\mathcal{l}}(\xi )X_2^{\mathcal{l}}+\frac{h_0}{2}\eta \sin \left[{\varphi }_{\mathcal{l}}(\xi ){\theta }_{\mathcal{l}}^0\right]\end{array}$$ (1)

and to the current configuration, ${\overrightarrow{f}}^1$, as

$$\begin{array}{l}{f}_1^1=y_1={\varphi }_{\mathcal{l}}(\xi )Y_1^{\mathcal{l}}+\frac{h_0}{2}\eta \cos [{\varphi }_{\mathcal{l}}(\xi ){\theta }_{\mathcal{l}}]\\ f_2^1=y_2={\varphi }_{\mathcal{l}}(\xi )Y_2^{\mathcal{l}}+\frac{h_0}{2}\eta \sin [{\varphi }_{\mathcal{l}}(\xi ){\theta }_{\mathcal{l}}]\end{array}$$ (2)

where $\overrightarrow{x}$ and $\overrightarrow{y}$ represents any point on the domain of a finite element in the initial and current configuration, respectively. The coordinates for both directions $i=\mathrm{1,2}$ of each node $\mathcal{l}$ along the reference line in the initial and current configurations are $X_i^{\mathcal{l}}$ and $Y_i^{\mathcal{l}}$, respectively. The initial nodal value of the cross-section angle is ${\theta }_{\mathcal{l}}^0$ and after deformation is denoted as ${\theta }_{\mathcal{l}}$. The cross section initial height is $h_0$, $\xi$ is the non-dimensional space variable in the direction of the reference line and $\eta$ follows the height direction. The shape functions ${\varphi }_{\mathcal{l}}(\xi )$ are obtained by Lagrange polynomials of any order.

Fig. 1
Current configuration mapping for a cubic approximation.

Fig. 2
Deformation mapping.

The deformation function can be written as a composition of the previous mappings, Eq. (1) and (2), as

$$\overrightarrow{f}={\overrightarrow{f}}^1\circ {({\overrightarrow{f}}^0)}^{-1}$$.(3)

Since only the gradient $A$ of the deformation function, but not the function itself, is necessary to obtain the strain field, as presented by (Bonet et al., 2000; Coda, 2003)

$$A=Grad(\overrightarrow{f})=A^1.{(A^0)}^{-1}$$ (4)

where

$$A_{ij}^0=\frac{\partial f_i^0}{\partial {\xi }_j}\text{and}{A}_{ij}^1=\frac{\partial f_i^1}{\partial {\xi }_j}$$.(5)

During the iterative solution strategy both $A^0$ and $A^1$ are numerical values calculated at the integration points resulting in a purely numerical procedure.

As the Saint-Venant-Kirchhoff constitutive law is employed, the Green-Lagrange strain tensor $E$ have to be calculated. This objective strain is given, for instance, by (Ogden, 1984)

$$E=\frac{1}{2}(C-I)=\frac{1}{2}(A^t\cdot A-I)$$ (6)

where $I$ is the second order identity tensor and $C=A^t\cdot A$ is the right Cauchy-Green stretch tensor.

As there is no relation between the cross-section angle and the slope of the reference line, the frame kinematic can be regarded as Reissner-type. It should be mentioned that the cross-section dimensions are maintained the same during motion, thus, to avoid volumetric locking, the constitutive equation is relaxed in order to exclude transverse expansions. The specific strain energy for the plane frame is presented in Section 4.

3 KINEMATICAL CONSTRAINTS DUE TO SLIDING CONNECTIONS

To introduce frictional effects in the equations of motion, it is required first to write the constraint equations imposed by the sliding connections. The curvilinear position - a new variable introduced in the system - is of particular importance as the friction force will act directly on it. In this section we summarize the description of the connections as prismatic and cylindrical joints.

Sliding connections are the ones that constrain relative translations between parts of the body. Fig. 3 illustrates both joints and their plane representation. In either case, a sliding node, at which the joint exists, is constrained to move over a trajectory comprised of path elements. The distinction between the prismatic and the cylindrical joint (understood as a sliding-pin joint for the plane case) is the relative rotation, which is allowed only by the last one.

Fig. 3
Sliding connections and its plane representation: a) prismatic and b) cylindrical (sliding-pin) joints.

Fig. 4 depicts a sliding connection, belonging to node $\widehat{P}$, and its path contact point $\overline{P}$. The connection is free to move along the path $s(\xi )$ defined by path finite elements, which may have an arbitrary roughness profile $\overrightarrow{r}(s)$. The new variable $s_P=s({\xi }_P^{})$ defining the curvilinear position and the cross-section orientation of the path point is also illustrated.

Fig. 4
Sliding connection over an arbitrary path (depicted for a prismatic joint).

The constraint equations, $\overrightarrow{c}$, can be written for both types of joints as a single expression

$$c_i={\widehat{Y}}_i^P-{\varphi }_{\mathcal{l}}({\xi }_P){\overline{Y}}_i^{\mathcal{l}}-\Delta {\theta }_P^0{\delta }_{i3}-r_i(s_P)(1-{\delta }_{(i)3})=0_i$$ (7)

where the upper bar $(\overline{•})$ is used to identify variables related to path elements and the upper hat $(\widehat{•})$ is used to define the sliding node. In the previous expression $i$ is the direction ($i=\mathrm{1,2,3}$ for prismatic joints and $i=\mathrm{1,2}$ for cylindrical joints) and ${\delta }_{ij}$ is the Kronecker delta. The difference of cross sections orientations at the initial configuration is $\Delta {\theta }_P^0={\widehat{\theta }}_P^0-{\overline{\theta }}_P^0$ and must be constant during the sliding process in the prismatic joint case to maintain a fixed relative angle.

In Eq. (7), the components of the roughness profile, obtained by its ‘height function’ $r_h(s)$, are given by

$$\begin{array}{l}{r}_1(s_P)=r_h(s)\cos \left[{\varphi }_{\mathcal{l}}({\xi }_P){\overline{\theta }}_{\mathcal{l}}\right]\\ r_2(s_P)=r_h(s)\sin \left[{\varphi }_{\mathcal{l}}({\xi }_P){\overline{\theta }}_{\mathcal{l}}\right]\end{array}$$.(8)

It is noteworthy that the curvilinear variable $s(\xi )$ represents an arch-length function defined by the non-dimensional coordinate $\xi$ and the path element coordinates. Also, as $r_h(s)$ is defined directly by the curvilinear position, the roughness profile is mesh-independent.

4 UNCONSTRAINED EQUATIONS OF MOTION

When dissipation occurs, the mechanical energy of the analyzed structure ${\Pi }_0$ is given by

$${\Pi }_0=\Pi -\mathcal{Q}$$ (9)

where $\mathcal{Q}$ represents the dissipation of an encompassing system of total energy $\Pi$. Studying this larger system, Eq. (9) can be rewritten as

$$\Pi ={\Pi }_0+\mathcal{Q}$$ (10)

or, making explicit the energy parcels of the new larger conservative system

$$\Pi =\mathcal{U}-\mathcal{P}+\mathcal{K}+\mathcal{Q}$$ (11)

where $\mathcal{U}$ is the stored elastic strain energy, $\mathcal{P}$ is the potential of conservative external forces and $\mathcal{K}$ is the kinetic energy of the body.

Following Lanczos (1970) and Gurtin et al. (Gurtin et al., 2010), it is not always possible to write down closed expressions for dissipative parcels but only its infinitesimal change. Thus, the equations of motion are stated from the variation of the energies present in Eq. (11), which is understood as the Principle of Stationary Total Energy

$$\delta \Pi =\delta \mathcal{U}-\delta \mathcal{P}+\delta \mathcal{K}+\delta \mathcal{Q}=0$$ (12)

in which the symbol $\delta$ means variation.

The total energy can be stated by writing the known expressions of the energies in Eq. (11) as function of the current configuration nodal parameters of the discretized body, grouped in the vector $\overrightarrow{\Upsilon }$, as

$$\Pi (\overrightarrow{\Upsilon })={\displaystyle {\int }_{V_0}^{}u(E(\overrightarrow{\Upsilon }))d{V}_0}-\overrightarrow{F}\cdot \overrightarrow{\Upsilon }-{\displaystyle {\int }_{s_0}^{}\overrightarrow{q}\cdot \overrightarrow{y}d{s}_0}+\frac{1}{2}{\displaystyle {\int }_{V_0}^{}{\rho }_0\dot{\overrightarrow{y}}\cdot \dot{\overrightarrow{y}}d{V}_0}+\mathcal{Q}(\overrightarrow{\Upsilon })$$ (13)

where the specific strain energy $u$ depends on the strain state $E$ of the body, Eq. (6), which is function of the nodal parameters $\overrightarrow{\Upsilon }$, as defined by the gradient of the deformation function in Eq. (4). Still in Eq. (13), $\overrightarrow{F}$ and $\overrightarrow{q}$ are the concentrated and distributed conservative external loads, respectively. The initial length of the frame reference line is $s_0$. The material mass density in the initial configuration, of volume $V_0$, is ${\rho }_0$. The material point velocity is denoted using the over-dot as $\dot{\overrightarrow{y}}$.

As mentioned before, the Saint-Venant-Kirchhoff constitutive relation is employed due to its simplicity and good representation of large displacements on solids that remain in the small to moderate strain regimen, which comprehends the majority of the usual applications in engineering. For the plane frame utilized, following Siqueira and Coda (2017), its specific energy is given as

$$u=\frac{E(1-\nu )}{2(1-2\nu )(1+\nu )}\left(E_{11}^2+E_{22}^2\right)+\frac{2\nu G}{(1-2\nu )}\left(E_{11}^{}{E}_{22}^{}\right)+G\left(E_{12}^2+E_{21}^2\right)$$ (14)

where $E$ is the longitudinal elastic parameter that approaches the Young modulus for small strains. The shear elastic modulus is $G=E/[2(1+\nu )]$, being $\nu$ a constant that reproduces the Poisson ratio for small strains. Assuming, in equation (14) $\nu =0$, except for the calculation of the shear elastic modulus, avoids locking problems. The second Piola-Kirchhoff stress tensor is easily obtained by the energy conjugacy property as

$$S=\frac{\partial u}{\partial E}$$.(15)

The equations of motion (geometric nonlinear dynamical equilibrium) are obtained by the development of the variations in eq. (13). Details regarding this development can be obtained for the employed plane frame element particular kinematics in Siqueira and Coda (2017) and for a general framework of positional finite elements in Siqueira and Coda (2019), for instance. Following these studies, the equilibrium can be written in a compact form as

$${\overrightarrow{F}}^{\mathrm{int}}-\overrightarrow{F}+M\cdot \ddot{\overrightarrow{\Upsilon }}+D\cdot \dot{\overrightarrow{\Upsilon }}=\overrightarrow{0}$$ (16)

where: ${\overrightarrow{F}}^{\mathrm{int}}=Grad(\mathcal{U})$ is the internal force vector; $\overrightarrow{F}$ collects all the external loads; $M$ results in a constant mass matrix for the present total Lagrangian formulation; $D$ is the external damping matrix arriving from $\delta \mathcal{Q}$ which is assumed as Rayleigh type; and $\dot{\overrightarrow{\Upsilon }}$ and $\ddot{\overrightarrow{\Upsilon }}$ are the velocity and acceleration vectors of the nodal parameters.

5 CONSTRAINED EQUATIONS OF MOTION

The dynamic equilibrium stated by Eq. (16) is called unconstrained as no restraints, such as the ones from the sliding connections, are present. Several consolidated methodologies to impose constraints on mechanical and structural applications can be found in the literature (Géradin and Cardona, 2001; Nocedal and Wright, 1999; Rao, 2009). Here, we employ the well-known Lagrange multiplier method along with the Principle of Stationary Total Energy to impose the sliding restrictions. Concerning the later introduction of friction dissipation, the multipliers are of great value since in Mechanics they might be understood as the contact forces between bodies, an essential information for the friction model.

The Principle of Stationary Total Energy is extended for the case of holonomic constraints by modifying the total energy through the introduction of a new potential $\mathcal{C}$, referred as the constraint potential, as

$$\Pi =\mathcal{U}-\mathcal{P}+\mathcal{K}+\mathcal{Q}+\mathcal{C}$$.(17)

When using Lagrange multipliers, the expression of the new potential is simply given by

$$\mathcal{C}=\overrightarrow{\lambda }\cdot \overrightarrow{c}$$ (18)

where $\overrightarrow{\lambda }$ represents the vector of multipliers, which are new variables of the system. Eq. (18) indicates the presence of a multiplier for each constraint equation in $\overrightarrow{c}$. It is worth mentioning that the constraint potential is null at the solution, therefore, the total energy is not altered.

Knowing the expression of $\mathcal{C}$, the first variation of the constrained energy, Eq. (17), is

$$\delta \Pi =\delta \mathcal{U}-\delta \mathcal{P}+\delta \mathcal{K}+\delta \mathcal{Q}+\delta \mathcal{C}=0$$ (19)

which, can be developed similarly to the unconstrained case leading to the constrained nonlinear equations of motion, expressed in a compact form as

$${\overrightarrow{F}}^{\mathrm{int}}-\overrightarrow{F}+M\cdot \ddot{\overrightarrow{\Upsilon }}+D\cdot \dot{\overrightarrow{\Upsilon }}+{\overrightarrow{F}}^{\text{con}}=\overrightarrow{0}$$ (20)

in which ${\overrightarrow{F}}^{\text{con}}$ represents the restriction forces arriving from the constraint potential. As the multipliers are new variables, the variation of $\mathcal{C}$ is organized in the following force vector, which separates the parameters $\overrightarrow{\Upsilon }$ (including $s_P$) and the multipliers

$$\delta \mathcal{C}=\delta \overrightarrow{\Upsilon }\cdot \nabla \overrightarrow{c}\cdot \overrightarrow{\lambda }+\delta \overrightarrow{\lambda }\cdot \overrightarrow{c}=\left\{\begin{array}{cc}\delta \overrightarrow{\Upsilon }& \delta \overrightarrow{\lambda }\end{array}\right\}\cdot \left\{\begin{array}{c}\nabla \overrightarrow{c}\cdot \overrightarrow{\lambda }\\ \overrightarrow{c}\end{array}\right\}=\left\{\begin{array}{cc}\delta \overrightarrow{\Upsilon }& \delta \overrightarrow{\lambda }\end{array}\right\}\cdot {\overrightarrow{F}}^{\text{con}}$$ (21)

where the tensor $\nabla \overrightarrow{c}$ represents the gradient of the constraint vector. The derivatives of the constraint equation for the sliding connections, Eq. (7), can be found in Siqueira and Coda (2017).

6 INTRODUCTION OF THE FRICTION FORCE IN THE SYSTEM

The friction force is included in the system directly in the Principle of Stationary Total Energy as part of the dissipative potential. As previously mentioned, dissipative potentials are introduced in their differential form since closed expressions might be unknown, as is the case for the dissipated friction energy ${\mathcal{Q}}_{\text{f}}$. However, the variation of this potential can be written as the work done by the friction force vector ${\overrightarrow{F}}^{\text{f}}$ on its displacement trajectory $\overrightarrow{d}$ as

$$\delta {\mathcal{Q}}_{\text{f}}={\overrightarrow{F}}^{\text{f}}\cdot \delta \overrightarrow{d}$$.(22)

To develop Eq. (22), parameters that describes the force displacement must be chosen. For that, the coordinates of the sliding node and its path contact point could be chosen. However, since in the previous formulation the curvilinear position $s_P$ is already used as an intrinsic variable, the displacement along the trajectory is simply the scalar expression $d=s_p-s_P^0$, being $s_P^0$ an arbitrary initial value, and its variation is $\delta d=\delta s_p$. As the friction force acts tangentially to the trajectory, with its value given by the scalar $F_{\text{f}}$, the dissipative parcel is introduced directly in the curvilinear position as

$$\delta {\mathcal{Q}}_{\text{f}}=F_{\text{f}}\delta s_P$$.(23)

To organize the equations of motion system, we make ${\overrightarrow{F}}^{\text{f}}=\left\{F_{\text{f}}\right\}$, the previous equation is rewritten as

$$\delta {\mathcal{Q}}_{\text{f}}=\left\{\delta s_P\right\}\cdot {\overrightarrow{F}}^{\text{f}}$$.(24)

Considering the correspondence of the friction force vector ${\overrightarrow{F}}^{\text{f}}$ to the system degrees of freedom, the equations of motion are restated to include frictional dissipation as

$${\overrightarrow{F}}^{\mathrm{int}}-\overrightarrow{F}+M\cdot \ddot{\overrightarrow{\Upsilon }}+D\cdot \dot{\overrightarrow{\Upsilon }}+{\overrightarrow{F}}^{\text{con}}+{\overrightarrow{F}}^{\text{f}}=\overrightarrow{0}$$.(25)

7 IMPROVED FRICTION MODEL

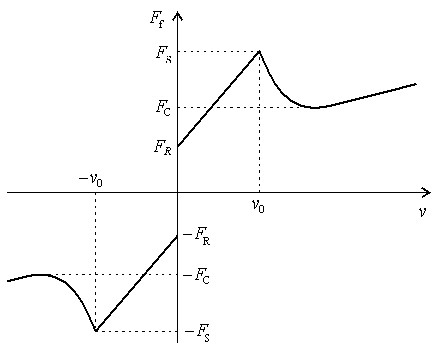
Given the way the friction force is incorporated in the equations of motion, Eq. (25), any expression may be easily applied without modifying its development. We start from the Coulomb friction model considering the Stribeck curve for the static and kinetic forces transition and a viscous effect. Fig. 5 shows the overall behavior of the friction force with the relative velocity among sliding bodies, $v$. This model considers the Stribeck curve using the expression proposed by Bo and Pavelescu (1982) and a linear evolution for the viscous friction, which occurs if lubricant layers are present on the surfaces. The expression for the friction force is written as

$$F_{\text{f}}=\left\{\begin{array}{ll}\left[F_{\text{C}}+\left(F_{\text{S}}-F_{\text{C}}\right)e^{-{\left(\left|v\right|/v_{\sigma }\right)}^{{\delta }_{\sigma }}}\right]\mathrm{sgn}(v)+\eta v\hfill & \text{if}v\ne 0\hfill \\ \min \left(F_{\text{S}},\left|F_{\text{R}}\right|\right)\mathrm{sgn}\left(F_{\text{R}}\right)\hfill & \text{if}v=0\hfill \end{array}\right.$$ (26)

with the static $F_{\text{S}}$ and kinetic $F_{\text{C}}$ friction forces given by

$$F_{\text{S}}={\mu }_s{F}_{\text{N}}\text{and}{F}_{\text{C}}={\mu }_k{F}_{\text{N}}$$ (27)

where, ${\mu }_s$ and ${\mu }_k$ are, respectively, the static and kinetic friction coefficients. $F_{\text{N}}$ is the absolute value of the contact force, orthogonal to the trajectory at the joint contact point, and $F_{\text{R}}$ is the resultant force on the sliding connection, tangential to the contact point. The viscous friction coefficient is $\eta$ and the Stribeck parameters are its decay velocity $v_{\sigma }$ and power ${\delta }_{\sigma }$. The sign function is represented by $\mathrm{sgn}(·)$.

Fig. 5
Friction model representation.

We highlight at this point that, for our application in sliding connections, the relative velocity $v$, tangential to the path, can be measured from the curvilinear position velocity, which will be important for the nonlinear solution procedure in Section 9.

For null relative velocity, that is, the rest state, second condition in Eq. (26), the tangential resultant force acting on the connection is required for comparison with the static friction value to evaluate the tendency of motion (in case $F_{\text{R}}$ is greater than $F_{\text{S}}$, or not, otherwise). Properly representing this condition is the key to simulate the stick-slip effect.

In numerical simulations, the transition from motion to rest states is challenging due to the absence of continuity at null speed, as expressed by Eq. (26), leading to instabilities in the response. For this reason, a linear interpolation between $F_{\text{S}}$ and $F_{\text{R}}$ is proposed here for the stabilization of the friction force at a range $[-v_0,v_0]$ of quasi-null velocities, as depicted in Fig. 6. The improved friction model is written as

$$F_{\text{f}}=\left\{\begin{array}{ll}\left[F_{\text{C}}+\left(F_{\text{S}}-F_{\text{C}}\right)e^{-{\left(\left|v\right|/v_{\sigma }\right)}^{{\delta }_{\sigma }}}\right]\mathrm{sgn}(v)+\eta v\hfill & \text{if}\left|v\right|>\left|v_0\right|\hfill \\ -F_S\mathrm{sgn}\left(F_{\text{R}}\right)\hfill & \text{if}\left|v\right|\le \left|v_0\right|\text{and}\left|F_R\right|\ge F_S\hfill \\ \frac{F_S-\left|F_R\right|}{\left|v_0\right|}v+F_R\hfill & \text{if}\left|v\right|\le \left|v_0\right|\text{and}\left|F_R\right|<F_S\hfill \end{array}\right.$$ (28)

where $v_0$ is the quasi-null speed limit. One should note that $F_C$ and $F_S$ are always positive as they are obtained from the absolute value of the normal force, Eq. (27), thus, the sign of the friction force in Eq. (28) depends on the values and signs of the relative velocity and resultant force.

Fig. 6
Improved friction model.

In the proposed approach, $F_{\text{R}}$ is not a constant value, but depends on the system own force state at a given time instant, which can even be null, if applicable. Therefore, the system response can be stabilized by means of a smooth transition from the motion state to rest state and vice versa.

It should be noted that $v_0$ is a new parameter introduced in the model to distinguish the movement when in the quasi-null velocity interval. For a better convergence of the iterative solution method, the recommended value of the limit velocity should be close to the relative stop speed of the bodies, but not too small, to still allow the smooth transition among forces at rest. Instead of adopting a fixed unknown arbitrary value, an estimative for this parameter can be obtained by

$$v_0=\frac{\left|F_{\text{S}}-F_{\text{R}}\right|}{m}\Delta t$$ (29)

being $m$ the mass of the sliding node. This estimative is updated along the solution process and presented good responses for general applications, as is illustrated in the examples section.

Known the coefficients of the model, which depends on the materials that make the sliding connection and its path, the forces required to calculate the friction force have to be related to the variables describing the joint. The normal force vector ${\overrightarrow{F}}^N$ is found from the component of the Lagrange multipliers vector due to the translational constraints, $\overrightarrow{\lambda }=\left\{{\lambda }_1,{\lambda }_2\right\}$, at the normal direction of the path at the contact point, defined by the normal vector ${\overrightarrow{\overline{N}}}^P$, as

$${\overrightarrow{F}}^N=\frac{\overrightarrow{\lambda }\cdot {\overrightarrow{\overline{N}}}^P}{‖{\overrightarrow{\overline{N}}}^P‖}\frac{{\overrightarrow{\overline{N}}}^P}{‖{\overrightarrow{\overline{N}}}^P‖}$$ (30)

and its absolute value, actually used in the calculation, is

$$F_{\text{N}}=‖{\overrightarrow{F}}^N‖=\frac{\left|\overrightarrow{\lambda }\cdot {\overrightarrow{\overline{N}}}^P\right|}{‖{\overrightarrow{\overline{N}}}^P‖}$$.(31)

In the plane case, the components of the normal vector are obtained from the tangent vector of the path finite element at the contact point, ${\overline{T}}_i^P={\varphi }_{\mathcal{l},\xi }({\xi }_P){\overline{Y}}_i^{\mathcal{l}}$ ($i=\mathrm{1,2}$), as ${\overline{N}}_1^P=-{\overline{T}}_2^P$ and ${\overline{N}}_2^P={\overline{T}}_1^P$.

The resultant force, equal to the inertial force at the sliding node, is obtained directly from the equilibrium equation, Eq. (25), considering only the sliding node degrees of freedom (positions and curvilinear variable), as

$${\overrightarrow{F}}^R=\overrightarrow{F}-{\overrightarrow{F}}^{\mathrm{int}}-{\overrightarrow{F}}^{\text{con}}$$ (32)

or, to identify the terms referred to the degrees of freedom of interest one writes

$$\left\{\begin{array}{c}{F}_{{\overline{Y}}_1^P}^R\\ F_{{\overline{Y}}_2^P}^R\\ F_{s_P}^R\end{array}\right\}=\left\{\begin{array}{c}{F}_{{\overline{Y}}_1^P}^{}\\ F_{{\overline{Y}}_2^P}^{}\\ F_{s_P}^{}\end{array}\right\}-\left\{\begin{array}{c}{F}_{{\overline{Y}}_1^P}^{\mathrm{int}}\\ F_{{\overline{Y}}_2^P}^{\mathrm{int}}\\ 0\end{array}\right\}-\left\{\begin{array}{c}{F}_{{\overline{Y}}_1^P}^{\text{con}}\\ F_{{\overline{Y}}_2^P}^{\text{con}}\\ F_{s_P}^{\text{con}}\end{array}\right\}$$ (33)

where $\overrightarrow{F}$ represents all the external loads, ${\overrightarrow{F}}^{\mathrm{int}}$ the internal force of the sliding element and ${\overrightarrow{F}}^{\text{con}}$ the connection constraint force. Subscripts ${\overline{Y}}_1^P$, ${\overline{Y}}_2^P$ and $s_P$ refer to the sliding node position degrees of freedom and the curvilinear position, respectively. In the definition of Eq. (32) and (33), being a quasi-null velocity case, the velocity-proportional external damping force was neglected. The friction force is also not present since its value is already considered indirectly through the constraint force at the curvilinear position direction.

As the tangential value of the resultant force $F_R$ is required, the tangent vector ${\overrightarrow{\overline{T}}}^P$ is used to decompose the Cartesian terms as

$$F_R=\frac{\left(F_{{\overline{Y}}_1^P}-F_{{\overline{Y}}_1^P}^{\mathrm{int}}-F_{{\overline{Y}}_1^P}^{\text{con}}\right){\overline{T}}_1^P+\left(F_{{\overline{Y}}_2^P}-F_{{\overline{Y}}_2^P}^{\mathrm{int}}-F_{{\overline{Y}}_2^P}^{\text{con}}\right){\overline{T}}_2^P}{‖{\overrightarrow{\overline{T}}}^P‖}+F_{s_P}-F_{s_P}^{\text{con}}$$.(34)

As expected from the physical meaning of the multipliers as contact forces, we have $F_{{\overline{Y}}_1^P}^{\text{con}}$ = ${\lambda }_1$ and $F_{{\overline{Y}}_2^P}^{\text{con}}$ =${\lambda }_2$, which can be obtained by developing the constraint force given in Eq. (21) for the constraint equation in (7).

8 TIME INTEGRATION

For the time discretization, as the description of the solid is made in a total Lagrangian reference, the inertial force in Eq. (25) is obtained using a constant mass matrix. Similarly, the assumed Rayleigh damping also renders a constant matrix. This allows the use of classical time approximations, originally developed for linear dynamics, for the material velocity and acceleration vectors. Paultre (2011) discuss the application of direct time integration on nonlinear systems.

As Lagrange multipliers are present in the system to introduce constraints, a time marching scheme capable of controlling deleterious high frequencies introduced by their presence is necessary (Rong et al., 2019; Géradin and Cardona, 2001). Here we employ the generalized-α method (Chung and Hulbert, 1993) design to numerically control the system high frequency content while retaining the important information of low frequency range.

To discretize the solution in time increments $\Delta t$, the forces in Eq. (25) are rewritten for specific auxiliary time instants $t+1-{\alpha }_f$ and $t+1-{\alpha }_m$ as

$${\overrightarrow{F}}_{t+1-{\alpha }_f}^{\mathrm{int}}-{\overrightarrow{F}}_{t+1-{\alpha }_f}+M\cdot {\ddot{\overrightarrow{\Upsilon }}}_{t+1-{\alpha }_m}+D\cdot {\dot{\overrightarrow{\Upsilon }}}_{t+1-{\alpha }_f}+{\overrightarrow{F}}_{t+1-{\alpha }_f}^{\text{con}}+{\overrightarrow{F}}_{t+1-{\alpha }_f}^{\text{f}}=\overrightarrow{0}$$.(35)

A linear combination of the type ${\overrightarrow{d}}_{t+1-\alpha }=\left(1-\alpha \right){\overrightarrow{d}}_{t+1}+\alpha {\overrightarrow{d}}_t$ is used to evaluate any vector in (35) at an auxiliary instant using its current value ${\overrightarrow{d}}_{t+1}$ and its past instant value ${\overrightarrow{d}}_t$. The parameter $\alpha$ may represent ${\alpha }_f$ or ${\alpha }_m$.

Nodal parameters velocity and acceleration vectors are written using the Newmark approximations with parameters $\beta$ and $\gamma$ as

$${\overrightarrow{\Upsilon }}_{t+1}={\overrightarrow{\Upsilon }}_t+\Delta t{\dot{\overrightarrow{\Upsilon }}}_t+\Delta t^2\left[\left(\frac{1}{2}-\beta \right){\ddot{\overrightarrow{\Upsilon }}}_t+\beta {\ddot{\overrightarrow{\Upsilon }}}_{t+1}\right]$$ (36)

and

$${\dot{\overrightarrow{\Upsilon }}}_{t+1}={\dot{\overrightarrow{\Upsilon }}}_t+\Delta t\left(1-\gamma \right){\ddot{\overrightarrow{\Upsilon }}}_t+\gamma \Delta t{\ddot{\overrightarrow{\Upsilon }}}_{t+1}$$.(37)

The time-discrete equations of motion results, using Eq. (36) and (37) in Eq. (35),

$$\left(1-{\alpha }_f\right)\left({\overrightarrow{F}}_{t+1}^{\mathrm{int}}+{\overrightarrow{F}}_{t+1}^{\text{con}}+{\overrightarrow{F}}_{t+1}^{\text{f}}-{\overrightarrow{F}}_{t+1}\right)+\left[\frac{\left(1-{\alpha }_m\right)}{\beta \Delta t^2}M+\frac{\left(1-{\alpha }_f\right)\gamma }{\beta \Delta t}D\right]{\overrightarrow{\Upsilon }}_{t+1}+{\overrightarrow{P}}_t=\overrightarrow{0}$$,(38)

with the vector that groups the terms of the previous time instant given by

$${\overrightarrow{P}}_t={\alpha }_f\left({\overrightarrow{F}}_t^{\mathrm{int}}+{\overrightarrow{F}}_t^{\text{con}}+{\overrightarrow{F}}_t^{\text{f}}-{\overrightarrow{F}}_t\right)+{\alpha }_{m}M\cdot {\ddot{\overrightarrow{\Upsilon }}}_t-\left(1-{\alpha }_m\right)M\cdot {\overrightarrow{T}}_t+{\alpha }_{f}D\cdot {\dot{\overrightarrow{\Upsilon }}}_t+\left(1-{\alpha }_f\right)D\cdot {\overrightarrow{R}}_t$$ (39)

with

$${\overrightarrow{T}}_t=\left(\frac{1}{2\beta }-1\right){\ddot{\overrightarrow{\Upsilon }}}_t+\frac{{\dot{\overrightarrow{\Upsilon }}}_t}{\beta \Delta t}+\frac{{\overrightarrow{\Upsilon }}_t}{\beta \Delta t^2}$$ (40)

and

$${\overrightarrow{R}}_t=\left(1-\frac{\gamma }{2\beta }\right)\Delta t{\ddot{\overrightarrow{\Upsilon }}}_t+\left(1-\frac{\gamma }{\beta }\right){\dot{\overrightarrow{\Upsilon }}}_t-\frac{\gamma {\overrightarrow{\Upsilon }}_t}{\beta \Delta t}$$.(41)

At the end of the step, velocity and acceleration vectors must be calculated from the approximations (36) and (37). To start the time march, the initial acceleration is evaluated from Eq. (25) using the initial configuration and velocity of the system.

Chung and Hulbert (1993) recommend obtaining the generalized-α method parameters from the high frequency region spectral radius ${\rho }_{\infty }\in \left[\mathrm{0,1}\right]$. In order to retain second order accuracy, to minimize numerical dissipation of the fundamental frequencies and maximize the numerical dissipation on the high frequencies range the α-parameters are calculated from

$${\alpha }_m=\frac{2{\rho }_{\infty }-1}{{\rho }_{\infty }+1}\text{and}{\alpha }_f=\frac{{\rho }_{\infty }}{{\rho }_{\infty }+1}$$,(42)

and the Newmark parameters by

$$\gamma =\frac{1}{2}-{\alpha }_m+{\alpha }_f\text{and}\beta =\frac{1}{4}{\left(1-{\alpha }_m+{\alpha }_f\right)}^2$$.(43)

To achieve unconditional stability in the presence of constraints, the relation ${\alpha }_m<{\alpha }_f\le 1/2$ must also be respected - proven for the linear case in Géradin and Cardona (2001). As a consequence of ${\alpha }_m<{\alpha }_f$, the situation without numerical dissipation, ${\rho }_{\infty }=1$, is not achieved. From the authors experience in most situations ${\rho }_{\infty }$ in the range 0.7 - 0.9 presents good results with small or negligible numerical dissipation even in nonlinear cases.

9 NONLINEAR SYSTEM SOLUTION PROCEDURE

To solve the resulting time-discrete nonlinear equations of motion, Eq. (38), for the variables $\left\{{\overrightarrow{\Upsilon }}_{t+1},{\overrightarrow{\lambda }}_{t+1}\right\}$ the equilibrium is restated as

$${\overrightarrow{g}}_{t+1}\left({\overrightarrow{\Upsilon }}_{t+1},{\overrightarrow{\lambda }}_{t+1}\right)=\left(1-{\alpha }_f\right)\left({\overrightarrow{F}}_{t+1}^{\mathrm{int}}+{\overrightarrow{F}}_{t+1}^{\text{con}}+{\overrightarrow{F}}_{t+1}^{\text{f}}-{\overrightarrow{F}}_{t+1}\right)+\left[\frac{\left(1-{\alpha }_m\right)}{\beta \Delta t^2}M+\frac{\left(1-{\alpha }_f\right)\gamma }{\beta \Delta t}D\right]{\overrightarrow{Y}}_{t+1}+{\overrightarrow{P}}_t=\overrightarrow{0}$$ (44)

where $\overrightarrow{g}$ is the residual of the Newton method (or mechanical unbalanced vector), null when ${\overrightarrow{\Upsilon }}_{t+1}$ and ${\overrightarrow{\lambda }}_{t+1}$ are a solution of the system of equations for a given time step $t+1$. Note that ${\overrightarrow{\lambda }}_{t+1}$ only appears in the terms ${\overrightarrow{F}}_{t+1}^{\text{con}}$ and ${\overrightarrow{F}}_{t+1}^{\text{f}}$.

A usual first order Taylor expansion can be employed to obtain the Newton method as

$$\left\{\begin{array}{c}\Delta {\overrightarrow{\Upsilon }}_{t+1}\\ \Delta {\overrightarrow{\lambda }}_{t+1}\end{array}\right\}=-{\left(H_{t+1}\right)}^{-1}\cdot \overrightarrow{g}\left({\overrightarrow{\Upsilon }}_{t+1}^0,{\overrightarrow{\lambda }}_{t+1}^0\right)$$ (45)

in which, the correction on a trial solution $\left\{{\overrightarrow{\Upsilon }}_{t+1}^0,{\overrightarrow{\lambda }}_{t+1}^0\right\}$ is repeated until the relative position norm - calculated as $\left|\right|\Delta \overrightarrow{\Upsilon }\left|\right|/\left|\right|\overrightarrow{X}\left|\right|$, where $\overrightarrow{X}$ is the initial nodal position vector of the body - is smaller than a given tolerance. It should be mentioned that the constraint equations, calculated from Eq. (7), can also be employed as a secondary convergence criterion. In the authors’ experience, for the examples tested, employing the adopted relative position criterion with a tolerance of 1.10^-8 results in small force errors along the iterative process, even for the imposed constraints.

The Hessian matrix $H_{t+1}$ (tangent operator), in Eq. (45), is given by

$$H_{t+1}=\nabla {\overrightarrow{g}}_{t+1}=\left(1-{\alpha }_f\right)\left(\nabla {\overrightarrow{F}}_{t+1}^{\mathrm{int}}+\nabla {\overrightarrow{F}}_{t+1}^{\text{con}}+\nabla {\overrightarrow{F}}_{t+1}^{\text{f}}\right)+\frac{\left(1-{\alpha }_m\right)}{\beta \Delta t^2}M+\frac{\left(1-{\alpha }_f\right)\gamma }{\beta \Delta t}D$$.(46)

The elastic part of the Hessian matrix, associated with the strain energy potential of the finite elements, is

$$\nabla {\overrightarrow{F}}_{t+1}^{\mathrm{int}}={\left.\frac{\partial {\overrightarrow{F}}^{\mathrm{int}}}{\partial \overrightarrow{\Upsilon }}\right|}_{t+1}={\displaystyle {\int }_{V_0}^{}\left({\left.\frac{\partial E}{\partial \overrightarrow{\Upsilon }}\right|}_{t+1}:\frac{{\partial }^{2}u}{\partial E\otimes \partial E}:{\left.\frac{\partial E}{\partial \overrightarrow{\Upsilon }}\right|}_{t+1}+S_{t+1}:{\left.\frac{{\partial }^{2}E}{\partial \overrightarrow{\Upsilon }\otimes \partial \overrightarrow{\Upsilon }}\right|}_{t+1}\right)d{V}_0}$$ (47)

in which $\otimes$ represents tensor product. From the specific strain energy expression, Eq. (14), and developing the Green strain derivatives, using Eq. (6) and (2), one develops this matrix particular expression for the plane frame finite element as seen in Siqueira and Coda (2017) and Coda and Paccola (2014).

The Hessian matrix parcel due the constraint potential of the sliding connections is written as

$$\nabla {\overrightarrow{F}}_{t+1}^{\text{con}}={\left.\frac{\partial {\overrightarrow{F}}^{\text{con}}}{\partial \left\{\overrightarrow{\Upsilon },\overrightarrow{\lambda }\right\}}\right|}_{t+1}={\left[\begin{array}{cc}\overrightarrow{\lambda }\cdot \nabla \left(\nabla \overrightarrow{c}\right)& \nabla \overrightarrow{c}\\ {\left(\nabla \overrightarrow{c}\right)}^t& 0\end{array}\right]}_{t+1}$$ (48)

where, $\nabla \left(\nabla \overrightarrow{c}\right)$ is a third order tensor that can be understood as the set of Hessian matrices due to each constraint equation $c_i$, Eq. (7), and $0$ is the null matrix.

It must be stressed that, the achieved value of $s_P$ in the solution process is not enough to update ${\overrightarrow{F}}^{\text{con}}$ and $\nabla {\overrightarrow{F}}_{t+1}^{\text{con}}$ as ${\xi }_P=\xi (s_P)$ is not explicitly written. The solution of this stage is done by adopting a least square method to find the non-dimensional coordinate from the converged values of the path element and the sliding node as described in detail by Siqueira and Coda (2017). Given the numerical value of the non-dimensional variable in the dimensionless space, the solution process continues and also the transition between path elements can be performed - which is straightforward when ${\xi }_P$ exceeds the space domain $[-\mathrm{1,1}]$.

As the friction force calculation is dependent on the tangential velocity $v={\dot{s}}_P$, Eq. (28), the solution procedure is improved by updating its value at each iteration by the following finite difference approximation

$v_{t+1}^{k+1}=\frac{{\left(s_P\right)}_{t+1}^{k+1}-{\left(s_P\right)}_t}{\Delta t}$,(49)

where $k+1$, is explicitly written to identify the value as belonging to the current iteration of a time step $t+1$. Consequently, the friction force is entirely defined by the main solution variables, of particular interest, the curvilinear position.

As ${\overrightarrow{F}}^{\text{f}}=\left\{F_{\text{f}}\right\}$, i.e., the friction force is a scalar properly placed at the system’s degree of freedom, the friction part of the Hessian matrix can be developed as

$$\nabla {\overrightarrow{F}}_{t+1}^{\text{f}}={\left.\frac{\partial F_{\text{f}}}{\partial s_p}\right|}_{t+1}$$,(50)

which is a scalar value to be added in the curvilinear position degree of freedom of the system’s matrix. Further developing Eq. (50), using Eq. (49) and (28), results

$${\left.\frac{\partial F_{\text{f}}}{\partial s_p}\right|}_{t+1}=\left\{\begin{array}{ll}\frac{1}{\Delta t}\left[\eta -\left(F_{\text{S}}-F_{\text{C}}\right)e^{-{\left(\left|v_{t+1}^{k+1}\right|/v_{\sigma }\right)}^{{\delta }_{\sigma }}}\frac{\delta {\left|v_{t+1}^{k+1}\right|}^{\delta -1}}{v_{\sigma }{}^{{\delta }_{\sigma }}}\right]\hfill & \text{if}\left|v_{t+1}^{k+1}\right|>\left|v_0\right|\hfill \\ \frac{1}{\Delta t}\frac{F_S-\left|F_R\right|}{\left|v_0\right|}\hfill & \text{if}\left|v_{t+1}^{k+1}\right|\le \left|v_0\right|\text{and}\left|F_R\right|<F_S\hfill \end{array}\right.$$ (51)

with $v_{t+1}^{k+1}$ updated in each iteration by Eq. (49).

Regarding the computational implementation, to reduce the time spent in updating the residual vector and Hessian matrix of the Newton method for each iteration, it should be noted that, due to the total Lagrangian description of the positional formulation, the mass and damping matrices, as well as the part $A^0$ of the deformation gradient, Eq. (4), are constants and can be stored before starting the time marching process.

10 EXAMPLES

Examples are presented to verify the correct response of the proposed improved friction model and its introduction on the finite element system and also to show the capabilities of the proposed formulation in describing engineering applications of interest including roughness.

10.1 Rabinowicz test

The Rabinowicz test is a one degree of freedom experiment largely used as a benchmark, Pennestrì et al. (2016), for testing friction models, particularly useful in verifying the model capability of representing the stick-slip behavior. Fig. 7a) depicts the test system with mass $m$, held by a spring with stiffness $k$, in contact with a belt moving horizontally with constant velocity $v$. Due to friction between the oscillator and belt, the mass initially sticks to the belt until the spring force exceeds the static friction value. At this point sliding takes place under the kinetic value of friction. After a while, the mass attaches again to the moving surface and the process is repeated.

Fig. 7
Geometry of the test: a) mass-spring and b) finite element bar scheme.

Parameters for the mass-spring system and friction were adopted the same as Pennestrì et al. (2016). To simulate the oscillator, one two-node (linear) frame element, Fig. 7b), is employed with a cylindrical joint at the end of the bar. This connection is free to slide over another finite element moving in the horizontal direction with velocity $v$ = 0.5 m/s and with all other degrees of freedom locked. A vertical force $P$ = 196.2 N is applied to manifest frictional effects at the contact point. In order to maintain small strains, to allow comparison with the reference, a $L$ = 1000 m bar is adopted with squared cross-section, $b_0$ = $h_0$ = 1.0 m, and Young modulus $E$ = 10 kPa. This results in an equivalent axial stiffness $k$ = $E{b}_0{h}_0/L$ = 10 N/m. Null Poisson ratio is used and the equivalent system mass $m$ = 20 kg is lumped at the joint node.

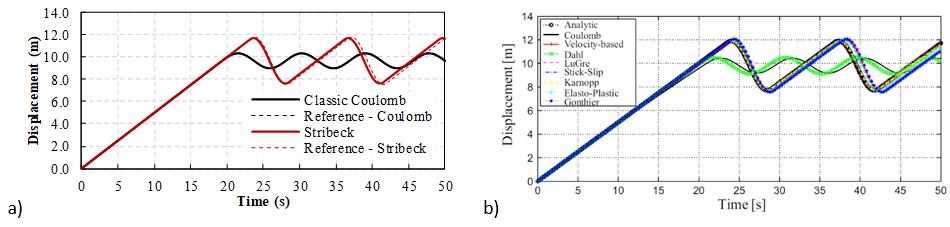
The sliding node displacement is shown in Fig. 8a) for the improved friction model under two different cases. The first considers the Stribeck effect, with parameters ${\mu }_s$ = 0.6, ${\mu }_k$ = 0.5, $v_{\sigma }$ = 0.05 m/s and ${\delta }_{\sigma }$ = 1.0, and the second case is the classic Coulomb model, only capable of representing kinetic friction. No viscous effect is present, $\eta$ = 0, in both cases. Results were obtained with a time increment $\Delta t$ = 1.0 ms with the generalized-α method parameter ${\rho }_{\infty }$ = 1.0.

Fig. 8
Displacement for the Rabinowicz test: a) improved model results and b) numerical results from Pennestrì et al. (2016) for different friction models.

Fig. 8b) depicts Pennestrì et al. (2016) results for the mass displacement due to different friction models evaluated in their work. No direct comparison can be performed with the reference models as they are not directly equivalent with the proposed improved model, or among themselves, as they consider different friction characteristics requiring parameters not present in the current model. For those parameters and models description we refer to Pennestrì et al. (2016) study.

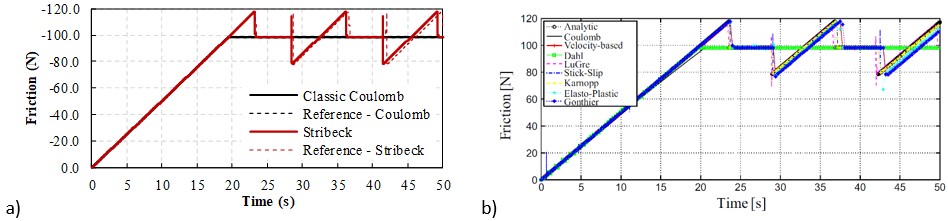
Compatible responses with Pennestrì et al. (2016) models are observed for both friction cases even for the relative velocity, Fig. 9, and friction force, Fig. 10. It is noticeable that, as the classic Coulomb model does not account for static friction, after the initial stiction phase, the system displays the harmonic oscillator behavior without maintaining null relative velocity and stiction again. For the Stribeck case a detail for the first relative motion of the system can be seen in Fig. 11 showing the variation between static and kinetic friction force captured by the improved model. Regarding processing time between models, for this example, the simulation for the Stribeck case is 15% longer than for the classic Coulomb model. The computation time was calculated by averaging the time spent in three separate simulations of each case (due to the influence of the operational system background tasks) on the same computer.

Fig. 9
Relative velocity for the Rabinowicz test: a) improved model results and b) numerical results from Pennestrì et al. (2016) for different friction models.

Fig. 10
Friction force for the Rabinowicz test: a) improved model results and b) numerical results from Pennestrì et al. (2016) for different friction models.

Fig. 11
Detail of the friction force evolution for the improved model showing the Stribeck effect.

To further analyze the improved friction model results, a reference solution is depicted in Fig. 8 to Fig. 11 for each case. As analytical solutions are not always available, the reference solution was obtained by employing a time step 100 times smaller to diminish the influence of the quasi-null speed range calculated by Eq. (29). For the classic Coulomb case, the reference solution after stiction is also the response of a harmonic oscillator subjected to the Couloumb friction force. The simulated response coincides perfectly for this case (overlapping curves). A difference in the response is observed after the initial stiction phase in the Stribeck case. This difference is anticipated as the friction force value in this situation is velocity dependent, due to the exponential term of the Stribeck curve expression, Eq. (26), which is null for the Coulomb case. Thus, the numerical solution procedure has a higher influence. Nevertheless, very good agreement with Pennestrì et al. (2016) models are observed.

10.2 Quick-return mechanism with friction

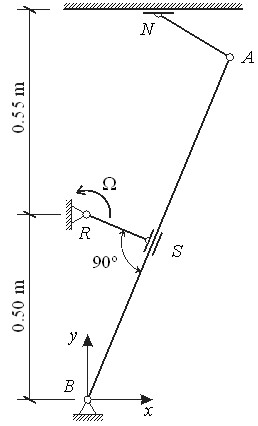
A classic quick-return mechanism is analyzed considering frictional dissipation, Fig. 12. This mechanism was proposed by Bauchau (2000) and also investigated by Siqueira and Coda (2017) employing positional frame finite elements, for the frictionless case. The system consists in a 1.0 m arm AB able to spin around a fixed support B and connected to a 0.25 m bar NA. The motion is imposed by a 0.20 m crank RS which turns around the fixed support R with a constant angular speed $\Omega$ = 5π rad/s and slides over the arm with a cylindrical joint S. The translational motion resulting from the mechanism input rotation is obtained by a cylindrical joint at point N, able to move horizontally over a fixed path.

Fig. 12
Initial configuration of the mechanism.

All bars have 5.98 cm squared cross section and density 1724.82 kg/m³. The arm is flexible with $E$ = 47.04 GPa and discretized by 10 cubic finite elements. To simulate the rigid behavior of the remaining bars a 10⁶ times greater Young modulus was adopted and 2 cubic frame elements were used for each bar. The shear elastic modulus is half the value of its corresponding Young modulus value for the whole mechanism. Lumped masses are placed at slider S (0.31 kg) and N (2.50 kg). Simulations were performed with a time increment $\Delta t$ = 0.1 ms and the generalized-α method parameter ${\rho }_{\infty }$ = 0.9.

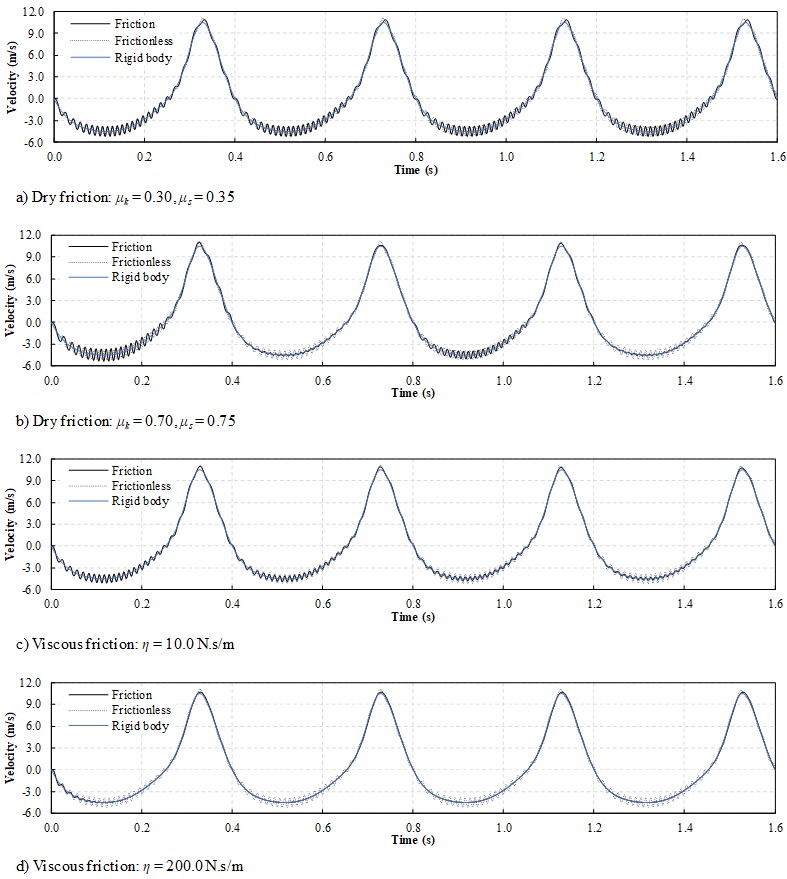
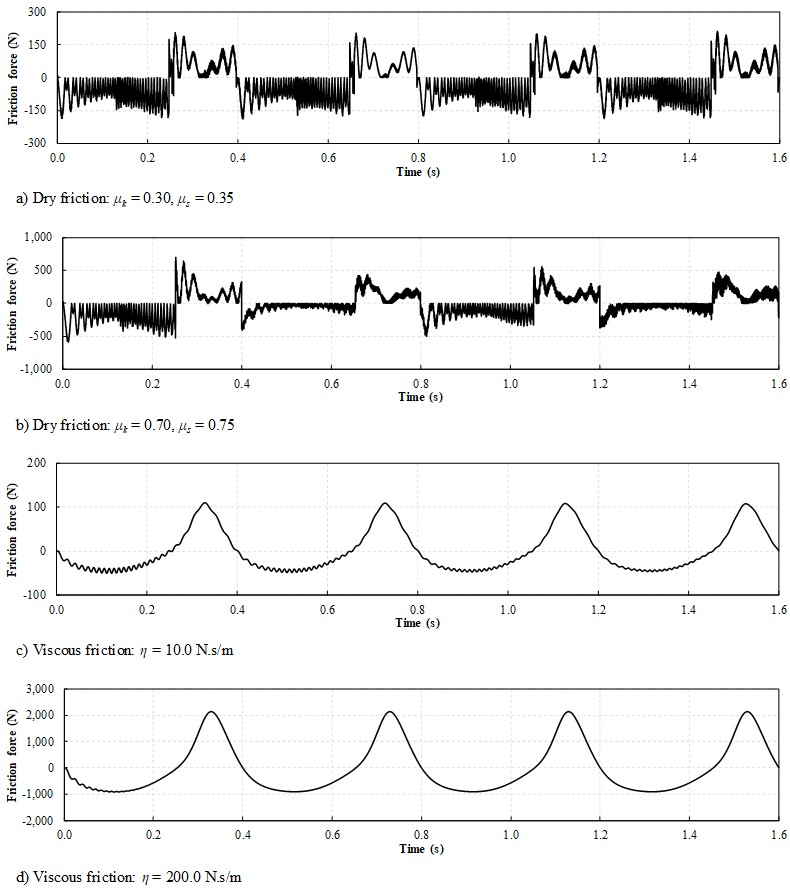
Four cases of friction were evaluated. As we are interested in the flexible arm deflection and the output velocity of the mechanism, attention is restricted to slider N. Tests with friction at slider S presented minor effects in the overall system response, thus dissipation at this joint was not considered. Two dry friction cases, one with ${\mu }_s$ = 0.35 and ${\mu }_k$ = 0.30 and another with ${\mu }_s$ = 0.75 and ${\mu }_k$ = 0.70, both with Stribeck curve parameters $v_{\sigma }$ = 0.10 m/s and ${\delta }_{\sigma }$ = 1.0, and two viscous friction situations, $\eta$ = 10.0 N.s/m and 200.0 N.s/m, are considered at the sliding connection N.

The first four cycles of the mechanism arm tip deflection (point A), evaluated orthogonally to a line that follows the arm spin at point B, are shown in Fig. 13. Interesting results for the deflection of the arm were obtained for different friction cases. Compared to the frictionless case, the situation with smaller dry friction coefficients presented slightly higher arm deflection along the cycles, Fig. 13a), but similar output velocity at slider N, Fig. 14a), even though a horizontal friction force, Fig. 15a), acts at this point. The output velocity for a frictionless rigid body case of the mechanism (simulated by adopting the same Young modulus for the arm AB as for the rigid parts) is also depicted in Fig. 14. It is clear that the arm flexibility promotes an oscillatory response of the output velocity around the rigid body response.

Fig. 13
Arm tip (point A) deflection for the quick-return mechanism.

Fig. 14
Slider N horizontal velocity for the quick-return mechanism.

Fig. 15
Friction force at slider N for the quick-return mechanism.

For the higher dry friction parameters adopted, however, the mechanism presents a curious behavior reducing its arm tip vibration amplitude in alternating cycles, Fig. 13b). The output velocity presented the same pattern, Fig. 14b). Friction forces, Fig. 15b), showed smaller values at the low amplitude cycles, than higher ones. Tests performed for even higher values of static and kinetic friction coefficients (${\mu }_s$ = 0.85 and ${\mu }_k$ = 0.80) showed that the same pattern occurs, but with less intense reduction of the deflection among cycles. Consequently, we understand that exist a range of friction parameters, in combination with this particular mechanism mass and stiffness, resulting in a very particular cycle-alternating nonlinear response. The physical interpretation of this response can be realized as slider N friction force affecting link NA force transmission to the flexible arm AB in a way that excites its transverse deflection at each two cycles and in the opposite direction of the crank (constant) excitation. This indicates the existence of a transverse motion along the arm (with a period twice as long as the duration of the mechanism cycle) decreasing the contact force in a cycle and increasing it on the next.

Cases with only viscous friction presented the expected reduction of vibration of the arm deflection, Fig. 13c) and d), and slider velocity, Fig. 14c) and d). For the larger friction coefficient case, although vibrations were quickly damped, higher values of arm deflection were observed indicating the difficulty of the crank to move the arm for the intensity of the friction force developed at slider N, Fig. 15d).

Independently of the friction force evolution aspect, Fig. 15, smoother for the velocity proportional viscous cases or discontinuous in dry friction cases, the mechanism response was correctly depicted showing sense alternance for its return and that the proposed improved friction model was capable of producing limited solutions for a system with several degrees of freedom.

10.3 Vehicle motion on bridge

A two-span bridge is analyzed considering the effect of a vehicle motion, Fig. 16. Pavement irregularities are considered by a roughness profile along the path of the wheels, modeled as cylindrical joints, Fig. 17. Before entering the bridge, the vehicle moves at a constant 100 km/h speed, after this moment its movement is released. Friction between the wheels and pavement is present during the whole analysis, which is performed until the car stops or reaches the end of the path.

Fig. 16
Initial configuration of the vehicle on a two-span bridge.

Fig. 17
Vehicle geometry and contact with the path.

The vehicle is modeled by 42 cubic finite elements with 6.73 cm squared cross section and has $E$ = 200.0 GPa, except for the suspension elements with $E$ = 1.5 GPa. Mass density ${\rho }_0$ = 7800.0 kg/m³ is adopted resulting in a total mass of 1500.0 kg. Each bridge span is modeled with 5 cubic frame elements. To have appropriate mass and stiffness, the bridge has a rectangular cross section, $h_0$ = 0.50 m and $b_0$ = 3.50 m, $E$ = 20.0 GPa and ${\rho }_0$ = 2500.0 kg/m³. The paths before and after the bridge are fixed and discretized by one finite element each. Shear elastic modulus for the whole system is half the value of its corresponding longitudinal one.

Structural damping, as Rayleigh type, is considered solely on the bridge to account for its proper dissipative behavior. Considering the bridge made of reinforce concrete, a damping ratio of 2,5% (Papageorgiou and Gantes, 2010) is employed for its first (1.03 Hz) and fourth (5.19 Hz) vibration modes. All four initial modes are related to bending. Thus, its Rayleigh damping matrix (mass and stiffness proportional) can be obtained as presented in classic dynamics textbooks, such as Paultre (2011). Since the present formulation is geometrically nonlinear, the bridge stiffness matrix, used for the modal analysis and to calculate a constant damping matrix, is assumed as the initial Hessian matrix.

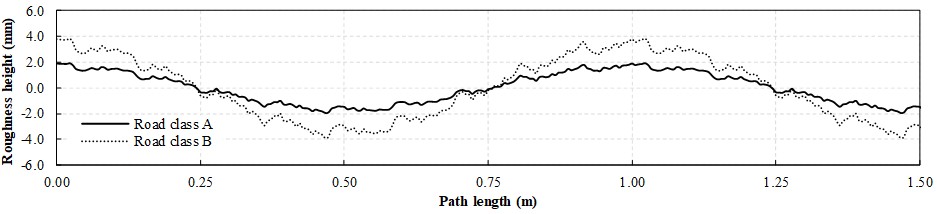
Dry friction parameters were adopted to consider contact between tire and asphalt as ${\mu }_s$ = 0.4, ${\mu }_k$ = 0.3, $v_{\sigma }$ = 1.0 m/s and ${\delta }_{\sigma }$ = 1.0. The pavement imperfection is obtained by a random roughness profile generated from a series of cosines as proposed by Yang and Lin (1995) using ISO 8608 (ISO, 1995) parameters for roads classes A and B, considered as in good traffic condition. The standard coefficients are the power spectral density function of 16.10^-6 m³, for class A, and 64.10^-6 m³, for class B. Both profiles were calculated employing 20 spatial frequencies equally distributed in the range from 1.0 to 10.0 cycle/m as recommended by Coussy et al. (1989) and Camara and Ruiz-Teran (2015). Also, as an actual wheel has finite dimensions, and its contact is not done in all the points of the path, a rigid tread band model is employed in order to maintain wheel tread band contact to the nearest point of the surface following Captain et al. (1979) and Chang et al. (2011). Both wheels have a 30.0 cm radius and the resulting roughness profiles are depicted in Fig. 18 for a representative part of the bridge path.

Fig. 18
Pavement roughness profiles for different ISO 8608 road classes.

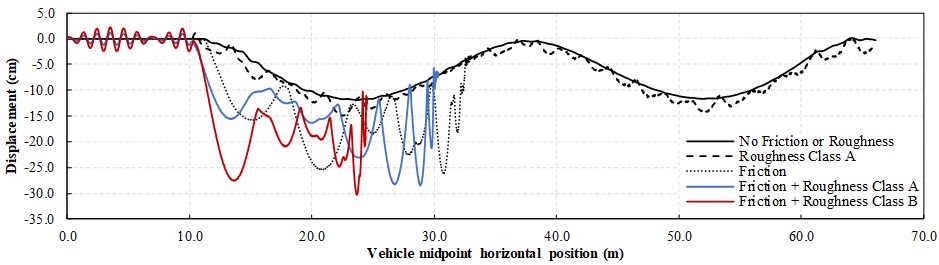
Both vehicle and bridge are subjected to their own weight during the whole analysis. Simulations were performed with a time increment $\Delta t$ = 0.1 ms and the generalized-α method parameter ${\rho }_{\infty }$ = 0.7. The front wheel curvilinear position evolution is depicted in Fig. 19 where is clear that the presence of friction stopped the vehicle before reaching the end of the bridge.

Fig. 19
Front wheel curvilinear position.

The pavement imperfections considered act primarily increasing vertical displacements of the vehicle, Fig. 20, and also the bridge, Fig. 21, but without friction dissipation the vehicle does not stop. For a frictionless situation, in presence of roughness, some resistance is found in its horizontal motion, as can be observed in Fig. 19 by the additional time (depicted for class A) the vehicle takes to reach the end of the path when compared to an smooth trajectory. The increase in the roughness of the road profile (from road class A to B) increases the friction force as depicted by Fig. 22.

Fig. 20
Vehicle midpoint vertical displacement.

Fig. 21
Bridge left span midpoint vertical displacement.

Fig. 22
Friction force at the front wheel.

From the vehicle midpoint horizontal position, Fig. 20, it can be observed that it stopped before the central support in all three cases where friction was considered. Thus, the bridge left mid-span deflection is not alleviated as for the frictionless situations, Fig. 21, when the vehicle passes on the right span. The vertical movement, manifested in the bridge even in the situation without roughness, is due to the horizontal friction force not aligned with the center of gravity of the vehicle, which generates a low frequency rotational vibration causing vertical movement in the region of the wheels, resulting in vertical forces transferred to the bridge. This aspect could only be captured due to the geometrically nonlinear description of the employed formulation.

11 CONCLUSIONS

Friction dissipation was successfully introduced in sliding connections commonly present in structures and mechanisms employing a total Lagrangian FEM formulation for plane frames based on a positional description of its kinematics. An improvement on a Coulomb friction model with Stribeck effect and viscous friction was proposed for a smoother description of the transition between motion and rest states of the joints. The improved model avoided instabilities for the friction force at null speed and is able to correctly represents frictional dissipation and capture the stick-slip effect since the resultant force could be calculated properly for the connections in the finite element system. The improved friction model is coupled with a mesh independent roughness strategy enabling general applications. Benchmarks and additional examples are used to verify the proposed model and to analyze engineering applications. Results were presented with successful responses for dynamical systems in which the consideration of friction is important. Future studies intent to extend this formulation to 3D applications.

References

• Ambrósio, J.A.C. (2003) Impact of Rigid and Flexible Multibody Systems: Deformation Description and Contact Models. In W. Schiehlen & M. Valášek, eds. Virtual Nonlinear Multibody Systems SE - 4. NATO ASI Series. Dordrecht, Netherlands: Springer Netherlands, pp. 57-81.
• Andersson, S., Söderberg, A., Björklund, S. (2007) Friction models for sliding dry, boundary and mixed lubricated contacts. Tribology International. 40(4), 580-587.
• Armstrong-Hélouvry, B., Dupont, P., De Wit, C.C. (1994) A survey of models, analysis tools and compensation methods for the control of machines with friction. Automatica. 30(7).
• Awrejcewicz, J., Grzelcyzk, D., Pyryev, Y. (2008) A novel dry friction modeling and its impact on differential equations computation and and Lyapunov exponents estimation. Journal of Vibroengineering. 10(4).
• Bauchau, O.A. (2000) On the modeling of prismatic joints in flexible multi-body systems. Computer Methods in Applied Mechanics and Engineering. 181(1-3), 87-105.
• Bo, L.C., Pavelescu, D. (1982) The friction-speed relation and its influence on the critical velocity of stick-slip motion. Wear. 82(3).
• Bonet, J., Wood, R.D., Mahaney, J., Heywood, P. (2000) Finite element analysis of air supported membrane structures. Computer Methods in Applied Mechanics and Engineering. 190(5-7), 579-595.
• Camara, A., Ruiz-Teran, A.M.M. (2015) Multi-mode traffic-induced vibrations in composite ladder-deck bridges under heavy moving vehicles. Journal of Sound and Vibration. 355, 264-283.
• Canudas de Wit, C., Lischinsky, P., Åström, K.J., Olsson, H. (1995) A New Model for Control of Systems with Friction. IEEE Transactions on Automatic Control. 40(3).
• Captain, K.M., Boghani, A.B., Wormley, D.N. (1979) Analytical Tire Models for Dynamic Vehicle Simulation. . 8(1), 1-32.
• Cha, H.-Y., Choi, J., Ryu, H.S., Choi, J.H. (2011) Stick-slip algorithm in a tangential contact force model for multi-body system dynamics. Journal of Mechanical Science and Technology. 25(7), 1687-1694.
• Chang, K.C., Wu, F.B., Yang, Y.B. (2011) Disk model for wheels moving over highway bridges with rough surfaces. Journal of Sound and Vibration. 330(20), 4930-4944.
• Chung, J., Hulbert, G.M. (1993) A Time Integration Algorithm for Structural Dynamics With Improved Numerical Dissipation: The Generalized-α Method. Journal of Applied Mechanics. 60(2), 371.
• Coda, H.B. (2003) An exact FEM geometric non-linear analysis of frames based on position description. In . IN: 17H INTERNATIONAL CONGRESS OF MECHANICAL ENGINEERING. 2003, São Paulo. São Paulo: ABCM.
• Coda, H.B., Paccola, R.R. (2014) A total-Lagrangian position-based FEM applied to physical and geometrical nonlinear dynamics of plane frames including semi-rigid connections and progressive collapse. Finite Elements in Analysis and Design. 91, 1-15.
• Coussy, O., Said, M., van Hoove, J.-P. (1989) The influence of random surface irregularities on the dynamic response of bridges under suspended moving loads. Journal of Sound and Vibration. 130(2), 313-320.
• Dahl, P.R. (1976) Solid friction damping of mechanical vibrations. AIAA Journal. 14(12), 1675-1682.
• Dupont, P., Hayward, V., Armstrong, B., Altpeter, F. (2002) Single state elastoplastic friction models. IEEE Transactions on Automatic Control. 47(5), 787-792.
• Géradin, M., Cardona, A. (2001) Flexible multibody dynamics: a finite element approach. Chichester: John Wiley & Sons.
• Gonthier, Y., McPhee, J., Lange, C., Piedbœuf, J.-C. (2004) A regularized contact model with asymmetric damping and dwell-time dependent friction. Multibody System Dynamics. 11(3), 209-233.
• Gurtin, M.E., Fried, E., Anand, L. (2010) The Mechanics and Thermodynamics of Continua. New York: Cambridge University Press.
• Hess, D.P., Soom, A. (1990) Friction at a lubricated line contact operating at oscillating sliding velocities. Journal of Tribology. 112(1), 147-152.
• Hsieh, C., Pan, Y.-C. (2000) Dynamic behavior and modelling of the pre-sliding static friction. Wear. 242(1-2), 1-17.
• ISO (1995) Mechanical Vibration — Road Surface Profiles — Reporting of Measured Data (ISO Standard No. 8608).
• Karnopp, D. (1985) Computer simulation of stick-slip friction in mechanical dynamic systems. Journal of Dynamic Systems, Measurement and Control, Transactions of the ASME. 107(1).
• Kikuuwe, R., Takesue, N., Sano, A., Mochiyama, H., Fujimoto, H. (2005) Fixed-step friction simulation: From classical coulomb model to modern continuous models. In 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS. pp. 1009-1016.
• Lanczos, C. (1970) The variational principles of mechanics. New York: Dover Publications .
• Leine, R.I., Van Campen, D.H., De Kraker, A., Van Den Steen, L. (1998) Stick-Slip Vibrations Induced by Alternate Friction Models. Nonlinear Dynamics. 16(1), 41-54.
• Marques, F., Flores, P., Pimenta Claro, J.C., Lankarani, H.M. (2016) A survey and comparison of several friction force models for dynamic analysis of multibody mechanical systems. Nonlinear Dynamics. 86(3), 1407-1443.
• Nocedal, J., Wright, S.J. (1999) Numerical optimization. New York: Springer.
• Ogden, R.W. (1984) Non-linear elastic deformations. Chichester: Ellis Horwood.
• Olsson, H., Åström, K.J., Canudas de Wit, C., Gäfvert, M., Lischinsky, P. (1998) Friction Models and Friction Compensation. European Journal of Control. 4(3), 176-195.
• Papageorgiou, A. V., Gantes, C.J. (2010) Equivalent modal damping ratios for concrete/steel mixed structures. Computers and Structures. 88(19-20), 1124-1136.
• Paultre, P. (2011) Dynamics of structures. Croydon: John Wiley & Sons.
• Pennestrì, E., Rossi, V., Salvini, P., Valentini, P.P. (2016) Review and comparison of dry friction force models. Nonlinear Dynamics. 83(4), 1785-1801.
• Rabinowicz, E. (1958) The intrinsic variables affecting the stick-slip process. Proceedings of the Physical Society. 71(4), 668-675.
• Rabinowicz, E. (1951) The nature of the static and kinetic coefficients of friction. Journal of Applied Physics. 22(11), 1373-1379.
• Rao, S.S. (2009) Engineering optimization: theory and practice. 4th ed. New Jersey: John Wiley & Sons.
• Rong, B., Rui, X., Tao, L., Wang, G. (2019) Theoretical modeling and numerical solution methods for flexible multibody system dynamics. Nonlinear Dynamics. 98(2), 1519-1553.
• Siqueira, T.M., Coda, H.B. (2016) Development of sliding connections for structural analysis by a total lagrangian FEM formulation. Latin American Journal of Solids and Structures. 13(11).
• Siqueira, T.M., Coda, H.B. (2019) Flexible actuator finite element applied to spatial mechanisms by a finite deformation dynamic formulation. Computational Mechanics. 64(6), 1517-1535.
• Siqueira, T.M., Coda, H.B. (2017) Total Lagrangian FEM formulation for nonlinear dynamics of sliding connections in viscoelastic plane structures and mechanisms. Finite Elements in Analysis and Design. 129, 63-77.
• Threlfall, D.C. (1978) The inclusion of Coulomb friction in mechanisms programs with particular reference to DRAM au programme DRAM. Mechanism and Machine Theory. 13(4).
• Yang, Y.-B., Lin, B.-H. (1995) Vehicle-Bridge Interaction Analysis by Dynamic Condensation Method. Journal of Structural Engineering. 121(11), 1636-1643.

Edited by

Editor: Marco L. Bittencourt

Publication Dates

• Publication in this collection
  13 Jan 2023
• Date of issue
  2023

History

• Received
  08 Oct 2022
• Reviewed
  30 Nov 2022
• Accepted
  15 Dec 2022
• Published
  19 Dec 2022