Numerical Modelling of Foamed Concrete Beam under Flexural Using Traction-Separation Relationship

Abstract

The aim of the current project is to carry out the FEA framework for predicting the flexural strength of notched foam concrete tested under three-point bending following the conducted experimental set-up. The investigated testing series have a variation of notch size opening in the foamed concrete beam. The Traction-separation relationship was used as a constitutive model to incorporate independent material properties and used in the modelling framework. Modelling techniques of 2D XFEM and CZM were adopted and later expanded to 3D XFEM models. Good agreement was found between the predicted structure response and experimental observation for all the investigated models. Crack was initiated at the crack tip and propagated to the beam edge under the applied load. It was found that the average discrepancies below 20% were found within XFEM techniques. Less agreement was found using the CZM models, partly due to the simplification of the adopted failure path. The modelling framework implemented in this project is potentially used as a predictive tool in estimating the flexural strength of the concrete beam with notches.

Keywords:
Concrete; Notched beam; Fracture; Finite element analysis (FEA); Strength prediction

Graphical abstract

1 INTRODUCTION

Any structures with discontinuities such as notches, cut-outs or cracks led to lower load-carrying capacity compared to continuous structures. These discontinuities give stress concentration; therefore, low resistance to applied load in notched structures is much expected. Failure and fracture are formed as the fracture energy of the material have exceeded upon the stress applied (Ahmed et al., 2016). Due to beam discontinuities, stress is concentrated at the notch tip; therefore, the crack initiation and propagations from the notch tip are perhaps not surprising (Xia et al., 2015). Concrete shows a stable non-linear fracture response under tension loading due to a fracture zone process zone (FPZ) ahead of the crack tip. Reasons for the establishment of FPZ in concrete associated with micro-cracks shielding, inclusion bridging and trans-granular fracture. In quasi-brittle materials such as concrete, the energy dissipated to form FPZ ahead of the crack tip is termed fracture energy to be regarded as a material property. The presence of localised micro-damage events to form new crack surface within FPZ at the crack tip can be represented by fracture energy values.

Incorporation of a foaming agent able to reduce the density of conventional concrete by promoting lightweight materials known as foamed concrete with a density ranging from 800 to 1800 kg/m2 (Shawnim and Mohammad, 2019). Foamed concrete is regarded as self-compacting concrete due to excellent self-flowing capacity (Jones et al., 2017). It has displayed booming attention in underground engineering and poor foundation to control imposed dead load (Fu et. al, 2020). The evolution of foam concrete has been reported in the literature by adding aluminium powder (Van et. al, 2019) and microsilica (Sherbin and Gorbach, 2020) to produce high-performance foamed concrete.

From experimental observations of notched foam concrete beam, it was found that crack occurred from the sharp notch tip to the beam edge. Crack exhibited during experimental observations was regarded as self-similar cracks where damages were taken place. Zhou and Chen (2019) performed a three-point bending test, and showed that cracking occured gradually as the force increased. Consistence crack pattern on the front and rear surfaces of the tested beam were obtained.

With the advancement of computing technology, numerical approaches are much favourable, particularly within a finite element modelling (FEM) framework (Wang et al., 2015). In earlier work, due to singularity stress occurred at the notch tip, FEM requires very fine mesh at the vicinity of the notch and further increases difficulties to model a sharp crack. Recently, the incorporation of traction-separation relationship in commercial software such as ABAQUS is able to define the damage to be driven by an energetic approach. This model requires fracture energy value to predict the structures strength of a concrete beam with stress concentrations (Náhlík et al., 2014). Fracture energy is regarded as unique material properties and independent of beam size, shape, structure, presence of the reinforcement and also loading condition. Nevertheless, fracture energy can be determined from experimental investigation and analytical analysis (Jaini et al., 2017). For analytical analysis, the fracture energy used available closed-form fracture energy formulations reported in Hillerborg model (1985), CEP-fib model (1993) and Bazant model (2002). Fracture energy estimation from the Hillerborg model acquires parameters of the total area under load-deflection profile, beam weight, beam dimensions and notch depth. However, compressive strength is essential to predict fracture energy in Bazant and CEB models. In the author point of view, fracture energy is regarded as a material property and has to be independently determined from available expressions instead of using calibrated values from available literature.

There are numbers of analytical approaches reported in the literature to provide strength prediction, but mostly are semi-empirical that requires experimental datasets in their closed-form expressions (Javadi and Rezania,2009). Advancing of computing technology promotes numerical approaches, the most powerful tools in predicting structures response of a structure subjected to applied load is finite element analysis (FEA). Modelling of such behaviour is complicated due to the presence of stress concentration at the notch tip. The presence of stress singularity at the crack tip is sensitive to mesh refinements that require extensive mesh refinement. However, considerable mesh refinements require large computational times and difficulties to reach convergence (Jadallah et al., 2016). The recent approach had led to the incorporation of traction-separation relationship to solve fracture and failure associated with stress concentration problems.

Supar and Ahmad (2017) incorporated a traction-separation relationship as constitutive models in multi-holes composite plates under quasi-static tensile loading. The traction-separation relationship requires independent measured material properties (maximum strength, σ_o and fracture energies, G _c ) and homogeneous elastic properties (E, v and concrete density, ρ) to provide faster and reasonably accurate results. These constitutive models can be implemented using two numerical techniques: cohesive zone modelling (CZM) and the extended finite element method (XFEM). Current work is aimed to develop a similar FEA framework by incorporating the traction-separation relationship to predict strength prediction of the notched foamed concrete beam. Suitable boundary conditions and loading applied are assigned to represent the physically three-point bending test. The predicted strength from these two techniques is then compared with experimental datasets.

2 EXPERIMENTAL STUDY

2.1 Preparation of Beam Specimens

Four different types of beam specimens, as specified in Table 1, were prepared for the three-point bending test. Briefly, FC-00 are the beam specimens without notch (also referred as control beam specimens), while FC-10, FC-20 and FC-30 are designed with a notch at the mid-span. The notched opening, a ₁ varies from 10 mm to 30 mm, but the notch height, a ₀ remains constant at 45 mm. The dimension of all beam specimens is 700 mm length, 150 mm width and 150 mm depth. Figure 1 shows the schematic diagram of beam specimens. These beam specimens were casting using foamed concrete with a density 1600k g/m³. The ratio of cement to sand, foam to cement and water to cement is 0.5, 0.7 and 0.55, resepectively The cube test of foamed concrete revealed that the compressive strength of foamed concrete at 28 days is 7.0 MPa.

Table 1
Designation and notch opening of beam specimens.

Beam designations	Notch opening size, a 1 (mm)
FC-00	0 (taken as unnotched strength,σ o )
FC-10	10
FC-20	20
FC-30	30

Figure 1
Schematic diagram of the three-point bending test.

2.2 Three-Point Bending Test

The three-point bending test was conducted to capture the force-deflection profiles of beam specimens. This experimental study was conducted using the Universal Testing Machine (UTM). Load cell and LDVT were utilized to capture the force-time history and displacement-time history, respectively. Figure 2 illustrates the setup of three-point bending test. As a preparation for the experimental study, beam specimens need to be inspected and placed between two simple supports with an effective span length of 600 mm. A concentrated load, P in term of a stroke at the constant rate of 0.40 mm/min, was imposed at the mid-span until the beam specimens experienced failure and break-up. During this period, the force that initiated cracking was simultaneously monitored, and its propagation was manually traced.

Figure 2
Experimental study of the three-point bending test.

It can be observed that the cracks from the edge notch up to the top surface of beam specimens. Figure 3 shows the crack propagation that experienced by the beam specimens. During the loaded stage, the fracture length is also increased. It was identified that the crack pattern occurred in the form of a flexural tension crack. Moslemi and Khoshravan (2015) agreed that as the force applied, the initial crack formed at the flexure zone right at the vicinity of maximum flexure moment. The crack length is just short that progressively initiated and continuously propagated until the shear zone as the load applied increased. The crack propagated diagonally from the corner crack tip associated with stress raisers until a certain distance and continuously propagated to the top of beam specimens. The magnitude of deflection and the maximum load depended on the crack zone. So, the value of fracture energy was able to be determined accurately since the propagation of cracks is dependent upon the actual strength of foamed concrete beam under investigations.

Figure 3
The crack pattern on the surface of FC-20.

Figure 4 shows the force-deflection profiles of beam specimens that were recorded from the three-point bending test. The un-notched beam specimen reached an ultimate force of 5969 N and associated deflection of 0.71 mm. However, the notched beam specimens, FC-10, FC-20 and FC-30 have a significant lower ultimate force at 2318 N, 2481 N and 2438 N, respectively. Among the notched beam specimens, the ultimate forces are insignificantly different. Thus, it can be deduced that the notch opening of 10 mm, 20 mm and 30 mm does not affect the strength capacity of beam specimens. Nevertheless, an increase in deflection was seen as the opening notch size increased.

Figure 4
Load versus stroke deflection from three-point bending test.

3 MODELLING TECHNIQUES

Commercial software ABAQUS CAE Version 6.14 was adopted during the pre-processing stage. The applied loading at the mid-span of the beam was modelled as applied displacement (to perform as applied force). As shown in Figure 4, the left support was modelled as pinned support, whereas the right support was a roller to imitate the actual experiment set-up acting as a simply supported beam. The surface interactions between two contacting surfaces are explicitly modelled by using the master-slave interactions. The master surface is able to penetrate into the slave surface; here, the combination of a surface to surface and finite sliding formulations were implemented. Besides, several reference points are located right at the support point to permit the restrain degree of freedom at a specified point. Furthermore, the beam model was assigned with tangential behaviour with friction coefficient to allow stress transfer along the crack surfaces. Earlier strength prediction works implemented 2D modelling using two numerical techniques, i.e., extended finite element method (XFEM) and cohesive zone modelling (CZM). Later, 3-D XFEM framework modelling was developed to explicitly model the out-of-plane beam deformation.

3.1 Material Properties

Bilinear constitutive models require material properties of maximum flexural strength (taken as the flexural strength of un-notched beam specimen) and fracture energy properties. Independent elastic and material properties, as given in Table 2, were incorporated within the modelling framework to govern the damage formation. The foamed concrete beam was assumed as a homogenous material. This is a simplification made in the model, although foamed concrete is anisotropic by nature as it consisted of cement, water and sand. The presence of voids on foamed concrete was totally ignored.

Table 2
Elastic and material properties of foamed concrete.

Elastic properties (Jaini et al., 2017)			Mechanical properties
E (GPa)	v	ρ (kg/m 3 )	σo (MPa)	Gc (kJ/m2)
12	0.2	1600	1.86	0.01885

The elastic properties, in term of Young’s Modulus, E, Poisson’s ratio, v and density, ρ were taken from a similar subset of foamed concrete reported in Jaini et al. (2017). However, the values of flexural strength, σ _o and fracture energy, G _c were calculated using semi-empirical equations. According to Abd. Rahman et al. (2017), the unnotched strength of foamed concrete can be independently estimated using the following equation:

${\sigma }_0=\frac{3P_{\max }S}{2B{\left(W-a_0\right)}^2}$ (1)

where P _max is the maximum load attained by the un-notched beam specimen, while S, B and W are the span, width and the depth of un-nocthed beam specimen, respectively, and a _o is the notch height. On the other hand, the fracture energy was predicted based on an equation proposed by Bazant (2002):

$G_F=2.5{\alpha }_0{\left(\frac{f_c}{0.058}\right)}^{0.40}{\left(1+\frac{D_{\max }}{1.94}\right)}^{0.43}{\left(\frac{w}{c}\right)}^{-0.18}$ (2)

where α ₀ is an aggregate shape factor (α ₀ = 1 for the rounded aggregate, α ₀ = 1.12 for the angular aggregate), f _c is the compressive strength of foamed concrete obtained from the cube test, D _max is the maximum aggregate size, and w/c is the water cement-ratio concrete.

3.2 2D XFEM Modelling

The In 2D modelling framework, there are five parts implemented, i.e. punch, two supports, a reinforced foamed concrete and a pre-defined crack. All of these parts were modelled differently based on their function. A punch and two simply supports were modelled as rigid parts, while the foamed concrete beam was modelled as a deformable part. The concrete beam was then partitioned and within the partition was assigned with XFEM region to limit the damage formation within the XFEM region only, as highlighted in red in Figure 5(a). XFEM technique used MaxPS damage formulation, where the crack was formed orthogonally to the maximum principal stress.

Concurrently, a small length of diagonal deformable pre-crack wire part was assigned from a notched edge to allow the crack to propagate with less computational effort. The diagonal crack was idealised to resemble with the experimental observations in all testing series, where the crack propagated diagonally from the notched edge, then propagated in a normal direction to the applied load. As the beam width was 100 mm, the plane strain model was implemented using the plane strain element (CPE8) (Wang and Hu,2019).

3.3 3D XFEM Modelling

Similar to 2D modelling, the 3D modelling framework consists of five parts, in which every part was explicitly modelled in their out-of-plane direction. To save the computational effort of the modelling, a pre-defined deformable shell extrusion crack was placed at the right corner sharp notch as the initial crack path to grow, as shown in Figure 5(b) below. The complexities of a concrete beam with discontinuities leading to difficulties to obtain as a structured mesh; therefore good mesh structure is able to perform better computational convergence (Li and Peng, 2012). At the vicinity of the notch, first-order incompatible brick element (C3D8I) meshes were made finer (as this region is the area of interest), and at the remaining areas, the meshes were made coarser, as given in Figure 6.

Figure 5
Pre-defined crack and XFEM regions

Figure 6
Meshing conducted within a notched concrete beam

3.4 2D CZM Modelling

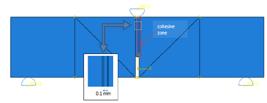
Compared to the XFEM modelling framework, CZM required an apriori crack path where cohesive elements were assigned to idealise fracture and failure on the damaged beam (Beaurepaire and Schuëller,2011). As the CZM region only restricted within a straight-line path, the crack growth does not precisely represent the experimental observation. In CZM model, a straight-line crack path with finite element thickness was adopted (current work used 0.1 mm element width) as cohesive zone by utilising partition function in ABAQUS, as shown in Figure 7, similar to the approach used in Koloor et al. (2019). A cohesive zone was assigned with a first-order 2-D cohesive element (ABAQUS element designation code as COH2D4).

Figure 7
Crack path region in CZM modelling framework

4 LOAD-DISPLACEMENT PROFILES

This section discussed on post-processing results of all techniques incorporated as previously described in Section 3. All the implemented techniques and associated computational times were then compared accordingly.

4.1 Sensitivity Studies

Two parametric studies were carried out earlier before strength predictions work to ensure the strength prediction modelling are free from mesh refinement and damage coefficient effects. In this sensitivity study, meshing was refined at the vicinity of the notched edge, as illustrated in Figure 8(a) (within red lines regions). These regions were chosen as fracture, and failure in the form of crack were initiated at the sharp corner of the notches. This is associated with the stress concentrations at the sharp edges due to plate discontinuity. This is consistent with experimental observations as reported by Zhou and Chen (2019).

The strength prediction of the foamed concrete with the variation of mesh refinements (given as element numbers around notch vicinity) are given in Figure 8(a). It was found that the strength predictions are independent of mesh refinements due to the constitutive model used in current work is driven by an energetic approach. Once the fracture energy from the applied load exceeded the fracture energy of the concrete mixture, G _c , crack is initiated and propagated. The fracture energy of the material is regarded as material properties, G _c and can be obtained from closed-form expression or independently determined. Therefore, strength prediction is free from the effects of mesh sizes. In the next modelling work of further testing series, a consistent element number of 5415 was chosen.

In the sensitivity study respecting the damage stabilisation coefficient, the strength prediction started to display the consistent value of the ultimate load at damage stabilisation coefficient of 1x10^-4, as plotted in red dotted line in Figure 8(b). This work was aimed to find a value that leads to actual results; therefore, the damage stabilisation coefficient of 1×10^-4 was found sufficient. A large value of damage stabilisation coefficient is associated with easy convergence; however, this leads to a large ill-physical result, which then leads overly strength predictions. On the other hand, small damage stabilisation coefficients lead to difficulties to obtain convergence but not sacrificing the results accuracy. Therefore, it is essential to determine the suitable value to obtain good strength prediction values with reasonable computational times. Therefore, the damage stabilisation of 1 × 10^-5 was chosen in throughout modelling works.

Figure 8
Strength prediction with respective of (a) mesh refinements and (b) damage stabilization parametric studies.

4.2 Consistency with experimental observations

Figure 9(a) shows the comparison of crack formation between XFEM modelling and experimental observation (given in Figure 9(c)). It can be seen that the formation of a crack in XFEM modelling is pretty similar to the actual experimental observation. The presence of slanting pre-crack directs the initial path of the crack propagation. As the load increase, the crack will form and continue moving upwards till it reaches the top surface of beam modelling. After the crack has separated the cracked concrete beam, the model processing has been completed and thus reached the last increment step.

Figure 9(b) shows the comparison of crack formation between CZM modelling and experimental observation. As mentioned before, the CZM method can only allow the crack path in a straight line due to the partition created. The element deletion and opening area in the CZM modelling refer to the failure of the concrete beam model. It represents the propagation of cracks that occurred within the actual cracked beam. CZM cracked beam model demonstrates simplistic failure patterns where the crack only propagates parallel to the beam cross-section.

Figure 9
Comparison of crack formation

4.3 Load-displacement curves

Figure 10 represents a typical load-displacement curve from the post-processing output of an XFEM model. The load-displacement profiles were plotted and labelled at specified points to highlight the fracture and damage process during the three-point bending test. There is no crack readily seen prior to point (a). This means that applied stress is less than the maximum stress that the concrete can sustain. At point (a), crack initiates as the applied fracture energy exceeds the fracture energy of the concrete. Within point (a) to point (b), it is expected that progressive micro-damage takes place prior to the ultimate strength of concrete. The micro-damage may arise from interfacial zones between aggregates and cement paste bonds and cohesive cracks within cement paste. These points (from (a) - (b)) is also known as damage zone length, where within these regions, the fracture and failure take place progressively.

Figure 10
Load-displacement curve from XFEM modelling (taken from 20 mm opening notch size model).

At point (b), the ultimate load was recorded, after which the subsequently applied load leads to catastrophic failures. As seen in Figure 10, the drastic load drop was seen to signify that crack separation occurred in a very short time interval before the beam exhibits full separation at point (d). As the applied load increased, stress also increased correspondingly. When the applied stress is larger than the maximum stress that the beam can resist, a crack started to form. This also indicated that the fracture energy applied to the concrete beam had exceeded the fracture energy of the concrete mixture.

Simultaneously, Figures 11 and 12 show the contour plot of steps increment from the posts-processing output at four identified stages as labelled in Figure 10 as point (a), (b), (c) and (d). As the applied load reach point (a) step 45, the crack started. As the stress increases, the crack propagates upwards parallel to the load applied until at step 83 when the model reaches the ultimate load. The crack length within step 45 to step 83 is known as a fracture process zone. Step 138 is the continuity of cracks with the increased displacement and not capable of carrying any additional load until step 229, where the crack reaches the top and fails. This modelling required 249 steps in total to complete.

Figure 12 indicates the status XFEM damage plot at the specified points labelled in Figure 10. When the element does not experience stress, it will be in blue colour (STATUS XFEM = 0). As the increments increased (associated with applied load increment), the beam elements started to demonstrate applied stress. When the fracture energy from the applied load is higher than material fracture energies (given as material input given to the ABAQUS as G_c values), the element failed and simultaneously changed from blue colour to red colour to indicate the element failure. (now STATUS XFEM is given as 1). Red colour to signify that a particular element has failed (to follow the actual experiment crack path as seen from experimental observation). As can be seen from Figure 12, the formation of crack initiation and crack propagations were in close agreement with experimental observations in Figure 9(c).

Figure 11
Damage plot of Von-Mises Stresses at specified points labelled in Figure 10..

In general, the curve profile in CZM models shown in Figure 13 is similar to the XFEM technique, but slightly over-predicted the strength prediction. In the CZM technique, the crack propagation has been defined earlier but does not follow the experimental observation crack path. The restriction in applying CZM is the crack path has to be modelled as a straight-line path, but experimental observations showed otherwise. As predicted, it demands more resistance load to form the initial crack. Furthermore, the distance from crack initiation to the top beam tends to be lengthier.

Figure 12
Damage plot of STATUSXFEM at specified points labelled in Figure 10.

Figure 13
Comparison of the load-displacement profile obtained from (a) XFEM and (b) CZM techniques with experimental work

5 VALIDATIONS WITH EXPERIMENTAL DATASETS

Table 3 depicts the strength prediction of 2-D XFEM modelling and experimental datasets. It can be seen that the agreement (below 20%) in all testing series investigated were obtained. This is considered within the reasonable agreement, albeit to fracture energies incorporated are predicted from Bazant formulations. It is worth noting that the implemented material properties (currently used traction-separation relationship as the constitutive model) were regarded as apparent values, which are predicted by the available model. The current XFEM modelling framework used a small slanting pre-crack of 10 mm, which is a considerably small crack introduction to ease the formation of crack initiation and crack propagation. The crack propagates normal to the loading path, which agrees well with experimental observations, as shown in Figure 9(c).

Table 3
Discrepancies of ultimate load from all modelling techniques with experimental datasets.

Crack opening (mm)	Pmax exp	2D XFEM		3D XFEM		2D CZM
		Pmax, 2D, XFEM	Error %	Pmax, 3D,XFEM	Error %	Pmax, CZM	Error %
10	2318.0	2738.5	18.14	2785	20.15	3161	36.37
20	2481.2	2926.3	17.94	3292	32.68	3348	34.95
30	2437.5	2889.0	18.52	2954	21.19	3455	41.75

As given in Figure 14(a), compared with XFEM modelling, less good agreements were obtained, ranging from 34 - 41%. This was partly due to the cohesive zone was assigned along normal to the sharp crack (where the cohesive zone was idealised as crack formation). This is somewhat opposed to experimental observation where the crack showed diagonal crack from corner notch to concrete compression extreme fibres. However, the cohesive zone only can be modelled in a straight line of small element size, which is a huge constraint of CZM modelling technique. This technique may perform well if the crack formation is along the net-section plane but less appropriate with a corner notch problem.

Average strength prediction from 3-D XFEM modelling framework was approximately 25% in all testing series investigated. Bear in mind that current 3-D XFEM modelling also introduced 10 mm pre-crack as the crack path to allow better computation effort. Better predictions in the foamed concrete beam were found with a small crack opening than the larger crack opening; however, there is no significant trend observed. This may be due to slight deformation along notch width, especially for the beam with larger notch width, which may not physically be shown in the model. The current model implemented homogenous concrete properties as the simplified model assumptions; therefore, the localised deformation due to composite behaviour may not well-represented.

Figure 14 (b) showed the comparison of strength prediction between 2-D and 3-D XFEM with experimental datasets. As explained previously, the crack initiation and crack propagation in both 2-D and 3-D was considered as a self-similar manner across the plate width. It was observed that not much improvements were obtained from the latter model, although the 3-D model explicitly modelled out-of-plane behaviour. 2-D models were considered sufficient as deformation across plate width has not contributed to additional plate bending behaviour and self-similar crack behaviour. The current XFEM model is driven by an energetic approach; therefore, the accuracy of the output was largely dependent upon material input. Both 2-D and 3-D models have implemented similar elastic and material input, which were estimated from relevant literature (not measured and considered as apparent values). However, these models were considered successful in order to capture the physical behaviour and consistency with the experimental observations.

Figure 14
Comparison of strength prediction between (a) 2D CZM and 2D XFEM models (b) 2D XFEM and 3D XFEM with experimental datasets (percentage indicates discrepancies with experimental datasets).

Figure 15
Comparison of computational time between 2-D and 3-D XFEM.

Figure 15 depicts the comparison of computational times between 2-D and 3-D XFEM modelling frameworks. As expected, large computational times were required in order to obtain a 3-D approach than 2-D models counterparts. This is because the 3-D model has more complex surface interactions between various parts, large element meshing and incorporation of 3-D element types. The computational times for 3-D models can go up to 23 times computational times than 2-D models counterparts. Despite not much improvement was readily seen in 3-D models, it was deduced that the 2-D model is sufficient to provide reasonable strength predictions.

The current modelling approach has made few assumptions to simplify the strength prediction work, partly due to insufficient information on material properties reported in the relevant literature. The mechanical properties such as elastic modulus and Poisson ratio are not measured but were taken as the estimated elastic properties from collections of foamed concrete work; however, the maximum tensile strength, σ _o was measured and available. On the other hand, fracture energies values were obtained from the closed-form expression of Bazant (2002) formulations. From the author point of view, the prediction can be improved if these properties were independently measured following code of practice provisions. The constitutive model incorporated maximum tensile strength and fracture energy values as material input as a traction-separation relationship. FEA model simplified the progressive micro-damage events in the concrete beam by implementing fracture energy value, G _c, where crack occurred when applied energy exerted exceeds G _c of the concrete (Bazant, 2002).

6 CONCLUSION

Experimental series has been conducted with the variation of notch opening size. Later, FEA modelling was conducted by adopting a traction-separation relationship based on state-of-the-art fracture mechanics fundamental using XFEM and CZM techniques. Sensitivity studies were carried out to assure the strength predictions were independent of mesh refinement and damage stabilisation coefficient adopted. Overall results showed that all FEA models obtained has a reasonably good agreement, where the average discrepancy between the predictions and experimental datasets were approximately 20%. The comparison series has been taken place by modelling 2D XFEM and CZM models, and later, 3D XFEM models were developed with explicitly modelled out-of-plane beam direction. From the validation work, XFEM and CZM showed that average discrepancies at 18% and 37%, respectively. This is due to XFEM allows the crack to grow independently, but CZM has to model the crack path in a straight line. XFEM modelling is then expanded to the 3D model, where the later modelling framework allows the deformation in the out-of-plane direction. Not much improvement was readily seen in the 3D model as fracture exhibited are self-similar crack, which is sufficient to be modelled within the 2D framework. Nevertheless, the current model implemented homogenous concrete properties as the simplified model assumptions; therefore, the localised deformation due to composite behaviour may not be well-represented.

Acknowledgement

The author would like to thank Research Fund FRGS Vot K325, Ministry of Higher Education Malaysia in providing financial support for this project work. On behalf of all authors, the corresponding author states that there is no conflict of interest.

References

• Ahmed, M., Mallick, J. and Abul Hasan, M. (2016). A Study of Factors Affecting the Flexural Tensile Strength of Concrete, Journal of King Sand University-Engineering Sciences, Vol.28 (2), pp. 147-156.
• Xia, H., Jian, W., Feng, Z., Niu, S. and Jun, D. (2015). An Experimental Investigation on the Failure Behavior of a Notched Concrete Beam Strengthened with Carbon Fiber-Reinforced Polymer, International Journal of Polymer Science, Vol. 2015 (3), pp. 1-17
• Shawnim, P. and Mohammad, F. (2019). Compressive Strength of Foamed Concrete in Relation to Porosity using SEM Images, Journal of Civil Engineering, Science and Technology, Vol.10 (1), pp. 33-44.
• Jones, M.R., Ozlutas, K., and Zheng, L. (2017). High-volume, ultra-low-density fly ash foamed concrete, Magazine of Concrete Research, Vol. 69(22), pp. 1146-1156.
• Fu, Y., Wang, X., Wang, L. and Li, Y. (2020). Foam Concrete: A State-of-the-Art and State-of-the-Practice Review, Advances in Material Science and Engineering, Vol.2020, pp. 1-25.
• Van, L.T., Kim, D.V., Xuan, H.N., Dinh, T.V., Bulgakov, B. and Bazhanora, S. (2019). Effect of Aluminium Powder on Light-weight Aerated Concrete Properties, E3S Web of Conferences Vol. 97(2), pp. 1 -10.
• Sherbin, S.A. and Gorbach, P.S. (2020). Foam Concrete Production with Addition of Microsilica, IOP Conference Series Materials Science and Engineering, Vol. 880, pp. 1-5.
• Zhou, R. and Chen, H.M. (2019). Mesoscopic Investigation of Size Effect in Notched Concrete Beams: The Role Fracture Process Zone. Engineering Fracture Mechanics, Vol. 212, pp. 136-152.
• Wang, L., Wang, G. and Alexander, C. (2015). Confluences among Big Data, Finite Element Analysis and High Performance Computing, American Journal of Engineering and Applied Sciences, Vol. 8 (4), pp 767-774.
• Náhlík, L., Hutař, P. and Štegnerová, K. (2014). Critical Applied Stresses for a Crack Initiation from a Sharp V-Notch, Fracture and Structural Integrity, Vol. 30, pp. 55-61.
• Jaini, Z.M., Abd Rahman, N., Rum, R.H.M and Haurula, M.M. (2017). Fracture Energy of Foamed Concrete: Numerical Modelling Using the Combined Finite-Discrete Element Method”. MATEC Web of Conferences, Vol.103:02030.
• Hillerborg, A. (1985). The Theoretical Basis of a Method to Determine the Fracture Energy of Concrete, Materials and Structure. Vol. 18(4), pp.291-296.
• Comite Euro-International du Beton. (1993). CEB-FIB Model Code 1990, Thomas Telford: Lausanne, Switzerland.
• Bazant, Z. P. (2002). Concrete Fracture Model Testing and Practice, Engineering Fracture Mechanics, Vol. 69, pp 165-205.
• Javadi, A.A. and Rezania, M. (2009). Intelligent finite element methods: An Evolutionary Approach to Constitutive Modelling, Advanced Engineering Infomatics, 2009, Vol. 23 (4), pp 442-451.
• Jadallah O., Bagni C., Askes H. and Susmel L. (2016). Microstructural length scale parameters to model the high-cycle fatigue behavior of notched plain concrete, International Journal of Fatigue, Vol. 82 (3), pp. 708-720.
• Supar, K. and Ahmad, H. (2017). Stress Distribution Study on Multi-holes Configurations in Woven Fabric Kenaf Composite Plates, IOP Conference Series: Materials Science and Engineering, Vol. 271, pp. 1-8.
• Moslemi, M. and Khoshravan, M. (2015). Cohesive Zone Parameters Selection for Mode-I Prediction of Interfacial Delamination, Journal of Mechanical Engineering, Vol. 61, pp. 507-516.
• Abd Rahman, N., Jaini. Z.M., Rum. R.H.M, Khairuddin, S.A. and Zamri, M.N. (2017). Effect of Span-to-Depth Ratio on the Fracture Energy of Foam Concrete, Key Engineering Materials, Vol.730, pp. 440-444.
• Wang, S. and Hu, S. (2019). Experimental Study of Crack Propagation in Cracked Concrete, Energies, Vol. 12, pp. 1-19.
• Li, Z. and Peng, S. (2012). An Adaptive Mesh Refinement Strategy for Immersed Boundary/Interface Methods. Communications in Computational Physics, Vol. 12 (2), pp. 515-527.
• Beaurepaire P. and Schuëller G. I. (2011). Modeling of the Variability of Fatigue Crack Growth using Cohesive Zone Elements. Engineering Fracture Mechanics, Vol. 78(12), pp 2399-2413.
• Koloor S., Rahimian S. M., Karimzadeh A., Hamdi M., Petrů M., and Tamin M. N. (2019). Nano-Level Damage Characterization of Graphene/Polymer Cohesive Interface under Tensile Separation, Polymers, Vol. 11(9), pp. 1-16.

Edited by

Editor:

Marco L. Bittencourt.

Publication Dates

• Publication in this collection
  19 July 2021
• Date of issue
  2021

History

• Received
  14 Nov 2020
• Reviewed
  01 May 2021
• Accepted
  21 May 2021
• Published
  24 May 2021