Abstract
The aim of this work was to experimentally evaluate the use of calcium carbonate as a pore-generating agent in ceramic compositions. Compositions that contained 50% kaolin, 20% limestone, and different concentrations of quartz and feldspar were prepared by uniaxial pressing. Samples were heat-treated at a heating rate appropriate to induce calcium carbonate degassing, and they were then sintered at 800, 900, and 1050 ºC. Tests of X-ray fluorescence, thermogravimetric analysis, porosimetry, and air permeation were performed. The composition (wt%) that contained 50% kaolin, 20% limestone, 20% feldspar, and 10% quartz and heat treated at 1050 ºC (k1 = 1.73×10-13 m² and k2 = 1.00×10-8 m) showed the highest level of permeability among the investigated samples. Fluid dynamics simulations showed that the prepared samples would exhibit a pressure drop greater than the range desired for applications that involve the filtration of aerosols, but alternatively would be suitable as substrates for asymmetric membranes in microfiltration applications.
ceramics; microporous materials; microstructure
Structural and fluid dynamic characterization of calcium carbonate-based porous ceramics
Lisandro SimãoI; Oscar Rubem Klegues MontedoI, * * e-mail: oscar.rkm@gmail.com ; Marcos Marques da Silva PaulaI; Luciano da SilvaI; Rafael Falchi CaldatoII; Murilo Daniel de Mello InnocentiniII
IInstituto de Engenharia e Tecnologia IDT, Universidade do Extremo Sul Catarinense UNESC, Av. Universitária, 1105, CEP 88806-000, Criciúma, SC, Brasil
IICurso de Engenharia Química, Universidade de Ribeirão Preto UNAERP, Av. Costábile Romano, 2201, CEP 14096-900, Ribeirão Preto, SP, Brasil
ABSTRACT
The aim of this work was to experimentally evaluate the use of calcium carbonate as a pore-generating agent in ceramic compositions. Compositions that contained 50% kaolin, 20% limestone, and different concentrations of quartz and feldspar were prepared by uniaxial pressing. Samples were heat-treated at a heating rate appropriate to induce calcium carbonate degassing, and they were then sintered at 800, 900, and 1050 ºC. Tests of X-ray fluorescence, thermogravimetric analysis, porosimetry, and air permeation were performed. The composition (wt%) that contained 50% kaolin, 20% limestone, 20% feldspar, and 10% quartz and heat treated at 1050 ºC (k1 = 1.73×1013 m2 and k2 = 1.00×108 m) showed the highest level of permeability among the investigated samples. Fluid dynamics simulations showed that the prepared samples would exhibit a pressure drop greater than the range desired for applications that involve the filtration of aerosols, but alternatively would be suitable as substrates for asymmetric membranes in microfiltration applications.
Keywords: ceramics, microporous materials, microstructure
1. Introduction
Porous ceramic materials are of great industrial interest because of their unique properties over a wide temperature range, such as their high chemical inertness, low thermal conductivity, high compressive strength, and high hardness, among other properties. These properties make porous ceramics useful in a variety of applications, including filters1, membranes2, sensors3, low-weight structural materials4, insulators5, biomaterials6, and catalyst supports7. In such applications, the porous ceramics are designed to exhibit different size distributions and pore morphologies8. For example, porous ceramics based on silicon carbide (SiC) have recently received significant attention from researchers due to their excellent structural properties, high thermal shock resistance, high hardness, and mechanical and chemical stability, particularly at high temperatures and in harsh environments. Because of these properties, such materials have been considered promising candidates for use as catalyst supports, gas sensors, thermal insulators, and other related applications9. Because of their physical-chemical characteristics, porous ceramic materials can also be used in environmental applications, such as sensing and the remediation of effluents through selective adsorption of chemical species10, and in engineering processes as substitutes for metallic and polymeric materials, especially those used at high temperatures11.
The energy economy is a very interesting advantage of the separation processes that involve porous ceramics because, in most cases, the ceramics promote separation without a phase change, and such processes are therefore energetically favorable. Moreover, the difficulty in reproducing results with porous ceramic materials is the main limitation of its use12,13. In this sense, various methods of preparing porous ceramics have been evaluated in recent years in attempts to obtain materials with complex geometries and microstructures designed for specific applications without the need for a machining step10.
With respect to porous ceramics, one of the oldest and still widely used preparation methods is related to the incorporation of organic products inside the ceramic bodies, which are removed during the heat treatment step. In this way, pores of different sizes are generated into the material depending on the particle size of the organic material inserted into the ceramic body14. Several known methods for the processing of porous ceramics also exist, such as the polymeric sponge method, the gel-casting method applied to foams, the incorporation of organic products to the ceramic powder, and the generation of bubbles in the suspension, which is associated with the control of the sintering conditions with the objective of achieving partial densification of the material15. The so-called direct forming techniques, which are based on ceramic bodies obtained from powder suspensions (slurries) in waterproof moulds, are also known. Therefore, microstructures with different pore sizes, which can vary over a wide size range from a few nanometers to some millimeters16, are obtainable. The processing method of porous ceramics based on the generation of gas bubbles in the ceramic suspension is related to the use of bubble-forming agents17, typically calcium carbonate, calcium hydroxide, aluminum sulfate, and hydrogen peroxide.
In this sense, the determination of the permeability of porous ceramics plays an important role and allows an evaluation of how easily a fluid permeates a porous media in relation to the structural characteristics of the medium, such as porosity, size and pore shape, and tortuosity, among other factors. Tortuosity, in particular, represents the ratio of the path in which the fluid travels into the pores and the thickness of the porous element18-20. Greater tortuosity in a porous medium allows a larger area of interaction between the layers of fluid and the pore walls. For example, in the case of ceramic substrates for use as catalysts, a change in the tortuosity may be used to increase the residence time of the reaction medium. Moreover, a compromise exists between the permeability and the mechanical behavior of the porous medium, particularly the compression strength, so that the structural demands of the system may be achieved. Permeability is also useful to quantify the power required to force a gas or a liquid to percolate a filtering membrane or a catalytic substrate in economical rates.
The experimental evaluation of the permeability of a porous material is based on equations that relate the dependence of the pressure drop (ΔP) and the superficial velocity (vs) of the fluid. The Forchheimer equation represents a reasonably accurate empirical expression to describe the resistance to fluid flow in porous media18:
where ΔP is the pressure drop calculated for compressible fluids (gas and vapors) using Equation 2:
where Pe and Ps are the absolute pressure of the fluid in the inlet and outlet of the sample, respectively, L is the sample thickness in the direction of flow, and µ and ρ are the absolute viscosity and the density of the permeating fluid, respectively. The parameters k1 and k2 represent properties of the porous medium and do not depend on the type of fluid or the flow speed. These parameters are known as the Darcian permeability coefficient and the non-Darcian coefficient, respectively18.
The Forchheimer equation is based on the assumption of continuous media, which is valid if the mean free path of the molecules of gas is significantly smaller than the dimensions of the permeable pore. This equation indicates that the pressure drop that results from the flow is the sum of two coexisting contributions; however, these contributions change in intensity as the fluid velocity increases. The term linear in velocity [µvs/k1] represents the energy dissipation due to the simple viscous action (friction). With increasing velocity, the curves, contractions, and extensions of the permeable channels generate secondary flow patterns, distortions in the pressure, and velocity fields on a microscopic scale. These effects enhance the dissipation of energy. This increase in dissipation leads to a nonlinear increase in the pressure drop, represented by the quadratic term in velocity [ρvs2/k2][21-26].
The permeability coefficients k1 and k2 are therefore parameters of proportionality that influence the viscous (linear) and inertial (quadratic) contributions to the total pressure drop (ΔP). Notably, k1 is expressed in square length dimensions, and k2 is expressed in length dimensions to maintain dimensional consistency in Equation 1.
Knowledge of the permeability coefficients k1 and k2 of a ceramic material is important because they are intrinsically related to the characteristics of the porous structure, such as the quantity, size, and morphology of the voids available for the fluid flow. Changes in the processing variables can increase interconnected porosity and pore size or can decrease the tortuosity and the roughness of the pores. These changes will result in an increase in k1 and k2, although the magnitudes of the changes will differ18,27-29.
Permeation is also highly susceptible to phenomena induced by the temperature during the processing of porous ceramic materials. Drying and sintering of green bodies are thermal processing steps that cause irreversible changes in the permeable porous structure. These phenomena occur through a reduction in the number of voids (due to densification) or through the creation of new voids and interconnections due to stresses caused by thermal expansion (microcracks) or even by the expansive removal of volatile and organic compounds (debinding and dehydration). The extent of these structural modifications on the permeability coefficients can be easily evaluated via permeability tests at room temperature before and after the heat treatments18,28.
Thus, this paper presents experimental results of permeability, porosity, and microstructure characterization related to the use of carbonates as pore-generating agents in different ceramic compositions.
2. Material and Methods
2.1. Preparation of formulations
Four compositions were used in this study, as shown in Table 1. They were prepared using appropriate amounts of raw commercial powders (diameter less than 37 µm) provided by Colorminas Colorifício e Mineração (Criciúma, Santa Catarina, Brazil). Each composition was homogenized for 15 min in a cylindrical wet ball mill that was internally coated and contained porcelain balls (33 wt% water content in the suspensions). Then, each suspension (slurry) was dried in a laboratory drier at 100 ± 5 ºC for 4 h. Each composition was subsequently humidified up to 7 wt% to obtain wet powders. Each powder was then passed throughout a 35-mesh ASTM sieve (aperture of 500 µm). The powders were then pressed in a uniaxial hydraulic press (steel die, pressure of 25 MPa) to obtain cylindrical pellets (27 mm in diameter and 12 mm thick).
2.2. Heat treatment
The thermal decomposition of the employed compositions was evaluated using thermogravimetric analysis (TGA Q500, TA Instruments, New Castle, USA, 10 ºC.min1 in air). The degassing temperatures of the samples were defined from the obtained thermograms. A sample of each compacted body was subjected to optical dilatometry (HSM ODHT Misura® 1400, Expert System Solutions, Modena, Italy; 5 ºC.min1 in air) to determine the dimensional behavior (ΔL/Lo, linear shrinkage, LS) of each sample with respect to temperature, i.e., to determine the sintering plot. After, the degassing and sintering temperatures were determined, the other compacted bodies were heat-treated in a laboratory kiln at 80, 350, 400, 450, 550, 650, 750, and 800 ºC (5 ºC.min1 heating rate and 30 min holding time) and subsequently at 800, 900, and 1050 ºC (10 ºC.min1 heating rate and 5 min holding time).
2.3. Physical characterization
The heat-treated test bodies were characterized using a variety of techniques. The chemical composition was determined by X-ray fluorescence spectrometry (XRF, Philips PW 2400, Eindhoven, The Netherlands). The relative densities of the green samples and sintered samples were calculated according to the ratio between the apparent density, as measured by immersion in mercury (Archimedes' principle) at 20 ºC, and the theoretical density of the solids, as determined by pycnometry. From the values of the apparent density (ρa) and theoretical density of the solids (ρs), the porosity (ε) of each body was determined according to Equation 3[30]:
The microstructural analysis of the sintered samples was performed using a scanning electron microscope (SEM, Jeol JSM-6390, Tokyo, Japan). The samples were transversally cut, ground, and polished with 1 mm alumina paste and then coated with a thin layer of a gold film for observation.
2.4. Fluid dynamics characterization
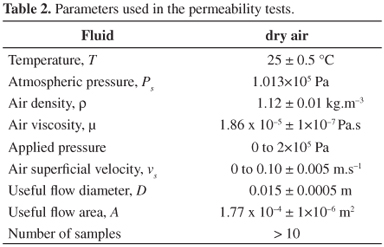
In this work, the air permeability tests were performed on samples heat-treated at different temperatures and with different formulations. Initially, each sample was dried in a laboratory drier at 100 ºC and was stored in a dry chamber that contained gel silica. To avoid air side leakage during the permeation test, the cylindrical lateral edge of each sample was sealed with silicone adhesive. For the test, the sample was fixed between two flexible rubber rings and was compressed within a cylindrical sample holder. The useful diameter for air flow in the test was 1.5 cm, which corresponds to a flow area of 1.77 cm2. After the sample holder was sealed, air from a compressor that was previously dried in a cylinder with gel silica was forced to flow through the sample. Table 2 shows the typical conditions for the tests.
The resulting flow rate was controlled using a valve and was measured by a flow meter or by a bubble meter after air was passed through the sample. The air pressure drop was measured before and after the sample using a digital micro manometer. Measurements of the resultant pressure drops were performed for each flow rate. At least ten pairs of flow-rate and pressure data were collected. The air superficial velocity (vs) was determined by dividing the flow rate (Q) by the flow area (A): vs = Q/A.
3. Results and Discussion
In the compositions tested in this study, the content of the pore-generating agent (calcium carbonate) was kept constant while the amount of flow agent (feldspar) was varied to control the sinterability and the amount of closed porosity. Table 3 shows the chemical compositions of the samples employed in this study after heat treatment at 1050 ºC. The major differences in composition are related to samples C-2 and C-4 because of the differences between feldspar and quartz contents. The contents of silica (SiO2) and alumina (Al2O3) were 61.08 and 16.93 wt%, respectively, for sample C-2 and 67.22 and 11.97 wt%, respectively, for sample C-4. Furthermore, alkaline earth oxides (CaO + MgO) were added by means of the addition of calcium carbonate, which was chosen to act as pore-generating agent (open porosity).The alkaline oxide contents (Na2O + K2O) are due mainly to the addition of feldspar and ranged from 5.15 wt% (C-2) to 3.24 wt% (C-4). The inclusion of these oxides is important to reduce the sintering temperature of the compositions during the formation of the viscous liquid phase during heat treatment31. All of the compositions employed showed residual volatile material at 1050 ºC, which was most likely due to non-reacted calcium carbonate.
Figure 1 shows the thermogram (TGA) for composition C-1; however, the same result was obtained for the other compositions because the limestone content was the same in all of the samples.
The total weight loss was approximately 15 wt% because of the initial moisture content of the powder and because of the carbon dioxide content in the calcium carbonate, which is the major constituent of the limestone used. Based on the TGA results, two heating rates were employed: one up to 800 ºC and the other at higher temperatures. Consequently, the heating program discussed in Section 2.2 was used for all of the investigated compositions to promote degassing and sintering of the samples. However, it is important to consider that the TGA tests were performed using a small sample (approximately 27 g) under conditions of thermal equilibrium at the heating rate used. In contrast, larger samples that were compacted using a hydraulic press were used for the heat treatment in a laboratory kiln; i.e., the sample preparation conditions differed significantly from those used for the TGA tests. Therefore, to guarantee comparable results for the samples used in the TGA tests, i.e., to eliminate all volatile material from the samples, we used higher temperatures in the kiln and/or a longer residence time in the temperature range where degassing occurred. In fact, Table 3 shows very low values for loss on ignition (LOI). We therefore concluded that the thermal program used in the laboratory kiln produced the same results as those used in the TGA tests.
Figure 2 shows sintering plots (LS × T) of compositions C-2 and C-4, which reveal the following thermal events: a) 840-870 ºC: onset of the sintering process (densification); b) ~ 930 ºC: ending of the sintering process; c) 1030 ºC: onset of the expansion process; and d) 1160 ºC: onset of fusion.
As evident in Figure 2, the sintering process started at the end of the degassing process of the material, which occurred over a temperature interval of 80 ºC. After the temperature interval between 930 and 1030 ºC, a dimensional stability was observed from which strong expansion occurred in the material. Thus, temperatures of 800, 900, and 1050 ºC were selected for the preparation of the samples.
Notably, the degassing process of the limestone and the expansion of material from 1030 ºC must have significantly modified the microstructure, particularly the porosity, of the obtained materials. In fact, the effects of these processes on the microstructure of the material are evident in Figure 3, which shows SEM micrographs obtained of the compositions sintered at 1050 ºC. This figure shows that two types of pores are typically observed: nearly spherical pores with diameters that range between 4 and 10 µm and irregularly shaped pores with diameters that vary between 15 and 30 µm. The former pore type must be related to degassing of the calcium carbonate particles, whereas the latter type is related to the residual porosity of the pressing process; the irregular pores were not removed during sintering. In this case, the time and temperature employed during the heat treatment of the samples were not sufficient to eliminate such porosity.
Figure 4 shows that the porosity increased as the sintering temperature was increased for all of the investigated compositions, which is opposite the behavior described in the literature32. Thus, the densification of the ceramic structure during the sintering has likely been compensated by other thermal phenomena, such as degassing, and by the occurrence of microcracks due to thermal expansion.
Figure 5 shows air permeation plots of samples C-2 and C-4, although compositions C-1 and C-3 showed the same behavior. The tested air velocity range (0 to 0.10 m.s1) is typical of those used in applications that involve aerosol filtration27. The fit of the Forchheimer equation to a parabolic function was satisfactory, with correlation coefficient (R2) greater than 0.999 for all of the curves. However, a certain inhomogeneity was observed in some compositions, as demonstrated by the data dispersion of ΔP/L as a function of vs. In general, the pressure drop (ΔP/L) decreased as the heat-treatment temperature was increased.
Figure 6 confirms the permeability of the investigated samples increased with the increased sintering temperature, which indicates that structural changes occurred in the porous medium. A comparison of Figure 4 and 6 reveals that the increase in porosity was one of the reasons for the progressive increase in permeability. A similar tendency was observed for the coefficients k1 and k2 for all of the investigated compositions. The differences in permeability between the investigated compositions were sharper when the sintering temperature was increased. The highest permeability was obtained for the composition prepared with a lower feldspar content and a higher quartz content (C-4) that was heat-treated at 1050 ºC.
As evident from the data shown in Figure 7, the samples investigated in this work exhibited permeability levels compatible with their application in microfiltration. Only composition C-1 showed permeability coefficients (k1 = 1.73 × 1013 m2 and k2 = 1.00 × 108 m) in good agreement with those used in granular and fibrous filters for aerosols. The most suitable k1 and k1 values for this application are on the order of k1 ≈ 1011 m2 and k2 ≈ 106 m[27].
The relative importance of the coefficients k1 and k2 to the analysis of permeability of a porous medium for a given application depends on the term that dominates the pressure drop over the flow, as specified in Equation 1. Thus, this analysis depends not only on the fluid velocity but also on its properties (density, viscosity) and the values of the coefficients k1 and k2. A useful criterion for this analysis is provided by the dimensionless group named Forchheimer number (Fo), which is defined as18:
The parameter Fo represents the ratio between the inertial forces and the viscous forces over the pressure drop of the flow fluid. Because the ratio k1/k2 has a length dimension, Fo can be understood as being similar to the Reynolds number, for which the characteristic dimension is the diameter of the pore structure. The substitution of Fo into the Forchheimer equation (Equation 1) yields:
Given that the total pressure drop through the porous medium is the sum of the viscous and inertial contributions, then:
Therefore, according to Equations 1, 5, and 6, the relative contributions of the inertial and viscous terms for the pressure drop can be determined by:
Thus, for Fo << 1, only the coefficient k1 is relevant, and Forchheimer equation (Equation 1) reduces to the Darcy law, in which ΔP ≈ ΔPviscous:
However, for Fo >> 1, the pressure drop in the porous medium will present a purely quadratic dependence on the fluid velocity, in which coefficient k2 (ΔP ≈ ΔPinertial) predominates. In this case, Equation 1 is simplified to:
For intermediary values of Fo, both inertial and viscous terms are relevant for the analysis of the pressure drop, and the complete Forchheimer equation (Equation 1) should be used. For reference, Table 4 shows the simulated values of Fo, the total pressure drop (ΔP), and the inertial and viscous contributions to the air permeation in a typical application of an aerosol filter at room temperature and pressure (T = 25 ºC, Po = Patm = 760 mm Hg, ρar = 1.19 kg.m3, µar = 1.86×105 Pa.s). The chosen air velocity for the simulation was 2 cm.s1; this value is typically used in the removal of fine particulate material by ceramic filters27.
As evident from the results in Table 4, for vs = 2 cm.s1, the pressure drop to the air flow for samples with a thickness of approximately 12 mm ranged from 25,423 to 189,029 Pa (250-1890 cm water column). Comparatively, these values are still significantly higher than those exhibited by commercial fibrous ceramic filter elements (1,000 to 2,000 Pa) operating in similar flow conditions27,33. Notably, however, the pressure drop exhibits an inertial contribution that is typically less than 5% in most compositions, which indicates the validity of Darcy's law to a velocity of up to 2 cm.s1.
Even though the developed ceramic compositions C-1 to C-4 were found to be incompatible with aerosol filtration applications due to the high pressure drop level, they still could act suitably as semi-permeable physical barriers (membranes) for other pressure-driven separations, including clarification, concentration or fractionation of process liquid streams34-36. The appeal of ceramic membranes for component separation is in situations of high pressures and temperatures, mechanical wear, exposure to organic solvents and other harsh chemical environments where polymeric membranes would fail37.
Filtration processes can be divided into five broad classes depending on the dimensions of the component to be separated: Particle filtration (PF), Microfiltration (MF), Ultrafiltration (UF), Nanofiltration (NF) and Reverse Osmosis (RO). PF refers to conventional media filtration, while the other four types are referred to as membrane filtrations. MF membranes are used to separate suspended particles (bacteria, protozoa, larger colloids, precipitates and coagulates) with diameters between 0.1 and 10 µm and are typically used in the production of drinking or process water. UF membranes are capable of retaining macromolecules (such as polysaccharides, proteins, sugars and polymers) with sizes ranging from 3 to 100 nm (or molecular weight ranging from 10,000-500,000 Da). NF membranes are able to remove contaminants smaller than 1 nm or soluble substances with molecular weight larger than 200 Da and are suitable for water softening and removal of pesticides, heavy metals, nitrates and odor or color substances in water treatment stations. RO membranes can effectively remove nearly all inorganic contaminants smaller than 0.1 nm or with molecular weight below 200 Da and are employed for desalinization of sea water, concentration of fruit juices and disinfection of drinking water38,39.
The permeation analysis of filtration membranes is typically based on Darcy's law, even though a specific terminology is employed to designate the relationship between pressure drop and the resulting fluid velocity34:
in which Jv [m/s] is the volumetric permeate flux, i.e., the volumetric flow rate Q [m3/s] passing through the membrane divided by the area exposed to flow A [m2], µ [Pa.s] is the permeate viscosity, Rm [m1] is the membrane resistance toward the flux and ΔP [Pa] is referred here as the transmembrane pressure difference.
It can be noted from inspection of Equations 9 and 11 that Rm relates to the Darcian permeability coefficient k1 by:
in which L [m] is the membrane thickness. Since membranes are processed according to a variety of configurations (tubular, spiral, flat-sheet or hollow-fiber arrangements) and thicknesses, their permeation features are better compared through the ratio Jv/ΔP, rather than through the flow resistance (Rm).
Despite some divergences in the literature34-39, typical permeation ranges for commercial filtration membranes are given in Table 5. For comparison purposes, Table 5 also gives the estimated ranges of Jv/ΔP for samples of compositions C-1 to C-4. Estimates were based on Equations 1 and 11 for water flow at 25 ºC (µ = 8.94×104 Pa.s and ρ = 997 kg/m3) with k1, k2 and L data from Table 4. Although samples C-1 to C-4 were not analyzed by mercury porosimetry, a rough estimate of their average pore size (dpore) can be obtained by Ergun-like equations, which relate the permeability coefficients k1and k2 with the apparent porosity of the medium (ε). Originally, Ergun equations were derived for packed columns of loose multisized particles/grains/fibers with an average particle diameter (dp)[40]. However, for porous media in which the solid matrix is continuous and the constitutive particles/grains/fibres are not individually recognizable, similar relationships can be derived by replacing dp by the average pore or cell size (dpore). In the present case, considering that only the Darcian coefficient k1 is required for flow analysis (validity of Darcy's law), then18:
Once known the experimental values of k1 and ε, Equation 13 can give a rough estimate of dpore for all tested compositions, as shown in Table 5. It is observed that while all samples presented permeation ranges higher than that typically found for microfiltration membranes and also presented pore sizes compatible with this application. Therefore, such compositions could be employed as substrates for asymmetric ceramic membranes or even microfiltration membranes for removal of particulate from liquid suspensions.
4. Conclusions
A study of the effect of calcium carbonate addition on a ceramic composition was performed to produce porous structures with sufficient permeability to allow their use in fluid dynamics applications. The results showed that the addition of limestone to a concentration of 20 wt.% caused an increase in porosity among the investigated compositions. This increase was due not only to the generation of pores by the degassing process of calcium carbonate from approximately 490 to 750 ºC but also due to the material expansion that occurred at approximately 1030 ºC. Air-flow tests conducted at room temperature indicated that the permeability coefficients k1 and k2 were approximately 1013 m2 and 109 m, respectively. An increase in the heat-treatment temperature from 800 to 1050 ºC resulted in an average 3-fold increase in the values of k1 and a 6-18-fold increase in k2. The composition prepared with 50 wt.% kaolin, 20 wt.% limestone, 20 wt.% feldspar, and 10 wt.% quartz that was heat treated at 1050 ºC showed the highest permeability (k1 = 1.73×1013 m2 and k2 = 1.00×108 m). Performance simulations performed with the samples showed that the Darcy's law is valid for applications in air flow at room temperature and pressure and at air velocities of less than 2 cm.s1. However, the obtained pressure drops are still higher than those recommended for aerosol filtration applications. Nevertheless, all compositions were found to present suitable permeation and pore size features to be used as substrates for asymmetric membranes or even microfiltration membranes for removal of suspended particles from liquid suspensions.
Acknowledgements
The authors are grateful to Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq/Brazil) for funding this work.
Received: January 18, 2013;
Revised: July 19, 2013
- 1. Taslicukur Z, Balaban C and Kuskonmaz N. Production of ceramic foam filters for molten metal filtration using expanded polystyrene. Journal of the European Ceramic Society. 2007; 27:637-40. http://dx.doi.org/10.1016/j.jeurceramsoc.2006.04.129
- 2. Li S and Crooks RM. Fabrication and Characterization of Single Pores for Modeling Mass Transport across Porous Membranes. Langmuir. 1999; 15:738-41. http://dx.doi.org/10.1021/la980871a
- 3. Seo D, Jung S, Lombardo SJ Feng ZC, Chen JK and Zhang Y. Fabrication and electrical properties of polymer-derived ceramic (PDC) thin films for high-temperature heat flux sensors. Sensor Actuators A 2011; 165:250-5. http://dx.doi.org/10.1016/j.sna.2010.11.013
- 4. Villar CEF, Nogueira REFQ, Carvalho LAM and Abreu HFG. Influence of pores on the failure of structural ceramic blocks. Construction and Building Materials 2008; 22:2376-1. http://dx.doi.org/10.1016/j.conbuildmat.2007.09.008
- 5. Park Y-H, Hinoki T and Kohyama A. Characteristic evaluation of liquid phase-sintered SiC materials by a nondestructive technique. Journal of Nuclear Materials 2009; 386-388:1014-7. http://dx.doi.org/10.1016/j.jnucmat.2008.12.202
- 6. Lemos AF and Ferreira JMF. Porous bioactive calcium carbonate implants processed by starch consolidation. Material Science and Engineering. 2000; 11:35-40. http://dx.doi.org/10.1016/S0928-4931(00)00134-X
- 7. Faure R, Rossignol F, Chartier T, Bonhomme C, Maitre A, Etchegoyen G et al. Alumina Foam Catalyst Supports for Industrial Steam Reforming Processes. Journal of the European Ceramic Society 2011; 31:303-12. http://dx.doi.org/10.1016/j.jeurceramsoc.2010.10.009
- 8. Ortega FS, Paiva AEM, Rodrigues JA and Pandolfelli VC. Propriedades mecânicas de espumas cerâmicas produzidas via "gelcasting". Cerâmica 2003; 49(309):1-5. http://dx.doi.org/10.1590/S0366-69132003000100002
- 9. Dey A, Kayal N and Chakrabarti O. Preparation of porous SiC ceramics by an infiltration technique. Ceramics International 2011; 37:223-30. http://dx.doi.org/10.1016/j.ceramint.2010.09.022
- 10. Ferreira OP, Alves OL, Macedo JS, Gimenez IF and Barreto LS. Ecomaterials: development and application of functional porous materials for environmental protection. Química Nova. 2007; 30:464-7. http://dx.doi.org/10.1590/S0100-40422007000200039
- 11. Sheppard LM. Porous ceramics: processing and applications. In: Ceramic Transactions-Porous Materials. Westerville: The American Ceramic Society; 1993. v. 31, p. 3-23.
- 12. Kingery WD, Bowen HK and Uhlmann DR. Introduction to Ceramics 2nd ed. New York: John Wiley & Sons; 1976. p. 1032.
- 13. Callister WD. Ciência e Engenharia de Materiais: Uma Introdução. 7th ed. Rio de Janeiro: LTC; 2008. p. 705.
- 14. Dutra RPS and Pontes LRA. Obtenção e análise de cerâmicas porosas com a incorporação de produtos orgânicos ao corpo cerâmico. Cerâmica 2002; 48:223-30. http://dx.doi.org/10.1590/S0366-69132002000400010
- 15. Montanaro L, Jorand Y, Fantozzi G and Negro A. Ceramic foams by powder processing. Journal of European Ceramic Society 1998; 18:1339-50. http://dx.doi.org/10.1016/S0955-2219(98)00063-6
- 16. Sepulveda P. Gelcasting foams for porous ceramics. American Ceramic Society Bulletim 1997; 76:61-5.
- 17. Sunderman E and Viedt J. Method of manufacturing ceramic foam bodies US Pat No. 3.745.201; 1973.
- 18. Innocentini MDM, Sepulveda P and Ortega FS. Cellular Ceramics: Structure, Manufacturing, Properties and Applications. Weinheim: Wiley-VCH; 2005. p. 313-40.
- 19. Innocentini MDM, Pardo ARF and Pandolfelli VC. Influence of air compressibility on the permeability evaluation of refractory castables. Journal of the American Ceramic Society 2000; 83:1536-8. http://dx.doi.org/10.1111/j.1151-2916.2000.tb01426.x
- 20. Innocentini MDM, Faleiros RK, Pisani R, Thijs I, Luyten J and Mullens S. Permeability of porous gelcast scaffolds for bone tissue engineering. Journal of Porous Materials 2010; 17:615-27. http://dx.doi.org/10.1007/s10934-009-9331-2
- 21. Scheidegger AE. The Physics of Flow Through Porous Media 3rd ed. Toronto: University of Toronto Press; 1974.
- 22. Innocentini MDM and Pandolfelli VC. Permeability of porous ceramics considering the Klinkenberg and inertial effects. Journal of the American Ceramic Society 2001; 84:941-4. http://dx.doi.org/10.1111/j.1151-2916.2001.tb00772.x
- 23. Hlushkou D and Tallarek U. Transition from creeping via viscous-inertial to turbulent flow in fixed beds. Journal of Chromatograph A. 2006; 1126:70-85. PMid:16806240. http://dx.doi.org/10.1016/j.chroma.2006.06.011
- 24. Noman R and Kalam MZ. Advances in Core Evaluation: Accuracy and Precision in Reserves Estimation. Philadelphia: Gordon and Breach Science Publishers; 1990. p. 447-462.
- 25. Seguin D, Montillet A and Comiti J. Experimental characterisation of flow regimes in various porous media-I: Limit of laminar flow regime. Chemical Engineering Science 1998; 53:3751-61. http://dx.doi.org/10.1016/S0009-2509(98)00175-4
- 26. Seguin D, Montillet A, Comiti J and Huet F. Experimental characterization of flow regimes in various porous media-II: Transition to turbulent regime, Chemical Engineering Science 1998; 53:3897-3909. http://dx.doi.org/10.1016/S0009-2509(98)80003-1
- 27. Innocentini MDM, Rodrigues VP, Romano RCO, Pileggi RG, Silva GM and Coury JR. Permeability optimization and performance evaluation of hot aerosol filters made using foam incorporated alumina suspension. Journal of Hazardous Materials 2009; 162:212-21. PMid:18565647. http://dx.doi.org/10.1016/j.jhazmat.2008.05.025
- 28. Barg S, Innocentini MDM, Meloni RV, Chacon WS, Wang H, Koch D et al. Physical and high-temperature permeation features of double-layered cellular filtering membranes prepared via freeze casting of emulsified powder suspensions. Journal of Membrane Science 2011; 383:35-43. http://dx.doi.org/10.1016/j.memsci.2011.08.003
- 29. Sepúlveda P, Ortega FS, Innocentini MDM and Pandolfelli VC. Properties of highly porous hydroxyapatite obtained by the gel-casting of foams. Journal of the American Ceramic Society 2001; 83:3021-4. http://dx.doi.org/10.1111/j.1151-2916.2000.tb01677.x
- 30. Rodrigues JA, Ortega FS, Paiva AEM, Villaboim ELG and Pandolfelli VC. The relation between porosity and elastic moduli of gelcast ceramic foams. Cerâmica 2004; 50:209-16. http://dx.doi.org/10.1590/S0366-69132004000300007
- 31. Montedo ORK, Floriano FJ, Oliveira J Fş, Angioletto E and Bernardin AM. Sintering behavior of LZSA glass-ceramics. Materials Research 2009; 12:197-200. http://dx.doi.org/10.1590/S1516-14392009000200014
- 32. Innocentini MDM, Pardo ARF, Menegazzo BA and Bittencourt LRM. Permeability of high-alumina refractory castables based on various hydraulic binders. Journal of the American Ceramic Society 2002; 85:1517-21. http://dx.doi.org/10.1111/j.1151-2916.2002.tb00306.x
- 33. Dey A, Kayal N, Chacon WS, Chakrabarti O, Innocentini MDM and Coury JR. Evaluation of Air Permeation Behavior of Porous SiC Ceramics Synthesized by Oxidation-Bonding Technique. International Journal of Applied Ceramic Technology 2012; 1-11.
- 34. Mulder M. Basic Principles of Membrane Technology. Kluwer academic Publishers; 1996. http://dx.doi.org/10.1007/978-94-009-1766-8
- 35. Porter MC. Handbook of Industrial Membrane Technology New Jersey: Noyes Publications; 1990.
- 36. Li K. Ceramic Membranes for Separation and Reaction West Sussex: John Wiley & Sons Ltd; 2007. http://dx.doi.org/10.1002/9780470319475
- 37. Scott K. Handbook of Industrial Membranes Oxford: Elsevier Advanced Technology; 2006.
- 38. Judd S and Jefferson B. Membranes for Industrial Wastewater Recovery and Re-use Oxford: Elsevier Science Ltd; 2003.
- 39. Cui ZF and Muralidhara HS. Membrane Technology - a Practical Guide to Membrane Technology and Applications in Food and Bioprocessing Oxford: Butterworth-Heinemann; 2010.
- 40. Ergun S. Fluid flow through packed columns. Chemical Engineering Progress. 1952; 48:89.
Publication Dates
-
Publication in this collection
10 Sept 2013 -
Date of issue
Dec 2013
History
-
Received
18 Jan 2013 -
Accepted
19 July 2013