Velocidade mínima para completar um loop circular vertical: uma abordagem cinemática

Minimum velocity to complete a vertical circular loop: a kinematic approach

Resumos

Neste simples estudo é mostrado um método alternativo para o problema clássico de se encontrar a velocidade mínima necessária para completar um loop vertical de raio $R$. Diferentemente da abordagem usual de livros introdutórios de física básica, que se utilizam do conceito de força (normal e peso), neste estudo são utilizados apenas conceitos de cinemática e geometria para encontrar o valor conhecido para a velocidade mínima $v_{\mathrm{\text{min}}}=\sqrt{gR}$.

Palavras-chave:
cinemática; movimento circular; movimento de projétil

In this simple study is presented an alternative method for the classic problem of finding the minimum velocity necessary to complete a vertical loop of radius $R$. Unlike the usual approaches of introductory textbooks of basic physics, which use the concept of force (normal and weight), in this study only kinematics and geometrics concepts are applied to find the known value for the minimum velocity $v_{\mathrm{\text{min}}}=\sqrt{gR}$.

Keywords:
kinematic; circular motion; projectile motion

1. Introdução

Encontrar a velocidade mínima, no topo da trajetória, para efetuar um loop circular vertical de raio $R$ é um problema expositivo comum em livros introdutórios de física básica [¹,²]. Essa específica aplicação das leis de Newton é muito interessante, pois é uma das primeiras vezes que é instigado algum interesse dos alunos de um primeiro curso de física básica na universidade. Desta forma, é interessante abordar esse problema utilizando-se, se possível, de mais de um método para responder a essa pergunta.

Além da forma usual abordada nos livros didáticos, que respondem qual seria a velocidade mínima para completar um loop vertical, existem estudos na literatura que abordam outras questões sobre esse tema. Em [³] foi analisada a possibilidade de um ser humano conseguir completar um loop vertical de três metros de raio apenas correndo. Eles concluíram que, embora teoricamente possível, este feito seria díficil de completar devido a falta de atrito para manter a velocidade e também devido a força-g que o corredor sentiria. Entretanto, um loop vertical já foi completado apenas correndo. Em 2014, Damien Walters completou um loop com aproximadamente metade do raio estudado, $R\simeq 1,5$ metros, e aparentemente sem muita dificuldade [⁴]. Isso demosntra como o loop vertical faz parte do nosso imaginário e também que esse estudo não é nada trivial.

O estudo de um loop vertical está intimamente conectado com o desenvolvimento de montanhas-russas de parques de diversões. Nesses trabalhos se faz uso dos conceitos de força e conservação da energia de tal forma a se encontrar a trajetória do loop vertical que produz certas características desejadas, e.g. força-g constante ou força normal constante durante todo o loop [⁵-⁸]. Várias formas são possíveis, todas relacionadas com as curvas cónicas. Para o caso de força normal constante em todo o loop a solução encontrada é a denominada curva clotóide, também conhecida como a espiral de Euler ou espiral de Cornu [⁶]. Interessante notar que até o ano de 1976 as montanhas-russas que possuíam um loop vertical tinham uma trajetória circular, tornando a experiência um tanto desconfortável devido a grande magnitude das forças-g envolvidas. Apenas em 1976 foi construída a primeira montanha-russa com a trajetória dada pela espiral de Euler e realmente utilizável em parques de diversões. Por essa razão sendo denomindada de The new revolution [⁹].

No estudo aqui apresentado será abordado apenas o problema clássico, ou seja, qual é a velocidade mínima necessária para completar um loop circular vertical de raio $R$. Entretanto, diferentemente da abordagem usual, essa pergunta será respondida utilizando apenas conceitos de cinemática e geometria: trajetória circular e trajetória de um projétil. Como serão utilizados apenas conceitos geométricos, esse método proposto para responder o problema não consegue determinar a forma da curva. Para esse fim é necessário ter conhecimento da dinâmica do movimento envolvido.

Esse artigo é divido nas seguintes partes: na seção 2. será relembrado sucintamente o método usual abordado nos livros didáticos, onde será apontado o conceito que os alunos normalmente têm mais dificuldade de compreensão. Na seção 3. será apresentada a solução utilizando apenas cinemática e geometria, onde serão aplicados três formas análogas para encontrar o resultado $v_{\mathrm{\text{min}}}=\sqrt{gR}$: diferencial, raio de curvatura e série de Taylor. E na seção 4. as conclusões serão apresentadas.

2. Abordagem usual

Na abordagem usual de livros didáticos de física básica, se argumenta que o ponto crítico para se responder a pergunta é o topo do loop. Consequentemente, é feito o diagrama de forças do objeto nessa posição. As duas forças que atuam no corpo, desprezando-se o atrito e a resistência do ar, são a força que a superfície do loop produz, denominada normal ($N$), e a força gravitacional que a Terra produz, denominada peso ($P=mg$). No topo do loop as duas forças apontam para o seu centro. Consequentemente, a segunda lei de Newton para a direção radial é dada por

(1) $$N+mg=m\frac{v^2}{R}.$$

Para encontrar a velocidade mínima é feito $N=0$, o que siginifica que o objeto não está mais em contato com a superfície do loop, muito embora o objeto ainda não tenha se movido na direção radial. Com essa argumentação temos que a aceleração radial do objeto ainda é dada pela aceleração centrípeta, $a_{cp}=v^2∕R$. Este é o instante que normalmente cria dúvidas nos alunos. Eles têm dificuldade em entender como o objeto perdeu contato com a superfície muito embora ele ainda não tenha se movido nesta direção. De fato, aparentemente temos uma contradição. Para tentarmos esclarecer essa aparente contradição, temos que olhar com mais detalhes para a força normal.

A normal é produzida pela resultante das forças de interação entre as moléculas das camadas externas das duas superfícies. Essa força é denominada de força de Van der Walls [¹⁰], e uma propriedade deste tipo de força é que a sua magnitude cai rapidamente com a separação entre as superfícies (tipicamente da ordem de algumas distâncias moleculares típicas). Denotando a distância na qual a força se torna desprezível por $\delta R$, temos que a força normal na posição $R-\delta R$, ou seja, um pequeno incremento abaixo do topo do loop, é nula, $N\left(R-\delta R\right)=0$. Entretanto, a aceleração centrípeta do objeto, nessa mesma posição, é dada por

(2) $$a_{cp}\left(R-\delta R\right)=\frac{v^2}{\left(R-\delta R\right)}.$$

Resolvendo a segunda lei de Newton para a velocidade, obtemos:

(3) $$v=\sqrt{g\left(R-\delta R\right)}.$$

Para encontrarmos o resultado conhecido para a velocidade mínima é necessário fazer a aproximação de que a distância típica na qual a força de Van der Walls é desprezível $\left(\delta R\right)$ é muito menor que o raio do loop. Quando é feita essa aproximação ($\delta R=0$), estamos afirmando que o objeto e o topo da superfície ocupam a mesma posição. Normalmente denominamos essa aproximação de “contato”, que é uma abstração matemática¹. Percebemos então que a dúvida reside na definição de contato em física [¹¹].

Na bordagem cinemática, que será apresentada na próxima seção, também é feita essa aproximação de que as duas superfícies (do loop e do objeto) estão em contato.

3. Abordagem cinemática

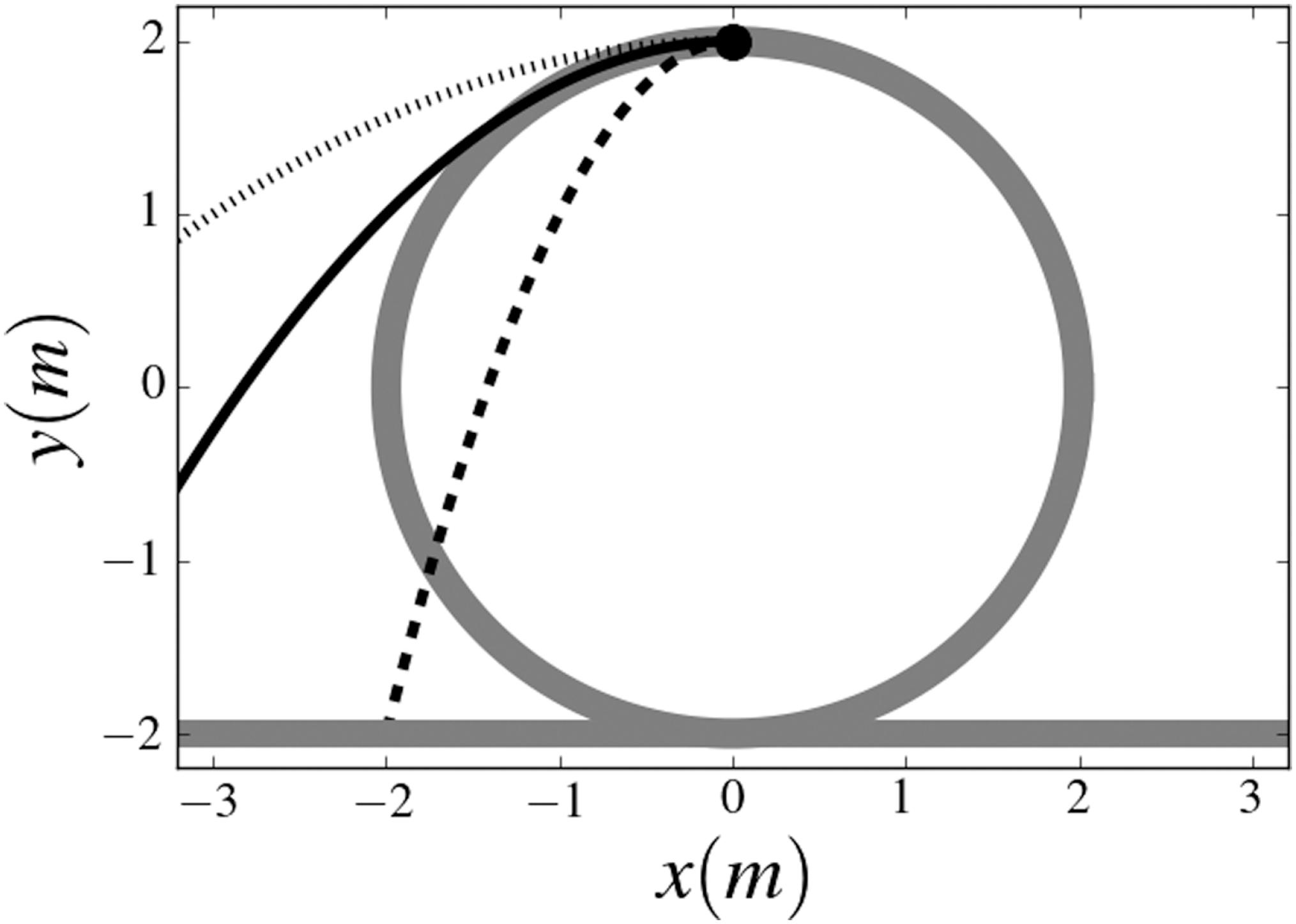
Utilizando argumentos de cinemática, a pergunta a ser feita para encontrar a velocidade mínima no topo de um loop vertical pode ser enunciada da seguinte forma: qual deve ser a velocidade inicial de um projétil, lançado por uma superfície circular vertical, de tal forma que a sua trajetória parabólica seja localmente igual a trajetória do loop? Na figura 1 são mostrados três exemplos de lançamentos com velocidades iniciais diferentes para um loop com raio de dois metros.

Figura 1
Três possíveis lançamentos do topo de um loop com $R=2$ metros. A linha tracejada é referente a uma velocidade inicial $v_0=0,5\sqrt{gR}$, a linha continua é referente a $v_0=\sqrt{gR}$ e a linha pontilhada para $v_0=1,5\sqrt{gR}$.

A seguir iremos responder essa pergunta de três formas análogas: utilizando o conceito de diferencial, raio de curvatura de uma curva e série de Taylor.

3.1. Diferencial

Uma forma de responder matematicamente essa pergunta é mostrando que num instante infinitesimal após o topo do loop, tanto a superfície circular quanto o movimento do projétil são exatamente iguais. Assim, quando o projétil se mover um infinitésimo na direção horizontal, $\mathrm{\text{d}}x$, após a posição do topo, ambos terão de cair a mesma altura $\mathrm{\text{d}}y$.

Consequentemente, temos de encontrar a trajetória da superfície do loop, $y_{\ell }\left(x\right)$, e do suposto projétil se não houvesse a superfície após a posição no topo, $y_p\left(x\right)$. Essas equações são dadas respectivamente por

(4) $$y_{\ell }\left(x\right)=\sqrt{R^2-x^2},$$

(5) $$y_p\left(x\right)=R-\frac{g}{2v_0^2}{x}^2.$$

Para escrevermos essas duas trajetórias utilizamos um referencial com origem no centro do loop e eixo vertical usual, perpendicular a Terra para cima e eixo horizontal da esquerda para direita como mostrado na figura 1. Além disso, utilizamos que a partícula executa o loop no sentido anti-horário e que no topo a sua velocidade inicial na direção vertical é zero.

Derivando as duas trajetórias com relação a variação na posição horizontal, obtemos:

(6) $$\frac{\mathrm{\text{d}}{y}_{\ell }}{\mathrm{\text{d}}x}=-\frac{x}{\sqrt{R^2-x^2}},$$

(7) $$\frac{\mathrm{\text{d}}{y}_p}{\mathrm{\text{d}}x}=-\frac{g}{v_0^2}x.$$

A velocidade mínima nessa abordagem é dada quando as duas derivadas são iguais,

(8) $$\frac{\mathrm{\text{d}}{y}_{\ell }}{\mathrm{\text{d}}x}=-\frac{x}{\sqrt{R^2-x^2}}=-\frac{g}{v_0^2}x=\frac{\mathrm{\text{d}}{y}_p}{\mathrm{\text{d}}x}.$$

Resolvendo para $v_0$ obtemos a seguinte relação:

(9) $$v_0^2=g\sqrt{R^2-x^2}.$$

Como estamos no topo do loop a posição horizontal da partícula é $x=0$. Dessa forma encontramos o resultado conhecido da velocidade mínima,

(10) $$v_0=\sqrt{gR}.$$

Essa abordagem cinemática deixa evidente a interpretação das diferenciais que aparecem nas equações (6) e (7). Algo que muitos alunos de física básica ainda possuem dificuldades em compreender.

3.2. Raio de curvatura

Esse problema também pode ser pensado em termos do raio de curvatura $\rho$ das duas curvas no topo do loop. O raio de curvatura de uma curva $y\left(x\right)$ é definido como sendo [¹²]

(11) $$\rho =\left|\frac{{\left(1+y^{\prime }\right)}^{3∕2}}{y^{\prime \prime }}\right|,$$

onde $y^{\prime }$ e $y^{\prime \prime }$ são, respectivamente, a primeira e segunda derivadas com relação a $x$. O raio de curvatura de um circulo é ${\rho }_{\ell }=R$, como deveria de ser, pois o raio de curvatura é definido de tal forma que para um círculo ele tenha valor igual ao seu raio.

Para a trajetória do projétil é mais interessante escrever o raio de curvatura na sua forma paramétrica, utilizando o tempo como parâmetro [¹²],

(12) $$\rho =\left|\frac{{\left({\dot{x}}^2+{\dot{y}}^2\right)}^{3∕2}}{\dot{x}\ddot{y}-\dot{y}\ddot{x}}\right|.$$

Neste caso as derivadas são efetuadas com relação ao tempo. Para o caso do projétil temos que o movimento na componente horizontal não tem aceleração, $\ddot{x}=0$, e a componente vertival tem aceleração constante dada pela aceleração da gravidade, $\ddot{y}=-g$. As velocidades de lançamento no topo do loop são dadas por: $\dot{x}=-v_0$ e $\dot{y}=0$. Consequentemente, obtemos que o raio de curvatura do projétil lançado é dado por

(13) $${\rho }_p=v_0^2∕g.$$

Dois casos limites são interessantes de ser enfatizados. No limite que $v_0\to \infty$ ou $g\to 0$ temos que ${\rho }_p\to \infty$, que é o raio de curvatura de um movimento horizontal, i.e., um movimento retilíneo e uniforme paralelo ao eixo $x$. Para o outro extremo, $v_0\to 0$ ou $g\to \infty$ temos que ${\rho }_p\to 0$. Neste caso o movimento é somente vertical, i.e., o objeto está em queda-livre perpendicular à superfície da Terra.

Para as duas curvas serem localmente iguais elas devem ter o mesmo raio de curvatura, ${\rho }_{\ell }={\rho }_p$, o que nos fornece $v_0=\sqrt{gR}$.

3.3. Série de Taylor

Uma outra forma de abordar a questão colocada é fazendo uso de série de Taylor. Neste caso não vamos apenas analisar a partícula no topo do loop, mas em qualquer posição na sua superfície. Ainda utilizando o referencial mostrado na figura 1, temos que as condições iniciais para um projétil lançado de qualquer posição do loop são dadas por:

(14) $$x_0=Rcos\theta ,$$

(15) $$v_{x0}=-v_0\mathrm{\text{sen}}\theta ,$$

(16) $$y_0=R\mathrm{\text{sen}}\theta ,$$

(17) $$v_{y0}=v_{0}cos\theta .$$

O ângulo $\theta$ é definido da forma usual, com relação ao semi-eixo positivo $x$ no sentido anti-horário.

A trajetória do loop, dada pela equação (4), pode ser expandida até segunda ordem em torno da posição inicial de lançamento $x_0$,

(18) $$\begin{array}{cc}\hfill & y_{\ell }\left(x\right)\simeq y_0-\frac{x_0}{\sqrt{R^2-x_0^2}}\left(x-x_0\right)\\ & \hfill -\frac{R^2}{2{\left(R^2-x_0^2\right)}^{3∕2}}{\left(x-x_0\right)}^2+\mathcal{O}{\left(x-x_0\right)}^3.\end{array}$$

Utilizando as condições iniciais, a trajetória do loop pode ser escrita como

(19) $$\begin{array}{cc}& y_{\ell }\left(x\right)\simeq R\mathrm{\text{sen}}\theta -\frac{cos\theta }{\mathrm{\text{sen}}\theta }\left(x-Rcos\theta \right)\\ & -\frac{1}{2R{\mathrm{\text{sen}}}^3\theta }{\left(x-Rcos\theta \right)}^2.\end{array}$$

A equação da trajetória de uma partícula lançada de qualquer posição angular $\theta$ do loop, com uma velocidade inicial de módulo $v_0$, é dada por

(20) $$\begin{array}{cc}& y_p\left(x\right)=R\mathrm{\text{sen}}\theta -\frac{cos\theta }{\mathrm{\text{sen}}\theta }\left(x-Rcos\theta \right)\\ & -\frac{g}{2v_0^2{\mathrm{\text{sen}}}^2\theta }{\left(x-Rcos\theta \right)}^2.\end{array}$$

Por comparação direta das equações (19) e (20), temos que os dois primeiros termos são idênticos, apenas os últimos termos diferem.

Para responder a pergunta proposta, ou seja, encontrar a velocidade mímina para efetuar o loop, as trajetórias devem ser iguais em torno da posição de lançamento, $y_{\ell }\left(x_0\right)=y_p\left(x_0\right)$. Desta forma encontramos que a velocidade inicial de um projétil que melhor se ajusta a trajetória de um circulo é

(21) $$v_0=\sqrt{gR\mathrm{\text{sen}}\theta }.$$

Essa relação é idêntica a encontrada anteriormente dada na equação (9) como esperado. Para o topo do loop temos $\theta =\pi ∕2$, fornecendo $v_0=\sqrt{gR}$.

Podemos notar que a equação (21) só têm solução física quando a partícula se encontra na parte superior do loop, ou seja, $0\le \theta \le \pi$. Este fato também era de se esperar, pois na sua parte inferior não existe a possibilidade do projétil acompanhar a superfície circular, ele sempre tentará atravessá-la, devido a direção da velocidade inicial de lançamento.

É interessante utilizar a série de Taylor para a trajetória do loop, por que esse método nos fornece uma forma de comparar as duas trajetórias não só na posição de lançamento, mas nos fornecendo uma estimativa do quão próximas elas são após o topo. A expansão da trajetória do loop em torno de $x=0$, ou seja, no seu topo, é dada por

(22) $$y_{\ell }=R-\frac{x^2}{2R}-\frac{x^4}{8R^3}+\mathcal{O}{\left(x\right)}^6.$$

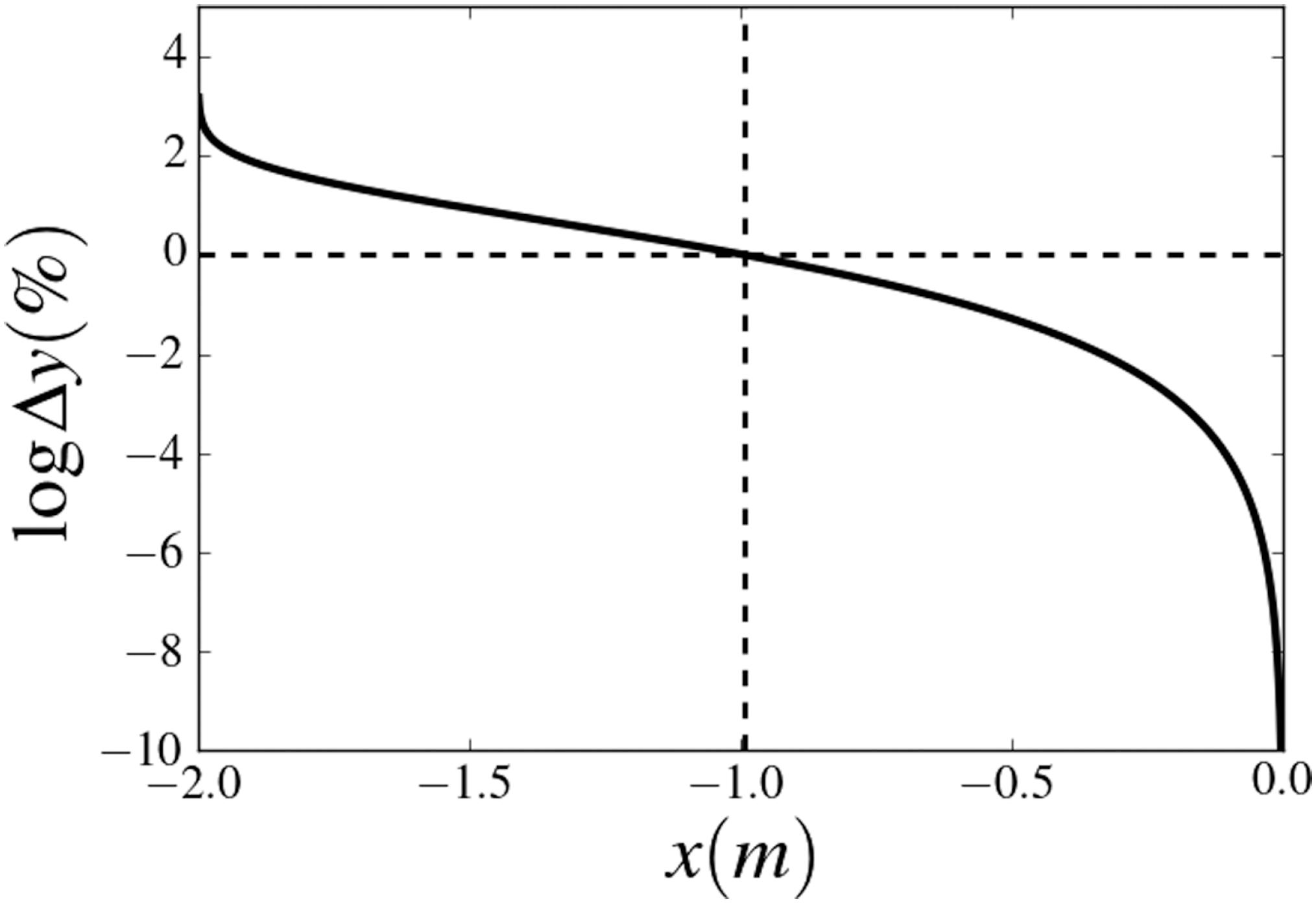
Essa expansão mostra que o projétil quando lançado com velocidade $v_0=\sqrt{gR}$ tem uma trajetória em torno de $x=0$ igual a trajetória do loop com precisão da ordem de $\mathcal{O}{\left(x\right)}^4$. Na figura 2 é mostrada a diferença percentual entre a trajetória do loop e da partícula com velocidade de lançamento $v_0=\sqrt{gR}$,

(23) $$\text{Δ}y=100\times \left|\frac{y_p\left(x\right)-y_{\ell }\left(x\right)}{y_{\ell }\left(x\right)}\right|.$$

Figura 2
Diferença percentual entre a trajetória do loop com $R=2$ metros e da partícula lançada no topo com velocidade $v_0=\sqrt{gR}$. As linhas tracejadas indicam a posição onde a diferença alcança $\text{Δ}y=1\%$.

Essa diferença se torna maior que $1\%$ em torno de $x\simeq -1$ metro, para o caso de um loop de dois metros de raio. A partícula estaria, com uma boa aproximação, em queda-livre até esse ponto.

4. Conclusão

Neste artigo foi analisado o problema clássico de física básica de determinar qual é a velocidade mínima para completar um loop circular vertical utilizando apenas conceitos de cinemática e geometria. Para encontrar essa velocidade mínima, utilizamos três métodos análogos para chegar ao resultado $v_{\mathrm{\text{min}}}=\sqrt{gR}$.

No primeiro método utilizamos o conceito de diferencial, que encontra a velocidade utilizando como argumentação que tanto a partícula quanto a superfície do loop devem cair um $\mathrm{\text{d}}y$ ao se mover um $\mathrm{\text{d}}x$ na horizontal. Acreditamos que esse seja um exemplo interessante para tentar esclarecer o conceito de diferencial para os alunos de um curso introdutório de física básica.

No segundo método foi utilizado o conceito de raio de curvatura, um conceito pouco abordado neste tipo de curso. Devido ao movimento de projéteis ser um dos poucos movimentos que os alunos têm familiaridade, acreditamos que este é um momento interessante para introduzir essa quantidade e esclarecer as suas características fundamentais.

No terceiro método, a trajetória da superfície do loop foi expandida utilizando o conceito de série de Taylor. Essa abordagem é interessante pois ela não esta restrita ao topo da trajetória, desta forma, explicitando o quão próximas são essas duas trajetórias após o lançamento do projétil. Por consequência nos fornece uma forma de quantificar a diferença entre o loop e o movimento do objeto lançado.

Um leitor atento deve ter percebido que poderíamos ter respondido a pergunta sobre a velocidade mínima, ainda utilizando somente conceitos de cinemática, de uma forma muito simples: a velocidade mínima para completar um loop vertical de raio $R$ é dada quando essa velocidade produz uma aceleração centrípeta exatamente igual a aceleração da gravidade, $g=v^2∕R$. Nessa argumentação utilizamos que a aceleração do projétil $\left(g\right)$ deve ser igual a “aceleração” da superfície do loop$\left(v^2∕R\right)$. De uma certa forma é o que foi feito neste estudo. Na abordagem diferencial fizemos que as velocidades do projétil e da superfície devem ser iguais. Com o raio de curvatura fizemos, indiretamente, que as acelerações devem ser iguais. E na abordagem com a série de Taylor igualamos as posições.

Agradecimentos

O autor gostaria de agradecer à Viviane Amorim e Aurelio Carnero pela leitura minuciosa do manuscrito e suas valiosas sugestões.

• 1
  Essa aproximação, ou melhor, a definição de contato, vai de encontro com o ditado popular que afirma que “dois corpos não ocupam o mesmo lugar no espaço ao mesmo tempo”.

Referências

• ^[1]
  D. Halliday, R. Resnick e J. Walker, Fundamentos de Física (LTC, Rio de Janeiro, 2008), v. 1, p. 137.
• ^[2]
  R.D. knight, Physics for Scientists and Engineers: A Strategic Approach (Pearson Education Inc, 2013), p. 204.
• ^[3]
  A. Armenti, Phys. Teach. 19, 624 (1981).
• ^[4]
  https://www.youtube.com/watch?v=OTcdutIcEJ4, acessado em 26/10/2017.
  » https://www.youtube.com/watch?v=OTcdutIcEJ4
• ^[5]
  R. Müller, Eur. J. Phys. 31, 835 (2010).
• ^[6]
  A.B. Nordmark and H. Essén, Eur. J. Phys. 31, 1307 (2010).
• ^[7]
  A.M. Pendrill, Phys. Educ. 40, 517 (2005).
• ^[8]
  A.M. Pendrill, Eur. J. Phys. 34, 1379 (2013).
• ^[9]
  https://en.wikipedia.org/wiki/The˙New˙Revolution˙(roller˙coaster), acessado em 26/10/2017.
  » https://en.wikipedia.org/wiki/The˙New˙Revolution˙(roller˙coaster)
• ^[10]
  A. Bettini, Course in Classical Physics 1 - Mechanics (Springer, Switzerland, 2016), p. 110.
• ^[11]
  M. Alonso and E.J. Finn, Física: Um Curso Univesitário (Edgard Blücher LTDA, São Paulo, 1972), v. 1, p. 156.
• ^[12]
  A.M. Munem, Cálculo (LTC, Rio de Janeiro, 2008), v. 2, p. 731.

Datas de Publicação

• Publicação nesta coleção
  2018

Histórico

• Recebido
  07 Nov 2017
• Revisado
  28 Nov 2017
• Aceito
  28 Nov 2017