Transformações de Lorentz na frente de luz

Lorentz transformations in the light front

Resumo

Nos cursos de relatividade em geral se estuda que as transformações de Lorentz são definidas num espaço com quatro dimensões: três espaciais e uma temporal. Neste trabalho colocamos em discussão uma forma alternativa para definir as transformações de Lorentz na frente de luz via espaço de Minkowski e suas propriedades. Dirac, em 1949, introduziu três formas distintas de dinâmica relativística possíveis, dependendo da escolha que fazemos das diferentes hipersuperfícies caracterizadoras. À primeira, denominou-se de forma instantânea. É a forma mais comum, cuja hipersuperfície é especificada pelas condições de contorno definidas em $t=0$ e a evolução do sistema ocorre para instantes $t>0$. A segunda, conhecida como forma pontual, tem como superfície caracterizadora uma hiperboloide, descrita pelas condições iniciais em $x^{\mu }{x}_{\mu }=a{}^2$, sendo $a$ uma constante e $t>0$. A terceira, conhecida como forma da frente de luz, tem sua hipersuperfície tangente ao cone de luz, sendo definida pelas condições iniciais em $x^{+}=\frac{c}{\sqrt{2}}(t+\frac{z}{c})=0$ e a evolução “temporal” prossegue para “instantes $x^{+}>0$”. Dessa forma, interpreta-se a variável $x^{+}$ como “tempo” na frente de luz. Os resultados aqui apresentados estão vinculados as transformações de Lorentz expressas nas coordenadas da frente de luz e suas consequências na expressão de diversas quantidades físicas de interesse.

Palavras-chave:
Transformação de Lorentz; Espaço de Minkowski; Frente de luz

Abstract

In undergraduate and graduate courses, one usually studies the Lorentz's transformation defined in four-dimensional space: three spatial dimensions and one temporal. In this work we present an alternative way for the Lorentz's transformations using the light front coordinates via Minkowski space-time and its properties. Dirac in one of his works, published in 1949, introduced three different forms of relativistic dynamics: the usual or most common one, called instant form, characterized by the hypersurface specified by the boundary conditions defined at $t=0$ and time evolution for the system at instances $t>0$; the point form, whose surface is a hyperboloid, and are described by the initial conditions $x^{\mu }{x}_{\mu }=a{}^2$ with the constant $a$ and $t>0$ and the light front form, whose hypersurface is tangent to the light cone, being defined by the initial conditions at $x^{+}=\frac{c}{\sqrt{2}}(t+\frac{z}{c})=0$ and the “time evolution” for “instances $x^{+}>0$”. Therefore, the variable $x^{+}$ plays the role of light-front “time”. The results we present here are connected to the study of Lorentz's transformations using light-cone coordinates and its consequences in the outcome expressions for diverse physical quantities of interest.

Keywords:
Lorentz Transform; Minkowski Space; Light Front

1. Introdução

Um postulado básico da física é que as leis da natureza devem ser independentes do observador que realiza as medidas de um dado evento. O conceito de relatividade surge pelo fato de que a observação de eventos é realizada por diversos referenciais. A cada observador pode-se associar um referencial no qual as suas medidas são determinadas. Dessa forma, embora a lei natural deva ser a mesma, dois observadores distintos podem registrar essa mesma lei sob pontos de vista diferentes (diferentes referenciais) – daí o conceito de relatividade dos fenômenos observados. O exemplo a seguir ajuda a esclarecer o que dissemos.

Um ponto no espaço bidimensional pode ser determinado por um conjunto de coordenadas cartesianas de eixos perpendiculares entre si, identificados como eixos $x$ e $y$. Desse modo, um ponto qualquer nesse espaço pode ser determinado univocamente pela relação $P=(x,y)$. Como exemplo, podemos tomar o ponto $P_1=(3,2)$. Nada nos impede de utilizar outro conjunto de coordenadas, $x^{{}^{\prime }}$ e $y^{{}^{\prime }}$, em rotação de ${45}^{\mathrm{o}}$ no sentido anti-horário em relação ao sistema de referência anterior. Desse modo, o ponto genérico se expressa agora como:

$$\begin{array}{r}P=(x{}^{\prime },y{}^{\prime })=(x\cos {45}^{\mathrm{o}}+y\sin {45}^{\mathrm{o}},-x\sin {45}^{\mathrm{o}}+y\cos {45}^{\mathrm{o}})\end{array}$$

e o particular ponto exemplificado antes se expressa agora como:

$$\begin{array}{r}{P}_1=(5\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2})\end{array}$$

O ponto $P_1$, nas novas coordenadas, parece diferente, mas representa o mesmo ponto de antes.

Então qual a vantagem de uma sobre a outra? Para pontos genéricos, nenhuma vantagem, mas para todos os pontos para os quais $x=\pm y,$ há uma simplificação nas novas coordenadas, uma delas se anula, ou seja, levam a pontos especificamente sobre $x^{{}^{\prime }}$ (ou $y^{{}^{\prime }}$).

Por exemplo, para o ponto $P_2=(2,2)$ em xy, temos $P_2=(2\sqrt{2},0)$ em $x^{{}^{\prime }}{y}^{{}^{\prime }}$, enquanto que para $P_3=(-2,2)$ em xy, temos $P_3=(0,2\sqrt{2})$ em $x^{{}^{\prime }}{y}^{{}^{\prime }}$. Isso ilustra o que discutiremos nesse trabalho em relação as transformações de Lorentz na relatividade especial quando utilizamos as coordenadas da frente de luz.

Na teoria da relatividade especial, a ideia do tempo absoluto é substituída por um tempo próprio para cada referencial inercial. Como consequência, passa a existir um espaço-tempo quadridimensional, sendo o tempo uma quarta dimensão. Dizer que o tempo é a quarta dimensão desse espaço deve ser entendido no sentido de que a quarta coordenada é definida pelo produto da velocidade da luz com o tempo, isto é, ct. Neste espaço, a métrica pode assumir uma aparência euclidiana, semelhante à métrica euclidiana tridimensional usada no espaço ordinário. Esta estrutura quadridimensional é chamada de universo de Minkowski [1]. Um acontecimento é definido por quatro coordenadas no espaço de Minkowski e a distância entre dois acontecimentos, ou seja, intervalo do universo é um invariante. O intervalo do universo é semelhante à distância entre dois pontos no espaço tridimensional.

Paul Adrien Maurice Dirac [2], em 1949, mostrou que é possível construir três formas de dinâmicas partindo da descrição do estado inicial de um sistema relativístico em qualquer superfície do espaço-tempo, ou seja, partículas se propagam no espaço avançando no tempo a partir do hiperplano também denotado como hipersuperfície em $t=0$, até um instante posterior $t>0$, sendo as mesmas definidas como: Forma Instantânea, que corresponde a Teoria Relativística com condições de contorno definidas em $t=0$; Forma Pontual, que consiste em estabelecer os dados iniciais sobre um ramo de um hiperboloide; E, finalmente a Forma Frontal, conhecida como Frente de Luz, na qual as condições iniciais são dadas em um hiperplano do espaço de Minkowski que contém a trajetória da luz (Figura 1), essa, por sua vez, será a forma de dinâmica que trataremos neste artigo.

Figura 1
Três formas de dinâmicas.

Neste artigo, o foco são as transformações de Lorentz nas coordenadas da frente de luz [3,4]. As transformações de Lorentz usuais (isto é, aquelas consideradas padrão no espaço-tempo de Minkowski $(z^0,\overrightarrow{z})$; onde $z^0=ct$, com referenciais inerciais $S$ e $S^{{}^{\prime }}$ movendo-se com velocidade constante relativa $v$ ao longo dos eixos $z$ paralelo a $z^{\prime }$) são tais que a coordenada tempo $t^{\prime }$ em $S^{\prime }$ é expressa em termos das coordenadas tempo $t$ e espaço $z$ em $S$; e similarmente, a coordenada espaço $z^{\prime }$ em $S^{\prime }$ é expressa em termos das coordenadas tempo $t$ e coordenada espaço $z$ em $S$. As coordenadas no espaço de Minkowski são construídas pela combinação linear entre a coordenada tempo $(ct)$ e coordenada espaço $(z)$, mas isso não se revela com as transformações de Lorentz na frente de luz, que se manifestam conectando apenas coordenadas similares, isto é, tempo em $S$ com tempo em $S^{\prime }$ e coordenada espacial em $S$ com coordenada espacial em $S^{\prime }$. Esse resultado é responsável pela introdução de profundas modificações nas estruturas algébricas das transformações de Lorentz [3 -6].

Neste trabalho discute-se essencialmente as transformações de Lorentz na relatividade especial e na sequência, a mesma transformação no espaço de Minkowski. Introduzimos as coordenadas na frente de luz, expressando as transformações de Lorentz nessas coordenadas, mostrando as suas peculiaridades inerentes e apresentamos alguns pontos distintivos dessas transformações na expressão de resultados de quantidades de interesse e em seguida finalizamos com as conclusões desse trabalho.

2. Transformações de Lorentz na relatividade especial

Sejam dois observadores inerciais movendo-se com velocidade relativa $\overrightarrow{v}$ constante. Um dos observadores faz suas medidas no sistema $S$ e o outro, em $S^{\prime }$. Isto não quer dizer que o sistema $S^{\prime }$ esteja em movimento e o sistema $S$, parado; o conceito de movimento é relativo. Quem está em $S$, vê o sistema $S^{\prime }$ se afastando com velocidade $\overrightarrow{v}$, mas quem está em $S^{\prime }$ vê, igualmente, o sistema $S$ se movendo com velocidade $-\overrightarrow{v}$. Ambos estão corretos.

De acordo com o princípio de Galileu, não há experiência alguma que possa ser feita, tanto em $S$ como em $S^{\prime }$, que mostre qual sistema está realmente em movimento. A situação é perfeitamente simétrica.

Consideremos que um observador em $S$ registre um evento, como um piscar de luz, pelo conjunto $(x,y,z,t)$. Para o observador em $S^{\prime }$, este mesmo evento é registrado por $(x^{\prime },y^{\prime },z^{\prime },t^{\prime })$. A transformação de um sistema referencial em outro é alcançada pelas transformações de Lorentz no espaço de quatro dimensões:

(1) $$\begin{array}{}& \{\begin{array}{l}c{t}^{{}^{\prime }}=\gamma (ct-\frac{v}{c}z)\\ z^{{}^{\prime }}=\gamma (z-vt)\\ x^{\prime }=x\\ y^{\prime }=y\end{array}\end{array}$$

onde $c$ é a velocidade da luz; e o fator de Lorentz é expresso por

$$\gamma =\frac{1}{\sqrt{1-{\beta }^2}},$$

em que utilizamos a notação bastante comum para o fator $\beta =v/c$.

A transformação inversa pode ser encontrada quando trocamos o sinal da velocidade, ficando da seguinte forma:

(2) $$\begin{array}{}& \{\begin{array}{l}ct=\gamma (c{t}^{{}^{\prime }}+\frac{v}{c}{z}^{\prime })\\ z=\gamma (z^{{}^{\prime }}+v{t}^{{}^{\prime }})\\ x=x^{\prime }\\ y=y^{\prime }\end{array}\end{array}$$

Esse é o resultado mais tradicional encontrado na literatura [1]. As transformações em (1) também podem ser expressas numa forma alternativa e mais simetrizada de notação para as diversas coordenadas: $x^0=ct;x^1=x;x^2=y\mathrm{e}{x}^3=z$

$$\{\begin{array}{l}{x}^{0^{{}^{\prime }}}=\gamma (x^0-\beta x^3)\\ x^{3^{{}^{\prime }}}=\gamma (x^3-\beta x^0)\\ x^{1^{\prime }}=x^1\\ x^{2^{\prime }}=x^2\end{array}.$$

Nas próximas seções vamos mostrar outras formas para representar as transformações de Lorentz.

3. Transformações de Lorentz no espaço Minkowski

Hermann Minkowski [7] sugeriu $\overrightarrow{x}=(x^1,x^2,x^3)$ e $x^4=ict$ como definições para as componentes de um espaço quadridimensional. Essas quatro coordenadas se transformam de um referencial inercial $S$ para outro $S^{{}^{\prime }}$ através das transformações de Lorentz. Albert Einstein [8], no seu livro The Meaning of Relativity, explica de forma didática que essas transformações de Lorentz podem ser vistas como uma rotação nas quatro dimensões.

Para obter as transformações de Lorentz via espaço de Minkowski, sem perda de generalidade, utilizamos apenas duas das quatro dimensões dadas, uma vez que duas delas sempre podem ser subentendidas. O resultado se mantém geral, mesmo com essa hipótese [9].

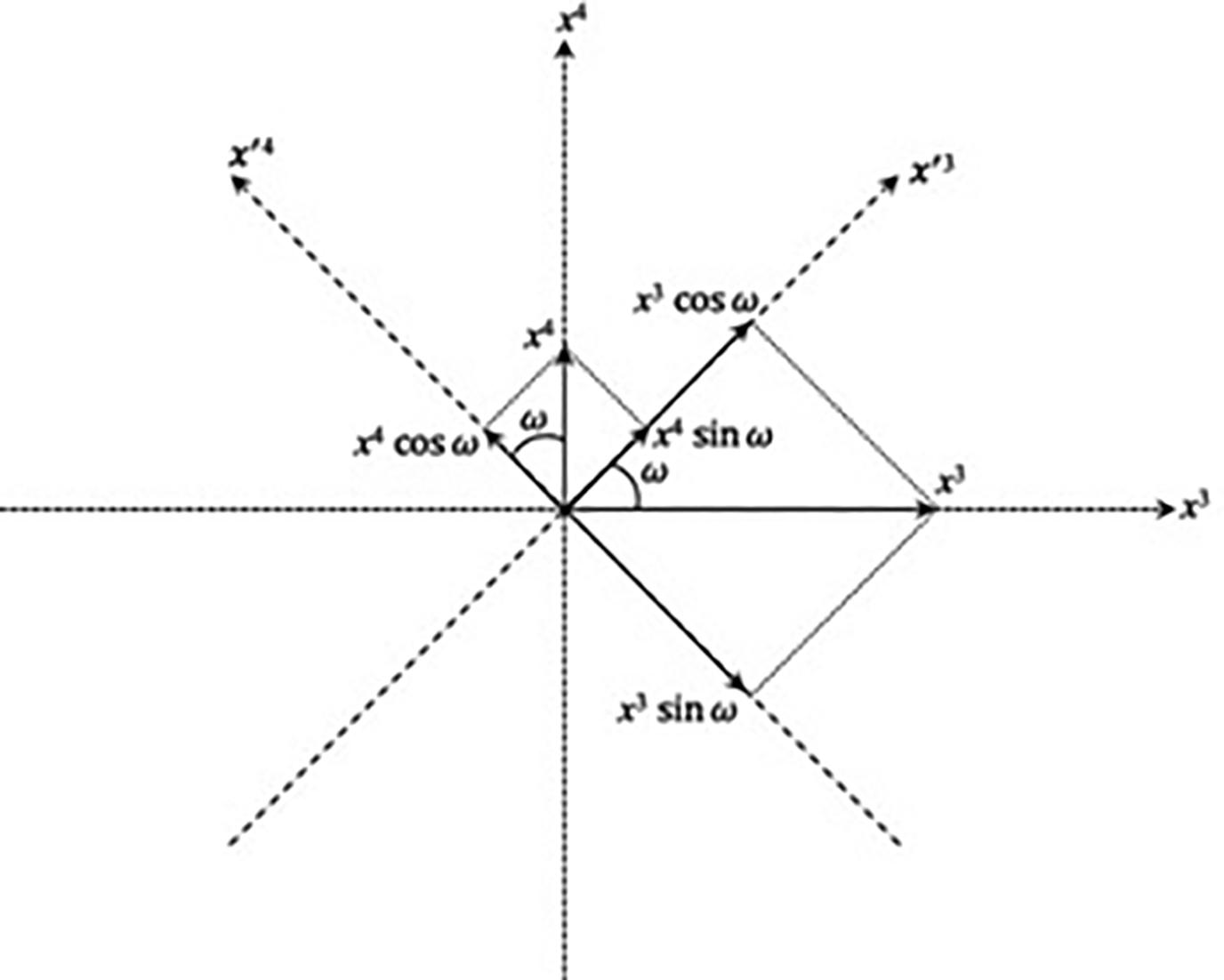
A Figura 2 mostra as coordenadas de posição $x^3$ e a coordenada temporal $x^4$ para representar um referencial $S$. Para um referencial $S^{{}^{\prime }}$, as coordenadas são $x^{{}^{\prime }3}$ e $x^{{}^{\prime }4}$. As transformações de Lorentz de $S^{{}^{\prime }}$ para $S$ se dá por rotação do espaço-tempo, como mostraremos na Figura 2.

Figura 2
Rotação no espaço de Minkowski.

No eixo ${x^{\prime }}^3$ temos duas projeções vindas do referencial $S$ e no eixo ${x^{\prime }}^4$ mais duas, ou seja:

(3) $$\begin{array}{}& \begin{array}{c}{x}^{{}^{\prime }3}=x^3\cos \omega +x^4\text{sen}\omega \\ x^{{}^{\prime }4}={-x}^3\text{sen}\omega +x^4\cos \omega \end{array}\end{array}$$

Sabendo que ${x^{\prime }}^3$ deve ser real e $x^4$ imaginário puro, obrigatoriamente $\cos \omega$ deve ser real e $\text{sen}\omega$ deve ser puramente imaginário, de modo que:

$$\omega =i\phi \{\begin{array}{c}\cos \omega =\cosh \phi \\ \text{sen}\omega =i\text{senh}\phi \end{array}$$

e usando a definição de Bjorken-Drell [10] em que $x^4=ict\equiv i{x}^0$, obtemos:

(4) $$\begin{array}{}& \{\begin{array}{l}{x^{\prime }}^3=x^3\cosh \phi -x^0\text{senh}\phi \\ x^{{}^{\prime }0}=-x^3\text{senh}\phi +x^0\cosh \phi \end{array}\end{array}$$

Se identificarmos a origem $O^{{}^{\prime }}({x^{\prime }}^3=0)$ com $x^3=vt=\frac{v}{c}{x}^0=\beta x^0$, encontraremos:

(5) $$\begin{array}{}& \tanh \phi =\beta ,\end{array}$$

e utilizando a identidade ${(\cosh \phi )}^2-{\left(\text{senh}\phi \right)}^2=1$ que, dividido por ${(\cosh \phi )}^2$, equivale:

$$1-{(\tanh \phi )}^2=\frac{1}{{(\cosh \phi )}^2}$$

Usando a equação (5) obtemos:

(6) $$\begin{array}{}& \cosh \phi =\frac{1}{\sqrt{1-{\beta }^2}}=\gamma \end{array}$$

Portanto, pelas identidades anteriores conclui-se que

(7) $$\begin{array}{}& \text{senh}\phi =\gamma \beta \end{array}$$

Dessa forma, as equações (4) se reduzem às equações das transformações de Lorentz na métrica de Bjorken-Drell, tornando-se:

$$\{\begin{array}{l}{x^{\prime }}^3=\gamma (x^3-\beta x^0)\\ x^{{}^{\prime }0}=\gamma (x^0-\beta x^3)\end{array}$$

Observe que o ângulo de rotação $\omega$ deve ser puramente imaginário para satisfazer os quesitos impostos pela equação (3), razão porque introduzimos um novo parâmetro real $\phi$ de tal modo que $\omega =i\phi$. Esse novo parâmetro $\phi$ está relacionado com a rapidez $\beta$ pela equação (5) acima. O parâmetro $\phi$ pode ser determinado da seguinte forma:

(8) $$\begin{array}{}& \tanh \phi =\frac{\text{senh}\phi }{\cosh \phi }=\beta \end{array}$$

Usando-se a propriedade:

$$\tanh \phi =\frac{v}{c}\to \frac{e^{\phi }-e^{-\phi }}{e^{\phi }+e^{-\phi }}=\frac{v}{c},$$

que pode ser reescrita como

$$e^{\phi }-e^{-\phi }=\frac{v}{c}(e^{\phi }+e^{-\phi }),$$

resultando em:

$$e^{2\phi }=\left(\frac{1+\frac{v}{c}}{1-\frac{v}{c}}\right)\equiv \frac{1+\beta }{1-\beta }$$

Portanto, isolando-se o ângulo, obtém-se que

(9) $$\begin{array}{}& \phi =\frac{1}{2}\mathrm{l}\mathrm{n}\left(\frac{1+\beta }{1-\beta }\right)\end{array}$$

Através dessas análises e levando-se em consideração a semelhança com a rotação usual no espaço de três dimensões, podemos formalmente interpretar geometricamente as transformações de Lorentz como uma ‘rotação’ por um ângulo imaginário $\omega$ no plano $(x^3,x^4)$ do espaço-tempo, em que o ‘ângulo imaginário’ é dado pelo produto da unidade imaginária $i$– com o parâmetro real $\phi$ acima obtido na equação (9).

4. Frente de luz

O uso das três formas de dinâmica relativística, criadas por Dirac, possibilita descrever o movimento de suas partículas, dependendo apenas do tipo de hiperplano escolhido para a evolução temporal do sistema [2]. A dinâmica de forma instantânea é a usual, que consiste em especificar os dados iniciais (a posição inicial e a velocidade) sobre a superfície $x^0=ct$. A forma pontual, cuja superfície é especificada pelas condições iniciais em $x^{\mu }{x}_{\mu }=a^2$ com $a$ constante e $x^0>0$, sendo a posição e velocidade iniciais definidas ao longo de um hiperboloide. A terceira formulação, a frente de luz, consiste em definir as condições iniciais sobre uma hipersuperfície tridimensional no espaço-tempo, formando um hiperplano de frente de luz que contém a trajetória da luz e avança com a velocidade da luz, $x^{+}=0$, o que implica em $t=-z/c$. As coordenadas da frente de luz são obtidas, particularmente, pelas transformações:

(10) $$\begin{array}{}& \{\begin{array}{l}{x}^{+}=\frac{1}{\sqrt{2}}(x^0+x^3)\\ x^{-}=\frac{1}{\sqrt{2}}(x^0-x^3)\\ {\overrightarrow{x}}^{\mathrm{\perp }}=x^1\overrightarrow{i}+x^2\overrightarrow{j}\end{array},\end{array}$$

onde $x^0=ct$ é a componente temporal e $x^1,x^2,x^3$ são as componentes espaciais $(x,y,z)$ respectivamente. O vetor ${\overrightarrow{x}}^{\mathrm{\perp }}$ está contido no plano $(x,y)$ e é transversal às componentes ${(x}^{+},x^{-})$. A coordenada $x^{+}$ é o parâmetro tempo na frente de luz [11] e as componentes $(x^{-},x^{\mathrm{\perp }})$ são associadas as posições espaciais na hipersuperfície da frente de luz.

Na Figura 3 vemos um plano tangente ao cone de luz que também é tangente à coordenada $x^{-}$ e perpendicular à coordenada $x^{+}$; esse plano define a frente de luz.

Figura 3
Frente de luz.

A transformação inversa para o espaço de Minkowski na métrica de Bjorken-Drell é dada por:

(11) $$\begin{array}{}& \{\begin{array}{l}{x}^0=\frac{\sqrt{2}}{2}(x^{+}+x^{-})\\ x^3=\frac{\sqrt{2}}{2}(x^{+}-x^{-})\end{array}\end{array}$$

onde $x^0=ct$ e $x^3=z$.

O jacobiano das transformações de coordenadas para aquelas associadas à frente de luz pode ser obtido pelo módulo do determinante

$$\left|J\right|=\parallel \begin{array}{ccc}\frac{\mathrm{\partial }{x}^0}{\mathrm{\partial }{x}^{+}}& \frac{\mathrm{\partial }{x}^0}{\mathrm{\partial }{x}^{-}}& \begin{array}{cc}\frac{\mathrm{\partial }{x}^0}{\mathrm{\partial }{x}^1}& \frac{\mathrm{\partial }{x}^0}{\mathrm{\partial }{x}^2}\end{array}\\ \frac{\mathrm{\partial }{x}^1}{\mathrm{\partial }{x}^{+}}& \frac{\mathrm{\partial }{x}^1}{\mathrm{\partial }{x}^{-}}& \begin{array}{cc}\frac{\mathrm{\partial }{x}^1}{\mathrm{\partial }{x}^1}& \frac{\mathrm{\partial }{x}^1}{\mathrm{\partial }{x}^2}\end{array}\\ \begin{array}{c}\frac{\mathrm{\partial }{x}^2}{\mathrm{\partial }{x}^{+}}\\ \frac{\mathrm{\partial }{x}^3}{\mathrm{\partial }{x}^{+}}\end{array}& \begin{array}{c}\frac{\mathrm{\partial }{x}^2}{\mathrm{\partial }{x}^{-}}\\ \frac{\mathrm{\partial }{x}^3}{\mathrm{\partial }{x}^{-}}\end{array}& \begin{array}{c}\begin{array}{cc}\frac{\mathrm{\partial }{x}^2}{\mathrm{\partial }{x}^1}& \frac{\mathrm{\partial }{x}^2}{\mathrm{\partial }{x}^2}\end{array}\\ \begin{array}{cc}\frac{\mathrm{\partial }{x}^3}{\mathrm{\partial }{x}^1}& \frac{\mathrm{\partial }{x}^3}{\mathrm{\partial }{x}^2}\end{array}\end{array}\end{array}\parallel$$

No caso da transformação do espaço de Minkowski com tensor métrico na representação de Bjorken-Drell para a frente de luz (10), o Jacobiano é igual $1$ [12,13].

A passagem de uma integral em um quadrivolume para outro sistema de coordenadas na frente de luz requer o uso do jacobiano, o que resulta:

$$\int {dx}^0{dx}^1{dx}^2{dx}^3=\left|J\right|\int {dx}^{+}{dx}^{-}{d^{2}x}^{\mathrm{\perp }}$$

Tem sido frequente o uso da frente de luz para estudos cinemáticos. Os campos de aplicações estendem-se destes sistemas com poucos núcleos [14] até estudos sobre estrutura de hádrons leves [15]. Isto se deve a possibilidade de tratar as funções de onda com um número pequeno de grau de liberdade, ou seja, usa-se um número fixo de partícula. Porém, dentro da limitação desse número fixo, não é levado em conta a mistura de componentes mais complexos do espaço de Fock. Na frente de luz, isso é conhecido como truncamento no espaço de Fock [16].

Do ponto de vista quântico, podemos definir o estado inicial do sistema em qualquer hipersuperfície para o qual a distância entre dois pontos sejam do tipo espaço, e, portanto sem conexão causal. A evolução quântica do sistema é dada pelo operador associado à translação temporal desta hipersuperfície. Uma vantagem do uso da frente de luz, na descrição de sistemas quânticos é que podemos realizar “boosts” sem envolver a dinâmica, e descrever a função de onda em diversos referenciais [16], conhecido como “boosts” cinemáticos.

Em Teoria Quântica de Campos usual, um truncamento no espaço de Fock é problemático [17]. Em geral, mudando-se de referencial, através de “boosts” há criação de pares, tornando-se inconveniente este tratamento, pois o número de partículas nesse referencial é diferente. É desejável, portanto, que essa dificuldade não exista e que seja possível encontrar uma descrição na qual o número de partículas não mude com o referencial, preservando essa descrição física.

Usando a frente de luz como ferramenta de cálculo, o problema é solucionado no que diz respeito a certos “boosts” [17]. Por exemplo, as funções de onda handrônica envolvendo quarks constituintes são covariantes por “boosts” cinemáticos [18]. Os geradores das transformações cinemáticas não produzem pares ao serem aplicados no estado quântico, por não conterem a dinâmica. Como consequência, a invariância dos observáveis físicos em geral é preservada via frente de luz [14-15].

5. Transformações de Lorentz na frente de luz

No sistema (4), na linha de ${x{}^{\prime }}^3$, fazendo-se a substituição de $x^0$ e $x^3$ com ajuda da transformação inversa da frente de luz (11), obtemos assim:

(12) $$\begin{array}{}& {\left(x^{+}-x^{-}\right)}^{{}^{\prime }}=\left(x^{+}-x^{-}\right)\cosh \phi -\left(x^{+}+x^{-}\right)\text{senh}\phi .\end{array}$$

Na segunda linha com $x^{{}^{\prime }0}$ da equação (4), tem-se:

(13) $$\begin{array}{}& {\left(x^{+}+x^{-}\right)}^{{}^{\prime }}=\left(x^{+}+x^{-}\right)\cosh \phi -\left(x^{+}-x^{-}\right)\text{senh}\phi .\end{array}$$

Somando as equações (12) e (13), resulta:

(14) $$\begin{array}{}& x^{{}^{\prime }+}=x^{+}\cosh \phi -x^{+}\text{senh}\phi \end{array}$$

De maneira análoga, calculando a diferença entre as equações (12) e (13), encontramos:

(15) $$\begin{array}{}& x^{{}^{\prime }-}=x^{-}\cosh \phi +x^{-}\text{senh}\phi .\end{array}$$

Assim, surge um sistema composto de duas equações na frente de luz:

(16) $$\begin{array}{}& \{\begin{array}{l}{x}^{{}^{\prime }+}=x^{+}\cosh \phi -x^{+}\text{senh}\phi \\ x^{{}^{\prime }-}=x^{-}\cosh \phi +x^{-}\text{senh}\phi \end{array}.\end{array}$$

O sistema (16) representa as transformações de Lorentz do espaço-tempo de Minkowski nas coordenadas da frente de luz.

Usando agora as definições para as funções hiperbólicas $\text{senh}\phi$ e $\cosh \phi$ podemos simplificar o sistema (16):

(17) $$\begin{array}{}& \{\begin{array}{l}\text{senh}\phi =\frac{e^{\phi }-e^{-\phi }}{2}\\ \cosh \phi =\frac{e^{\phi }+e^{-\phi }}{2}\end{array}\end{array}$$

Da primeira relação do sistema da equação (16), $x^{{}^{\prime }+}=x^{+}(\cosh \phi -\text{senh}\phi )$ com a ajuda da relação (17) temos:

(18) $$\begin{array}{}& x^{{}^{\prime }+}=x^{+}(\frac{e^{\phi }+e^{-\phi }}{2}-\frac{e^{\phi }-e^{-\phi }}{2})\end{array}$$

que finalmente resulta em:

$$x^{{}^{\prime }+}=x^{+}{e}^{-\phi }$$

Para $x^{{}^{\prime }-}$ em (16), utilizando-se das definições (17), segue que:

$$x^{{}^{\prime }-}=x^{-}(\frac{e^{\phi }+e^{-\phi }}{2}+\frac{e^{\phi }-e^{-\phi }}{2})$$

que, simplificando, resulta em

$$x^{{}^{\prime }-}=x^{-}{e}^{\phi }$$

Dessa forma, os resultados para as transformações de Lorentz na frente de luz, podem ser escritas resumidamente da seguinte forma:

(19) $$\begin{array}{}& \{\begin{array}{l}{x}^{{}^{\prime }+}=e^{-\phi }{x}^{+}\\ {x^{{}^{\prime }-}=e}^{\phi }{x}^{-}\end{array}\end{array}$$

onde $\phi$ está representado na equação (9).

O resultado (19) mostra que a coordenada temporal na frente de luz $x^{+}$ não interfere com a coordenada espacial $x^{-}$ em uma transformação entre referenciais, diferentemente das transformações de Lorentz expressas em (1) ou em (4). Por exemplo, a transformação para a coordenada temporal $t(x^0)$ em (1) possui a coordenada $z(x^3)$. Esse aspecto das transformações de Lorentz nas coordenadas da frente de luz, portanto, são típicas de uma transformação de escala na coordenada.

6. Algumas consequências das transformações de Lorentz na frente de luz

Nos textos sobre relatividade especial é comum encontrar a descrição nos seguintes termos: quando o corpo observado está em repouso num determinado referencial dizemos que o corpo está no seu sistema próprio. Ao intervalo de tempo em tal sistema denominamos tempo próprio. Analogamente, ao comprimento de uma barra denominamos de comprimento próprio.

Outra forma equivalente de abordarmos essa situação é o intervalo de tempo próprio entre dois eventos que ocorrem no mesmo lugar. Um intervalo de tempo não próprio (ou impróprio) seria aquele medido por dois relógios em dois lugares diferentes. Portanto, se $d\tau$ for um intervalo de tempo próprio, temos a expressão:

(20) $$\begin{array}{}& dt=\gamma d\tau \end{array}$$

onde $dt$ é o tempo impróprio, que estabelece uma relação entre eles. Esta equação descreve a dilatação temporal.

No caso do comprimento próprio $L_0$ uma régua em $S^{{}^{\prime }}$, teria a seguinte relação:

(21) $$\begin{array}{}& L=\frac{L_0}{\gamma }\end{array}$$

onde $L$ é o comprimento impróprio e esta equação descreve a contração espacial.

Na frente de luz ocorre uma situação semelhante. Se colocarmos um relógio em $S^{{}^{\prime }}$observado por $S$, o tempo próprio na frente de luz${\mathrm{\Delta }{x}^{\prime }}^{+}$ é dado por

(22) $$\begin{array}{}& {\mathrm{\Delta }x}^{+}=e^{\phi }{\mathrm{\Delta }{x}^{\prime }}^{+}\end{array}$$

sendo ${\mathrm{\Delta }x}^{+}$ o tempo impróprio na frente de luz.

Uma régua em $S^{{}^{\prime }}$ na frente de luz, observado por $S$, tem-se o comprimento próprio na frente de luz${\mathrm{\Delta }{x}^{\prime }}^{-}$:

(23) $$\begin{array}{}& {\mathrm{\Delta }x}^{-}=e^{-\phi }{\mathrm{\Delta }{x}^{\prime }}^{-}\end{array}$$

Para comparar os efeitos cinemáticos da dilatação temporal e contração espacial entre os dois sistemas de coordenadas é definido um fator de dilatação temporal nas coordenadas usuais como:

(24) $$\begin{array}{}& {\mathrm{\Gamma }}_{tempo}=\frac{dt}{d\tau }=\gamma \end{array}$$

e para contração espacial temos:

(25) $$\begin{array}{}& {\mathrm{\Gamma }}_{espacial}=\frac{L}{L_0}=\frac{1}{\gamma }\end{array}$$

Na frente de luz o fator de dilatação temporal é dado por:

(26) $$\begin{array}{}& {\mathrm{\Gamma }}_{x^{+}}=\frac{{\mathrm{\Delta }x}^{+}}{{\mathrm{\Delta }{x}^{\prime }}^{+}}=e^{\phi }\end{array}$$

e o fator de contração espacial na frente de luz é definido como:

(27) $$\begin{array}{}& {\mathrm{\Gamma }}_{x^{-}}=\frac{{\mathrm{\Delta }x}^{-}}{{\mathrm{\Delta }{x}^{\prime }}^{-}}=e^{-\phi }\end{array}$$

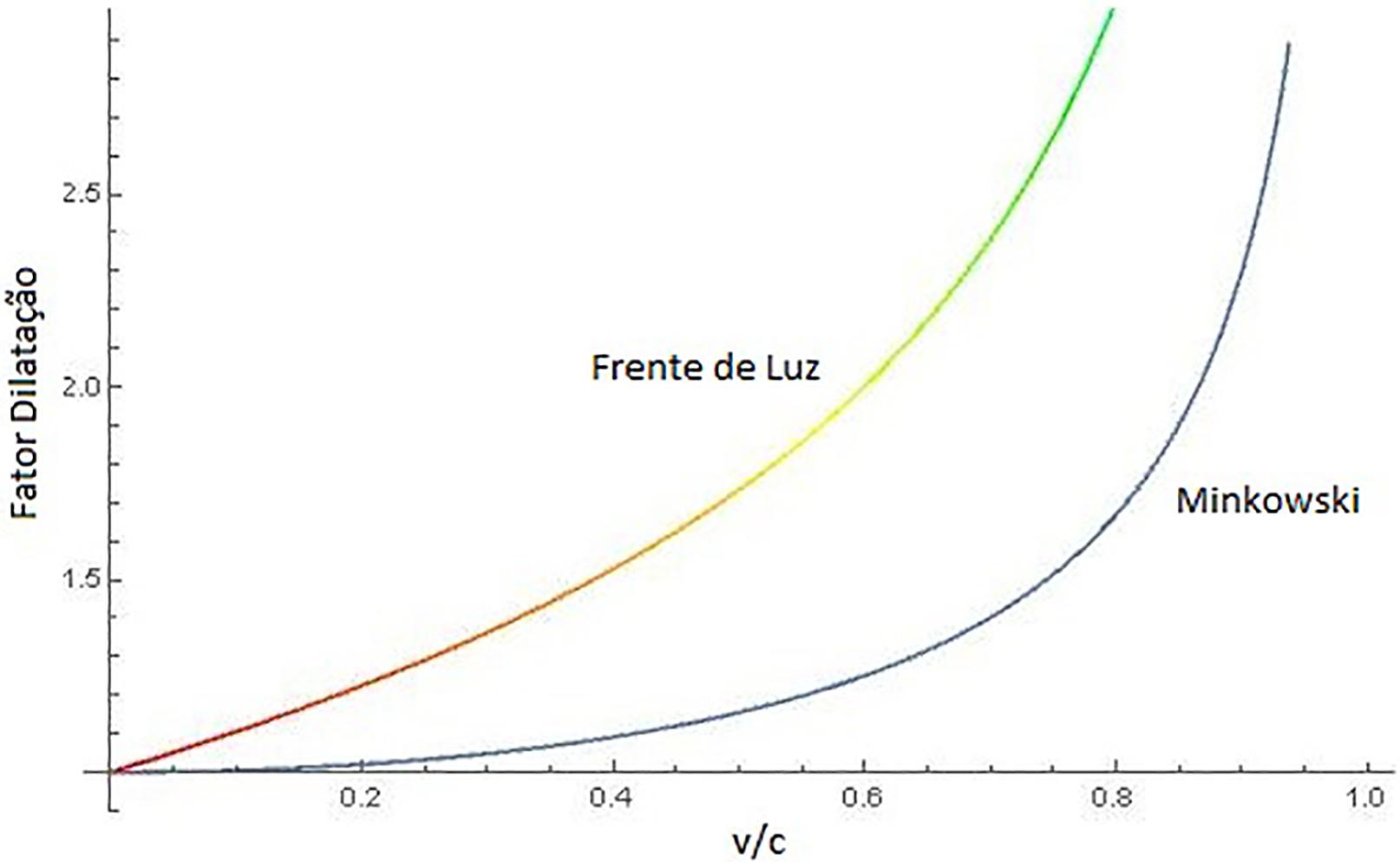
Na Figura 4 mostramos os efeitos da dilatação temporal utilizando os distintos fatores (24) e (26) em função de $v/c$ variando do repouso, $v=0$ a $v=c$. Observa-se ainda na Figura 4, que o efeito da dilatação está presente nos dois sistemas de coordenadas: de Minkowski e da frente de luz. Contudo, o comportamento do fator de dilatação não é equivalente entre os dois sistemas de coordenadas, uma vez que, no sistema da frente de luz, a transformação ocorre puramente como um fator de escala nas equações (19) como função de uma única variável ${x^{\prime }}^{\pm }=f(x^{\pm })$, e no sistema de Minkowski, tempo e espaço nas equações (1) aparecem como função de duas componentes das coordenadas ${x^{\prime }}^3=f(x^3,x^0)$, basicamente.

Figura 4
Comparação entre a dilatação do tempo em Minkowski e na frente de luz.

A Figura 5, no caso do efeito de contração espacial (25) e (27), mostra as curvas para as coordenadas no espaço de Minkowski e na frente de luz. Na Figura 5 é observado um efeito relativístico importante. Para $v=c$ o fator de contração espacial (25) é nulo, o mesmo acontece para o fator de contração na frente de luz (27). Esse efeito pode ser entendido, fisicamente, como uma contração do comprimento de uma barra em dado referencial que se move com velocidade $v$, sendo a mesma cada vez mais próxima da velocidade da luz $c$, e no limite de $v=c$ o comprimento é nulo. O mesmo efeito pode ser interpretado na frente de luz, ou seja, no limite de $v=c$ uma barra, nas coordenadas da frente de luz, tem comprimento nulo.

Figura 5
Comparação da contração espacial em Minkowski e na frente de luz.

Os efeitos relativísticos são semelhantes em ambas coordenadas. As medidas do tempo e espaço feitas separadamente não são invariantes. Mas, medidas da distância entre dois eventos no espaço-tempo são invariantes. Assim, as transformações de Lorentz e a relatividade da simultaneidade fazem com que os intervalos de tempo e as distâncias sejam diferentes para observadores situados em diferentes referenciais inerciais.

No entanto, há uma grandeza associada às coordenadas espaço e tempo que é invariante em relação às transformações de Lorentz, denominada de intervalo no espaço-tempo:

(28) $$\begin{array}{}& {(\mathrm{\Delta }S)}^2={\left(c\mathrm{\Delta }t\right)}^2-\left({\mathrm{\Delta }x}^2+{\mathrm{\Delta }y}^2+{\mathrm{\Delta }z}^2\right)\end{array}$$

ou, para o caso de uma dimensão espacial:

(29) $$\begin{array}{}& {\left(\mathrm{\Delta }S\right)}^2={\left(c\mathrm{\Delta }t\right)}^2-{\left(\mathrm{\Delta }z\right)}^2\end{array}$$

Usando as transformações de Lorentz (1) demonstra-se que ${\left(\mathrm{\Delta }S\right)}^2={\left(\mathrm{\Delta }S{}^{\prime }\right)}^2$, ou seja, o intervalo espaço-tempo em $S$ é igual a $S^{\prime }$.

No caso da frente de luz o intervalo no espaço-tempo é obtido a partir da equação (29) com a substituição de (11), o que resulta em:

(30) $$\begin{array}{}& {\left(\mathrm{\Delta }S\right)}^2={\mathrm{\Delta }x}^{+}{\mathrm{\Delta }x}^{-}\end{array}$$

Usando as transformações de Lorentz na frente de luz (22) e (23) em (30), chegamos a expressão:

(31) $$\begin{array}{}& {\left(\mathrm{\Delta }S\right)}^2={\mathrm{\Delta }x}^{+}{\mathrm{\Delta }x}^{-}=e^{\phi }{\mathrm{\Delta }{x}^{\prime }}^{+}{e}^{-\phi }{\mathrm{\Delta }{x}^{\prime }}^{-}={\left(\mathrm{\Delta }{\mathrm{S}}^{\prime }\right)}^2\end{array}$$

O resultado (31) mostra que na frente de luz a condição de invariância para o intervalo espaço-tempo é preservado.

Como ressaltamos antes, a física permanece a mesma (como no exemplo simples introdutório, as coordenadas (2,2) em xy e $(2\sqrt{2},0)$ em $x^{{}^{\prime }}{y}^{{}^{\prime }}$ representam o mesmo ponto $P$ no espaço bidimensional), embora as expressões matemáticas utilizadas para descrevê-la pareçam diferentes! Note que na ilustração inicial, com a mudança de coordenadas (rotação), o valor de uma das variáveis se torna zero, de modo que essencialmente, a descrição do ponto considerado se faz pelo valor de uma única coordenada; semelhantemente, quando utilizamos a rotação nas coordenadas da frente de luz para as transformações de Lorentz, as mesmas são funções apenas de uma coordenada quando são transformadas de um sistema para outro. Nas transformações usuais de Lorentz temos, basicamente, ${x^{\prime }}^3=f(x^3,x^0)$ ou ${x^{\prime }}^0=f(x^0,x^3)$ como função de duas coordenadas. Na frente de luz temos ${x^{\prime }}^{+}=f(x^{+})$ e ${x^{\prime }}^{-}=f(x^{-})$, ou seja, as transformações de Lorentz na frente de luz são apenas em função de uma coordenada $x^{+}$ ou $x^{-}$.

7. Conclusão

Neste artigo apresentamos uma técnica alternativa para se estudar a relatividade especial. Essa técnica é uma mudança de coordenadas do espaço-tempo de Minkowski para um sistema de coordenadas conhecida como frente de luz.

O resultado para os fenômenos de dilatação temporal e de contração espacial usando a frente de luz, aparentemente, parece não corresponder ao obtido via espaço-tempo de Minkowski. No entanto, a invariância dos intervalos espaço-tempo é preservada.

Os fatores de dilatação e contração, vistos nas Figuras 4 e 5, são diferentes pelo fato de serem calculados em sistemas de coordenadas diferentes. Podemos entender essa diferença utilizando a analogia com o que acontece no caso em que determinamos a posição de um determinado ponto no espaço utilizando coordenadas cartesianas em rotação de ${45}^{\mathrm{o}}$. Os valores desses pontos são diferentes nas respectivas coordenadas, mas a distância entre dois pontos fica preservada.

Qual a vantagem prática de se utilizar as coordenadas na frente de luz? Como vimos, o uso das coordenadas da frente de luz no estudo da dinâmica relativística possibilita a introdução de algumas simplificações nas expressões matemáticas necessárias para o estudo da relatividade de Einstein.

Nos grandes aceleradores de partículas, como o CERN, prótons e antiprótons são acelerados a velocidades próximas à velocidade da luz e colocados em rotas de colisão para o estudo das interações entre as partículas elementares. Essas interações são descritas utilizando-se tanto a ferramenta da mecânica quântica como a relatividade de Einstein, de modo que o referencial mais adequado para analisar o fenômeno é justamente o referencial da frente de luz [14 -17].

Agradecimentos

Ao CNPq 315519/2018-5, CAPES e FAPESB – PIE 0013/2016 pelo apoio. Um importante agradecimento ao revisor anônimo por suas perguntas e sugestões ao texto. A Vera Lucia Fouchy que nos ajudou no texto.

Referências

• [1] P.A. Tipler e R.A. Llewellyn, Física moderna (LTC, São Paulo, 2014).
• [2] P.M.A. Dirac, Rev. Mod. Phys. 21, 392 (1949).
• [3] A.T. Suzuki, J.H. Sales e L.A. Soriano, Physical Review D 88, 025036 (2013).
• [4] J.H. Sales, A.T. Suzuki e L.A. Soriano, Revista Brasileira de Ensino de Física 37, 3309 (2015).
• [5] J.H. Sales e A.T. Suzuki, Communications in Theoretical Physics 60, 55 (2013).
• [6] J.H. Sales e A.T. Suzuki, Communications in Theoretical Physics 55, 1029 (2011).
• [7] H. Minkowski, Annalen der Physik 352, 927 (1907).
• [8] A. Einstein, The Meaning of Relativity(Princeton University Press, Princeton, 1923).
• [9] S. Weinberg, The Quantum Theory of Fields (Cambridge University Press, London, 2005).
• [10] J.D. Bjorken, Physical Review 179, 1547 (1969).
• [11] J.H.O. Sales, A.T. Suzuki e G.S. Santos, Few-Body Systems 56, 587 (2015).
• [12] J.H.O. Sales, T. Frederico, B.V. Carlson e P.U. Sauer, Physical Review C. Nuclear Physics 61, 044003 (2000).
• [13] J.H.O. Sales, T. Frederico, B.V. Carlson e P.U. Sauer, Physical Review C. Nuclear Physics 63, 064003 (2001).
• [14] J. Carbonell, B. Desplanques, V.A. Karmanov e J.F. Mathiot, Phys. Rep. 300, 215 (1998).
• [15] S.J. Brodsky, H.C. Pauli e S. Pinski, Phys. Rep. 301, 299 (1998).
• [16] J.P. Vary e F. Wölz, Light-Front Quantization and Non-Perturbative QCD (International Institute of Theoretical and Applied Physics, Ames, 1997).
• [17] R.J. Perry, A. Harindranath e K.G. Wilson, Phys. Rev. Lett. 65, 2959 (1990).
• [18] B.D. Keister e W.N. Polizou, Adv. Nucl. Phys. 20, 225 (1991).

Datas de Publicação

• Publicação nesta coleção
  15 Jun 2020
• Data do Fascículo
  2020

Histórico

• Recebido
  17 Out 2019
• Revisado
  20 Mar 2020
• Aceito
  25 Mar 2020