Densidade de carga elétrica num condutor retilíneo finito

Electrical charge density in finite rectilinear conductor

ARTIGOS GERAIS

Densidade de carga elétrica num condutor retilíneo finito

(Electrical charge density in finite rectilinear conductor)

Renê Robert

Departamento de Eletricidade da UFPR, CP 19047, Curitiba, Pr, 81531-990

RESUMO

Mostram-se dois métodos numéricos para o cálculo da distribuição de carga elétrica num condutor filiforme de comprimento finito e pequeno diâmetro. Os resultados numéricos são comparados com uma solução analitica aproximada mostrando boa concordância de resultados.

ABSTARCT

Two numerical methods for the calculation of electrical charge distribution on a finite linear wire of small diameter are shown. The obtained results are compared with an approximated analytical solution showing good results.

1 Introdução

Nos últimos anos tem-se discutido bastante o problema da distribuição de carga em um fio condutor retilíneo de comprimento finito, mantido a um potencial , sendo que nenhum aborda o problema fazendo uso de técnicas numéricas. Do ponto de vista histórico este problema é bastante antigo^[5], pois foi resolvido analiticamente, de forma aproximada, em 1878 por J. C. Maxwell, sendo provavelmente um de seus últimos trabalhos de pesquisa em eletricidade e magnetismo^[6].

A maioria dos problemas de cálculo de campos elétricos e magnéticos apresentam soluções analíticas somente quando a geometria é extremamente simples. Nos problemas práticos esta geometria simples não existe e as dificuldades para obter soluções analíticas são insuperáveis. No passado, do ponto de vista técnico, este problema foi contornado em parte com o uso de técnicas experimentais ou gráficas. Atualmente lança-se mão de técnicas numéricas, pois essas são em geral as únicas possíveis^[7]. Observa-se há algum tempo uma tendência em apresentar as técnicas numéricas para o cálculo de campos em livros de texto de eletromagnetismo o que é desejável para que os estudantes se tornem familiarizados com os diversos procedimentos.

Nosso objetivo é mostrar como obter a solução do problema da distribuição de cargas num fio retilíneo, finito e mantido a um potencial fixo utilizando duas técnicas numéricas simples: método de simulação de cargas e método dos momentos, e em seguida os resultados obtidos são comparados com aqueles calculados analiticamente. Estas técnicas podem ser usadas para resolver outros problemas simples, tais como a distribuição de carga em placas com formato retangular ou circular.

2 Método de simulação de carga

O princípio básico do método de simulação de carga (CSM) é muito simples^[8]. Considere um condutor mantido a um potencial f 0 dentro do vácuo. A região de interesse é externa ao condutor. Sejam n cargas pontuais Q_j , { j = 1,2,3,...,n } localizadas próximas à superfície do condutor, na região interna do mesmo e posicionadas pelo vetor _j . Este processo é em geral chamado de discretização do problema. O potencial elétrico num ponto P externo ao condutor posicionado pelo vetor _i , é dado pela equação

em que p_ij = . Quando coloca-se o ponto definido pelo vetor _i sobre m pontos no contorno do condutor, a equação (1) pode ser escrita como

A equação (2) forma um sistema de m equações lineares com n incógnitas. Para nosso problema basta fazer m = n e o método é então chamado de método de simulação de carga convencional. A equação (2), quando escrita sob forma matricial, toma a forma

Em geral, com este método pode-se chegar a erros da ordem de 0,001% para valores grandes de n. Contudo, em pontas, cantos e eletrodos muito finos esta precisão dificilmente é alcançada.

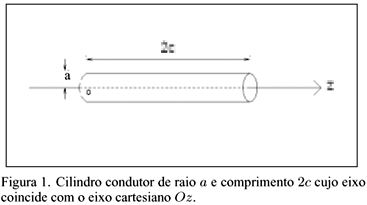
Considere um condutor retilíneo de comprimento 2c e raio a, sendo a < < c, mantido a um potencial constante f₀ , conforme mostra a figura 1. Dividamos o comprimento 2c sobre o eixo oz em n - 1 partes iguais e coloquemos cargas pontuais Q_j em cada um dos n pontos. Analogamente dividamos a superfície do fio em n - 1 partes iguais cujos pontos batiza-se pela letra i. O elemento de matriz p_ij pode ser escrito como em que D = é a distância entre duas cargas consecutivas.

Como exemplo numérico façamos: c = 0,5m, a = 0,001m, f₀ = 1V, 4pe₀ = 111,2626pF/m e n = 1000. Utilizando o software Mathematica^®, o cálculo numérico das cargas Q_j fica simples e rápido. A figura 2 mostra o resultado obtido, em que a densidade linear de carga vale _j = .

3 Método dos momentos

O método dos momentos (MM) é conceitualmente simples e muito usado em engenharia^[9]. Para a finalidade deste trabalho vamos usar um caminho mais simples e adequado ao nível de graduação^[10]. O potencial elétrico gerado por uma distribuição de cargas linear num ponto é dado pela equação:

em que (z¢) é a densidade de carga linear sobre o fio da figura 1, localizada pelo vetor ¢. Quando conhecemos o potencial f() e desconhecemos (z¢) a equação (5) constitui uma equação integral de Fredholm de 1^a. espécie. Para resolver numericamente esta equação integral, dividamos o fio em n - 1 partes de comprimento D = e chamemos de _j a densidade linear de carga de cada parte. A equação (5) pode ser escrita para pontos sobre a superfície do fio como:

Dividindo a superfície do fio em n partes tal que z = + (i - 1)D i = { 1,2,3...,n } a equação (6) pode ser escrita como:

em que d = .

Fazendo como antes, c = 0,5m, a = 0,001m, f₀ = 1V, D @ 0,001m, 4pe₀ = 111,2626pF/m, n = 1000 e usando o Mathematica^® para o cálculo da equação (7), isto é, do sistema de n equações lineares com n incógnitas obtém-se o resultado espelhado na figura 3.

4 Comparação entre os resultados numéricos e analítico

Em artigo recente, J.D. Jackson^[4,5] deduziu uma equação aproximada que permite calcular a densidade de carga em um fio retilíneo de comprimento 2c e secção transversal circular de raio a. Esta equação até a ordem de O () é dada por

em que L = 2ln (), x = e ₀ = . Quando o fio for mantido a um potencial f₀ = 1V, ₀ = 8,0533pC/m para o fio acima especificado.

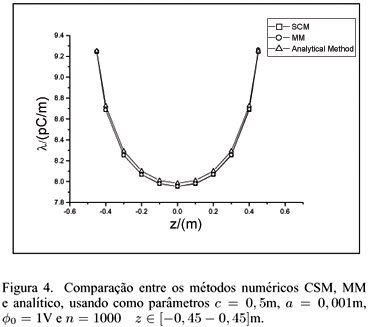
Na figura 4 mostram-se os resultados obtidos com os métodos CSM, MM e a expressão analítica fornecido pela equação (8). Os cálculos são executados no intervalo do comprimento do condutor [-0,45m,0,45m]. A maior diferença entre os resultados numéricos é de 0,2% e entre os resultados analítico e numéricos é de 0,4%. A figura 5 mostra que a diminuição do raio a do fio diminui o valor da densidade de carga e esta torna-se mais uniforme^[1,4] , sendo os resultados numéricos e analíticos compatíveis entre si. É importante frisar que os cálculos numéricos não fornecem bons resultados nos extremos do fio.

Uma informação adicional a se obter do calculo numérico é a capacitância do fio. Usando o método SCM obtém-se para a capacitância do fio acima especificado o valor. C = 8,499pF, quando n = 1000. A fórmula do artigo de J.D. Jackson^[4] fornece o valor, C = 8,457pF correspondendo portanto a uma diferença de 0,5%. O leitor interessado pode consultar outras referências^[11-14] para o cálculo da distribuição de cargas em um fio mantido a potencial constante.

5 Conclusão

Uma grande quantidade de problemas práticos em eletrostática e na aproximação quase-estática, não envolvem a determinação de potenciais de uma dada distribuição de cargas, mas requerem que seja encontrado a distribuição de cargas que corresponde a alguns conjuntos de potenciais dados. O primeiro problema não é de todo fácil, pois, mesmo nos casos em que a distribuição das cargas pode ser descrita com simplicidade razoável, a avaliação da integral para o cálculo do campo pode ser difícil. Por outro lado, o problema inverso é de solução muito mais difícil, e soluções analíticas de fato somente existem para um número limitado de casos. Muitos problemas reais só podem ser tratados com sucesso por técnicas numéricas.

Recebido em 15 de Outubro, 2003

Aceito em 28 de Novembro, 2003

• [1] D. J. GRIFFITHS and Y. LI, Charge Density on a Conducting Needle, Am. J. Phys. 64(6), June 1996. p. 706-714.
• [2] R. H. GOOD, Comment on ''Charge Density on a Conducting Needle'' , Am. J. Phys. 65(2), February 1997, p.155-156.
• [3] M. ANDREWS, Equilibrium Charge Density on Conducting Needle, Am. J. Phys. 65(9), September 1997, p.846-850.
• [4] J. D. JACKSON, Charge Density on Thin Straight Wire, Revisited, Am. J. Phys. 68(9), September 2000, p. 789-799.
• [5] J. D. JACKSON, Charge Density on a Thin Straight wire: The First Visit, Am. J. Phys. 70(4), April 2002, p.409-410.
• [6] J. C. MAXWELL, The Scientific Papers of James Clerk Maxwell, Edited by W. D. Nivens, 2 vols. Bound as one, Dover Pub. Inc., N.Y. p.672-680.
• [7] K. J. BINNS, P. J. LAWRENSON and C. W. TROBRIDGE, The Analytical and Numerical Solution of Electric and Magnetic Field, John Willey & Sons, Baffins Lane, 1992.
• [8] N. H. MALIK, A Review of the Charge Simulation Method and its Application, IEEE Transactions on Electric Insulation, vol.24 n.1 February 1989, p.3-20.
• [9] R. HARRINGTON, Matrix Methods for Field Problems, Proceedings of the IEEE, vol.55, n.2, February 1967, p.136-149.
• [10] L. L. TSAI and C.E SMITH, Moment Methods in Electromagnetics for Undergraduates, IEEE Transactions on Education, vol.21, n.1, February 1978, p.14-22.
• [11] P. SILVESTER, Modern Electromagnetic Field, Prentice-Hall Inc., Englewood Cliffs, N.J., 1968, p.90-93.
• [12] J. R REITZ, F. J. MILFORD and R.W. CHRISTY, Foundations of Electromagnetic Theory, Addison Wesley Publishing Co., Reading Massachusetts, 1993, p.84-89.
• [12] N. N. O. SADIKU, Electromagnetics, Oxford University Press, N.Y., 1995, p.721-733.
• [13] S. RATNAJEEVAN, H. HOOLE, P. RATNAMAHILAN and P. HOOLE, Engineering Electromagnetics, Oxford University Press, N.Y., 1996, p.176-179.

Datas de Publicação

• Publicação nesta coleção
  05 Maio 2004
• Data do Fascículo
  Dez 2003

Histórico

• Recebido
  15 Out 2003
• Aceito
  28 Nov 2003