Resúmenes
En este trabajo se estudian algunos sistemas mecánicos y electrostáticos intrínsecamente no lineales. Mostramos, a través de la expansión en serie de Taylor de la energía potencial, que en límite de pequeñas oscilaciones estos sistemas no realizan movimientos armónicos simples. Por tanto, incluso para pequeñas oscilaciones algunos sistemas oscilantes se comportan como osciladores no lineales.
Palabras clave:
Oscilador armónico simple; Oscilador no lineal; Energía potencial; Expansión en serie de Taylor
In this work some intrinsically non-linear mechanical and electrostatic systems are studied. We show, through the Taylor series expansion of the potential energy, that at the limit of small oscillations these systems do not perform simple harmonic movements. Therefore, even for small oscillations some oscillating systems behave like non-linear oscillators.
Keywords:
Simple harmonic oscillator; Non-linear oscillator; Potential energy; Taylor series expansion
1. Introducción
Muchos sistemas oscilatorios son en realidad no lineales, y el caso de oscilaciones lineales es una situación restringida y excepcional. Si la fuerza de restitución no tiene una dependencia lineal con el desplazamiento o si la fuerza de amortiguamiento es no lineal con la velocidad, el movimiento alrededor de un punto de equilibrio estable será no lineal. La ecuación general de movimiento para una partícula que realiza oscilaciones no lineales, en el caso unidimensional, en el marco de la teoría clásica, es una ecuación diferencial no lineal de la forma [11. J.B. Marion, Dinámica Clásica de las Partículas y Sistemas (Reverté, Barcelona, 1998).]
donde, m es la masa del sistema; x es la posición de la partícula; f(x) es la fuerza de restitución, proporcional a potencias de x mayores a uno; y es un término de amortiguamiento. El principio de superposición no se cumple para la ecuación (1), por tanto, si se conocen dos soluciones particulares, la suma de éstas no conduce a una solución general del problema. Las oscilaciones no lineales ocurren en muchos sistemas reales tanto a nivel macroscópico como microscópico, y así, están presentes en diversidad de campos científicos, no solo en física, mecánica y matemática, sino también en electrónica, química, biología y astronomía. Efectos no lineales son responsables de muchas propiedades físicas importantes, por ejemplo, la expansión térmica y la conductividad térmica en los sólidos [22. C. Kittel, Introducción a la Física del Estado Sólido (Reverté, Barcelona, 1997), 3 ed.]. Las comunicaciones por radio y televisión no existirían sin elementos no lineales. La forma en que el ser humano ve y oye también se basa en no linealidades en el ojo y el oído [33. T.L. Chow, Classical Mechanics (CRC Press, Boca Raton, 2013), 2 ed.].
Aunque las oscilaciones y efectos no lineales son de gran importancia, en los libros de texto de física básica [44. R.A. Serway y J.W. Jewett, Física para Ciencias e Ingeniería (Thomson Learning, 2005), v. 1, 7 ed., 55. D. Halliday, R. Resnick y J. Walker, Física (CECSA, Ciudad de México, 1993), v. 1, 4 ed.] y artículos académicos [66. E. Maor, The Physics Teacher 10 , 377 (1972).] se limita el análisis a las oscilaciones armónicas, tema al que se le da gran relevancia. Esto se hace por la sencillez del modelo y porque éste es el fundamento teórico para analizar situaciones más complicadas, como la propagación de ondas electromagnéticas [77. R.K. Wangsness, Campos Electromagnéticos (Limusa, Ciudad de México, 2001).], el modelo cuántico de oscilador armónico [88. L. De la Peña, Introducción a la Mecánica Cuántica (Universidad Nacional Autónoma de México, Ciudad de México, 2006), 3 ed.] y la cuantización del campo electromagnético [99. C.C. Gerry y P.L. Knight, Introductory Quantum Optics (Cambridge University Press, Cambridge, 2005).], entre otros aspectos.
Un análisis de oscilaciones no lineales se presenta en algunos textos de nivel intermedio/avanzado como Marion [11. J.B. Marion, Dinámica Clásica de las Partículas y Sistemas (Reverté, Barcelona, 1998).], Chow [33. T.L. Chow, Classical Mechanics (CRC Press, Boca Raton, 2013), 2 ed.], Baierlein [1010. R. Baierlein, Newtonian Dinamics (McGrawHill, New York, 1983).] y Cveticanin[1111. L. Cveticanin, Strongly Nonlinear Oscillators: Analytical Solutions (Springer, Berlin, 2014).], también se pueden mencionar los artículos académicos de Hanggi-Riseborough [1212. P. Hanggi y P. Riseborough, Am. J. Phys. 51 , 347 (1983).] y Thomsen [1313. J.S. Thomsen, Am. J. Phys. 56 , 123 (1988).].
Un artículo académico donde se aborda el tema de osciladores intrínsecamente no lineales de forma clara, y en el que basamos nuestro trabajo, es el artículo de Mohazzabi [1414. P. Mohazzabi, Am. J. Phys. 72 , 492 (2004).]. En dicho trabajo, se hace una descripción general del cálculo del periodo de oscilación de una partícula con energía potencial proporcional a |x|n (n≠2), y se consideran algunos sistemas mecánicos y electrostáticos para los que se presenta esta situación aún cuando x sea pequeño.
El proposito de este artículo es presentar otro conjunto de sistemas mecánicos y electrostáticos, distintos a los de Mohazzabi, que exhiben oscilaciones intrínsecamente no lineales.
El artículo está organizado de la siguiente manera: en la Sección 2 2. Teoría En el caso de oscilaciones armónicas, la energía potencial tiene la forma [4, 5] (2) V ( x ) = 1 2 k x 2 . La fuerza correspondiente será, por tanto, (3) F ( x ) = - k x , la cual corresponde a la fuerza de Hooke, que da origen al movimiento armónico simple. En los casos en que la función energía potencial no es armónica, se puede aproximar a la forma cuadrática de la ecuación (2) si la energía de la partícula es ligeramente mayor que la energía potencial mínima [1]. Esta aproximación es válida cuando las amplitudes son pequeñas (aproximación de pequeñas oscilaciones). Si la energía es apreciablemente mayor que la energía potencial mínima, la amplitud no puede ser considerada pequeña y no se puede usar la aproximación armónica; por consiguiente las expresiones para la energía potencial y para la fuerza, dadas en las ecuaciones (2) y (3), no serán apropiadas. La derivada de la fuerza lineal es simétrica respecto a la posición de equilibrio (x=0), en tal caso la magnitud de la fuerza ejercida sobre la partícula es la misma en −x y x, pero la dirección es opuesta en los dos casos. Debido a esto en una situación simétrica, la primera corrección a una fuerza lineal (3) debe ser un término proporcional a x3 [1] (4) F ( x ) ≅ - k x + ε x 3 , donde ε es una cantidad pequeña comparada con k. La energía potencial correspondiente a dicha fuerza es, (5) V ( x ) = 1 2 k x 2 - 1 4 ε x 4 . De esta forma, en términos generales, si la energía potencial se puede expandir en serie de Taylor alrededor de la posición de equilibrio y el coeficiente de segundo orden se anula, tendremos un oscilador intrínsecamente no lineal [14]. Así, para un oscilador intrínsecamente no lineal, se puede proponer una función energía potencial simétrica de la forma (6) V ( x ) = b | x | n , con n ≠ 2 , donde b y n son constantes reales positivas. Para los casos particulares n=4 y 6, la ecuación (1), con γ = 0 se puede escribir como (7) m d 2 x d t 2 + 4 b x 3 = 0 , n = 4 , (8) m d 2 x d t 2 + 6 b x 5 = 0 , n = 6 . Las ecuaciones (7) y (8) tienen soluciones exactas que se pueden escribir en términos de funciones elípticas de Jacobi sn y cn , respectivamente [15, 16]. Para la energía potencial (6), el periodo de oscilación de una partícula de masa m estará dado por (9) T = 2 2 π Γ ( 1 n + 1 ) Γ ( 1 n + 1 2 ) A 1 - n 2 m b , donde A es la amplitud de las oscilaciones y Γ(z) es la función Gamma. Una deducción de la ecuación (9) se muestra en el Apéndice. La ecuación (9) indica que, para n≠2, el periodo de un oscilador intrínsecamente no lineal siempre dependerá de la amplitud, como se muestra en la Figura 1. Se nota que si n < 2 el periodo se incrementa al aumentar la amplitud, pero en el caso n > 2 el aumento de amplitud genera una disminución del periodo y si n=2 (oscilador lineal), el periodo es constante. Figura 1 Periodo como una función de la amplitud para distintos valores de n. Se considera m/b = 4. , presentamos la descripción teórica general de los osciladores intrínsecamente no lineales. En la Sección 3 3. Ejemplos de Osciladores Intrínsecamente No Lineales 3.1. Partícula deslizándose sobre dos planosinclinados Comencemos con un ejemplo relativamente sencillo, planteado en el texto de Alonso-Finn [17]. Se asume que una partícula de masa m de desliza, sin fricción, de arriba hacia abajo de los planos inclinados mostrados en la Figura 2. En este caso la energía potencial de la partícula es Figura 2 Partícula deslizándose sin fricción sobre dos planos inclinados. (10) V = m g y , donde y puede ser escrito como y = β|x| (β es una constante real positiva). Así, (11) V = m g β | x | . La expresión (11) tiene la estructura de la ecuación (6) con b = mgβ y n=1. Por tanto, este sistema es un oscilador intrínsecamente no lineal, con periodo dado por la ecuación (9) (12) T = 2 2 π Γ ( 2 ) Γ ( 3 2 ) A g β = 4 2 A g β . 3.2. Masa unida a un resorte Consideremos un sistema estudiado en el artículo de Mohazzabi [14]. Se asume que una partícula de masa m atada a un resorte se desliza sin fricción por una barra recta, como se muestra en la Figura 3. Si la masa m se encuentra en la posición x, su energía potencial es Figura 3 Masa unida a un resorte deslizando por una barra recta sin fricción. (13) V ( x ) = k ( l - l 0 ) 2 , donde l=l02+x2, entonces, (14) V ( x ) = k l 0 2 [ 1 + ( x l 0 ) 2 - 1 ] 2 . Asumiendo que el sistema realiza pequeñas oscilaciones, o sea, x≪l0, (15) V ( x ) = ( k 4 l 0 2 ) x 4 . La expresión (15) tiene la misma estructura de la ecuación (6) con b=(k4l02) y n=4. Por tanto, usando (9), el periodo estará dado por (16) T = 4 2 π Γ ( 5 4 ) Γ ( 3 4 ) l 0 A m k = 13.1451 l 0 A m k . 3.3. Masa unida a dos resortes Consideremos una partícula de masa m conectada a dos resortes de igual constante elástica k pero diferentes longitudes sin estirar, d1 y d2, como se muestra en la Figura 4. Se asume que el sistema oscila sobre una superficie horizontal sin fricción. Figura 4 Masa unida a dos resortes oscilando sobre una superficie sin fricción. La energía potencial está dada por (17) V ( x ) = 1 2 k ( l 1 - d 1 ) 2 + 1 2 k ( l 2 - d 2 ) 2 , donde l1=d12+x2 y l2=d22+x2. Por tanto, (18) V ( x ) = 1 2 k d 1 2 [ 1 + ( x d 1 ) 2 - 1 ] 2 + 1 2 k d 2 2 [ 1 + ( x d 2 ) 2 - 1 ] 2 . Asumiendo que el sistema realiza pequeñas oscilaciones, o sea, x≪d1 y x≪d2 se tiene (19) V ( x ) = 1 8 k ( d 1 2 + d 2 2 d 1 2 d 2 2 ) x 4 . La expresión (19) tiene la misma estructura de la ecuación (6) con b=18k(d12+d22d12d22) y n=4. Por tanto, usando (9), el periodo estará dado por (20) T = 8 π d 1 d 2 d 1 2 + d 2 2 Γ ( 5 4 ) Γ ( 3 4 ) 1 A m k , = 10.4883 d 1 d 2 d 1 2 + d 2 2 A m k . 3.4. Disco uniformemente cargadocon un agujero Se asume un disco uniformemente cargado de radio a y densidad de carga superficial + σ, como se muestra en la Figura 5. El disco tiene un pequeño agujero en su centro y una carga puntual −q, ubicada en el eje x, se mueve bajo la acción atractiva del campo eléctrico creado por el disco, pasando a través del agujero. Figura 5 Disco uniformemente cargado con un agujero en su centro. Para un disco uniformemente cargado, el potencial electrostático está dado por [18, 19] (21) ϕ ( x ) = σ 2 ε 0 [ x 2 + a 2 - | x | ] , y la energía potencial de la carga −q será (22) V ( x ) = - q σ 2 ε 0 [ x 2 + a 2 - | x | ] . Si x≪a podemos hacer la aproximación x2 + a2≈a2, tal que (23) V ( x ) = - q σ 2 ε 0 ( a - | x | ) . Además, cambiando apropiadamente la escala de la energía obtenemos (24) V ( x ) = q σ 2 ε 0 | x | . Comparando la expresión (24) con la ecuación (6), b=qσ2ε0 y n=1, entonces, según (9), el periodo estará dado por (25) T = 4 π Γ ( 2 ) Γ ( 3 2 ) m A ε 0 q σ = 8 m A ε 0 q σ . 3.5. Sistema masa-resorte deslizándoseen una pista circular Se considera una partícula de masa m atada a un resorte y deslizándose sobre una pista circular sin fricción, en el plano xy, como se indica en la Figura 6. Figura 6 Masa conectada a un resorte y deslizando por una pista circular. En este problema la energía potencial está dada por (26) V = V e + V g , donde Ve es la energía potencial elástica y Vg es la energía potencial gravitacional. Para este problema (27) V g = m g y , donde y está dada por la ecuación de la circunferencia (28) ( y + l 0 + r ) 2 + x 2 = r 2 , de manera que (29) y = r 2 - x 2 - ( l 0 + r ) , y por tanto, (30) V g ( x ) = m g [ r 2 - x 2 - ( l 0 + r ) ] , = m g r [ 1 - ( x r ) 2 - 1 ] - m g l 0 . La energía potencial elástica es de la forma (31) V e = 1 2 k ( l - l 0 ) 2 , donde, según la Figura 6, (32) l 2 = ( l 0 + d ) 2 + x 2 . En esta expresión podemos escribir d en términos de x usando (29) (33) d = r - y = 2 r + l 0 - r 2 - x 2 . Reemplazando (33) en (32), obtenemos (34) l 2 = ( l 0 + 2 r + l 0 - r 2 - x 2 ) 2 + x 2 , = c - 4 ( r + l 0 ) r 2 - x 2 , donde c=4l02+8l0r+5r2. Por lo tanto, (35) l = c - 4 ( r + l 0 ) r 2 - x 2 . Con lo cual, la ecuación (31) se puede escribir como (36) V e ( x ) = 1 2 k [ c - 4 ( r - l 0 ) r 1 - ( x r ) 2 - l 0 ] 2 . Reemplazando (30) y (36) en (26) obtenemos (37) V ( x ) = 1 2 k [ c - 4 ( r - l 0 ) r 1 - ( x r ) 2 - l 0 ] 2 + m g r [ 1 - ( x r ) 2 - 1 ] - m g l 0 . Si se asume la condición de pequeñas oscilaciones (x≪r), (38) 1 - ( x r ) 2 = 1 - 1 2 ( x r ) 2 , (39) c - 4 ( r - l 0 ) r 1 - ( x r ) 2 = 4 ( r + l 0 ) r c 4 ( r + l 0 ) r - 1 + 1 2 ( x r ) 2 . Para simplificar la expresión se considera que l0 = r, entonces, (40) c 4 ( r + l 0 ) r = 17 8 , y (41) c - 4 ( r - l 0 ) r 1 - ( x r ) 2 = 2 2 r [ 9 8 + 1 4 ( x r ) 2 ] . Haciendo los reemplazos correspondientes, la energía potencial total (37) queda escrita así, (42) V ( x ) = 1 2 k [ 2 2 r [ 9 8 + 1 4 ( x r ) 2 ] - r ] 2 + m g r [ 1 - 1 2 ( x r ) 2 - 1 ] - m g r , = 9 2 k r 2 ( 9 8 - 1 2 ) - m g r + [ ( 9 4 - 1 2 ) k - m g 2 r ] x 2 + k 4 r 2 x 4 . Reescalando la energía se tiene (43) V ( x ) = [ ( 9 4 - 1 2 ) k - m g 2 r ] x 2 + k 4 r 2 x 4 . Lo cual corresponde a una energía potencial no armónica. Adicionalmente, si los parámetros del problema se restringen a (44) ( 9 4 - 1 2 ) k - m g 2 r = 0 , tal que, (45) k = 1 ( 9 4 - 1 2 ) m g 2 r ≈ 0.324 m g r , la energía potencial total tendrá la siguiente forma (46) V ( x ) = k 4 r 2 x 4 Por último, comparando la expresión (46) con la ecuación (6), b=k4r2 y n=4. Entonces, según (9), el periodo estará dado por (47) T = 4 2 π r Γ ( 5 4 ) Γ ( 3 4 ) 1 A m k = 7.4164 r A m k . , se presentan cinco sistemas oscilantes que exhiben oscilaciones no lineales. Una posible relación entre la descripción clásica, hecha en este trabajo, y la descripción cuántica se realiza en la Sección 4 4. Conexión con Osciladores Cuánticos Se puede notar que, según la aproximación WKB, para una partícula de masa m y energía potencial V(x), la regla de cuantización de Bohr-Sommerfeld se puede escribir como [20] (48) ∫ x 1 x 2 2 m [ E - V ( x ) ] d x = ( η + 1 2 ) ℏ π , donde E es la energía total, ℏ es la constante de Planck racionalizada (ℏ = h/2π), x1 y x2 son los puntos de retorno, en los que E = V(x), y η = 0,1,2,3,…. En el caso de que la energía potencial sea de la forma (6) se obtiene [21, 22] (49) E = [ ( η + 1 2 ) h b 1 / n 4 ( 2 m ) 1 / 2 Γ ( 1 n + 3 2 ) Γ ( 3 2 ) Γ ( 1 n + 1 ) ] 2 n n + 2 . Como h = 2πℏ, Γ(32)=π/2 y además, Γ(1n+32)=Γ(1n+12+1)=(1n+12)Γ(1n+12) [23], podemos escribrir (49) en la forma (50) E = [ ( η + 1 2 ) ℏ π 2 m ( 1 n + 1 2 ) b 1 / n Γ ( 1 n + 1 2 ) Γ ( 1 n + 1 ) ] 2 n n + 2 . La ecuación (50) se puede seguir reescribiendo de manera apropiada como (51) E n + 2 2 n = ( η + 1 2 ) ℏ π 2 m ( 1 n + 1 2 ) 4 π m 2 ( E 1 - n 2 ) 1 n 4 π m 2 ( E 1 - n 2 b ) 1 n Γ ( 1 n + 1 ) Γ ( 1 n + 1 2 ) , = ( η + 1 2 ) 2 π ℏ ( 1 n + 1 2 ) E 1 n - 1 2 1 T , E n + 2 2 n T E 1 n - 1 2 = ( η + 1 2 ) h ( 1 n + 1 2 ) , E T = ( n + 2 2 n ) ( η + 1 2 ) h . donde hemos utilizado la expresión del periodo como función de la energía, ver ecuación (A11) del Apéndice. Para el caso lineal (oscilador armónico simple) n = 2 y T = 2π/ω, donde ω es la frecuencia angular de oscilación, las ecuaciones (50) y (51) se reducen a la expresión cuántica de la energía E=(η+12)ℏω. a través de la aproximación WKB. En la Sección 5 5. Conclusiones Hemos ilustrado, a través de ejemplos sencillos, que aún en el límite de pequeñas oscilaciones algunos sistemas mecánicos y electrostáticos ejecutan movimientos oscilatorios no lineales. En todos los casos estudiados, una característica de los osciladores intrínsecamente no lineales es que el periodo de oscilación depende de la amplitud. Esto muestra que la aproximación armónica no siempre es apropiada para describir sistemas oscilantes de amplitud pequeña. presentamos las conclusiones y en el Apéndice se muestra una deducción de la expresión del periodo de los osciladores no lineales.
2. Teoría
En el caso de oscilaciones armónicas, la energía potencial tiene la forma [44. R.A. Serway y J.W. Jewett, Física para Ciencias e Ingeniería (Thomson Learning, 2005), v. 1, 7 ed., 55. D. Halliday, R. Resnick y J. Walker, Física (CECSA, Ciudad de México, 1993), v. 1, 4 ed.]
La fuerza correspondiente será, por tanto,
la cual corresponde a la fuerza de Hooke, que da origen al movimiento armónico simple.
En los casos en que la función energía potencial no es armónica, se puede aproximar a la forma cuadrática de la ecuación (2) si la energía de la partícula es ligeramente mayor que la energía potencial mínima [11. J.B. Marion, Dinámica Clásica de las Partículas y Sistemas (Reverté, Barcelona, 1998).]. Esta aproximación es válida cuando las amplitudes son pequeñas (aproximación de pequeñas oscilaciones).
Si la energía es apreciablemente mayor que la energía potencial mínima, la amplitud no puede ser considerada pequeña y no se puede usar la aproximación armónica; por consiguiente las expresiones para la energía potencial y para la fuerza, dadas en las ecuaciones (2) y (3), no serán apropiadas.
La derivada de la fuerza lineal es simétrica respecto a la posición de equilibrio (x=0), en tal caso la magnitud de la fuerza ejercida sobre la partícula es la misma en −x y x, pero la dirección es opuesta en los dos casos. Debido a esto en una situación simétrica, la primera corrección a una fuerza lineal (3) debe ser un término proporcional a x3 [11. J.B. Marion, Dinámica Clásica de las Partículas y Sistemas (Reverté, Barcelona, 1998).]
donde ε es una cantidad pequeña comparada con k. La energía potencial correspondiente a dicha fuerza es,
De esta forma, en términos generales, si la energía potencial se puede expandir en serie de Taylor alrededor de la posición de equilibrio y el coeficiente de segundo orden se anula, tendremos un oscilador intrínsecamente no lineal [1414. P. Mohazzabi, Am. J. Phys. 72 , 492 (2004).]. Así, para un oscilador intrínsecamente no lineal, se puede proponer una función energía potencial simétrica de la forma
donde b y n son constantes reales positivas.
Para los casos particulares n=4 y 6, la ecuación (1), con γ = 0 se puede escribir como
Las ecuaciones (7) y (8) tienen soluciones exactas que se pueden escribir en términos de funciones elípticas de Jacobi sn y cn , respectivamente [1515. Wolfram Language & System Documentation Center, disponible en: https://reference.wolfram.com/language/ref/JacobiSN.html.
https://reference.wolfram.com/language/r...
, 1616. Wolfram Language & System Documentation Center, disponible en: https://reference.wolfram.com/language/ref/JacobiCN.html
https://reference.wolfram.com/language/r...
].
Para la energía potencial (6), el periodo de oscilación de una partícula de masa m estará dado por
donde A es la amplitud de las oscilaciones y Γ(z) es la función Gamma. Una deducción de la ecuación (9) se muestra en el Apéndice.
La ecuación (9) indica que, para n≠2, el periodo de un oscilador intrínsecamente no lineal siempre dependerá de la amplitud, como se muestra en la Figura 1. Se nota que si n < 2 el periodo se incrementa al aumentar la amplitud, pero en el caso n > 2 el aumento de amplitud genera una disminución del periodo y si n=2 (oscilador lineal), el periodo es constante.
3. Ejemplos de Osciladores Intrínsecamente No Lineales
3.1. Partícula deslizándose sobre dos planosinclinados
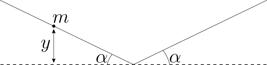
Comencemos con un ejemplo relativamente sencillo, planteado en el texto de Alonso-Finn [1717. M. Alonso y E.J. Finn, Física. Mecánica (Fondo Educativo Interamericano, Bogotá, 1970), v. 1.]. Se asume que una partícula de masa m de desliza, sin fricción, de arriba hacia abajo de los planos inclinados mostrados en la Figura 2. En este caso la energía potencial de la partícula es
donde y puede ser escrito como y = β|x| (β es una constante real positiva). Así,
La expresión (11) tiene la estructura de la ecuación (6) con b = mgβ y n=1. Por tanto, este sistema es un oscilador intrínsecamente no lineal, con periodo dado por la ecuación (9)
3.2. Masa unida a un resorte
Consideremos un sistema estudiado en el artículo de Mohazzabi [1414. P. Mohazzabi, Am. J. Phys. 72 , 492 (2004).]. Se asume que una partícula de masa m atada a un resorte se desliza sin fricción por una barra recta, como se muestra en la Figura 3. Si la masa m se encuentra en la posición x, su energía potencial es
donde , entonces,
Asumiendo que el sistema realiza pequeñas oscilaciones, o sea, x≪l0,
La expresión (15) tiene la misma estructura de la ecuación (6) con y n=4. Por tanto, usando (9), el periodo estará dado por
3.3. Masa unida a dos resortes
Consideremos una partícula de masa m conectada a dos resortes de igual constante elástica k pero diferentes longitudes sin estirar, d1 y d2, como se muestra en la Figura 4. Se asume que el sistema oscila sobre una superficie horizontal sin fricción.
La energía potencial está dada por
donde y . Por tanto,
Asumiendo que el sistema realiza pequeñas oscilaciones, o sea, x≪d1 y x≪d2 se tiene
La expresión (19) tiene la misma estructura de la ecuación (6) con y n=4. Por tanto, usando (9), el periodo estará dado por
3.4. Disco uniformemente cargadocon un agujero
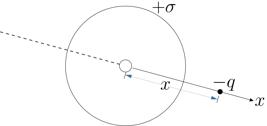
Se asume un disco uniformemente cargado de radio a y densidad de carga superficial + σ, como se muestra en la Figura 5. El disco tiene un pequeño agujero en su centro y una carga puntual −q, ubicada en el eje x, se mueve bajo la acción atractiva del campo eléctrico creado por el disco, pasando a través del agujero.
Para un disco uniformemente cargado, el potencial electrostático está dado por [1818. R.A. Serway y J.W. Jewett, Física para Ciencias e Ingeniería (Thomson Learning, 2005), v. 2, 7 ed., 1919. W.E. Gettys, F.J. Keller y M.J. Skove, Física Clásica y Moderna (McGraw-Hill, Madrid, 1991).]
y la energía potencial de la carga −q será
Si x≪a podemos hacer la aproximación x2 + a2≈a2, tal que
Además, cambiando apropiadamente la escala de la energía obtenemos
Comparando la expresión (24) con la ecuación (6), y n=1, entonces, según (9), el periodo estará dado por
3.5. Sistema masa-resorte deslizándoseen una pista circular
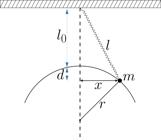
Se considera una partícula de masa m atada a un resorte y deslizándose sobre una pista circular sin fricción, en el plano xy, como se indica en la Figura 6.
En este problema la energía potencial está dada por
donde Ve es la energía potencial elástica y Vg es la energía potencial gravitacional. Para este problema
donde y está dada por la ecuación de la circunferencia
de manera que
y por tanto,
La energía potencial elástica es de la forma
donde, según la Figura 6,
En esta expresión podemos escribir d en términos de x usando (29)
Reemplazando (33) en (32), obtenemos
donde . Por lo tanto,
Con lo cual, la ecuación (31) se puede escribir como
Reemplazando (30) y (36) en (26) obtenemos
Si se asume la condición de pequeñas oscilaciones (x≪r),
Para simplificar la expresión se considera que l0 = r, entonces,
y
Haciendo los reemplazos correspondientes, la energía potencial total (37) queda escrita así,
Reescalando la energía se tiene
Lo cual corresponde a una energía potencial no armónica. Adicionalmente, si los parámetros del problema se restringen a
tal que,
la energía potencial total tendrá la siguiente forma
Por último, comparando la expresión (46) con la ecuación (6), y n=4. Entonces, según (9), el periodo estará dado por
4. Conexión con Osciladores Cuánticos
Se puede notar que, según la aproximación WKB, para una partícula de masa m y energía potencial V(x), la regla de cuantización de Bohr-Sommerfeld se puede escribir como [2020. Y. Peleg, R. Pnini, E. Zaarur y E. Hecht, Schaum’s Outline of Quantum Mechanics (McGraw-Hill, New York, 2010), 2 ed.]
donde E es la energía total, ℏ es la constante de Planck racionalizada (ℏ = h/2π), x1 y x2 son los puntos de retorno, en los que E = V(x), y η = 0,1,2,3,….
En el caso de que la energía potencial sea de la forma (6) se obtiene [2121. U.P. Sukhatme, Am. J. Phys. 41 , 1015 (1973)., 2222. D.J.W. Geldart y D. Kiang, Am. J. Phys. 54 , 131 (1986).]
Como h = 2πℏ, y además, [2323. M. Abramowitz y I.A. Stegun (eds), Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables (Dover, New York, 1965).], podemos escribrir (49) en la forma
La ecuación (50) se puede seguir reescribiendo de manera apropiada como
donde hemos utilizado la expresión del periodo como función de la energía, ver ecuación (A11) del Apéndice.
Para el caso lineal (oscilador armónico simple) n = 2 y T = 2π/ω, donde ω es la frecuencia angular de oscilación, las ecuaciones (50) y (51) se reducen a la expresión cuántica de la energía .
5. Conclusiones
Hemos ilustrado, a través de ejemplos sencillos, que aún en el límite de pequeñas oscilaciones algunos sistemas mecánicos y electrostáticos ejecutan movimientos oscilatorios no lineales. En todos los casos estudiados, una característica de los osciladores intrínsecamente no lineales es que el periodo de oscilación depende de la amplitud. Esto muestra que la aproximación armónica no siempre es apropiada para describir sistemas oscilantes de amplitud pequeña.
Agradecimientos
Los autores agradecen a la Universidad Surcolombiana por el apoyo durante la realización de este trabajo.
Apéndice Deducción de la ecuación (9)
Se considera una partícula de masa m oscilando bajo la influencia de una función energía potencial
donde b y n son constantes positivas (n no necesariamente es entero).
La energía mecánica de la partícula estará dada por
A partir de la cual podemos encontrar
Por lo tanto,
Para determinar el periodo de oscilación, T, se tiene en cuenta que, debido a la simetría de V(x), en una oscilación la partícula recorre la distancia 4A, donde A es la amplitud del movimiento. Por tanto,
donde se ha tenido en cuenta que, en el intervalo 0≤x≤A, los valores de x son positivos y podemos hacer |x| = x.
Para resolver la integral que aparece en (A5) se hace el cambio de variables
con lo cual
además, de (A6)
tal que
De esta forma los nuevos límites de integración son
En la ecuación (A9b) se usó la relación entre la energía total y la amplitud
Ahora se reemplaza (A6), (A7), (A9a) y (A9b) en (A5)
donde se ha tenido en cuenta la identidad
Referencias
-
1.J.B. Marion, Dinámica Clásica de las Partículas y Sistemas (Reverté, Barcelona, 1998).
-
2.C. Kittel, Introducción a la Física del Estado Sólido (Reverté, Barcelona, 1997), 3 ed.
-
3.T.L. Chow, Classical Mechanics (CRC Press, Boca Raton, 2013), 2 ed.
-
4.R.A. Serway y J.W. Jewett, Física para Ciencias e Ingeniería (Thomson Learning, 2005), v. 1, 7 ed.
-
5.D. Halliday, R. Resnick y J. Walker, Física (CECSA, Ciudad de México, 1993), v. 1, 4 ed.
-
6.E. Maor, The Physics Teacher 10 , 377 (1972).
-
7.R.K. Wangsness, Campos Electromagnéticos (Limusa, Ciudad de México, 2001).
-
8.L. De la Peña, Introducción a la Mecánica Cuántica (Universidad Nacional Autónoma de México, Ciudad de México, 2006), 3 ed.
-
9.C.C. Gerry y P.L. Knight, Introductory Quantum Optics (Cambridge University Press, Cambridge, 2005).
-
10.R. Baierlein, Newtonian Dinamics (McGrawHill, New York, 1983).
-
11.L. Cveticanin, Strongly Nonlinear Oscillators: Analytical Solutions (Springer, Berlin, 2014).
-
12.P. Hanggi y P. Riseborough, Am. J. Phys. 51 , 347 (1983).
-
13.J.S. Thomsen, Am. J. Phys. 56 , 123 (1988).
-
14.P. Mohazzabi, Am. J. Phys. 72 , 492 (2004).
-
15.Wolfram Language & System Documentation Center, disponible en: https://reference.wolfram.com/language/ref/JacobiSN.html
» https://reference.wolfram.com/language/ref/JacobiSN.html -
16.Wolfram Language & System Documentation Center, disponible en: https://reference.wolfram.com/language/ref/JacobiCN.html
» https://reference.wolfram.com/language/ref/JacobiCN.html -
17.M. Alonso y E.J. Finn, Física. Mecánica (Fondo Educativo Interamericano, Bogotá, 1970), v. 1.
-
18.R.A. Serway y J.W. Jewett, Física para Ciencias e Ingeniería (Thomson Learning, 2005), v. 2, 7 ed.
-
19.W.E. Gettys, F.J. Keller y M.J. Skove, Física Clásica y Moderna (McGraw-Hill, Madrid, 1991).
-
20.Y. Peleg, R. Pnini, E. Zaarur y E. Hecht, Schaum’s Outline of Quantum Mechanics (McGraw-Hill, New York, 2010), 2 ed.
-
21.U.P. Sukhatme, Am. J. Phys. 41 , 1015 (1973).
-
22.D.J.W. Geldart y D. Kiang, Am. J. Phys. 54 , 131 (1986).
-
23.M. Abramowitz y I.A. Stegun (eds), Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables (Dover, New York, 1965).
Fechas de Publicación
-
Publicación en esta colección
04 Jun 2021 -
Fecha del número
2021
Histórico
-
Recibido
22 Mar 2021 -
Revisado
02 Mayo 2021 -
Acepto
06 Mayo 2021