Physical and mathematical modeling of inclusion behavior in a tundish with gas curtain

Abstract

Gas injection in the tundish has been considered as an alternative to optimizing inclusion removal from steels. In the present study, physical and mathematical modeling were used to investigate the effect of gas injection in the tundish on the inclusion removal efficiency. The physical model is a 1/3 reduced scale of an industrial two-strand tundish of 40 tons. The inclusion removal efficiency was quantified using the APS III probe, which counts particles leaving the tundish during the test. Different locations for the gas injection plug were evaluated. Additionally, a mathematical model was developed using commercial CFD software CFX. The predictions of the mathematical model were validated by the physical model results, comparing the efficiency of inclusion removal. The proposed model includes a new boundary condition to describe the behavior of the particles at the free surface, implemented by a special subroutine. The model enabled the identification of appropriate conditions: plugs located at 0.56 or 0.84m from the tundish inlet with gas injection with the flow rate of 3NL/min.

Keywords:
tundish; inclusions; gas injection; physical modeling; mathematical modeling

1. Introduction

The increasing demand for high-quality steels requires continuous improvement and strict control of the process by the steel companies. The last metallurgical vessel through which molten steel flows before solidification in the continuous casting mold is the tundish. Therefore, the appropriate project and operation of a tundish are essential to obtain cleaner steels. To enhance inclusion removal, flow modifiers such as dams and weirs have been introduced into the tundish. These devices are designed to direct the steel flow toward the top surface and to increase the effective residence time of steel in the tundish. Both effects intensify inclusion flotation (Sahai, 2016; Chen et al., 2014; Chattopadhyay et al., 2010). In addition to the flow modifiers, the injection of inert gas has been considered (Chang et al., 2016; Zhang et al., 2006).

Several studies suggest that inert gas bubbling at the bottom of the tundish enhances inclusion removal. Gas curtains could play a role similar to the flow modifiers. Some authors also stated the possibility of inclusion removal by attachment of the inclusions to the bubbles. However, the probability of this event is very small, even for microbubbles (Rogler, 2004; Arcos-Gutierrez et al., 2012).

The majority of the studies on inclusion removal by gas injection have been carried out through physical and mathematical modeling. Usually, the predictions are based on flow characteristics in the tundish, such as Residence Times Distribution (RTD) curves (Cwudzinski, 2018; Neves and Tavares, 2017). There are few studies dedicated to simulating the inclusion removal in physical models. Some authors investigated the behavior of inclusions using mathematical models. Cwudzinski (2010), using the Euler-Lagrange mathematical model considering integral capture of the inclusion at the free surface, obtained removal rates from 88% for inclusions of 10 µm. Using the same approach, Ramos-Bandeiras et al. (2003) showed that, at least, 70% of the inclusions were eliminated from the molten steel. Both results demonstrated that removal efficiency is almost independent of inclusion sizes. Industrial tests of gas injection in the tundish (Kumar et al., 2009; Meijie et al., 2011) have shown that the number of inclusions found in the solid metal was significant. Kumar et al. (2009) observed a reduction of 33 to 70% in inclusions of size greater than 50 µm and a reduction of 13 to 36% in inclusions of 25 to 50 µm. Therefore, the classical Euler-Lagrange model seems to have limitations in predictions of inclusion removal rates.

Ruckert et al. (2009) and Warzecha et al. (2013) achieved satisfactory results in an attempt to overcome the prediction of overestimated inclusion flotation rates. The authors proposed a special boundary condition for the free surface in the mathematical model, which limits the capture of the inclusions based on their velocity. However, the studies did not include gas injection in the tundish.

The present study aimed at evaluating the efficiency of removal of inclusions in a tundish equipped with a gas injection system and flow modifiers using mathematical and physical modeling. The inclusions were simulated by hollow borosilicate microspheres. The on-line counting of the inclusions at the exit of the tundish was carried out using the Aqueous Particle Sensor 3 probe (APS III). Furthermore, a special boundary condition to describe the behavior of the particles at the free surface was proposed in the mathematical model.

2. Methodology

The present study investigated fluid flow and efficiency of inclusion removal for different tundish configurations. The physical and mathematical models are described below.

2.1 Physical model

The physical model is a 1/3 reduced scale of a real two-strand tundish. A schematic view of the physical apparatus is illustrated in Figure 1. The characteristics of the tundish are presented in Table 1. For the configurations with gas injection, two porous plugs were installed at the tundish bottom, equidistant from the center. Produced with the same material used in industrial plants, the plugs have dimensions of 0.150x0.02m and thickness of 0.02m, covering the full width of the bottom of the tundish. The plugs were located at 0.28, 0.56 and 0.84m from the tundish inlet. The water and gas flow rates were estimated based on the Froude and modified Froude numbers according to geometric and dynamic similarity criteria Mazumdar et al. (1999). The water flow rate is 50 L/min and the gas flow rate is 3NL/min in each porous plug, corresponding to flow rates of 779L/min and 46.76NL/min in the industrial tundish, respectively (Mendonça, 2016). The configuration without gas injection was also studied.

Figure 1
Schematic view of the physical model of the tundish.

Table 1
Characteristics of the physical model of the tundish.

	Parameters	Value
Tundish	Width: upper/lower (m)	0.33/0.155
	Steel level (m)	0.276
	Length: upper/lower (m)	2.76/2.66
Ladle shroud	Diameters: internal/	0.026
	external (m)	0.037
	Distance from the bottom (m)	0.18
Weirs	Distance from the bottom (m)	0.07
	Distance from the centre (m)	0.48
	Thickness (m)	0.01
Dams	Height (m)	0.12
	Distance from the centre (m)	0.75
	Thickness (m)	0.01
Tundish outlet	Diameter (m)	0.065
	Distance from the centre (m)	1.128

The inclusion removal efficiency was quantified using the APS III (Aqueous Particle Sensor 3), which counts particles online during the test. Its operation is based on the existence of a difference in electrical conductivity between the particle and the working fluid. The fluid with a suspension of particles simulating inclusion passes through a narrow orifice. Two electrodes apply a constant electric current to the orifice. When a particle passes through the orifice, the voltage leap is recorded and its magnitude indicates the particle size (Chakraborty, 2010).

Each test with the APS III was performed in triplicate. In addition to the different tundish configurations, bench tests were carried out for reference of particles size distribution in the tundish inlet flow.

Hollow borosilicate microspheres were used to simulate inclusions. They were introduced into the ladle shroud with a flow rate of 68 ml/min (1.13x10^-6 m³/s) by a peristaltic pump. The particle storage had a concentration of 1 kg/m³. Each test lasted approximately 6 theoretical residence times. The efficiency of particle removal was evaluated according to the methodology applied by Chakraborty (2010).

Experimental tests for RTD curves were also performed on the physical model to validate the results of the mathematical model, by comparison of these curves. The ‘pulse-input’ method was employed. In this method, a salt solution, named tracer, is introduced rapidly into the water supply (ladle shroud) and the change in salt concentration is measured by a conductivity meter in the tundish outlet. The RTD curve is a plot of dimensionless concentration of salt into the dimensionless time. The curve (C) and dimensionless time (θ) are defined by Equations 1 and 2 (Sahai and Emi, 1996).

(1) $\mathit{C}=\frac{\mathit{c}}{\mathit{q}/{\mathit{V}}_{\mathit{tund}}}$

(2) $\mathit{\theta }=\frac{\mathit{t}}{{\mathit{t}}_{\mathit{theoritical}}}$

where c is the concentration of tracer in the output (kg/m³) over time t (s), q is the mass of the tracer injected (kg) and V_tund is the tundish volume (m³). Additionally, a camera was used to take images of the gas curtain in order to evaluate the average bubble size to be used in the mathematical model. 84 samples of bubbles were measured through equivalent diameter definition.

2.2 Mathematical model

In the mathematical modeling, the air/water fluid flow was described by the Eulerian-Eulerian approach, while the trajectories of the particles (discrete phase) were described by the Eulerian-Lagrangian formulation.

In the Eulerian-Eulerian approach, both phases interpenetrate and interact with each other. The continuity and momentum equations for each phase are solved together. The continuity equations for gaseous and liquid phases are given by Equations 3 and 4, respectively.

(3) $\frac{\mathit{\partial }\left({\mathit{r}}_{\mathit{g}}{\mathit{\rho }}_{\mathit{g}}\right)}{\partial \mathit{t}}=-\left(\nabla .{\mathit{r}}_{\mathit{g}}{\mathit{\rho }}_{\mathit{g}}{\mathbf{v}}_{\mathit{g}}\right)$

(4) $\frac{\mathit{\partial }\left({\mathit{r}}_{\mathit{l}}{\mathit{\rho }}_{\mathit{l}}\right)}{\mathit{\partial }\mathit{t}}=-\left(\nabla .{\mathit{r}}_{\mathit{l}}{\mathit{\rho }}_{\mathit{l}}{\mathbf{v}}_{\mathit{l}}\right)$

where l and g represent the liquid and gaseous phases, the term r is the volume fraction, r is the density of the fluid (kg/m³), v is the velocity vector (m/s). Each phase has its governing equations. The momentum equation for the liquid phase can be expressed by:

(5) $\frac{\mathit{\partial }\left({\mathit{\rho }}_{\mathit{l}}{\mathit{r}}_{\mathit{l}}{\mathbf{v}}_{\mathit{l}}\right)}{\mathit{\partial }\mathit{t}}=-\left(\nabla .{\mathit{\rho }}_{\mathit{l}}{\mathit{r}}_{\mathit{l}}{\mathbf{v}}_{\mathit{l}}{\mathbf{v}}_{\mathit{l}}\right)-{\mathit{r}}_{\mathit{l}}\nabla \mathit{p}-\left(\nabla .{\tau }_{\mathit{l}}\right)+{\mathit{r}}_{\mathit{l}}{\mathit{\rho }}_{\mathit{l}}\mathbf{g}+{\mathit{M}}_{\mathit{lg}}$

The corresponding momentum equation for the gaseous phase is:

(6) $\frac{\mathit{\partial }\left({\mathit{\rho }}_{\mathit{g}}{\mathit{r}}_{\mathit{g}}{\mathbf{v}}_{\mathit{g}}\right)}{\mathit{\partial }\mathit{t}}=\left(\nabla .{\mathit{\rho }}_{\mathit{g}}{\mathit{r}}_{\mathit{g}}{\mathbf{v}}_{\mathit{g}}{\mathbf{v}}_{\mathit{g}}\right)-{\mathit{r}}_{\mathit{g}}\nabla \mathit{p}-\left(\nabla .{\tau }_{\mathit{g}}\right)+{\mathit{r}}_{\mathit{g}}{\mathit{\rho }}_{\mathit{g}}\mathbf{g}+{\mathit{M}}_{\mathit{gl}}$

The Boussinesq proposal was used to introduce the effects of turbulence (Seshadri et al., 2010).

(7) ${\tau }_{\mathit{l}}={\mathit{r}}_{\mathit{l}}{\mathit{\mu }}_{\mathit{eff}}\left[\nabla {\mathbf{v}}_{\mathit{l}}+{\left(\nabla {\mathbf{v}}_{\mathit{l}}\right)}^{\mathit{T}}\right]$

(8) ${\tau }_{\mathit{g}}={\mathit{r}}_{\mathit{g}}{\mathit{\mu }}_{\mathit{g}}\left[\nabla {\mathbf{v}}_{\mathit{g}}+{\left(\nabla {\mathbf{v}}_{\mathit{g}}\right)}^{\mathit{T}}\right]$

(9) ${\mathit{\mu }}_{\mathit{eff}}={\mathit{\mu }}_{\mathit{l}}+{\mathit{\mu }}_{\mathit{t}}$

where g is the gravity vector, µ_g represents the gas viscosity (kg/m s), µ_eff is the effective viscosity that is the liquid viscosity µ_l combined with turbulent viscosity µ_t. The term M_lg (kg m/s) is the transfer of momentum between the phases. M_lg is analogue to M_gl (ANSYS, 2015).

In this study, only the drag force was considered for transfer momentum. The Grace model was considered for drag coefficient calculations (Grace et al., 1976). This model considers the distortion of spherical bubbles to ellipsoids. Additionally, the interfacial tension air/water in the drag model was considered to be 0.072N/m (Vargaftik et al., 1983).

To describe the effects of turbulence within the tundish, the k-e turbulence model was adopted (Seshadri et al., 2010). The conservation equations for the turbulent kinetic energy k are given by Equation 10. The turbulent dissipation e is represented by Equation 11.

(10) $\frac{\mathit{\partial }\left({\mathit{r}}_{\mathit{l}}{\mathit{\rho }}_{\mathit{l}}\mathit{k}\right)}{\mathit{\partial }\mathit{t}}=-\left(\nabla .{\mathit{\rho }}_{\mathit{l}}{\mathit{r}}_{\mathit{l}}{\mathbf{v}}_{\mathit{l}}\mathit{k}\right)+\left(\nabla .\frac{{\mathit{\mu }}_{\mathit{t}}}{{\sigma }_{\mathit{K}}}\nabla \mathit{k}\right)+{\mathit{G}}_{\mathit{k}}-{\mathit{r}}_{\mathit{l}}{\mathit{\rho }}_{\mathit{l}}\epsilon$

(11) $\frac{\mathit{\partial }\left({\mathit{r}}_{\mathit{l}}{\mathit{\rho }}_{\mathit{l}}\epsilon \right)}{\mathit{\partial }\mathit{t}}=-\left(\nabla .{\mathit{\rho }}_{\mathit{l}}{\mathit{r}}_{\mathit{l}}{\mathbf{v}}_{\mathit{l}}\epsilon \right)+\left(\nabla .\frac{{\mathit{\mu }}_{\mathit{t}}}{{\sigma }_3}\nabla \epsilon \right)+\frac{\epsilon }{\mathit{k}}\left({\mathit{C}}_1{\mathit{G}}_{\mathit{k}}-{\mathit{r}}_{\mathit{l}}{\mathit{\rho }}_{\mathit{l}}{\mathit{C}}_2\epsilon \right)$

(12) ${\mathit{G}}_{\mathit{k}}={\mathit{\mu }}_{\mathit{t}}\left[\nabla {\mathbf{v}}_{\mathit{l}}+{\left(\nabla {\mathbf{v}}_{\mathit{l}}\right)}^{\mathit{T}}\right]:\nabla {\mathbf{v}}_{\mathit{l}}$

(13) ${\mathit{\mu }}_{\mathit{t}}={\mathit{C}}_{\mathit{\mu }}\mathit{\rho }{\mathit{k}}^2/\epsilon$

The term G_k is the generation rate of turbulent kinetic energy. The following values have been taken for constants: C_µ =0.09, σ_k = 1.0, σ_ε =1.30, C₁ =1.44, C₂ =1.92.

For the simulation of the movement of the particles, a discrete phase model was used. This model is described as follows:

(14) ${\mathit{m}}_{\mathit{p}}\frac{\mathit{d}{\mathbf{v}}_{\mathit{p}}}{\mathit{dt}}={\mathit{m}}_{\mathit{p}}\mathbf{g}-{\mathit{\rho }}_{\mathit{l}}{\mathit{V}}_{\mathit{p}}\mathbf{g}+\frac{1}{2}{\mathit{\rho }}_{\mathit{l}}{\mathit{C}}_{\mathit{D}}{\mathit{A}}_{\mathit{p}}\left|{\mathbf{v}}_{\mathit{l}}-{\mathbf{v}}_{\mathit{p}}\right|\left({\mathbf{v}}_{\mathit{l}}-{\mathbf{v}}_{\mathit{p}}\right)$

(15) ${\mathit{C}}_{\mathit{D}}=\max \left(\frac{24}{{\mathit{Re}}_{\mathit{p}}}\left(1+0.1\mathit{5}{\mathit{Re}}_{\mathit{p}}^{0.687}\right),0.44\right)$

(16) ${\mathit{Re}}_{\mathit{p}}=\frac{{\mathit{\rho }}_{\mathit{l}}{\mathit{d}}_{\mathit{p}}\left|{\mathbf{v}}_{\mathit{p}}\mathbf{-}{\mathbf{v}}_{\mathit{l}}\right|}{{\mathit{\mu }}_{\mathit{l}}}$

where v_p is the particle velocity (m/s), m_p is the particle mass (kg), V_p is the particle volume (m³), A_p is the particle projected area (m²), C_D is the drag coefficient, Re_p is the particle Reynolds number and d_p is the particle diameter (m). The effects of the chaotic behavior of the particles due to turbulence are described by the discrete random walk model. In this model, the random components of the particle velocity v'_p are proportional to the local effective energy of turbulence.

(17) ${\mathbf{v}}_{\mathit{p}}^{\text{'}}=\varsigma {\left(\frac{\mathit{2}\mathit{k}}{\mathit{3}}\right)}^{1/2}$

where ς is a random number.

The boundary conditions for the water/air flow were established according to the physical conditions:

Walls: non-slip and free slip conditions were assumed for the liquid and gaseous phases, respectively;

Free surface: degassing and free slip conditions were assumed for the gases and liquid phase, respectively;

Tundish outlet: atmospheric pressure assumed;

Plug gas injection: inlet condition for gases, the mass flow rate was specified. Therefore, the average bubble diameter (2.75mm) was set for all cases with gas injection;

Symmetry: two planes of symmetry were considered.

The particle behaviors were calculated from the converged steady-state water/air flow simulation. Therefore, only the particles species were considered. The coupling of the pair fluid/particle is one-way, in other words, only the fluid phases affect the movement of the particles. Ten thousand particles of each size were introduced in the tundish inlet. The reference for the range of particle size was the bench tests. It was assumed that all particles are reflected on the walls. Usually, the majority of studies consider the capture of all particles that reach the free surface. Since this simplification is not appropriate, an additional boundary condition was implemented via a subroutine in Ansys-CFX. Therefore, the standard boundary condition results and the implemented boundary condition results are presented and compared.

Since the modeling assumes a steady fluid, the forces acting on the particles near the free surface can be considered to be the total buoyancy force and drag force. In this case, the forces act only in the vertical direction and the force balance is equal to:

(18) ${\mathbf{F}}_{\mathit{B}}={\mathbf{F}}_{\mathit{D}}$

The buoyancy force is defined by Equation 19. Considering the validity of Stokes Law, the drag force can be described by Equation 20.

(19) ${\mathbf{F}}_{\mathit{B}}=\frac{\mathit{\pi }{\mathit{d}}_{\mathit{p}}^3}{6}\mathbf{g}\left({\mathit{\rho }}_{\mathit{l}}-{\mathit{\rho }}_{\mathit{p}}\right)$

(20) ${\mathbf{F}}_{\mathit{D}}=3{\mathit{\pi }\mathit{\mu }}_{\mathit{l}}{\mathit{d}}_{\mathit{p}}{\mathbf{v}}_{\mathit{t}}$

where v_t is the terminal velocity (m/s).

(21) ${\mathbf{v}}_{\mathit{t}}=\frac{1}{18}{\mathit{d}}_{\mathit{p}}^2\mathbf{g}\frac{\left({\mathit{\rho }}_{\mathit{l}}-{\mathit{\rho }}_{\mathit{p}}\right)}{{\mathit{\mu }}_{\mathit{l}}}$

The present study proposes to consider the terminal velocity as a critical velocity for the particle. The slip velocity of each particle reaching the surface is compared with the critical velocity. If the relative velocity of the particle is smaller, it is trapped. Otherwise, the particle is reflected. To solve the governing equations, the academic version of CFD software ANSYS CFX 17.1 was used and unstructured tetrahedral meshes were employed. The second-order advection scheme High Resolution was applied and the root means square convergence criterion was set as 10^-6. For the mesh independence test, three meshes were considered: 100000, 142000 and 226000 nodes. Due to the two planes of symmetry, the calculations were carried out in one quarter of the tundish. The particle simulations parameters were set as 900s for maximum tracking time, 50m for maximum distance and 5000 for maximum number of integration steps. All computations were performed with a Windows 10 PC with Intel i7 and 16 GB RAM. The computation time was approximately 5 hours per each case.

3. Results and discussion

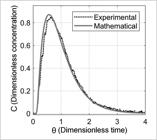
Regarding the mesh independence test, the chosen one was the mesh with 142000 nodes in which there was no more variation in RTD curves. The experimental RTD curves of the tundish were used to validate the mathematical model. Figure 2 presents the RTD curves for the configuration with the gas injection of 3NL/min at 0.560m from the ladle shroud. The calculated curve adequately represents the experimental curve.

Figure 2
Comparison of the RTD curve from the mathematical model with the experimental RTD curve, according to Equations 1 and 2.

The flow patterns of the fluid water are presented in Figures 3 and 4. The velocity fields and the contours of the velocity at the free surface and symmetry plane of the tundish are plotted. Figure 5 presents the trajectories of 30 µm particles. For shortening, only two cases are presented: tundish without gas injection and tundish with a gas injection having a flow rate of 3NL/min at 0.560m from the ladle shroud.

Figure 3
Flow field in the tundish without gas injection.

Figure 4
Flow field in the tundish with gas injection of 3NL/min at 0.56m from the ladle shroud.

Figure 5
Trajectories of 30 µm particles in the tundish without gas injection (a) and in the tundish with gas injection of 3NL/min at 0.56m from the ladle shroud (b).

From Figures 3, it is observed that the weir and dam promote a recirculation zone between them. With the gas curtain (Figure 4), a more pronounced flow from the bottom towards the free surface can be noticed and a new recirculation zone is formed between the plug and the dam. The particles trajectories reflect these characteristics of the flow. In Figure 6 (b), the particles move to the free surface following the gas curtain.

Figure 6
Results obtained from the tundish without gas injection (a) and with gas injection at 0.28m from the ladle shroud (b).

The removal particle index is defined by the Equation 22,

(22) $\mathit{Particle}\mathit{removal}\mathit{index}=\frac{{\mathit{N}}_{\mathit{in}}-{\mathit{N}}_{\mathit{out}}}{{\mathit{N}}_{\mathit{in}}}*100\%$

where N_in is the number of particles of a particular size range injected within the tundish and N_out is the number of particles of that particular size range leaving the tundish. In the physical model, the N_in was quantified through the bench tests and the N_out was counted by the APS III, located in the tundish outlet. Regarding the mathematical model, the N_in is set and the N_out is a result of the simulations.

The removal indexes obtained with the standard boundary condition and the implemented boundary condition of the mathematical model are compared to the experimental removal indexes in Figures 6 and 7. The experimental indexes are presented with their respective error bar, which corresponds to one standard deviation. The abbreviation BC refers to boundary condition.

Figure 7
Results obtained from the tundish with gas injection at 0.56m (a) and 0.84m(b) from the ladle shroud.

The standard boundary condition overestimates the particle removal results when compared to the experimental data. It is observed that the proposed boundary condition considerably reduces the particle removal indexes for all the cases. The comparison indicates a good agreement between the measured and the calculated removal indexes. For the case without gas injection and the case with the plug located at 0.84m from the tundish inlet, the proposed mathematical model predicts indexes greater than the experimental data. The tundish without gas injection presents higher velocities near the free surface when compared to the other configurations. Possibly, the capture criterion should be stricter, with the critical velocity being less than the particle terminal velocity. Additional studies regarding the definition of the critical velocity are needed.

Another limitation of the model is related to the reversal of bath inclusions. It could explain the case with the plug located at 0.84m from the tundish inlet. The gas curtain implies certain agitation at the free surface that could provoke the return of trapped particles to the bath. This effect could be an issue to the above case given the fact that the plug is close to the outlet tundish. It is noteworthy that the implemented subroutine restricts the particle entrapment based on their slip velocities, but does not consider the reversion of the particles that are already trapped at the free surface. In the discrete model, once trapped, the particle is not tracked anymore. Although feasible in physical models, the reversal of bath inclusions is unlikely in industrial practice, given the inclusion/slag thermodynamic interactions.

When the gas injection is present, unlike the standard boundary condition, the proposed boundary condition exhibits removal indexes dependent on particle sizes. These dependencies were also observed in the experimental data and industrial tests (Kumar et al., 2009; Meijie et al., 2011).

It is verified that gas injection with flow rate of 3L/min leads to a significant gain in the efficiency of particle removal when compared to the case without gas injection. Plug locations of 0.56 and 0.84m from the tundish inlet enabled similar particle removal efficiencies that were considerably greater than the indexes obtained with the plug location of 0.28m from the tundish inlet. Possibly, this case presented lower efficiency due to high turbulent energy in the region close to the tundish inlet.

4. Summary and conclusions

The inclusion removal in the tundish with gas injection was evaluated through physical and mathematical modeling. The results suggest that the gas curtains increase the efficiency of inclusion removal. However, the plug location seems to affect the inclusion removal index. The greater indexes were achieved with the plugs located at 0.56 and 0.84m from the ladle shroud. A new boundary condition to describe the behavior of the particles at the free surface was proposed and implemented in the mathematical model. Its use provided inclusion removal predictions in good agreement with the experimental data, permitting additional investigations. Further studies regarding the definition of the critical velocity could enhance the correspondence between mathematical and experimental results. The results indicated that the inclusion removal indexes are dependent on particle sizes, as observed in industrial tests, reported in literature.

Acknowledgments

This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001 and Pró-Reitoria de Pesquisa - Universidade Federal de Minas Gerais (PRPq/UFMG).

References

• ANSYS. Workshop CFx: introduction to multiphase systems. [S. l.]: Ansys, Inc., 2015.
• ARCOS-GUTIERREZ, H.; BARRETO, J.; GARCIA-HERNANDEZ, S.; RAMOS-BANDEIRAS, A. Mathematical analysis of inclusion removal from liquid steel by gas bubbling in a casting tundish. Journal of Applied Mathematics, v. 12, p. 1-16, 2012.
• CHAKRABORTY, A. Development of an on-line aqueous particle sensor to study the performance of inclusions in a 12 tonne, delta shaped full scale water model tundish 2010. 118 f. Thesis (Master of Engineering) - McGill University, Montreal, 2010.
• CHANG, S.; CAO, X.; ZOU, Z.; ISAC, M.; GUTHRIE, R. Microbubble swarms in a full-scale water model tundish. Metallurgical and Materials Transactions B, v. 47, p. 2732-2743, 2016.
• CHEN, D.; XIE X.; LONG, M.; ZHANG, M.; ZHANG, L.; LIAO, Q. Hydraulics and mathematics simulation on the weir and gas curtain in tundish of ultrathick slab continuous casting. Metallurgical and Materials Transactions B, v. 45, p. 392-398, 2014.
• CWUDZINSKI, A. Numerical simulation of liquid steel flow and behaviour of non-metallic inclusions in one strand slab tundish with subflux turbulence controller and gas permeable barrier. Ironmaking and Steelmaking, v. 37, n. 3, p. 169-180, 2010.
• CWUDZINSKI, A. Physical and mathematical modeling of bubbles plume behaviour in one strand tundish. Metallurgical Research & Technology, v. 115, n. 1, p. 1-8, 2018.
• GRACE, J. R.; WAIREGI, T.; NGUYEN, T. H. Shapes and velocities of single drops and bubbles moving freely through immiscible liquids. Transactions of the Institution of Chemical Engineers, v. 54, n. 3, p. 167-173, 1976.
• GUTHRIE, R. I. L.; LI, M. In situ detection of inclusions in liquid metals: Part I. Mathematical modeling of the behavior of particles traversing the electric sensing zone. Metallurgical and Materials Transactions B, v. 32, p. 1067-1079, 2001a.
• GUTHRIE, R. I. L.; LI, M. In situ detection of inclusions in liquid metals: Part II. Metallurgical applications of LiMCA systems. Metallurgical and Materials Transactions B, v. 32, p. 1081-1093, 2001b.
• KUMAR, D. S.; RAJENDRA, T.; PRASAD, R.; SARKAR, A.; RANJAN, M. Forced flotation of inclusions in tundish. Ironmaking and Steelmaking, v. 36, n. 6, p. 470-5, 2009.
• MAZUMDAR, D.; GUTHRIE, R. The physical and mathematical modeling of continuous casting tundish systems. ISIJ International, v. 39, n. 6, p. 524-547, 1999.
• MEIJIE, Z.; HUAZHI, G.; AO, H.; HONGXI, Z.; CHENGJI, D. Numerical simulation and industrial practice of inclusion removal from molten steel by gas bottom-blowing in continuous casting tundish. Journal of Mining and Metallurgy, v. 47, n. 2, p. 137-147, 2011.
• MENDONÇA, A. F. G. Avaliação do efeito da injeção de gás sobre a flotação de inclusões em um distribuidor de lingotamento contínuo 2016. 188 f. Dissertação (Mestrado em Engenharia Metalúrgica, Materiais e de Minas) - Escola de Engenharia, Universidade federal de Minas gerais, Belo Horizonte, 2016.
• NEVES, L.; TAVARES, R. P. Analysis of the mathematical model of the gas bubbling curtain injection on the bottom and the walls of a continuous casting tundish. Ironmaking and Steelmakin, v. 44, n. 8, p. 559-567, 2017.
• RAMOS-BANDERAS, A.; MORALES, R. D.; BARRETO, J.; SOLORIO-DIAZ, G. Modelling study of inclusion removal by bubble flotation in the tundish. Steel Research International, v. 77, n. 5, p. 325-335, 2006.
• RAMOS-BANDERAS, A.; MORALES, R. D.; GARCÍA-DEMEDICES, L.; DÍAZ-CRUZ, M. Mathematical simulation and modeling of steel flow with gas bubbling in trough type tundishes. ISIJ International, v. 43, n. 5, p. 653-662, 2003.
• ROGLER, J. P. Modeling of inclusion removal in a tundish by gas bubbling 2004. 67 f. Thesis (Master of Chemical Engineering) - Ryerson University, Toronto, 2004.
• RUCKERT, A.; WARZECHA, M.; KOITZSCH, R.; PAWLIK, M.; PFEIFER, H. Particle distribution and separation in continuous casting tundish. Steel Research International, v. 80, n. 8, p. 568-574, 2009.
• SAHAI, Y.; EMI, T. Melt flow characterization in continuous casting tundishes. ISIJ International, v. 36, n. 6, p. 667-672, 1996.
• SAHAI, Y. Tundish technology for casting clean steel: a review. Metallurgical and Materials Transactions B, v. 47, p. 2095-2106, 2016.
• SESHADRI, V.; TAVARES, R. P.; SILVA, C. A.; SILVA, I. A. Transport phenomena: fundamentals and applications in metallurgical and materials engineering. São Paulo: Associação Brasileira de Metalurgia, Materiais e Mineração - ABM, 2010. 810 p. (Metallurgical, Materials and Mining Collection - Textbooks, v. 2).
• WARZECHA, M.; MERDER, T.; WARZECHA, P.; STRADOMSKI, G. Experimental and numerical investigations on non-metallic inclusions distribution in billets casted at a multi-strand continuous casting tundish. ISIJ International, v. 53, n. 11, p. 1983-1992, 2013.
• VARGAFTIK, N. B.; VOLKOV, B. N.; VOLJAK, L. D. International tables of the surface tension of water. Journal of Physical and Chemical Reference Data, v. 12, p. 817-820, 1983.
• ZHANG, L.; TANIGUCHI, S. Fundamentals of inclusion removal from liquid steel by bubble formation. International Materials Reviews, v.45, n.2, p. 59-82, 2000.

Publication Dates

• Publication in this collection
  30 Sept 2020
• Date of issue
  Oct-Dec 2020

History

• Received
  03 Feb 2020
• Accepted
  27 June 2020