Numerical formulation for nonlinear analysis of concrete and steel shells with deformable connections

Abstract

A two-dimensional interface finite element capable of associating flat shell elements positioned one above the other was developed. The implemented interface element can physically simulate the contact between the flat shell elements and connect the reference planes of the shell elements above and below it. The formulation presented allows consideration of nonlinear behavior for the deformable connection as well as for the concrete and steel materials that make up the shell structure. One of the practical applications analyzed in this research is the numerical simulation of composite floors formed by a reinforced concrete slab connected to steel beams through a deformable connection. In this case, the concrete slab and the steel beams are discretized by flat shell elements and the deformable connection is discretized by two-dimensional interface elements. Experimental and numerical results from literature were used to validate the implemented elements. In the two examples analyzed, the results obtained for the displacements were close, with the difference, in the first case, being associated with uncertainties during the experimental test and in the second, the difference in theories used in the formulation of the implemented elements.

Key words:
two-dimensional interface element; flat shell element; composite floor; deformable connection

1. Introduction

A formulation of a two-dimensional interface finite element that can numerically simulate a deformable connection between structural elements and be analyzed by flat shell elements is presented. Practical civil construction components, such as composite floors, beams, and pillars, have a deformable connection between different materials. Among these, composite floors formed by a reinforced concrete slab connected to steel beams by shear connectors are the most common. In general, the structural analysis and design for this element are based on simplified models that can generate significant errors (e.g., by using bar elements to represent the elements). Therefore, the effect of the variation of the normal stress along the width of the concrete slab or shear lag is not considered, and if torsion effects on the beam are significant, it is necessary to accurately represent the warping. One way to better represent the mechanical behavior of this structural element and an optimized design is to model the concrete slab and steel beams by flat shell elements and to model the deformable connection by interface elements.

The interface element was initially developed to work in conjunction with two- and three-dimensional elements that represent a thin layer of material or the contact between two distinct materials, such as the case of soil–structure interaction. The first study on interface elements was by Goodman et al. (1968). In that study, the interface element was used to simulate the slip and separation between two bodies in contact.

To represent two distinct materials, Kalikin and Li, (1995) used two-dimensional interface elements with zero thickness to model the problem of contact between the soil and a shallow foundation. Subsequently, Carol et al. (2001) used an interface element of zero thickness to analyze the cracking process in concrete elements.

For the analysis of the ultimate capacity of a composite beam with a deformable connection, Sousa and Silva (2007) developed an interface element capable of simulating longitudinal slip and vertical uplift at the contact between materials of a composite section. The implemented interface element works in conjunction with one-dimensional beam elements implemented by considering Euler–Bernoulli beam theory, the physical nonlinearity of materials, and the possibility of generic cross sections.

Sousa and Silva (2009) presented a family of interface elements for the numerical analysis of composite beams with longitudinal deformable connections. The proposal of these elements includes formulations to be employed with Euler–Bernoulli beam theory, Tymoshenko's beam theory, different numbers of nodes in the elements, and different integration processes for the displacements along the element.

Sousa and Silva (2010) presented an analytical solution for composite beams with multiple layers. This solution was used to verify the ability of the interface element to simulate composite beam problems with more than one shear plane.

The interface element implemented in the present study is associated with flat shell elements above and below it. According to Batoz et al. (2010), the first analysis of a shell structure using the finite element method was performed using a set of flat shell elements to approximate the true shell shape. Owing to the simplicity of the formulation. computational efficiency, and application flexibility, shell elements are extensively used in practice.

According to Hughes (1987), Reissner–Mindlin's plate theory, which includes transverse shear strain, has promoted the development of several interpolation schemes of nodal displacements, because, in this case, translations and rotations are interpolated independently. Because of this, shell elements have recently been obtained based on Reissner–Mindlin’s theory, and these are superior to the elements obtained according to Kirchhoff's classic plate theory in the numerical analyses of thick shells. In the case of thin shells, shear strain tends to be very small and may lead to problems in the evaluation of these elements in the analysis using Reissner – Mindlin’s theory (the shear locking effect). To avoid this, a slightly higher discretization is recommended when thin shells are obtained, as well as reduced numerical integration of the shear strain.

One of the practical applications analyzed in this study is the numerical simulation of composite floors formed by a reinforced concrete slab connected to steel beams through a deformable connection. Despite the prodigious use of composite floors in construction, few numerical and experimental studies on composite floors can be found in literature. A vast majority of studies focus on simplification of the problem, modeling the floor as a composite beam. One of the most relevant articles for the study of composite floors is that of Nie et al. (2008), which introduces a new definition of the effective width for the final resistance calculations of composite beams subjected to a bending moment using a commonly accepted rectangular stress distribution.

Izzuddin et al. (2004) developed a shell element to simulate concrete slabs reinforced by cold-rolled steel sheets. The formulation, as in the present article, is based on Reissner–Mindlin’s plate theory, but with a modification that makes the proposed element capable of simulating orthotropic geometry and the discontinuity of the material between the adjacent ribs.

In this study, a two-dimensional interface finite element capable of associating flat shell elements positioned one above the other was developed. The implemented interface element can physically simulate the contact between the flat shell elements and connect the reference planes of the shell elements above and below it or side by side. The formulation presented allows consideration of nonlinear behavior for the deformable connection as well as for the concrete and steel materials that make up the shell structure.

One of the practical applications analyzed herein is the numerical simulation of composite floors formed by a reinforced concrete slab connected to steel beams through a deformable connection. In this case, the concrete slab and the steel beams are discretized by flat shell elements and the deformable connection is discretized by two-dimensional interface elements.

Experimental and numerical results from the literature were used to validate the implemented elements. Two examples were analyzed, and their results demonstrated the efficiency of the implemented element.

2. Materials and methods

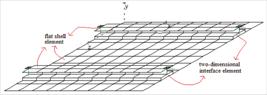
Figure 1 shows a composite floor formed by a concrete slab connected to two steel beams. In the discretization of the composite floor, a two-dimensional interface element is used to make the connection between the flat shell elements and to simulate a possible deformable connection in the contact between the concrete slab and the steel beams.

Figure 1
Composite floor discretized by flat shell and interface elements.

2.1 Flat shell element

The flat shell finite element implemented for the nonlinear analysis of a steel and reinforced concrete shell has nine nodes and five degrees of freedom per node, as shown in Figure 2. Because of the independence between translation and rotational degrees of freedom, the formulation described in this section accounts for shear deformation; therefore, it is applicable to thick shells. In the case of thin shells, attention should be given to possible numerical errors resulting from shear locking. To avoid this, we can refine the finite element mesh and use reduced integration in the evaluation of shear strain.

Figure 2
Nine-node multilayer flat shell element.

In the analysis of physical nonlinearity, a multilayer element is used and specific characteristics are considered for each layer. These include, for example, different mechanical properties and independent stress–strain relationships. For other characteristics and more details of the flat shell element, consult Huang et al. (1999, 2003a, 2003b) and Silva and Dias (2018a).

Using the kinematic assumptions of Reissner–Mindlin's plate theory, we obtain the displacement equations given by:

(1) $u\left(x,y,z\right)=u^0\left(x,y\right)+z{\theta }_y\left(x,y\right)$

(2) $v\left(x,y,z\right)=v^0\left(x,y\right)+z{\theta }_x\left(x,y\right),\text{and}$

(3) $w\left(x,y,z\right)=w^0\left(x,y\right)$

where u⁰, v⁰, and w⁰ represent the translations of the reference plane of the flat shell element in the x, y, and z directions, respectively; θ_x and θ_y are the rotations of the sections in relation to the x and axes, respectively; and z is the position of the fiber along the thickness of the flat shell element. To simplify the notation, the zero superscript is omitted in the following equations.

In the definition of the strain–displacement equations, the Green–Lagrange relations were used by considering Von Karman’s hypothesis, which implies that the derivatives of u and v in relation to y, and z are small and can be neglected, while the variation of w can be also be neglected:

(4) ${\epsilon }_x=u_{,x}+z{\theta }_{y,x}+1/2{\left(w_{,x}\right)}^2$

(5) ${\epsilon }_y=v_{,y}-z{\theta }_{x,y}+1/2{\left(w_{,y}\right)}^2$

(6) ${\epsilon }_{xy}=1/2(u_{,y}+z{\theta }_{y,y}+v_x-z{\theta }_{x,x}+w_{,x}{w}_{,y}$

(7) ${\epsilon }_{xz}=1/2\left({\theta }_y+w_{,x}\right)$

(8) ${\epsilon }_{yz}=1/2\left(-{\theta }_x+w_{,y}\right)$

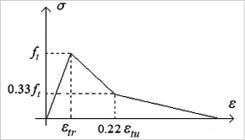
Geometric nonlinearity is observed in Eqs. (4) and (5): Another nonlinearity of the problem is defined by the stress–strain relationship of steel and concrete for a uniaxial stress state. For concrete under compression, the curve defined by the CEB-FIP model code (2010) was used. For the concrete under tension, the stress–strain curve of Figure 3 was adopted, as suggested by Rots et al. (1984) and also used by Huang et al. (1999, 2003a).

Figure 3
Stress–strain relationship for concrete in tension.

Herein, ε_tu = 10ε_tr was adopted, and, for the concrete tension strength, the relationship f_t = 0.3321 √f_c (ASCE, 1982) was used, where f_c is the concrete compressive strength in MPa. For the steel, the stress– strain curve defined by linear segments was adopted, where values of the limits of stresses and strain are presented in the application examples.

For the physical and geometric nonlinear analysis, an incremental method with displacement control was used. At each step of the incremental method, a linear material with a modulus of elasticity given by the tangent to the strain–strain curve was considered. In this manner, the stress–strain relationship can be obtained by using Hooke's law for the problem analyzed. Following the constitutive matrix for materials under stress levels inside and outside, the failure region was defined.

The materials exhibited orthotropic behavior inside the failure region (after cracking or crushing of concrete and after yielding of the steel); that is, they exhibited different characteristics for each principal direction. By considering the layers in the plane stress state, the principal directions were calculated, as indicated herein by subscripts 1 and 2, where 1 indicates the direction of the greater principal strain. If the principal strains (ε₁ and ε₂) are within the failure region, the materials are considered orthotropic with the stress–strain relationship decoupled to the principal directions; in this way, the constitutive matrix of the material is given by:

(9) $D_{12}=\left[\begin{array}{ccccc}{E}_1& 0& 0& 0& 0\\ & E_2& 0& 0& 0\\ & & \frac{1}{2}\left(G_1+G_2\right)& 0& 0\\ & & & G_1& 0\\ \mathrm{Sim}\_& & & & G_2\end{array}\right]$

where E₁ and E₂ are given by tangents to the material stress–strain curve at points ε = ε_α and G_α = 0.5E_α / (1+v) for α =1, 2. The stiffness matrix in the direction of the x–y axes (D_xy) can be obtained from D₁₂ and the angle ϕ of rotation of the principal axes in relation to the x–y axes:

(10) $D_{xy}=\left[\begin{array}{ccccc}{d}_{11}& d_{12}& d_{13}& 0& 0\\ & d_{22}& d_{23}& 0& 0\\ & & d_{33}& 0& 0\\ & & & d_{44}& d_{45}\\ Sim\_& & & & d_{55}\end{array}\right]$

where

(11) $d_{11}=E_1{\cos }^4\varphi +E_2{\sin }^4\varphi +1/2\left(G_1+G_2\right){\sin }^2\left(2\varphi \right)$

(12) $d_{12}=1/4{\sin }^2\left(2\varphi \right)\left(E_1+E_2-4\left(G_1+G_2\right)\right)$

(13) $d_{13}=1/2{\sin }^2\varphi \left(E_1{\cos }^2\varphi -E_2{\sin }^2\varphi -\left(G_1+G_2\right)\cos \left(2\varphi \right)\right)$

(14) $d_{22}=E_1{\sin }^4\varphi +E_2{\cos }^4\varphi +1/2\left(G_1+G_2\right){\sin }^2\left(2\varphi \right)$

(15) $d_{23}=1/2{\sin }^2\varphi \left(E_1{\sin }^2\varphi -E_2{\cos }^2\varphi +\left(G_1+G_2\right)\cos \left(2\varphi \right)\right)$

(16) $d_{33}=1/4{\sin }^2\left(2\varphi \right)\left(E_1+E_2\right)+1/2\left(G_1+G_2\right){\cos }^2\left(2\varphi \right)$

(17) $d_{44}=G_1{\cos }^2\varphi +G_2{\sin }^2\varphi$

(18) $d_{45}=1/2\left(G_1-G_2\right)\sin \left(2\varphi \right)$

(19) $d_{55}=G_1{\sin }^2\varphi +G_2{\cos }^2\varphi$

For the particular case of isotropic material, observed when the principal strain is outside the failure region, we have E₁ = E₂ = E and G₁ = G₂ = G, and the D_xy matrix of Eq. (10) reduces to the traditional form of Reissner–Mindlin’s plate theory.

In the definition of the internal force vector and tangent stiffness matrix, it is assumed that the displacements and rotations have quadratic variations along the element and can be written in terms of the nodal displacements. For details on how to obtain the numerical formulation of this element, consult Silva and Dias (2018a).

2.2 Two-dimensional interface element

The 18-node two-dimensional interface element is responsible for simulating the deformable connection and making the connection between 9-node flat shell elements, as shown in Figure 4. The orientation of the degrees of freedom follows analogously to that of the flat shell element of Section 2.1.

Figure - 4
Two-dimensional interface element associated with flat shell elements.

The two-dimensional interface element has, in addition to the function of physically simulating the contact between the flat shell elements, the function of connecting the reference surfaces of the flat shell elements above and below it. For this, reference surfaces are defined, which in this case are taken as the mid-plane of the element to be discretized into flat shell elements. I n this way, the thickness or distance between the upper and lower nodes of the two-dimensional element is taken as the sum of half of the upper and lower thickness of the elements connected by the two-dimensional element. Although this thickness is not zero, its actual physical thickness is always zero.

The interface element physically represents only the contact between the flat shell elements. The relative displacement equations in this contact can be obtained from the displacement equations for the shell elements below (α = 1) and above (α = 2) the interface element. The equations of longitudinal (s_l) , transversal (s_t) , and vertical (s_v) relative displacement in directions x, y, and z shown in Figure 4 are given as

(20) $s_l\left(x,y\right)=u_2^0\left(x,y\right)-u_1^0\left(x,y\right)-h_2/2{\theta }_{y2}\left(x,y\right)-h_1/2{\theta }_{y1}\left(x,y\right)$

(21) $s_t\left(x,y\right)=v_1^0\left(x,y\right)-v_2^0\left(x,y\right)-h_2/2{\theta }_{x2}\left(x,y\right)+h_1/2{\theta }_{x1}\left(x,y\right)$

(22) $s_v\left(x,y\right)=w_2^0\left(x,y\right)-w_1^0\left(x,y\right)$

In Eqs. (20) - (22), u⁰_a , v⁰_a, and w⁰_a represent the translational displacements of the midplane (or any reference plane) of the flat shell elements; θ_xa and θ_ya represent the rotations with respect to the x and y axes, which are independent of the position along the thickness, the hypothesis of the maintenance of the plane section; and h₁ and h₂ are the thicknesses of the flat shell elements below and above, respectively, the interface element. In the following equations, the index 0 will be omitted to simplify the notation.

Because E_Sb, E_Vb, and E_Nb are the deformable connection stiffnesses of the interface element in the direction of the relative displacements s_l , s_t , and s_v, the forces per unit area that emerge at this interface are S_b = E_Sb s_l , V_b = E_Vb s_t, and N_b = E_Nb s_v. Applying a compatible virtual deformation field to an interface element of Figure 4, we have, through the principle of virtual work,

(23) $\delta W_{\mathrm{int}}={\displaystyle {\int }_A\left(S_b\delta s_l+V_b\delta s_t+N_b\delta s_2\right)}dA$

Substituting the variation of the relative displacements in Eq. (23) of the principle of virtual work, we have

(24) $\delta W_{\mathrm{int}}={\displaystyle {\int }_A\left[S_b\left(\delta u_2-\delta u_1\right)+V_b\left(\delta v_1-\delta v_2\right)+N_b\left(\delta w_2-\delta w_1\right)-h_2/2S_b\delta {\theta }_{y2}-h_1/2S_b\delta {\theta }_{y1}+h_1/2V_b\delta {\theta }_{x1}+h_2/2V_b\delta {\theta }_{x2}\right]}dA$

In the finite element approximation based on displacements, the displacement equations are approximated by the shape functions associated with the nodal displacements (q). Because the lower and upper degrees of freedom are independently interpolated and the order of these followed the same order as that for the flat shell element shown in Section 2.1, the shape functions for the two-dimensional interface element are the same as those adopted for the flat shell element.

Analogous to the flat shell element, we arrive at the internal force vector and stiffness matrix of the two-dimensional interface element given by Eq. (25). For the element in question, shape functions given by quadratic polynomials represented by the column vector Φ of nine terms were adopted:

(25) $\begin{array}{cc}{f}_{\mathrm{int}}={\displaystyle {\int }_A\left\{\begin{array}{c}-S_b\Phi \\ -V_b\Phi \\ -N_b\Phi \\ \frac{h_1}{2}{V}_b\Phi \\ -\frac{h_1}{2}{S}_b\Phi \\ S_b\Phi \\ V_b\Phi \\ N_b\Phi \\ \frac{h_2}{2}{V}_b\Phi \\ -\frac{h_2}{2}{S}_b\Phi \end{array}\right\}dA}& K={\displaystyle {\int }_A\left\{\begin{array}{c}-\Phi {\left(\frac{\partial S_b}{\partial q}\right)}^T\\ -\Phi {\left(\frac{\partial V_b}{\partial q}\right)}^T\\ -\Phi {\left(\frac{\partial N_b}{\partial q}\right)}^T\\ \frac{h_1}{2}\Phi {\left(\frac{\partial V_b}{\partial q}\right)}^T\\ -\frac{h_1}{2}\Phi {\left(\frac{\partial S_b}{\partial q}\right)}^T\\ \Phi {\left(\frac{\partial S_b}{\partial q}\right)}^T\\ \Phi {\left(\frac{\partial V_b}{\partial q}\right)}^T\\ \Phi {\left(\frac{\partial N_b}{\partial q}\right)}^T\\ \frac{h_2}{2}\Phi {\left(\frac{\partial V_b}{\partial q}\right)}^T\\ -\frac{h_2}{2}\Phi {\left(\frac{\partial S_b}{\partial q}\right)}^T\end{array}\right\}dA}\end{array}$

S_b, V_b , and N_b can be obtained directly from the force per unit area versus the relative displacement curve. The derivatives of these force terms in relation to nodal displacements are given by

(26) $\frac{\partial S_b}{\partial q}=\left\{\begin{array}{c}-\Phi E_{Sb}\\ {\rm O}\\ {\rm O}\\ {\rm O}\\ -\frac{h_1}{2}\Phi E_{Sb}\\ \Phi E_{Sb}\\ {\rm O}\\ {\rm O}\\ {\rm O}\\ -\frac{h_2}{2}\Phi E_{Sb}\end{array}\right\},\frac{\partial V_b}{\partial q}=\left\{\begin{array}{c}{\rm O}\\ -\Phi E_{Vb}\\ {\rm O}\\ \frac{h_1}{2}\Phi E_{Vb}\\ {\rm O}\\ {\rm O}\\ \Phi E_{Vb}\\ {\rm O}\\ \frac{h_2}{2}\Phi E_{Vb}\\ {\rm O}\end{array}\right\}\text{and}\frac{\partial N_b}{\partial q}=\left\{\begin{array}{c}{\rm O}\\ {\rm O}\\ -\Phi E_{Nb}\\ {\rm O}\\ {\rm O}\\ {\rm O}\\ {\rm O}\\ \Phi E_{Nb}\\ {\rm O}\\ {\rm O}\end{array}\right\}$

where O is a column vector with nine null terms.

3. Results

3.1 Steel–concrete composite floor

Nie et al. (2008) numerically and experimentally evaluated a floor formed by a reinforced concrete slab connected by shear connectors to five steel beams. In their model, the load was applied through three hydraulic jacks in increments of 2 kN until rupture. During the test, displacements, strain, and slip were monitored. Figure 5 shows the composite floor with the geometric parameters of the slab, steel beams, reinforcing bars, and shear connector. Load P is applied to the three longitudinal beams and divided into four points on each beam.

Figure 5
Composite steel–concrete slab (in units of mm) (Nie et al. 2008).

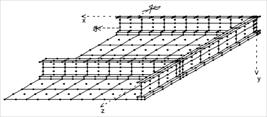
In this work, the slab and the I-shaped steel profile were simulated by a nine-node flat shell element, and the deformable connection was represented by a two-dimensional interface element of 18 nodes, as shown in Figure 6.

Figure 6
Steel–concrete composite slab discretized in flat shell and interface elements.

Among the results provided by Nie et al. (2008), the numerical and experimental load–displacement curves of the composite floor are shown. In the analysis using the elements implemented in this study, f_c = 30.3 MPa, ε_c2 = 0.2%, ε_cu = 0.35%, and v = 0.17 for the concrete. For the reinforcement bars and steel beam, a stress–strain curve defined by elastic-perfectly plastic-hardening trilinear model was used. The four points that define the tensioned part of the curve are: (0;0), (0.1432%; 295 MPa), (0.23%; 295 MPa) e (2%; 448 MPa) (steel beams), and (0;0), (0.1845%; 380 MPa), (0.2%; 380 MPa) e (4.5%; 478 MPa) (reinforcement bars). For both steels E_s = 206000 MPa, v = 0.30, and compression behavior equal in traction was admitted. For the longitudinal and transverse stiffness of the deformable connection between the steel beams and the concrete slab, the equation of Ollgaard et al. (1971) or Aribert (1992) was used: S_b = S_bu (1 - e^C1Sl)^C2, with C₁ = 0.7 mm^-1 and C₂ = 0.4. The ultimate strength of the connector can be obtained through the equations described in the technical norms and textbooks on the subject. For stud connectors of 6 mm in diameter, spaced every 60 mm, with f_eu = 450 MPa surrounded by concrete of f_ck = 30.3 MPa we have F_u = 13434 N (connector ultimate load) and S_bu = 2239 kPa (connection stiffness in the contact area). For the vertical stiffness at the contact interface, a high stiffness (E_Nb = 10⁹ kPa) was considered, that is, the total interaction for the vertical uplift.

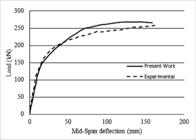
Figure 7 illustrates the results obtained from the numerical analyses using the elements developed in the present study and results of the experimental model of Nie et al. (2008).

Figure - 7
Load–displacement curve for midspan vertical displacement.

It is observed that the result obtained by using the implemented elements is relatively close to that obtained from the experimental test, demonstrating the effectiveness of the implemented elements.

3.2 Elastic line

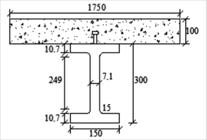
In this example, the elastic line of a fixed composite beam with a 10 m span was subjected to a concentrated force of 50 kN at the midspan is analyzed. The cross section of the composite beam was composed of a concrete slab, with E_c = 13 GPa and v = 0.2, connected to an I-shaped steel profile (IPE 30 0), with E_s = 200 GPa and v = 0. 30. Figure 8 shows the cross section with the dimensions.

Figure 8
Cross section of the mixed section (in units of mm).

Figure 9 shows the discretization of the composite beam in flat shell elements and a two-dimensional interface. From the figure, it is observed that the concrete slab was discretized by 20 flat shell elements. The steel beam had four divisions in the longitudinal direction, and, for each division, there were two flat shell elements for the flange and one for the web. For the two-dimensional interface elements, four elements were used.

Figure 9
Discretization of the fixed composite beam.

The influence of longitudinal stiffness variation on vertical displacement along the length of the beam was evaluated. The values of longitudinal stiffness used were E_Sb = 10³ kPa and E_Sb = 10⁷ kPa Because transverse and vertical displacements at the contact interface were not allowed, values for the stiffnesses of E_Vb = 10⁷ kPa and E_Nb = 10⁷ kPa respectively, were adopted.

In the following figures, Shell9+int6 is the result for the composite beam analyzed by using the nine-node flat shell element and the six-node interface element implemented by Silva and Dias (2018b). Shell9+Int18 is the result obtained by simulating the composite beam through the 9-node shell element and the 18-node interface element implemented in this study. BeamTQ+IntTQ is the result obtained by simulating the steel beam with the three-node beam element (BeamTQ) and the six-node interface element (IntTQ); both are elements presented in Sousa and Silva (2007), wherein the beam theory of Timoshenko was used in the formulation and quadratic interpolation for translation and rotation. REF is the result obtained by Brighenti and Bottoli (2014), which simulates the beam with beam elements based on Euler–Bernoulli beam theory.

The responses for the three analyses (Shell9+Int18, Shell9+Int6, and BeamTQ+IntTQ) are shown in Figure 10, and they are practically the same. The difference observed when compared with the response indicated by REF in Figure 10 is due to the difference between the theories used in the simulation of the problem, because Shell9+Int6, Shell9+Int18, and BeamTQ+IntTQ account for the shear strain, which is not considered in the REF analysis. The effects of shear lag (normal stress variation along the slab width) and poisson, which are verified when simulating the problem using flat shell elements and do not appear in the beam analysis, do not cause this difference because the responses are practically identical for the Timoshenko beam analysis (BeamTQ+IntTQ) and for the Reisner– Mindlin’s plate analysis (Shell9+Int6 or Shell9+Int18).

Figure 10
Elastic line of composite fixed–fixed beam with E_Sb = 10³ kPa.

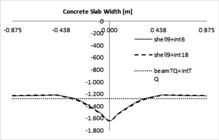
Figure 11 shows the variation along the width of the concrete slab of normal stress obtained in the most compressed fiber. It can be seen from the figure that the results obtained by Shell9+Int6 and Shell9+Int18 analyses are very close to each other. The response obtained from the BeamTQ+IntTQ analysis does not exhibit normal stress variation along the width because it simulates the problem by considering beam theory with flexion in only one plane. Figure 11 shows that, although the plate analysis reveals a shear lag effect, the areas bound by the curves and the horizontal axis are close together, generating the same contribution for the concrete slab in the beam and plate analyses.

Figure 11
Stress variation in the most compressed fiber along the concrete slab width for E_Sb = 10³ kPa.

Similar to Figure 10, it can be seen from Figure 12 that both the 6- and 18-node interface elements give almost identical results, but they present a different relationship from that of the BeamTQ+IntTQ analyses. In this case, the shear lag and poisson effect were significant and caused this difference, as evidenced by studying the variation of the normal stress along the width of the concrete slab in the analyses using flat shell and beam elements.

Figure 12
Elastic line of fixed composite beam with E_Sb = 10⁷ kPa.

Figure 13 shows that the area bound by the curves and the horizontal axis for the plate analysis is larger than the area found using Timoshenko beam analysis (for the same load). Therefore, greater stiffness is found when the problem is simulated through the beam theory of Timoshenko, which generated a smaller displacement, as shown in Figure 12. This effect, which also manifests when using Euler–Bernoulli beam theory, generated a smaller displacement in the REF analysis to compensate for the difference in the response between the flat shell elements and the Euler–Bernoulli beam element shown in Figure 10. That is, a reduction of the concrete slab width should be made so that the displacement and the area defined by the region bound by the beam theory curve and the horizontal axis are the same as in the plate analysis. Therefore, it is concluded that beam analysis may generate an overestimation of the bending stiffness of the composite beam.

Figure 13
Stress variation in the most compressed fiber along the concrete slab width for E_Sb = 10⁷ kPa.

4. Conclusions

Formulations of the flat shell and two-dimensional interface finite elements are presented for the numerical analysis of shell structures with possible deformable connections. The most practical case would be the composite floors formed by reinforced concrete slabs associated with steel beams by means of a deformable connection.

Two examples were analyzed to verify the potential usefulness of the elements implemented in this study. Some other examples have been evaluated by other researchers using numerical methods, commercial software, and experimental tests. The results demonstrate that the implemented elements are a useful tool for structural analysis in some practical situations.

Acknowledgment

The authors would like to thank the Federal University of Ouro Preto, PROPEC, CNPq, and FAPEMIG for their financial support.

References

• AMERICAN SOCIETY OF CIVIL ENGINEERS. Finite element analysis of reinforced concrete. New York: ASCE, 1982.
• ARIBERT, J. M. Slip and uplift measurements along the steel and concrete interface of various types of composite beams. In: MAZZOLANI, F. M. (ed.). Testing of metals for structures: proceedings of the international RILEM workshop. London: Taylor & Francis, 1992. p. 395–407.
• BATOZ, J. L.; HAMMADI, F.; ZHENG, C.; ZHONG, W. On the linear analysis of plates and shells using a new-16 degrees of freedom flat shell element. Computers and Structures, v.78, p. 11-20, 2000.
• BRIGHENTI, R.; BOTTOLI, S. A novel finite element formulation for beams with composite cross-section. International Journal of Mechanical Sciences, v.89, p.112-122, 2014.
• CAROL, I.; LÓPEZ, C. M.; ROA O. Micromechanical analysis of quasi-brittle materials using fracture-based interface elements. International Journal for Numerical Methods in Engineering, v. 52, p. 193-215, 2001.
• GOODMAN, R. E.; TAYLOR, R. L.; BREKKE, T. L. A model for the mechanics of jointed rock. Journal of the Soil Mechanics and Foundations Division, v. 94, n. 3, p. 637-659, May 1968.
• HUANG, Z.; BURGESS, I. W.; PLANK, R. Nonlinear analysis of reinforced concrete slabs subjected to fire. ACI Structural Journal, v. 96, n. 1, p. 127-135, 1999.
• HUANG, Z.; BURGESS, I. W.; PLANK, R. J. Modelling membrane action of concrete slabs in composite buildings in fire. Part I: theoretical development. Journal of Structural Engineering, v.129, n.8, 2003a. DOI 10.1061/(ASCE)0733-9445129:8.
  » https://doi.org/10.1061/(ASCE)0733-9445129:8
• HUANG, Z.; BURGESS, I. W.; PLANK, R. J. Modelling membrane action of concrete slabs in composite buildings in fire. Part II: validations. Journal of Structural Engineering, v.129, n.8, 2003b. DOI 10.1061/(ASCE)0733-9445129:8(1103).
  » https://doi.org/10.1061/(ASCE)0733-9445129:8(1103)
• HUGHES, T. J. R. The finite element method: linear static and dynamic finite element analysis. Englewood Cliffs, N.J.: Prentice-Hall, 1987.
• INTERNATIONAL FEDERATION FOR STRUCTURAL CONCRETE. Model Code 2010: first complete draft – Volume 1 Germany: fib, CEB-FIP, 2010. 318 p. (fib Bulletin 55).
• IZZUDIN, B. A.; TAO, X. Y.; ELGHAZOULI, A. Y. Realistic modeling of composite and reinforced concrete floor slabs under extreme loading. Journal of Structural Engineering, v. 130, p. 1972-1984, 2004.
• KALIAKIN, V. N.; LI, J. Insight into deficiencies associated with commonly used zero thickness interface elements. Computers and Geotechnics, v. 17, p. 225-252, 1995.
• LAM, D.; EHAB, E. Behavior of headed stud shear connectors in composite beam. Journal of Structural Engineering, v. 131, p. 96-107, 2005.
• NIE, J.; FANA, J.; CAI, C. S. Experimental study of partially shear-connected composite beams with profiled sheeting. Engineering Structures, v. 30, p. 1-12, 2008.
• OLLGARD, J. G.; SLUTTER, R. G.; FISHER, J. W. Shear strength of stud connectors in lightweight and normal-weight concrete. AISC Engineering Journal, v. 8, n. 2, p. 55-64, 1971.
• ROTS J. G.; KUSTERS, G. M. A.; BLAAUWENDRAAD, J. The need for fracture mechanics options in finite element models for concrete structures. In: INTERNATIONAL CONFERENCE ON COMPUTER AIDED ANALYSIS AND DESIGN OF CONCRETE STRUCTURES, 1984, Split. Proceedings [...]. Split: [s. n.], 1984. v.1, part 1, p. 19–32.
• SILVA , A. R.; DIAS, L. E. S. Numerical analysis of the effect of partial interaction in the evaluation of the effective width of composite beams. Revista IBRACON de Estruturas e Materiais, v. 4, p. 757-778, 2018a.
• SILVA, A. R.; DIAS, L. E. S. An interface element for numerical analysis of flat plate/shell elements with deformable connection. Latin American Journal of Solids and Structures, v 15, n. 2, 2018b.
• SOUSA JR., J. B. M.; SILVA, A. R. Nonlinear analysis of partially connected composite beams using interface elements. Finite Elements in Analysis and Design, v.43, n. 11-12, p. 954-964, 2007.
• SOUSA JR., J. B. M.; SILVA, A. R. A family of interface elements for the analysis of composite beams with interlayer slip. Finite Elements in Analysis and Design, v. 45, p. 305-314, 2009.
• SOUSA JR., J. B. M.; SILVA, A. R. Analytical and numerical analysis of multilayered beams with interlayer slip. Engineering Structures, v. 32, p. 1671-1680, 2010.

Publication Dates

• Publication in this collection
  21 July 2021
• Date of issue
  Jul-Sep 2021

History

• Received
  13 Sept 2020
• Accepted
  09 Mar 2021