Estimating the rock mass deformation modulus: A comparative study of empirical methods based on 48 rock mass scenarios

Abstract

The rock mass deformation modulus, E_rm, is an input parameter for most numerical modeling to verify the deformation behavior of rocks due to rock engineering activities within/on it. Among the most common methodologies used for estimating this parameter, empirical correlations based on rock mass classification schemes (e.g., RQD, RMR, GSI, and Q) stand out the most, principally because of their low cost when compared to the other methods. Herein, the main correlations used in practice are evaluated and comparted for 48 different rock quality scenarios, previously characterized and classified according to rock mass classification systems. The results obtained by each of the empirical correlations demonstrated that normalized correlations, that is, based on the ratio of the rock mass and intact rock modulus, E_rm/E_i, underestimate the E_rm values when compared to those results obtained from not-normalized correlations in the scenarios of better quality rock masses. For poor quality rock mass scenarios, both non-normalized and normalized correlation presented similar results. The correlations proposed by Hoek and Diederichs (2006) and Galera et al. (2007) estimated more central Erm values when compared to the other correlations, for all quality scenarios, while the Mitri et al. (1994) and Sonmez et al. (2006) methods estimated most high and low values of E_rm, respectively.

Keywords:
deformation modulus; empirical methods; classification schemes; rock masses

1. Introduction

The deformation modulus of the rock mass, E_rm, is an essential input parameter for many analyses of jointed rock mass behavior that includes deformations (Hoek and Diederichs, 2006). It can be estimated directly through field tests or indirectly by using empirical relationships based on classification schemes, e.g., Rock Quality Designation (Deere et al., 1967), Rock Mass Rating (Bieniawski, 1973, 1989), Q-System (Barton et al., 1974) and Geological Strength Index (Hoek, 1994). Considering that field tests are time-consuming, expensive, and often difficult to be conducted, as reported by Zhang (2016), the second approach is often used by the rock mechanics community to estimate the rock mass deformation modulus.

From the various empirical correlations proposed for estimating E_rm, standing out are those using as input parameters the RQD index (Coon and Merritt, 1970; Gardner, 1987; Zhang and Einstein, 2004), the RMR number (Bieniawski, 1978; Serafim and Pereira, 1983; Nicholson and Bieniawski, 1990; Mitri et al., 1994; Read et al., 1999; Gokceoglu et al., 2003; Ramamurthy, 2004; Sonmez et al., 2006; Galera et al., 2007; Lowson and Bieniawski, 2013), the Q-value (Barton et al., 1980; Grimstad and Barton, 1993; Barton, 1995; Pamström and Singh, 2001; Barton, 2002; Ramamurthy, 2004), and the GSI (Hoek and Brown, 1997; Hoek et al., 2002; Gokceoglu et al., 2003; Hoek and Diederichs, 2006).

Because of the number of correlations in literature, this article will evaluate their behavior in determining the deformation modulus of the rock mass for 48 different rock quality scenarios, previously characterized and classified according to rock mass classification systems.

2. Rock mass classification systems (RMCS) and their indices

A reliable prediction of rock mass behavior under different stress conditions is critical for the design of most rock engineering projects. However, this is not a trivial task due to the heterogeneous and anisotropic characteristics of the rock material and the scale effect existing in jointed rock masses. These features combined make conventional laboratory and field tests, which are necessary to estimate the mechanical parameters of this geomaterial for this purpose, an extremely cost-effective solution.

Dealing with this limitation, different rock mass classification systems (RMCS) were proposed to be used as a guide for different rock engineering applications, taking into consideration the individual characteristics of the intact rock and the discontinuities within the rock masses. Among these RMCS, the classification schemes designed by Deere et al. (1967), Bieniawski (1973, 1978), Barton et al. (1974), and Hoek (1994) have been widely used to quantify the rock mass quality based on their indices, i.e., RQD, RMR, Q e GSI, respectively.

First, the Rock Quality Designation (RQD) index was idealized by Dr. Don U. Deere in 1964 and later presented for the first time in published form by Deere et al. (1967), as reported by Deere and Deere (1988). It represents a modified borehole core recovery percentage in which all the pieces of sound core over 10 cm long are summed and divided by the length of the core run, allowing a measurement of the rock mass quality. The RQD index ranges from 0 to 100%, where high RQD values will identify a rock mass with good quality, while an RQD ranging from 0 to 50% are indicative of poor quality rock mass (Deere et al., 1967). Although the RQD is a single-based parameter, only considering the discontinuity frequency within the rock mass, it is still widely used for estimating the rock’s mechanical properties, e.g., the deformation modulus (Zhang and Einstein, 2004).

The Rock Mass Rating (RMR) system, also known as the Geomechanics Classification, was introduced first by Bieniawski (1973) and later modified over the years by the author until its last version presented by Bieniawski (1989). This system allows classification of the rock mass quality based on six different parameters: (1) the uniaxial compressive strength of the intact rock; (2) the RQD; (3) the spacing of discontinuities; (4) the condition of discontinuities; (5) the groundwater conditions; and (6) the orientation of discontinuities. Each of these parameters will attribute a rating for the rock mass, which combined, generate the overall RMR value of it, varying from 0 to 100. In a direct comparison to Deere’s index, the RMR provides a much more realistic quality condition of the jointed geomaterial due to the numbers of variables analyzed.

Almost one year after the first publication of Bieniawski’s classification scheme, Barton et al. (1974) introduced a new system to classify rock masses for engineering purposes, the Q-system. Similar to the Geomechanics Classification, this system also provides a numerical assessment of the rock mass quality using six parameters: (1) the RQD; (2) the number of joint sets; (3) the roughness of the discontinuities; (4) the degree of alteration of the discontinuities; (5) the water inflow; and (6) the stress conditions. The numerical value of Q ranges on a logarithmic sale from 0.001, for exceptionally poor rock mass quality, up to 1000, for exceptionally good rock mass quality. The main difference between the RMR and Q indices lies in the fact that the first uses the compressive strength of the intact rock as an input parameter, while the second takes into account the stress condition of the rock mass. Besides that, for similar conditions of discontinuities within the rock mass, i.e., spacing, aperture, roughness, infilling and weathering, they attribute different weightings to compose their indices.

Lastly, the Geological Strength Index (GSI) was designed by Hoek (1994) as a tool to describe a rock mass qualitatively based upon geological observations. According to the author, the GSI use as input parameters the two major features that most influence the mechanical properties of a rock mass, i.e., the overall structure conditions, also described as the blockiness (Hoek and Brown, 2019), and the surface condition of the discontinuities. Besides describing the rock mass quality, Hoek’s index is frequently used for numerical modeling in jointed rock masses, since it is used to determine the empirical constants of the generalized Hoek-Brown failure criterion (Hoek et al., 2002).

Although the RQD, RMR, Q, and GSI systems were introduced as an alternative methodology to evaluate the rock mass quality for rock engineering practices, especially to overcome the limitation of testing these jointed geomaterials as a conventional engineering material, e.g., human-made materials and soils, they were designed initially for different applications. Under these circumstances, these systems have both their strengths and weaknesses that need to be assessed individually according to some variables, such as the in-situ site accessibility conditions, the experience of the engineering and geological staff, and the previously recorded local geological features.

3. Empirical methods

This study selected the most relevant empirical methods presented in literature to estimate the deformation modulus of jointed rock masses based on their qualitative index values derived from Deere’s (1967), Bieniawski’s (1973,1989), Barton’s (1974, 2002), and Hoek’s (1994) classification schemes. Table 1 presents the RQD based correlations, where all of them are normalized, i.e., expressed in terms of the deformation ratio, E_rm/E_i. Coon and Merritt’s (1970) and Gardner’s (1987) correlations are very similar, the only difference is that the first is only applied for RQD > 57%, while the second gives an arbitrary value of E_rm/E_i for RQD < 57%. The correlation proposed by Zhang and Einstein (2004) can be applied for the full range for RQD.

Table 1
RQD-based methods.

Author (s)	Empirical Method	Eq.
Coon and Merritt (1970)	$\frac{E_{\mathrm{rm}}}{E_i}=0.0231\mathrm{RQD}-1.32$	(1)
Gardner (1987)	$\frac{E_{\mathrm{rm}}}{E_i}=0.0231\left(\mathrm{RQD}\right)-1.32\ge 0.15$	(2)
Zhang and Einstein (2004)	$\frac{E_{\mathrm{rm}}}{E_i}=k\left({10}^{0.0186\mathrm{RQD}-1.91}\right)$	(3)

• where E_rm and E_i are the deformation modulus of the rock mass and intact rock, respectively, and k is a constant parameter ranging from 0.2 to 1.8.

Since the Rock Mass Rating system, alias Geomechanics Classification, initially presented by Bieniawski (1973), was probably the most used classification scheme during the '80s and '90s, many authors suggested correlations to estimate deformation modulus of rock masses using this system. These methods can be divided into two major groups, the non-normalized equations, and the normalized equations, and are summarized in Tables 2 and 3, respectively. Among the non-normalized correlations, the ones proposed by Bieniawski (1978), Equation 5, for RMR > 50, and Serafim and Pereira (1983), Equation 6, for RMR ≤ 56, stand out in literature. While for the normalized correlations, Nicholson and Bieniawski’s (1990), Equation 11, and Sonmez et al.’s (2006), Equation 12, are commonly used for estimating the deformation modulus of rock masses using an RMR number for numerical modeling.

Table 2
RMR-based methods (non-normalized).

Author (s)	Empirical Method	Eq.
Bieniawski (1978)	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]=1.76\mathrm{RMR}-84.3$	(4)
Bieniawski (1978)	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]=2\mathrm{RMR}-100$	(5)
Serafim and Pereira (1983) a	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]={10}^{\left(\mathrm{RMR}-10\right)/40}$	(6)
Read et al. (1999)	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]=0.0001{\left(\mathrm{RMR}\right)}^3$	(7)
Gokceoglu et al. (2003)	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]=0.0736{\mathit{e}}^{\left(0.0755\mathrm{RMR}\right)}$	(8)
Galera et al. (2007) b	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]=0.0876\mathrm{RMR}$	(9)
Galera et al. (2007) c	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]=0.0876\mathrm{RMR}+1.056\left(\mathrm{RMR}-50\right)+0.015{\left(\mathrm{RMR}-50\right)}^2$	(10)

• ^a
  RMR ≤ 56.
• ^b
  RMR ≤ 50.
• ^c
  RMR < 50.

Table 3
RMR-based methods (normalized).

Author (s)	Empirical Method	Eq.
Nicholson and Bieniawski (1990)	$\frac{E_{\mathrm{rm}}}{E_i}=\frac{1}{100}\left[0.0028{\mathrm{RMR}}^2+0.9\exp \left(\frac{\mathrm{RMR}}{22.82}\right)\right]$	(11)
Mitri et al. (1994)	$\frac{E_{\mathrm{rm}}}{E_i}=0.5\left\{1-\left[\cos \left(\pi x\frac{\mathrm{RMR}}{100}\right)\right]\right\}$	(12)
Sonmez et al. (2006)	$\frac{E_{\mathrm{rm}}}{E_i}={10}^{\left(\mathrm{RMR}-1000\right)\left(100-\mathrm{RMR}\right)/4000\exp \left(\frac{-\mathrm{RMR}}{100}\right)}$	(13)
Galera et al. (2007)	$\frac{E_{\mathrm{rm}}}{E_i}={\mathit{e}}^{\frac{\mathrm{RMR}-100}{36}}$	(14)
Lowson and Bieniawski (2013) a	$E_{\mathrm{rm}}=14+\left(E_i-14\right)\left[1-{\left(\frac{100-\mathrm{RMR}}{44}\right)}^{\mathrm{RMR}/70}\right]$	(15)

• ^a
  RMR > 56.

Regarding the empirical methods developed based on the Q-value, most of the proposed correlation is indicated for fair, good and very good rock qualities, e.g., Equations 16 and 17, proposed by Grimstad and Barton (1993) and Barton (1995), respectively. For weak rocks, Barton's (2002) correlation, Equation 19, is recommended, which takes the strength of intact rock into account. Table 4 summarizes these Q based methods, which all are not-normalized equations.

Table 4
Q-based methods.

Author (s)	Empirical Method	Eq.
Grimstad and Barton (1993) a	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]=25\log \left(Q\right)$	(16)
Barton (1995) a	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]=10Q^{\left(1/3\right)}$	(17)
Palmström and Singh (2001) b	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]=8x{Q}^{\left(0.4\right)}$	(18)
Barton (2002)	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]=10{\left(Qx\frac{{\sigma }_{\mathrm{ci}}}{100}\right)}^{1/3}$	(19)

• where s_ci is the uniaxial compressive strength of the intact rock.
• ^a
  Q > 1.
• ^b
  1 < Q < 30.

Lastly, because of its direct link to the Hoek-Brown empirical constants and consequently to other engineering parameters, such as the Mohr-Coulomb strength parameters, i.e., cohesive strength and the angle of friction, several empirical methods for estimating rock mass deformation using GSI have been proposed. Among these methods, Table 5 presents several GSI-based methods to estimate the deformation modulus of rock masses, in which the generalized Hoek and Diederichs correlation, Equation 23, stands as the only normalized equation.

Table 5
GSI-based methods.

Author (s)	Empirical Method	Eq.
Hoek et al. (2002)a	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]=\left(1-D/2\right)\sqrt{\frac{{\sigma }_{\mathrm{ci}}}{100}}{10}^{\frac{\mathrm{GSI}-10}{40}}$	(20)
Hoek et al. (2002)b	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]=\left(1-D/2\right){10}^{\frac{\mathrm{GSI}-10}{40}}$	(21)
Gokceoglu et al. (2003)	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]=0.1451{\mathit{e}}^{\left(0.0654\mathrm{GSI}\right)}$	(22)
Hoek and Diederichs (2006)	$E_{\mathrm{rm}}\left[\mathrm{GPa}\right]=100\left(\frac{1-D/2}{1+{\mathit{e}}^{\left(75+25D-\mathrm{GSI}\right)/11}}\right)$	(23)
Hoek and Diederichs (2006)	$E_{\mathrm{rm}}=E_I\left(0.02+\frac{1-D/2}{1+{\mathit{e}}^{\left(60+15D-\mathrm{GSI}\right)/11}}\right)$	(24)

• where D is the disturbance factor of rock mass. ^a σ_ci ≤ 100 MPa. ^b σ_ci > 100 MPa.

4. Scenarios database

To assess the behavior of the empirical correlations presented above, they were applied to estimate the deformability modulus of rock masses from a database of different lithologies, previously characterized and classified according to the rock mass classifications systems, i.e., RQD, RMR, Q, and GSI. Table 6 presents the database of 48 scenarios selected.

Table 6
The 48 rock mass scenarios database.

Scs.	Rock Type	σci	Ei	RQD	RMR	Q	GSI	Author (s)
S1	Schist	20.0	14.0a	2.0	31	0.010	32	Coşar (2004)
S2	Schist	21.0	14.7a	21.1	34	0.480	39
S3	Schist	79.0	55.3a	13.3	44	0.090	40
S4	Schist	32.0	22.4a	16.1	31	0.200	38
S5	Schist	24.0	16.8a	19.9	34	0.540	40
S6	Limestone	13.0	9.1a	12.2	36	0.180	37
S7	Conglomerate	15.0	6.0a	93.5	58	18.750	52
S8	Shale	55.0	15.0	80.0	70	19.990	77	Bieniawski (1990)
S9	Basalt	70.0	32.0	90.0	74	11.250	79
S10	Limestone	50.0	26.0	94.0	59	6.150	55	Shafiei and Dusseault (2008)
S11	Evaporite	30.0	18.0	78.0	52	1.400	45
S12	Sandstone	95.0	40.0	80.0	55	5.340	66	Shafiei et al. (2007)
S13	Sandstone	20.0	11.6	42.0	30	0.410	45
S14	Slate	44.0	41.9	59.0	42	1.930	53
S15	Conglomerate	5.1	3.0	35.0	16	0.031	15	Shafiei et al. (2008)
S16	Conglomerate	57.0	19.9a	80.0	65	12.600	70	Heydari et al. (2019)
S17	Shale	38.0	11.4a	40.0	50	1.100	49
S18	Phyllite	30.0	18.0a	26.0	27	0.040	28	Genis et al. (2007) and Genis (2010)
S19	Phyllite	1.5	0.9a	10.0	11	0.002	13
S20	Breccia	15.0	4.4a	28.0	24	0.045	28
S21	Granodiorite	30.8	13.3	50.0	36	0.600	38
S22	Granodiorite	26.0	10.4a	24.0	29	0.330	33
S23	Sandstone	55.0	31.0	50.0	58	3.420b	53	Dalgiç (2002)
S24	Mudstone	31.0	12.0	50.0	46	0.540b	41
S25	Basalt	142.0	40.0	15.0	38	0.630	43	Özsan and Akin (2002)
S26	Andesite	93.0	41.2	41.0	34	0.560	41
S27	Tuff	24.0	11.6	10.0	21	0.110	31
S28	Basalt	52.7	39.3	60.0	36	0.130	31c	Kocbay and Kilic (2006)
S29	Schist/Slate	44.0	26.4a	44.0	30	0.120	25c	Özsan and Karpuz (1996)
S30	Quartzite	104.3	39.1a	58.0	50	1.170	45c
S31	Basalt	40.6	30.9	62.0	56	1.030	48	Gurocak et al. (2007)
S32	Tuff	8.2	2.2	25.0	34	0.156	32
S33	Limestone	62.3	31.4	69.0	48	1.880	43	Basarir et al. (2005)
S34	Sandstone	64.7	27.2	34.0	38	0.450	33
S35	Diabase	32.3	23.5	28.0	24	0.120	19
S36	Schist	24.3	12.9	10.0	28	0.020	22	Rasouli (2009)
S37	Andesite	169.8	17.3	21.0	41	0.197	35
S38	Schist	68.1	11.6	12.0	34	0.021	30
S39	Schist	20.0	13.5	16.0	46	0.425	38	Riaz et al. (2016)
S40	Marble	50.0	42.5	21.5	43	1.183	40
S41	Schist	20.0	13.5	43.5	48	1.435	42
S42	Marble/Phyllite	40.0	22.0	19.0	33	0.392	32
S43	Schist	20.0	13.5	10.0	23	0.100	26
S44	Tuff	18.5	10.9	85.0	26	0.070	29	Kaya et al. (2011)
S45	Tuff	29.4	10.6	89.0	30	0.074	35
S46	Granite	74.0	31.5a	N/A	24	0.800	19	Basarir (2006)
S47	Diorite	60.0	25.5a	N/A	21	0.050	16
S48	Gneiss	85.0	44.6a	N/A	69	17.800	80	Sapigni et al. (2003)

• where σ_ci is in MPa and E_i is in GPa. Scs. = Scenarios. ^a Estimated values using modulus ratio (MR) described by Hoek and Diederichs (2006). ^b Estimated values using Barton's (1995) correlation. ^c Estimated values using Hoek's (1994) correlation. The disturbance factor used for all scenarios was 0.

Respecting the chosen database described in Table 6, the authors took into consideration grouping them according to the following criteria: (i) lithology variability; (ii) wide range of jointed rock mass quality; (iii) availability of mechanical properties of the intact rock previously estimated through direct or indirect tests; (iv) multiple classifications for the same site using the RMCS discussed in this study; and (v) sites characterized for different civil engineering purposes, e.g., underground excavations and dam foundations.

For the comparative study between the correlations, the 48 scenarios were divided into two groups, taking into consideration the similarity between the quality of the rock mass. The first group, SG-I, consists of the poor quality rock mass scenarios, while the second group, SG-II, comprises the rock mass with better quality. The scenarios presented in SG-I are: S1, S2, S4, S5, S6, S13, S15, S18, S19, S20, S21, S22, S27, S29, S32, S34, S35, S36, S38, S42, S43, S44, S45, S46, and S47. The SG-II group covers the following scenarios: S3, S7, S8, S9, S10, S11, S12, S14, S16, S17, S23, S24, S25, S26, S28, S30, S31, S33, S37, S39, S40, S41, and S48. Table 7 gives the descriptive statistics of both groups.

Table 7
Descriptive statistical of SG-I and SG-II.

#	RQD (%)			RMR			Q			GSI
	Max.	Min.	Mean	Max.	Min.	Mean	Max.	Min.	Mean	Max.	Min.	Mean
SG-1	89	2	28.36	38	11	28.18	0.8	0.002	0.214	45	13	29.4
SG-2	94	13	55.22	74	34	51.39	19.99	0.09	4.739	80	31	50.67

5. Comparative analysis and results

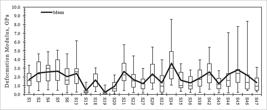
The first comparative study considered the variation of estimated values for each scenario, based on the application of the possible correlations available. Regarding the results of the SG-I, Figure 1 shows the box-whisker plots displaying the distribution of E_rm estimated of the scenarios in this group. In summary, Equations (12) and (19) were responsible for estimating the maximum deformation modulus in 28% (S1, S15, S19, S20, S36, and S38), 20% (S4, S18, S29, S34, and S42) and 28% (S2, S5, S21, S22, S27, S46, and S47) of the scenarios analyzed, respectively.

Figure 1
Box-whisker plots displaying the distribution of E_rm estimated for the scenarios in SG-I.

On the other hand, the correlation suggested by Equation (13) estimated in 80% (S2, S4, S13, S15, S18, S19, S20, S21, S22, S27, S29, S32, S34, S35, S42, S43, S44, and S45) the minimum values for the SG-I. Equation (3), which is a RQD-based method proposed by Zhang and Einstein (2004), was responsible for estimating the other 20% minimum values in this group. Equations (14), (20), (22), (23) and (24) gave the closest result to the mean in each study scenario, especially the generalized equation of Hoek and Diederichs (2006).

Regarding the group with better quality rock masses, SG-II, Figure 2 shows the distribution behavior of E_rm calculated for each scenario in this group. Equations (7) and (12) estimated almost 61% (S3, S11, S12, S17, S23, S24, S25, S26, S28, S30, S31, S33, S39, and S40) of the maximum scenarios’ values of rock mass deformation modulus. It was Equation (23), however, that estimated the highest values (S8, S9, S16, and S48). In common, these are the highest quality rock mass scenarios in SG-II.

Figure 2
Box-whisker plots displaying distribution of E_rm estimated for the scenarios in SG-II.

In contrast, Equations (3), (8) and (13) were responsible for estimating the minimum deformation modulus in 17% (S12, S14, S26, S48), 26% (S3, S23, S25, S37, S39 and S40) and 22% (S7, S10, S11, S16 and S24) of the scenarios analyzed, respectively. For the rock quality range in SG-II, Equations (11) and (24) estimated values of deformation modulus with closest result to the mean in each study scenario.

Based on the results presented above, it is noticed that non-normalized correlations tend to estimate higher values of deformation modulus as rock quality increases in most cases. In order to show this behavior, Figure 3 presents a comparison between the arithmetic mean for each scenario of the E_rm estimated using the normalized and non-normalized correlations.

Figure 3
Estimated average values of rock mass deformation modulus for non-normalized (NN) and normalized (N) empirical correlations.

For some scenarios with good rock mass quality, e.g., S8, S9, S16, and S48, there is noticeably a higher peak of the deformation modulus calculated by the non-normalized equations when compared with the normalized ones. In these cases, Equations (4), (5), (7), and (9) estimated E_rm values up to 3 times more than the values obtained using Equations (11) to (15) and (24).

For the weak rock mass scenarios, the difference between the not-normalized and the normalized correlations is much smaller. There are even situations where normalized equations give higher values, e.g., S3 and S40, which are justified by the mathematical function of the correlations used. In both scenarios cited, the correlation proposed by Mitri et al. (1994), which is a function of cosine, estimates higher values for poor to fair quality rock masses when compared with other normalized and not-normalized equations.

For the third and final analysis of this study, the behavior of the estimated deformation modulus values was considered, based on the same type of classification system for each scenario. Regarding the RQD-based methods, Figure 4 presents the range of rock mass deformation modulus calculated using Equations (1) to (3). For the scenarios with rock masses with RQD > 64%, Equations (1) and (2) estimated higher values of E_rm compared to the values estimated by Equation (3). In total, Equation (3) only overestimated E_rm values in less than 7% of the total scenarios (S14, S28, and S31). Consequently, the correlation proposed by Zhang and Einstein (2004) predicted more conservative values for the scenarios analyzed in this study.

Figure 4
Rock mass deformation modulus estimated values using RQD-based correlations.

In relation to the values estimated using the RMR-based correlations for the all the 48 scenarios (Figure 5), Equations (9) and (14) presented the mean values for poorer quality rocks, while Equations (11) and (14) presented average values for rocks with better quality. On the other hand, Equations (12) and (13) resulted in overestimated and underestimated values of E_rm, respectively, for the full range of rock mass quality.

Figure 5
Rock mass deformation modulus estimated values using RMR-based correlations.

Concerning the empirical methods that use Barton’s (1974) Q-value as an input parameter for estimating the deformation modulus of rock masses, Figure 6 gives the behavior of the E_rm values estimated using Equations (16) to (19). For the low-quality rocks scenarios, i.e., from the SG-I group, Equation (19) were the only that could be used, and yet resulted in overestimated values compared to other classification scheme methods, as pointed out before. For the scenarios with better rock mass quality, in general, Equations (16) to (17), when applicable, estimated similar E_rm values.

Figure 6
Rock mass deformation modulus estimated using Q-based correlations.

To conclude, the GSI-based methods, among the other systems, were responsible for estimating the greatest variation of rock mass deformation modulus, especially for the scenarios from the SG-II group. Taking into consideration only the estimated values using Equations (20) to (24), as illustrated in Figure 7, it is remarkable that these equations estimated similar E_rm values for scenarios formed by rock masses with poor qualities, putting in evidence the generalized equation of Hoek and Diederichs (2006).

Figure 7
Rock mass deformation modulus estimated using GSI-based correlations.

6. Conclusions

Herein, analyzed and compared were the main empirical correlations derived from the most used rock mass classification schemes (RQD, RMR, Q, and GSI) for estimating the rock mass deformation modulus. A database with 48 different scenarios of rock masses from different lithologies, previously characterized and classified according to rock mass classification systems, was used to achieve these goals. From the results discussed earlier, the conclusions obtained are as follow:

1. For both poor and good quality rock mass scenarios, the correlations proposed by Hoek and Diederichs (2006) and Galera et al. (2007), Equations (14) and (24), respectively, estimated more central Erm values when compared to the other correlations.

2. Concerning the non-normalized and normalized equations, it is noticed that for higher quality rock masses, the former tends to estimate higher values of Erm when compared to the latter. However, for conditions of rock masses with lower quality, they behave more similarly.

3. Sonmez et al.’s (2006) method estimated the lower value of Erm among all 24 correlations for most scenarios, mainly for those in the SG-I group. On the other hand, Mitri et al.’s (1994) method estimated the highest values of Erm, mainly for those in the SG-II.

4. Due to the number of different methods proposed for estimating deformation modulus, the authors of this article recommend, when possible, that three or more methods should be used to give a good confidence range of values.

Acknowledgments

The authors gratefully acknowledge the National Council for Scientific and Technological Development (CNPq) for their financial support.

References

• BARTON, N. The influence of joint properties in modelling jointed rock masses. In: ISRM CONGRESS, 8th, 1995, Tokyo, Japan. Proceedings […]. [S. l.]: International Society for Rock Mechanics and Rock Engineering, 1995.
• BARTON, N. Some new Q-value correlations to assist in site characterisation and tunnel design. International Journal of Rock mechanics and Mining Sciences, v. 39, n. 2, p. 185-216, 2002.
• BARTON, N.; LIEN, R.; LUNDE, J. Engineering classification of rock masses for the design of tunnel support. Rock Mechanics ,v. 6, n. 4, p. 189-236, 1974.
• BARTON, N. et al. Application of Q-system in design decisions concerning dimensions and appropriate support for underground installations. In: BERGMAN, M. (ed.). Subsurface space. Oxford: Pergamon, 1981. p. 553-561.
• BASARIR, H. Engineering geological studies and tunnel support design at Sulakyurt dam site, Turkey. Engineering geology , v. 86, n. 4, p. 225-237, 2006.
• BASARIR, H.; OZSAN, A.; KARAKUS, M. Analysis of support requirements for a shallow diversion tunnel at Guledar dam site, Turkey. Engineering Geology , v. 81, n. 2, p. 131-145, 2005.
• BIENIAWSKI, Z. T. Engineering classification of jointed rock masses. Civil Engineer in South Africa , v. 15, n. 12, 1973.
• BIENIAWSKI, Z. T. Determining rock mass deformability: experience from case histories. International Journal of Rock mechanics and Mining Sciences & Geomechanics Abstracts, v. 15, n.5, p. 237-247, 1978.
• BIENIAWSKI, Z. T. Engineering rock mass classifications New York: John Wiley & Sons, 1989. 251 p.
• BIENIAWSKI, Z. T. Tunnel design by rock mass classifications. Washington, DC: Department of the Army, 1990. (Technical Report GL-79-19).
• COON, R. F.; MERRITT, A. H. Predicting in situ modulus of deformation using rock quality indexes. In: DETERMINATION of the in situ modulus of deformation of rock. West Conshohocken, PA: ASTM International, 1970.
• COSAR, S. Application of rock mass classification systems for future support design of the Dim Tunnel near Alanya.2004. Thesis (Master of Science in Mining Engineering) - Middle East Technical University, Ankara, 2004.
• DALGIÇ, S. A comparison of predicted and actual tunnel behaviour in the Istanbul Metro, Turkey. Engineering Geology , v. 63, n. 1-2, p. 69-82, 2002.
• DEERE, D. U. et al. Design of surface and near-surface construction in rock. In: US SYMPOSIUM ON ROCK MECHANICS (USRMS), 8th, 1966, Minneapolis, Minnesota. Proceedings […]. [S. l.] : American Rock Mechanics Association, 1967.
• DEERE, D. U.; DEERE, D. W. The rock quality designation (RQD) index in practice. In: KIRKALDIE, L. (ed.). Rock classification systems for engineering purposes.West Conshohocken, PA: ASTM International, 1988. p. 91-101.
• GALERA, J. M.; ÁLVAREZ, M.; BIENIAWSKI, Z. T. Evaluation of the deformation modulus of rock masses using RMR: comparison with dilatometer tests. In: ISRM WORKSHOP, 2007, Madrid, Spain. Proceedings […]. [S. l.] : ISRM, 2007. p. 71-77.
• GARDNER, W. S. Design of drilled piers in the Atlantic Piedmont. In: SMITH, R. E. (ed.). Foundations and excavations in decomposed rock of the Piedmont province. Reston, Virginia: ASCE, 1987. p. 62-86.
• GENIŞ, M. Assessment of the dynamic stability of the portals of the Dorukhan tunnel using numerical analysis. International Journal of Rock mechanics and Mining Sciences , v. 47, n. 8, p. 1231-1241, 2010.
• GENIŞ, M. et al. Engineering geological appraisal of the rock masses and preliminary support design, Dorukhan Tunnel, Zonguldak, Turkey. Engineering Geology , v. 92, n. 1-2, p. 14-26, 2007.
• GOKCEOGLU, C.; SONMEZ, H.; KAYABASI, A. Predicting the deformation moduli of rock masses. International Journal of Rock mechanics and Mining Sciences , v. 40, n. 5, p. 701-710, 2003.
• GRIMSTAD, E.; BARTON, N. Updating of the Q-system for NMT. In: INTERNATIONAL SYMPOSIUM ON SPRAYED CONCRETE: MODERN USE OF WET MIX SPRAYED CONCRETE FOR UNDERGROUND SUPPORT, 1993, Fagernes, Oslo, Norway. Proceedings […]. Oslo: Norwegian Concrete Association, 1993.
• GUROCAK, Z.; SOLANKI, P.; ZAMAN, M. M. Empirical and numerical analyses of support requirements for a diversion tunnel at the Boztepe dam site, eastern Turkey. Engineering Geology ,v. 91, n. 2-4, p. 194-208, 2007.
• HEYDARI, S. et al. An investigation of the relationship between muck geometry, TBM performance, and operational parameters: A case study in Golab II water transfer tunnel. Tunnelling and Underground Space Technology , v. 88, p. 73-86, 2019.
• HOEK, E. Strength of rock and rock masses. ISRM News Journal , v. 2, n. 2, p. 4-16, 1994.
• HOEK, E.; BROWN, E. T. Practical estimates of rock mass strength. International Journal of Rock mechanics and Mining Sciences , v. 34, n. 8, p. 1165-1186, 1997.
• HOEK, E.; BROWN, E. T. The Hoek-Brown failure criterion and GSI - 2018 edition. Journal of Rock Mechanics and Geotechnical Engineering , v. 11, n. 3, p. 445-463, 2019.
• HOEK, E.; CARRANZA-TORRES, C.; CORKUM, B. Hoek-Brown failure criterion-2002 edition. Proceedings of NARMS-Tac ,v. 1, n. 1, p. 267-273, 2002.
• HOEK, E.; DIEDERICHS, M. S. Empirical estimation of rock mass modulus. International Journal of Rock mechanics and Mining Sciences , v. 43, n. 2, p. 203-215, 2006.
• KAYA, A. et al. Analysis of support requirements for a tunnel portal in weak rock: a case study from Turkey. Scientific Research and Essays ,v. 6, n. 31, p. 6566-6583, 2011.
• KOCBAY, A.; KILIC, R. Engineering geological assessment of the Obruk dam site (Corum, Turkey). Engineering Geology , v. 87, n. 3-4, p. 141-148, 2006.
• LOWSON, A. R.; BIENIAWSKI, Z. T. Critical assessment of RMR based tunnel design practices: a practical engineer’s approach. In: RAPID EXCAVATION AND TUNNELLING CONFERENCE, 2013, Washington, DC, USA. Proceedings […] . Englewood, Colorado: SME, 2013. p. 23-26.
• MITRI, H. S.; EDRISSI, R.; HENNING, J. G. Finite-element modeling of cable-bolted stopes in hard-rock underground mines. Transactions-Society for Mining Metallurgy and Exploration Incorporated , v. 298, p. 1897-1902, 1994.
• NICHOLSON, G. A.; BIENIAWSKI, Z. T. A nonlinear deformation modulus based on rock mass classification. International journal of Mining and geological engineering , v. 8, n. 3, p. 181-202, 1990.
• ÖZSAN, A.; AKIN, M. Engineering geological assessment of the proposed Uruş dam, Turkey. Engineering Geology , v. 66, n. 3-4, p. 271-281, 2002.
• ÖZSAN, A.; KARPUZ, C. Geotechnical rock-mass evaluation of the Anamur dam site, Turkey. Engineering Geology , v. 42, n. 1, p. 65-70, 1996.
• PALMSTRÖM, A.; SINGH, R. The deformation modulus of rock masses-comparisons between in situ tests and indirect estimates. Tunnelling and Underground Space Technology , v. 16, n. 2, p. 115-131, 2001.
• RAMAMURTHY, T. A geo-engineering classification for rocks and rock masses. International Journal of Rock mechanics and Mining Sciences , v. 41, n. 1, p. 89-101, 2004.
• RASOULI, M. Engineering geological studies of the diversion tunnel, focusing on stabilization analysis and support design, Iran. Engineering Geology , v. 108, n. 3-4, p. 208-224, 2009.
• READ, S. A. L.; PERRIN, N. D.; RICHARDS, L. R. Applicability of the Hoek-Brown failure criterion to New Zealand greywacke rocks. In: ISRM CONGRESS, 9th, 1999, Paris, France. Proceedings […] . [S. l.] : International Society for Rock Mechanics and Rock Engineering, 1999.
• RIAZ, A. et al. Tunnel support design by comparison of empirical and finite element analysis of the Nahakki tunnel in mohmand agency, Pakistan. Studia Geotechnica et Mechanica ,v. 38, n. 1, p. 75-84, 2016.
• SAPIGNI, M.; LA BARBERA, G.; GHIROTTI, M. Engineering geological characterization and comparison of predicted and measured deformations of a cavern in the Italian Alps. Engineering Geology , v. 69, n. 1-2, p. 47-62, 2003.
• SERAFIM, J. L; PEREIRA, J. P. Consideration of the geomechanical classification of Bieniawski. In: INTERNATIONAL SYMPOSIUM ON ENGINEERING GEOLOGY AND UNDERGROUND CONSTRUCTION, 1983, Lisboa, Portugal. Proceedings […] . [S. l.] : SPG - Sociedade Portuguesa de Geotecnia, 1983. p. 33-44.
• SHAFIEI, A. et al. Rock mass characterization along lot no. 6 of Dez-Qomroud Tunnel Project in Iran. In: ISRM INTERNATIONAL SYMPOSIUM, 5th; ASIAN ROCK MECHANICS SYMPOSIUM, 2008, Tehran, Iran. Proceedings […]. [S. l.]: International Society for Rock Mechanics and Rock Engineering, 2008.
• SHAFIEI, A.; DUSSEAULT, M. B. Rock Mass Characterization at Kangir Dam Site in Iran. In: ISRM INTERNATIONAL SYMPOSIUM, 5th; ASIAN ROCK MECHANICS SYMPOSIUM, 2008, Tehran, Iran. Proceedings […] . [S. l.] : International Society for Rock Mechanics and Rock Engineering, 2008.
• SHAFIEI, A.; HEIDARI, M.; DUSSEAULT, M. B. Rock mass characterization at the proposed Khorram-Roud Dam site in Western Iran. In: CANADA-US ROCK MECHANICS SYMPOSIUM, 1st, 2007, Vancouver, Canada. Proceedings […] [S. l.]: American Rock Mechanics Association, 2007.
• SONMEZ, H. et al. Estimation of rock modulus: for intact rocks with an artificial neural network and for rock masses with a new empirical equation. International Journal of Rock mechanics and Mining Sciences , v. 43, n. 2, p. 224-235, 2006.
• ZHANG, L.; EINSTEIN, H. H. Using RQD to estimate the deformation modulus of rock masses. International Journal of Rock mechanics and Mining Sciences , v. 41, n. 2, p. 337-341, 2004.
• ZHANG, L. Evaluation of rock mass deformability using empirical methods-A review. Underground Space, v. 2, n. 1, p. 1-15, 2017.

Publication Dates

• Publication in this collection
  15 Jan 2021
• Date of issue
  Jan-Mar 2021

History

• Received
  11 Nov 2019
• Accepted
  05 Oct 2020