Evaluation of the impact of cluster formation in a direct reduction shaft furnace through numerical simulation

Abstract

The Direct Reduction (DR) process has been growing worldwide, and there are strong context suggestions that it will grow even more. One of these factors is the environmental pressure that occurs worldwide, and there are already projects to migrate Blast Furnace route steel plants to the Direct Reduction (DR) route, due to its smaller carbon footprint. Considering the importance of this process and the challenges of carrying out experimental tests on a pilot scale, an adequate way to evaluate the process and its impacts is through numerical simulations. There are different techniques applied to models that describe the counter-current reactor in the DR process, but none of them account for the clustering phenomenon. Clustering occurs because of the sintering of the metallic iron on the surface of the pellets in such a way that they attach to each other, forming clusters that hinder the gas flow through the shaft. The present study attempted to adapt a numerical model of a DR process to account for the effect of the cluster formation. Some clustering index equations from literature and some developed as part of this study were used and tested in the model, as a function of temperature, by varying the solid volume fraction in the control unit. The equation that resulted in the adjusted output closest to the current empirical value was implemented in the model and proved to be successful.

Keywords:
iron ore; direct reduction; simulation; clustering

1

Introduction

DRI (direct reduced iron) production in 2019 reached 108.1 Mt, representing an increase of 7.3% compared to the year 2018. It was the fourth consecutive year of increase. More than 75% of this DRI production comes from a reduction process in shaft furnaces (Midrex, 2020). Some countries such as India, Iran, Algeria, USA and Russia have stood out in this scenario due to new projects and plant reconditioning. In addition, the need for technologies with lower greenhouse gas emissions is a relevant driver for new investments in the future. It is estimated that a DR route with a 100% H₂ atmosphere may reduce emissions by approximately 80% compared to a conventional Blast Furnace route (Costa et al., 2013, Arens et al., 2017, Hille, 2018, Ahman et al., 2018, Dorndorf, 2018, Hybrit, 2018). However, the process has some challenges in its operation to guarantee dynamic process control and product quality. One of the challenges is the sintering of metallic iron formed at high temperatures and the associated reducing atmosphere causing the formation of clusters(Zhang et al, 2012, Yi et al, 2013, Battle, 2014, Alencar, 2016).This condition comes from when some raw material with a high susceptibility for sticking enters the shaft furnace. So, an increase in the bed pressure is noted, which tends to increase gradually.

The reduction process that takes place inside a direct reduction reactor is complex, as it involves a set of thermochemical reactions in a heterogeneous phase system. In this context, a huge number of models have already been developed trying to represent the DR process. These models range from single-particle approaches to multiparticle and components models with topochemical and grain models (Venkateswaran and Brimacombe, 1977, Yu and Gillis, 1981, Takenaka and Kimura, 1986, Negri, 1991 and 1995, Parisi and Laborde, 2004, Piotrowski et al., 2005,, Pineau et al., 2006, Thurnhofer, 2006, Valipour et al., 2006, Ajbar et al., 2011, Nouri, 2011, Costa et al., 2013, Shams and Moazeni, 2015, Kazemi, 2017, Castro, 2018, Rocha et al., 2019). Since the DR process can be summarized as a counter-current bed composed of solid and gas into a mass and heat transfer, the most acceptable and useful models correspond to numerical models that comprise the multi interaction and multiple phase theory.

The insertion of elements and components that best describe the phenomena associated with the direct reduction process is a continuous target to achieve better operational predictability and quality values. A recent example that can be cited is the study of the particle shape factor charged in a Corex reactor (You et al., 2019). But, there are still no models that consider the phenomenon of clustering formation impacting the bed’s permeability and its stability.

In this sense, the present study used data from other studies (Pereira, 2012, Alencar, 2016, Griscom et al., 2000) concerning the clustering index in different temperatures to provide enough data to establish parameters and correlations that could be added in a model based on transport equations applied to reactive multiphase and multicomponent systems in order to estimate the impact of cluster formation inside the bed on the operational parameters.

2

Methodology

2.1

Clustering index experiment

The standard test to measure the susceptibility of clustering formation is the ISO11256. This test is based on an isothermal reduction at 850 °C in a reducing atmosphere composed of CO and H₂. At the end of the test, the reduced mass is weighed and put into a tumbling cycle. At the end of each revolution, the mass in the form of a cluster is weighed and subjected to the drum again (ISO, 2007). Eq.1 shows how the international standard ISO11256 standard establishes the clustering index.

(1)$$Cl=\frac{100}{8\times m_r}\times \sum _{i=1}^8{\mathrm{c}\mathrm{m}}_i$$

Where: m_r is the total mass after reduction and cm_i is the mass (g) of the cluster portion after each revolution “i”.

Previous studies (Pereira, 2012, Zhang et al., 2012, Yi et al., 2013, Alencar, 2015 and 2016) evaluated the metallic iron morphology present at different pellet clusters considering different reduction temperatures. According to these studies, as the reduction temperature increases, the clustering index also rises. Based on these data, it was possible to formulate Equations 2, 3, 4 and 5 that correlate with the clustering index (CI) as a function of temperature. Three of these equations consider the effect of temperature as linear and one considers the effect as exponential. All of them were evaluated in this study.

(2)$$C/1(\mathrm{\%})=0.38\times T\left({}^{°}\mathrm{C}\right)-308.67\text{ (Alencar, 2015) }$$

(3)$$C/2(\mathrm{\%})=0.445\times T\left({}^{°}\mathrm{C}\right)-376.75\text{ (Alencar, 2015) }$$

(4)$$C/3(\mathrm{\%})=0.435\times T\left({}^{°}\mathrm{C}\right)-347.25\text{ (Alencar, 2015) }$$

(5)$$Cl4(\mathrm{\%})=0.0004\mathrm{e}0.0122\times T\left({}^{°}\mathrm{C}\right)\text{ (Alencar, 2015) }$$

2.2

Modeling concept

a

General conditions

The mathematical modeling of the DR process in the shaft furnace can be represented by the transport equation of momentum, energy and chemical species (Melaaen, 1992, Castro et al., 2018, Patankar, 2018, Rocha et al., 2019). In this approach, two phases can be discriminate, gas and solid. The gas phase is represented by the reductant gas injected in the reduction zone, the gas generated in the reduction reaction and reform, the cooling gas, and the carburization reaction. The solid phase is the metallic burden, that is composed of pellets and lump. The model can also represent the size distribution, divided into granulometric ranges for the pellets and lump. In this implementation, kinetic constants were assumed to be the same for all materials. Thus, the reduction rate is different due to physical characteristics, such as size, shape factor and porosity.

The principle of solid arrangement in the control volume is assumed. Thus, this approach considers that the gas phase fills the voids. Therefore, as in the rule of continuity, then Equation 6 can be applied.

(6)$${\epsilon }_{\mathrm{g}}+{\epsilon }_{\mathrm{s}}=1$$

The term ε_g in the above equation corresponds to the gas fraction and the ε_s is the solid fraction in the volume. To calculate the solid fraction in the volume, the mixture rule is applied according to Equation 7.

(7)$${\epsilon }_{\mathrm{s}}=\sum {\mathrm{f}}_{\mathrm{m}}$$

The granulometric ranges for pellets and lumps in the solid phase are represented by the index “m” in the above equation.

b.

Process governing equations and boundary conditions

For each phase considered in the control volume, the conservation rule is applied. Thus the momentum, energy and chemical species transport equation can be calculated. To represent the industrial process, the corresponding boundary conditions are applied in these equations. The fluxes and volumetric composition to the reduction and cooling gas inlet are assumed to be known. For the gas phase, the reduction and cooling zone are considered. Due to pressure difference, the gas does not pass from one zone to another. The solids assume movement against the upward gas flow and it is allowed to pass through these two zones. In the wall region, the gas is non-slip, and for the interaction with the solid particles, a friction coefficient is adopted. To represent the cooling of the refractories, a heat exchange coefficient is applied to the walls. For the two phases, the flows are assumed to be completely developed at the outlet.

Equations 8 to 11 represent the phase momentum, mass conservation, energy, and chemical species, respectively.

(8)$$\frac{\mathrm{\partial }\left({\rho }_i{\epsilon }_i{u}_i\right)}{\mathrm{\partial }t}+\mathrm{div}\left({\rho }_i{\epsilon }_i{\overrightarrow{U}}_i{u}_j\right)=\mathrm{div}\left({\epsilon }_i{\mu }_i\mathrm{grad}\left(u_j\right)\right)-\mathrm{grad}\left({\epsilon }_i{P}_i\right)-F_i^k$$

(9)$$\frac{\mathrm{\partial }\left({\rho }_i{\epsilon }_i\right)}{\mathrm{\partial }t}+\mathrm{div}\left({\rho }_i{\epsilon }_i{\overrightarrow{U}}_i\right)=\sum _{n=1}^{\text{nreacts }}{R}_n^i$$

(10)$$\frac{\mathrm{\partial }\left({\rho }_i{\epsilon }_i{h}_i\right)}{\mathrm{\partial }t}+\mathrm{div}\left({\rho }_i{\epsilon }_i{\overrightarrow{U}}_i{h}_j\right)=\mathrm{div}\left(\frac{k_i}{c_{pi}}\left(h_j\right)\right)+\sum _{n=1}^{n\text{ reacts }}{R}_n^i\mathrm{\Delta }{h}_n^{\mathrm{\prime }}+E_i$$

(11)$$\frac{\mathrm{\partial }\left({\rho }_i{\epsilon }_i{\phi }_i\right)}{\mathrm{\partial }t}+\mathrm{div}\left({\rho }_i{\epsilon }_i{\overrightarrow{U}}_i{\phi }_{i,\text{ specie }}\right)=\mathrm{div}\left({\epsilon }_i{D}_{\text{specie }}^{\text{bulk }}grad\left({\phi }_{i,\text{ specie }}\right)\right)+\sum _{n=1}^{\text{nreacts }}{M}_{\text{specie }}{R}_n^i$$

In the above equations, the index i and j represent the phases and velocity components, and n represents the chemical reactions. The terms μ, ε, ρ are the dynamic viscosity volumetric fractions and phase densities, respectively. U and u are vectors and velocity components. P is the pressure and F are the exerted strength by other phases. Cp, k and ∆H are heat capacity, thermal conductivity and heat due to chemical reactions, respectively. R is the reaction rates and M is the molecular weight of the species.

c.

Phase interactions

Regarding phase interactions, the model considers the momentum, energy and mass changes. The momentum interactions are modeled by semi-empirical equations (Eq. 12 and 13) with adjusted constants to the shaft furnace process.

Momentum interaction:

(12)$$F_g^s=-F_s^g=\left[\sum _m{f}_m{F}_m\right]|{\overrightarrow{U}}_g-{\overrightarrow{U}}_s|(u_g-u_s)$$

(13)$$F_m=150{\mu }_g\frac{1}{|{\overrightarrow{U}}_g-{\overrightarrow{U}}_s|}{\left(\frac{{\epsilon }_m}{(1-{\epsilon }_m)d_m{\phi }_m}\right)}^2+1.75{\rho }_g\left(\frac{{\epsilon }_m}{(1-{\epsilon }_m)d_m{\phi }_m}\right)$$

The indexes g and s indicate gas and solid respectively, m is the granulometric range of the solid phase component, f is the volume fraction of the granulometric range of the component in the solid phase, F is the interaction strength between the phases, d is the mean diameter of the granulometric range of the component in the solid phase and φ is the mean shape factor in the granulometric range of the component in the solid phase.

d.

Convection and radiation energy transfer

Equation 14 is applied to modeling the heat transfer between the solid phase components and the gas phase.

(14)$$E_g^s=-E_s^g=\frac{6{\epsilon }_m}{d_m{\phi }_m}\frac{k_g}{d_m{\phi }_m}[2+0.39{\left(\frac{\rho \left|U_g\right|}{{\mu }_g}\left(d_m{\phi }_m\right)\right)}^{\frac{1}{2}}{\left(\frac{{\mu }_g{C}_{pg}}{k_g}\right)}^{\frac{1}{3}}](T_g-T_m)$$

The above equation is accountable for convective and radiation heat transfer among the phases and T is the phase temperature.

e

Phase Properties

Based on its components, the mixing rule is used to calculate the solid and gaseous phase properties. From the ideal gas law, we can determine the gas-phase density.

(15)$${\rho }_g=\frac{P_g}{R{T}_g}\sum {\varnothing }_{j,g}{M}_j$$

In the above equation, the subscript j means the gas species. The viscosities of these components are determined as follows (Bird et al., 1960, Reid et al., 1988).

(16)$${\mu }_g=2.6693\times {10}^{-6}\frac{1}{{\mathrm{\Omega }}_{\mu ,j}}\sqrt{\frac{M_j{T}_g}{{\sigma }_j}}$$

The terms that appear in the equation are presented below:

(17)$${\mathrm{\Omega }}_{\mu ,j}=\frac{1.16145}{{\left(T^{\ast }\right)}^{0.14874}}+\frac{0.52487}{\exp \left(0.77320T^{\ast }\right)}+\frac{0.52487}{\exp \left(2.43787T^{\ast }\right)}$$

(18)$$T^{\ast }=\frac{K_{\mathit{\text{Boltzmann }}}{T}_g}{{ϵ}_j}$$

The Eucken´s polyatomic gas approximation is used to determine the thermal conductivities for the components (Wilke, 1950, Neufeld et al., 1972).

(19)$$K_j=M_j(c_{p,j}+\frac{5R}{4M_j})$$

The wilke method (Wilke, 1950) is used to determine the viscosity and thermal code of the phase.

(20)$${\lambda }_g={\mathrm{\Sigma }}_{j\in g}\left[\frac{{\gamma }_{j,g}{\lambda }_j}{\sum _{jj\in g}\left({\gamma }_{jj,}{\chi }_{j,jj}\right)}\right](\lambda =\mu ,k)$$

(21)$${\gamma }_{j,g}=\frac{\left({\varnothing }_{j,g}/M_j\right)}{\sum _{jj\in g}\left({\varnothing }_{j,g}/M_j\right)}$$

(22)$${\chi }_{j,jj}={\{1+\left({\lambda }_j/{\lambda }_{jj}\right){\left(M_{jj}/M_j\right)}^{1/4}\}}^2$$

Where it is possible to determine the binary diffusivity of the gas species according to the equation below.

(23)$$D_{j,k}^T=0.0018583\times {10}^{-4}\frac{T^{1/2}\sqrt{\left(\frac{1}{M_j}\right)+\left(\frac{1}{M_k}\right)}}{\left(P_g/101325\right){\sigma }_{ave}^2{\mathrm{\Omega }}_{ave}}$$

The terms of the above equation are determined as follows:

(24)$${\sigma }_{ave}=0.5({\sigma }_j+{\sigma }_k)$$

(25)$${\mathrm{\Omega }}_{ave}=\frac{1.06036}{{\left(T^{\ast }\right)}^{0.15610}}+\frac{0.19300}{\exp \left(0.47635T^{\ast }\right)}+\frac{1.03587}{\exp \left(1.5299T^{\ast }\right)}+\frac{1.76474}{\exp \left(3.89411T^{\ast }\right)}$$

(26)$$T^{\ast }=\frac{K_{\text{Boltzmann }}{T}_g}{{\in }_{ave}}$$

(27)$${\in }_{ave}=\sqrt{{\in }_j{\in }_k}$$

The above terms are: Boltzmann constant and σ and ∈ which are related to the collision gas types (Bird et al., 1960, Reid et al., 1988).

The equation below defines the gas temperature as a function of gas composition and enthalpy.

(28)$$H_g=\sum _{j\in g}{\varnothing }_{j,g}[\mathrm{\Delta }{H}_{j,g}^{298k}+{\int }_{298k}^{Tg}{C}_{p,j}(T)dT]$$

(29)$$C_{p,j}(T)=a_j+b_{j}T+c_j{T}^{-2}$$

Based on the solid properties, the component’s heat capacity are calculated as a function of temperature.

(30)$$C_{p,k}=a_k+b_k+T_s+\frac{C_k}{T_s^2}$$

(31)$$C_{p,s}=\sum _{k\in s}{C}_{p,k}{\varnothing }_{k,s}$$

(32)$$H_s={\mathrm{\Sigma }}_{k\in s}{\varnothing }_k[\mathrm{\Delta }{H}_k^{298k}+{\int }_{298k}^{Ts}{C}_{p,k}(T)dT]$$

Considering the intra-bed radiation and the limit layer convection, the thermal conductivity is determined (Bird et al., 1960, Reid et al., 1988, Akiyama et al., 1992).

(33)$$K_{s,e,ff}=(1-{\epsilon }_s)(k_g+a)+{\epsilon }_s{[\frac{2}{k_s}+{(\frac{k_g}{0.274}+b)}^{-1}]}^{-1}$$

The term e_s is the emissivity of solid components and the above constants are determined as follows:

(34)$$a=\alpha {[1+\left(\frac{1-{\epsilon }_s}{{\epsilon }_s}\right)\left(\frac{1-{\mathrm{e}}_s}{{\mathrm{e}}_s}\right)]}^{-1}$$

(35)$$b=\alpha \left(\frac{{\mathrm{e}}_s}{2-{\mathrm{e}}_s}\right)$$

(36)$$\alpha =0.1952d_s{\left(\frac{T_s}{100}\right)}^3\left(\frac{4.184}{3600}\right)$$

f

Numerical solution

The model uses the finite volume method (FVM) to discretize the equation of mass, energy, momentum and species taking into account a general coordinate system (Piotrowski et al., 2005, Pineau et al., 2006). These equations are integrated over a controlled volume; thus, a set of algebraic equations is created. The power-law scheme is used to determine the algebraic equation coefficients (Pineau et al., 2006). To improve the coupling of the pressure and velocity fields, the SIMPLE algorithm technique is used iteratively. To efficiently solve the algebraic equation system, the tridiagonal matrix algorithm based on the line by line solution is used. To improve the convergence, the alternated direction implicit is applied in the model solver. The solution is obtained iteratively to a stationary condition. The solution accuracy is reached by convergence criteria of 10-6 for the energy and momentum equation. The convergence target to the mass balance equation considers a difference of 0.01.

2.3

Pellets clustering modeling

Taking into account the tests and results mentioned above where it is possible to obtain a correlation between temperature and clustering index, the model applied the equations to consider the presence of pellet clusters inside the DR reactor.

All equations formulated were applied in the model considering the increase of the solid fraction in the control volume and consequently decreasing the gas permeability to the region. In order to increase the solid volume fraction, the mean diameter d_m of each solid component is recalculated as a function of CI (Eq. 37), where CI is the Clustering Index in decimal format.

(37)$$d_m=d_m\ast (1-Cl)$$

The empirical equations (Parisi and Laborde, 2004) for the solid fraction component ε_m are actualized according to the new diameter in Equation 38:

(38)$${\epsilon }_m=1-0.403{\left[100d_m\right]}^{0.14}$$

The sum of solid fraction components is used to determine the gas volume fraction (Eq. 39).

(39)$${\epsilon }_s=1-\sum {\epsilon }_m$$

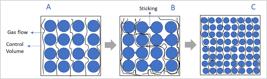
Figure 1 schematically shows the configuration of the control volumes in different aspects. Scenario A shows a reference situation with the pellets’ average diameter (d_m). Scenario B demonstrates the real aspect of the pellets that, under reduction and high temperatures, faces softening, deformations, and the sticking phenomena, leading to the gas flow disturbance. On the other hand, scenario C is the representation of the approach given in the present study, where the smaller diameter of the pellets generates a greater packing factor and, consequently, greater pressure drop, resulting in the same practical effect observed in scenario B.

Figure 1
Schematic representative diagram of the control volume:

(A) condition without clustering, (B) real flow condition with clustering and (C) condition with clustering as represented in the model.

3

Results and discussion

The evaluation of the clustering equations with different temperatures was validated, aiming similar results that were achieved in two industrial cases. In both scenarios, the reactor was a shaft furnace type and the impact of the clustering index was converted into relative productivity. After comparing and defining the best prediction equation for CI and its impact on solid volume fraction, new temperature scenarios were tested to evaluate the sensibility related to it.

3.1

Validation of the reference model with industrial data

Before starting the tests involving the new elements in the model, such as the equation that correlates solids fraction as a function of the clustering index, an initial validation of the model was carried out based on a shaft furnace's industrial data from a mill located in MENA. Tables 1 and 2 show, respectively, the main operational data of this industrial reactor and the predominant gas composition in the reduction and cooling zones.

Table 1
Industrial data from a shaft furnace reactor.

Process Parameters
Solid temperature [ºC]	33
Reduction Gas Temperature [ºC]	985
Reduction gas Flow rate [Nm3/min]	2764
Cooling Gas Temperature [ºC]	30
Cooling Gas Flow rate [Nm3/min]	850
Number of bustle gas inlets	72
Bustle gas diameter [mm]	120

Table 2
Gas composition used in the reactor and model.

Gas composition
	N2	O2	CO	CO2	H2	H2O	CH4	C2H6
Reduction gas Composition [vol%]	3.44	0.0	28.98	2.32	53.66	6.4	4.98	0.1
Cooling gas Composition [vol%]	6.13	0.0	0.92	1.24	6.06	3.5	82.15	0.0

It can be seen in Table 1 that the operational practice of the selected reactor is in line with the typical modus operandi of DR plants, where the raw material pellet enters the reactor at room temperature, and the bustle gas temperature is around 1000 °C (Atsushi, 2010). In addition, Table 2 shows that the reduction gas composition has an H₂/CO ratio of approximately 1.85, which is a value that guarantees good conditions for reduction kinetics and thermal balance in the system (Capriotti, 2012). Finally, the cooling gas is very rich in CH₄ to favor the carburization and self-reforming process inside the reactor.

The pellet burden used in this validation step also represented the market share consumed by this mill studied. Three pellets from different suppliers were simulated according to chemical and granulometric quality highlighted in Tables 3 and 4.

Table 3
Raw material chemical composition.

	FeT	FeO	SiO2	Al2O3	CaO	MgO	P
Pellet A	67.72	NA	1.61	0.46	0.78	0.07	0.022
Pellet B	67.79	0.13	1.37	0.41	0.84	0.12	0.042
Pellet C	67.81	0.31	0.81	0.17	0.94	0.61	0.027

Table 4
Raw material particle size distribution.

Materials		Range 1	Range 2	Range 3	Range 4	Range 5
Pellet A (50% in burden)	Size distribution (mm)	16	12.5	10.0	8	- 5
	Fraction (%)	1.6	55.4	35.5	6.5	0.2
Pellet B (10% in burden)	Size distribution (mm)	16	12.5	10.0	8	-5
	Fraction (%)	1.4	53.5	42.1	2.4	0.6
Pellet C (40% in burden)	Size distribution (mm)	16	12.5	10.0	8	-5
	Fraction (%)	2.9	36.6	51.7	2.5	0.6

According to Table 3, all pellets in the mix have similar iron content. However, the acid gangue content is lower in pellet C, which also has the highest values of CaO and MgO. Meanwhile pellets A and B are very similar in general, but pellet B has higher binary basicity and higher phosphorus content. In terms of size distribution, Table 4 presents in detail the particle size fractions of each pellet tested in the simulation. These data are one of the model inputs and are used to calculate the average particle size and consequently the bed porosity. Through Table 4, it is possible to say that pellet A has the distribution of larger pellets, while pellet C has the distribution of smaller pellets. The most used pellet in the reactor is A (50%), followed by C (40%) and B (10%).

Table 5 summarizes the simulation comparing the results obtained from the model based on transport equations, multiphase and multicomponent systems with the industrial results provided by the studied mill. It appears that the key process parameters, such as metallization, carburation and production in the model were comparable to the industrial values collected. There are no values in the remaining parameters similar to the industrial averages, but were within the confidence interval of the industrial values measured over 30 days.

Table 5
DRI and process parameters evaluated.

Parameters	Average metallization (%)	Average Carburization (%)	Top gas - (CO2 / CO+CO2) (%)	Top gas - (H2O / H2+H2O) (%)	Pressure Drop (atm)	Production (t/h)
Industrial Data	93.8	2.3	46.1	44.4	0.97	128
Model Result	93.75	2.35	48.11	46.76	1.09	128

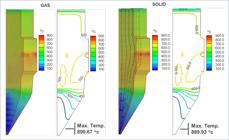
Figure 2 shows the temperature profile of solids and gas. The results obtained in the simulation are aligned with what is expected for an typical industrial operation. First, the temperatures of solids and gases are close to each other and the highest temperature observed inside the reactor in both cases is slightly lower than the bustle gas temperature because after entering the shaft, the bustle gas expands its volume and subsequently experiences a slight pressure drop. In addition, the regions of higher temperatures in the reduction zone are close to the walls, whereas the cooling zone presents lower temperatures due to the carburization reaction with CH₄, which is endothermic.

Figure 2
Solid and gas thermal profile.

3.2

CI approach results

In all tests performed, each of these equations generated a CI that replaced the Eq. 15 and led to different outputs of the solid fraction and consequently permeability. The CIs that result from each equation for different temperature ranges are shown in Table 6.

Table 6
Temperature and its relative CI for each equation tested.

TemperatureoC	CI1	CI2	CI3	CI4
850	14.33	22.50	1.50	12.76
900	33.33	44.25	23.75	23.48
950	52.33	66.00	46.00	43.20
1000	71.33	87.75	68.25	79.52
1050	90.33	109.50	90.50	146.34

All cases/equations had a version called “Adjusted” that represents the return to the base case's original condition for Dp (pressure drop). This understanding reflects the operational practices that always aim to work within an ideal range of Dp in order to keep operational safety and stability. Thus, all four evaluation cases use equations that correct the solid fraction volume, which decreases the permeability and increases the Dp of the reactor. Therefore, in the adjusted cases, the Dp is reestablished, correcting gas flow and/or temperature, and thus these adjusted cases lead to lower productivity, as shown in Table 7.

Table 7
DRI and process parameters for each case evaluated.

	Base case	CI1	Adjusted	CI2	Adjusted	CI3	Adjusted	CI4	Adjusted
Production (t/h)	128.00	128.00	96.50	128.00	104.00	128.00	96.00	128.00	100.50
Dp (atm)	1.030	1.36	1.029	1.26	1.032	1.51	0.979	1.28	1.024
Metalization (%)	93.28	93.89	93.80	93.84	93.70	93.93	93.39	93.73	93.46
CO2/(CO+CO2) (%)	46.00	46.88	49.27	46.79	48.53	46.94	49.34	46.71	48.87
H2O/(H2+H2O) (%)	43.96	43.90	43.39	43.93	43.53	43.86	43.54	43.87	43.48

Such numerical simulation results in Table 7 were contrasted with the practical experience based on two real situations involving two DR shaft furnace reactors from different locations. In one case, a pellet consumes a CI of 10%, which was replaced by another pellet of the same supplier, but with a CI of 39%. In the other case, the same pellet with a 10% Clustering Index was changed by one with a 13% CI. The impacts in both scenarios were similar. It was necessary to reduce the temperature and flow rate of the bustle gas over a period and, as a result, the furnace productivity decreased. Even though they are different furnaces, dealing with the data in both cases led to a correlation, where each additional 1% CI in the burden would result in a relative decrease of production around 0.83%. Table 8 presents the data from each numerical simulation based on the four equations formulated. Figure 3 shows the decrease of production-related to each 1% of CI, aiming to highlight the best value compared to the empirical rule.

Table 8
DRI production loss according to each CI equation.

Equation	Decrease of production t/h	Relative decrease %
CI1	31.5	24.61
CI2	32.0	25.00
CI3	24.0	18.75
CI4	27.5	21.48

Figure 3
Decrease of production for each 1% Clustering Index.

It can be seen from Table 8 and Figure 3 that the Equations CI1 and CI4 are the ones that come closest to the industrial value of 0.83%. However, when observing Table 6, it is noted that extrapolating the Equation CI4 to temperature values just above 1000 °C would result in CI values above 100%, which is something impossible. Therefore, the most suitable equation considered to represent the impact of the clustering inside the reactor was the Equation CI1.

3.3

Temperature Influence on CI

Figure 4 depicts the influence of the bustle gas temperature on CI. Each slice of the furnace represented by the letters in Figure 4 refers to a simulation made at a specific bustle gas temperature in its steady state. As can be seen, the fraction of solids (clusters) increases with increasing bustle gas temperature, where Equation Cl1 was applied to conduct this investigation. This aspect is in line with the industrial reports of buildup problems (Costa et al., 2013, Voelker, 2019) because clusters usually concentrate. In more severe cases, these clusters can accumulate inside the furnace and drastically obstruct the permeability, requiring a maintenance cold stop. This is why reactors cannot be found operating at bustle gas temperatures much higher than 1000°C.

Figure 4
Evolution of solid fraction according to bustle gas temperature simulated: (a) 985°C, (b) 1025°C, (c) 1035°C and (d) 1050°C.

4.

Conclusions

The experience of seeking literary references about the temperature impact on the formation of the clusters and associating these equations with the solid’s fraction volume and their respective bed permeability was novel and successfully tested using an adjusted mathematic approach. Based on this study, new evaluations of potential coating agents may be performed more assertively through laboratory tests and the developed numerical model, saving costs and time with more complex and industrial tests. In addition, from the data obtained with this study, it can be stated that:

• The adaptation of a pre-existing model based on the finite volumes method focusing on the RD process was suitable to assess the impact of the cluster formation inside a DR shaft furnace reactor.

• From the equations evaluated in this study, the Equation CI1 (CI1 (%) = 0.38 x T (°C) - 308.67) was the one that showed the best adherence to the empirical result of real case studies.

• This equations for clustering modelling used in different temperatures presented the same industrial trend, starting with the reactor walls and going towards the center.

Acknowledgment

The authors would like to thank CAPES-PROEX, CNPq and FAPEMIG for stimulating and supporting research.

References

• AHMAN, M. et al. Hydrogen steelmaking for a low-carbon economy: a joint LU-SEI working paper for the HYBRIT project. Lund: Lunds universitet, 2018. (EESS report n. 109).
• AJBAR, A.; ALHUMAIZI, K.; SOLIMAN, M. Modelling and parametric studies of direct reduction reactor. Ironmaking & Steelmaking, v. 38, n. 6, p. 401-411, 2011.
• AKIYAMA, T.; HOHTA, H.; TAKAHASHI, R.; WASEDA, Y.; YAGI, J. Measurement and modeling of thermal conductivity for dense iron oxide and porous iron ore agglomerates in stepwise reduction. ISIJ International, v. 32, n. 7, p. 829-837, 1992.
• ALENCAR, J. Avaliação do efeito da temperatura na morfologia do ferro metálico e na formação da colagem em diferentes tipos de pelotas de redução direta 2015. Dissertação (Mestrado em Engenharia Metalúrgica, Materiais e de Minas) – Escola de Engenharia, Universidade Federal de Minas Gerais, Belo Horizonte, 2015.
• ALENCAR, J.; RESENDE, V.; CASTRO, L. Effect of temperature on morphology of metallic iron and formation of clusters of iron ore pellets. Metallurgical and Materials Transactions B, v. 47, n. 1, p. 85-88, 2016.
• ARENS M.; WORRELL E.; EICHHAMMER W.; HASANBEIGI A.; ZHANG Q. Pathways to a low-carbon iron and steel industry in the medium-term- the case of Germany. Journal of Cleaner Production, v. 163, p. 84-98, 2017.
• ATSUSHI, M.; UEMURA, H.; SAKAGUCHI, T. Midrex processes. Kobelco Technology Review, v. 29, p. 50-57, 2010.
• BATTLE, T. et al. The direct reduction of iron. In: SEETHARAMAN, S. (ed.). Treatise on process metallurgy. [S. l.]: Elsevier, 2014. v. 3, p. 89-176.
• BIRD, R.; STEWARTAND, W.; LIGHTFOOT, E. Transport phenomena NewYork: John Wiley&Sons, 1960. (A Wiley International Edition).
• CAPRIOTTI, L. Process parameters. In: CAPRIOTTI, L. Direct reduction process [S. l.]: Development Maximize Technology, 2012.
• COSTA, A.; WAGNER, D.; PATISSON, F. Modelling a new, low CO₂ emissions, hydrogen steelmaking process. Journal of Cleaner Production, v. 46, p. 27-35, 2013.
• CASTRO, J. et al. Mathematical modeling of the shaft furnace process for producing DRI based on the multiphase theory. REM - International Engineering Journal, v. 71, n. 1, p. 81-87, 2018.
• CASTRO, J. et al. Mathematical modeling of the shaft furnace process for producing DRI using self-reducing pellets. In: 2019-SUSTAINABLE INDUSTRIAL PROCESSING SUMMIT, 2019, Flogen Star Outreach. Proceedings […]. [S. l.]: SIPS, 2019. p. 171-172.
• DORNDORF, M.; DUARTE, P.; ARGENTA, P.; MAGGIOLINO, S.; MARCOZZI, M. Transforming the steelmaking process. Steel Times International, v.42, n.7, p. 29-32, 2018.
• GRISCOM, G.; METIUS, J.; KOPFLE. Coating Agents. Direct from Midrex, Charlotte, n. 2, p. 3-6, Apr./Jun. 2000.
• HILLE, V.; REDENIUS, A. SALCOS - schrittweise, flexible Dekarbonisierung auf basis bewährter Technologie. Stahl und Eisen, v.138, n.11, p. 95-101, 2018.
• HYBRIT. Fossil-free steel: Summary of Findings from HYBRIT Pre-Feasibility Study 2016–2017. [S. l.]: HYBRIT, 2018. Available at: https://ssabwebsitecdn.azureedge.net/-/media/hybrit/files/hybrit_brochure.pdf Accessed: 20 may 2020.
  » https://ssabwebsitecdn.azureedge.net/-/media/hybrit/files/hybrit_brochure.pdf
• INTERNATIONAL ORGANIZATION FOR STANDARDIZATION. ISO 11256: Iron ore pellets for shaft direct-reduction feedstocks - Determination of the clustering index. Genebra: ISO, 2007. 13 p.
• KAZEMI, M.; POUR, M.; SICHEN, D. Experimental and modeling study on reduction of hematite pellets by hydrogen gas. Metallurgical and Materials Transactions B, v. 48, n. 2, p. 1114-1122, 2017.
• MELAAEN, M. Calculation of fluid flows with staggered and nonstaggered curvilinear nonorthogonal grids-the theory. Numerical Heat Transfer, Part B Fundamentals, v. 21, n. 1, p. 1-19, 1992.
• MIDREX. World direct reduction statistics [S. l.]: MIDREX, 2020. Available at: https://www.midrex.com/insight/world-dri-production-exceeds-108m-tons-in-2019/ Accessed: 20 May 2021.
  » https://www.midrex.com/insight/world-dri-production-exceeds-108m-tons-in-2019/
• NEGRI, E.; ALFANO, D.; ORLANDO, M.; CHIOVETTA, M. Direct reduction of hematite in a moving-bed reactor. Analysis of the water gas shift reaction effects on the reactor behavior. Industrial & Engineering Chemistry Research, v. 30, n. 3, p. 474-482, 1991.
• NEUFELD, P.; JANZEN, A.; AZIZ, R. Empirical equations to calculate the transport collision integrals for Lennard-Jones potentials. Journal Chemical Physics, vol. 57, n. 3, p.1100-1102, 1972.
• NOURI, S.; EBRAHIM, H.; JAMSHIDI, E. Simulation of direct reduction reactor by the grain model. Chemical Engineering Journal, v. 166, n. 2, p. 704-709, 2011.
• PARISI, D.; LABORDE, M. Modeling of counter current moving bed gas-solid reactor used in direct reduction of iron ore. Chemical Engineering Journal, v. 104, n. 1-3, p. 35-43, 2004.
• PATANKAR, S. Numerical heat transfer and fluid flow [S. l.]: CRC Press, 2018.
• PEREIRA, J. Avaliação da utilização de diferentes materiais para diminuição da tendência de colagem de pelotas durante o processo de redução direta 2012. Dissertação (Mestrado em Engenharia Metalúrgica, Materiais e de Minas) – Escola de Engenharia, Universidade Federal de Minas Gerais, Belo Horizonte, 2012.
• PINEAU, A.; KANARI, N.; GABALLAH, I. Kinetics of reduction of iron oxides by H₂: Part I: Low temperature reduction of hematite. Thermochimica Acta, v. 447, n. 1, p. 89-100, 2006.
• PIOTROWSKI, K. et al. Effect of gas composition on the kinetics of iron oxide reduction in a hydrogen production process. International Journal of Hydrogen Energy, v. 30, n. 15, p. 1543-1554, 2005.
• REID, R.; PRAUSNITZ, J.; POLING, B. The properties of gases and liquids New York: McGraw-Hill, 1987.
• SHAMS, A.; MOAZENI, F. Modeling and simulation of the MIDREX shaft furnace: reduction, transition and cooling Zones. JOM, v. 67, n. 11, p. 2681-2689, 2015.
• TAKENAKA, Y. et al. Mathematical model of direct reduction shaft furnace and its application to actual operations of a model plant. Computers & Chemical Engineering, v. 10, n. 1, p. 67-75, 1986.
• THURNHOFER, A. et al. Iron ore reduction in a continuously operated multistage lab-scale fluidized bed reactor-Mathematical modeling and experimental results. Metallurgical and Materials Transactions B, v. 37, n. 4, p. 665-673, 2006.
• VALIPOUR, M.; HASHEMI, M.; SABOOHI, Y. Mathematical modeling of the reaction in an iron ore pellet using a mixture of hydrogen, water vapor, carbon monoxide and carbon dioxide: an isothermal study. Advanced Powder Technology, v. 17, n. 3, p. 277-295, 2006.
• VENKATESWARAN, V.; BRIMACOMBE, J. Mathematical model of the SL/RN direct reduction process. Metallurgical and Materials Transactions B, v. 8, n. 2, p. 387-398, 1977.
• VOELKER, B. Methods for mitigating the buildup of direct reduced iron clusters on the walls of a direct reduction furnace Depositor: Midrex Technologies. U.S. 2017/0292168A1, Deposit: 12 Apr. 2017. Concession: 6 Aug. 2019.
• WILKE, C. A viscosity equation for gas mixtures. The Journal of Chemical Physics, v. 18, n. 4, p. 517-519, 1950.
• YI, L.; HUANG, Z.; JIANG, T. Sticking of iron ore pellets during reduction with hydrogen and carbon monoxide mixtures: behavior and mechanism. Powder Technology, v. 235, p. 1001-1007, 2013.
• YOU, Y. et al. Investigating the effect of particle shape on the charging process in melter gasifiers in COREX. Powder Technology, v. 351, p. 305-313, 2019.
• YU, K.; GILLIS, P. Mathematical simulation of direct reduction. Metallurgical and Materials Transactions B, v. 12, n. 1, p. 111-120, 1981.
• ZHANG, B. et al. A comparative study of influence of fluidized conditions on sticking time during reduction of Fe₂O₃ particles with CO. Powder Technology, v. 225, p. 1-6, 2012.

Publication Dates

• Publication in this collection
  20 Sept 2021
• Date of issue
  Oct-Dec 2021

History

• Received
  17 May 2021
• Accepted
  09 July 2021