Abstract
This research work aims to investigate the dynamic structural behaviour and assess the human comfort of footbridges, when subjected to pedestrian walking, based on experimental tests and tuning of finite element model. Therefore, the investigated structure is associated to a real pedestrian footbridge, spanning 24.4m, located at the campus of the State University of Rio de Janeiro (UERJ), Rio de Janeiro, Brazil. Initially, an experimental modal testing was conducted using two data acquisition strategies. After that the experimental forced vibration tests were performed on the footbridge, considering the pedestrians walking with different step frequencies. In sequence of the study, a finite element model was developed based on the ANSYS computational program. The experimental footbridge tests were used for the calibration of results on the numerical model. Finally, a human comfort assessment was performed, based on the comparisons between the results (peak accelerations), of the dynamic experimental monitoring and the recommendations provided by design guides SÉTRA, HIVOSS and AISC.
Keywords:
footbridges; experimental monitoring; dynamic analysis; human comfort
Resumo
Este trabalho de pesquisa tem como objetivo investigar o comportamento estrutural dinâmico e avaliar o conforto humano de passarelas, quando submetidas à caminhada de pedestres, com base em testes experimentais e calibrações dos modelos em elementos finitos. Assim sendo, a estrutura investigada corresponde a uma passarela de pedestres real, com vão de 24,4 m, localizada no campus da Universidade do Estado do Rio de Janeiro (UERJ), Rio de Janeiro, Brasil. Inicialmente, os ensaios para obtenção dos parâmetros modais foram realizados utilizando-se duas estratégias para aquisição dos dados. Em seguida, foram realizados testes experimentais de vibração forçada sobre a passarela, considerando os pedestres caminhando com diferentes frequências de passo. Na sequência do estudo, um modelo de elementos finitos foi desenvolvido com base no uso do programa computacional ANSYS. Os testes experimentais da passarela foram utilizados para a calibração dos resultados no modelo numérico. Finalmente, foi realizada uma avaliação do conforto humano, com base nas comparações entre os resultados (acelerações de pico), da monitoração experimental dinâmica e das recomendações fornecidas pelos guias de projeto SÉTRA, HIVOSS e AISC.
Palavras-chave:
passarelas; monitoração experimental; análise dinâmica; conforto humano
1. Introduction
Pedestrian footbridges are more and more becoming the modern landmarks of urban areas. On the other hand, structural engineers, with their experience and knowledge coupled with the use of newly developed materials and technologies, have produced pedestrian footbridges with daring structures. These facts have generated very slender pedestrian footbridges, sensitive to dynamic excitation, and, consequently, changed the serviceability and ultimate limit states associated with their design. A direct consequence of this design trend is a considerable increase in excessive vibration problems.
Several authors [1[1] Debona GL. Experimental monitoring and numerical modelling on the dynamic structural response of pedestrian footbridges. PhD Thesis (In Portuguese). Civil Engineering Post-graduate Programme, PGECIV. State University of Rio de Janeiro, UERJ. Rio de Janeiro/RJ, Brazil, 2016.
[2] Brownjohn JMW, Fu TN. Vibration excitation and control of a pedestrian footbridge by individuals and crowds. Shock and Vibration, 12: 333-347, 2005.
[3] Fernandes H. Dynamic behaviour of footbridges modelled as beams subjected to pedestrian-induced vertical direction vibrations. PhD Thesis (In Portuguese). Graduate Program in Mechanical Engineering, PPGEM, Federal University of Paraíba, UFPB, João Pessoa/PB, Brazil, 2007.
[4] Brownjohn JMW, Fok P, Roche M, Omenzetter P. Long span steel pedestrian bridge at Singapore Changi Airport. Part 2: crowd loading tests and vibration mitigation measures. Structural Engineer; 82 (16): 28-34, 2004.
[5] Bocian M, Macdonald JHG, Burn JF. Biomechanically inspired modelling of pedestrian-induced vertical self-excited forces. American Society of Civil Engineers (ASCE), 2013.
[6] Silva JGS da, Debona GL. Effect of the pedestrian-structure dynamic interaction on the vibration serviceability of steel-concrete composite footbridges. Proceedings of the 8th International Conference on Advances in Steel Structures, ICASS 2015, Lisbon, Portugal; pp. 1-15, 2015.
[7] Pfeil MS, Costa NPA, Pimentel RL, Vasconcelos RP. Analytic-numerical model for walking person-footbridge structure interaction. Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal; pp: 1079-1085, 2014.-8[8] Alonso JFJ, Saez A, Caetano E, Cunha A. Proposal and calibration of a human-structure interaction biomechanical model by the resolution of the inverse dynamic problem. Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal; pp: 975-982, 2014.] have published important scientific works related to the vibration serviceability assessment of pedestrian footbridges, based on experimental data and modelling of the dynamic structural behaviour, considering finite element analysis. It is noteworthy that research papers [1[1] Debona GL. Experimental monitoring and numerical modelling on the dynamic structural response of pedestrian footbridges. PhD Thesis (In Portuguese). Civil Engineering Post-graduate Programme, PGECIV. State University of Rio de Janeiro, UERJ. Rio de Janeiro/RJ, Brazil, 2016.
[2] Brownjohn JMW, Fu TN. Vibration excitation and control of a pedestrian footbridge by individuals and crowds. Shock and Vibration, 12: 333-347, 2005.
[3] Fernandes H. Dynamic behaviour of footbridges modelled as beams subjected to pedestrian-induced vertical direction vibrations. PhD Thesis (In Portuguese). Graduate Program in Mechanical Engineering, PPGEM, Federal University of Paraíba, UFPB, João Pessoa/PB, Brazil, 2007.
[4] Brownjohn JMW, Fok P, Roche M, Omenzetter P. Long span steel pedestrian bridge at Singapore Changi Airport. Part 2: crowd loading tests and vibration mitigation measures. Structural Engineer; 82 (16): 28-34, 2004.
[5] Bocian M, Macdonald JHG, Burn JF. Biomechanically inspired modelling of pedestrian-induced vertical self-excited forces. American Society of Civil Engineers (ASCE), 2013.
[6] Silva JGS da, Debona GL. Effect of the pedestrian-structure dynamic interaction on the vibration serviceability of steel-concrete composite footbridges. Proceedings of the 8th International Conference on Advances in Steel Structures, ICASS 2015, Lisbon, Portugal; pp. 1-15, 2015.
[7] Pfeil MS, Costa NPA, Pimentel RL, Vasconcelos RP. Analytic-numerical model for walking person-footbridge structure interaction. Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal; pp: 1079-1085, 2014.-8[8] Alonso JFJ, Saez A, Caetano E, Cunha A. Proposal and calibration of a human-structure interaction biomechanical model by the resolution of the inverse dynamic problem. Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal; pp: 975-982, 2014.] using experimental data and numerical analysis related to the human dynamic force associated with pedestrians walking confirm the ability of the people to act as a shock absorber for the structural system’s dynamic response [2[2] Brownjohn JMW, Fu TN. Vibration excitation and control of a pedestrian footbridge by individuals and crowds. Shock and Vibration, 12: 333-347, 2005.].
On the other hand, an increase of the structural system damping rate when a pedestrian crowd is crossing the footbridge in continuous flow was also reported [3[3] Fernandes H. Dynamic behaviour of footbridges modelled as beams subjected to pedestrian-induced vertical direction vibrations. PhD Thesis (In Portuguese). Graduate Program in Mechanical Engineering, PPGEM, Federal University of Paraíba, UFPB, João Pessoa/PB, Brazil, 2007.-4[4] Brownjohn JMW, Fok P, Roche M, Omenzetter P. Long span steel pedestrian bridge at Singapore Changi Airport. Part 2: crowd loading tests and vibration mitigation measures. Structural Engineer; 82 (16): 28-34, 2004.]. However, Bocian et al. [5[5] Bocian M, Macdonald JHG, Burn JF. Biomechanically inspired modelling of pedestrian-induced vertical self-excited forces. American Society of Civil Engineers (ASCE), 2013.] and Silva [6[6] Silva JGS da, Debona GL. Effect of the pedestrian-structure dynamic interaction on the vibration serviceability of steel-concrete composite footbridges. Proceedings of the 8th International Conference on Advances in Steel Structures, ICASS 2015, Lisbon, Portugal; pp. 1-15, 2015.] have observed that for different step frequency values, the structural damping can be influenced positively or negatively, resulting in different dynamic structural responses.
In his investigation, Ohlsson [9[9] Ohlsson S. Floor vibrations and human discomfort. PhD Thesis. Chalmers University of Technology, Switzerland, 1982.] reported that a moving pedestrian increased the mass and damping of the structural system and that the measured force on a rigid surface was different from the measurement on flexible structures. Baumann and Bachmann [10[10] Baumann K and Bachmann H. Durch menschen verursachte dynamische lasten und deren auswirkungen auf balkentragwerke. Report 7501-3, Institute of Structural Engineering (IBK), Swiss Federal Institute of Technology (ETH), Switzerland, 1988.] reported that dynamic loading factors were 10% smaller on flexible surfaces when compared to rigid surfaces. This fact was also confirmed by Pimentel [11[11] Pimentel RL. Vibration performance of pedestrian bridges due to human-induced loads. PhD Thesis, University of Sheffield, United Kingdom, 1997.], who observed a reduction in the natural frequency of the footbridge when subjected to pedestrian walking. Ebrahimpour et al. [12[12] Ebrahimpour RL, Sack PD, Cleek V. Computing crowd loads using a nonlinear equation of motion. Proceedings of the 4th International Conference on Civil and Structural Engineering Computing; pp: 47-52, Civil-Comp Press, United Kingdom, 1989.] concluded from their experimental data that the damping and mass of the structure are dependent on the amount of people walking. Ebrahimpour and Sack [13[13] Ebrahimpour A, Sack RL. Design live loads for crowds in motion. Conference Proceedings of Building an International Community of Structural Engineers; pp: 420-427, 1996.] also concluded that dynamic loading factors decrease as the number of people increases over the structure.
Another relevant aspect that has been investigated is related to the differences in the pedestrian footbridges’ natural frequency values when occupied by a crowd of people [14[14] Butz C, Feldmann M, Heinemeyer C, Sedlacek G, Chabrolin B, Lemaire A, Lukic M, Martin PO, Caetano E, Cunha A, Goldack A, Keil A, Schlaich M. Advanced load models for synchronous pedestrian excitation and optimised design guidelines for steel footbridges. European Comission; pp: 1-167, 2008.-15[15] Barker C, Mackenzie D. Calibration of the UK National Annex. Proceedings of the International Conference Footbridge 2008: Footbridges for Urban Renewal, Porto, Portugal, 2008.]. Other investigations [16[16] Venuti F, Racic V, Corbetta A. Pedestrian-structure interaction in the vertical direction: coupled oscillator-force model for vibration serviceability assessment. Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal; pp: 915-920, 2014.] have demonstrated that the effects of the decisions assigned to each pedestrian to change its direction (trajectory), frequency, speed and step distance; to overcome other pedestrians; or even to change their attitude when walking, should be included in the dynamic analysis in addition to the pedestrian-structure dynamic interaction.
Hence, the frequencies of the actions associated with pedestrians (walking or running) may coincide with the fundamental frequency of the structure (resonance), and dynamic effects cannot be neglected. It is also known that the dynamic response of the footbridges in resonance with the human-induced dynamic loads is amplified when compared to the static response. This way, these structures may vibrate excessively and cause human discomfort.
Therefore, considering the increasing number of reported excessive vibration problems in pedestrian structures [16[16] Venuti F, Racic V, Corbetta A. Pedestrian-structure interaction in the vertical direction: coupled oscillator-force model for vibration serviceability assessment. Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal; pp: 915-920, 2014.-17[17] Ingólfsson EL. Pedestrian-induced lateral vibrations of footbridges. PhD Thesis. DTU Civil Engineering. Technical University of Denmark - DTU. Lyngby, Denmark, 2011.], this research study aims to develop an analysis methodology to investigate the dynamic structural behaviour of footbridges when subjected to the walking of pedestrians. The test structure is related to an existing pedestrian footbridge, based on an internal reinforced concrete footbridge, spanning 24.4 m, constituted by concrete beams and slabs and currently being used for pedestrian crossing, located on the campus of the State University of Rio de Janeiro (UERJ), Rio de Janeiro, Brazil.
2. Investigated pedestrian footbridge and finite element modelling
The investigated structure is related to an existing pedestrian footbridge located in the campus of the State University of Rio de Janeiro (UERJ), Rio de Janeiro/RJ, Brazil [1[1] Debona GL. Experimental monitoring and numerical modelling on the dynamic structural response of pedestrian footbridges. PhD Thesis (In Portuguese). Civil Engineering Post-graduate Programme, PGECIV. State University of Rio de Janeiro, UERJ. Rio de Janeiro/RJ, Brazil, 2016.]. The structural system is based on a simply supported internal reinforced concrete pedestrian footbridge spanning 24.4 m, constituted by concrete beams and slabs, and being currently used for people crossing, see Figures 1 and 2. The concrete presents a 14 MPa specified compression strength and a 1.78 x 1010 N/m² Young’s Modulus. The material properties of the concrete were obtained in the original drawings of the footbridge structural project. Is fair to mention that this pedestrian footbridge was constructed at the end of the 70’s and the material properties are in fact real and were widely used in the design practice at Rio de Janeiro/RJ, Brazil, at that time. The total mass of the investigated structure is equal to 66200 kg [1[1] Debona GL. Experimental monitoring and numerical modelling on the dynamic structural response of pedestrian footbridges. PhD Thesis (In Portuguese). Civil Engineering Post-graduate Programme, PGECIV. State University of Rio de Janeiro, UERJ. Rio de Janeiro/RJ, Brazil, 2016.].
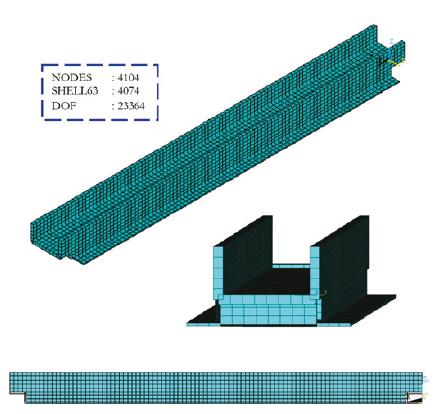
The developed finite element model adopted the usual mesh refinement techniques present in finite element method simulations, based on the ANSYS computational program [18[18] ANSYS Swanson Analysis Systems, Inc., P. O. Box 65, Johnson Road, Houston, PA, 15342-0065. Release 11.0, SP1 UP20070830, ANSYS, Inc. is a UL registered ISO 9001:2000 Company. Products ANSYS Academic Research, Using FLEXlm v10.8.0.7 build 26147, Customer 00489194. 2007.], as illustrated in Figure 3. In this computational model, all the reinforced concrete sections were represented by shell finite elements (SHELL63). This finite element has both bending and membrane capabilities. The element has six degrees of freedom at each node: translations in the nodal x, y, and z directions and also rotations about the nodal x, y, and z axes. The final computational model has presented 4104 nodes and 4074 finite elements, which resulted in a numeric model with 23364 degrees of freedom, see Figure 3. The boundary conditions (supports) were adopted according to the structural design and the footbridge supports were numerically modelled based on a traditional simply supported system.
3. Experimental modal analysis
The experimental modal analysis of the footbridge was conducted through dynamic monitoring, “in loco”, through the installation of accelerometers on the structure connected to an ADS-2002 data acquisition system and through a Polytec PDV-100 laser vibrometry system, with the aid of a Dytran impact hammer, a modal exciter (shaker) TV 51140-M and the dynamic loadings of the people, see Table 1. Modal analysis tests were carried out in order to obtain the natural frequencies and vibration modes of the structure, the time functions associated with the accelerations in relevant structural sections of the footbridge, the damping coefficients and the experimental modal mass values.
This way, two different techniques commonly used in dynamic experimental monitoring of structures (Brandt [19[19] Brandt A. Noise and vibration analysis. Signal analysis and experimental procedures. 1st Edition. John Wiley & Sons, Inc., 2011.], Cunha and Caetano [20[20] Cunha A, Caetano E. Experimental modal analysis of civil engineering structures. Journal of Sound and Vibration; 40(6):12-20, 2006.]) was used in this study: single-input multiple-output (SIMO) and single-input single-output (SISO). Before the experimental modal tests, the behaviour of the main vibration modes of the structure was investigated, in order to find the common points on the footbridge that would excite as many modes as possible. After that, three points were chosen in this analysis, aiming to obtain the Frequency Response Functions (FRFs) and the Fast Fourier Transforms (FFTs) of the investigated footbridge.
In the experimental tests, several points of interest were used to study the footbridge dynamic behaviour. These sections were used to read or even to excite the structure (randomly modified, according to the results to be obtained and expected). These points on interest (1/4; 1/2 and 3/4 of footbridge span) are illustrated in Figure 4. It must be emphasized that numerous modal tests have been performed on the structure and only the most interesting test results will be presented in this research work.
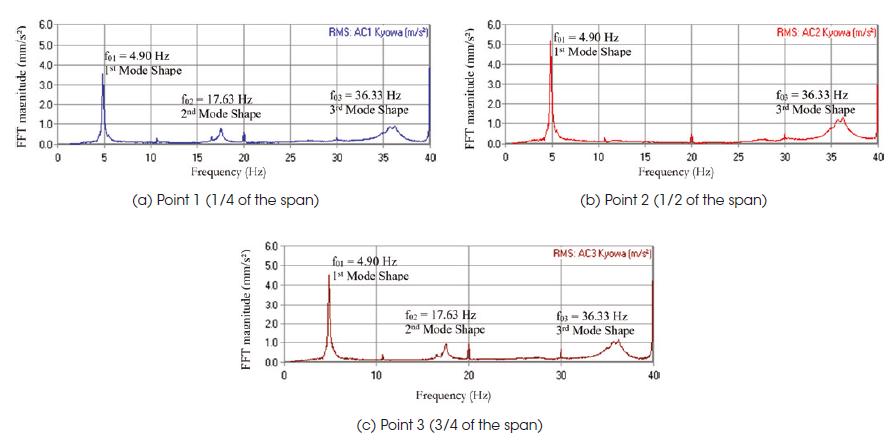
Initially, the first modal analysis test (Test 1: ADS-2002 system) was carried out considering the simplest manner, i.e. one person (mp = 95 kg) jumped at the footbridge central section (Point 2: see Figure 4). The modal analysis results were measured using three resistive Kyowa accelerometers (see Figure 5a), located at Points 1, 2 and 3 (1/4, 1/2 and 3/4 of the footbridge span, respectively: see Figure 4). A data acquisition system ADS-2002 manufactured by LYNX Electronic Technology was used in this investigation (see Figure 5b). This system is based on signal conditioners that return the sign of the variation in engineering value (specific deformation, acceleration and force), controlled by a computer. The FFT magnitudes corresponding to the output responses associated with the three accelerometers used in the experimental modal analysis of the investigated footbridge are presented in Figure 6.
After that, the second experiment (Test 2: PDV-100 and the Dytran impact hammer) was performed, based on a single-input single-output technique, combining the Polytec vibrometer PDV-100 and the Dytran impact hammer, as shown in Figure 7. In this test, the excitation provided by the Dytran impact hammer was located at footbridge middle span (Point 2: see Figure 4), and the velocities, in the time domain, were measured at Points 1, 2 and 3 (1/4, 1/2 and 3/4 of the footbridge span, respectively: see Figure 4). The input and output parameters of the dynamic response were properly measured, defining the vibrations of the footbridge. The basic functioning of the Laser Doppler Vibrometry (LDV) methodology is related to a laser beam focused on the tested structure so that the relative movement between the laser and the structure causes the presence of the Doppler Effect, i.e. the relative change in wavelength and frequency of a wave when the observer and the source are moving [19[19] Brandt A. Noise and vibration analysis. Signal analysis and experimental procedures. 1st Edition. John Wiley & Sons, Inc., 2011.]. To do this experimental test, the PDV-100 was positioned on the concrete slab of the investigated footbridge and properly isolated to avoid vibrations. In this situation, the upper footbridge was used as a non-vibrating reference system. The FRFs and the coherence curves of the dynamic response, based on 10 impacts on the footbridge for averaging, associated to the output signals obtained in the experimental modal analysis of the structure are presented in Figure 8. It is noteworthy that the coherence curves represent an very important data in the execution of the experimental tests, due to the fact that these curves show how the dynamic response can be representative of the reality or not. These coherence curves are based on a scale from 0 to 1, where 0 represents 0% of representativeness and 1 represents 100% of representativeness.
Experimental FRF magnitudes and consistency curves of the footbridge vibration modes (Test 2)
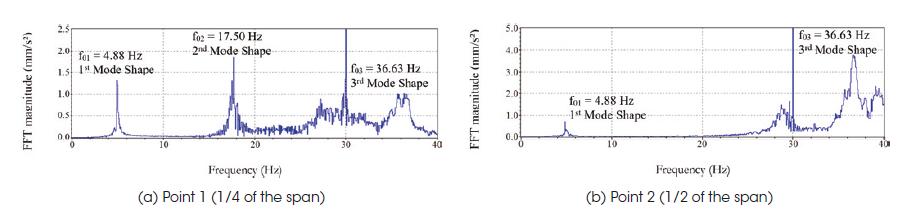
In sequence of the experimental analysis, the third modal vibration test (Test 3: Modal Exciter and PDV-100) was performed using the Modal Exciter (Shaker) TV 51140-M and the BAA 1000 power amplifier, as illustrated in Figure 9. The dynamic excitation was located at 1/4 of structure span (Point 1: see Figure 4), and the velocities, in the time domain, were obtained at Points 1 and 2 (1/4 and 1/2 of the footbridge span, respectively: see Figure 4), in modal analysis after the excitation. In this test, only the dynamic response parameters were measured and the impact input data was not obtained. The velocities in the time domain were measured using the Laser Vibrometry System PDV 100 (see Figure 9). The SGenerator app installed on the iPad A1459 was used to generate square wave signals connected to the power amplifier (BAA 1000) and the vibration exciter (Shaker) for this modal analysis test. The experimental FFT magnitudes of the pedestrian footbridge mode shapes are described by Figure 10.
The damping ratios were obtained via dynamic experimental monitoring of the tests previously described (Tests 1 to 3) and the results were summarized and presented in Table 2. In this investigation, the damping coefficients were obtained experimentally in Test 1 using the logarithm decrement filtering the respective vibration modes. In Tests 2 and 3, the “3Db Bandwidth” method [19[19] Brandt A. Noise and vibration analysis. Signal analysis and experimental procedures. 1st Edition. John Wiley & Sons, Inc., 2011.] was used in the frequency domain, according to Equation (1). This equation is valid for low damping coefficients (ξ < 0.1) [19[19] Brandt A. Noise and vibration analysis. Signal analysis and experimental procedures. 1st Edition. John Wiley & Sons, Inc., 2011.]. In this situation, the upper (fs) and lower (fi) frequencies were defined as half of the maximum peak value squared that occurs (or 3dB), as presented in Equation (1).
Where:
ξ = damping coefficient;
fs = upper frequency in Hz;
fi = lower frequency in Hz;
fd = damped natural frequency in Hz.
In Tests 2 and 3, the critical damping corresponding to the vibration modes was obtained through the “Band Cursor” tool available in the “Polytec Vibrometer Software”. This tool has the extensive peak analysis capability enhanced by a band cursor that provides statistical parameters and harmonic oscillator curve adjustment, adjusted to the vibration peaks of the dynamic response, by plotting the harmonic cursor up to 12 lines in the order of the base frequency of the structure.
In order to obtain the experimental modal mass values, some parameters need to be known from the experimental tests (the resonance peaks, the vibration mode magnitude and the vibration mode damping). In this investigation, these parameters were obtained through the VibSoft 5.1 software, based on the experimental data related to Test 2 (Test 2: PDV-100 and the Dytran impact hammer), in the frequency domain and also considering a bandwidth of 3dB [21[21] Prislan R. Laser doppler vibrometry and modal testing. University of Ljubljana, 2008.]. Considering these parameters and based on the use of Equations (2) and (3) [21[21] Prislan R. Laser doppler vibrometry and modal testing. University of Ljubljana, 2008.], the modal mass was calculated as the inverse of the modal constant at the point of maximum modal amplitude of the footbridge.
Where:
Ar = modal constant for the r mode;
|H| = Magnitude of the mode (displacement / force);
Ωr = natural frequency in rad/s of the r mode;
xr = damping of the r mode;
mr = modal mass of the r mode.
The experimental modal mass values obtained for the first and second vertical vibration modes of the analysed pedestrian footbridge were equal to 33402 kg and 29529 kg, respectively. The modal mass value of the third vibration mode was not obtained due to the fact that this mode shape presents a resonance peak very close to other modes, falling under the restrictions of the adopted method utilised to obtain the modal mass.
Based on the two strategies used for the dynamic experimental monitoring of the footbridge, three natural frequencies of the structure were identified, corresponding to the vertical vibration of the system (bending mode shapes); the damping coefficients and the modal mass values were identified as well. It is worth emphasizing that the agreement between the dynamic structural responses of the investigated footbridge obtained experimentally indicates a positive validation of the developed experimental tests.
4. Calibration of natural frequencies and vibration modes
The footbridge natural frequencies and vibration modes were determined with the aid of numerical simulations, based on the finite element method using the ANSYS computational program [18[18] ANSYS Swanson Analysis Systems, Inc., P. O. Box 65, Johnson Road, Houston, PA, 15342-0065. Release 11.0, SP1 UP20070830, ANSYS, Inc. is a UL registered ISO 9001:2000 Company. Products ANSYS Academic Research, Using FLEXlm v10.8.0.7 build 26147, Customer 00489194. 2007.]. The numerical results were compared with the obtained experimental results, according to Tables 1 and 2 and also Figures 11 and 12.
The investigated footbridge dynamic response (modal analysis) was analysed and the numerical model was calibrated with the experimental results, through the addition of the mass corresponding to the finishing coat on the floor slab and longitudinal beams, which was included to the concrete structure right after its construction process, and was not predicted in the original structural design. Besides that, it can be emphasized that the dynamic behaviour of the footbridge was consistent in comparison with the experimental results, when the boundary conditions (supports) were modelled using a traditional simply supported model.
The numerical analysis carried out by Debona [1[1] Debona GL. Experimental monitoring and numerical modelling on the dynamic structural response of pedestrian footbridges. PhD Thesis (In Portuguese). Civil Engineering Post-graduate Programme, PGECIV. State University of Rio de Janeiro, UERJ. Rio de Janeiro/RJ, Brazil, 2016.] showed natural frequencies of 4.90 Hz and 16.92 Hz for the first two vertical vibration modes of the structure, as presented in Table 2 and Figure 11, with modal mass of 31275 kg and 27488 kg for these modes shapes, respectively. The modal mass of the first vibration mode is equal to half of the total mass of the footbridge [1[1] Debona GL. Experimental monitoring and numerical modelling on the dynamic structural response of pedestrian footbridges. PhD Thesis (In Portuguese). Civil Engineering Post-graduate Programme, PGECIV. State University of Rio de Janeiro, UERJ. Rio de Janeiro/RJ, Brazil, 2016.].
It must be emphasized that the natural frequency values of the investigated footbridge were coherent and reliable when compared with the experimental values, with differences between 1% and 7%, when the first, second and third vibration modes were investigated, as presented in Table 2. On the other hand, the modal mass values determined by the finite element modelling were compared with the experimental values (first and second vibration modes), obtained by the peak picking method. The analysed results presented small differences, 6% to 8%, demonstrating a very well correlation between the experimental and numerical values.
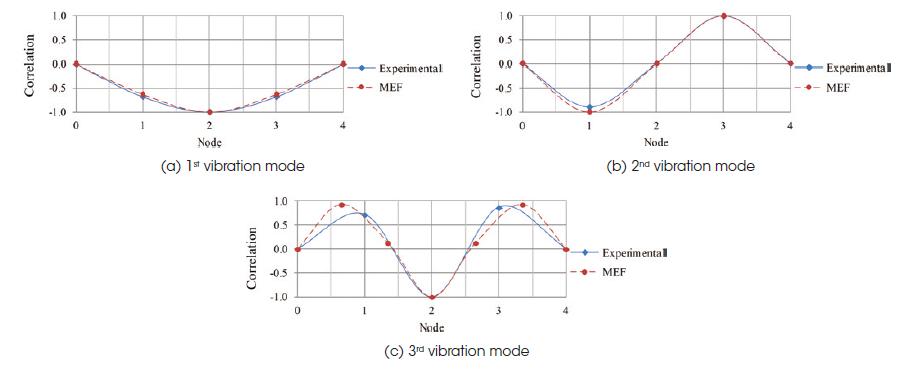
In sequence, Figure 11 illustrates the footbridge bending mode shapes, obtained based on numerical modelling, and Figure 12 presents the comparison between the first three experimental mode shapes, obtained via experimental monitoring, based on the modal analysis test (Test 1: ADS-2002 system), and the three corresponding vibration modes obtained by finite element modelling (Figure 11). This comparison is related to the correlation of the experimental amplitudes obtained in the frequency domain and the amplitudes of the numerical mode shapes.
It should also be noted that the experimental footbridge mode shapes obtained using the accelerometers precisely coincided with those generated through the numerical modal analysis, except for the third vibration mode, see Figure 12. However, it’s important to point out that the modal curves were generated by point’s approximation and these points coincide in both cases; showing that a better approximation between modes (experimental and numerical) can be obtained by increasing the number of the adopted reference points, see Figure 12.
Based on the results presented in Table 2 and Figures 11 and 12, it can be seen that the obtained experimental dynamic structural response agreed very well when the different strategies used in the experimental tests were investigated, as well as with the numerical results (Tests 1, 2 and 3: see Tables 1 and 2 and Figures 11 and 12). These results (experimental and numerical) are very important for the evaluation of the dynamic structural response of the investigated structural model to know its behaviour when subjected to walking human loads.
5. Experimental forced vibration analysis
Considering the experimental forced vibration analysis, the human walking excitation on the investigated reinforced concrete pedestrian footbridge was performed based on two control groups: the first one was intended to excite the structural model to cause a resonance motion with a controlled step frequency; the second one was related to freely random people crossing the footbridge as it occurs normally during in service life. The obtained data related to these experimental tests were recorded by the acquisition system ADS-2002 using resistive Kyowa accelerometer located at Point 2 (see Figure 4). Figures 13 to 16 show the typical layouts (photos and typical walking paths) and Table 3 describes the forced vibration tests.
To control the step of each pedestrian and to maintain the synchronization of the rhythm of the group of people that moved on the structure a metronome was used. This device was connected to a loudspeaker so that it was possible to produce sound pulses of regular duration. The representative unit of the metronome is the “bpm” (beats per minute). Therefore, each sound beating corresponds to the contact of each step of the pedestrian on the structure.
Initially, the value in the metronome was set at 96 bpm (fp = 1.60 Hz, slow walking) and at 147 bpm (fp = 2.45 Hz, fast walking), so that the second harmonic (2 x 2.45 Hz = 4.90 Hz) and the third harmonic (3 x 1.60 Hz = 4.80 Hz) of pedestrians walking that synchronously crossed the footbridge could force a resonant movement with the first vertical vibration mode (f01 = 4.90 Hz, see Table 2). Thereafter, in order to perform additional tests, the metronome value was changed: 102 bpm (fp = 1.70 Hz) in order to induce pedestrians to cross the structure at a slow walk; 120 bpm (fp = 2.00 Hz), inducing pedestrians to cross the structure at a normal walking pace and 138 bpm (fp = 2.30 Hz) considering the pedestrians to cross the structure at a fast walk. After these experimental trials, pedestrians randomly walked on the studied footbridge. The forced vibration tests were performed in such a way that the structure was excited through human walking performed by people at slow, normal, fast or random walking paces with the measured frequencies in the metronome. The walking was distributed in such a way as to have equal spacing between individuals, measured by a timer with equal time between pedestrians.
In relation to the data analysis (footbridge accelerations), the experimental signs were acquired with a sampling rate equal to 100 Hz. In addition, a fifth order Butterworth low pass filter with a cut-off frequency of 50 Hz was used in the investigation. The Fast Fourier Transform (FFT) functions of the experimental accelerations presented in this analysis were obtained based on the theory of signal processing [19[19] Brandt A. Noise and vibration analysis. Signal analysis and experimental procedures. 1st Edition. John Wiley & Sons, Inc., 2011.-20[20] Cunha A, Caetano E. Experimental modal analysis of civil engineering structures. Journal of Sound and Vibration; 40(6):12-20, 2006.]. The duration of each acquisition was in the range between 15 and 60s and the initial parts of each signal were discarded to collect only the part of in which the pedestrian flow was steady. It should be noted that a Hanning window was used to minimize the effects of using a non-integer number of cycles on an FFT, reducing the amplitude of the discontinuities at the edges of each finite sequence.
The experimental results associated to the dynamic structural response of the footbridge (vertical accelerations) are presented in Figures 17 to 21, considering 8 people walking on the concrete slab, aiming to illustrate the general behaviour of the dynamic response. These results were obtained in the time and frequency domain, respectively; corresponding to the output response associated with the Kyowa accelerometers (Point 2: see Figure 4). It should be emphasized that the horizontal axes of the graphs present the time in “hour: minute: second” and frequency in Hz, respectively and the vertical axes present the accelerations and the FFTs magnitude.
Dynamic structural response of the footbridge due to slow walking of 8 people (fp = 1.60 Hz)
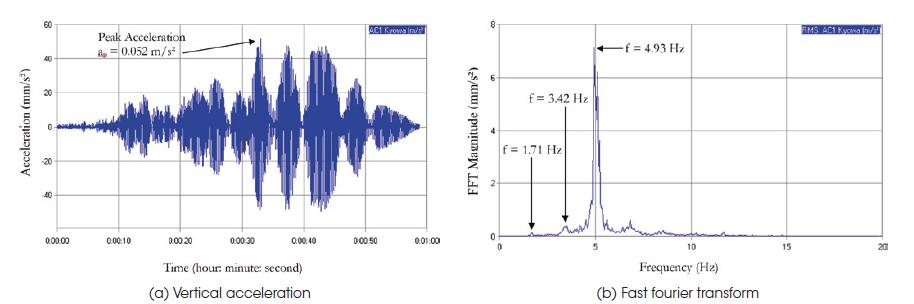
Dynamic structural response of the footbridge due to slow walking of 8 people (fp = 1.70 Hz)
Dynamic structural response of the footbridge due to normal walking of 8 people (fp = 2.00 Hz)
Dynamic structural response of the footbridge due to fast walking of 8 people (fp = 2.30 Hz)
Dynamic structural response of the footbridge due to fast walking of 8 people (fp = 2.45 Hz)
In sequence, Table 4 presents the peak accelerations values of the investigated footbridge, obtained through dynamic experimental monitoring. The maximum acceleration values found in this experimental investigation are respectively equal to 0.075 m/s2 (fp = 1.60 Hz: slow walking; see Figure 17) and 0.052 m/s2 (fp = 1.70 Hz: slow walking; see Figure 18), considering 8 people in slow walking on the structural model, respectively; 0.030 m/s2 (fp = 2.00 Hz: normal walking), for 12 pedestrians in normal walking on the footbridge; 0.114 m/s2 (fp = 2.30 Hz: fast walking), for 12 people in fast walking on the structure; 0.157 m/s2 (fp = 2.45 Hz: resonance) for 12 people in resonance walking on the footbridge and 0.046 m/s2 for 14 people walking freely on the footbridge concrete slab (random walking), as presented in Table 4.
The results demonstrated that the maximum peak acceleration value occurred when the pedestrians are walking in resonance with relation to the second harmonic (2 x 2.45 Hz = 4.90 Hz) of the dynamic action. It should be noted that pedestrian synchronization difficulties occur in the step frequency and in the permanence of the distance between individuals. This fact is explained by the length of the step of each pedestrian being unique and the difficulty of some individuals to remain in synchronized movement. Another important factor was the logistical difficulty of the experimental tests performed using cable accelerometers, due to the fact that the cables coupled in the accelerometer of the first pedestrians walking on the footbridge were dragged along the structure span involuntarily, causing uncontrolled situations of the human step, due to the concern of the pedestrian in not stepping on the cables. The composition of humans walking in a single row and the number of pedestrians were limited, showing that in future experimental tests, accelerometers without cabling can be used for better synchronization.
6. Human comfort assessment
In this section of the paper, the footbridge human comfort levels are investigated. The results of all human walking tests are summarised in Table 4. It can be noted from Table 4 results that the human comfort criterion proposed by the SÉTRA [22[22] Technical Guide Footbridges: Assessment of Vibrational Behaviour of Footbridges under Pedestrian Loading. SÉTRA: Service d’Études Techniques des Routes et Autoroutes, 2006.] and HIVOSS [23[23] HIVOSS “Human Induced Vibration of Steel Structures”. Design of Footbridges Guideline. Research Fund for Coal and Steel, 2008.] technical guides was satisfied for the sixteen investigated walking situations. It means that the experimental acceleration values lie in range of 0.0 to 0.50 m/s² (see Table 4), which corresponds to a maximum human comfort for the investigated pedestrian footbridge.
On the other hand, regarding the AISC technical guide [24[24] Murray TM, Allen DE, Ungar EE, Davis DB. Vibrations of Steel-Framed Structural Systems due to Human Activity. Second Edition. Steel Design Guide Series. American Institute of Steel Construction, AISC, 2016.], even though the acceleration limit of 0.15 m/s² for indoor footbridges is respected in most of investigated situations (slow, normal, fast, resonance and random walking cases: see Table 4), the peak acceleration value of 0.157 m/s² for the resonance case slight overpass this limit (alim=0.15 m/s²). This way, it is interesting to point out that a person standing on the investigated structure can perceive an acceleration value equal to 0.034 m/s² (just perceptible), and 0.10 m/s² (clearly perceptible), based on the indication of human perceptibility thresholds for vertical vibrations (person standing) proposed by Bachmann et al. [25[25] Bachmann H et al., Vibration problems in structures - practical guidelines, Basel (Switzerland):Institut für Baustatik und Konstruktion, Birkhäuser, 1995.].
Finally, the authors would like to emphasize that this investigation will continue based on the development of a mathematical model, aiming to numerically simulate the pedestrian-structure dynamic interaction, considering the use of biodynamic models of people. This way, the results of the pedestrian walking vibration tests can also be validated and represented by FEM simulations. These models simulate the dynamic characteristics of the pedestrians (mass, stiffness and damping) and have been used as an efficient alternative to better evaluate human comfort rather than the traditional “force-only” model widely used for dynamic analysis of footbridges.
7. Conclusions
This research work analysed experimentally and numerically the dynamic structural behaviour of an internal reinforced concrete pedestrian footbridge spanning 24.4m, constituted by concrete beams and slabs and being currently used for pedestrian crossing located in the campus of the State University of Rio de Janeiro (UERJ), Rio de Janeiro/RJ, Brazil. Thus, the main conclusions of the present investigation are:
-
1. Modal Analysis: The modal analysis of the investigated structure was performed both experimentally and numerically. The modal testing of the footbridge was performed by dynamic monitoring through accelerometers installed on the concrete slab as well as by a vibrometer device based on a Laser Doppler Vibrometry methodology. Then, these experimental results were calibrated with a three-dimensional finite element model based on the use of ANSYS program. It must be emphasized that a good agreement between the experimental and numerical results was obtained. The highest energy transfer peak contribution related to the dynamic structural response of the analysed footbridge is associated to the vertical bending vibration mode with frequency equal to 4.90 Hz [f01 = 4.90 Hz].
-
2. Forced Vibration Experimental Tests: The maximum acceleration values (peak accelerations values), related to the central section of the investigated span (L = 24.4 m), respectively, are equal to 0.075 m/s2 (fp = 1.60 Hz; ap = 0.075 m/s2; slow walking: 8 pedestrians); (fp = 1.70 Hz; ap = 0.052 m/s2; slow walking: 8 pedestrians); 0.030 m/s2 (fp = 2.00 Hz; ap = 0.030 m/s2; normal walking: 12 pedestrians); 0.114 m/s2 (fp = 2.30 Hz; ap = 0.114 m/s2; fast walking: 12 pedestrians); 0.157 m/s2 (fp = 2.45 Hz; ap = 0.157 m/s2; resonance: 12 pedestrians) and 0.046 m/s2 (ap = 0.046 m/s2; random walking: 14 pedestrians).
-
3. Human Comfort Assessment: The experimental dynamic analysis, carried out by sixteen human walking loading cases (slow, normal, fast, resonance and random walking) have shown that the obtained accelerations values satisfied the current human comfort design criteria, apart from the resonance case (ap=0.157 m/s²), which slight overpass the AISC proposed limit equal to 0.15 m/s², when twelve persons crossed the footbridge. Based on the peak acceleration values (experimental tests), observations made at the footbridge location and also several interviews with the participants of the experimental tests, it was concluded that the investigated pedestrian footbridge attends the human comfort criteria. On the other hand, it is interesting to point out that a person standing on the footbridge concrete slab can perceive the accelerations values for vertical vibrations, as the traffic density on the footbridge increases.
Finally, the authors would like to emphasize the understanding of the necessity of a study based on the evaluation of the pedestrian footbridge dynamic interaction effect, associated to crowd situations, considering experimental tests and numerical modelling, using representative biodynamic models to simulate the pedestrians, aiming to contribute with a more realistic assessment of the dynamic structural behaviour and human comfort evaluation of footbridges subjected to pedestrian walking.
8. Acknowledgements
The authors gratefully acknowledge the financial support for this work provided by the Brazilian Science Foundation’s CAPES, CNPq and FAPERJ.
9. References
-
[1]Debona GL. Experimental monitoring and numerical modelling on the dynamic structural response of pedestrian footbridges. PhD Thesis (In Portuguese). Civil Engineering Post-graduate Programme, PGECIV. State University of Rio de Janeiro, UERJ. Rio de Janeiro/RJ, Brazil, 2016.
-
[2]Brownjohn JMW, Fu TN. Vibration excitation and control of a pedestrian footbridge by individuals and crowds. Shock and Vibration, 12: 333-347, 2005.
-
[3]Fernandes H. Dynamic behaviour of footbridges modelled as beams subjected to pedestrian-induced vertical direction vibrations. PhD Thesis (In Portuguese). Graduate Program in Mechanical Engineering, PPGEM, Federal University of Paraíba, UFPB, João Pessoa/PB, Brazil, 2007.
-
[4]Brownjohn JMW, Fok P, Roche M, Omenzetter P. Long span steel pedestrian bridge at Singapore Changi Airport. Part 2: crowd loading tests and vibration mitigation measures. Structural Engineer; 82 (16): 28-34, 2004.
-
[5]Bocian M, Macdonald JHG, Burn JF. Biomechanically inspired modelling of pedestrian-induced vertical self-excited forces. American Society of Civil Engineers (ASCE), 2013.
-
[6]Silva JGS da, Debona GL. Effect of the pedestrian-structure dynamic interaction on the vibration serviceability of steel-concrete composite footbridges. Proceedings of the 8th International Conference on Advances in Steel Structures, ICASS 2015, Lisbon, Portugal; pp. 1-15, 2015.
-
[7]Pfeil MS, Costa NPA, Pimentel RL, Vasconcelos RP. Analytic-numerical model for walking person-footbridge structure interaction. Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal; pp: 1079-1085, 2014.
-
[8]Alonso JFJ, Saez A, Caetano E, Cunha A. Proposal and calibration of a human-structure interaction biomechanical model by the resolution of the inverse dynamic problem. Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal; pp: 975-982, 2014.
-
[9]Ohlsson S. Floor vibrations and human discomfort. PhD Thesis. Chalmers University of Technology, Switzerland, 1982.
-
[10]Baumann K and Bachmann H. Durch menschen verursachte dynamische lasten und deren auswirkungen auf balkentragwerke. Report 7501-3, Institute of Structural Engineering (IBK), Swiss Federal Institute of Technology (ETH), Switzerland, 1988.
-
[11]Pimentel RL. Vibration performance of pedestrian bridges due to human-induced loads. PhD Thesis, University of Sheffield, United Kingdom, 1997.
-
[12]Ebrahimpour RL, Sack PD, Cleek V. Computing crowd loads using a nonlinear equation of motion. Proceedings of the 4th International Conference on Civil and Structural Engineering Computing; pp: 47-52, Civil-Comp Press, United Kingdom, 1989.
-
[13]Ebrahimpour A, Sack RL. Design live loads for crowds in motion. Conference Proceedings of Building an International Community of Structural Engineers; pp: 420-427, 1996.
-
[14]Butz C, Feldmann M, Heinemeyer C, Sedlacek G, Chabrolin B, Lemaire A, Lukic M, Martin PO, Caetano E, Cunha A, Goldack A, Keil A, Schlaich M. Advanced load models for synchronous pedestrian excitation and optimised design guidelines for steel footbridges. European Comission; pp: 1-167, 2008.
-
[15]Barker C, Mackenzie D. Calibration of the UK National Annex. Proceedings of the International Conference Footbridge 2008: Footbridges for Urban Renewal, Porto, Portugal, 2008.
-
[16]Venuti F, Racic V, Corbetta A. Pedestrian-structure interaction in the vertical direction: coupled oscillator-force model for vibration serviceability assessment. Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal; pp: 915-920, 2014.
-
[17]Ingólfsson EL. Pedestrian-induced lateral vibrations of footbridges. PhD Thesis. DTU Civil Engineering. Technical University of Denmark - DTU. Lyngby, Denmark, 2011.
-
[18]ANSYS Swanson Analysis Systems, Inc., P. O. Box 65, Johnson Road, Houston, PA, 15342-0065. Release 11.0, SP1 UP20070830, ANSYS, Inc. is a UL registered ISO 9001:2000 Company. Products ANSYS Academic Research, Using FLEXlm v10.8.0.7 build 26147, Customer 00489194. 2007.
-
[19]Brandt A. Noise and vibration analysis. Signal analysis and experimental procedures. 1st Edition. John Wiley & Sons, Inc., 2011.
-
[20]Cunha A, Caetano E. Experimental modal analysis of civil engineering structures. Journal of Sound and Vibration; 40(6):12-20, 2006.
-
[21]Prislan R. Laser doppler vibrometry and modal testing. University of Ljubljana, 2008.
-
[22]Technical Guide Footbridges: Assessment of Vibrational Behaviour of Footbridges under Pedestrian Loading. SÉTRA: Service d’Études Techniques des Routes et Autoroutes, 2006.
-
[23]HIVOSS “Human Induced Vibration of Steel Structures”. Design of Footbridges Guideline. Research Fund for Coal and Steel, 2008.
-
[24]Murray TM, Allen DE, Ungar EE, Davis DB. Vibrations of Steel-Framed Structural Systems due to Human Activity. Second Edition. Steel Design Guide Series. American Institute of Steel Construction, AISC, 2016.
-
[25]Bachmann H et al., Vibration problems in structures - practical guidelines, Basel (Switzerland):Institut für Baustatik und Konstruktion, Birkhäuser, 1995.
Publication Dates
-
Publication in this collection
13 July 2020 -
Date of issue
May-Jun 2020
History
-
Received
04 Feb 2019 -
Accepted
20 Dec 2019 -
Published
26 May 2020