Abstracts
Abstract
Research on behavior of flat slabs under punching shear, performed by Kinnunen, Regan and Muttoni influenced the main design recommendations. Meanwhile, studies about strut and tie model developed by Schlaich for beams, deep beams and corbels also influenced these design codes. This work aimed to adapt the strut and tie model for the punching shear resistance analysis in flat slabs. The punching shear resistance of 30 flat slabs verified through strut and tie model was compared to the one designed following Brazilian, American and European codes recommendation. Subsequently, this same model was validated by comparing the test results of 32 flat slabs. The strut and tie model results, when compared with the test results, showed a better average than those from codes, and the modified strut and tie model can become an alternative for punching shear strength prediction.
Keywords:
flat slab; punching shear; strut and tie model
Resumo
Pesquisas sobre punção em lajes lisas, realizadas por Kinnunen, Regan e Muttoni influenciaram sobremaneira as principais recomendações normativas. Enquanto isso, os estudos sobre o modelo de bielas e tirantes desenvolvido por Schlaich para vigas, vigas paredes e consolos também influenciaram essas normas. Este trabalho teve o objetivo de adaptar o modelo de bielas e tirantes para a análise da resistência à punção em lajes lisas. Comparou-se a resistência à punção de 30 lajes lisas calculadas via modelo de bielas e tirantes com a resistência calculadas pelas normas brasileira, americana e européia. Posteriormente, este mesmo modelo foi validado comparando com os resultados experimentais de 32 lajes lisas. Os resultados do modelo de bielas e tirantes, quando comparados aos experimentais, apresentaram melhor média que as estimativas normativas, podendo o modelo modificado se tornar uma alternativa para estimar a resistência ao puncionamento.
Palavras-chave:
laje lisa; punção; modelo de bielas e tirantes
1 INTRODUCTION
Punching shear is a type of fragile failure that occurs in flat slabs. The reaction of the column on the slab leads to the appearance of principal stresses that create a punching shear cone. This cone can cause the slab to completely disconnect with the column, providing a redistribution of efforts and a possible progressive collapse in the structure. The strut and tie model (STM) was developed by Schlaich et al. [11 J. Schlaich, K. Schafer, and M. Jennewein, "Toward a consistent design of structural concrete," PCI-Journal Chic., vol. 32, no. 3, pp. 74–150, May./Jun. 1987.] through an idealization of an imaginary truss within the structure, in the ultimate limit state, where the compression fields are called struts and are the truss bars represented by concrete, while the tensile fields are called ties and are the bars of the truss represented by the reinforcements. Subsequently, Schäfer & Schlaich [22 K. Schafer and J. Schlaich, Consistent design of structural concrete using strut and tie models, in Colóquio sobre Comportam. Projeto de Estrut, Rio de Janeiro, RJ, Brasil, 1988.], [33 K. Schafer and J. Schlaich, "Design and detailing of structural concrete using strut-and-tie models," Struct. Eng. (Lond.), vol. 69, no. 06, pp. 113–125, 1991.] defined criteria for choosing the most appropriate truss model for each structural part. Currently, this model is extremely well accepted in the analysis of beams, wall beams, corbels, etc.
The recent inclusion of STM for the most diverse analyzes in the concrete standards, together with the simplicity of the method, justify its adaptation for analysis of punching in flat slabs. Furthermore, it is a subject of great scientific utility due to the high potential for application in flat slabs with the most diverse contour conditions and physical and mechanical properties, including shear reinforcement. Thus, to present an alternative to satisfactorily estimate the punching shear resistance of reinforced concrete flat slabs, the modified STM was applied to tested slabs from works in the literature and the results found were better than those estimated by the codes analyzed here.
2 PUNCHING SHEAR IN FLAT SLABS
The first relevant mechanical model for punching shear analysis in flat slabs came with the studies by Kinnunen & Nylander [44 S. Kinnunen and H. Nylander, Punching of Concrete Slabs Without Shear Reinforcement, no. 158, Stockholm, Sweden: Transactions of the Royal Institute of Technology, 1960, 112 pp.]. They tested 61 circular slabs without shear reinforcement on circular columns. Experimental observations on cracks and deformations were the basis for the classic model. As the load increased, radial cracks appeared on the top face of the slab and, subsequently, a circumferential crack outlined “slices” of a slab. These “slices” of the slab were deformed by rotating around a center, causing the crushing of the compressed area on the bottom face of the slab. The model by Kinnunen & Nylander [44 S. Kinnunen and H. Nylander, Punching of Concrete Slabs Without Shear Reinforcement, no. 158, Stockholm, Sweden: Transactions of the Royal Institute of Technology, 1960, 112 pp.] correlates the punching shear resistance of the flat slab with the balance of forces that cause this crushing of the compressed area of the slab (Figure 1).
Mechanical model by Kinnunen & Nylander [44 S. Kinnunen and H. Nylander, Punching of Concrete Slabs Without Shear Reinforcement, no. 158, Stockholm, Sweden: Transactions of the Royal Institute of Technology, 1960, 112 pp.].
It is also worth highlighting the important contribution of Regan's and Regan & Bræstrup’s experimental works [5], [6], [7]. In these works, the author has always tried to calibrate the equations adopted by the codes with the experimental findings of the various analyzed slabs. One of the most important findings in these publications was that the increase in the bending reinforcement rate increases the punching shear resistance to slab.
Muttoni [88 A. Muttoni, "Punching shear strength of reinforced concrete slabs without transverse reinforcement," ACI Struct. J. Farmington Hills, vol. 105, no. 4, pp. 440–450, Jul./Aug. 2008.] developed the theory of critical shear cracking observing that the punching shear resistance curve in flat slabs was inversely proportional to the slab rotation curve. Thus, the increase in the opening of the critical crack causes the punching shear failure in the slab (Figure 2). Based on this observation, the author considered the load-rotation relationship, thus being able to find a value for the slab punching shear resistance.
Muttoni's Critical Shear Crack Theory [88 A. Muttoni, "Punching shear strength of reinforced concrete slabs without transverse reinforcement," ACI Struct. J. Farmington Hills, vol. 105, no. 4, pp. 440–450, Jul./Aug. 2008.].
The most interesting thing is to note that the three different theories validate themselves. For example: Regan [55 P. E. Regan, "Symmetric punching of reinforced concrete slabs," Mag. Concr. Res. Lond., vol. 38, no. 136, pp. 115–128, Sep 1986.], [66 P. E. Regan, Behavior of Reinforced Concrete Flat Slabs, Report 89. London: Construction Industry Research and Information Association (CIRIA), Feb. 1981, 89 pp.], [77 P. E. Regan and M. W. Bræstrup, Punching Shear in Reinforced Concrete (Bulletin d›Information, No. 168). London: Comité Euro-International du Béton, Jan. 1985, 232 pp.] states that increasing the reinforcement rate increases the punching shear resistance. With the increase in the reinforcement rate, there is a reduction in the rotation observed by Muttoni [88 A. Muttoni, "Punching shear strength of reinforced concrete slabs without transverse reinforcement," ACI Struct. J. Farmington Hills, vol. 105, no. 4, pp. 440–450, Jul./Aug. 2008.], which confirms the increase of the punching shear resistance. With the reduction of the slab rotation, there is a reduction of the compression in the compressed zone of Kinnunen & Nylander [44 S. Kinnunen and H. Nylander, Punching of Concrete Slabs Without Shear Reinforcement, no. 158, Stockholm, Sweden: Transactions of the Royal Institute of Technology, 1960, 112 pp.] which confirms the increase of the punching shear resistance.
2.1 STM applied to flat slabs
Muttoni [88 A. Muttoni, "Punching shear strength of reinforced concrete slabs without transverse reinforcement," ACI Struct. J. Farmington Hills, vol. 105, no. 4, pp. 440–450, Jul./Aug. 2008.] showed that the critical crack appears in the compression strut, with the slab rotation. Kinnunen & Nylander [44 S. Kinnunen and H. Nylander, Punching of Concrete Slabs Without Shear Reinforcement, no. 158, Stockholm, Sweden: Transactions of the Royal Institute of Technology, 1960, 112 pp.] found experimentally that after the slab rotation, the compressed zone, in the STM represented by the CCC node, is crushed in the instant of the punching shear failure. Putting this two information together, in this article, a STM was conceived where the punching shear failure was characterized when the model's CCC node was crushed.
In this work, to estimate the punching shear resistance in flat slabs, without shear reinforcement, a STM was proposed for each axis. One STM on the X axis, with the bending reinforcement of the X axis, and another on the Y axis, with the reinforcement of the Y axis. It was assumed as a model hypothesis that the ties would be the longitudinal reinforcement within the central band “c+1.5·d”. The struts would be the compression fields that would connect the CCC node to the tie (Figure 3). The limit compression stress of 0.85·fc was adopted for the CCC node, as recommended by NBR 6118 [99 Associação Brasileira de Normas Técnicas, Design of Concrete Structures – Procedure, NBR 6118, 2014.]. The value of the punching shear load estimated by this method is the sum of the vertical reactions of the X-axis and Y-axis models, through the balance of forces at the CCC node (Equation 1).
The values of Tx, Ty, tg(θ)x and tg(θ)y can be found using equations 2, 3, 4 and 5.
Where:
VSTM = punching shear resistance for flat slab without shear reinforcement via STM;
fc = compressive resistance of concrete;
As, x e As, y = steel area on the x and y axes, respectively;
fs, x e fs, y = stress in the longitudinal reinforcements of the x and y axes, respectively (fs, x = Es, x·εs, x ≤ fy, x and fs, y = Es, y·εs, y ≤ fy, y);
d = (dx + dy)/2 = average effective depth;
Tx e Ty = normal forces in the ties of the x and y axis models, respectively;
hNode, x e hNode, y = height of the CCC node for the x and y axes, respectively;
zx e zy = distance between the axis of the longitudinal reinforcement and half the height of the node for the x and y axes, respectively;
cx e cy = dimensions of the support on the x and y axes, respectively;
(θ)x e (θ)y = inclination angle of the compressed strut for models on the x and y axes, respectively.
Figure 4 shows the STM on the X axis with the efforts made compatible with the strains of the slab. In the study, the efforts of the Bx strut crush the CCC node, and how the STM is inside of a slab in flexure, in the face between the node and the strut the stress and the strain were considered 0.85·fc and 3.5‰, respectively. Tension in the longitudinal reinforcement (fsx) can be estimated by comparing the factors kh node, x with kLim, x. The relation kh node, x if less than or equal to kLim, x indicates that the reinforcements have yielded (fs, x = fy, x), otherwise, the reinforcements would be in the elastic regime (fs, x = Es, x·εs, x). The same procedure applies to STM on the Y axis.
Other researchers had similar ideas for estimating punching shear resistance in slabs. In 2012, Rizk, Marzouk and Tiller [1010 E. Rizk, H. Marzouk, and R. Tiller, "Design of thick concrete plates using strut-and-tie model," ACI Struct. J. Farmington Hills, vol. 109, no. 5, pp. 677–686, 2012.] devised a STM for calculating the punching shear resistance for thick flat slabs. The peculiarity of this model was the conical shape, simulating the punching shear failure cone. In 2016, Bompa & Onet [1111 D. V. Bompa and T. Onet, "Punching shear strength of rc flat slabs at interior connections to columns," Mag. Concr. Res. Lond., vol. 68, no. 1, pp. 24–42, 2016.] also suggested an alternative equation based on STM for punching shear. The model proposed in this work was a function directly of the Mohr-Coulomb theory for plane stress state. Unlike these studies, the STM proposed in this work originated from the classic Schlaich truss and through the balance of the efforts of the CCC node in the punching shear failure.
2.2 Code recommendations
2.2.1 ACI 318 [1212 American Concrete Institute, Building Code Requirements for Structural Concrete and Commentary, ACI 318M-14, 2014.]
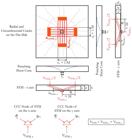
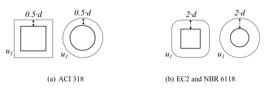
The American code [1212 American Concrete Institute, Building Code Requirements for Structural Concrete and Commentary, ACI 318M-14, 2014.] estimates the punching shear failure load (VACI), for flat slabs without shear reinforcement, through the lowest result among Equations 6, 7 and 8. Being fc the compressive strength of concrete (limited to 70 MPa), βc the ratio between the largest and smallest column dimensions, αs the constant that assumes a value equal to 40 for internal columns or 30 for edge columns or 20 for corner columns, d the effective depth and u1 the control perimeter according to ACI 318 (Figure 5).
2.2.2 Eurocode 2 (EC2)
The European code EC2 [1313 British Codes Institution, Design of Concrete Structures, Part 1, General codes and codes for buildings, DD ENV, EUROCODE 2, 2010.] estimates the punching shear failure load (VEC), for flat slabs without shear reinforcement, according to Equation 9. In this equation, ρl is the longitudinal reinforcement rate and not greater than 0.02, and u1 is the control perimeter according to EC2 (Figure 5).
EC2 recommends that the 0.18 coefficient is divided by a safe factor γc. However, in this research, it was decided to remove any safe factor (γc = 1.0), to compare code estimates with experimental results.
2.2.3 NBR 6118
The Brazilian code estimates the punching shear failure load (VNBR), for flat slabs without shear reinforcement, according to Equation 10. Being: and u1 equal to the control perimeter according to NBR 6118 (Figure 5). It is worth mentioning that NBR 6118 does not limit the size effect (ξ) nor the longitudinal reinforcement rate (ρl), different of the EC2.
Unlike EC2, NBR 6118 has a formula with the coefficient 0.13 with a safe factor already built in. Using the same reasoning as EC2, it was decided to remove this safe factor, for this reason, the NBR 6118 coefficient was 0.18 (1.4 · 0.13 = 0.18).
2.3 Analyzed slabs
In this research, 30 idealized flat slabs of reinforced concrete without shear reinforcement were initially analyzed, divided into 3 groups of 10 slabs each. In group A, slabs A1 to A10 varied only the reinforcement rates (ρ) between 0.59% to 1.10%. In group B, slabs B1 to B10 varied only the compressive strength of the concrete (fc) between 30 MPa and 48 MPa. In group C, slabs C1 to C10 varied only the width (c) of the square supports between 120 mm to 165 mm (Table 1) (Figure 6). All 30 slabs had a height (h) equal to 180 mm, an effective depth (d) equal to 160 mm, reinforcement yield stress (fy) equal to 500 MPa and a size of 2220 mm × 2220 mm. These slabs should be tested experimentally, in another stage of the research, therefore, the choice of this reduced size. It is also worth mentioning that this research is purely qualitative, where it was intended to compare the slabs of reduced size between them. At no time was the intention to do a quantitative research, where the models are correlated with full-scale prototypes. In addition, in this same article, in order to validate the strut and tie model proposed, the model results were compared with the experimental results of 32 flat slabs (18 by Regan [55 P. E. Regan, "Symmetric punching of reinforced concrete slabs," Mag. Concr. Res. Lond., vol. 38, no. 136, pp. 115–128, Sep 1986.], [66 P. E. Regan, Behavior of Reinforced Concrete Flat Slabs, Report 89. London: Construction Industry Research and Information Association (CIRIA), Feb. 1981, 89 pp.], [77 P. E. Regan and M. W. Bræstrup, Punching Shear in Reinforced Concrete (Bulletin d›Information, No. 168). London: Comité Euro-International du Béton, Jan. 1985, 232 pp.], 1 by Marzouk & Hussein [1414 H. Marzouk and A. Hussein, "Experimental investigation on the behavior of high-strength concrete slabs," ACI Struct. J. Farmington Hills, vol. 88, no. 6, pp. 701–713, Nov./Dec. 1991.], 6 by Moe [1515 J. Moe, Shearing Strength of Reinforced Concrete Slabs and Footings Under Concentrated Loads. Development Department Bulletin D47, Skokie, Illinois: Portland Cement Association, Apr. 1961, 129 pp.] and 7 by Elstner & Hognestad [1616 R. C. Elstner and E. Hognestad, "Shearing strength of reinforced concrete slabs," ACI Struct. J. Farmington Hills, vol. 53, no. 1, pp. 29–58, Jul 1956.]).
To calculate the reinforcement rate of the codes, only the reinforcements within the central band “c+6d” were considered, as recommended by EC2 and NBR6118, and for the adopted STM, only the reinforcements within the central band “c+1.5d” were considered. The hypothesis that the width “c+1.5d” was the most adequate was proven when the results of the STM (VSTM) were compared, using bands of “c+d”, “c+1.5d” and “c+2d”, with the experimental results (Vu) presented in the course of that paper. The ratio (VSTM/Vu), when using the “c+d” band, presented an average equal to 0.87, standard deviation equal to 0.11 and coefficient of variation equal to 12.26%, when using the “c+1.5d”, presented an average of 0.97, standard deviation equal to 0.11 and a variation coefficient of 11.51% and when using the “c+2d”, presented an average equal to 1.04, standard deviation equal to 0.14 and a variation coefficient equal to 13.06%.
3 RESULTS AND DISCUSSIONS
It was observed that the STM results for group A slabs were closer to the EC2 estimates, with the average of (VSTM/VEC) equal to 0.93, while they were farther from the ACI 318 estimates, with the average (VSTM/VACI) equal to 1.14 (Table 2). Figure 7 shows that STM, NBR 6118 and EC2 increase the punching shear resistance with the increase in the bending reinforcement rate, while the ACI 318 remains constant.
It was noted that the STM results for group B slabs were closer to the EC2 estimates, with the average of (VSTM/VEC) equal to 1.02, followed by NBR 6118, with the average of (VSTM/VNBR) equal to 0.96, while ACI 318 again presented the most distant results, with the average of (VSTM/VACI) equal to 1.31 (Table 2). Figure 8 shows that STM, NBR 6118, EC2 and ACI 318 increase the resistance with the increasing of the compressive resistance of the concrete.
It was observed that the STM results for group C slabs were closer to the EC2 estimates, with the average of (VSTM/VEC) equal to 0.93, followed by NBR 6118, with the average of (VSTM/VNBR) equal to 0.88, while ACI 318 again presented the most distant results, with the average of (VSTM/VACI) equal to 1.27 (Table 2). Figure 9 shows that the STM, NBR 6118, EC2 and ACI 318 increase the resistance with the increasing of the size of the support, and for supports with c ≤ 140 mm, the results of the STM move away from the results of the EC2.
Table 2 shows that as the size of the support decreases, the result of the STM decreases to a greater proportion than the codes estimates. Particularly in EC2, the slabs C5 (c = 140mm), C4 (c = 135mm), C3 (c = 130mm), C2 (c = 125mm) and C1 (c = 120mm) presented the VSTM/VEC ratios of 0.93, 0.88, 0.84, 0.79 and 0.74, respectively. This is because Equation 3 overestimates the height of the node and consequently underestimates punching shear resistance (VSTM), for columns with width less than or equal to 140 mm.
To approximate the results of STM and EC2, for slabs with supports of c ≤ 140 mm, a hypothetical value of cnew, x and cnew, y can be used in the calculation of STM, according to Equations 11 and 12.
These equations arose from the observation that the correction factor that brings the results from STM to EC2 (kx e ky) is linearly proportional to the relation of the support width (cx e cy) divided by the slab height (h). With this simple correction, for slabs with c ≤ 140 mm, the ratios (VSTM/VEC) of slabs C5 to C1 that were from 0.93 to 0.74, as shown in Table 2, became 1.01 to 1.00.
To validate the model experimentally, the punching shear resistance of 32 flat slabs was calculated (18 by Regan [55 P. E. Regan, "Symmetric punching of reinforced concrete slabs," Mag. Concr. Res. Lond., vol. 38, no. 136, pp. 115–128, Sep 1986.], [66 P. E. Regan, Behavior of Reinforced Concrete Flat Slabs, Report 89. London: Construction Industry Research and Information Association (CIRIA), Feb. 1981, 89 pp.], [77 P. E. Regan and M. W. Bræstrup, Punching Shear in Reinforced Concrete (Bulletin d›Information, No. 168). London: Comité Euro-International du Béton, Jan. 1985, 232 pp.], 1 by Marzouk & Hussein [1414 H. Marzouk and A. Hussein, "Experimental investigation on the behavior of high-strength concrete slabs," ACI Struct. J. Farmington Hills, vol. 88, no. 6, pp. 701–713, Nov./Dec. 1991.], 6 by Moe [1515 J. Moe, Shearing Strength of Reinforced Concrete Slabs and Footings Under Concentrated Loads. Development Department Bulletin D47, Skokie, Illinois: Portland Cement Association, Apr. 1961, 129 pp.] and 7 by Elstner & Hognestad [1616 R. C. Elstner and E. Hognestad, "Shearing strength of reinforced concrete slabs," ACI Struct. J. Farmington Hills, vol. 53, no. 1, pp. 29–58, Jul 1956.]), using the STM, and compared with the experimental results (Table 3). The results in general were satisfactory. When compared with the experimental results, STM was the one with the best average, with (VSTM/Vu) equal to 0.97, followed by NBR 6118 with (VNBR/Vu) equal to 1.04 and EC2 with (VEC/Vu) equal to 0.87, while ACI was the one with the worst average with (VACI/Vu) equal to 0.76.
Data and experimental results from slabs of Regan [55 P. E. Regan, "Symmetric punching of reinforced concrete slabs," Mag. Concr. Res. Lond., vol. 38, no. 136, pp. 115–128, Sep 1986.], [66 P. E. Regan, Behavior of Reinforced Concrete Flat Slabs, Report 89. London: Construction Industry Research and Information Association (CIRIA), Feb. 1981, 89 pp.], [77 P. E. Regan and M. W. Bræstrup, Punching Shear in Reinforced Concrete (Bulletin d›Information, No. 168). London: Comité Euro-International du Béton, Jan. 1985, 232 pp.], Marzouk & Hussein [1414 H. Marzouk and A. Hussein, "Experimental investigation on the behavior of high-strength concrete slabs," ACI Struct. J. Farmington Hills, vol. 88, no. 6, pp. 701–713, Nov./Dec. 1991.], Moe [1515 J. Moe, Shearing Strength of Reinforced Concrete Slabs and Footings Under Concentrated Loads. Development Department Bulletin D47, Skokie, Illinois: Portland Cement Association, Apr. 1961, 129 pp.] and Elster & Hognestad [1616 R. C. Elstner and E. Hognestad, "Shearing strength of reinforced concrete slabs," ACI Struct. J. Farmington Hills, vol. 53, no. 1, pp. 29–58, Jul 1956.].
However, the result of the slab V/1 via STM stood out negatively, presenting the ratio (VSTM/Vu) equal to 0.50. This slab had the support with c = 54 mm. When recalculated using Equations 11 and 12, the ratio (VSTM/Vu) went from 0.50 to 1.27. However, it is worth mentioning that for this slab, the result that came closest to the experimental one was ACI (VACI/Vu) with 0.92, followed by STM (VSTM/Vu) with 1.27, EC2 (VEC/Vu) with 1.28 and NBR 6118 (VNBR/Vu) with 1.47.
4 CONCLUSIONS
In this work, a STM adapted for the calculation of punching shear resistance in flat slabs was presented. The results of this model were compared with codes for the analysis of 30 slabs, divided into 3 groups of 10 slabs: with different: average compressive strength fc (group A), bending reinforcement rate ρ (group B) and dimension of the support c (group C). In addition, the results of this model were also compared with the experimental results of 32 flat slabs, 18 by Regan [55 P. E. Regan, "Symmetric punching of reinforced concrete slabs," Mag. Concr. Res. Lond., vol. 38, no. 136, pp. 115–128, Sep 1986.], [66 P. E. Regan, Behavior of Reinforced Concrete Flat Slabs, Report 89. London: Construction Industry Research and Information Association (CIRIA), Feb. 1981, 89 pp.], [77 P. E. Regan and M. W. Bræstrup, Punching Shear in Reinforced Concrete (Bulletin d›Information, No. 168). London: Comité Euro-International du Béton, Jan. 1985, 232 pp.], 1 by Marzouk & Hussein [1414 H. Marzouk and A. Hussein, "Experimental investigation on the behavior of high-strength concrete slabs," ACI Struct. J. Farmington Hills, vol. 88, no. 6, pp. 701–713, Nov./Dec. 1991.], 6 by Moe [1515 J. Moe, Shearing Strength of Reinforced Concrete Slabs and Footings Under Concentrated Loads. Development Department Bulletin D47, Skokie, Illinois: Portland Cement Association, Apr. 1961, 129 pp.] and 7 by Elstner & Hognestad [1616 R. C. Elstner and E. Hognestad, "Shearing strength of reinforced concrete slabs," ACI Struct. J. Farmington Hills, vol. 53, no. 1, pp. 29–58, Jul 1956.]. When compared with the experimental results, it was observed that the STM results were the ones that came closest, followed by the NBR6118 estimates. When analyzing the 30 slabs of groups A, B and C, it was noted that the STM results were closer to the results of EC2 and NBR 6118. For columns with width less than or equal to 140 mm, the results of the proposed model decrease more than the norms, however, when the correction using the cnew (cnew, x = kx⋅c e cnew, y = ky⋅c) was used, the results of the modified strut and tie model returned to the EC2 estimates again. Finally, it was noted that the ACI 318 underestimated the resistance of the slabs more than the other codes and the STM. However, more theoretical, computational, and experimental analyzes are needed for more comprehensive conclusions.
ACKNOWLEDGEMENTS
The authors thank the Federal University of Pará (UFPA) and the Vale of Acarau State University (UVA) for the interaction for the development of this research.
-
Financial support: None.
-
How to cite: R. J. C. Silva, D. R. C. O. de Oliveira, N. G. B. de Albuquerque, T. A. Gomes, and A. K. L. L. Nzambi,“ Punching shear in flat slabs by strut and tie model,” Rev. IBRACON Estrut. Mater., vol. 14, no. 5, e14506, 2021, https://doi.org/10.1590/S1983-41952021000500006
REFERENCES
-
1J. Schlaich, K. Schafer, and M. Jennewein, "Toward a consistent design of structural concrete," PCI-Journal Chic., vol. 32, no. 3, pp. 74–150, May./Jun. 1987.
-
2K. Schafer and J. Schlaich, Consistent design of structural concrete using strut and tie models, in Colóquio sobre Comportam. Projeto de Estrut, Rio de Janeiro, RJ, Brasil, 1988.
-
3K. Schafer and J. Schlaich, "Design and detailing of structural concrete using strut-and-tie models," Struct. Eng. (Lond.), vol. 69, no. 06, pp. 113–125, 1991.
-
4S. Kinnunen and H. Nylander, Punching of Concrete Slabs Without Shear Reinforcement, no. 158, Stockholm, Sweden: Transactions of the Royal Institute of Technology, 1960, 112 pp.
-
5P. E. Regan, "Symmetric punching of reinforced concrete slabs," Mag. Concr. Res. Lond., vol. 38, no. 136, pp. 115–128, Sep 1986.
-
6P. E. Regan, Behavior of Reinforced Concrete Flat Slabs, Report 89. London: Construction Industry Research and Information Association (CIRIA), Feb. 1981, 89 pp.
-
7P. E. Regan and M. W. Bræstrup, Punching Shear in Reinforced Concrete (Bulletin d›Information, No. 168). London: Comité Euro-International du Béton, Jan. 1985, 232 pp.
-
8A. Muttoni, "Punching shear strength of reinforced concrete slabs without transverse reinforcement," ACI Struct. J. Farmington Hills, vol. 105, no. 4, pp. 440–450, Jul./Aug. 2008.
-
9Associação Brasileira de Normas Técnicas, Design of Concrete Structures – Procedure, NBR 6118, 2014.
-
10E. Rizk, H. Marzouk, and R. Tiller, "Design of thick concrete plates using strut-and-tie model," ACI Struct. J. Farmington Hills, vol. 109, no. 5, pp. 677–686, 2012.
-
11D. V. Bompa and T. Onet, "Punching shear strength of rc flat slabs at interior connections to columns," Mag. Concr. Res. Lond., vol. 68, no. 1, pp. 24–42, 2016.
-
12American Concrete Institute, Building Code Requirements for Structural Concrete and Commentary, ACI 318M-14, 2014.
-
13British Codes Institution, Design of Concrete Structures, Part 1, General codes and codes for buildings, DD ENV, EUROCODE 2, 2010.
-
14H. Marzouk and A. Hussein, "Experimental investigation on the behavior of high-strength concrete slabs," ACI Struct. J. Farmington Hills, vol. 88, no. 6, pp. 701–713, Nov./Dec. 1991.
-
15J. Moe, Shearing Strength of Reinforced Concrete Slabs and Footings Under Concentrated Loads. Development Department Bulletin D47, Skokie, Illinois: Portland Cement Association, Apr. 1961, 129 pp.
-
16R. C. Elstner and E. Hognestad, "Shearing strength of reinforced concrete slabs," ACI Struct. J. Farmington Hills, vol. 53, no. 1, pp. 29–58, Jul 1956.
Edited by
Publication Dates
-
Publication in this collection
14 June 2021 -
Date of issue
2021
History
-
Received
12 Feb 2020 -
Accepted
01 Sept 2020