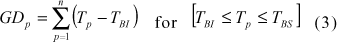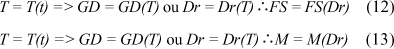Abstracts
The temporal variation of cumulative dry matter can be represented by a sigmoidal curve and the temporal variation of nutrient uptake follows this characteristic shape. Therefore, modeling the temporal variation of cumulative dry matter allows estimating nutrient uptake along the crop cycle. The objective of this study was to propose a sine model to estimate dry matter and macronutrient uptake, and to estimate the moments of maximum N and K uptake rates for the rice crop. The field experiment was carried out on a wetland area of Piracicaba, SP, Brazil, consisting of an Humic Haplaquept. The chosen rice variety was IAC 103, a middle season cycle and high yield. Observed variables were dry matter of different plant parts (root, leaf and stem, and panicle) and macronutrient contents per unit dry matter. A sine model was proposed for the cumulative variation of these variables, based on biological events that occurred during the crop cycle. The temporal variation of nutrient uptake was estimated and a lower accuracy was observed for K uptake. The maximum absorption rate for N and K was found at 56% of the relative development of the crop, corresponding to 60 days after emergence in this experiment. The proposed model presented a satisfactory behavior to define the order of magnitude of estimated dry matter and macronutrient uptake by the rice crop and maximum N and K uptake rates.
modeling; sine function; macronutrients
A variação temporal do acúmulo de fitomassa seca pode ser representada por curva de tipo sigmoidal e a variação temporal do acúmulo de nutrientes acompanha essa forma característica. Conseqüentemente, a modelagem da variação temporal do acúmulo de fitomassa seca permite estimar a extração de nutrientes ao longo do ciclo da cultura. O objetivo do trabalho foi propor um modelo senoidal para estimar a fitomassa seca e extração de macronutrientes pela cultura de arroz, bem como determinar a época de máxima taxa de extração de N e K. O experimento foi conduzido em Piracicaba, SP num Gleissolo Eutrófico, horizonte A chernozênico, textura média a argilosa. Foi utilizada a variedade IAC 103, caracterizada por ser de ciclo médio e de alto rendimento. As variáveis observadas foram a fitomassa seca em diferentes compartimentos da planta (raiz, folha e colmo e panícula) e os teores de macronutrientes por unidade de fitomassa seca. Propõe-se um modelo senoidal, cuja base matemática é fundamentada em eventos biológicos que acontecem ao longo do ciclo da cultura. Estimou-se a variação temporal da extração de nutrientes pela cultura, observando-se menor aderência na estimativa da extração de K. A máxima taxa de absorção de N e K foi observada a 56% do desenvolvimento relativo, equivalente a 60 DAE no estudo. O modelo proposto apresentou adequado desempenho para definir ordem de grandeza dos valores de fitomassa seca e extração de macronutrientes pela cultura de arroz, bem como para estimar a máxima taxa de absorção de N e K.
modelagem; modelo senoidal; macronutrientes
CROP SCIENCE
Logistic rice model for dry matter and nutrient uptake
Modelo logístico para fitomassa e extração de nutrientes para a cultura de arroz
Axel García y García; Durval Dourado-Neto* * Corresponding author < dourado@esalq.usp.br> ; Maria del Valle Basanta; Ramiro Fernando López Ovejero; José Laércio Favarin
USP/ESALQ - Depto. de Produção Vegetal, C.P. 9 - 13418-900 - Piracicaba, SP - Brasil
ABSTRACT
The temporal variation of cumulative dry matter can be represented by a sigmoidal curve and the temporal variation of nutrient uptake follows this characteristic shape. Therefore, modeling the temporal variation of cumulative dry matter allows estimating nutrient uptake along the crop cycle. The objective of this study was to propose a sine model to estimate dry matter and macronutrient uptake, and to estimate the moments of maximum N and K uptake rates for the rice crop. The field experiment was carried out on a wetland area of Piracicaba, SP, Brazil, consisting of an Humic Haplaquept. The chosen rice variety was IAC 103, a middle season cycle and high yield. Observed variables were dry matter of different plant parts (root, leaf and stem, and panicle) and macronutrient contents per unit dry matter. A sine model was proposed for the cumulative variation of these variables, based on biological events that occurred during the crop cycle. The temporal variation of nutrient uptake was estimated and a lower accuracy was observed for K uptake. The maximum absorption rate for N and K was found at 56% of the relative development of the crop, corresponding to 60 days after emergence in this experiment. The proposed model presented a satisfactory behavior to define the order of magnitude of estimated dry matter and macronutrient uptake by the rice crop and maximum N and K uptake rates.
Keywords: modeling, sine function, macronutrients
RESUMO
A variação temporal do acúmulo de fitomassa seca pode ser representada por curva de tipo sigmoidal e a variação temporal do acúmulo de nutrientes acompanha essa forma característica. Conseqüentemente, a modelagem da variação temporal do acúmulo de fitomassa seca permite estimar a extração de nutrientes ao longo do ciclo da cultura. O objetivo do trabalho foi propor um modelo senoidal para estimar a fitomassa seca e extração de macronutrientes pela cultura de arroz, bem como determinar a época de máxima taxa de extração de N e K. O experimento foi conduzido em Piracicaba, SP num Gleissolo Eutrófico, horizonte A chernozênico, textura média a argilosa. Foi utilizada a variedade IAC 103, caracterizada por ser de ciclo médio e de alto rendimento. As variáveis observadas foram a fitomassa seca em diferentes compartimentos da planta (raiz, folha e colmo e panícula) e os teores de macronutrientes por unidade de fitomassa seca. Propõe-se um modelo senoidal, cuja base matemática é fundamentada em eventos biológicos que acontecem ao longo do ciclo da cultura. Estimou-se a variação temporal da extração de nutrientes pela cultura, observando-se menor aderência na estimativa da extração de K. A máxima taxa de absorção de N e K foi observada a 56% do desenvolvimento relativo, equivalente a 60 DAE no estudo. O modelo proposto apresentou adequado desempenho para definir ordem de grandeza dos valores de fitomassa seca e extração de macronutrientes pela cultura de arroz, bem como para estimar a máxima taxa de absorção de N e K.
Palavras-chave: modelagem, modelo senoidal, macronutrientes
INTRODUCTION
An understanding of the processes involving crop growth and development, in addition to the adoption of adequate decision-making tools, is essential for better results to be obtained in the production process, and modeling is one tool utilized for the integration of the processes that take place along the crop cycle. Simulation models are utilized to verify theories and test hypotheses, improve the knowledge on a given process, feeding databases with the acquired information and allowing grain yield estimates to be obtained (Munakata, 1995; Boote et al., 1996).
Modeling procedures try to represent the interaction between environmental and plant factors, allowing for a more detailed study and prediction of the processes of interest. The ideal situation is to formulate a model that is sufficiently complex to describe the phenomenon, by utilizing original data, without making its practical use difficult (Pereira & Machado, 1987). On the other hand, every model is a simplification of the system to be studied and cannot contemplate all existing variables, which results in a less than exact prediction of reality (Penning de Vries, 1987).
During growth and development of rice plants, dry mass increases along the growth cycle, and nutrient uptake is subject to great variations (Murayama, 1995). The amount of dry phytomass varies as a function of variety, environmental factors and nutrient availability, but the accumulation pattern is similar in nearly all rice materials. In high yield varieties, almost half of the total dry phytomass comes from the grain, resulting in a harvest index of 0.5 (Fernández et al., 1985).
Along the development of the crop, nutrient uptake varies as a function of the plant stage, and a sigmoidal-type curve best describes the absorption progress. During the early stages nutrient uptake is low, followed by a period in which the absorbed amount increases, and this behavior is described by a curve that is similar in shape to a straight line. As the cycle draws to an end, when the plant is mature, nutrient absorption becomes very low or null once again (Malavolta, 1980).
Crop cycles can be characterized by the thermal unit approach, which presumes the plant needs to accumulative a given amount of calories sum to develop. In this context, three temperature thresholds can be identified as relevant: a lower threshold (baseline) temperature (TBI), an optimal temperature (TO), and an upper threshold temperature (TBS) (Kropff et al., 1995), which, in the case of rice, correspond to 8oC, 30oC and 42oC, respectively (Gao et al., 1992).
The relative development of the crop (Dr) at a given time is the ratio between the actual caloric sum (GDp, oC.day) and the caloric sum that corresponds to the physiological maturity stage (GDpmƒ, oC.day). On a daily scale it can be estimated the equation:
where Tp is the mean air temperature (oC) on the p-th day after emergence. The caloric sum at the physiological maturity stage is defined by the equation:
where T(t) refers to the temporal variation of temperature on a daily scale, between emergence (t=0) and the physiological maturity stage (t=tpmƒ), and tpmƒ corresponds to the time necessary, in days after emergence, to attain the physiological maturity stage. The previous expression can be approximated by the Gilmore & Rogers method (1958), according to equation (3):
If Tminp<TBI, then Tp=TBI and if Tmaxp>TBS, then Tmaxp=TBS.
During vegetative growth, nutrients N, P, K and S are intensely absorbed. In terms of characterization, the nutrient uptake curve varies obeying the development conditions of the plant and presents a certain shape for each type of nutrient. Macronutrients in the rice plant can be classified into three groups: (1): N, P and S; (2): K and Ca; and (3): Mg. Nutrients in group 1 are rapidly absorbed by plants along the cycle, with the bulk of accumulation occurring until the onset of booting, and are drained from the stem to the panicle at the ripening stage. Nutrients in group 2 are absorbed along the crop cycle, with the bulk of accumulation occurring until the ripening stage. Draining to the panicles is minimal. Accumulation of Mg occurs especially during the period between panicle initiation and booting (Murayama, 1995). The amount of nutrients extracted from the soil by the crop is quite variable (Perdomo et al., 1985 and Bastos, 1999). In soils that present high organic matter contents, the plant utilizes nutrients quantitatively in the sequence N>K>P, while in average fertility soils the sequence is K>N>P.
The objective of this study was to propose a sine model to estimate dry phytomass accumulation and macronutrient uptake, and to determine the moments when the uptake rate of nitrogen and potassium by the rice crop are maximum.
MATERIAL AND METHODS
The experiment was carried out in Piracicaba-SP Brazil, 22º 12'S, 47º 38'W, 550 m altitude, in an Humic Haplaquept, with a chernozemic A horizon, intermediate to clayey texture and textural class defined as silty clay loam.The chosen rice variety was IAC 103, characterized by middle cycle, high yield, with long, thin grain, and moderate susceptibility to rice blast disease. Sowing was performed mechanically on September 28, 1999, with a row spacing of 0.34 m and 10 seeds per meter. Fertilization at sowing was performed based on soil analysis. The crop was irrigated by flooding and water management consisted of maitaining a mean water depth of 0.10 m until physiological maturity. The experiment was conducted as a randomized block design with ten treatments (sampling seasons) (n=3).
Ten samplings were performed along the crop cycle by removing two plants per plot, from a total of three plots, to determine dry phytomass and macronutrient content per plant compartment (root, leaf and stem, panicle). The dry phytomass of the aerial part in the i-th sampling season (DPPAi) corresponds to the sum of dry phytomass of leaf and stem (DPFCi) and panicle (DPPi), while the total dry phytomass in the i-th sampling season (TDPi) corresponds to the sum of dry phytomass in the aerial part plus root (DPRi).
The extraction (Eij; kg ha-1) of the j-th macronutrient, up to the i-th sampling season was calculated according to equation (4).
where Mji refers to the content of the j-th nutrient (g kg-1) at the i-th sampling season. The relative total dry phytomass at the i-th sampling season (TDPri) is the ratio between TDPi and the maximum total dry phytomass (TDPmax) observed along the crop cycle (5).
The mean Mji content corresponds to the product of the mean nutrient content in the nc compartments, weighted by the corresponding dry phytomass (6).
A linear model was then adjusted to pairs of data Mji and Dri, to estimate the mean content of the j-th nutrient  , g kg-1), in the i-th sampling season, as shown in equation (7).
, g kg-1), in the i-th sampling season, as shown in equation (7).
where aj and bj refer to the empirical parameters of the j-th macronutrient.
The proposed sine model was adjusted to pairs of data TDPri (5) and Dri (1), and the estimated relative total dry phytomass in the i-th sampling season ( ) was obtained, as described by equation (8).
) was obtained, as described by equation (8).
By rearranging equations (7) and (8) it is possible to estimate the extraction of the j-th nutrient in the i-th sampling season, according to equation (9).
The relative total dry phytomass accumulation rate was estimated by deriving the original function as a function of relative development and obtaining equation (10).
By obtaining the second derivative, equation (11), and making it equal to zero, it was possible to determine the point of maximum total dry phytomass accumulation rate.
The crop cycle was characterized in terms of relative development (Dr), equation (1), and caloric sum (°C.d), equation (3).
The empirical parameter b was determined by non-linear regression analysis, using the least squares method (minimization of the sum of squares of deviations between observed and estimated values) and Newton-Raphson's iterative procedure.
Proposed model
To develop the proposed model, the first step was to devise a structure based on theoretical considerations inherent to the growth, development and nutrient uptake rate in the rice crop. At the moment of plant emergence (Dr=0), the phytomass is negligible and, consequently, the accumulation rate is null. (Table 1, case 1).
In the other extreme, the maximum value attained by the total dry phytomass occurs at the physiological maturity stage (Table 1, case 2), the total dry phytomass accumulation beling maximum (Table 1, case 3) and, consequently, the accumulation rate null (Table 1, case 4).
Along the crop cycle occurs a single point of maximum, total dry phytomass accumulation rate (Table 1, case 5), as well as a period of positive and increasing (Table 1, case 6) and positive and decreasing rates (Table 1, case 7). The temporal variation of dry phytomass and the accumulation of macronutrients have a sigmoidal shape, which is a fact demonstrated in several studies (Malavolta, 1980; Fageria, 1984; Penning de Vries, 1987; Kropff et al., 1995; Yin, 1996; Dourado Neto, 1999).
Since the crop cycle can be characterized in terms of GD or Dr, the temporal variations of dry phytomass (DP) and nutrient (M) accumulations in the plant can be expressed according to equations (12) and (13), respectively.
To propose an equation that addresses the pre-established conditions (Table 1), the following structure was obtained for the model given by equation (8).
To generalize the proposed model, the empirical coefficient b was introduced into equation (8), which corresponds to the shape factor for the growth curve in order to extrapolate the result for other location and interpolate the prediction between any two measured time intervals. The flow chart in Figure 1 illustrates the general procedure utilized.
RESULTS AND DISCUSSION
Dry phytomass and macronutrient accumulation
The temporal variation of the total dry phytomass accumulation corresponds to the sum of dry phytomass in the root and aerial part of the plant (Figure 2), which in turn corresponds to the sum of leaf and stem, and panicle dry phytomass (Figure 3).
Differences were detected between phytomass sampling seasons and means were compared (all against all) between sampling seasons (Table 2) to determine equal dry phytomass accumulation moments (a=0.05). The beginning stages of the crop (Seedling, Four-leaf stage and Onset of tillering) were equal in terms of dry phytomass accumulation, and differentiation started to occur at full tillering.
Growth was slow until 40 to 50 days after emergence onset of tillering (Table 2). At internode elongation (55 DAE), dry phytomass accumulation was intensified, and the beginning of the sigmoidal trend can be observed at the stage that corresponds to panicle exsertion. These results are similar to those obtained by Fageria (1984).
The observed temporal variation in total dry phytomass accumulation occurred as expected: slow initial growth, with a period of rapid growth until a maximum was reached at the physiological maturity stage, with an observed tendency to become stabilized. Until the fourth sampling season the dry phytomass accumulation is low, becoming more intense from maximum tillering onward (Table 3). This fact can be identified at the a = 0.05 significance level in the comparison of means (Table 2). Similar results were reported by Fageria (1984), in experiments conducted under irrigation and different levels of applied phosphorus.
The macronutrient most extracted by the crop was nitrogen, followed by potassium and sulfur. The order of absorption of primary macronutrients was N>K>P, while for secondary macronutrients the order was S>Mg>Ca (Table 3).
The general order of absorption was: N>K>S>P>Mg>Ca. Fageria (1999) reported that in irrigated rice the macronutrient accumulation order is K>N>P>Mg>Ca, while the order observed in the present work is cited by the same author as a trait of dryland rice under conditions observed in cerrado soils.
Modeling and estimation of temporal variation in dry phytomass accumulation and macronutrient uptake
Models were obtained for: (i) estimate of total dry phytomass in the crop on the p-th day after emergence; (ii) estimate of the mean content of the j-th macronutrient on the p-th day after emergence; and (iii) extraction of the j-th macronutrient on the p-th day after emergence. Figure 1 shows a summary of the procedure utilized to obtain these models.
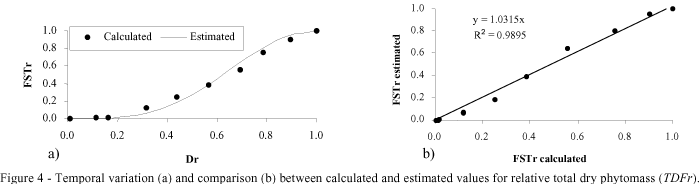
After adjusting the sine model to the observed data, a value was obtained for the empirical coefficient b = 1.877, which can be interpreted as the numerical value that incorporates the inter-relations not controled and not considered in the process. In other words, studies under diverse scenarios and climatic conditions are needed to produce a generalized value for b. The proposed model was satisfactorily adjusted to the calculated data (Figure 4a), demonstrating that the model estimate fits the experimental data (Figure 4b).
The result for the estimate of extraction of the j-th macronutrient on the p-th day after emergence can be observed in Figure 5. With the exception of K (Figure 6), the model adequately estimated the temporal variation of nutrient uptake.
As described in equation (11), a macronutrient absorption rate was obtained in kg ha-1 d-1. The plants attained the maximum absorption rate for all macronutrients in the period that corresponds to the reproductive stage. N and K were more extracted by the end of the internode elongation stage, Ca and Mg at panicle initiation, and P and S at the booting stage. Nutrients P, Ca, Mg and S were slowly absorbed initially, on the contrary to what was observed for N and K (Figure 7).
When the observed results are compared to those presented by Murayama (1995), the stages of maximum absorption are different in terms of groups of macronutrients, with the exception of Mg. According to that author, N, P and S belong to the group of maximum extraction at the booting stage, K and Ca to the beginning of the ripening stage and Mg to panicle initiation. In spite of that, Murayama (1995) reports that the observed patterns do not necessarily characterize the macronutrient absorption rate by the rice plant.
To establish the best season for N and K application as sidedressing, a maximum uptake rate for these nutrients was obtained when the uptake acceleration was null. To that effect, the second derivative of the original function [equation (11)] of the proposed model was equaled to zero (d2Te/dDAE2=0) (Figure 8).
With respect to sidedressing, in both cases the fertilizer should be applied until 60 DAE, when panicle initiation occurs.
CONCLUSIONS
The model proposed to estimate total dry phytomass and macronutrient uptake (N, P, K, Ca, Mg and S) for the rice crop had adequate performance and can be utilized to define the order of magnitude of the variables under consideration; The estimate for maximum absorption rate of nitrogen and potassium established that the application of these macronutrients should be carried out until 56% of the relative development (equivalent to 60 DAE in this study) of the crop, at panicle initiation.
Received March 5, 2002
Accepted April 30, 2003
- BASTOS, A.R.R. Nutrição mineral e produção de cultivares de arroz (Oryza sativa L.) em solos de várzea inundados. Lavras: ESAL, 1999. 89p. (Dissertação - Mestrado)
- BOOTE, K.J.; JONES, J.W.; PICKERING, N.B. Potential uses and limitations of crop models. Agronomy Journal, v.88, p.704-716, 1996.
- DOURADO-NETO, D. Modelos fitotécnicos referentes à cultura de milho. Piracicaba: USP/ESALQ, 1999. 227p. (Tese - Livre Docência)
- FAGERIA, N.K.Adubação e nutrição mineral da cultura do arroz Rio de Janeiro: Campus; Goiânia: EMBRAPA, cnpaf, 1984. 341p.
- FAGERIA, N.K. Nutrição mineral. In: VIEIRA, N.R.A.; SANTOS, A.B. dos; SANT'ANA, E.P. (Ed.) A cultura do arroz no Brasil Santo Antônio de Goiás: Embrapa Arroz e Feijão, 1999. cap.7, p.173-195.
- FERNÁNDEZ, F.; vergara, B.S.; YAPIT, N.; GARCIA, O. Crecimiento y etapas de desarrollo de la planta de arroz. In: TASCÓN, J.E.; GARCIA, D.E. (Ed). Arroz: investigación y producción. Cali: CIAT, 1985. p.83-101.
- GAO, L.Z.; JIN, Z.Q.; HUANG, Y.; ZHANG, L.Z. Rice clock model - a computer model to simulate rice development. Agricultural and Forest Meteorology, v.60, p.1-16, 1992.
- GILMORE , E.; ROGERS, J. S. Heat units as a method of measuring maturity in corn. Agronomy Journal, n.50, p.611-615. 1958.
- KROPFF, M.J.; MATTEWS, R.B.; van LAAR, H.H.; ten BERGE, H.F.M. The rice model Oryza1 and its testing. In: MATTHEWS, R.B.; KRPFF, M.J.; BACHELET, D.; van LAAR, H.H. (Ed.) Modeling the impact of climate change on rice production in Asia Manila: International Rice Research Institute, 1995. p.27-50.
- MALAVOLTA, E. Elementos da nutrição mineral de plantas São Paulo: Ceres, 1980. 251p.
- MUNAKATA, K. Simulation of population photosynthesis and dry matter production. In: MATSUO, T.; KUMAZAWA, K.; ISHII, R.; ISHIHARA, K.; HIRATA, H. (Ed.) Science of the rice plant Tokyo: Physiology, Food and Agricultural Policy Research Center, 1995. v.2, p.671-684.
- MURAYAMA, N. Development and senescence. In: MATSUO, T.; KUMAZAWA, K.; ISHII, R.; ISHIHARA, K.; HIRATA, H. (Ed.) Science of the rice plant Tokyo: Physiology, Food and Agricultural Policy Research Center, 1995. v.2, p.119-132.
- PENNING de VRIES, F.W.T. Some opportunities for using crop models in rice. In: INTERNATIONAL WORKSHOP ON THE IMPACT OF WEATHER PARAMETERS ON GROWTH AND YIELD OF RICE, Los Banõs, Philippines, 1987. Proceedings Los Baños: International Rice Research Institute, 1987. p.291-300.
- PERDOMO, M.A.; GONZALEZ, J.; GALVIS, C. de; GARCIA, E.; ARREGOCÉS, O. Los macronutrientes en la nutrición de la planta de arroz. In: TASCON, J.E.; GARCIA, D.E. (Ed.) Arroz: investigación y producción. Cali: CIAT, 1985. p.103-132.
- PEREIRA, A.R.; MACHADO, E.C. Análise quantitativa do crescimento de comunidade vegetal Campinas: Instituto Agronômico, 1987. 33p. (Boletim Técnico, 114).
- YIN, X. Quantifying the effects of temperature and photoperiod on phenological development to flowering in rice. Wageningen: Wageningen Agricultural University 1996. 173p. (Thesis - Ph.D.)
Publication Dates
-
Publication in this collection
12 Aug 2003 -
Date of issue
2003
History
-
Accepted
30 Apr 2003 -
Received
05 Mar 2002