ABSTRACT:
The system of differential equations proposed by Oltjen et al. [1986Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97., named Davis Growth Model (DGM)] to represent cattle growth has been parameterized with data from Bos taurus (British) and Bos indicus (Nellore) breeds. The DGM has been successfully used for simulation and decision support in the United States. However, the effect of about 30 years of genetic improvement and the use of different breeds may affect the model parameter values, which also may need to be re-estimated for crossbred animals. The aim of this study was to estimate parameter values and confidence intervals for the DGM with growth and body composition data from Zebu crossbred animals. Confidence intervals and asymptotic distribution were generated through nonparametric bootstrap with data from a field experiment conducted in Brazil. The parameters showed normal probability distribution for most scenarios. The rate constant for deoxyribonucleic acid (DNA) synthesis had a minimum increase of 156 % and the maximum of 389 %, compared to the original values and the maintenance requirement had a minimum increase of 126 % and maximum of 160 % compared to the original values. Lower limits of 95 % confidence intervals for the parameters related to maintenance and protein accretion rates were higher than the original estimates of the DGM, evidencing genetic differences of the Zebu crossbred animals in relation to the original DGM parameters.
Keywords:
asymptotic distribution; calibrating; cattle growth; nonparametric bootstrap; ordinary differential equations
Introduction
Non-linear growth functions (e.g., Bhowmick & Bhattacharya, Gompertz, Logistic, Von Bertalanffy, Weibull and Richards), with parameters estimated by regression, describe animal growth (Bhowmick and Bhattacharya, 2014Bhowmick, A.R.; Bhattacharya, S. 2014. A new growth curve model for biological growth: some inferential studies on the growth of Cirrhinus mrigala. Mathematical Biosciences 254: 28–41.; Chizzotti et al., 2008Chizzotti, M.L.; Tedeschi, L.O.; Valadares Filho, S.C. 2008. A meta-analysis of energy and protein requirements for maintenance and growth of Nellore cattle. Journal of Animal Science 86: 1588–1597.; Forni et al., 2009Forni, S.; Piles, M.; Blasco, A.; Varona, L.; Oliveira, H.N.; Lôbo, R.B.; Albuquerque, L.G. 2009. Comparison of different nonlinear functions to describe Nelore cattle growth. Journal of Animal Science 87: 496–506.; Freetly et al., 2011Freetly, H.C.; Kuehn, L.A.; Cundiff, L.V. 2011. Growth curves of crossbred cows sired by Hereford, Angus, Belgian Blue, Brahman, Boran, and Tuli bulls, and the fraction of mature body weight and height at puberty. Journal of Animal Science 89: 2373–2379.; Marinho et al., 2013Marinho, K.N.S.; Freitas, A.R.; Falção, A.J.S.; Dias, F.E.F. 2013. Nonlinear models for fitting growth curves of Nellore cows reared in the Amazon Biome. Revista Brasileira de Zootecnia 42: 645–650.; Nesetrilová, 2005Nesetrilová, H. 2005. Multiphasic growth models for cattle. Czech Journal of Animal Science 8: 347–354.). However, they have limited capacity to estimate body composition (i.e., fat and protein), thus, neglecting the possible interactions between metabolism and composition of gain dynamics (NRC, 1996National Research Council [NRC]. 1996. Nutrient Requirements of Beef Cattle. 7ed. The National Academies Press, Washington, DC, USA. p. 234.).
Mathematical models for beef cattle growth by France et al. (1987)France, J.; Gill, M.; Thornley, J.H.M.; England, P. 1987. A model of nutrient utilization and body composition in beef cattle. Animal Production 44: 371–385., Hoch and Agabriel (2004)Hoch, T.; Agabriel, J. 2004. A mechanistic dynamic model to estimate beef cattle growth and body composition. 1. Model description. Agricultural Systems 81: 1–15., Oltjen et al. (1986)Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97., Tedeschi et al. (2004)Tedeschi, L.O.; Fox, D.G.; Guiroy, P.J. 2004. A decision support system to improve individual cattle management. 1. A mechanistic, dynamic model for animal growth. Agricultural Systems 79: 171–204., Williams and Bennett (1995)Williams, C.B.; Bennett, G.L. 1995. Application of a computer model to predict optimum slaughter end points for different biological types of feeder cattle. Journal of Animal Science 73: 2903–2915. and Williams and Jenkins (2003)Williams, C.B.; Jenkins, T.G. 2003. A dynamic model of metabolizable energy utilization in growing and mature cattle. II. Metabolizable energy utilization for gain. Journal of Animal Science 81: 1382–1389. are potentially more useful than the models mentioned in the previous paragraph, as they express variables including metabolism and nutrient availability. The model described by Oltjen et al. (1986)Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97., named Davis Growth Model (DGM), and updated by Oltjen et al. (2000)Oltjen, J.W.; Pleasants, A.B.; Soboleva, T.K.; Oddy, V.H. 2000. Second-generation dynamic cattle growth and composition models. p. 197–209. In: McNamara, J.P.; France, J.; Beever, D.E., eds. Modelling nutrient utilization in farm animals. CAB International, Wallingford, UK. was chosen for this study because it is one of the most parsimonious, interpretable and easy for computational implementations.
Although there are several studies on nutritional requirements of cattle in Brazil (Marcondes et al., 2010aMarcondes, M.I.; Chizzotti, M.L.; Valadares Filho, S.C.; Gionbelli, M.P.; Paulino, P.V.R.; Paulino, M.F. 2010a. Energy requirements of zebu beef cattle. p. 81–106. In: Valadares Filho, S.C.; Marcondes, M.I.; Chizzotti, M.L.; Paulino, P.V.R., eds. Nutrient requirements of zebu beef cattle BR-CORTE. 2ed. UFV, Viçosa, MG, Brazil., bMarcondes, M.I.; Chizzotti, M.L.; Valadares Filho, S.C.; Gionbelli, M.P.; Paulino, P.V.R.; Paulino, M.F. 2010b. Protein requirements of zebu beef cattle. p. 107–126. In: Valadares Filho, S.C.; Marcondes, M.I.; Chizzotti, M.L.; Paulino, P.V.R., eds. Nutrient requirements of zebu beef cattle BR-CORTE. 2ed. UFV, Viçosa, MG, Brazil.; Paulino et al., 2010Paulino, P.V.R.; Fonseca, M.A.; Henriques, L.T.; Valadares Filho, S.C.; Detmann, E. 2010. Nutritional requirements of nellore cows and calves. p. 167–185. In: Valadares Filho, S.C.; Marcondes, M.I.; Chizzotti, M.L.; Paulino, P.V.R., eds. Nutrient requirements of zebu beef cattle BR-CORTE. 2ed. UFV, Viçosa, MG, Brazil.; Sainz et al., 2006Sainz, R.D.; Barioni, L.G.; Paulino, P.V.; Valadares Filho, S.C.; Oltjen, J.W. 2006. Growth patterns of Nellore vs British beef cattle breeds assessed using a dynamic, mechanistic model of cattle growth and composition. p. 160–170. In: Kebreab, E.; Dijkstra, J.; Bannink, A.; Gerrits, W.J.J.; France, J., eds. Nutrient digestion and utilization in farm animals: modeling approaches. CAB International, Wallingford, UK.; Valente et al., 2013Valente, E.E.L.; Paulino, M.F.; Detmann, E.; Valadares Filho, S.C.; Cardenas, J.E.G.; Dias, I.F.T. 2013. Requirement of energy and protein of beef cattle on tropical pasture. Acta Scientiarum 35: 417–424.), the DGM parameterization for Zebu genetics explored under Brazilian conditions has never included the estimation of parameter distribution by nonparametric bootstrap and statistical inferences.
In this context, this study aimed to calibrate parameters of the DGM to adapt it to the British (Bos taurus) × Zebu (Bos indicus) crossbred genotypes, to study the asymptotic distribution of the parameters of the mathematical model based on a nonparametric bootstrap method, and to estimate the confidence intervals for these parameters.
Materials and Methods
The methods are described in three subsections: Data, describing the experiment; Model, with a detailed description of variables and parameters from the DGM; Computational Statistics, which describes the procedures of algorithms to solve Ordinary Differential Equations (ODE), objective function optimization methods, and nonparametric bootstrap.
Data
Data for parameter estimation was obtained from a trial conducted in Campo Grande, Mato Grosso do Sul (MS) State, Brazil (20°26′39″ S, 54°43′24,6″ W and altitude of 500.25 m), in 2007. All procedures with animals were conducted according to the Embrapa Beef Cattle and University of São Paulo ethical standards established by the College of Agriculture Commission. The data comprised 27 crossbred cattle ½ Red Angus × ¼ Caracu × ¼ Nellore [RCN, n = 8 female (F) and 10 young bulls (M)] and Red Angus × Nellore (RN, n = 5 F and 4 M). Before weaning, the animals were raised in two systems: pasture system (PS) and confined system (CS). In PS, cows and their calves (cow-calf pairs) were kept on pasture with a mineral supplement (15 % Na, 11 % Ca, 9 % P, 1 % Mg, 7 % S, 6.691 ppm Zn, 2.829 ppm Fe, 1.153 ppm Cu, 797 ppm Mn, 90 ppm I, 31 ppm S and 24 ppm Co, dry matter basis). Intake and body composition of cow-calf pairs were not evaluated in the PS. In the CS, calves were fed with the same diet [2.3 Mcal ME kg−1 dry matter (DM) basis, 13 % crude protein (CP)] with cows on an ad libitum basis from 33 days of age until weaning. The DM intake of each cow was adjusted individually in 28-day intervals to minimize change in body weight (BW) and to keep Body Condition Scores (BCS) constant [diet and management are presented in detail in Albertini et al. (2012)Albertini, T.Z.; Medeiros, S.R.; Torres Júnior, R.A.; Zocchi, S.S.; Oltjen, J.W.; Strathe, A.B.; Lanna, D.P.D. 2012. A methodological approach to estimate the lactation curve and net energy and protein requirements of beef cows using nonlinear mixed-effects modeling. Journal of Animal Science 90: 3867–3878.]. After weaning (225 ± 14 days), animals from both systems were individually fed a total mixed diet (2.84 Mcal ME kg−1 DM, 14 % CP, DM basis) in individual stalls. Animals were slaughtered when they reached 6 mm of subcutaneous fat in the 12–13th ribs (feedlot maximum period was 147 days).
At the beginning of the feedlot period, the initial chemical body composition was derived from the slaughter of two to four animals of each genotype. In addition, at the end of feedlot period, animals were slaughtered and retained energy was estimated based on the composition of the 9–10–11th ribs.
Empty body chemical composition was estimated from linear regressions of percentage of water and fat in the 9–10–11th ribs. The original Hankins and Howe (1946)Hankins, O.G.; Howe, P.E. 1946. Estimation of the Composition of Beef Carcass Cuts. USDA, Washington, DC, USA. (Technical Bulletin, 26.). methodology was modified, so that the entire rib sections (bones and soft tissue) were ground. The composition of the entire 9–10–11th ribs was used. Protein and ash in the empty body were calculated from the estimated fat and water using the 80:20 ratio of protein and ash in the fat-free DM (Bonilha et al., 2011Bonilha, S.F.M.; Tedeschi, L.O.; Packer, I.U.; Razook, A.G.; Nardon, R.F.; Figueiredo, L.A.; Alleoni, G.F. 2011. Chemical composition of whole body and carcass of Bos indicus and tropically adapted Bos Taurus breeds. Journal of Animal Science 89: 2859–2866.; Reid et al., 1955Reid, J.T.; Wellington, G.H.; Dunn, H.O. 1955. Some relationships among the major chemical components of the bovine body and their application to nutritional investigations. Journal of Dairy Science 38: 1344–1359.). The energy concentration used for protein and fat was 5.497 and 9.390 Mcal kg−1 of Empty Body Weight (EBW), respectively.
The variables used to parameterize the DGM were based on the information collected in the post-weaning period: gender, genetic group, age, production system, initial body weight (BWi), kg; feedlot period (FP), d; DMI: dry matter intake (DMI), kg DMI d−1; initial shrunk body weight (BWji), kg; final shrunk body weight (BWjf), kg; initial empty body weight (BWzi), kg; final empty body weight (BWzf), kg; initial protein body weight (PROT_BWzi), kg; initial fat body weight (FAT_BWzi), kg; final protein body weight (PROT_BWzf), kg; final fat body weight (FAT_BWzf), kg. The aggregated dataset is summarized in Tables 1 and 2.
Summary descriptive analysis [mean, standard deviation (SD), minimum (Min) and maximum (Max)] of the model input variables for 13 crossbred females.
Summary descriptive analysis [mean, standard deviation (SD), minimum (Min) and maximum (Max)] of the model input variables for 14 crossbred bulls.
Model
The DGM contains three state variables corresponding to deoxyribonucleic acid (DNA) mass, protein mass (PROT) and fat mass (FAT) totals. The DGM was originally proposed by Oltjen et al. (1986)Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97. and updated by Oltjen et al. (2000)Oltjen, J.W.; Pleasants, A.B.; Soboleva, T.K.; Oddy, V.H. 2000. Second-generation dynamic cattle growth and composition models. p. 197–209. In: McNamara, J.P.; France, J.; Beever, D.E., eds. Modelling nutrient utilization in farm animals. CAB International, Wallingford, UK.. The proposal for this model is based on concepts of hyperplasia and hypertrophy of the animal, described by the following set of ODE:
where k1 is the rate constant for DNA synthesis; k2 is the rate constant for protein synthesis; k3 is the rate constant for protein degradation; DNAmax is the maximum quantity of DNA in the whole body; PROT is the protein in the EBW; NUT1 and NUT2 are the effects of energy intake on growth (Oltjen et al., 1986Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97.; Oltjen et al., 2000Oltjen, J.W.; Pleasants, A.B.; Soboleva, T.K.; Oddy, V.H. 2000. Second-generation dynamic cattle growth and composition models. p. 197–209. In: McNamara, J.P.; France, J.; Beever, D.E., eds. Modelling nutrient utilization in farm animals. CAB International, Wallingford, UK.), reported in equations 4 and 5:
and
where
is the ratio between the observed metabolizable energy intake (MEI, Mcal d−1) and the metabolizable energy intake reference (MEInorm Mcal d−1),
where MEBW is the mature EBW (600 kg for females and 900 kg for intact males).
The fat deposition rate is calculated by the ratio of the amount of residual energy and the average energy value of lipids, according to eq. (3), where FAT is the fat mass; EProt and Efat are the energy concentrations of protein and fat, respectively; NEm and NEg are net energy for maintenance and gain contents of the feed, respectively; and MEMAINT is the metabolizable energy requirements for maintenance
where α is the parameter to be estimated and represents the maintenance requirement of animals and EBW can be estimated as
The parameters of interest in the DGM are k1, k2, k3, DNAmax and α (Eq. 1, 2 and 3). However, k2 and k3, are highly correlated, thus, it is not feasible to adjust the two parameters simultaneously. An alternative mentioned in the literature (Oltjen et al., 1986Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97.; Sainz et al., 2006Sainz, R.D.; Barioni, L.G.; Paulino, P.V.; Valadares Filho, S.C.; Oltjen, J.W. 2006. Growth patterns of Nellore vs British beef cattle breeds assessed using a dynamic, mechanistic model of cattle growth and composition. p. 160–170. In: Kebreab, E.; Dijkstra, J.; Bannink, A.; Gerrits, W.J.J.; France, J., eds. Nutrient digestion and utilization in farm animals: modeling approaches. CAB International, Wallingford, UK.) was to keep the value of k2 at 0.0461.
The gain composition and the dilution of maintenance requirements are two predominant processes to explain growth and food conversion efficiency into body tissues. The mechanistic process from the DGM allows the biological understanding of the growth process in detail through the evaluation of changes in underlying growth parameter (k1 and α). Furthermore, the DGM enables the evaluation of trajectories of DNA mass and fat and protein tissue pools over time.
Computational statistics
A multivariate analysis of covariance (ANCOVA) was carried out to check for differences between the means of treatments and to cluster the treatments that were not significantly different. The parameters used to perform the multivariate analysis of covariance were individually fitted, k1 and α by DGM, simultaneously. The statistical model for this analysis was:
where i = 1, …, b is the ith index of the breeds (RCN and RN); j = 1, …, s is the jth index of the systems (PS and CS); k = 1, …, g is the kth index of the gender (F and M); l are replicates of each treatment (unbalanced experiment); p = 1, … , v is the pth index of the response variables (DNA accretion rate and energy requirement for maintenance); yijklp is the multivariate vector of observations of pth variable under the effect of ith breed, jth system, kth gender and lth repetition; μ is the general multivariate vector of constants inherent for all observations; αip is the multivariate vector of effects of the ith breed in pth variable; βjp. is the multivariate vector of effects of the ith system in pth variable; γkp is the multivariate vector of effects of the kth gender in pth variable; (β × γ)jkp is the multivariate vector of interaction effects between jth system and kth gender in pth variable; ρijklp is the covariate (multivariate vector of effects from initial weights associated with observations yijklp); and εijklp, is the multivariate vector of errors associated with observations yijklp, (εijklp ~ N2(0, Σ)).
The multivariate ANCOVA showed no significant difference in mean vectors in relation to the breeds (data not reported). Nonparametric bootstrap resampling was run taking into account the following groups: females PS, females CS, males PS and males CS (reported in Tables 1 and 2). We performed 300 resampling nonparametric bootstraps for each group and determined the confidence interval of Biased Corrected Percentile Bootstrap (BCPB, Efron, 1979Efron, B. 1979. Bootstrap methods: another look at the jackknife. The Annals of Statistics 7: 1–26.; Efron, 1981Efron, B. 1981. Nonparametric standard errors and confidence intervals. Canadian Journal of Statistics 9: 139–172.).
The DGM was implemented in the R software (Development Core Team, version 3.1.0, 2014) and the function ode() of the deSolve package (Soetaert et al., 2010Soetaert, K.; Petzoldt, T.; Setzer, R.W. 2010. Solving differential equations in R: package deSolve. Journal of Statistical Software 33: 1–25.) for numerical solution of initial first-order problems was used. The solution was achieved using the lsoda integration method with absolute and relative error tolerances of 10−6.
Parameter values were determined using the downhill simplex optimization algorithm described by Nelder and Mead (1965)Nelder, J.A.; Mead, R. 1965. A simplex algorithm for function minimization. Computer Journal 7: 308–313. to minimize the residuals sum of squares. The residual sum of squares of the DGM was calculated in Eq. (11):
where t = 1, 2,…, n; u = 1,…, m; n is the number of animals and m is the number of response variables, namely the protein mass and fat mass endpoint; Res is the residual sum of squares of all observations of the sample; ŷtu and ytu are the predicted and observed values, respectively, of the tth individual in the uth variable of the DGM; and σμ is the standard deviation of the uth variable of the DGM. The standard deviation was used as a weighting factor for terms to become dimensionless, so it is important for different model variables that have different units and magnitudes. The function optim() and “stats” package from the R statiscal software (R Core Team, 2014) was used to minimize Eq. (11).
The Nelder-Mead method optimizes nonlinear and multidimensional models requiring only an objective function without the need to be derived to find a solution (Press et al., 1990Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. 1990. Numerical recipes in C: the art of scientific computing. Cambridge University Press, New York, NY, USA.). The method uses an initial simplex [a set of vectors (points) in an M-dimensional space], where each vertex represents a possible solution. The number of simplex vertices is equal to the number of parameters to be fitted plus one. The scaling coefficients of the Nelder-Mead method for the reflection factor (β), the contraction factor (λ) and expansion factor (γ) received values suggested by Press et al. (1990)Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. 1990. Numerical recipes in C: the art of scientific computing. Cambridge University Press, New York, NY, USA., i.e., 1.0, 0.5 and 2.0, respectively. The tolerance limit was 10−8 and the maximum number of interactions was 500.
Model evaluation
In this section, we present several techniques for mathematical comparison of the models. These techniques are necessary to support decisions and to demonstrate the success of a model, presenting evidence to promote their acceptance and use for certain purposes. All predictions obtained through the model fit can be rewritten in the form of a simple linear regression, represented by the observed and predicted values according to the Eq.
where x is the predicted values; y is the observed values; β0 and β1 are intercept and slope, respectively.
The regression was evaluated according to the following statistical hypothesis:
If the null hypotheses were not rejected, it was concluded that the equations accurately estimated the observed values. The slope and the intercept were evaluated separately to identify specific problems of fitting. For all comparisons, 0.05 was established as the critical level of probability for type I error. The parameters β0 and β1 were evaluated separately and simultaneously to assess whether the bias was represented by a constant (evaluated by the intercept difference of parametric value zero) or by a tendency of percentage bias (evaluated by the slope deviation of parametric value 1).
Estimates were evaluated using the estimate value of the mean square error of the prediction (MSEP) and its components (Tedeschi, 2006Tedeschi, L.O. 2006. Assessment of the adequacy of mathematical models. Agricultural Sciences 89: 225–247.):
where x is the predicted values; y is the observed values; and n is the number of observations.
The prediction of accuracy was determined by estimating the correlation concordance coefficient (CCC), or reproducibility index, as described by Tedeschi (2006)Tedeschi, L.O. 2006. Assessment of the adequacy of mathematical models. Agricultural Sciences 89: 225–247.. The CCC indicates models with good accuracy and precision (when close to 1.0) or models with problem of reproducibility (when close to 0.0). The smallest mean square error of prediction indicates the best model in the evaluation.
Other methods used for model evaluation were the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC), which were calculated, respectively, by Eqs. (15) and (16):
where p is the number of parameter settings of the estimated model and n is the number of observations. The best performances of the model are provided by the lowest values of AIC and BIC. is the variance of the estimated model;
is the variance of the estimated model;
Results and Discussion
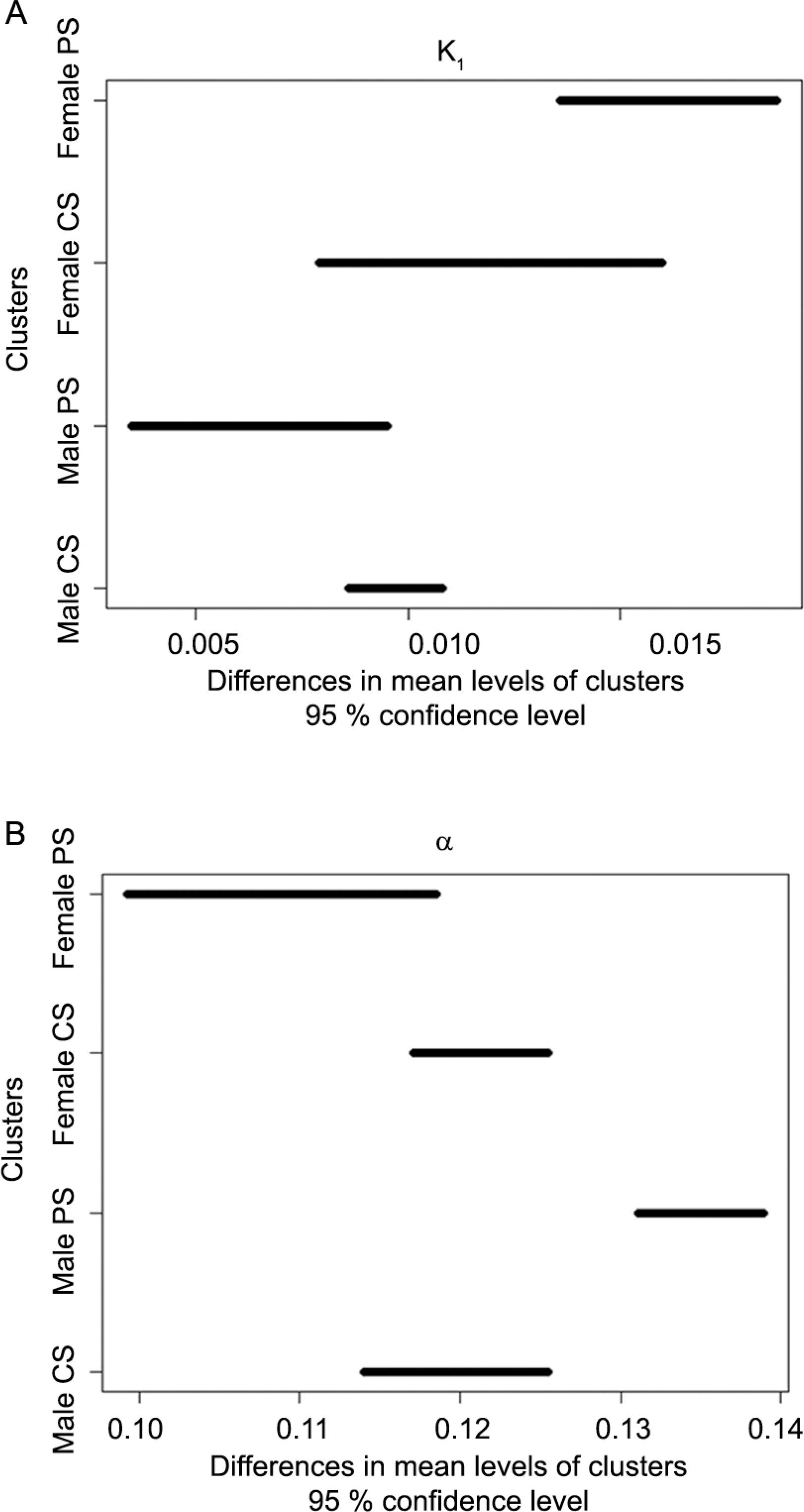
The results of the nonparametric bootstrap with the new parameterization of the model are shown in Table 3. The Kolmogorov-Smirnov (KS) normality test showed normal distribution for all parameters (p > 0.05), except for k1 (females PS). This shows that the probability distribution is not the same, highlighting differences between groups like females PS and males CS (Figures 1A and B). The model parameter fitting and parameter correlation structures are important to characterize the behavior of a system in response to multiple variations (climate, genotypes, nutritional diet, system, and other factors). The adjusted model for the four specific scenarios ensures greater predictability and can be a useful tool to adapt systems to higher profitability. The negative correlation between the rate constant for addition of DNA and the maintenance requirement energy of animal was found for intact males PS (Figure 2C). This correlation indicates that the animals with faster lean tissue deposition also have better performance because they tend to dilute the energy for maintenance with the greater proportion of energy intended for tissue deposition. The joint dispersion matrices of the nonparametric bootstrap estimates, Pearson correlation and frequency histograms for k1 and α, are shown in Figures 2A, B, C and D.
Descriptive measures, Kolmogorov-Smirnov (KS) normality test (p value) and confidence intervals for the average Davis Growth Model (DGM) parameters with 95 % of confidence.
Confidence intervals of Biased Corrected Percentile Bootstrap for the mean Davis Growth Model parameters with 95 % of confidence, A) parameter k1 and B) parameter α (PS: Pasture System; CS: Confined System).
Joint dispersion matrixes of the nonparametric bootstrap estimates, the Pearson correlation, and frequency histograms for k1 and α to the Davis Growth Model A) Female PS (Pasture System); B) Female CS (Confined System); C) Male PS; D) Male CS.
There was no difference between the PS and CS systems within the female gender, considering the parameters k1 and α simultaneously. There was no difference in the CS level change for PS level, regarding the gender factor, in weight gain (k1). This was an expected result, since PS animals have a similar growth rate during the compensatory gain compared to CS animals (Table 3). The results show significant differences, about a, between males PS and males CS, with the largest maintenance of energy average for males PS (Table 3). This behavior in male animals was expected because animals from CS were slaughtered in a shorter time during the feedlot in relation to animals from PS (Table 2).
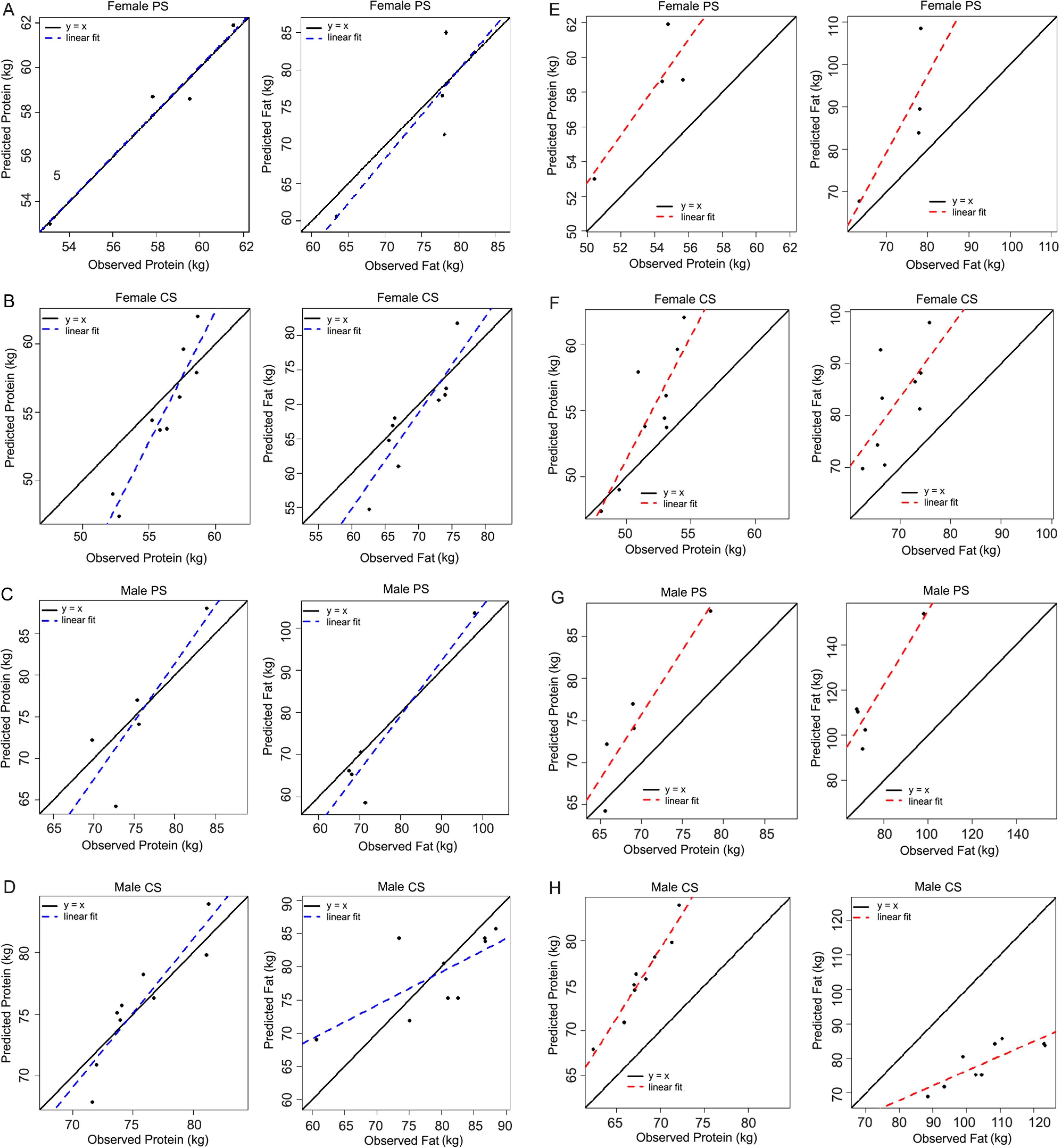
The reparametrized model in this study (Figures 3A, B, C and D) improved predictions of the original parameters (Bos Taurus reference bull, Figures 3E, F, G and H). The bias of the proposed new parameters calculated considering average protein and fat concentration are smaller than the bias considering calculated average predictions of protein and fat concentration using the original calibration of the model by Oltjen et al. (1986)Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97., respectively (Table 4). The evaluation of the model (Table 5) using the criteria MSEP, CCC, intercept, slope, AIC, and BIC corroborate the results shown in Figures 3A, B, C, D, E, F, G, and H, indicating improvement in performance of the model with new estimates of the current study compared to the original estimates by Oltjen et al. (1986)Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97.. Therefore, this fitted model was provisionally accepted for growth simulation of Nellore (Bos indicus) and Nellore crossbred animals, although pending further evaluations with an independent dataset.
Observed and predicted values for protein and fat. (A – D) modified parameters; (E – H) original parameters (Bos Taurus reference bull); PS: Pasture System; CS: Confined System.
Comparison of average predictions of protein and fat between the new calibrations proposed in this study and calibrations using the original values of Oltjen et al. (1986)Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97..
Evaluation of Davis Growth Model (DGM) with the estimates obtained by bootstrap analysis of the current study and evaluation using the original estimates of model Oltjen et al. (1986)Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97..
In this study, k1 and α values were higher than the original DGM parameters (Oltjen et al., 1986Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97.). In the study conducted by Oltjen et al. (1986)Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97., k1 had a minimum increase of 156 % and the maximum of 389 % compared to the original values (k1 = 0.00429, Table 6), while α had a minimum increase of 126 % and the maximum of 160 % compared to the original values (α = 0.086, Table 6). Previous study involving reparameterization of the model with Nellore bulls by Sainz et al. (2006)Sainz, R.D.; Barioni, L.G.; Paulino, P.V.; Valadares Filho, S.C.; Oltjen, J.W. 2006. Growth patterns of Nellore vs British beef cattle breeds assessed using a dynamic, mechanistic model of cattle growth and composition. p. 160–170. In: Kebreab, E.; Dijkstra, J.; Bannink, A.; Gerrits, W.J.J.; France, J., eds. Nutrient digestion and utilization in farm animals: modeling approaches. CAB International, Wallingford, UK. estimated rates for k1, k3 and α (k1 = 0.00304, k3 = 0.1300, and α = 0.0768), keeping fixed k2 (0.0479) and DNAmax (462 g). Compared to Sainz et al. (2006)Sainz, R.D.; Barioni, L.G.; Paulino, P.V.; Valadares Filho, S.C.; Oltjen, J.W. 2006. Growth patterns of Nellore vs British beef cattle breeds assessed using a dynamic, mechanistic model of cattle growth and composition. p. 160–170. In: Kebreab, E.; Dijkstra, J.; Bannink, A.; Gerrits, W.J.J.; France, J., eds. Nutrient digestion and utilization in farm animals: modeling approaches. CAB International, Wallingford, UK., k1 had a minimum increase of 220 % and the maximum of 549 %; α had a minimum increase of 141 % and the maximum of 178 % (Table 7). Breeds and genetic improvement are the possible causes of parameter changes.
Percentage of change of the current values of the parameters in relation to the original values of Oltjen et al. (1986)Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97..
Percentage of change of the current values of the parameters in relation to the original values of Sainz et al. (2006)Sainz, R.D.; Barioni, L.G.; Paulino, P.V.; Valadares Filho, S.C.; Oltjen, J.W. 2006. Growth patterns of Nellore vs British beef cattle breeds assessed using a dynamic, mechanistic model of cattle growth and composition. p. 160–170. In: Kebreab, E.; Dijkstra, J.; Bannink, A.; Gerrits, W.J.J.; France, J., eds. Nutrient digestion and utilization in farm animals: modeling approaches. CAB International, Wallingford, UK..
There are two hypotheses to explain the higher values of k1 and α compared to previous research: 1) heterosis (maximum for RN and lower for RCN) increased the value of the parameters when compared with Zebu genotype (i.e., Nellore used by Sainz et al., 2006Sainz, R.D.; Barioni, L.G.; Paulino, P.V.; Valadares Filho, S.C.; Oltjen, J.W. 2006. Growth patterns of Nellore vs British beef cattle breeds assessed using a dynamic, mechanistic model of cattle growth and composition. p. 160–170. In: Kebreab, E.; Dijkstra, J.; Bannink, A.; Gerrits, W.J.J.; France, J., eds. Nutrient digestion and utilization in farm animals: modeling approaches. CAB International, Wallingford, UK.); and 2) the experiment was conducted with animals from herds selected by Embrapa in 2010, three to seven generations after the Sainz et al. (2006)Sainz, R.D.; Barioni, L.G.; Paulino, P.V.; Valadares Filho, S.C.; Oltjen, J.W. 2006. Growth patterns of Nellore vs British beef cattle breeds assessed using a dynamic, mechanistic model of cattle growth and composition. p. 160–170. In: Kebreab, E.; Dijkstra, J.; Bannink, A.; Gerrits, W.J.J.; France, J., eds. Nutrient digestion and utilization in farm animals: modeling approaches. CAB International, Wallingford, UK. and Oltjen et al. (1986)Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97. studies. These cases reinforce both the improvement through crossing and selection, as well as genetic progress associated with increased k1 and α. In Brazil as in other countries, weight is the main selection criteria with moderate to high genetic correlation with growth curve parameters (Meyer, 1995Meyer, K. 1995. Estimates of genetic parameters for mature weight of Australian beef cows and its relationship to early growth and skeletal measures. Livestock Production Science 44: 125–137.; Mignon-Grasteau, 1999Mignon-Grasteau, S. 1999. Genetic parameters of growth curve parameters in male and female chickens. British Poultry Science 40: 44–51.), and potentially with k1 and α.
Conclusions
The parameters showed normal probability distribution for most scenarios. Confidence intervals produced through bootstrap inferred that model parameters differ from the original values determined by Oltjen et al. (1986)Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97.. Breeds and genetic improvement are the possible causes of parameter changes. Intact male animals of the pasture system showed negative correlation between the protein deposition rate and requirement for energy maintenance, indicating that the animals with faster lean tissue deposition also have better performance because they tend to dilute the energy cost for maintenance, with a greater proportion of energy used for tissue deposition. We highlight that the generalization of this finding demands studies with larger populations. The new estimates of parameter values, instead of the originals, can be used for predictive purposes for crossbred cattle.
Acknowledgements
The authors express their thanks to Coordination for the Improvement of Higher Level Personnel (CAPES) and Brazilian Agricultural Research Corporation (Embrapa) for providing scholarship and University of São Paulo/ESALQ academic formation by the first author, the Embrapa Beef Cattle, Animal Nutrition and Growth Laboratory – USP/ESALQ and São Paulo State Foundation for Research Support (FAPESP) for providing the data and grants, as well the Embrapa Eastern Amazon and Embrapa Agricultural Informatics by the scientific partnership group of the Pecus and Animal-Change network.
References
- Albertini, T.Z.; Medeiros, S.R.; Torres Júnior, R.A.; Zocchi, S.S.; Oltjen, J.W.; Strathe, A.B.; Lanna, D.P.D. 2012. A methodological approach to estimate the lactation curve and net energy and protein requirements of beef cows using nonlinear mixed-effects modeling. Journal of Animal Science 90: 3867–3878.
- Bonilha, S.F.M.; Tedeschi, L.O.; Packer, I.U.; Razook, A.G.; Nardon, R.F.; Figueiredo, L.A.; Alleoni, G.F. 2011. Chemical composition of whole body and carcass of Bos indicus and tropically adapted Bos Taurus breeds. Journal of Animal Science 89: 2859–2866.
- Bhowmick, A.R.; Bhattacharya, S. 2014. A new growth curve model for biological growth: some inferential studies on the growth of Cirrhinus mrigala. Mathematical Biosciences 254: 28–41.
- Chizzotti, M.L.; Tedeschi, L.O.; Valadares Filho, S.C. 2008. A meta-analysis of energy and protein requirements for maintenance and growth of Nellore cattle. Journal of Animal Science 86: 1588–1597.
- Freetly, H.C.; Kuehn, L.A.; Cundiff, L.V. 2011. Growth curves of crossbred cows sired by Hereford, Angus, Belgian Blue, Brahman, Boran, and Tuli bulls, and the fraction of mature body weight and height at puberty. Journal of Animal Science 89: 2373–2379.
- France, J.; Gill, M.; Thornley, J.H.M.; England, P. 1987. A model of nutrient utilization and body composition in beef cattle. Animal Production 44: 371–385.
- Forni, S.; Piles, M.; Blasco, A.; Varona, L.; Oliveira, H.N.; Lôbo, R.B.; Albuquerque, L.G. 2009. Comparison of different nonlinear functions to describe Nelore cattle growth. Journal of Animal Science 87: 496–506.
- Efron, B. 1979. Bootstrap methods: another look at the jackknife. The Annals of Statistics 7: 1–26.
- Efron, B. 1981. Nonparametric standard errors and confidence intervals. Canadian Journal of Statistics 9: 139–172.
- Hankins, O.G.; Howe, P.E. 1946. Estimation of the Composition of Beef Carcass Cuts. USDA, Washington, DC, USA. (Technical Bulletin, 26.).
- Hoch, T.; Agabriel, J. 2004. A mechanistic dynamic model to estimate beef cattle growth and body composition. 1. Model description. Agricultural Systems 81: 1–15.
- Marinho, K.N.S.; Freitas, A.R.; Falção, A.J.S.; Dias, F.E.F. 2013. Nonlinear models for fitting growth curves of Nellore cows reared in the Amazon Biome. Revista Brasileira de Zootecnia 42: 645–650.
- Marcondes, M.I.; Chizzotti, M.L.; Valadares Filho, S.C.; Gionbelli, M.P.; Paulino, P.V.R.; Paulino, M.F. 2010a. Energy requirements of zebu beef cattle. p. 81–106. In: Valadares Filho, S.C.; Marcondes, M.I.; Chizzotti, M.L.; Paulino, P.V.R., eds. Nutrient requirements of zebu beef cattle BR-CORTE. 2ed. UFV, Viçosa, MG, Brazil.
- Marcondes, M.I.; Chizzotti, M.L.; Valadares Filho, S.C.; Gionbelli, M.P.; Paulino, P.V.R.; Paulino, M.F. 2010b. Protein requirements of zebu beef cattle. p. 107–126. In: Valadares Filho, S.C.; Marcondes, M.I.; Chizzotti, M.L.; Paulino, P.V.R., eds. Nutrient requirements of zebu beef cattle BR-CORTE. 2ed. UFV, Viçosa, MG, Brazil.
- Meyer, K. 1995. Estimates of genetic parameters for mature weight of Australian beef cows and its relationship to early growth and skeletal measures. Livestock Production Science 44: 125–137.
- Mignon-Grasteau, S. 1999. Genetic parameters of growth curve parameters in male and female chickens. British Poultry Science 40: 44–51.
- National Research Council [NRC]. 1996. Nutrient Requirements of Beef Cattle. 7ed. The National Academies Press, Washington, DC, USA. p. 234.
- Nelder, J.A.; Mead, R. 1965. A simplex algorithm for function minimization. Computer Journal 7: 308–313.
- Nesetrilová, H. 2005. Multiphasic growth models for cattle. Czech Journal of Animal Science 8: 347–354.
- Oltjen, J.W.; Pleasants, A.B.; Soboleva, T.K.; Oddy, V.H. 2000. Second-generation dynamic cattle growth and composition models. p. 197–209. In: McNamara, J.P.; France, J.; Beever, D.E., eds. Modelling nutrient utilization in farm animals. CAB International, Wallingford, UK.
- Oltjen, J.W.; Bywater, A.C.; Baldwin, R.L.; Garrett, W.N. 1986. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62: 86–97.
- Paulino, P.V.R.; Fonseca, M.A.; Henriques, L.T.; Valadares Filho, S.C.; Detmann, E. 2010. Nutritional requirements of nellore cows and calves. p. 167–185. In: Valadares Filho, S.C.; Marcondes, M.I.; Chizzotti, M.L.; Paulino, P.V.R., eds. Nutrient requirements of zebu beef cattle BR-CORTE. 2ed. UFV, Viçosa, MG, Brazil.
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. 1990. Numerical recipes in C: the art of scientific computing. Cambridge University Press, New York, NY, USA.
- Reid, J.T.; Wellington, G.H.; Dunn, H.O. 1955. Some relationships among the major chemical components of the bovine body and their application to nutritional investigations. Journal of Dairy Science 38: 1344–1359.
- Sainz, R.D.; Barioni, L.G.; Paulino, P.V.; Valadares Filho, S.C.; Oltjen, J.W. 2006. Growth patterns of Nellore vs British beef cattle breeds assessed using a dynamic, mechanistic model of cattle growth and composition. p. 160–170. In: Kebreab, E.; Dijkstra, J.; Bannink, A.; Gerrits, W.J.J.; France, J., eds. Nutrient digestion and utilization in farm animals: modeling approaches. CAB International, Wallingford, UK.
- Soetaert, K.; Petzoldt, T.; Setzer, R.W. 2010. Solving differential equations in R: package deSolve. Journal of Statistical Software 33: 1–25.
- Tedeschi, L.O. 2006. Assessment of the adequacy of mathematical models. Agricultural Sciences 89: 225–247.
- Tedeschi, L.O.; Fox, D.G.; Guiroy, P.J. 2004. A decision support system to improve individual cattle management. 1. A mechanistic, dynamic model for animal growth. Agricultural Systems 79: 171–204.
- Valente, E.E.L.; Paulino, M.F.; Detmann, E.; Valadares Filho, S.C.; Cardenas, J.E.G.; Dias, I.F.T. 2013. Requirement of energy and protein of beef cattle on tropical pasture. Acta Scientiarum 35: 417–424.
- Williams, C.B.; Bennett, G.L. 1995. Application of a computer model to predict optimum slaughter end points for different biological types of feeder cattle. Journal of Animal Science 73: 2903–2915.
- Williams, C.B.; Jenkins, T.G. 2003. A dynamic model of metabolizable energy utilization in growing and mature cattle. II. Metabolizable energy utilization for gain. Journal of Animal Science 81: 1382–1389.
Edited by
Publication Dates
-
Publication in this collection
Jan-Feb 2017
History
-
Received
14 July 2015 -
Accepted
26 Apr 2016