ABSTRACT
A similarity hypothesis recently presented to describe horizontal infiltration into homogeneous soils, developed for coarse-textured soils like sieved marine sand, implies that the soil water retention function θ(h) is the mirror image of an extended Boltzmann transform function θ(λ2). A second hypothesis applicable to vertical infiltration suggests that the soil water retention function θ(h) is also the mirror image of the soil water profile θ(z). Using previously published infiltration data, we investigated whether these two similarity solutions successfully describe infiltration into two “normal” soils. Although the theory using the first similarity assumption adequately describes horizontal cumulative infiltration and infiltration rate into both soils, it fails to estimate soil water distributions measured between soil profiles. The second similarity solution for vertical infiltration into either soil completely fails to coincide with measured soil water distributions, cumulative infiltration and infiltration rate.
Boltzmann function; mirror image; wetting front
Introduction
Hydraulic transport and retention properties of water-unsaturated soils are strikingly complex, therefore, obtaining simple solutions for describing infiltration into soils remains a lingering challenge. After the classical concepts of Darcy (1856)Darcy, H. 1856. The public fountains in the city of Dijon = Les fontaines publique de la ville de Dijon. Dalmont, Paris (in French)., Boltzmann (1894)Boltzmann, L. 1894. For the integration of the diffusion equation with variable diffusion coefficients = Zur Integration der Diffusionsgleichung bei variabeln Diffusionscoefficienten. Annalen der Physik (Leipzig) 53: 959-964 (in German). and Buckingham (1907)Buckingham, E. 1907. Studies on the movement of soil moisture. Bulletin Nº 38. U.S. Dept. of Agriculture. Bureau of soils, Washington, D.C., Green and Ampt (1911)Green, W.H.; Ampt, G.A. 1911. Studies in soil physics: I. The flow of air and water through soils. Journal of Agriculture Science 4: 1-24. developed an equation to estimate water infiltration into a sandy soil subjected to specific initial and boundary conditions. Today, the Green and Ampt equation as well as Richard’s equation (1931), developed while he conducted research for his PhD degree, are now commonplaces in soil physics and hydrology textbooks. Moreover, since Philip (1955)Philip, J.R. 1955. Numerical solution of equations of the diffusion type with diffusivity concentration-dependent. Transactions of Faraday Society 51: 885-892. published a numerical solution of Richard's equation for water infiltrating into a homogeneous soil, his achievement has been universally used as a classical solution known as the Richard's equation.
Recently, Prevedello et al. (2008)Prevedello, C.L.; Loyola, J.M.T.; Reichardt, K.; Nielsen, D.R. 2008. New analytic solution of Boltzmann transform for horizontal water infiltration into sand. Vadose Zone Journal 7: 1170-1177. focused on soil water content distribution [θ(x,t)] during horizontal infiltration to estimate infiltration into homogeneous soils using measured values of K for specific values of θ and the soil water retention curve θ(h), Richard's equation and an extension of the historic 1894 Boltzmann transform function. As illustrated in Figure 1A, this similarity hypothesis
– A: Illustration of similarity hypothesis between θ(h) and θ(λ2) for horizontal infiltration, and B: Illustration of similarity hypothesis between θ(h) and θ(z) for vertical downward infiltration.
implies that the soil water retention function θ(h) is the mirror image of an extended Boltzmann transform function θ(λ2). For vertical infiltration, Prevedello et al. (2009)Prevedello, C.L.; Loyola, J.M.T.; Reichardt, K.; Nielsen, D.R. 2009. New analytic solution related to the Richards, Philip, and Green-Ampt equations for infiltration. Vadose Zone Journal 8: 127-135. published another similarity hypothesis
illustrated in Figure 1B and showed that θ(h) is the mirror image of the soil water profile θ(z).
Recognizing that these similarity solutions are approximations of classical solutions of Richard's equation, Prevedello et al. (2008Prevedello, C.L.; Loyola, J.M.T.; Reichardt, K.; Nielsen, D.R. 2008. New analytic solution of Boltzmann transform for horizontal water infiltration into sand. Vadose Zone Journal 7: 1170-1177., 2009Prevedello, C.L.; Loyola, J.M.T.; Reichardt, K.; Nielsen, D.R. 2009. New analytic solution related to the Richards, Philip, and Green-Ampt equations for infiltration. Vadose Zone Journal 8: 127-135.) specifically stated that the use and acceptance of the hypotheses remained open for future research. Here, without deriving additional mirror image hypotheses, we merely explore the potential use and associated restrictions of the two recent similarity hypotheses illustrated in Figure 1.
Theory
Similarity solution for horizontal infiltration
With the analytic integral of Eq. [1] introduced into the equation of continuity subject to the initial and boundary conditions
where subscript i refers to initial, 0 to saturated and t is the infiltration time.
Prevedello's similarity solution for horizontal infiltration is
Integrating Eq. [3] between the boundary conditions θi and θ0, the cumulative infiltration i(t) at the soil surface x = 0 is
The derivative of Eq. [4] with respect to time t defines the infiltration rate q0(t) at the soil surface
Similarity solution for vertical downward infiltration
After introducing Eq. [2] into Richards' equation and integrating it subject to the initial and boundary conditions
where subscript i refers to initial, 0 to saturated and t is the infiltration time.
Prevedello's similarity solution for vertical downward infiltration is
The soil water content profile θ(z,t) during infiltration is obtained from Eq. [6] using measured values of the soil water retention curve.
Materials and Methods
The similarity solutions of Prevedello et al. (2008Prevedello, C.L.; Loyola, J.M.T.; Reichardt, K.; Nielsen, D.R. 2008. New analytic solution of Boltzmann transform for horizontal water infiltration into sand. Vadose Zone Journal 7: 1170-1177. and 2009Prevedello, C.L.; Loyola, J.M.T.; Reichardt, K.; Nielsen, D.R. 2009. New analytic solution related to the Richards, Philip, and Green-Ampt equations for infiltration. Vadose Zone Journal 8: 127-135.) are here tested with measurements of water infiltrating into laboratory columns of Columbia silt loam and Hesperia sandy loam (Davidson et al., 1963Davidson, J.M.; Nielsen, D.R.; Biggar, J.W. 1963. The measurement and description of water flow through Columbia silt loam and Hesperia sandy loam. Hilgardia 34: 601-617.). Their measured soil water properties and wetting parameters are given in Table 1.
− Saturated hydraulic conductivity K0, saturated volumetric water content θ0, residual water content θr, initial water content θi, and wetting parameters of van Genuchten (1980) a, ι, m and n for Marine sand, Columbia silt loam and Hesperia sandy loam, used to calculate θ(h) and K(θ ) functions by Mualem (1976).
During horizontal and vertical infiltration into the Columbia and Hesperia soils, the matric potential head h0 at their soil surfaces was maintained at -2 cm. Values of x[h(θ),t], i(t) and q0(t) from Eqs. [3 through 5] as well as θ(z,t) obtained from Eq. [6] were compared with those from classical solutions of the Richards' equation derived by Philip (1955)Philip, J.R. 1955. Numerical solution of equations of the diffusion type with diffusivity concentration-dependent. Transactions of Faraday Society 51: 885-892..
Results and Discussion
Horizontal infiltration
Calculations made from Eqs. [3, 4 and 5] presented in Figures 2 through 4 illustrate the comparisons of the Prevedello similarity solutions to measured observations and classical solutions of Richards' equation for three different infiltration times. From Figure 2, it is readily apparent that all of the similarity calculations for the Marine sand are nearly identical to those stemming from the classical solution of Philip, as stated in Prevedello et al. (2008)Prevedello, C.L.; Loyola, J.M.T.; Reichardt, K.; Nielsen, D.R. 2008. New analytic solution of Boltzmann transform for horizontal water infiltration into sand. Vadose Zone Journal 7: 1170-1177..
− Soil water content measured within horizontal columns of Marine sand as well as cumulative infiltration versus the square root of time and infiltration rate at soil surface as a function of time.
− Soil water content measured within horizontal columns of Hesperia sandy loam as well as cumulative infiltration versus the square root of time and infiltration rate at the soil surface as a function of time.
Based on the Columbia silt loam measurements, graphs of soil water content profiles, cumulative infiltration and infiltration rate are presented in Figure 3. Indeed, cumulative infiltration and infiltration rate derived from the similarity solution successfully approximate those from the classical solution. However, it is immediately obvious that the similarity solution fails to estimate the distributions of the soil water measured within the profile. The similarity solution describes gradually flattening sigmoid-shaped wetting fronts rather than the persistently abrupt measured wetting fronts and those calculated from the classical solution of Richards' equation.
− Soil water content measured within horizontal columns of Columbia silt loam as well as cumulative infiltration versus the square root of time and infiltration rate at the soil surface as a function of time.
The results from the Hesperia sandy loam illustrated in Figure 4 are consistent with those from the Columbia silt loam. In other words, the similarity hypothesis successfully describes both cumulative infiltration and rate of infiltration, but fails to predict the abrupt shape of the measured wetting fronts.
Vertical infiltration
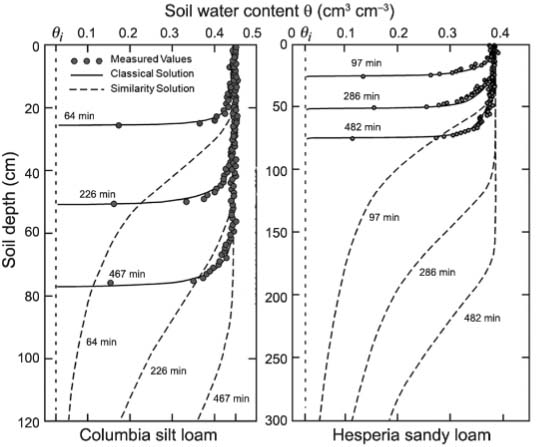
We now verify that Prevedello et al. (2009)Prevedello, C.L.; Loyola, J.M.T.; Reichardt, K.; Nielsen, D.R. 2009. New analytic solution related to the Richards, Philip, and Green-Ampt equations for infiltration. Vadose Zone Journal 8: 127-135. was correct to limit the use of Eq. [6] to describe infiltration into only coarse textured soils. Figure 5 illustrates the results of using Eq. [6] to describe infiltration experiments into vertical columns of the two fine-textured soils.
− Measured, classical solutions and similarity solutions of soil water content within vertical columns of Columbia silt loam and Hesperia sandy loam during vertical infiltration.
From the figure, we first verify and notice for both soils that the measured soil water content distributions are accurately described by the classical solution of Richards' equation using measured soil water properties and wetting parameters given in Table 1. Hence, we are confident that the soil water content distributions calculated with the similarity solution Eq. [6] based on those same properties and parameters are erroneous and do not come close to reality. Indeed, the cumulative amounts of water infiltrating the Columbia profile calculated from the similarity solution are more than 2 times greater than reality. And the results observed for the Hesperia soil are also erroneous – the similarity calculations are more than 5 times greater than experimentally measured values. From these results, we conclude that the utility of the 2009 Prevedello similarity assumption is correctly limited to coarse-textured soils.
Looking Ahead
We anticipate further attempts to create mirror images of soil water profiles, soil water functions and related properties during infiltration and redistribution. Achieving simple solutions for water transport and retention in soils of different physical and chemical characteristics during this century shall remain a lingering challenge for soil scientists.
Acknowledgements
We wish to express thanks to the Brazilian National Council for Scientific and Technological Development (CNPq) for scholarships of the three authors. Our gratitude is also expressed to Prof. Dr. Donald R. Nielsen for the review of the manuscript.
References
- Boltzmann, L. 1894. For the integration of the diffusion equation with variable diffusion coefficients = Zur Integration der Diffusionsgleichung bei variabeln Diffusionscoefficienten. Annalen der Physik (Leipzig) 53: 959-964 (in German).
- Buckingham, E. 1907. Studies on the movement of soil moisture. Bulletin Nº 38. U.S. Dept. of Agriculture. Bureau of soils, Washington, D.C.
- Darcy, H. 1856. The public fountains in the city of Dijon = Les fontaines publique de la ville de Dijon. Dalmont, Paris (in French).
- Davidson, J.M.; Nielsen, D.R.; Biggar, J.W. 1963. The measurement and description of water flow through Columbia silt loam and Hesperia sandy loam. Hilgardia 34: 601-617.
- Green, W.H.; Ampt, G.A. 1911. Studies in soil physics: I. The flow of air and water through soils. Journal of Agriculture Science 4: 1-24.
- Mualem, Y. 1976. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resources Research 12: 513-522.
- Philip, J.R. 1955. Numerical solution of equations of the diffusion type with diffusivity concentration-dependent. Transactions of Faraday Society 51: 885-892.
- Prevedello, C.L.; Loyola, J.M.T.; Reichardt, K.; Nielsen, D.R. 2008. New analytic solution of Boltzmann transform for horizontal water infiltration into sand. Vadose Zone Journal 7: 1170-1177.
- Prevedello, C.L.; Loyola, J.M.T.; Reichardt, K.; Nielsen, D.R. 2009. New analytic solution related to the Richards, Philip, and Green-Ampt equations for infiltration. Vadose Zone Journal 8: 127-135.
- Richards, L.A. 1931. Capillary conduction of liquids through porous materials. Physics 1: 318-333.
- van Genuchten, M.Th. 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal 44: 892-898.
Edited by
Publication Dates
-
Publication in this collection
Jul-Aug 2016
History
-
Received
21 Sept 2015 -
Accepted
26 Jan 2016