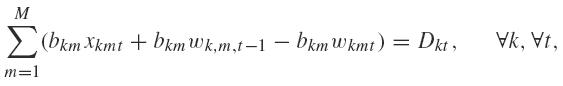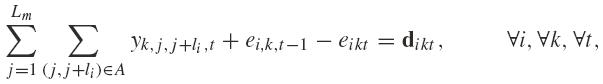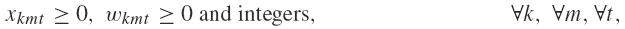ABSTRACT.
Two important optimization problems occur in the planning and production scheduling inpaper industries: the lot sizing problem and the cutting stock problem. The lot sizing problem must determine the quantity of jumbos of different types of paper to be produced in each machine over a finite planning horizon. These jumbos are then cut in order to meet the demand of items for each period. In this paper, we deal with the integration of these two problems, aiming to minimize costs of production and inventory of jumbos, as well as the trim loss of paper generated during the cutting process. Two mathematical models for the integrated problem are considered, and these models are solved both heuristically and using an optimization package. Attempting to get lower bounds for the problem, relaxed versions of the models also have been solved. Finally, computational experiments are presented and discussed.
Keywords:
integrated problem; cutting stock problem; lot sizing problem; paper industry
RESUMO.
Dois importantes problemas de otimização combinatória ocorrem no planejamento da produção em indústrias papeleiras: o problema de dimensionamento de lotes e o problema de corte de estoque multiperíodo. O problema de dimensionamento de lotes deve determinar a quantidade de bobinas jumbos de diferentes tipos de papel (gramaturas) a serem produzidos em cada máquina, ao longo de um horizonte de planejamento finito. Estes jumbos são então cortados para atender a demanda de itens para cada período. Neste trabalho, tratamos da integração desses dois problemas, procurando minimizar custos com produção e estoque dos jumbos, como também a perda de papel durante o processo de corte. Duas modelagens matemáticas para o problema integrado foram consideradas, e os modelos foram resolvidos heuristicamente usando um pacote de otimização. Procurando obter limitantes inferiores para o problema, foram resolvidas versões relaxadas dos modelos. Finalmente, experimentos computacionais são apresentados e discutidos.
Palavras-chave:
Problema integrado; problema de corte de estoque; problema de dimensionamento de lotes; indústria de papel
1 INTRODUCTION
The relevance of studying problems, that arises in the planning and production scheduling of manufacturing industries, comes from the need of these industries to optimize their processes and resources. In the paper industry, for example, the production planning involves decisions of jumbos production (big reels of paper) to subsequently be cut, producing final items, which can be smaller reels or rectangles (A4, letter, cutsize, etc).
The Cutting Stock Problem (CSP) consists in the optimization of the cutting process of major units (objects), available for the production of a set of smaller units (items). The demand for the items are known and must be fullfiled. The objective is to optimize some criteria, such as minimize the material trim-loss. Such problems are being intensively investigated in the last decades, since Gilmore & Gomory's 77 P.C. Gilmore & R.E. Gomory. A linear programming approach to the cutting stock problem. Operations Research, 9 (1961), 848-859.), (88 P.C. Gilmore & R.E. Gomory. A linear programming approach to the cutting stock problem - Part II. Operations Research, 11 (1963), 863-888.), (99 P.C. Gilmore & R.E. Gomory. Multi-stage cutting stock problems of two and more dimensions. Operations Research, 13 (1965), 94-120.) pioneer works which proposed the column generation procedure, allowing the solution of real problems.
The Lot Sizing Problem (LSP) consists in determining the amount of products to be produced in each period along a finite time planning horizon, in order to attend a known demand and optimize an objective function, such as minimizing the production and inventory costs 2525 W.W. Trigeiro, L.G. Thomas & J.O. McClain. Capacitated lot sizing with setup times. Management Science, 35 (1989), 353-366.. Reviews on the LSP can be found in Buschkühl et al. 22 L. Buschkül, F. Sahling, S. Helber & H. Tempelmeier. Dynamic capacitated lot-sizing problems: a classification and review of solution approaches. OR Spectrum, 32 (2010), 231-261., Drexl & Kimms 44 A. Drexl & A. Kimms. Lot sizing and scheduling - survey and extensions. European Journal of Operational Research, 99 (1997), 221-235., Jans & Degraeve 1313 R. Jans & Z. Degraeve. Modeling industrial lot sizing problems: a review. International Journal of Production Research, 46 (2008), 1619-1643. and Karimi et al. 1515 B. Karimi, S.M.T. Fatemi Ghomi & J.M. Wilson. The capacitated lot sizing problem: a review of models and algorithms. OMEGA, 31 (2003), 365-378..
In general, the LSP and the CSP are treated separately and sequentially. Firstly, the LSP is solved and subsequently, the CSP is solved. However, this approach may increase the total cost, especially if the cutting process is economically relevant. Therefore, researches started to consider the integration of these two problems.
Farley 55 A.A. Farley. Mathematical programming models for cutting-stock problems in the clothing industry. Operational Research Society, 1 (1988), 41-53. published a study on the CSP integrated to the planning and scheduling problem applied to the clothing industry. In the paper industry, we can cite the works of Respício & Captivo 2222 A. Respício & M.E. Captivo. Integrating the cutting stock problem in capacity planning, Department of Informatics and Centre of Operational Research. University of Lisbon, Portugal (2002). which present a mathematical model and a branch-and-price method. Also regarding the paper industry, Correia et al. 33 M.H. Correia, J.F. Oliveira & J.S. Ferreira. Reel and sheet cutting at a paper mill. Computers & Operations Research, 31 (2004), 1223-1243. presented a heuristic procedure to generate cutting patterns which are added in a linear programming model. Still considering applications in the paper industry, Poltroniere et al. 1919 S.C. Poltroniere, K.C. Poldi, F.M.B. Toledo & M.N. Arenales. Coupling cutting stock-lot sizingproblems in the paper industry. Annals of Operations Research, 157 (2008), 91-104. proposed a mathematical model which considers the integration of the LSP and the one-dimensional CSP in a planning horizon divided into periods. Planning decisions of jumbos manufacturing and the cutting stage are interdependent problems. Both are not trivial combinatorial optimization problems. The authors proposed two heuristic methods for the solution based on the Lagrangian relaxation of the integration constraints, which proved to be appropriated to address the integrated problem.
In 2006, Gramani & França 1010 M.C.N. Gramani & P.M. França. The combined cutting stock and lot-sizing problem in industrial processes. European Journal of Operational Research, 174 (2006), 509-521. studied the integration of the LSP and the two-dimensional CSP applied to the furniture industry. Extensions of the model proposed in 2006 and new solution approaches were proposed in Gramani et al. 1111 M.C.N. Gramani, P.M. França & M.N. Arenales. A Lagrangian relaxation approach to a coupled lot-sizing and cutting stock problem. International Journal of Production Economics, 119 (2009), 219-227.), (1212 M.C.N. Gramani, P.M. França & M.N. Arenales. A linear optimization approach to the combined production planning model. Journal of the Franklin Institute, 348(7) (2010), 1523-1536.. In 2008, Ghidini 66 C.T.L.S. Ghidini. Otimização de processos acoplados: programação da produção e corte de estoque. Tese de doutorado, ICMC, USP, São Carlos, SP (2008). proposed a model for the integrated problem which enables the anticipation of some products and inventory, and two heuristic methods to solve a simplificated version of the mathematical model. Santos et al. 2323 S.G. Santos, S.A. Araujo & S. Rangel. Integrated cutting machine programming and lot sizing in furniture industry. Revista Eletrônica Pesquisa Operacional para o Desenvolvimento, 3 (2011),249-266. presented a mixed integer optimization model for the integrated problem in the furniture industry, where two sets of previously generated cutting patterns were considered. Alem & Morabito 11 D. Alem & R. Morabito. O problema combinado de planejamento da produção e corte de estoque sob incertezas: aplicação em fábricas de móveis de pequeno porte. Gestão & Produção, 20(1) (2013), 111-133. proposed three robust modeling to deal with uncertainties on demand and costs, also for a furniture industry.
Leão 1616 A.A.S. Leão. Extensões em problemas de corte: padrões compartimentados e problemas acoplados. Tese de doutorado, ICMC, USP, São Carlos, SP (2013). studied mathematical formulations for the LSP coupled with the one-dimensionalCSP. Three variations were considered, regarding the number of available machines and the number of types of objects in stock. They also presented a column generation procedure to solve the mathematical model proposed by Poltroniere et al. 1919 S.C. Poltroniere, K.C. Poldi, F.M.B. Toledo & M.N. Arenales. Coupling cutting stock-lot sizingproblems in the paper industry. Annals of Operations Research, 157 (2008), 91-104.. In the present paper we have implemented a similar column generation procedure.
Recently, Silva et al. 2424 E. Silva, F. Alvelos & J.M. Valério de Carvalho. Integrating two-dimensional cutting stock and lot-sizing problems. Journal of Operational Research Society, 65 (2014), 108-123. proposed two integer programming models for the integrated two-dimensional cutting stock and lot sizing problem. In both of the models, the anticipation of the production of items and the storage of unusued objects are allowed. Motivated by challenges that arise in the paper industry, Kallrath et al. 1414 J. Kallrath, S. Rebennack & R. Kusche. Solving real-world cutting stock-problems in the paper industry: mathematical approaches, experience and challenges. European Journal of OperationalResearch, 238(1) (2014), 374-389. presented several approaches to model and solve one-dimensional and two-dimensional CSP.
Considering the related literature, the main contributions of this paper are: the proposition of a new mathematical model based on an arc flow model by Valério de Carvalho 2626 J.M. Valério de Carvalho. Exact solution of bin packing problem using column generation andbranch-and-bound. Annals of Operations Research, 86 (1999), 629-659.), (2727 J.M. Valério de Carvalho. LP models for bin packing and cutting stock problems. European Journal of Operational Research, 141 (2002), 253-273. for which we have tried to solve considering all the possible arcs (columns) and using an optimization package; the extension of the Lagrangian heuristic proposed by Poltroniere et al. 1919 S.C. Poltroniere, K.C. Poldi, F.M.B. Toledo & M.N. Arenales. Coupling cutting stock-lot sizingproblems in the paper industry. Annals of Operations Research, 157 (2008), 91-104., allowing anticipation on the cut of some items between periods; the computational experiments that show the quality of the proposed approaches both for solving the problem and for obtaining lower bounds. We remark that the present paper is an extension of two previous conference papers: Poltroniere et al. 2020 S.C. Poltroniere, S.A. Araujo & K.C. Poldi. Modelos matemáticos para o problema de corte de estoque integrado ao planejamento da produção em indústrias de papel, in "Anais do XLVI Simpósio Brasileiro de Pesquisa Operacional", pp. 3652-3663, Salvador, BA, Brazil (2014). and Poltroniere et al. 2121 S.C. Poltroniere, S.A. Araujo & K.C. Poldi. Otimização de problemas integrados na indústria papeleira, in " Proceeding Series of the Brazilian Society of Applied and Computational Mathematics", Vol. 3, n. 2, Vitória, ES, Brazil (2015)..
This paper is organized as follows: Section 2 presents the mathematical models considered for the integrated problem. Section 3 provides a description of three methods to solve the proposed models. Computational experiments are presented and discussed in Section 4 and in Section 5, the main conclusions of this research are presented.
2 MATHEMATICAL MODELS FOR THE INTEGRATED PROBLEM
In Poltroniere et al. 1919 S.C. Poltroniere, K.C. Poldi, F.M.B. Toledo & M.N. Arenales. Coupling cutting stock-lot sizingproblems in the paper industry. Annals of Operations Research, 157 (2008), 91-104., the integrated problem has been modeled based on Gilmore & Gomory's 88 P.C. Gilmore & R.E. Gomory. A linear programming approach to the cutting stock problem - Part II. Operations Research, 11 (1963), 863-888. approach, assuming a stock of different width jumbos in limited quantities. Their model is presented in Section 2.1 In Section 2.2, a new integrated model is presented based on Valério de Carvalho's 2626 J.M. Valério de Carvalho. Exact solution of bin packing problem using column generation andbranch-and-bound. Annals of Operations Research, 86 (1999), 629-659.), (2727 J.M. Valério de Carvalho. LP models for bin packing and cutting stock problems. European Journal of Operational Research, 141 (2002), 253-273. approach.
2.1 Integrated model using the approach of Gilmore & Gomory (LCGG)
In the industrial process of production and cutting of paper, the LSP is considered to decide the weight of jumbos (big reels of paper) to be produced in each period of a horizon planning. The jumbos are produced in parallel machines, which are capacited and have particular performances. Later, the jumbos are cut into smaller reels of known widths to fulfill the demand. Paper of different types (thickness) must be produced and changing from one type to another causes significant loss of either paper (setup cost) or machine time (setup time), which are sequence dependents.
Consider the following notation and data.
-
• Indices:
-
t = 1, ..., T number of periods in the planning horizon;
-
k = 1, ..., K number of types (thickness) of paper;
-
m = 1, ..., M number of paper machines (machine m produces jumbos of width Lm );
-
j = 1, ..., Nm number of cutting pattern for jumbos of width Lm ;
-
i = 1, ..., Nf number of ordered items;
-
{1, ..., Nf} = S(1) ∪ S(2) ∪ ... ∪ S(K), where S(k) = {i, if the item i is type k paper}.
-
• Parameters:
-
ckmt production cost (ton) for a jumbo of type k paper being made in machine m in period t;
-
hkt inventory cost (ton) for a jumbo of type k paper at the end of period t;
-
skmt setup cost for machine m producing a jumbo of type k paper in period t;
-
cpkt cost for each centimeter of type k paper lost during the cutting process in period t;
-
σit cost for stock (ton) of final items i in period t;
-
Cmt capacity (ton) of machine m in period t;
-
dkt vector of ordered quantities of final items of type k paper in period t. Its size is |S(k)| and each component dikt means the number of final items i, i ∈ S(k), ordered in period t.
-
ηk vector of weight of final items of type k paper (the weight of final item i of type k paper and width li is given by ηik = ρkli );
-
ρk specific weight for jumbo of type k paper;
-
Dkt demand (ton) of type k paper in period t;
-
bkm weight of jumbo of type k paper produced in machine m(bkm = Lm ρk );
-
fkm paper lost (ton) in setting up machine m to produce a jumbo of type k paper;
-
ajm vector associated to cutting pattern j for jumbo of width Lm . Its size is |S(k)| and each component aijm means the number of items i, i ∈ S(k), cut according to cutting pattern j for the jumbo of width Lm ;
-
pjm paper waste (cm) in cutting pattern j used to cut a jumbo of width Lm ;
-
Q big number.
-
• Decision variables:
-
xkmt number of jumbos of type k paper produced in machine m in period t;
-
wkmt number of jumbos of type k paper produced in machine m stored at the end of period t;
-
zkmt binary variables that means if there was production or not of jumbos of type k paper in machine m in period t;
-
yj kmt number of jumbos of type k paper produced in machine m in period t which are cut according to the cutting pattern j;
-
ekt vector of final items of type k paper stored at the end of period t. Its size is |S(k)| and each component eikt means the number of final items i, i ∈ S(k), stored at the end of period t.
So, the mathematical model for the integrated (CSP and LSP) problem is given by (Poltroniere et al. 1919 S.C. Poltroniere, K.C. Poldi, F.M.B. Toledo & M.N. Arenales. Coupling cutting stock-lot sizingproblems in the paper industry. Annals of Operations Research, 157 (2008), 91-104.):
Minimize
subject to
The objective function (2.1) is a composition of various costs: jumbo production and inventory costs, setup costs, final item inventory costs and waste cost in a cutting process, where the waste is given by F(k, t) =  . The inventory balancing constraints are given in (2.2), i.e., the total quantity produced (ton) plus the stock from the previous period which have to meet the demand plus the stock for the next time period. Parameter Dkt depends on the unknown waste in the cutting process. As defined, it should be Dkt = Σi ∈ S(K)ηikdikt + waste. On the other hand, parameter Dkt can be determined by Dkt =
. The inventory balancing constraints are given in (2.2), i.e., the total quantity produced (ton) plus the stock from the previous period which have to meet the demand plus the stock for the next time period. Parameter Dkt depends on the unknown waste in the cutting process. As defined, it should be Dkt = Σi ∈ S(K)ηikdikt + waste. On the other hand, parameter Dkt can be determined by Dkt =  .
.
Constraints (2.3) assure that the capacity of paper machines must be respected in each period, considering the total quantity of produced paper and the waste of paper due to changing types. Constraints (2.4) are set zkmt = 1 in case of xkmt > 0. If xkmt = 0, then optimality criterium forces zkmt = 0. Constraints in (2.5) are the item inventory balancing equations. Constraints (2.6) limit the number of jumbos cut, which were previously produced. These are the coupling constraints that involve decisions concerning the production of jumbos and the cutting of them. Constraints (2.7)-(2.10) define the domain of the decision variables.
2.2 Integrated model using the approach of Valério de Carvalho (LCVC)
Valério de Carvalho (2626 J.M. Valério de Carvalho. Exact solution of bin packing problem using column generation andbranch-and-bound. Annals of Operations Research, 86 (1999), 629-659.) proposes an alternative formulation for the CSP, considering stock of identical objects. It is a problem of minimal flow with additional constraints imposing the fulfill of demand. The extention of this model, in order to consider several types of stock objects is presented in Valério de Carvalho (2727 J.M. Valério de Carvalho. LP models for bin packing and cutting stock problems. European Journal of Operational Research, 141 (2002), 253-273.), and this is the approach used in the integrated model proposed in this paper.
In addition to the parameters and decision variables defined in Section 2.1, consider Lmax the width of the larger jumbo in stock; the set of vertices V = {0, 1, ..., Lmax}; the set of arcs A = {(d, e) : 0 ≤ d < e ≤ Lmax and e - d = li for every 1 ≤ i ≤ Nf}, which means that there is an oriented arc between two vertices if there is an item of the corresponding size. Also consider extra arcs between (d, d + 1, d = 0, 1, ..., Lmax - 1) related to wastes in the cutting process. The number of variables is polynomial, as a function of the width of the jumbos and the number of items, and is on the order O(Nf · Lmax). Some reduction criteria proposed in Valério de Carvalho (2626 J.M. Valério de Carvalho. Exact solution of bin packing problem using column generation andbranch-and-bound. Annals of Operations Research, 86 (1999), 629-659.), (2727 J.M. Valério de Carvalho. LP models for bin packing and cutting stock problems. European Journal of Operational Research, 141 (2002), 253-273.) were implemented.
Then, determining a valid cutting pattern for jumbo of width Lm is modeled as the problem of determining a path between the vertices 0 and Lm in the graph G = (V, A). The arcs which form a path define a cutting pattern and the length of these arcs define the size of the items to be cut. The decision variable ykijt represents the number of items of type k paper and width j - i cut in the cutting pattern in period t. Furthermore, Flkmt is the number of jumbos oftype k paper produced in machine m cut in period t (can be seen as a feedback arc, from vertex Lm to vertex 0).
The proposed model, called LCVC (Lot Cutting Valério de Carvalho), is given by:
Minimize
subject to
The objective function (2.11) is equivalent to (2.1). Observe that in the last parcel, the evaluation of the waste of material is done in a smoothing different, but equivalent, way. Constraints (2.12), (2.13), (2.14), (2.15) and (2.17) are, respectively, equivalent to (2.2), (2.3), (2.4), (2.5) and (2.6). Constraints (2.18)-(2.21) define the domain of the decision variables. The main difference of this model is in constraints (2.16) which are the flow conservation constraints. They ensure that a flow corresponds to a valid cutting pattern, because an item is either placed at the border of the object or immediately after another item.
3 SOLUTION METHODS FOR THE INTEGRATED PROBLEM
3.1 Solving the LCGG model with Column Generation and Rounding Heuristic
Solving the (2.1)-(2.10) model is, in general, a difficult task for several reasons, including the great number of variables (one variable for each cutting pattern) and the integrality constraints on these variables. In order to overcome these difficulties, a column generation procedure based on Gilmore & Gomory 77 P.C. Gilmore & R.E. Gomory. A linear programming approach to the cutting stock problem. Operations Research, 9 (1961), 848-859.), (88 P.C. Gilmore & R.E. Gomory. A linear programming approach to the cutting stock problem - Part II. Operations Research, 11 (1963), 863-888. is applied to the linear relaxation of the problem. The Restricted Master Problem (RMP) is defined regarding a subset of feasible cutting patterns. In this paper, we considered the homogeneous cutting patterns (cutting patterns with only one type of items and this type of item is placed as many times as it fits) to build the initial constraints matrix for the RMP. Other cutting patterns are not, initially, considered, and they are generated during the method's iterations. After solving the RMP, which is a linear programming problem, its associated dual variables are considered and a subproblem, which is a knapsack problem, is solved in order to determine whether there are cutting patterns which improve the current solution or not, i.e., a cutting pattern with negative reduced cost. Attractive columns are added and a new RMP is solved. This procedure is repeated until there are no more columns that improve the RMP solution. By the end of this process, regarding only the columns (cutting patterns) in the optimal solution for the linear relaxed problem, the decision variables are turned to integers and the integer problem is solved by Cplex.
3.2 Solving the LCGG model with LotCutting Heuristic and Items Anticipation
Two heuristic methods have been proposed by Poltroniere et al. 1919 S.C. Poltroniere, K.C. Poldi, F.M.B. Toledo & M.N. Arenales. Coupling cutting stock-lot sizingproblems in the paper industry. Annals of Operations Research, 157 (2008), 91-104. to solve the (2.1)-(2.10) model. These are named as LotCutting and CuttingLot heuristics and are based on the Lagrangian relaxation of the integration constraints (2.6). Such constraints are added to the objective function (2.1), weighted by Lagrangian multipliers. Thus, the problem is decomposed into two subproblems: lot sizing (LSP) and cutting stock (CSP), which are treated separately and iteratively.
In the model proposed by Poltroniere et al. 1919 S.C. Poltroniere, K.C. Poldi, F.M.B. Toledo & M.N. Arenales. Coupling cutting stock-lot sizingproblems in the paper industry. Annals of Operations Research, 157 (2008), 91-104., a CSP for each type of paper k must be solved over a planning horizon divided into periods. The items inventory at the end of each period t, given by the variables vector ekt, should be considered. There is an interdependence between the cut decisions in different periods due to these variables. This problem is called a multiperiod CSP. However, the methods proposed by the authors solve the multiperiod CSP ignoring the items stock variables. Then, KT cutting stock problems (one for each type of paper k and each period t) were solved considering these variables to be zero.
In this paper, we propose an extension of the LotCutting Heuristic that allows the anticipation on the cut of some items between periods. Firstly, the heuristic solves the LSP in which the objective function is to minimize inventory, setup and production costs, subject to constraints (2.2)-(2.4), (2.8) and (2.9), in the same way as in Poltroniere et al. 1919 S.C. Poltroniere, K.C. Poldi, F.M.B. Toledo & M.N. Arenales. Coupling cutting stock-lot sizingproblems in the paper industry. Annals of Operations Research, 157 (2008), 91-104.. The solution obtained from the LSP provides the jumbos inventory for the multiperiod CSP. Then, the multiperiod CSP is solved by minimizing the waste and item inventory costs, subject to (2.5), (2.6) and (2.10). Initially, the inventory variables are ignored. Then, the problems (one for each tickness) are decomposed by periods. Thus, a CSP for each period is solved, considering as jumbos inventory the sum of the availability of this period with the stock of the previous period, after the cutting of the demanded items. From the solution obtained for each period and based on the dual variables associated with constraints (2.5), anticipations on the cut of some items from a period t to period t - 1 are performed, regarding the inventory constraints. In this way, we seek to improve the use of the jumbos inventory in order to generate better combinations of items which would decrease the paper waste during the cutting process. Each CSP was solved by the simplex method with column generation procedure proposed by Gilmore & Gomory 77 P.C. Gilmore & R.E. Gomory. A linear programming approach to the cutting stock problem. Operations Research, 9 (1961), 848-859.), (88 P.C. Gilmore & R.E. Gomory. A linear programming approach to the cutting stock problem - Part II. Operations Research, 11 (1963), 863-888. and considering the integrality relaxation.
3.3 Solving the LCVC model with an optimization package
The (2.11)-(2.21) arc flow model presents many symmetric solutions, i.e., several alternative solutions that correspond to the same set of cutting patterns. So, Valério de Carvalho 2626 J.M. Valério de Carvalho. Exact solution of bin packing problem using column generation andbranch-and-bound. Annals of Operations Research, 86 (1999), 629-659.), (2727 J.M. Valério de Carvalho. LP models for bin packing and cutting stock problems. European Journal of Operational Research, 141 (2002), 253-273. presented some reduction criteria that allow the elimination of some arcs and therefore reducing the number of symmetric solutions, without eliminating any valid cutting patterns. This procedure reduces the number of variables (columns) in the problem. We adapted two of these criteria to our model. The first one consists in ordering the items according to their size and including them in a cutting pattern in decreasing order. The second reduction criterion applied to our model is that the first loss arc is inserted in our graph at a distance from the beginning of the object that is equal to the size of the smallest item. The idea is to put the losses arcs at the end of the object. After applying the reduction criteria, the arc flow model is solved by the branch-and-cut method of the Cplex package with a limited amount of time.
4 COMPUTATIONAL EXPERIMENTS
In this section, lower bounds and upper bounds are presented based on the mathematical models and solution methods presented in Section 2 and 3. We used the set of instances generated by Poltroniere et al. 1919 S.C. Poltroniere, K.C. Poldi, F.M.B. Toledo & M.N. Arenales. Coupling cutting stock-lot sizingproblems in the paper industry. Annals of Operations Research, 157 (2008), 91-104.: 27 classes, containing 10 instances each, ranked according to the number of demanded items (Nf = 5, 10, 20), the number of types (thickness) of paper (K = 2, 4, 6) and the number of periods (T = 8, 10, 12). M = 2 machines, and machine one produces jumbos of width L 1 = 540 cm and the machine two produces jumbo of width L 2 = 460 cm; specific weight ρk = 2kg/cm. The model parameters were generated by simulating situations found in the paper industry, as follows:
-
ckmt ∈ [0.015 0.025] · bkm , with bkm = Lm ρ;
-
skmt ∈ [0.03 0.05] · ckmt; hkt ∈ [0.0000075 0.0000125]; fkm ∈ [0.01 0.05] · bkm ;
-
cpkt = ikt = 0.5 · hkt, i ∈ S(k);
 · 10; σ
· 10; σ -
li ∈ [0.1 0.3] ·
 ;
; -
dikt ∈ [0 300]. If dikt ≤ 50, then dikt = 0 (in order to avoid low demand);
-
Cmt = Cap, with Cap =
 ·
·  .
.
The LotCutting Heuristic with Items Anticipation, described in Section 3.2, allows the anticipation on the cut of some items based on dual variables associated to constraints of stock balancing. We considered Dkt = (1 + θ)Σ i ∈ S ( K ) ηikdikt . Then, a tolerance on the total produced paper is added in order to cover the waste during the cutting process, preventing the problem to be infeasible. We started with θ = 0 and increased the demand by 1% in each step of the algorithm,until the problem is feasible or to upper bound of θ = 10%. These values obtained for θ are used in the other methods in order to obtain the values of Dkt .
The methods described in Section 3.1. and 3.3. were solved by optimization package AMPL/Cplex 12.6 and the LotCutting heuristic (Section 3.2.) was coded in Delphi. Computational tests were run in a Intel (R) Core (TM) Corel i7-4770K, with 3.5 GHz and 32 GB of RAM.
4.1 Lower bounds for the integrated problem
Relaxed versions of the models presented in Section 2 were solved with the attempt to provide lower bounds for the instances and consequently to have a test parameter for the quality of the heuristic solutions. Table 1 presents the lower bounds obtained by two types of relaxations, Relaxation A and Relaxation B, described as follows.
Relaxation A: The problem variables were relaxed, i.e., the production and inventory variables, the setup binary variables, which are considered continuous between 0 and 1, and those related to the cutting patterns frequencies. However, the variables related to the knapsack problem are kept integer. For the LCGG model this is exactly the procedure described in Section 3.1 without the rounding procedure. For the LCVC model we consider the procedure described in Section 3.3 relaxing all the variables except the ykijt variables.
Relaxation B: In order to try to improve the quality of the lower bounds, the LCVC model was solved with the setup variables as binary variables and all the other variables relaxed, i.e., all the decision variables were considered to be continuous (including the variables related to the knapsack problem). It is worth noticing that it is only possible to ensure that we have lower bounds when the model is optimally solved, and the LCVC model was solved to optimality, for all instances. This relaxation cannot be applied to the LCGG model considering the column generation approach, because first we would solve the linear relaxation of the problem and, after that, we would consider the setup variables as integer and try to solved the integer problem considering the set of column from the optimal solution of the linear relaxation. However, this procedure would be an heuristic procedure and there is no guarantee that it provides a lower bound.
The column "O.F.", in Table 1, shows the average value of the total costs obtained by the instances of each class. This average was evaluated considering only the instances for which all heuristic methods found a feasible solution. The column "Time" shows the average computational time, in seconds, necessary to solve the 10 instances of each class. Considering the Relaxation A, the quality of the lower bounds obtained by LCGG model is better than LCVC model, but LCVC is faster than LCGG. Relaxation B provided better lower bounds than Relaxation A only in classes 12 and 18.
4.2 Heuristic solutions
Table 2 provides the heuristic results obtained by: the solution of the LCGG model, using column generation and a rounding heuristic (described in Section 3.1). Firstly, the optimal solution of the linear relaxation is obtained. Subsequently, considering only the columns of this optimal solution, a limit of 600 seconds is given for the package to find an integer solution; thesolution obtained by LotCutting Heuristic with Items Anticipation, described in Section 3.2. For the solution of LCVC model (described in Section 3.3), the variables of the original model were considered integers, and the computational time was limited to 600 seconds attempting to obtain an exact solution. However, the LCVC model was unable to find feasible solutions in 600 seconds.
In the solution of the two models, presented in Tables 1 and 2, the parameter θ was taken as the tolerance used in the LotCutting Heuristic. The average of these tolerances for the 10 examples of each class is given in the third column of the Table 2. In column "O.F." the average value of the total costs obtained by the instances of each class is shown. This average was calculated between the instances for which all methods found a feasible solution. The column "Sol" provides the number of solved instances in each class and the column "Time" shows the computational time, in seconds, necessary to solve the 10 instances of each class. Finally, the column "GAP" indicates the average gap between the solution obtained by the heuristic (HS) and the lower bound obtained by relaxation A of the LCGG model (AGG). The GAP is given by 100 *  .
.
Comparing the number of feasible solutions obtained by each method, we have 233 solutions for the LotCutting/ItemsAnticipation and 242 for the Column Generation Rounding Heuristic. When the number of items increases to 20, both heuristics have difficulties in solving the problem. We observe that the computational time of the LotCutting heuristic with Items Anticipation is relatively low since the biggest of them was of 175.8 seconds when the heuristic was applied in the instances of class 18. The quality of the results obtained by the solution of the LCGG model, using column generation and a rounding heuristic, is better than the LotCutting heuristic. Furthermore, the average gap obtained for each class shows the quality of the solution when compared to the lower bound.
The results obtained during the experiments confirm the good performance of the Items Anticipation Heuristic used to solve the multiperiod CSP. The total cost (i.e., the sum of the waste costs with the stock costs of jumbos and items) was lower when compared to the total cost obtained by solving the CSP without allowing the anticipation of items. According to Poltroniere 1818 S.C. Poltroniere. "Otimização do processo de corte integrado à produção de bobinas: modelo e métodos de solução". Tese de doutorado, ICMC, USP, São Carlos, SP (2006)., the average decrease in the material waste is 9.1% for the instances with 5 types of items and 16.7% for the instances with 10 types of items.
5 CONCLUSIONS AND FUTURE PERSPECTIVES
This research considers the mathematical formulation for an integraded (cutting stock and lot sizing) problem in a paper industry. A model from the literature (Poltroniere et al. 1919 S.C. Poltroniere, K.C. Poldi, F.M.B. Toledo & M.N. Arenales. Coupling cutting stock-lot sizingproblems in the paper industry. Annals of Operations Research, 157 (2008), 91-104.) is revisited and, in addition, a new mathematical model (LCVC) based on an arc flow model 2626 J.M. Valério de Carvalho. Exact solution of bin packing problem using column generation andbranch-and-bound. Annals of Operations Research, 86 (1999), 629-659.), (2727 J.M. Valério de Carvalho. LP models for bin packing and cutting stock problems. European Journal of Operational Research, 141 (2002), 253-273. is proposed. These two mathematical models were implemented and solved using Ampl/Cplex 12.6. Relaxed versions of the models were, also, solved aimming to obtain lower bounds for the solution of the integrated problem.
Furthermore, we proposed an extension of the LotCutting Heuristic to solve the Poltroniere et al.'s 1919 S.C. Poltroniere, K.C. Poldi, F.M.B. Toledo & M.N. Arenales. Coupling cutting stock-lot sizingproblems in the paper industry. Annals of Operations Research, 157 (2008), 91-104. model, that allows the anticipation on the cut of some items between periods. The solutions obtained by the LotCutting Heuristic with Items Anticipation and the heuristic solutions obtained by Cplex, presented in Table 2, were satisfactory. For some examples, the upper bounds were better than those from the literature, for example, in Poltroniere et al. 1919 S.C. Poltroniere, K.C. Poldi, F.M.B. Toledo & M.N. Arenales. Coupling cutting stock-lot sizingproblems in the paper industry. Annals of Operations Research, 157 (2008), 91-104..
The presented results show that the considered relaxations provided good lower bounds for the integrated problem, especially those obtained by the LCGG model, in the relaxations whose results are presented in Table 1. Furthermore, it is important to emphasize that these bounds are not too far from the heuristic solutions presented in Table 2, what allows observing the quality of the heuristics.
The proposition of the LCVC model was motivated by the good results obtained by Poldi & Araujo 1717 K.C. Poldi & S.A. Araujo. Mathematical models and a heuristic method for the multiperiod one-dimensional cutting stock problem. Annals of Operations Research, 238 (2016), 497-520. in a multiperiod cutting stock problem. However, this good performance does not happen for the model proposed in this paper, which is much harder than the one proposed by Poldi & Araujo 1717 K.C. Poldi & S.A. Araujo. Mathematical models and a heuristic method for the multiperiod one-dimensional cutting stock problem. Annals of Operations Research, 238 (2016), 497-520.. So, new researches are needed to try to overcome this difficulty, for instance, the implementation of a columns generation procedure for solving the LCVC model.
ACKNOWLEDGMENTS
This work was partially funded by the Brazilian agencies CNPq and FAPESP (2010/10133-0 and 2013/07375-0). The authors are grateful to the anonymous referees for their constructive suggestions.
References
-
1D. Alem & R. Morabito. O problema combinado de planejamento da produção e corte de estoque sob incertezas: aplicação em fábricas de móveis de pequeno porte. Gestão & Produção, 20(1) (2013), 111-133.
-
2L. Buschkül, F. Sahling, S. Helber & H. Tempelmeier. Dynamic capacitated lot-sizing problems: a classification and review of solution approaches. OR Spectrum, 32 (2010), 231-261.
-
3M.H. Correia, J.F. Oliveira & J.S. Ferreira. Reel and sheet cutting at a paper mill. Computers & Operations Research, 31 (2004), 1223-1243.
-
4A. Drexl & A. Kimms. Lot sizing and scheduling - survey and extensions. European Journal of Operational Research, 99 (1997), 221-235.
-
5A.A. Farley. Mathematical programming models for cutting-stock problems in the clothing industry. Operational Research Society, 1 (1988), 41-53.
-
6C.T.L.S. Ghidini. Otimização de processos acoplados: programação da produção e corte de estoque. Tese de doutorado, ICMC, USP, São Carlos, SP (2008).
-
7P.C. Gilmore & R.E. Gomory. A linear programming approach to the cutting stock problem. Operations Research, 9 (1961), 848-859.
-
8P.C. Gilmore & R.E. Gomory. A linear programming approach to the cutting stock problem - Part II. Operations Research, 11 (1963), 863-888.
-
9P.C. Gilmore & R.E. Gomory. Multi-stage cutting stock problems of two and more dimensions. Operations Research, 13 (1965), 94-120.
-
10M.C.N. Gramani & P.M. França. The combined cutting stock and lot-sizing problem in industrial processes. European Journal of Operational Research, 174 (2006), 509-521.
-
11M.C.N. Gramani, P.M. França & M.N. Arenales. A Lagrangian relaxation approach to a coupled lot-sizing and cutting stock problem. International Journal of Production Economics, 119 (2009), 219-227.
-
12M.C.N. Gramani, P.M. França & M.N. Arenales. A linear optimization approach to the combined production planning model. Journal of the Franklin Institute, 348(7) (2010), 1523-1536.
-
13R. Jans & Z. Degraeve. Modeling industrial lot sizing problems: a review. International Journal of Production Research, 46 (2008), 1619-1643.
-
14J. Kallrath, S. Rebennack & R. Kusche. Solving real-world cutting stock-problems in the paper industry: mathematical approaches, experience and challenges. European Journal of OperationalResearch, 238(1) (2014), 374-389.
-
15B. Karimi, S.M.T. Fatemi Ghomi & J.M. Wilson. The capacitated lot sizing problem: a review of models and algorithms. OMEGA, 31 (2003), 365-378.
-
16A.A.S. Leão. Extensões em problemas de corte: padrões compartimentados e problemas acoplados. Tese de doutorado, ICMC, USP, São Carlos, SP (2013).
-
17K.C. Poldi & S.A. Araujo. Mathematical models and a heuristic method for the multiperiod one-dimensional cutting stock problem. Annals of Operations Research, 238 (2016), 497-520.
-
18S.C. Poltroniere. "Otimização do processo de corte integrado à produção de bobinas: modelo e métodos de solução". Tese de doutorado, ICMC, USP, São Carlos, SP (2006).
-
19S.C. Poltroniere, K.C. Poldi, F.M.B. Toledo & M.N. Arenales. Coupling cutting stock-lot sizingproblems in the paper industry. Annals of Operations Research, 157 (2008), 91-104.
-
20S.C. Poltroniere, S.A. Araujo & K.C. Poldi. Modelos matemáticos para o problema de corte de estoque integrado ao planejamento da produção em indústrias de papel, in "Anais do XLVI Simpósio Brasileiro de Pesquisa Operacional", pp. 3652-3663, Salvador, BA, Brazil (2014).
-
21S.C. Poltroniere, S.A. Araujo & K.C. Poldi. Otimização de problemas integrados na indústria papeleira, in " Proceeding Series of the Brazilian Society of Applied and Computational Mathematics", Vol. 3, n. 2, Vitória, ES, Brazil (2015).
-
22A. Respício & M.E. Captivo. Integrating the cutting stock problem in capacity planning, Department of Informatics and Centre of Operational Research. University of Lisbon, Portugal (2002).
-
23S.G. Santos, S.A. Araujo & S. Rangel. Integrated cutting machine programming and lot sizing in furniture industry. Revista Eletrônica Pesquisa Operacional para o Desenvolvimento, 3 (2011),249-266.
-
24E. Silva, F. Alvelos & J.M. Valério de Carvalho. Integrating two-dimensional cutting stock and lot-sizing problems. Journal of Operational Research Society, 65 (2014), 108-123.
-
25W.W. Trigeiro, L.G. Thomas & J.O. McClain. Capacitated lot sizing with setup times. Management Science, 35 (1989), 353-366.
-
26J.M. Valério de Carvalho. Exact solution of bin packing problem using column generation andbranch-and-bound. Annals of Operations Research, 86 (1999), 629-659.
-
27J.M. Valério de Carvalho. LP models for bin packing and cutting stock problems. European Journal of Operational Research, 141 (2002), 253-273.
Publication Dates
-
Publication in this collection
Sep-Dec 2016
History
-
Received
20 Dec 2015 -
Accepted
10 Aug 2016