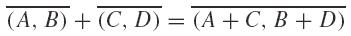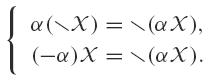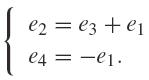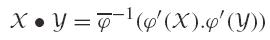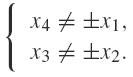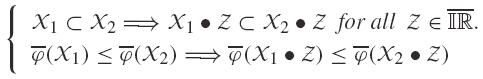ABSTRACT.
In this paper one proposes to use a new approach of interval arithmetic, the so-called pseudo-intervals (1), (5), (13). It uses a construction which is more canonical and based on the semi-group completion into the group, and it allows to build a Banach vector space. This is achieved by embedding the vector space into free algebra of dimensions higher than 4. It permits to perform linear algebra and differential calculus with pseudo-intervals. Some numerical applications for interval matrix eigenmode calculation, inversion and function minimization are exhibited for simple examples.
Keywords:
Pseudo-intervals arithmetic; free algebra; inclusion function; linear algebra; differential calculus; optimization
RESUMO.
Neste artigo é proposto o uso de uma nova abordagem de aritmética intervalar, os chamados pseudo-intervalos (1), (5), (13). Essa abordagem utiliza uma construção que é mais canônica e baseada na completude de semi-grupos em um grupo, e permite a construção de espaços vetoriais de Banach. Isso é alcançado através da imersão do espaço vetorial em uma álgebra livre de dimensão maior que 4. Desta forma é possível realizar álgebra linear e cálculo diferencial com pseudo-intervalos. Algumas aplicações numéricas para o cálculo do espectro de matrizes intervalares, inversão e minimização de funções são mostradas como exemplos.
Palavras-chave:
Aritmética pseudo-intervalar; álgebra livre; inclusão de funções; álgebra linear; cálculo diferencial; otimização
1 INTRODUCTION
Intervals are mathematical objects which allow to describe quantities with uncertainity due to the lack of knowledge of the studied phenomenon or experimental measurement accuracy. This is common in natural sciences and engineering. Even if nowadays we consider R.E. Moore 2020 R.E. Moore. PhD thesis. Standford university, (1962).), (2121 R.E. Moore. Interval analysis. Prentice Hall, Englewood Cliffs, NJ, (1966).), (2222 R.E. Moore. A test for existence of solutions to nonlinear systems. SIAM J. Numer. Anal., 14(4) (1977), 611-615.), (2929 C.T. Yang & R.E. Moore. Interval analysis i. LMSD-285875, Lockheed Aircraft Corporation, Missiles and Space Division, Sunnyvale, California, (1959).), (3030 Wayman Strother, R.E. Moore & C.T. Yang. Interval integrals. LMSD-703073, Lockheed Aircraft Corporation, Missiles and Space Division, Sunnyvale, California, IX(4) (1960), 241-245. as the first mathematician who has proposed a rigorous framework for intervalcomputations, the famous Archimedes from Syracuse (287-212 b.C) proposed 23 centuries before a two-sides bounding of π: 3 + 10/71 < π < 3 + 1/7.
Interval arithmetic, and interval analysis (IA) have been introduced as a computing framework which allows to perform analysis by computing mathematic bounds. Its extensions of the areas in applied and computational mathematics are important: non-linear problems, partial differential equations, inverse problems, global optimization and set inversion 11 B. Durand, A. Kenoufi & J.F. Osselin. System adjustments for targeted performances combining symbolic regression and set inversion. Inverse problems for science and engineering, (2013).), (1313 A. Kenoufi. Probabilist set inversion using pseudo-intervals arithmetic. Trends in Applied and Computational Mathematics, 15 (1) (2014), 97-117.), (1414 O. Didrit, L. Jaulin, M. Kieffer & E. Walter. Introduction to interval Analysis. SIAM 2009, Applied interval Analysis. Springer-Verlag, London, (2001).), (2020 R.E. Moore. PhD thesis. Standford university, (1962).), (2121 R.E. Moore. Interval analysis. Prentice Hall, Englewood Cliffs, NJ, (1966).), (2222 R.E. Moore. A test for existence of solutions to nonlinear systems. SIAM J. Numer. Anal., 14(4) (1977), 611-615.), (3030 Wayman Strother, R.E. Moore & C.T. Yang. Interval integrals. LMSD-703073, Lockheed Aircraft Corporation, Missiles and Space Division, Sunnyvale, California, IX(4) (1960), 241-245.), (3232 T. Sunaga. Theory of an interval Algebra and its Application to Numerical Analysis. Number 2. RAAG Memoirs, (1958).. It finds a large place of applications in controllability, automation, robotics, embedded systems, biomedical, haptic interfaces, form optimization, analysis of architecture plans, etc.
Several softwares and computational libraries to perform calculations with intervals such as INTLAB77 http://www.ti3.tu-harburg.de/rump/intlab/.
http://www.ti3.tu-harburg.de/rump/intlab...
, INTOPT90, GLOBSOL1212 R.B. Kearfott. Rigorous Global Search: Continuous Problems. Academic Publishers, (1996)., and Numerica2727 Yves Deville, Pascal Van Hentenryck & Laurent Michel. Numerica: A Modelling Language for Global Optimization. MIT Press, (1997). have been developed those last decades. But, due to the lack of distributivity of IA, their Achille's heel remains the construction of the inclusion function from the natural one. Some approaches using boolean inclusion tests, series or limited expansions of the natural function where the derivatives are computed at a certain point of the intervals, have been developed to circumvent this problem 11 B. Durand, A. Kenoufi & J.F. Osselin. System adjustments for targeted performances combining symbolic regression and set inversion. Inverse problems for science and engineering, (2013).), (1313 A. Kenoufi. Probabilist set inversion using pseudo-intervals arithmetic. Trends in Applied and Computational Mathematics, 15 (1) (2014), 97-117.), (1414 O. Didrit, L. Jaulin, M. Kieffer & E. Walter. Introduction to interval Analysis. SIAM 2009, Applied interval Analysis. Springer-Verlag, London, (2001).. Nevertheless, those transfers from real functions to functions defined on intervals are not systematic and not given by a formal process. This yields to the fact that the inclusion function definition has to be adapted to each problem with the risk to miss the primitive scope. Moreover, linear algebra and differential calculus need to be performed in the framework of vector space theory and not within semi-group one.
This article reminds first in Section 2 the definition and characteristics of the intervals semi-group IR and the construction of its associated vector space 11 B. Durand, A. Kenoufi & J.F. Osselin. System adjustments for targeted performances combining symbolic regression and set inversion. Inverse problems for science and engineering, (2013).), (55 N. Goze. PhD thesis, N-ary algebras and interval arithmetics. University of Haute-Alsace, (2011).), (1313 A. Kenoufi. Probabilist set inversion using pseudo-intervals arithmetic. Trends in Applied and Computational Mathematics, 15 (1) (2014), 97-117.). A systematic way to build inclusion functions, i.e. interval-valued functions defined on 11 B. Durand, A. Kenoufi & J.F. Osselin. System adjustments for targeted performances combining symbolic regression and set inversion. Inverse problems for science and engineering, (2013).), (1313 A. Kenoufi. Probabilist set inversion using pseudo-intervals arithmetic. Trends in Applied and Computational Mathematics, 15 (1) (2014), 97-117., only examples of interval matrix eigenmode calculation, inversion, and minimization of interval functions are exhibited in each section. We have choosen python programming langage 2828 http://www.python.org.
http://www.python.org...
to implement pseudo-intervals arithmetic. The main reason is that it is a free object-oriented langage, with a huge number of numerical libraries.Another advantage of python is that first, it is possible to link the source code with others written in C/C++, FORTRAN, and second, it interacts easily with other calculations tools such as SAGE 3131 http://www.sagemath.org.
http://www.sagemath.org...
and Maxima 1919 http://maxima.sourceforge.net.
http://maxima.sourceforge.net...
in order to perform formal calculations. But here, one presents pure numerical applications in python. , is presented in Section 2. In Section 3, one shows that
, is presented in Section 2. In Section 3, one shows that  , and how to get an associative and distributive arithmetic of intervals, called pseudo-intervals arithmetic, by embedding the vector space into a free algebra with dimension 4, 5, or 7 (
, and how to get an associative and distributive arithmetic of intervals, called pseudo-intervals arithmetic, by embedding the vector space into a free algebra with dimension 4, 5, or 7 ( can be endowed with a Banach space topology and allows differential calculus. Since a new algorithm for set inversion within pseudo-intervals framework has already been presented in previous papers
can be endowed with a Banach space topology and allows differential calculus. Since a new algorithm for set inversion within pseudo-intervals framework has already been presented in previous papers
2 AN ALGEBRAIC APPROACH FOR INTERVALS
An interval X is defined as a non-empty, closed and connected set of real numbers. One writes real numbers as intervals with same bounds, ∀a ∈ ℝ, a ≡ [a, a]. We denote by 𝕀ℝ = 𝒫1 the set of intervals of ℝ. The arithmetic operations on intervals, called Minkowski or classical operations, are defined such that the result of the corresponding operation on elements belonging to operand intervals belongs to the resulting interval. That is, if ⋄ ∈ {+, -, *, /} denotes one of the usual operations, one has, if X and Y are bounded intervals of ℝ,
Although, X - X = 0, and hence a substraction in the usual sense cannot be obtained. In many problems using interval arithmetic, that is the set 𝕀ℝ with the Minkowski operations, there exists an informal transfers principle which allows, to associate with a real function f a function define on the set of intervals 𝕀ℝ which coincides with f on the interval reduced to a point. But this transferred function is not unique. For example, if we consider the real function f(x) = x
2 + x = x(x + 1), we associate naturally the functions  is provided with a pseudo-inverse operation, it does not satisfy
is provided with a pseudo-inverse operation, it does not satisfy  (X) = X(X +1) and
(X) = X(X +1) and  : 𝕀ℝ → 𝕀ℝ given by
: 𝕀ℝ → 𝕀ℝ given by  (X) = X2 + X. These two functions do not coincide. Usually this problem is removed considering the most interesting transfers. But the qualitative "interesting" depends of the studied model and it is not given by a formal process.
(X) = X2 + X. These two functions do not coincide. Usually this problem is removed considering the most interesting transfers. But the qualitative "interesting" depends of the studied model and it is not given by a formal process.
In this paper, we determine a natural extension X \ Y does not correspond to the semantical difference of intervals and the interval \ X has no real interpretation. But these anti-intervals have a computational role. of 𝕀ℝ provided with a vector space structure. The vectorial substraction
of 𝕀ℝ provided with a vector space structure. The vectorial substraction
An algebraic extension of the classical interval arithmetic, called generalized interval arithmetic 2121 R.E. Moore. Interval analysis. Prentice Hall, Englewood Cliffs, NJ, (1966).), (3232 T. Sunaga. Theory of an interval Algebra and its Application to Numerical Analysis. Number 2. RAAG Memoirs, (1958).) s been proposed first by M. Warmus 3333 Mieczyslaw Warmus. Calculus of approximations. Bull. Acad. Pol. Sci., C1, III(IV (5)) (1956), 253-259.), (3434 Mieczyslaw Warmus. Approximations and inequalities in the calculus of approximations. classification of approximate numbers. Bull. Acad. Pol. Sci. math. astr. & phys., IX(4) (1961), 241-245.. It has been followed in the seventies by H.J. Ortolf and E. Kaucher 88 E. Kaucher. Ueber metrische und algebraische Eigenschaften einiger beim numerischen Rechnen auftretender Raume. Dissertation, Universitaet Karlsruhe, (1973).), (99 E. Kaucher. Algebraische erweiterungen der intervallrechnung unter erhaltung der ordnungs und verbandstrukturen computing. 1 (1977), 65-79.), (1010 E. Kaucher. Ueber eigenschaften und en der anwendungsmoeglichkeiten der erweiterten intervallrechnung und des hyperbolischen fastkoerpers ueber r computing. 1 (1977), 81-94.), (1111 E. Kaucher. Interval analysis in the extended interval space ir computing. 2 (1980), 33-49.), (2424 H.J. Ortolf. Eine verallgemeinerung der intervallarithmetik. geselschaft fuer mathematik und datenverarbeitung. Bonn, 11 (1969), 1-71.. In this former interval arithmetic, the intervals form a group with respect to addition and a complete lattice with respect to inclusion.In order to adapt it to semantic problems, Gardenes et al. have developed an approach called modal interval arithmetic 22 A. Trepat, E. Gardenes & H. Mielgo. Modal intervals: Reason and ground semantics. Lecture Notes in Computer Science, Springer-Verlag, Berlin, Heidelberg, 212 (1986), 27-35.), (33 L. Jorba, R. Calm, R. Estela, H. Mielgo, A. Trepat, E. Gardenes & M.A. Sainz. Modal intervals. Reliable Computing, 7 (2001), 77-111.), (44 E. Gardenes. Fundamentals of sigla, an interval computing system over the completed set of intervals. Computing, 24 (1980), 161-179.. S. Markov and others investigate the relation between generalized intervals operations and Minkowski operations for classic intervals and propose the so-called directed interval arithmetic, in which Kaucher's generalized intervals can be viewed as classic intervals plus direction, hence the name directed interval arithmetic 1515 S.M. Markov. Extended interval arithmetic involving infinite intervals. Mathematica Balkanica, New Series, 6(3) (1992), 269-304.), (1616 S.M. Markov. On directed interval arithmetic and its applications. J. UCS, 1(7) (1995), 510-521.. In this arithmetic framework, proper and improper intervals are considered as intervals with sign 1717 S.M. Markov. On the Foundations of Interval Arithmetic. Scientific Computing and Validated Numerics Akademie Verlag, Berlin, (1996).. Interesting relations and developments for proper and improper intervals arithmetic and for applications can be found in literature 2323 E. Popova, N. Dimitrova & S. M. Markov. Extended Interval arithmetic: New Results and Applications. Computer Arithmetic and Enclosure Methods. Elsevier Sci. Publishers B.V., (1992).), (2626 E.D. Popova. Multiplication distributivity of proper and improper intervals. Reliable Computing, 7(2) (2001), 129-140.), (2525 E.D. Popova. All about generalized interval distributive relations. i. complete proof of the relations. Sofia, (2000)..
Our approach 11 B. Durand, A. Kenoufi & J.F. Osselin. System adjustments for targeted performances combining symbolic regression and set inversion. Inverse problems for science and engineering, (2013).), (55 N. Goze. PhD thesis, N-ary algebras and interval arithmetics. University of Haute-Alsace, (2011).), (1313 A. Kenoufi. Probabilist set inversion using pseudo-intervals arithmetic. Trends in Applied and Computational Mathematics, 15 (1) (2014), 97-117., that we remind below in this article, is similar to the previous ones in the sense that intervals are extended to generalized intervals; intervals and anti-intervals correspond respectively to the proper and improper ones. However one uses a construction which is more canonical and based on the semi-group completion into a group, which allows then to build the associated real vector space, and to get an analogy with directed intervals.
2.1 The real vector space 𝕀ℝ
Let 𝕀ℝ be the set of intervals. It is in one to one correspondence and can be represented as a point in the half-plane of ℝ2, 𝒫1 = {(a, b) ∈ ℝ2, a ≤ b}. The set 𝒫2 = {(a, b) ∈ ℝ2, a ≥ b} is the set of anti-intervals. 𝕀ℝ is closed for the addition and endowed with a regular semi-group structure. The multiplication * is not globally defined.
We recall briefly the construction proposed by Markov (1818 M. Markov. Isomorphic embeddings of abstract interval systems. Reliable Computing, (3) (1997), 199-207.) to define a structure of abelian group. As (𝕀ℝ, +) is a commutative and regular semi-group, the quotient set, denoted by  , associated with the equivalence relations:
, associated with the equivalence relations:
(A, B) ~ (C, D) ⟺ A + D = B + C,
for all A, B, C, D ∈ 𝕀ℝ, is provided with a structure of abelian group for the natural addition:
where A, B). We denote by  is the equivalence class of (
is the equivalence class of ( the inverse of
the inverse of  for the interval addition.
for the interval addition.
We have X = [-a, -a], and  where -
where - =
=  . If X = [a, a], a ∈ ℝ, then
. If X = [a, a], a ∈ ℝ, then  . In this case, we identify X = [a, a] with a and we denote always by ℝ the subset of intervals of type [a, a].
. In this case, we identify X = [a, a] with a and we denote always by ℝ the subset of intervals of type [a, a]. =
=  =
=
Naturally, the group 2 by the isomorphism a - c, b - d). We find the notion of generalized interval and this yields immediately to the following result: → (
→ ( is isomorphic to the additive group ℝ
is isomorphic to the additive group ℝ
Proposition 1. Let 𝒳 =  ∈
∈  , and l: 𝕀ℝ ⟼ ℝ which gives the interval length. Thus
, and l: 𝕀ℝ ⟼ ℝ which gives the interval length. Thus
-
If l(Y) < l(X), there is an unique A ∈ 𝕀ℝ \ ℝ such that 𝒳 =
 ,
, -
If l(Y) > l(X), there is an unique A ∈ 𝕀ℝ \ ℝ such that 𝒳 =
 ,
, =
= -
If l(Y) = l(X), there is an unique A = α ∈ ℝ such that 𝒳 =
 =
=  .
.
Any element 𝒳 = A ∈ 𝕀ℝ - ℝ is said positive and we write 𝒳 > 0. Any element 𝒳 = A ∈ 𝕀ℝ - ℝ is said negative and we write 𝒳 < 0. We write 𝒳 ≥ 𝒳' if 𝒳 \ 𝒳' ≥ 0. For example if 𝒳 and 𝒳' are positive, 𝒳 ≥ 𝒳' ⇔ l(𝒳) ≥ l(𝒳'). The elements  with α ∈ ℝ* are neither positive nor negative.
with α ∈ ℝ* are neither positive nor negative. with
with  with
with
In 1818 M. Markov. Isomorphic embeddings of abstract interval systems. Reliable Computing, (3) (1997), 199-207., one defines on the abelian group  , a structure of quasi linear space. Our approach is a little bit different. We propose to construct a real vector space structure. We consider the external multiplication:
, a structure of quasi linear space. Our approach is a little bit different. We propose to construct a real vector space structure. We consider the external multiplication:
defined, for all A ∈ 𝕀ℝ, by
for all α > 0. If α < 0 we put β = -α. So we put:
We denote α 𝒳 instead of α · 𝒳. This operation satisfies
-
1. For any α ∈ ℝ and 𝒳 ∈
 we have:
we have:
-
2. For all α, β ∈ ℝ, and for all 𝒳, 𝒳' ∈
 , we have
, we have
Theorem 1. The triplet (and 𝒳2 = ofdetermine a basis of.

 . So dimℝ
. So dimℝ , +, .) is a real vector space and the vectors 𝒳1 =
, +, .) is a real vector space and the vectors 𝒳1 =  = 2
= 2
Proof. We have the following decompositions:
The linear map
defined by
is a linear isomorphism and 2. is canonically isomorphic to ℝ
is canonically isomorphic to ℝ
Definition 1. (is called the vector space of pseudo-intervals. , +, )
, +, )
2.2 A 4-dimensional free algebra associated with 𝕀ℝ
Consider the following subset of 𝒫1:
One observes that the semi-group 𝕀ℝ can be identified to 𝒫1,1 ∪ 𝒫1,2 ∪ 𝒫1,3. Let us consider as well the following vectors of ℝ2
They correspond to the intervals [1, 1],[0, 1],[-1, 0], and [-1, -1]. Any point of 𝒫1,1 ∪ 𝒫1,2 ∪ 𝒫1,3 admits the decomposition
(a, b) = α1e1 + α2e2 + α3e3 + α4e4
With αi ≥ 0. The dependance relations between the vectors ei are
Thus there exists a unique decomposition of (a, b) in a chosen basis such that the coefficients are non negative. These basis are {e1, e2} for 𝒫1,1, {e2, e3} for 𝒫1,2, {e3, e4} for 𝒫1,3. Let us consider the free algebra of basis {e1, e2, e3, e4} whose products correspond to the Minkowski products. The multiplication table is
Definition 2. This algebra is associative and its elements are called pseudo-intervals.
2.3 Pseudo-intervals product
Let φ: 4 the natural injective embedding, F ⊂ 𝒜4 the linear subspace generated by{e
1 - e
2 + e
3, e
1 + e
4}, ψ the canonical embedding from 𝒜4 to 𝒜4/F and φ' = ψ ○ φ 11 B. Durand, A. Kenoufi & J.F. Osselin. System adjustments for targeted performances combining symbolic regression and set inversion. Inverse problems for science and engineering, (2013).), (55 N. Goze. PhD thesis, N-ary algebras and interval arithmetics. University of Haute-Alsace, (2011).), (1313 A. Kenoufi. Probabilist set inversion using pseudo-intervals arithmetic. Trends in Applied and Computational Mathematics, 15 (1) (2014), 97-117.. We identify an interval with its image in 𝒜4. The application φ is not bijective. Its image on the elements 𝒳 =  → 𝒜
→ 𝒜 =
=  is
is
Theorem 2. The multiplication
is distributive with respect the addition.
Proof. Practically the multiplication of two intervals will so be made: let X, Y ∈ ℝ. Thus X = Σαiei , Y = Σβiei with αi, βi ≥ 0 and we have the product
this product is well defined because  . This product is distributive because
. This product is distributive because ∈
∈
Remark. We have
We shall be careful not to return in 𝕀ℝ during the calculations as long as the result is not found. Otherwise we find the semantic problems of the distributivity.
We extend naturally the map φ: 𝕀ℝ → 𝒜4 to  by
by
for every A ∈ 𝕀ℝ.
2.4 Pseudo-intervals division
Division between intervals can also be defined with solving X · Y = (1, 0, 0, 0) in 𝒜4 or in a isomorphic algebra 𝒜4'. In 𝒜4 we consider the change of basis
This change of basis shows that 𝒜4 is isomorphic to 𝒜4'
The unit of 𝒜4' is the vector e 1 + e 2. This algebra is a direct sum of two ideals: 𝒜4' = I 1 + I 2 where I 1 is generated by e 1 and e 4 and I 2 is generated by e 2 and e 3. It is not an integral domain, that is, we have divisors of 0. For example e 1 · e 2 = 0.
Proposition 2. The multiplicative group 𝒜4* of invertible elements of 𝒜4 is the set of elements x = (x 1 , x 2 , x 3 , x 4) such that
This means that the invertible intervals do not contain 0. If x ∈ 𝒜4* we have:
2.5 Pseudo-intervals monotonicity property
Let us compute the product of pseudo-intervals using the product in 𝒜4 and compare it with the Minkowski product. Let X = [a, b] and Y = [c, d] two intervals.
Lemma 1. If X and Y are not in the same piece 𝒫1, i, then X ● Y corresponds to the Minkowski product.
Proof. i) If X ∈ 𝒫1,1 and Y ∈ 𝒫1,2 then φ(X) = (a, b - a, 0, 0) and φ(Y) = (0, d, -c, 0). Thus
ii) If X ∈ 𝒫1,1 and Y ∈ 𝒫1,3 then φ(X) = (a, b -a, 0, 0) and φ(Y) = (0, 0, d -c, -d). Thus
iii) If X ∈ 𝒫1,2 and Y ∈ 𝒫1,3 then φ(X) = (0, b, -a, 0) and φ(Y) = (0, 0, d -c, -d). Thus
Lemma 2. If X an Y are both in the same piece 𝒫1,1 or 𝒫1,3 , then the product X ● Y corresponds to the Minkowski product.
The proof is analogous to the previous.
Let us assume that X = [a, b] and Y = [c, d] belong to 𝒫1,2. Thus φ(X) = (0, b, -a, 0) and φ(Y) = (0, d, -c, 0). We obtain
XY = (be 2 - ae 3)(de 2 - ce 3) = (bd + ac)e 2 + (-bc - ad)e 3.
Thus
[a, b][c, d] = [bc + ad, bd + ac].
This result is greater that all the possible results associated with the Minkowski product. However, we have the following property:
Proposition 3 Monotony property: Let 𝒳1, 𝒳2 ∈  . Then
. Then
The order relation on 𝒜4 that ones uses here is
Proof. Let us note that the second property is equivalent to the first. It is its translation in  . We can suppose that 𝒳1 and 𝒳2 are intervals belonging moreover to 𝒫1,2: φ(𝒳1) = (0, b, -a, 0), φ(𝒳2) = (0, d, -c, 0). Ifφ(𝒵) = (z1, z2, z3, z4), then
. We can suppose that 𝒳1 and 𝒳2 are intervals belonging moreover to 𝒫1,2: φ(𝒳1) = (0, b, -a, 0), φ(𝒳2) = (0, d, -c, 0). Ifφ(𝒵) = (z1, z2, z3, z4), then
Thus
But (b - d), -(a - c) ≤ 0 and z2, z3 ≥ 0. This implies  (𝒳1 ● 𝒵) ≤
(𝒳1 ● 𝒵) ≤  (𝒳2 ● 𝒵).
(𝒳2 ● 𝒵).
2.6 The algebras 𝒜n and a better result of the product
We can refine the product to become closer to Minkowski's one. Consider the one dimensional extension 𝒜4 ⊕ ℝe5 = 𝒜5, where e5 is a vector corresponding to the interval [-1, 1] of 𝒫1,2. The multiplication table of 𝒜5 is
The piece 𝒫1,2 is written 𝒫1,2 = 𝒫1,2,1 ∪ 𝒫1,2,1 where 𝒫1,2,1 = {[a, b], -a ≤ b} and 𝒫1,2,2 = {[a, b], -a ≥ b}. If X = [a, b] ∈ 𝒫1,2,1 and Y = [c, d] ∈ 𝒫1,2,2, thus
φ(X) . φ(Y) = (0, b + a, 0, 0, -a).(0, 0, -c -d, 0, d) = (0, -(a + b)(c + d), 0, 0, a(c + d) + bd).
Thus we have
X ● Y = [-bd -ac -ad, -bc].
Example. Let X = [-2, 3] and Y = [-4, 2]. We have X ∈ 𝒫1,2,1 and Y ∈ 𝒫1,2,2. The product in 𝒜4 gives
X ● Y = [-16, 14].
The product in 𝒜5 gives
X ● Y = [-12, 10].
The Minkowski product is
[-2, 3].[-4, 2] = [-12, 8].
Thus the product in 𝒜5 is better than the product in 𝒜4 with respect to the partial order. Let's go further. Considering a partition of 𝒫1,2, we can define an extension of 𝒜4 of dimension n, the choice of n depends on the approach wanted of the Minkowski product. For example, let us consider the vector e6 corresponding to the interval [-1, 1/2]. Thus the Minkowsky product gives e6 * e6 = e7 where e7 corresponds to[-1/2, 1]. This yields to the fact that 𝒜6 is not an associative algebra but it is the case for 𝒜7 whose table of multiplication is
Example. Let X = [-2, 3] and Y = [-4, 2]. The decomposition on the basis {e1, ..., e7} with positive coefficients writes
X = e5 + 2e7, Y = 2e6.
X ● Y = (e5 + 2e7)(4e6) = 4e5 + 8e6 = [-12, 8].
We obtain now the Minkowski product.
Remark 1. Pseudo-intervals division can be defined as well in 𝒜5 and 𝒜7.
2.7 Inclusion functions
It is necessary for some problems to extend the definition of a function defined for real numbers f: ℝ → ℝ to function defined for intervals [f]: 𝕀ℝ → 𝕀ℝ such as [f]([a, a])=f(a) for any a ∈ ℝ. It will be convenient to have the same formal expression for f and [f]. Usually the lack of distributivity in Minkowski arithmetic does not give the possibility to get the same formal expressions. But with the pseudo-intervals arithmetic we have presented, there is no data dependency anymore and one can define easily inclusion functions from the natural one. For example, let's extend to intervals the real functions f0(x) = x2 - 2x + 1, f1(x) = (x - 1)2, f2(x) = x(x - 2) + 1. Usually, with the Minkwoski operations, the three expressions of this same function for the interval X = [3, 4] are [f]0(X) = [2, 11], [f]1(X) = [4, 9] and [f]2(X) = [6, 12]. Data dependancy occurs when the variable appears more than once in the function expression. The deep reason of that is the lack of distributivity in Minkowski arithmetic. But within the arithmetic developed in 𝒜4 or higher dimension free algebras [nicolas], this problem vanishes. For example: with X = [3, 4] and since X ∈ 𝒫11,
Since e 1 = (1, 0, 0, 0), e 2 = (0, 1, 0, 0) and with means of product table, one has
and
Thus, [f]0(X) = [f]1(X) = [f]2(X) = [4, 9] and the inclusion function is defined univoquely regardless the way to write the original one.
On the other hand, the construction of the inclusion function depends on the type of problem one deals with. If one aims to perform set inversion for example, it has to be done in the semi-group 𝕀ℝ. But, the substraction is not defined in 𝕀ℝ. This problem can be circumvented by replacing it with an addition and a multiplication with the interval e 4 = [-1, -1]. This maintains the associativity and distributivity of arithmetic and permits to introduce a pseudo-substraction. For example: if f(x) = x 2 - x = x(x - 1) for real numbers, one defines [f](X) = X 2 + e 4 · X. One reminds the product [-1, -1]·[a, b] is equal to [-b, -a]. Due to the fact that the arithmetic is now associative and distributive, one does not have data dependency anymore and [f](X) = X 2 + e 4 · X = X · (X + e 4). The last term corresponds to the transfer of x(x - 1). Division can be transferred to the semi-group in the same way by replacing 1/x = x -1 with Xe 4.
Taylor polynomial expansions, differential calculus and linear algebra operations are defined only in a vector space. Therefore the transfer for the vector space is done directly. This permits to get infinitesimal intervals with the substraction and to compute derivatives. This is of course not allowed and not possible into the semi-group. From 𝕀ℝ to the vector space X. This means that [a, b] substraction is the anti-interval [-a, -b] addition. One of the most important consequence is that it is possible to transfer some functions directly to the pseudo-intervals. For example, it is easy to prove analytically in  with means of Taylor expansion.
with means of Taylor expansion. , f: x ⟼ -x is transferred to [f]: X ≡
, f: x ⟼ -x is transferred to [f]: X ≡  =
=  ⟼
⟼  that [exp]
that [exp] ≡ \
≡ \
2.8 Numerical linear algebra examples
One uses the 𝒜7 pseudo-intervals arithmetic for simple examples of linear algebra computations where matrix elements are intervals.
2.8.1 Interval matrix diagonalization
As an example, we would like to compute the largest eigenmode of the matrix M whose elements are intervals centered around a certain real number with a radius є:
If one uses scilab to compute the spectrum of the previous matrix without radius (є = 0), the highest eigenvalue is approximatively 16.345903 and the corresponding eigenvector is (0.4728057, 0.5716783, 0.6705510). In order to show that arithmetics and interval algebra developed above are robust and stable, let's try to compute the highest eigenvalue of an interval matrix. One uses here the iterate power method, which is very simple and constitute the basis of several powerful methods such as deflation and others.
The Figures 1 and 2 show clearly for different value of є the stability of the multiplication, and the largest eigenmode is recovered when є = 0. The other eigen modes can be computed with the deflation methods for example which consists to withdraw the direction spanned by the eigenvector associated to the highest eigenvalue to the matrix by constructing its projector and to do the same. Several methods are available and efficient to achieve that 66 A.S. Householder. The theory of matrices in numerical analysis. Dover Publications, (1975).), (3535 W.T. Vetterling, B.P. Flannery, W.H. Press & S.A. Teukolsky. Numerical Recipes in C: The Art of Scientific Computing, 2nd Ed. Cambridge University Press, New York, (1992).. We have choosen to compute only the highest eigenvalue and its corresponding eigenvector in order to show simply the efficiency of our new arithmetic.
Largest eigenvalue convergence computed with iterate power method to the value computed with scilab 16.345903.
Eigenvector components associated to the largest eigenvalue convergence computed with iterate power method to the eigenvector computed with scilab (0.4728057, 0.5716783, 0.6705510).
2.8.2 Interval matrix inversion
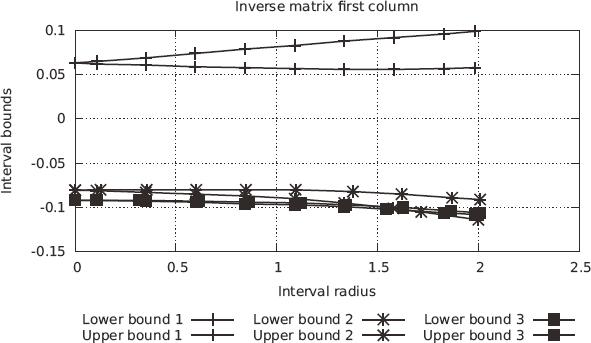
Let's define the matrix X whose elements are intervals centered around a certain real number with a radius є:
Scilab inversion function gives numerically for є = 0
We would like to use the well-known Schutz-Hotelling algorithm 66 A.S. Householder. The theory of matrices in numerical analysis. Dover Publications, (1975).), (3535 W.T. Vetterling, B.P. Flannery, W.H. Press & S.A. Teukolsky. Numerical Recipes in C: The Art of Scientific Computing, 2nd Ed. Cambridge University Press, New York, (1992). to inverse the matrix X since it uses simple arithmetic operations:
The elements of inverse matrix columns are exhibited on Figures 3, 4, 5 and are converging to the right values when є = 0.
3 TOPOLOGY OF 𝕀ℝ
One shows in this section that  can be endowed with the metric topology of a Banach space. This permits to define correctly continuity and differentiability of functions.
can be endowed with the metric topology of a Banach space. This permits to define correctly continuity and differentiability of functions.
3.1 Banach space structure of 𝕀ℝ
Any element 𝒳 ∈  or
or  . We define its length l(𝒳) as the length of A and its center as c(A) or -c(A) in the second case.
. We define its length l(𝒳) as the length of A and its center as c(A) or -c(A) in the second case. is written
is written
Theorem 3. The map || || : → ℝ+
given by
||𝒳|| = l(𝒳) + |c(𝒳)|
for any 𝒳 ∈ is a norm.
Proof. We have to verify the following axioms:
1) If ||𝒳|| = 0, then l(𝒳) = |c(𝒳)| = 0 and 𝒳 = 0.
2) Let λ ∈ ℝ. We have
||λ𝒳|| = l(λ𝒳) + |c(λ𝒳)| = |λ| · l(𝒳) + |λ| · |c(𝒳)| = |λ| · ||𝒳||.
3) One considers that I refers to 𝒳 and J refers to 𝒳' thus 𝒳 =  or =
or =  . We have to study the two different cases:
. We have to study the two different cases:
i) If 𝒳 + 𝒳' =  , then
, then or
or
ii) Let𝒳 + 𝒳' = K + J = I and =
=  then
then  . If
. If
that is
So we have a norm on  .
.
Theorem 4. The normed vector space is a Banach space.
Proof. In fact, all the norms on ℝ2 are equivalent and ℝ2 is a Banach space for any norm. The vector space  is then isomorphic to ℝ2. Thus, it is complete.
is then isomorphic to ℝ2. Thus, it is complete.
Remarks.
1. To define the topology of the normed space 0 = a, b) ∈ ℝ2. We assume that χ0 = A
1, ..., A
4 the points A
1 = (a - ε, b - ε), A
2 = (a + ε/2, b - ε/2), A
3 = (a + ε, b + ε), A
4 = (a - ε/2, b + ε/2). If 0 < a < b, then the ε-neighborhood of χ0 = A
1, A
2, A
3, A
4. for ε a positive infinitesimal number. We can give a geometrical representation, considering χ
for ε a positive infinitesimal number. We can give a geometrical representation, considering χ and ε an infinitesimal real number. Let
and ε an infinitesimal real number. Let  is represented by the parallelograms whose vertices are
is represented by the parallelograms whose vertices are  represented by the point (
represented by the point ( , it is sufficient to describe the ε-neighborhood of any point χ0 ∈
, it is sufficient to describe the ε-neighborhood of any point χ0 ∈
2. We can consider another equivalent norms on  . For example
. For example
||𝒳|| = ||\𝒳|| = max{|x|, |y|}
where 𝒳 =  , but the initial one has a better geometrical interpretation.
, but the initial one has a better geometrical interpretation.
3.2 Continuity and differentiability in 𝕀ℝ
As 0 = X
0, ε) = {X ∈  is a Banach space, we can describe a notion of differential function on it. Consider 𝒳
is a Banach space, we can describe a notion of differential function on it. Consider 𝒳 .
. . The norm ||.|| defines a topology on
. The norm ||.|| defines a topology on  whose a basis of neighborhoods is given by the balls ℬ(
whose a basis of neighborhoods is given by the balls ℬ( in
in  =
=  , ||𝒳 \ 𝒳0|| < ε}. Let us characterize the elements of ℬ(X0, ε). 𝒳0 =
, ||𝒳 \ 𝒳0|| < ε}. Let us characterize the elements of ℬ(X0, ε). 𝒳0 =
Proposition 4. Consider 𝒳0 = inand ε ~ 0, ε > 0. Then every element of ℬ(X
0, ε) is of type 𝒳 = and satisfies

 =
= 
l(X) ∈ B ℝ(l(X 0), ε1) and c(X) ∈ B ℝ(c(X 0), ε2)
with ε1, ε2 ≥ 0 and ε1 + ε2 ≤ ε, where B ℝ(x, a) is the canonical open ball in ℝ of center x and radius a.
Proof. First case: Assume that 𝒳 =  =
=  . We have
. We have
If l(X) ≥ l(X0) we have
As l(X) - l(X0) ≥ 0 and |c(X) - c(X0)| ≥ 0, each one of this term if less than ε. If l(X) ≤ l(X0) we have
||𝒳 \ 𝒳0|| = l(X0) - l(X) + |c(X0) - c(X)|.
and we have the same result.
Second case: Consider 𝒳 =  =
=  . We have
. We have
and
||𝒳 \ 𝒳0|| = l(X0) + l(X) + |c(X0) + c(X)|.
In this case, we cannot have ||𝒳 \ 𝒳0|| < ε thus X ∉ ℬ(X0, ε).
Definition 3. A function f:→is continuous at 𝒳0
if

∀ε > 0, ∃η such that ||𝒳 \ 𝒳0|| < η implies ||f(𝒳) \ f(𝒳0)|| < ε.
Consider (𝒳1, 𝒳2) the basis of  given in Section 2. We have
given in Section 2. We have
If f is continuous at 𝒳0 so
f(𝒳) \ f(𝒳0) = (f 1(𝒳) - f 1(𝒳0)) 𝒳1 + (f 2(𝒳) - f 2(𝒳0)) 𝒳2.
To simplify notations let α = f 1(𝒳) - f 1(𝒳0) and β = f 2(𝒳) - f 2(𝒳0). If ||f(𝒳) \ f(𝒳0)|| < ε, and if we assume f 1(𝒳) - f 1(𝒳0) > 0 and f 2(𝒳) - f 2(𝒳0) > 0 (other cases are similar), then we have
Thus f 1(𝒳) - f 1(𝒳0) < ε. Similarly,
and this implies that f 2(𝒳) - f 2(𝒳0) < ε.
Corollary 1. f is continuous at 𝒳0 if and only if f 1 and f 2 are continuous at 𝒳0 .
Definition 4. Consider 𝒳0
inand f:→continuous. We say that f is differentiable at 𝒳0
if there exists a linear function g:→such that




||f(𝒳) \ f(𝒳0) \ g(𝒳 \ 𝒳0)|| = o(||𝒳 \ 𝒳0||).
Examples.
• f(𝒳) = 𝒳. This function is continuous and differentiable at any point. Its derivative is f'(𝒳) = 1.
• f(𝒳) = 𝒳2. Consider 𝒳0 = X
0, ε). We have =
=  and 𝒳 ∈ ℬ(
and 𝒳 ∈ ℬ(
Given ε > 0, let η =  , thus if ||𝒳 \ 𝒳0|| < η, we have ||𝒳2 \ 𝒳20|| < ε and f is continuous and differentiable. It is easy to prove that f'(𝒳) = 2𝒳 is its derivative.
, thus if ||𝒳 \ 𝒳0|| < η, we have ||𝒳2 \ 𝒳20|| < ε and f is continuous and differentiable. It is easy to prove that f'(𝒳) = 2𝒳 is its derivative.
• Consider P = a0 + a1X + ... + anXn ∈ ℝ[𝕏]. We define f: f(𝒳) = a
0𝒳2 + a
1𝒳 + ... + an
n
𝒳n where 𝒳n = 𝒳 - 𝒳n
-1. From the previous example, all monomials are continuous and differentiable, it implies that f is continuous and differentiable as well. →
→  with
with
• Consider the function Q 2 given by Q 2([x, y]) = [x 2, y 2] if |x| < |y| and Q 2([x, y] = [y 2, x 2] in the other case. This function is not differentiable.
3.3 Minimization examples
One uses the 𝒜7 pseudo-intervals arithmetic for simple examples of inclusion function minimization with first and second order methods such as respectively fixed-step gradient descent and Newton-Raphson ones.
3.3.1 Fixed-step gradient descent method
Let's minimize the function x ⟼ x · exp(x) with fixed-step gradient method which belongs to the so-called gradient descent method 3535 W.T. Vetterling, B.P. Flannery, W.H. Press & S.A. Teukolsky. Numerical Recipes in C: The Art of Scientific Computing, 2nd Ed. Cambridge University Press, New York, (1992).. This example is very simple but it shows that the result is garanted to be found within the final interval. One sets initial guess interval to [-5, 2], fixed-step of descent to10-2, finite difference step to 10-3 and accuracy of gradient to 10-3. The results shown in Figures 6, 7) show that for any initial guess the interval width decreases to converge to real point minimum.
Convergence of the fixed-step gradient algorithm for the function x ⟼ x · exp(x) to an interval centered around [-1, -1] = -1.
Convergence of the fixed-step gradient algorithm for the derivative of the function x ⟼ x · exp(x) to an interval centered around [0, 0] = 0.
3.3.2 Newton-Raphson method
Let's optimize the same function x ⟼ x · exp(x) with a second order method such as the Newton-Raphson one, which is the basis of all second order methods such as Newton or quasi-Newton's ones 3535 W.T. Vetterling, B.P. Flannery, W.H. Press & S.A. Teukolsky. Numerical Recipes in C: The Art of Scientific Computing, 2nd Ed. Cambridge University Press, New York, (1992).. One sets initial guess interval to [0, 10], finite difference step to 10-3 and accuracy of gradient to10-9. One can state on Figures (8, 9) that it finds the same minimum which is an interval centered around -1.
Convergence of the Newton-Raphson algorithm for the function x ⟼ x · exp(x) to an interval centered around [-1, -1] = -1.
Convergence of the Newton-Raphson algorithm for the derivative of the function x ⟼ x · exp(x) to an interval centered around [0, 0] = 0.
4 CONCLUSION
We have presented a better algebraic way to do calculations on intervals, called pseudo-intervals vector space or free algebra. This approach 11 B. Durand, A. Kenoufi & J.F. Osselin. System adjustments for targeted performances combining symbolic regression and set inversion. Inverse problems for science and engineering, (2013).), (55 N. Goze. PhD thesis, N-ary algebras and interval arithmetics. University of Haute-Alsace, (2011).), (1313 A. Kenoufi. Probabilist set inversion using pseudo-intervals arithmetic. Trends in Applied and Computational Mathematics, 15 (1) (2014), 97-117. is done by embedding the space of intervals into a free algebra of dimension belonging to {4, 5, 7}. It permits to obtain all the basic arithmetic operators with distributivity and associativity. We have shown that when one increases the representative algebra dimension, the multiplication result will be closer to the usual Minkowski product. It is now possible to build inclusion functions from the natural ones in a systematicway. Thus, it allows to build all algebraic operations and functions on intervals and avoids completely the wrapping effects and data dependance. One has exhibited some simple examples of applications: minimization, diagonalization and inversion of matrices which clearly state that the arithmetic is stable and that if the initial data are known with uncertainity (belonging to an interval), it is thus possible to estimate with accuracy the point solution of the problem, a real number or an interval centered around it. This pseudo-intervals arithmetic seems to be a promising and powerful computation framework in several domains of sciences and engineering, such as physics, mechanics of structure, or finance for instance.
5 ACKNOWLEDGEMENTS
The author thanks Michel Gondran for useful and interesting discussions.
REFERENCES
-
1B. Durand, A. Kenoufi & J.F. Osselin. System adjustments for targeted performances combining symbolic regression and set inversion. Inverse problems for science and engineering, (2013).
-
2A. Trepat, E. Gardenes & H. Mielgo. Modal intervals: Reason and ground semantics. Lecture Notes in Computer Science, Springer-Verlag, Berlin, Heidelberg, 212 (1986), 27-35.
-
3L. Jorba, R. Calm, R. Estela, H. Mielgo, A. Trepat, E. Gardenes & M.A. Sainz. Modal intervals. Reliable Computing, 7 (2001), 77-111.
-
4E. Gardenes. Fundamentals of sigla, an interval computing system over the completed set of intervals. Computing, 24 (1980), 161-179.
-
5N. Goze. PhD thesis, N-ary algebras and interval arithmetics. University of Haute-Alsace, (2011).
-
6A.S. Householder. The theory of matrices in numerical analysis. Dover Publications, (1975).
-
7http://www.ti3.tu-harburg.de/rump/intlab/
» http://www.ti3.tu-harburg.de/rump/intlab/ -
8E. Kaucher. Ueber metrische und algebraische Eigenschaften einiger beim numerischen Rechnen auftretender Raume. Dissertation, Universitaet Karlsruhe, (1973).
-
9E. Kaucher. Algebraische erweiterungen der intervallrechnung unter erhaltung der ordnungs und verbandstrukturen computing. 1 (1977), 65-79.
-
10E. Kaucher. Ueber eigenschaften und en der anwendungsmoeglichkeiten der erweiterten intervallrechnung und des hyperbolischen fastkoerpers ueber r computing. 1 (1977), 81-94.
-
11E. Kaucher. Interval analysis in the extended interval space ir computing. 2 (1980), 33-49.
-
12R.B. Kearfott. Rigorous Global Search: Continuous Problems. Academic Publishers, (1996).
-
13A. Kenoufi. Probabilist set inversion using pseudo-intervals arithmetic. Trends in Applied and Computational Mathematics, 15 (1) (2014), 97-117.
-
14O. Didrit, L. Jaulin, M. Kieffer & E. Walter. Introduction to interval Analysis. SIAM 2009, Applied interval Analysis. Springer-Verlag, London, (2001).
-
15S.M. Markov. Extended interval arithmetic involving infinite intervals. Mathematica Balkanica, New Series, 6(3) (1992), 269-304.
-
16S.M. Markov. On directed interval arithmetic and its applications. J. UCS, 1(7) (1995), 510-521.
-
17S.M. Markov. On the Foundations of Interval Arithmetic. Scientific Computing and Validated Numerics Akademie Verlag, Berlin, (1996).
-
18M. Markov. Isomorphic embeddings of abstract interval systems. Reliable Computing, (3) (1997), 199-207.
-
19http://maxima.sourceforge.net
» http://maxima.sourceforge.net -
20R.E. Moore. PhD thesis. Standford university, (1962).
-
21R.E. Moore. Interval analysis. Prentice Hall, Englewood Cliffs, NJ, (1966).
-
22R.E. Moore. A test for existence of solutions to nonlinear systems. SIAM J. Numer. Anal., 14(4) (1977), 611-615.
-
23E. Popova, N. Dimitrova & S. M. Markov. Extended Interval arithmetic: New Results and Applications. Computer Arithmetic and Enclosure Methods. Elsevier Sci. Publishers B.V., (1992).
-
24H.J. Ortolf. Eine verallgemeinerung der intervallarithmetik. geselschaft fuer mathematik und datenverarbeitung. Bonn, 11 (1969), 1-71.
-
25E.D. Popova. All about generalized interval distributive relations. i. complete proof of the relations. Sofia, (2000).
-
26E.D. Popova. Multiplication distributivity of proper and improper intervals. Reliable Computing, 7(2) (2001), 129-140.
-
27Yves Deville, Pascal Van Hentenryck & Laurent Michel. Numerica: A Modelling Language for Global Optimization. MIT Press, (1997).
-
28http://www.python.org
» http://www.python.org -
29C.T. Yang & R.E. Moore. Interval analysis i. LMSD-285875, Lockheed Aircraft Corporation, Missiles and Space Division, Sunnyvale, California, (1959).
-
30Wayman Strother, R.E. Moore & C.T. Yang. Interval integrals. LMSD-703073, Lockheed Aircraft Corporation, Missiles and Space Division, Sunnyvale, California, IX(4) (1960), 241-245.
-
31http://www.sagemath.org
» http://www.sagemath.org -
32T. Sunaga. Theory of an interval Algebra and its Application to Numerical Analysis. Number 2. RAAG Memoirs, (1958).
-
33Mieczyslaw Warmus. Calculus of approximations. Bull. Acad. Pol. Sci., C1, III(IV (5)) (1956), 253-259.
-
34Mieczyslaw Warmus. Approximations and inequalities in the calculus of approximations. classification of approximate numbers. Bull. Acad. Pol. Sci. math. astr. & phys., IX(4) (1961), 241-245.
-
35W.T. Vetterling, B.P. Flannery, W.H. Press & S.A. Teukolsky. Numerical Recipes in C: The Art of Scientific Computing, 2nd Ed. Cambridge University Press, New York, (1992).
Publication Dates
-
Publication in this collection
Sep-Dec 2016
History
-
Received
13 Oct 2014 -
Accepted
30 Aug 2016