Produto funcional de grafos

Produto funcional de grafos

A.R.G. Lozano^I,*; A.S.Siqueira^II; S. Jurkiewicz^III; C.V.P. Friedmann^IV

^IDepartamento de Matemática da FFP-UERJ, Escola de Ciências, Educação, Letras, Artes e Humanidades da UNIGRANRIO, Grupo de Pesquisa em Matemática Discreta e Computacional. E-mail: [e-mail]

^IIEscola de Ciências, Educação, Letras, Artes e Humanidades da UNIGRANRIO, Grupo de Pesquisa em Matemática Discreta e Computacional. E-mail: [e-mail]

^IIIPrograma de Engenharia da Produção da COPPE-UFRJ. E-mail: [e-mail]

^IVDepartamento de Matemática da FFP-UERJ, Grupo de Pesquisa em Matemática Discreta e Computacional. E-mail: [e-mail]

RESUMO

O trabalho apresenta uma generalização do produto cartesiano de grafos que denominamos de produto funcional de grafos. Provam-se algumas propriedades do novo produto e mostra-se uma aplicação do mesmo, que consiste em gerar grafos regulares que admitem coloração com folga Δ com Δ + 1cores.

Palavras-chave: produto funcional de grafos, coloração com folga, grafo suporte.

ABSTRACT

The paper presents a generalization of the Cartesian product of graphs, called functional product. We prove some properties of the new product and show an application, that consist in generate regular graphs that admits I-range coloring with Δ + Δ colors.

Keywords: functional product of graphs, range coloring, support graph.

1 INTRODUÇÃO

Em 2008 Lozano, Jurkiewicz e Friedmann [8] apresentaram um algoritmo para troca completa de informações que não dependia da topologia da rede. Para isto, usaram a coloração total equilibrada dos grafos correspondentes às topologias mais comuns e mostraram que tais colorações satisfaziam a Conjectura de Vizing, ou seja, os grafos podiam ser coloridos totalmente com, no máximo, Δ + 2 cores. Posteriormente Lozano, Siqueira e Jurkiewicz [12] provaram que, se um grafo regular pode ser colorido com folga Δ com Δ + 1 cores então a coloração de vértices pode ser completada obtendo-se uma coloração total equilibrada com, no máximo, Δ + 2 cores. O resultado acima citado serviu como motivação para estudar a possibilidade de se construir famílias de grafos regulares com as características mencionadas. Para auxiliar nesta construção, introduziu-se o conceito de produto funcional de grafos e suas propriedades, que são explorados na terceira seção deste artigo. Em seguida apresentamos uma das maneiras de obter estas fam ílias de grafos regulares usando o produto funcional, e finalizamos com uma seção onde são expostas as perspectivas de trabalhos futuros. Neste texto, os grafos são simples, não orientados e sem laços.

2 DEFINIÇÕES BÁSICAS E NOTAÇÕES

Ao longo do artigo serão usadas as notações listadas a seguir:

• {u, v}ou uv denota uma aresta do grafo G, onde u e v são adjacentes;

• d_G(v) ou d(v) se não houver ambiguidade, denota o grau do vértice v no grafo G;

• Δ (G) ou Δ se não houver ambiguidade, denota o grau máximo do grafo G;

• N_G (v) ou N(v) se não houver ambiguidade, denota o conjunto de os todos vértices adjacentes ao vértice v no grafo G;

• F(X) denota o conjunto de todas as bijeções de X em X;

• D(G) denota o digrafo obtido pela substituição de cada aresta uv do grafo G pelos arcos (u, v)e (v, u), mantendo o mesmo conjunto de vértices;

•

denota o conjunto dos digrafos que satisfazem as seguintes condições:

1. (u, v) e um arco do digrafo se, e somente se, (v, u) também é um arco do digrafo,

2. Não existem dois arcos iguais.

• Se ∈ , G() denota o grafo obtido pela substituição de cada par de arcos (u, v) e (v, u) de pela aresta uv, mantendo o mesmo conjunto de vétices;

• I_n denota o conjunto de números naturais {0, 1, 2, 3, 4, ..., n -1};

• Se A é um conjunto, |A|denota a cardinalidade de A;

• E(X) ou E se não houver ambiguidade, denota o conjunto de arestas (arcos) do grafo (digrafo) X;

• V (X) ou V se não houver ambiguidade, denota o conjunto de vértices do grafo (digrafo) X;

• C_n denota o ciclo de n vértices;

• K_n denota o grafo completo de n vértices.

Definição 2.1. [3] Sejam um grafo G(V, E), um conjunto S ⊂(E ∪V), um número natural k e um conjunto arbitrário C = {c₁, c₂, ..., c_k} cujos elementos são denominados de cores. Uma coloração f: S → C.

Na definição acima, se S = V então tem-se uma coloração de vértices. No caso de S = E, trata-se de uma coloração =E ∪V , ent˜f euma coloracao de arestas e finalmente, se S = E ∪V, então f é uma coloração total. Se x ∈ S e f (x) = c_i , i ∈ {1, 2, ..., k}, diz-se que x possui ou está colorido com a cor c_i .

Definição 2.2. [3] Sejam um grafo G(V, E), um conjunto S ⊂(E ∪ V)e um conjunto de cores C = {c₁, c₂, ..., c_k }, onde k é um número natural. Uma coloração f: S → C do grafo G com as cores de Cé uma coloração própria , se para todo par x, y ∈ S tem-se que, se x e adjacente ou incidente a y então f (x) ≠ f (y).

Deste ponto em diante, todas as colorações neste trabalho serão consideradas próprias e sobrejetivas, a menos que explicitamente se especifique o contrário.

Definição 2.3. [15] Dados um grafo G(V, E), um conjunto S ⊂(E ∪V) e um conjunto de cores C = {c₁, c₂, ..., c_k }, onde k é um número natural. Uma coloração f: S → C do grafo G com as cores de é uma colocaração equilibrada, se para todo par i, j ∈ {1, 2, ..., k} tem-se que, ||f ^-1(c_i )| - |f ^-1(c_j )|| < 1, sendo |f ^-1(c _i )| e |f ^-1(c_j)| as cardinalidades dos conjuntos dos elementos de S que possuem as cores c_i e c_j, respectivamente.

Definição 2.4. [5] Sejam um grafo G(V, E), um conjunto de cores C = {c₁, c₂, ..., c_k}, onde k é um número natural, e um número natural p, tal que p< Δ(G). Uma aplicação f: S → C é uma coloração de vértices do grafo G com as cores de C com folga p, se para todov ∈ V tem-se que se d (v) < p, então |c (N(v))| = d(v), caso contrário, |c(N(v))| = p, sendo |c(N(v))| a cardinalidade do conjunto das cores da vizinhança de v.

Definição 2.5 própria de arestas com [15] Um grafo G é de classe 1 se admite uma coloracI(G) cores, caso contrário é de classe 2.

3 PRODUTO FUNCIONAL DE GRAFOS

Nesta seção é apresentada a definição de produto funcional de grafos, para este fim, é necessário definir aplicações, denominadas aplicações de ligação, que associam cada aresta de um fator com uma bijeção definida no conjunto de vértices do outro. Esta bijeção indica como será feita a ligação dos vértices do grafo produto. O produto cartesiano de grafos pode ser visto como um produto funcional, onde a todas as arestas são associadas à aplicação identidade correspondente.

Definição 3.1. Os digrafos₁(V₁,E₁) e ₂(V₂,E₂) são ditos funcionalmente ligados pelas aplicações f₁:E₁ → F(V₂) e f₂:E₂ → F(V₁) se f₁e f₂são tais que:

1. Se para todo arco (u, v) ∈ E₁se (v, u) ∈ E₁, então f₁((u, v)) = (f₁((v, u)))^-1;

2. Se para todo (x, y) ∈ E₂se (y, x) ∈ E₂, então f₂((x, y)) = (f₂((y, x)))^-1;

3. Para todo par de arcos (u, v) ∈ E₁e (x, y) ∈ E₂, tem-se que f₂((x, y))(u) ≠ v ou f₁((u, v))(x) ≠ y.

As aplicações f ₁ e f ₂ são denominadas aplicações de ligação.

Definição 3.2. Sejam dois grafos G₁(V₁, E₁) e G₂(V₂, E₂). Se D(G₁) e D(G₂) são funcionalmente ligados pelas aplicações f₁ : E(D(G₁)) →F(V₂) e f₂ : E(D(G₂)) → F(V₁), então os grafos G₁(V₁, E₁) e G₂(V₂, E₂) são ditos funcionalmente ligados pelas mesmas aplicações.

Definição 3.3. Sejam ₁(V₁, E₁) e ₂(V₂, E₂) digrafosfuncionalmente ligados pelas aplicações f₁ : E₁ → F(V₂) e f₂ : E₂ → F(V₁).O produto funcional do digrafo ₁pelo digrafo ₂segundo as aplicações f₁e f₂, denotado por(₁, f₁) × (₂, f₂), é o digrafo, V^*,E^*) = definido por

• V^* = V₁ × V₂.

• ((u, x), (v, y)) ∈ E^* se, e somente se, uma das seguintes condições for verdadeira:

1. (u, v) ∈ E₁e f₁((u, v))(x) = y;

2. (x, y) ∈ E₂e f₂((x, y))(u) = v.

A Figura 1 apresenta dois digrafos com suas respectivas aplicações de ligação e o digrafo obtido como resultado do produto de ambos os pares.

Definição 3.4. Sejam G₁(V₁, E₁) e G₂(V₂, E₂) grafos funcionalmente ligados pelas aplicações f₁ : E(D(G₁)) → F(V₂) e f₂ : E(D(G₂)) → F(V₁). O produto funcional do grafo G₁ grafo G₂, denotado por (G₁, f₁) × (G₂, f₂), é o grafo G((V^*, E^*)), sendo (V^*, E^*) = (D(G₁), f₁) × (D(G₂), f₂).

E interessante notar que o Produto Cartesiano de Grafos é um caso particular do Produto Funcional de Grafos definido acima, quando f₁e f₂ atribuem a identidade a todos os arcos dos digrafos correspondentes. A seguir será definido um tipo especial de bijeção, denominado rotação.

Definição 3.5 Dado um número natural n, uma rotaçao em In é uma bijeção f : I_n → In definida como segue:

f(i) = (i + k)( mod n),

Definição 3.6. Sejam n um número natural e A um conjunto finito tal que |A| = n. Uma bijeção f: A → A é uma rotação em A, se existem, uma bijeção h: I_n → A e uma rotação r em I_n tais que f (h(i)) = h(r(i)), para todo i ∈ I_n.

Observe que, na definição acima, se h(i) e representado por x_i , tem-se que f (h(i)) = h(r(i)) = xr(i). Isso significa que para conhecer a rotação, basta conhecer o valor em x₀. Neste texto r_i (A) denotaráarotação em A tal que r(h(0)) = h(i). Se não existir ambiguidade, tal rotação será representada simplesmente por r_i.

A Figura 2 representa o produto funcional do caminho P₃ por ele mesmo, associado a duas diferentes aplicações de ligação (as rotações r₁e r₂). Na figura, cada vérticedaforma (v_i , v_j ) é representado por v_iv_j e as linhas descontínuas descrevem as arestas do produto cartesiano usual de grafos.

Os teoremas a seguir mostram algumas proriedades do produto funcional.

Teorema 3.1. Sejam G₁(V₁, E₁) e G₂(V₂, E₂) grafos funcionalmente ligados pelas aplicações f₁ : E(D(G₁)) → F(V₂) e f₂ : E(D(G₂)) → F(V₁). Então os grafos G^* (V^*, E^*) = ( G₁, f₁) ×( G₂, f₂) e G**(V^**, E^**) = (G₂, f₂) × (G₁, f₁) são isomorfos. Neste sentido, o produto funcional de grafos é comutativo.

Demonstração. Sejam E^'₁ = E(D(G₁)) e E^'₂ = E(D(G₂)). Provaremos que dados dois vértices (u, x) ∈ V^* e (v, y) ∈ V^*, então a aresta {(u, x), (v, y)} ∈ E^* se, e somente se, a aresta {(x, u), (y, v)} ∈ E^**. Tem-se que {(u, x), (v, y)} ∈ E^* se, e somente se:

1- (u, v) ∈ E₁^'e f₁((u, v))(x) = y e (v, u) ∈ E₁^'e f₁(v, u)(y) = (f₁((u, v)))^-1(y) = x ou

2- (x, y) ∈ E₂^'e f₂((x, y))(u) = v e (y, x) ∈ E₂^'e f₂(y, x)(v) = (f₂((x, y)))^-1(v) = u. {(x, u), (y, v)} ∈ E^** se, e somente se:

3- (x, y) ∈ E₂e f₂ ((x, y))(u) =v e (y, x) ∈ E₂e f₂(y, x)(v) = ( ₂f((x, y)))^-1(v) = u ou

4- (u, v) ∈ E₁e f₁((u, v))(x) = y e (v, u) ∈ E₁e f₁(v, u)(y) = ( f₁((x, y)))^-1(y) = x. Como 1 é equivalente a 4 e 2 é equivalente a 3 o teorema está provado.

Teorema 3.2. Sejam G₁ = (V₁, E₁) e G₂ = (V₂, E₂) grafos funcionalmente ligados pelas aplicações f₁ : E₁ → F(V₂) e f₂ : E₂ → F(V₁). Para todo vértice (u, x) do grafo G^* = (V^*, E^*) = (G₁, f₁) × (G₂, f₂) tem-se que: d_G*((u, x)) = d_G1 (u) + d_G2 (x).

Demonstração. Para cada (u, x) ∈ V^*, denota-se por E_G*((u, x)) o conjunto de arestas incidentes nesse vértice no grafo G^*. Constrói-se a aplicação h₁ : N_G1 (u) → E_G* ((u, x)) da seguinte forma: h₁(v) = {(v, y), (u, x)} onde y ∈ V₂ e tal que f₁((u, v))(x) = y com (u, v) ∈ E(D(G₁)); y existe pois f₁((u, v)) é bijetiva. Por outro lado h é injetiva, pois se v₁, v₂ ∈ N_G1 (u) e v₁ ≠ v₂ então necessariamente (v₁, y₁)(u, x) = (v₂, y₂)(u, x) independentemente do valor de y₁ e y₂. De forma semelhante, construimos h₂ :N_G2 (x) → E_G*((u, x)). Se uma aresta é incidente em (u, x) no grafo G^*ela tem a forma {(u, v) ∈ E(D(G₁)) tal que f₁((u, v))(x) = y ou (x, y) ∈ E(D(G₂)) tal que f₂((x, y))(u) = v. Por construção de h₁e h₂ tem-se que h₁(N_G1 (u)) ∪ h₂(N_G2 (v)) = E_G*((u, x)). Por outro lado, se {(u, x), (v, y)} ∈ h₁(N(u)) e {(u, x), (v, y)} ∈ h₂(N(v)) então existem arcos (u, v) ∈ E (D(G₁)) e (x, y) ∈ E(D(G₂)) tais que f₁((u, v))(x) = y e f₂((x, y))(u) = v o que contradiz a condição 3 da definição de aplicações de ligação logo, h₁(NG₁(u))∩h₂ (NG₂ (v)) = Φ.

Podemos agora construir a bijeção

h: N_G1 (u) ∪N_G2 (x) → E_G* ((u, v)), definida por

O que conclui a prova do teorema.

Do teorema anterior se obtém, de forma imediata, o seguinte corolário.

Corolário 3.2.1. Sejam G₁ = (V₁, E₁) e G₂ = (V₂, E₂) grafos funcionalmente ligados pelas aplicações f₁ : E₁ → F(V₂) e f₂ : E₂ → F(V₁), então o grafo G^*= (V ^*, E^* ) = (G₁, f₁) × (G₂, f₂) tem grau máximo Δ(G^*) = Δ (G₁) + Δ (G₂).

Em relação a conexidade, o produto funcional de grafos conexos não é necessarimamente conexo como mostra a Figura 3, mas também e possível obter um grafo conexo como resultado do produto funcional de dois grafos desconexos. O teorema abaixo oferece uma condição que garante a conexidade do grafo produto funcional, caso os fatores sejam conexos.

Teorema 3.3. Dados dois grafos G₁ =(V₁, E₁) e G₂ = (V₂, E₂) conexos e funcionalmente ligados pelas aplicações f₁ : E₁ → F(V₂) e f₂ : E₂ → F(V₁), se f₁ou f₂atribui a identidade a todos os arcos do digrafo correpondente, então o produto funcional de G₁por G₂segundo f₁e f₂é conexo.

Demonstração. Sem perda de generalidade, suponhamos que f₂ atribui a identidade a todos os arcos de D(G₂). Sejam G^* (V^*, E^*) = (G₁, f₁) × (G₂, f₂), (u, x) e (v, y) dois vértices de G^*. Como G₁ = v em G₁. Sejam agora z₁ = f₁((u, x₁))(x), z_i+1 = f₁((x_i, x_i+1))(z_i), i = 1, ..., p -1, consequentemente existe um caminho P₁ = (u, x)(x₁, z₁)(x₂, z₂) ∙∙∙(v, z_p) em G^*. Como G₂ é conexo, existe um caminho z_py₁ ∙∙∙y_q com y_q = y em G₂, e como f₂(e)(v) = v para toda aresta e ∈ E,₂ então P₂ = (v, zp)(v, y1) ∙∙∙(v, y) é um caminho em G^* A união de P₁ e P₂ proporciona um caminho entre (u, x) e (v, y).

O Produto Cartesiano de dois Grafos é conexo se, e somente se, ambos os fatores forem conexos, e para mais detalhes, pode-se consultar [14, 11]. Observe que esse resultado é uma consequência do teorema anterior, pois no Produto Cartesiano de Grafos, as aplicações de ligação f₁ e f₂ atribuem a identidade a todos os arcos dos digrafos correpondentes. Esse teorema impõe uma condição forte sobre uma das aplicações de ligação para que o produto funcional seja conexo. Mas, neste artigo, tal condição é suficiente para construir famílias de grafos conexos que admitem coloração com folga I com Δ+Δ cores, que foi a motivação inicial para a introdução do produto funcional. De qualquer forma, uma proposta de trabalho futuro e determinar condicoes mais fracas para as aplicações de ligação.

4 UMA APLICAÇÃO DO PRODUTO FUNCIONAL

Nesta seção, mostraremos alguns resultados relativos à construção de famílias de grafos regulares que admitem uma coloração com folga Δ com Δ +1 cores. Para um estudo mais detalhado, bem como outros resultados pode-se consultar [12]. Muitos grafos usados como grafos suporte para topologias de redes de interconexão, são obtidos mediante o produto cartesiano de grafos, como é o caso do hipercubo, mas nem sempre estes grafos admitem uma coloração com folga Δ com Δ +1 cores (como é o caso do toro C₃ × C₅, ilustrado na Figura 4). Com uma modificação adequada, pode-se obter um grafo que admite a coloração desejada mantendo as caracteristicas dos grafos suporte de redes (no que diz repeito à diâmetro, conexidade, regularidade, etc). As definições e teoremas a seguir exploram a ideia anterior.

Definição 4.1 (Grafo k-suporte). Dado um número natural k, k> 3, o grafo G = (V, E), é um k-suporte se satisfaz as seguintes condições

1. G é um grafo regular de grau k -3;

2. Existe uma aplicação f : E(G) → F(I_k), tal que G e C_k estão funcionalmente ligados por f e Id, onde Id: E(C_k) → F(I_|V|) é a aplicação que a cada arco de D(C_k)faz corresponder a função identidade;

3. O grafo G^*= (f₁, G) × (Id, C_k) pode ser colorido com folga Δ(G^*) com Δ(G^*) +1 cores.

Teorema 4.1. Se G(V, E) é um grafo k-regular de classe 1, então G é (k +3)-suporte.

Demonstração. Sejam V ={v₁, v₂, ..., v_n}, V (C_k+3) = {u₀, u₁, ..., u_k+2}, C = {2, 3, 4 ..., k +1} um conjunto e c: E → C, uma coloração de arestas de G usando o conjunto C. Dividiremos o restante da prova em dois casos:

Caso 1. k = Δ é par:

Denotamos por i' o número (k +3) - i, para todo i ∈ {2, 3, ...,(+1)}. Veja agora que i + i' = 0 (mod k +3), e que para cada par {i, i' } o subgrafo G_i (V_i , E_i ) induzido pelo conjunto de arestas {e ∈ E : c(e) = i ou c(e) = i' } é um grafo regular de grau 2 e que V = V_i . Logo, as componentes conexas de cada subgrafo G_i , são ciclos G_i1, ..., G_iti , onde t_i é um número natural, t_i < e cada ciclo G_ij está associado a dois ciclos orientados e em D(G). Definimos as aplicações f₁ : E(D(G)) → V (C_Δ+3), f₂ :E(D(C_Δ+3)) → V como segue:

f₂(x) = Id(x) para todo arco x ∈ D(C_Δ+3), onde Id representa a função identidade.

Sejam agora G^*= (f₁, G₁) × (f₂, C_k+3), V^*= V(G^*), E^*= E(G^*), A coloração f : V^*→ {0, 1, ..., (k +2)} definida por: f ((vi , uj)) = j, i = 1, 2, ..., n; j = 0, 1, 2, ..., (k +2) é uma coloração com folga Δ(V ^*) com Δ(V^*) +1 "cores" do grafo G^*. O conjunto de "cores" {0, 1, ..., (k +2)}possui k +3 elementos pelo corolário 3.2.1 G^* é um grafo regular de grau Δ(G) + Δ(C_k+3) = k +2. Para analisar que a coloração tem folga Δ(G^*), observe que por simetria basta analisar um vétice de V^*, por exemplo (v₁, u₀), seja N_G(v₁) = {x₂, ..., x_k+1}, por facilidade e sem perder generalidade vamos supor que c(v₁x_j) = j , j ∈ {2, ..., k +1} (na verdade cada aresta incidente a v₁ possui uma cor diferente) então os extremos dos arcos de (f₁,1) × (f₂,_Δ+3) que tem como origem (v₁, u₀) são (v₁, u₁), (v₁, u_k+2), (x₂, u₂), (x₃, u₃), (x₄, u₄), ..., (x_k+1, u_k+1) coloridos com as "cores" 1, k +2, 2, 3, ..., k +1 respectivamente, logo a coloração possui folga Δ.

Caso 2. k = Δ(G)é ímpar:

Observe que 2 +(k +1) = 3 + k = 4 + (k -1)∙∙=∙ + = + = k + 3, e denotamos por i' o número (k +3)- i, para todo i ∈ {2, 3, ..., ( +1)}. Agora o subgrafo G_i(V_i , E_i) induzido pelo conjunto de arestas {e ∈ E : c(e) = i ou c(e) = i'} i ∈ {2, 3, ..., (+ 1)} é um grafo regular de grau 2, e o subgrafo G_a, com a =, + 1 induzido pelo conjunto de arestas {e ∈ E : c(e) = + 1} é um emparelhamento perfeito, e o raciocinio seguido no caso 1, é válido, o que prova o teorema.

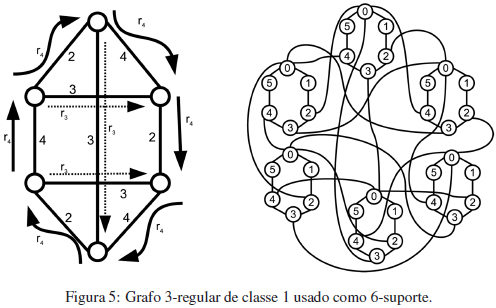
A Figura 5(a) mostra um grafo 3-regular de classe 1, colorido com os elementos do conjunto {2, 3, 4}. As setas indicam que ao fazer o produto funcional no sentido indicado é usada a rotação r₃ ou r₄ segundo o caso. Já no sentido contrário a r₄, éusada r₂ pois 4 +2 = 0 (mod 6), e no sentido contrário a r₃ eusada ´r₃ pois 3 +3 = 0 (mod 6). A Figura 5(b) ilustra o produto funcional com o ciclo C6, mas como o número de arestas é muito grande, foram representadas apenas as arestas que tem como extremo o vértice 0 de algum ciclo.

Teorema 4.2. Se G(V, E) = é um grafo completo então G é um (|V| + 2)-suporte.

Demonstração Seja G(V, E) = K_n. Se n é par então G é de classe 1 e o teorema está provado, logo vamos supor que n é ímpar. Sejam V = {v₀, v₁, ..., v_n-1} e c : E → C = {0, 1, 2, ..., n} uma coloração de arestas de G definida por c(v_i, v_j) = (i +j )(mod n); i, j ∈ {0, 1, ..., n -1}; i ≠ j . É claro que c, é própria pois fixando i 0 ∈ {0, 1, ..., n -1} temos que (i₀ + j₀) ≡(i0 + j1)(mod n) se, e somente se, j₀ ≡ j₁ (mod n). Antes de continuar com a prova do teorema, provaremos a seguinte, propriedade de c: se c₀ ∈ C está ausente no vértice v_i0 e c({vi₀ , vi₁ }) = 0, então c'₀ está ausente no vértice vi₁, onde c₀ denota o inverso aditivo de c₀ (mod n). Observe inicialmente que para todo i ∈{0, 1, 2, ..., n -1}, a cor i está ausente no vértice v_i .De fato,(i + i) ≡(i + j )(mod n), se, e somente se, i ≡ j (mod n), ecomo i, j ∈{0, 1, ..., n -1}, então i = j , mas G não possui laços, por outro lado (i + j ) = 0 (mod n) se, e somente se, (i + j ) = 0 (mod n), isto é, j = i (mod n), de onde segue imediatamente a propriedade. Para cada i ∈ {0, 1, 2, ...n -1}, denotamos por e_i a aresta {v_i, v_i}. Agora para cada par de cores {i, i'} i ∈{1, 2, ...,}, o subgrafo gerado pelo conjunto de arestas {e ∈ E : c(e) = i ou c(e) = i'} ∪ {e_i} é um grafo regular de grau 2 cujo conjunto de vértices é V , logo G foi decomposto em grafos 2-regulares e podemos utilizar o mesmo raciocínio do teorema 4.1, usando as rotações r₂, r₃, ..., r e suas inversas definidas em I_n+2 nos respectivos ciclos orientados.

A Figura 6 mostra um K₃ sendo usado como 5-suporte. Novamente foram omitidas as arestas não adjacentes a vértices rotulados com 0.

5 CONCLUSÕES

O produto funcional é uma generalização do produto cartesiano, e que apresenta algumas das propriedades deste, como a comutatividade e o fato de que o grau máximo do grafo produto seja a soma dos graus máximos dos grafos fatores. Por outro lado, o produto funcional mostrou-se eficiente para construir grafos que de alguma forma "herdam" boas propriedades dos fatores, como foi mostrado na seção anterior, e ainda oferece mais "liberdade" que o produto cartesiano usual na hora de definir as adjacências do grafo produto. Para o futuro, pretende-se estudar o comportamento de algumas invariantes de grafos, assim como condições mais fracas para garantir a conexidade do produto quando os fatores sejam conexos.

Recebido em 27 outubro, 2012

Aceito em 7 junho, 2013

• [1] R.M. Barbosa & M.R.C. Santana. Produtos de Grafos Zm-bem-cobertos. Tema, 13(2012),75-83.
• [2] V.A. Bojarshinov. Edge and total coloring of interval graphs. Disc. Appl. Math., 114(2001),23-28.
• [3] J. Bondy & U. Murty. "Graph Theory with Applications", North-Holland, New York, (1976).
• [4] C.N. Campos & C.P. Mello. A result on the total coloring of power of cycles. Disc. Appl. Math., 155(2007),585-597.
• [5] C.V.P. Friedmann, A.R.G. Lozano, L. Markenzon & C.F.E.M. Waga. Total coloring of Block-cactus graphs. The journal of combinatorial mathematics and combinatorial computing, 78(2011),273-283.
• [6] W. Imrich, S. Klavzar & D. Rall. "Topics in Graph Theory: Graphs and Their Cartesian Products", A.K. Peters Ltd., (2008).
• [7] A. Kemnitz & M. Marangio. Total colorings of cartesian products of graphs. Congres. Numer., 165(2003),99-109.
• [8] A.R.G.Lozano, S. Jurkiewicz & C.V.P. Friedmann. Coloração total equilibrada de grafos, um modelo para redes de interconexão. Pesquisa Operacional, 28(2008),161-171.
• [9] A.R.G.Lozano."Coloração Total Equilibrada de Grafos", Tese de Doutorado, COPPE, UFRJ, Riode Janeiro, RJ, (2005).
• [10] K. Prnaver & B. Zmazek. On the total chormatic number of direct products graphs. J. Appl. Math. Comput., (2009).
• [11] G. Sabidussi. Graph multiplication. Math. Z., 72(1960),446-457.
• [12] A.S. Siqueira. "Coloração total equilibrada em subfam ílias de grafos regulares". Tese de Doutorado, COPPE, UFRJ, Rio de Janeiro, RJ, (2011).
• [13] X. Tan, H. Chen & J. Wu. Total coloring of planar graphs without adjacent 4-cycles. The Eighth International Symposium on Operational Research and its Applications, China (2009),20-22.
• [14] V.G. Vizing. The Cartesian product of graphs. Vyc. Sis., 9(1963),30-43.
• [15] H. Yap. "Total colorings of graphs", Springer, Berlin, (1996).

*

Autor correspondente: Abel Rodolfo Garcia Lozano

Datas de Publicação

• Publicação nesta coleção
  11 Out 2013
• Data do Fascículo
  Ago 2013

Histórico

• Recebido
  27 Out 2012
• Aceito
  07 Jun 2013