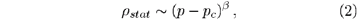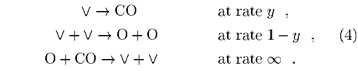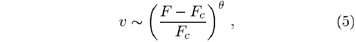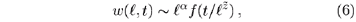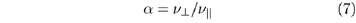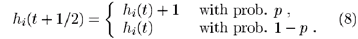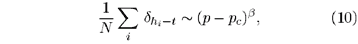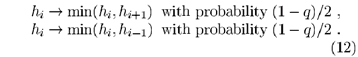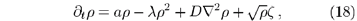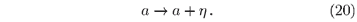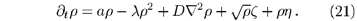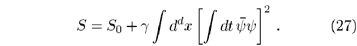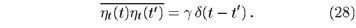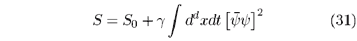Abstract
Directed percolation is one of the most prominent universality classes of nonequilibrium phase transitions and can be found in a large variety of models. Despite its theoretical success, no experiment is known which clearly reproduces the critical exponents of directed percolation. The present work compares suggested experiments and discusses possible reasons why the observation of the critical exponents of directed percolation is obscured or even impossible.
On possible experimental realizations of directed percolation
Haye Hinrichsen
Theoretische Physik, Fachbereich 10,
Gerhard-Mercator-Universität Duisburg,
D-47048 Duisburg, Germany
Received 1 November 1999
Directed percolation is one of the most prominent universality classes of nonequilibrium phase transitions and can be found in a large variety of models. Despite its theoretical success, no experiment is known which clearly reproduces the critical exponents of directed percolation. The present work compares suggested experiments and discusses possible reasons why the observation of the critical exponents of directed percolation is obscured or even impossible.
I Introduction
Physical phenomena far from thermal equilibrium are very common in nature. For example, many systems are subjected to an external flow of energy or particles which keeps them away from equilibrium. Similarly, dynamic systems starting with a nonequilibrium initial state may need a long time to reach thermal equilibrium. Theories of systems out of equilibrium are more difficult than equilibrium statistical mechanics since the partition sum is no longer given by the Gibbs ensemble. On the other hand, nonequilibrium systems may exhibit a potentially richer behavior than systems at thermal equilibrium. Therefore, the study of nonequilibrium phenomena is a field of growing interest, both theoretically and experimentally.
A particularly interesting topic is the investigation of phase transitions far from equilibrium [1]. The theoretical interest in nonequilibrium phase transitions mainly stems from the emergence of universal features of the associated critical behavior. The concept of universality was originally introduced by experimentalists in the context of equilibrium systems in order to describe the observation that order parameters of various apparently unrelated systems may display the same type of singular behavior near the transition. These singularities are associated with a certain set of critical exponents which characterizes the universality class of the transition. The subsequent development of powerful theoretical concepts such as scaling, renormalization group, and conformal invariance supported this hypothesis and established universality as a paradigm of equilibrium statistical mechanics.
Because of this success, theoretical physicists are nowadays trying to transfer the idea of universality to nonequilibrium phase transitions. However, in the nonequilibrium case the emerging picture remains less clear. Although universality certainly exists on the level of simple models, the experimental evidence of universal behavior under nonequilibrium conditions is still very poor. Therefore, it is not yet known to what extent the concept of universality can be applied to nonequilibrium critical phenomena.
An important example is the universality class of Directed Percolation (DP) which describes continuous phase transitions from a spreading (wet) phase into an absorbing (dry) state [2]. The DP universality class is extremely robust with respect to the choice of the dynamic rules and covers a large variety of models with applications ranging from catalytic reactions [3] and interface growth [4] to turbulence [5]. The observed robustness led Janssen and Grassberger [6] to the conjecture that a continuous phase transition from a fluctuating active phase into a single absorbing state should belong to the DP universality class, provided that the model uses short-range dynamics without special attributes such as additional symmetries or quenched randomness. In fact, DP is the canonical universality class for nonequilibrium phase transitions into absorbing states. Thus it may be as important as the Ising universality class in equilibrium statistical mechanics.
Despite this success in theoretical statistical physics, the critical behavior of DP, especially the set of critical exponents, has not yet been confirmed experimentally. The lack of experimental evidence is indeed surprising, especially since a large number of possible experimental realizations have been suggested in the past. As Grassberger emphasizes in a summary on open problems in DP [7]:
"...there is still no experiment where the critical behavior of DP was seen. This is a very strange situation in view of the vast and successive theoretical efforts made to understand it. Designing and performing such an experiment has thus top priority in my list of open problems.".
The aim of the present work is to review the most important experiments which have been suggested so far and to discuss their specific problems which could obscure the verification of the critical exponents. After a brief introduction to DP in Sect.II we will first discuss certain catalytic reactions on two-dimensional surfaces which mimic the dynamic rules of DP. As described in Sect. IV, DP may also be realized in certain wetting experiments where the interface between air and liquid undergoes a depinning transition. Another possible realization may be provided by systems of flowing sand on an inclined plane (see Sect. V). However, in none of these experiments could the predicted critical exponents be confirmed convincingly.
What might be the reason for the apparent lack of experimental evidence? It seems that the basic features of DP, which can easily be implemented on a computer, are quite difficult to realize in nature. One of these theoretical assumptions is the existence of an absorbing state. In real systems, however, a perfect non-fluctuating state cannot be realized. For example, a poisoned catalytic surface is not completely frozen, it will rather always be affected by small fluctuations. Although these fluctuations are strongly suppressed, they could still be strong enough to 'soften' the transition, making it impossible to quantify the critical exponents.
Another reason might be the influence of quenched disorder due to spatial or temporal inhomogeneities. In most experiments frozen randomness is expected to play a significant role. For example, a real catalytic surface is not fully homogeneous but characterized by certain defects leading to spatially quenched disorder. As shown in Ref. [8], this type of disorder may affect or even destroy the critical behavior of DP. Technical details concerning quenched disorder are summarized in the Appendix Appendix .
II Directed Percolation
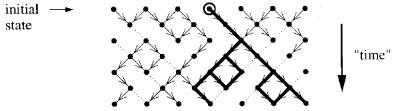
Directed percolation was introduced by Broadbent and Hammersley [9] in 1957 as an anisotropic variant of ordinary percolation [10]. The aim was to describe the connectivity of directed random media such as porous rocks in a gravitational field. Assuming that water can only move downwards, the permeability of a rock will depend on the average connectivity of its pores. One of the simplest models is directed bond percolation. As shown in Fig. 1, neighboring sites (pores) of a diagonal square lattice are connected by bonds (channels) which are open with probability p and otherwise closed. Because of the gravitational field, the bonds function as 'valves' wherefore the spreading agent can only percolate along the given direction, as indicated by the arrows.
Directed bond percolation on a diagonal square lattice. Open (closed) bonds are represented as solid (dashed) lines. The spreading agent, introduced at the site marked by the circle, flows downwards through open bonds, generating a certain cluster (bold bonds).
Depending on the actual configuration of open bonds, each site generates a certain cluster of connected sites. A cluster of this kind would correspond to the maximal spreading range if the water was injected into a single pore. Below a certain threshold p < pc all clusters are finite, i.e., the material is impermeable on large scales. However, above the critical value a cluster may become infinite so that water can percolate over arbitrarily long distances (cf. Fig. 2).
Regarding the given direction as 'time', DP may be interpreted as a d + 1-dimensional dynamic process describing the spreading of some non-conserved agent. For example, we may enumerate the sites in Fig.1 horizontally by a spatial coordinate i and vertically by a discrete time variable t. Then, for a given state at time t, we can determine the state at time t + 1 by means of certain stochastic updates [11].
Interpreting active sites as particles A and inactive sites as vacancies  , the particles can either destroy themselves or produce an offspring. Moreover, if two particles reach the same site, they coagulate to a single particle. Therefore, DP may be regarded as a reaction-diffusion process
, the particles can either destroy themselves or produce an offspring. Moreover, if two particles reach the same site, they coagulate to a single particle. Therefore, DP may be regarded as a reaction-diffusion process
Depending on the ratio between offspring production and self destruction, the process may either remain active or reach the empty state from where it cannot escape. This is the so-called absorbing state of DP systems. For a special realization of DP, the so-called contact process [12], the existence of a continuous transition between survival and extinction could be proven rigorously [13]. Near the transition the stationary density of active sites vanishes as a power law
where b is the critical exponent associated with the order parameter r. Moreover, the DP process is characterized by a spatial and a temporal correlation length diverging at the transition as
As already mentioned, a large variety of models show essentially the same properties at the transition, forming the DP universality class. The DP class corresponds to a specific field theory [14] and is characterized by the three critical exponents b,n^,n||. Despite its simplicity, DP has not yet been solved exactly. However, the critical exponents can easily be estimated by computer simulations. The most accurate estimates are summarized in Table I. Notice that in d > 4 spatial dimensions fluctuations become irrelevant so that the exponents are given by their mean field values.
III Catalytic reactions
It is well known that under specific conditions certain catalytic reactions mimic the microscopic rules of DP models. For example, the Ziff-Gulari-Barshad (ZGB) model, which was designed in order to describe the catalytic reaction CO + O ® CO2 on a platinum surface [3], displays a DP transition. In the ZGB model a gas composed of CO and O2 molecules with fixed concentrations y and 1-y, respectively, is brought into contact with a catalytic material. The catalytic surface is represented by a square lattice whose sites can either be vacant ( ), occupied by a CO molecule, or occupied by an O atom. CO molecules fill any vacant site at rate y, whereas O2 molecules dissociate on the surface into two O atoms and fill pairs of adjacent vacant sites at rate 1-y. Finally, neighboring CO molecules and O atoms recombine instantaneously to CO2 and desorb from the surface. On the lattice the three processes correspond to the reaction scheme
), occupied by a CO molecule, or occupied by an O atom. CO molecules fill any vacant site at rate y, whereas O2 molecules dissociate on the surface into two O atoms and fill pairs of adjacent vacant sites at rate 1-y. Finally, neighboring CO molecules and O atoms recombine instantaneously to CO2 and desorb from the surface. On the lattice the three processes correspond to the reaction scheme
Therefore, if the whole lattice is entirely covered either with CO or O, the system is trapped in a catalytically inactive state. These 'poisoned' states are the two absorbing configurations of the ZGB model. As shown in Fig. 3, the corresponding phase diagram displays two absorbing phases. For y < y1 0.389 the system evolves into the O-poisoned state whereas for y > y2
0.389 the system evolves into the O-poisoned state whereas for y > y2 0.525 it always reaches the CO-poisoned state. Between these two values the model is catalytically active. The two transitions into the absorbing phases are different in character, namely discontinuous at y = y2 and continuous at y = y1 (see Fig. 3). Motivated by the DP conjecture, Grinstein et al. [15] expected the latter to belong to the DP universality class. In order to verify this hypothesis, extensive numerical simulations were performed. Initially it was believed that the critical exponents were different from those of DP [16], while later the transition at y = y1 was found to belong to DP [17]. Very precise estimates of the critical exponents were recently obtained in Ref. [18], confirming the DP conjecture. DP exponents were also obtained in a simplified version of the ZGB model [19]. These theoretical models therefore suggest that certain catalytic reactions could serve as an experimental realization of DP.
0.525 it always reaches the CO-poisoned state. Between these two values the model is catalytically active. The two transitions into the absorbing phases are different in character, namely discontinuous at y = y2 and continuous at y = y1 (see Fig. 3). Motivated by the DP conjecture, Grinstein et al. [15] expected the latter to belong to the DP universality class. In order to verify this hypothesis, extensive numerical simulations were performed. Initially it was believed that the critical exponents were different from those of DP [16], while later the transition at y = y1 was found to belong to DP [17]. Very precise estimates of the critical exponents were recently obtained in Ref. [18], confirming the DP conjecture. DP exponents were also obtained in a simplified version of the ZGB model [19]. These theoretical models therefore suggest that certain catalytic reactions could serve as an experimental realization of DP.
Catalytic reactions in theory (left) and experiment (right). The schematic graphs show the concentrations of oxygen (solid line) and carbon monoxide (dashed line) as a function of the CO adsorption rate.
In real catalytic reactions, however, only the discontinuous transition at y = y2 can be observed. The schematic graph on the right-hand side of Fig. 3 shows the reaction rates as functions of the CO pressure measured in a catalytic reaction on a Pt(210) surface [22]. Although the experiment was designed in order to investigate the technologically interesting regime of high activity close to the first-order phase transition, it clearly indicates that poisoning with oxygen does not occur. Instead the reactivity increases almost linearly with the CO pressure. Similar results were obtained for Pt(111) and for other catalytic materials. Thus, so far there is no experimental evidence for the DP transition predicted by the ZGB model.
One may speculate why the DP transition is obscured or even destroyed under experimental conditions. A possible reason might be the reaction chain being much more complicated than in the ZGB model [23]. Moreover, the O-poisoned system might not be in a perfect absorbing state, i.e., the surface can still adsorb CO molecules although it is satured with carbon monoxide. Another possibility is thermal (nonreactive) desorption of oxygen which - in the DP language - would correspond to spontaneous creation of active sites due to an external field [24]. Finally, defects and inhomogeneities of the catalytic material could lead to an effective (spatially quenched) disorder. As shown in the Appendix Appendix , this type of disorder is marginal. It can therefore seriously affect the critical behavior and even modify the values of the exponents.
For a long time microscopic details were difficult to study experimentally. However, novel techniques such as scanning tunneling microscopy (STM) led to an enormous progress in the understanding of catalytic reactions. They also point at various unexpected subtleties. For example, recent experiments revealed that the reactions preferably take place at the perimeter of oxygen islands [25]. Furthermore, it was observed that the adsorbed CO molecules on Pt(111) may form three different rotational patterns representing the c(4×2) structure of CO on platinum, leading to three competing absorbing states [26]. Moreover, the STM technique allows one to trace individual molecular reactions and to determine the corresponding reaction rates. In addition, the influence of defects such as terraces on catalytic reactions can be quantified experimentally [27]. We may therefore expect a considerable progress in the understanding of catalytic reactions in near future.
IV Growing interfaces
Various models for interface growth exhibit a roughening or depinning transition which can be related to DP. In this Section we discuss three examples, namely transitions of depinning interfaces in random media, polynuclear growth processes, and solid-on-solid growth with evaporation at the edges of plateaus.
IV.1 Depinning transitions
Depinning transitions of driven interfaces provide a very promising class of experiments which could be related to DP [28]. In these experiments a liquid is pumped through a porous medium. If the driving force F is sufficiently low the liquid cannot move through the medium since the air/liquid interface is pinned at certain pores. Above a critical threshold, however, the interface starts moving through the medium with an average velocity v. Close to the transition, v is expected to scale as
where q is the velocity exponent. Moreover, in the moving phase F > Fc the interface roughness averaged over length l should obey the usual scaling law for roughening interfaces [29]
where a is the so-called roughening exponent. One of the first experiments in 1 + 1 dimensions was performed by Buldyrev et al., who studied the wetting of paper in a basin filled with suspensions of ink or coffee [30]. Measuring the interface width they found the roughness exponent a = 0.63(4). In various other experiments the values are scattered between 0.6 and 1.25. This is surprising since the Kardar-Parisi-Zhang (KPZ) class [31, 32], the canonical universality class for roughening interfaces, predicts the exponent a = 1/2 which is smaller than the experimentally observed values.
It is believed that the large values of a are due to inhomogeneities of the porous medium. Due to these inhomogeneities, the interface does not propagate uniformly by local fluctuations as in the KPZ equation, it rather propagates by avalanches. In the literature two universality classes for this type of interfacial growth have been proposed. In case of linear growth the interface should be described by a random field Ising model [33], leading to the exponents a = 1,  = 4/3, and q = 1/3 in 1 + 1 dimensions. In the presence of a KPZ-type nonlinearity, however, the roughening process should exhibit a depinning transition which is related to DP [4, 34]. Notice that the underlying DP mechanism of depinning transitions differs significantly from an ordinary directed percolation process in a porous medium subjected to a gravitational field (cf. Sect. VI). In the latter case the spreading agent is restricted to percolate along a given direction, i.e., the flow is strictly unidirectional. In depinning experiments, however, water may flow both along the pumping force and - even more easily - in the opposite direction, as will be explained below.
= 4/3, and q = 1/3 in 1 + 1 dimensions. In the presence of a KPZ-type nonlinearity, however, the roughening process should exhibit a depinning transition which is related to DP [4, 34]. Notice that the underlying DP mechanism of depinning transitions differs significantly from an ordinary directed percolation process in a porous medium subjected to a gravitational field (cf. Sect. VI). In the latter case the spreading agent is restricted to percolate along a given direction, i.e., the flow is strictly unidirectional. In depinning experiments, however, water may flow both along the pumping force and - even more easily - in the opposite direction, as will be explained below.
A simple model exhibiting a depinning transition is shown in Fig. 4. In this model the pores are represented by cells of a diagonal square lattice. The liquid can flow to neighboring cells by crossing the edges of the cell. Depending on the direction of the flow these edges can either be open or closed. For simplicity we assume that all edges are permeable in downwards direction, whereas in upwards direction they can only be crossed with a certain probability p. Thus, by starting with a horizontal row of wet cells at the bottom, we obtain a compact cluster of wet cells, as illustrated in Fig. 4. The size of the cluster (and therewith the penetration depth of the liquid) depends on p. If p is large enough, the cluster is infinite, corresponding to a moving interface. If p is sufficiently small, the cluster is bound from above, i.e., the interface becomes pinned.
Simple model exhibiting a depinning transition. The pores are represented by cells on a diagonal square lattice. The permeability across the edges of the cells depends on the direction of flow: In the downwards direction all edges are permeable whereas in the upwards direction they are permeable with probability p and impermeable otherwise. The right panel of the figure shows a particular configuration of open (dashed) and closed (solid) edges. Pumping in water from below, the interface becomes pinned along a directed path of solid lines, leading to a finite cluster of wet cells (shaded region). The dashed arrow represents an open path in order to illustrate the flow.
The depinning transition is related to DP as follows. As can seen in the figure, a pinned interface may be interpreted as a directed path along impermeable edges running from one boundary of the system to the other. Obviously, the interface becomes pinned only if there exists a directed path of impermeable bonds connecting the boundaries of the system. Hence the depinning transition is related to an underlying DP process running perpendicular to the direction of growth. The pinning mechanism is illustrated in Fig. 5, where a supercritical DP cluster propagates from left to right. The cluster's backbone, consisting of bonds connecting the two boundaries, is indicated by bold dots. The shaded region denotes the resulting cluster of wet cells. As can be seen, the interface will be pinned at the lowest lying branch of the DP backbone. Therefore, the roughening exponent coincides with the meandering exponent
of the backbone. Moreover, by analyzing the dynamics of the moving interface, it can be shown that the dynamic critical exponents are given by q = a and  = 1. Thus, depinning transitions in inhomogeneous porous media may serve as experimental realizations of the DP universality class.
= 1. Thus, depinning transitions in inhomogeneous porous media may serve as experimental realizations of the DP universality class.
Comparing the prediction (7) with the result a = 0.63(4) obtained by Buldyrev et al. [30] we find an excellent coincidence, confirming the validity of the model introduced above. Therefore, this experiment can be regarded as a first experimental evidence of DP exponents. However, only one exponent has been verified, and it is not fully clear how accurate and reproducible these exponents are. Further experimental effort in this direction would be desirable.
Similar experiments were carried out in 2 + 1 dimensions with a spongy-like material used by florists, as well as fine-grained paper rolls [35]. In this case, however, the exponent a is not related to 2 + 1-dimensional DP, instead it corresponds to the dynamic exponent of percolating directed interfaces in 2 + 1 dimensions. In experiments as well as in numerical simulations a roughness exponent a = 0.50(5) was obtained.
In order to perform a depinning experiment which can easily be reproduced, Dougherty and Carle measured the dynamical avalanche distribution of an air/water interface moving through a porous medium made of glass beads [36]. Assuming an underlying DP process, the distribution P(s) of avalanche sizes s is predicted to behave algebraically. In the experiment, however, a stretched exponential behavior P(s) ~ s-be-s/L is observed even for small flowing rates. The estimates for the exponent b are inconclusive; they depend on the time window of the measurement and vary between -0.5 and 0.85. Even more recently Albert et al. proposed a method allowing to identify the universality class by measuring the propagation velocity of locally tilted parts of the interface [37]. Their results suggest that interfaces propagating in glass beads are not described by a DP depinning process, but to be related instead to the random-field Ising model. From the theoretical point of view this is surprising since linear growth of the interface is a special case which requires fine-tuning of certain parameters. Further experimental effort would be needed to understand these findings.
IV.2 Polynuclear growth
A completely different DP mechanism is responsible for roughening transitions in so-called polynuclear growth (PNG) models [38, 39, 40]. A key feature of PNG models is the use of parallel updates, leading to a maximal propagation velocity of one monolayer per time step. For a high adsorption rate the interface is smooth, propagating at maximal velocity v = 1. Decreasing the adsorption rate below a certain critical threshold, PNG models exhibit a roughening transition to a rough phase with v < 1. In contrast to equilibrium roughening transitions, which only exist in d ³ 2 dimensions, PNG models have a roughening transition even in one spatial dimension.
Probably the simplest PNG model investigated so far is defined by the following dynamic rules [38]. In the first half time step atoms 'nucleate' stochastically at the surface by
In the second half time step the islands grow deterministically in lateral direction by one step. This type of growth may be expressed by the update rule
where j runs over the nearest neighbors of site i.
The relation to DP can be established as follows. Starting from a flat interface hi(0) = 0, let us interpret sites at maximal height hi(t) = t as active sites of a DP process. The adsorption process (8) turns active sites into the inactive state with probability 1-p, while the process (9) resembles offspring production. Therefore, if p is large enough, the interface is smooth and propagates with maximal velocity v = 1. This situation corresponds to the active phase of DP. Therefore, we expect the density of sites at maximal height to scale as
where N denotes the system size. Below a critical threshold, however, the density of active sites at the maximum height hi(t) = t vanishes; the growth velocity is smaller than 1 and the interface evolves into a rough state. Although this mapping to DP is not exact, numerical simulations suggest that it still remains valid on a qualitative level. More specifically, it turns out that PNG models are related to a unidirectionally coupled hierarchy of DP processes [41].
A closely related class of models was introduced in order to describe the growth of colonial organisms such as fungi and bacteria [42], motivated by recent experiments with the yeast Pichia membranaefaciens on solidified agarose film [43]. By varying the concentration of polluting metabolites, different front morphologies were observed. The model proposed in [42] aims to explain these morphological transitions on a qualitative level. A careful analysis of the dynamic rules shows that models for fungal growth and PNG models are very similar in character. They both employ parallel dynamics and exhibit a DP-related roughening transition.
Concerning experimental realizations of PNG models, one major problem - apart from quenched disorder - is the use of parallel updates. The type of update is crucial; by using random-sequential updates the transition is lost since in this case there is no maximum velocity. However, in realistic experiments atoms do not move synchronously, but the adsorption events are rather randomly distributed in time. Therefore, random sequential updates might be more appropriate to describe such experiments. It thus remains an open question to what extent PNG processes can be realized in nature. In fact, it would be interesting to see if PNG can be generalized to random-sequential dynamics.
IV.3 Growth with evaporation at the edges of plateaus
DP-related roughening transitions can also be observed in certain solid-on-solid growth processes with random-sequential updates [44, 45]. As a key feature of these models, atoms may desorb exclusively at the edges of existing layers, i.e., at sites which have at least one neighbor at a lower height. By varying the growth rate, such growth processes display a roughening transition from a non-moving smooth phase to a moving rough phase.
A simple solid-on-solid model for this type of growth is defined by the following dynamic rules [44]: For each update a site i is chosen at random and an atom is adsorbed
or desorbed at the edge of a plateau
Moreover, the growth process is assumed to be restricted, i.e., updates are only carried out if the resulting configuration obeys the constraint
The qualitative behavior of this model is illustrated in Fig. 7. For small q the desorption processes (12) dominate. If all heights are initially set to the same value, this level will remain the bottom layer of the interface. Small islands will grow on top of the bottom layer but will be quickly eliminated by desorption at the island edges. Thus, the interface is effectively anchored to its bottom layer and a smooth phase is maintained. The growth velocity v is therefore zero in the thermodynamic limit. As q is increased, more islands on top of the bottom layer are produced until above qc  0.189, the critical value of q, they merge forming new layers at a finite rate, giving rise to a finite growth velocity. In an infinite system the growth velocity scales near the transition as
0.189, the critical value of q, they merge forming new layers at a finite rate, giving rise to a finite growth velocity. In an infinite system the growth velocity scales near the transition as
Since the propagation velocity fluctuates locally, the interface evolves into a rough state according to the predictions of the KPZ equation. The same type of critical behavior is observed in similar models without the restriction (13).
Restricted solid-on-solid growth model exhibiting a roughening transition from a non-moving smooth to a moving rough phase. Monomers are randomly deposited whereas desorption takes place only at the edges of plateaus.
At the transition the dynamics of the model is related to DP as follows. Starting with a flat interface at zero height, let us consider all sites with hi = 0 as particles A of a DP process. Growth according to Eq. (11) corresponds to spontaneous annihilation A® . Conversely, desorption may be considered as a particle creation process. However, since atoms may only desorb at the edges of plateaus, particle creation requires a neighboring active site, corresponding to offspring production A ® 2A. These rules resemble (although not exactly) the dynamics of a DP process. In contrast to PNG models, the DP process takes place at the bottom layer of the interface. Moreover, the roughening transition does not depend on the use of either parallel or random-sequential updates. However, if composite particles instead of monomers are deposited on the surface, the universality class may change due to additional symmetries [46].
. Conversely, desorption may be considered as a particle creation process. However, since atoms may only desorb at the edges of plateaus, particle creation requires a neighboring active site, corresponding to offspring production A ® 2A. These rules resemble (although not exactly) the dynamics of a DP process. In contrast to PNG models, the DP process takes place at the bottom layer of the interface. Moreover, the roughening transition does not depend on the use of either parallel or random-sequential updates. However, if composite particles instead of monomers are deposited on the surface, the universality class may change due to additional symmetries [46].
With respect to experimental realizations of the dynamic rules (11)-(12) we note that atoms are not allowed to diffuse on the surface. This assumption is rather unnatural since in most experiments the rate for surface diffusion is much higher than the rate for desorption back into the gas phase. Therefore, it will be difficult to realize this type of homoepitaxial growth experimentally. However, in a different setup, the above model could well be relevant [47]. As illustrated in Fig. 8, a laterally growing monolayer could resemble the dynamic rules (11) and 12) by identifying the edge of the monolayer with the interface of the growth model. In this case 'surface diffusion', i.e. diffusion of atoms along the edge of the monolayer, is highly suppressed. Moreover, in single-step systems (such as fcc(100) surfaces) it would also be possible to implement the restriction (13).
Possible experimental realization of the growth process defined in Eqs.(11) and (12) by lateral growth of a monolayer on a substrate.
V Flowing granular matter
It has been shown recently that simple systems of flowing sand on an inclined plane, e.g. the experiments performed by Douady and Daerr [48, 49], could serve as experimental realizations of DP [50]. In the Douady-Daerr experiment glass beads with a diameter of 250-425 mm are poured uniformly at the top of an inclined plane covered by a rough velvet cloth (see Fig. 9). As the beads flow down, a thin layer settles and remains immobile. Increasing the angle of inclination f by Df the layer becomes dynamically unstable, i.e., by locally perturbing the system at the top of the plane an avalanche of flowing granular matter will be generated. In the experiment these avalanches have the shape of a fairly regular triangle with an opening angle q. As the increment Dj decreases, the value of q decreases, vanishing as
with a certain critical exponent x. The experimental results suggest the value x = 1 [49].
In order to explain the experimentally observed triangular form of the avalanches, Bouchaud et al. proposed a mean-field theory based on deterministic equations taking the actual local thickness of the flowing avalanche into account [51]. This theory predicts the exponent x = 1/2. Another explanation assumes that flowing sand may be associated with a nearest-neighbor spreading process [50]. Considering the avalanche as a cluster of active sites while identifying the vertical coordinate of the plane with time and the increment of inclination Dj with p - pc the opening angle is expected to scale as
where n|| and n^ are the scaling exponents of the spreading process under consideration.
Simplified drawing of the Douady-Daerr experiment. At a given angle f a layer of a certain thickness settles. Perturbing the layer locally with a stick leads to an avalanche of flowing sand.
To support this scaling argument, a simple lattice model was introduced which mimics the physics of flowing sand [50]. The model exhibits a transition from an inactive to an active phase with avalanches whose compact shapes reproduce the experimental observations. On laboratory scales the model predicts the exponent x = 1, corresponding to the universality class of compact directed percolation (CDP) which is characterized by the exponents [52]
The CDP behavior, however, is only an initial transient and crosses over to DP after a very long time. Thus the Douady-Daerr experiment - performed on sufficiently large scales - may serve as a physical realization of DP. Irregularities of the layers thickness may affect the spreading properties of avalanches. However, such inhomogeneities can be considered as a kind of spatio-temporally quenched disorder which is irrelevant on large scales (see Appendix Appendix ). Thus, in contrast to the previous examples, the problem of quenched disorder does not play a major role in this type of experiments.
The crossover from CDP to DP is very slow and presently not accessible in the experiments. To illustrate the crossover, two avalanches are plotted on different scales in Fig. 10. The left one represents a typical avalanche within the first few thousand time steps. As can be seen, the cluster appears to be compact. However, as shown in the right panel of Fig. 10, the cluster breaks up into several branches after a very long time. As a precondition for DP behavior, initially compact avalanches should thus be able to break up into several branches. Only then is it worthwhile to optimize the experimental setup and to measure the critical exponents quantitatively.
Typical clusters generated at criticality on small and large scales, illustrating the crossover from CDP to DP.
More recent experimental studies [53] confirm that for high angles of inclination critical avalanches do split up into several branches (see Fig. 11). Yet here the avalanches have no well defined front, the propagation velocity of separate branches rather depends on their thickness. It is therefore no longer possible to interpret the vertical axis as a time coordinate. Moreover, it is not yet known how the spreading process depends on correlations in the initial state. As shown in Ref. [54], such long-range correlations may change the values of certain dynamic critical exponents. However, recent studies of a single rolling grain on an inclined rough plane [55] support that there are presumably no long-range correlations due to a 'memory' of rolling grains. By means of molecular dynamics simulations it was shown that the motion of a rolling grain consists of many small bounces on each grain of the supporting layer. Therefore, the rolling grain quickly dissipates almost all of the energy gain from the previous step and thus forgets its history very fast. For this reason it seems to be unlikely that quenched disorder of the prepared layer involves long-range correlations. Therefore, flowing granular matter seems to be a promising candidate for an experimental realization of DP.
Avalanches splitting up into several branches, observed in recent experiments with high angle of inclination (reprinted with kind permission from A. Daerr).
VI Other Applications
This section discusses other applications which are less promising to serve as experimental realizations of DP, although they are frequently quoted in the literature.
Porous media: One example is percolating water in a porous medium subjected to an external driving force. The medium could be a porous rock in a gravitational field where neighboring pores are connected by channels with a certain probability. Depending on this probability, the penetration depth is either finite or the water may "percolate" over infinitely long distances through the medium. Due to the external driving force, the flow in the medium is assumed to be strictly unidirectional, i.e., the water can only flow downwards (in contrast to the depinning models of Section IV.1). Although this application is quite natural, it is extremely difficult to realize experimentally. For example, by studying natural sandstone a broad distribution of pore sizes was observed [56]. Although these experiments are concerned with isotropic percolation, similar difficulties are expected in the directed case.
Epidemics: Another frequently quoted applications of DP is the spreading of epidemics without immunization [12, 13, 57]. Here infection and recovery resemble the reaction-diffusion scheme (1). If the rate of infection is very low, the infectious disease will disappear after some time. If infections occur more frequently, the disease may spread and survive for a very long time. However, spreading processes in nature are usually not homogeneous enough to reproduce the critical behavior of DP. Moreover, in many realistic spreading processes short-range interactions are no longer appropriate. This situation emerges, for example, when an infectious disease is transported by insects. The motion of the insects is typically not a random walk, rather occasional flights over long distances may occur before the next infection takes place. On the level of theoretical models such long-range interactions may be described by Lévy flights [60], leading to continuously varying critical exponents [61].
Forest fires: A closely related problem is the spreading of forest fires [58]. Tephany et al. studied the propagation of flame fronts on a random lattice both under quiescent conditions and in a wind tunnel [59]. The experimental estimates of the critical exponents at the spreading transition are in rough agreement with the predictions of isotropic and directed percolation, respectively. However, the accuracy of these costly experiments remains limited.
Calcium dynamics: DP transitions may also occur in certain kinetic models for the dynamics of Calcium ions in living cells. Ca2+ ions play an important physiological role as second messenger for various purposes ranging from hormonal release to the activation of egg cells by fertilization [62, 63]. The cell uses nonlinear propagation of increasing intracellular Ca2+ concentration, a so-called calcium wave, as a tool to transmit signals over distances which are much longer than the diffusion length. For example, propagating Ca2+ waves can be observed in the immature Xenopus laevis oocyte [64]. So far theoretical work focused mainly on deterministic reaction-diffusion equations in the continuum which explain various phenomena such as solitary and spiral waves [65]. This mean-field type approach, however, ignores the influence of fluctuations. Yet, near the transition between survival and extinction of Ca2+, activity fluctuations may play an important role. Recently improved models have been introduced which take also the stochastic nature of Calcium release into account [66, 67]. As expected, the transition in one of these models belongs to the DP universality class [67]. However, from the experimental point of view it seems to be impossible to confirm or disprove this conjecture. On the one hand, the size of a living cell is only a few order of magnitude larger than the diffusion length, leading to strong finite-size effects in the experiment. On the other hand, inhomogeneities as well as internal structures of the cell give rise to a completely unpredictable form of quenched noise which may be correlated in space and time. Therefore, it seems to be impossible to identify the universality class of the transition in actual experiments. It would be rather an achievement to find clear evidence for the very existence of a phase transition between survival and extinction of propagating calcium waves. For quantitative experiments, it would be interesting to reproduce the dynamics of Calcium in a well-defined environment, e.g., on an artificial membrane [24].
Directed polymers: DP is also related to the problem of directed polymers [68]. In contrast to DP, which is defined as a local process, the directed polymer problem selects directed paths in a random medium by global optimization. Under certain conditions, namely a bimodal distribution of random numbers, both problems were shown to be closely related [69]. More specifically, the roughness exponent of the optimal path in a directed polymer problem is predicted to cross over from the KPZ value 2/3 to the DP value n||/n^  0.63 at the transition point. Directed polymers were used to describe the propagation of cracks [70]. However, it is rather unlikely that crack experiments can reproduce the tiny crossover from KPZ to DP.
0.63 at the transition point. Directed polymers were used to describe the propagation of cracks [70]. However, it is rather unlikely that crack experiments can reproduce the tiny crossover from KPZ to DP.
Turbulence: Finally, DP has also been considered as a toy model for turbulence. According to Ref. [5], the front between turbulent and laminar flow should exhibit the critical behavior of DP. For example, the velocity of the front should scale algebraically with a combination of DP exponents. However, these predictions are based rather on heuristic arguments than on rigorous results. In fact, in many respects turbulent phenomena show a much richer behavior than DP.
VII Conclusions
Directed percolation has kept theoretical physicists fascinated for more than forty years. Several reasons make directed percolation so appealing. First of all, DP is a very simple model in terms of its dynamic rules. Nevertheless, the DP phase transition turns out to be highly nontrivial. In fact, DP belongs to the very few critical phenomena which have not yet been solved exactly in one spatial dimension. Therefore, the critical exponents are not yet known analytically. High-precision estimates indicate that they might be given rather by irrational than by simple fractional values.
Moreover, DP is extremely robust. It stands for a whole universality class of phase transitions from a fluctuating phase into an absorbing state. In fact, a large variety of models display phase transitions belonging to the DP universality class. Thus, on the theoretical level, DP plays the role of a standard universality class similar to the Ising model in equilibrium statistical mechanics.
In spite of its simplicity, no experiment is known confirming the values of the critical exponents quantitatively. An exception may be the wetting experiment performed by Buldrey et al. where the value of the roughness exponent a coincides with n^/n|| within less than 10%. However, since the results of similar experiments are scattered over a wide range, further experimental effort would be needed in order to confirm the existence of DP in this type of systems.
Apart from difficulties to realize a non-fluctuating absorbing state, a fundamental problem of DP experiments is the emergence of quenched disorder due to certain inhomogeneities of the system. Depending on the type of disorder, even weak inhomogeneities might obscure or even destroy the DP transition. Therefore, the most promising experiments are those where quenched disorder is irrelevant on large scales. This is the case, for example, in wetting experiments (Section IV) and systems of flowing granular matter (Section V).
In spite of all these difficulties, many physicists believe that DP should have a counterpart in reality, mostly because of its simplicity and robustness. Therefore, Grassberger's message remains valid: The experimental realization of DP is an outstanding problem of top priority.
Acknowledgements: I would like to thank R. Dickman for carefully reading the manuscript. I would also like to thank A. Daerr and O. Biham for fruitful suggestions and discussions.
Appendix
A. Quenched disorder
On a coarse-grained scale the temporal evolution of a DP process without quenched disorder is described by the Langevin equation [6]
where z(x, t) denotes an uncorrelated Gaussian noise:
The noise z(x, t) represents the intrinsic fluctuations of the DP process due to the stochastic nature of the dynamic rules. The parameter a controls the rate for offspring production and can be thought of as a being measure of the percolation probability p-pc.
Quenched disorder may be introduced by random variations of the parameter a, i.e., by adding another noise field h:
Thus, the resulting Langevin equation reads
The noise h is quenched in the sense that quantities like the particle density are averaged over many independent realizations of the intrinsic noise z while the disorder field h is kept fixed. In the following we distinguish three different types of quenched disorder:
A. Spatially quenched disorder hs(x).
B. Temporally quenched disorder ht(t).
C. Spatio-temporally quenched disorder hst(x, t).
These variants of quenched disorder differ in how far they affect the critical behavior of DP. In the following we review some of the main results.
A.1 Spatially quenched disorder
For spatially quenched disorder, the noise field h is defined through the correlations
where the bar denotes the average over independent realizations of the disorder field (in contrast to averages á¼ñ over the intrinsic noise z). The parameter g is an amplitude which controls the intensity of disorder. In order to find out whether this type of noise affects the critical behavior of DP, let us consider the properties of the Langevin equation under the scaling transformation
where L is a dilatation factor while z = n||/n^ and c = b/n^ are the critical exponents of DP. In absence of quenched disorder, the Langevin equation turns out to be invariant under rescaling if
where dc = 4 is the upper critical dimension of DP. These values are consistent with the DP mean field exponents b = 1, n^ = 1/2, and n|| = 1, which are valid in d ³ 4 dimensions. Checking the scaling behavior of the additional term rhs in Eq. (21) at the critical dimension, we observe that it scales as
i.e., spatially quenched disorder is a marginal perturbation. Therefore, it may seriously affect the critical behavior at the transition.
The same result is obtained by considering the field-theoretic action. Without quenched noise, DP is described by the action of Reggeon field theory [72]
where y(x, t) represents the local particle density while ['(y)](x, t) denotes the Martin-Siggia-Rosen response field. As shown by Janssen [73], spatially quenched noise can be taken into account by adding the term
By simple power counting we can prove that this additional term is indeed a marginal perturbation. Janssen showed by a field-theoretic analysis that the stable fixed point is shifted to an unphysical region, leading to runaway solutions of the flow equations in the physical region of interest. Therefore, spatially quenched disorder is expected to crucially disturb the critical behavior of DP. The findings are in agreement with earlier numerical results by Moreira and Dickman [74] who reported non-universal logarithmic behavior instead of power laws. Later Cafiero et al. [75] showed that DP with spatially quenched randomness can be mapped onto a non-Markovian spreading process with memory, in agreement with previous results.
From a more physical point of view, spatially quenched disorder in 1+1 dimensional systems was studied by Webman et al. [8]. It turns out that even very weak randomness drastically modifies the phase diagram. Instead of a single critical point one obtains a whole phase of very slow glassy-like dynamics. The glassy phase is characterized by non-universal exponents which depend on the percolation probability and the disorder amplitude. For example, in a supercritical 1+1 dimensional DP process without quenched disorder the boundaries of a cluster propagate at constant velocity v. However, in the glassy phase v decays algebraically with time. The corresponding exponent turns out to vary continuously with the mean percolation probability. The power-law behavior is due to 'blockages' at certain sites where the local percolation probability is small. Similarly, in the subcritical edge of the glassy phase, the spreading agent becomes localized at sites with high percolation probability. In d >1, however, numerical simulations indicate that a glassy phase does not exist.
A.2 Temporally quenched disorder
Temporally quenched disorder is defined by the correlations
In this case the additional term scales as a relevant perturbation rht® L-z/2-crht. Therefore, we expect the critical behavior and the associated critical exponents to change entirely. In the field-theoretic formulation this corresponds to adding a term of the form
The influence of spatio-temporally quenched disorder was investigated in detail by I. Jensen [76]. Employing series expansion techniques he demonstrated that the three exponents b, n^, n|| vary continuously with the disorder strength. Thus the transition no longer belongs to the DP universality class. A field-theoretic explanation of these findings is still missing.
A.3 Spatio-temporally quenched disorder
For spatio-temporally quenched disorder, the noise field h is uncorrelated in both space and time:
In Reggeon field theory, this would correspond to the addition of the term
which is an irrelevant perturbation. Spatio-temporally quenched disorder is expected in systems where each time step is associated with a new set of spatial degrees of freedom. Examples include water in porous media subjected to a gravitational field as well as flowing sand on an inclined plane. In these systems the critical behavior of DP should remain valid on large scales.
References
[1] J. Marro and R. Dickman, Nonequilibrium phase transitions in lattice models Cambridge University Press, Cambridge, 1999).
[2] W. Kinzel, in Percolation Structures and Processes, edited by G. Deutscher, R. Zallen, and J. Adler, Ann. Isr. Phys. Soc. 5 (Adam Hilger, Bristol, 1983), p. 425.
[3] R. M. Ziff, E. Gulari, and Y. Barshad, Phys. Rev. Lett. 56, 2553 (1986).
[4] L. H. Tang and H. Leschhorn, Phys. Rev. A 45, R8309 (1992).
[5] Y. Pomeau, Physica D 23, 3 (1986).
[6] H. K. Janssen, Z. Phys. B 42, 151 (1981); P. Grassberger, Z. Phys. B 47, 365 (1982).
[7] P. Grassberger, Directed percolation: results and open problems, in Nonlinearities in complex Systems, Proceedings of the 1995 Shimla Conference on Complex Systems, edited by S. Puri et al. (Narosa Publishing, New Dehli, 1997).
[8] I. Webman, D. ben-Avraham, A. Cohen, and S. Havlin, Phil. Mag. B 77, 1401 (1998).
[9] S. R. Broadbent and J. M. Hammersley, Proc. Camb. Phil. Soc. 53, 629 (1957).
[10] D. Stauffer and A. Aharony, Introduction to Percolation Theory (Taylor & Francis, London, 1992).
[11] E. Domany and W. Kinzel, Phys. Rev. Lett. 53, 311 (1984).
[12] T. E. Harris, Ann. Prob. 2, 969 (1974).
[13] T. M. Liggett, Interacting Particle Systems (Springer, Berlin, 1985).
[14] P. Grassberger and K. Sundermeyer, Phys. Lett. B 77, 220 (1978). J. L. Cardy and R. L. Sugar, J. Phys. A 13, L423 (1980); H. K. Janssen, Z. Phys. B 42, 151 (1981).
[15] G. Grinstein, Z. W. Lai, and D. A. Browne, Phys. Rev. A 40, 4820 (1989).
[16] P. Meakin, J. Chem. Phys. 93, 2903 (1990).
[17] I. Jensen, H. C. Fogedby, and R. Dickman, Phys. Rev. A 41, 3411 (1990).
[18] C. A. Voigt and R. M. Ziff, Phys. Rev. E 56, R6241 (1997).
[19] T. Aukrust, D. A. Browne, and I. Webman, Phys. Rev. A 41, 5294 (1990).
[20] Currently the most precise estimates for the DP exponents are given in: I. Jensen, cond-mat/9906036 (unpublished).
[21] I. Jensen, Phys. Rev. A 45, R563 (1992).
[22] M. Ehsasi, M. Matloch, O. Frank, J. H. Block, K. Christmann, F. S. Rys, and W. Hirschwald, J. Chem. Phys. 91, 4949 (1989).
[23] R. M. Eiswirth, K. Krischer, and G. Ertl, Appl. Phys. A 51, 79 (1990).
[24] R. Dickman, private communication.
[25] J. Wintterlin, S. Völkening, T. V. W. Janssens, T. Zambelli, and G. Ertl, Science 278, 1931 (1997).
[26] H. Hinrichsen, Phys. Rev. E 55, 219 (1997).
[27] T. Zambelli, J. Wintterlin, J. Trost, and G. Ertl, Science 273, 1688 (1996).
[28] A.L. Barabási and H.E. Stanley, Fractal concepts in surface growth (Cambridge University Press, U.K., 1995).
[29] F. Family and T. Vicsek, J. Phys. A 18, L75 (1985).
[30] S. V. Buldyrev, A. L. Barabási, F. Caserta, S. Havlin, H. E. Stanley, and T. Vicsek, Phys. Rev. A 45, R8313 (1992).
[31] M. Kardar, G. Parisi, and Y.-C. Zhang, Phys. Rev. Lett. 56, 889 (1986).
[32] T. Halpin-Healy and Y.-C. Zhang, Phys. Rep. 254, 215 (1995).
[33] T. Nattermann, S. Stepanow, and L. H. Tang, Journal de Phys. II 2, 1483 (1992).
[34] H. A. Makse, S. Buldyrev, H. Leschhorn, and H. E. Stanley, Europhys. Lett. 41, 251 (1998).
[35] S. V. Buldyrev, A. L. Barabási, S. Havlin, J. Kertész, H. E. Stanley, and H. S. Xenias, Physica A 191, 220 (1992).
[36] A. Dougherty and N. Carle, Phys. Rev. E 58, 2889 (1998).
[37] R. Albert, A. L. Barabási, N. Carle, and A. Dougherty Phys. Rev. Lett. 81, 2926 (1998).
[38] J. Kertész and D. E. Wolf, Phys. Rev. Lett. 62, 2571 (1989).
[39] C. Lehner, N. Rajewsky, D. E. Wolf and J. Kertész, Physica A 164, 81 (1990).
[40] A. Toom, J. Stat. Phys. 74, 91 (1994); ibid 74, 111 (1994).
[41] U.C. Täuber, M.J. Howard, and H. Hinrichsen, Phys. Rev. Lett. 80, 2165 (1998); Y.Y. Goldschmidt, Phys. Rev. Lett. 81, 2178 (1998); Y.Y. Goldschmidt, H. Hinrichsen, M.J. Howard, and U.C. Täuber, Phys. Rev. E 59, 6381 (1999); H.K. Janssen, cond-mat/9901188.
[42] J.M. López and H.J. Jensen, Phys. Rev. Lett. 81, 1734 (1998).
[43] T. Sams, K. Sneppen, M. H. Jensen, C. Ellegaard, B. E. Christensen, and U. T. Thrane, Phys. Rev. Lett. 79, 313 (1997).
[44] U. Alon, M.R. Evans, H. Hinrichsen and D. Mukamel, Phys. Rev. Lett. 76, 2746 (1996);.
[45] U. Alon, M.R. Evans, H. Hinrichsen and D. Mukamel, Phys. Rev. E 57, 4997 (1998).
[46] H. Hinrichsen and G. Ódor, Phys. Rev. Lett. 82,1205 (1999); Phys. Rev. E 60, 3842 (1999).
[47] suggested by O. Biham, private communication.
[48] S. Douady and A. Daerr, in Physics of Dry Granular Media, edited by H. J. Herrmann et al., (Kluwer Academic Publishers, New York, 1998), p.339.
[49] A. Daerr and S. Douady, Nature 399, 241 (1999).
[50] H. Hinrichsen, A. Jiménez-Dalmaroni, Y. Rozov, and E. Domany, preprint cond-mat/9908103, to appear in Phys. Rev. Lett.; preprint cond-mat/9909376, submitted to J. Stat. Phys.
[51] J. P. Bouchaud and M. E. Cates, Granular Matter 1, 101 (1998).
[52] R. Dickman and A. Yu. Tretyakov, Phys. Rev. E 52, 3218 (1995).
[53] A. Daerr, private communication (1999).
[54] H. Hinrichsen and G. Ódor, Phys. Rev. E 58, 311 (1998); Comp. Phys. Comm. 121, 392 (1999).
[55] S. Dippel, G. G. Batrouni, and D. E. Wolf, Phys. Rev. E 54, 6845 (1996).
[56] R. Hilfer, T. Rage, and B. Virgin, Physica A 241, 105 (1997).
[57] D. Mollison, J. Roy. Stat. Soc. B 39, 283 (1977).
[58] E. V. Albano, J. Phys. A 27, L881 (1994).
[59] H. Tephany, J. Nahmias, and J. A. M. S. Duarte, Physica A 242, 57 (1997).
[60] J.-P. Bouchaud and A. Georges, Phys. Rep. 195, 127 (1990).
[61] H. K. Janssen, K. Oerding, F. van Wijland, Eur. Phys. J. B 7, 137 (1999); H. Hinrichsen and M. Howard, Eur. Phys. J. B 7, 635 (1999).
[62] M. J. Berridge, Nature 361, 315 (1993).
[63] J. Keizer, Y.-X. Li, J. Rinzel, and S. Stojilkovic, Mol. Biol. Cell 6, 945 (1995).
[64] J. Lechleiter and D. Clapham, Cell 69, 283 (1992).
[65] L. F. Jaffe, Cell Calcium 14, 736 (1993); M. Falcke, "Inositol 1,4,5-trisphosphate Induced Calcium Waves'', in Transport and Structure in Biophysical and Chemical Phenomena (Springer Verlag, in press).
[66] J. Keizer and G. D. Smith, Bioph. Chem. 72, 87 (1998).
[67] M. Bär, M. Falcke, H. Levine, and L. Tsimring, "Discrete stochastic modeling of calcium channel dynamics'', submitted to Phys. Rev. Lett.
[68] D. A. Huse and C. Henley, Phys. Rev. Lett. 54, 2708 (1985).
[69] E. Perlsman and S. Havlin, The directed polymer - directed percolation transition, preprint cond-mat/9904106.
[70] J. Kertész, V. K. Horváth, and F. Weber, Fractals 1, 67 (1992).
[71] H. Chaté and P. Manneville, in New Trends in Pattern Forming Phenomena, edited P. Coullet and P. Huerre (Plenum press, New York, 1990).
[72] P. Grassberger and K. Sundermeyer, Phys. Lett. B 77, 220 (1978). J. L. Cardy and R. L. Sugar, J. Phys. A 13, L423 (1980); H. K. Janssen, Z. Phys. B 42, 151 (1981).
[73] H. K. Janssen, Phys. Rev. E 55, 6253 (1997).
[74] A. G. Moreira and R. Dickman, Phys. Rev. E 54, 1 (1996); R. Dickman and A. G. Moreira, Phys. Rev. E 57, 5060 (1998).
[75] R. Cafiero, A. Gabrielli, and M. A. Muñoz, Phys. Rev. E 57, 5060 (1998).
[76] I. Jensen, Phys. Rev. Lett. 77, 4988 (1996).
- [1] J. Marro and R. Dickman, Nonequilibrium phase transitions in lattice models Cambridge University Press, Cambridge, 1999).
- [2] W. Kinzel, in Percolation Structures and Processes, edited by G. Deutscher, R. Zallen, and J. Adler, Ann. Isr. Phys. Soc. 5 (Adam Hilger, Bristol, 1983), p. 425.
- [3] R. M. Ziff, E. Gulari, and Y. Barshad, Phys. Rev. Lett. 56, 2553 (1986).
- [4] L. H. Tang and H. Leschhorn, Phys. Rev. A 45, R8309 (1992).
- [5] Y. Pomeau, Physica D 23, 3 (1986).
- [6] H. K. Janssen, Z. Phys. B 42, 151 (1981);
- P. Grassberger, Z. Phys. B 47, 365 (1982).
- [7] P. Grassberger, Directed percolation: results and open problems, in Nonlinearities in complex Systems, Proceedings of the 1995 Shimla Conference on Complex Systems, edited by S. Puri et al. (Narosa Publishing, New Dehli, 1997).
- [8] I. Webman, D. ben-Avraham, A. Cohen, and S. Havlin, Phil. Mag. B 77, 1401 (1998).
- [9] S. R. Broadbent and J. M. Hammersley, Proc. Camb. Phil. Soc. 53, 629 (1957).
- [10] D. Stauffer and A. Aharony, Introduction to Percolation Theory (Taylor & Francis, London, 1992).
- [11] E. Domany and W. Kinzel, Phys. Rev. Lett. 53, 311 (1984).
- [12] T. E. Harris, Ann. Prob. 2, 969 (1974).
- [13] T. M. Liggett, Interacting Particle Systems (Springer, Berlin, 1985).
- [14] P. Grassberger and K. Sundermeyer, Phys. Lett. B 77, 220 (1978).
- J. L. Cardy and R. L. Sugar, J. Phys. A 13, L423 (1980);
- H. K. Janssen, Z. Phys. B 42, 151 (1981).
- [15] G. Grinstein, Z. W. Lai, and D. A. Browne, Phys. Rev. A 40, 4820 (1989).
- [16] P. Meakin, J. Chem. Phys. 93, 2903 (1990).
- [17] I. Jensen, H. C. Fogedby, and R. Dickman, Phys. Rev. A 41, 3411 (1990).
- [18] C. A. Voigt and R. M. Ziff, Phys. Rev. E 56, R6241 (1997).
- [19] T. Aukrust, D. A. Browne, and I. Webman, Phys. Rev. A 41, 5294 (1990).
- [21] I. Jensen, Phys. Rev. A 45, R563 (1992).
- [22] M. Ehsasi, M. Matloch, O. Frank, J. H. Block, K. Christmann, F. S. Rys, and W. Hirschwald, J. Chem. Phys. 91, 4949 (1989).
- [23] R. M. Eiswirth, K. Krischer, and G. Ertl, Appl. Phys. A 51, 79 (1990).
- [25] J. Wintterlin, S. Völkening, T. V. W. Janssens, T. Zambelli, and G. Ertl, Science 278, 1931 (1997).
- [26] H. Hinrichsen, Phys. Rev. E 55, 219 (1997).
- [27] T. Zambelli, J. Wintterlin, J. Trost, and G. Ertl, Science 273, 1688 (1996).
- [28] A.L. Barabási and H.E. Stanley, Fractal concepts in surface growth (Cambridge University Press, U.K., 1995).
- [29] F. Family and T. Vicsek, J. Phys. A 18, L75 (1985).
- [30] S. V. Buldyrev, A. L. Barabási, F. Caserta, S. Havlin, H. E. Stanley, and T. Vicsek, Phys. Rev. A 45, R8313 (1992).
- [31] M. Kardar, G. Parisi, and Y.-C. Zhang, Phys. Rev. Lett. 56, 889 (1986).
- [32] T. Halpin-Healy and Y.-C. Zhang, Phys. Rep. 254, 215 (1995).
- [33] T. Nattermann, S. Stepanow, and L. H. Tang, Journal de Phys. II 2, 1483 (1992).
- [34] H. A. Makse, S. Buldyrev, H. Leschhorn, and H. E. Stanley, Europhys. Lett. 41, 251 (1998).
- [35] S. V. Buldyrev, A. L. Barabási, S. Havlin, J. Kertész, H. E. Stanley, and H. S. Xenias, Physica A 191, 220 (1992).
- [36] A. Dougherty and N. Carle, Phys. Rev. E 58, 2889 (1998).
- [37] R. Albert, A. L. Barabási, N. Carle, and A. Dougherty Phys. Rev. Lett. 81, 2926 (1998).
- [38] J. Kertész and D. E. Wolf, Phys. Rev. Lett. 62, 2571 (1989).
- [39] C. Lehner, N. Rajewsky, D. E. Wolf and J. Kertész, Physica A 164, 81 (1990).
- [40] A. Toom, J. Stat. Phys. 74, 91 (1994); ibid 74, 111 (1994).
- [41] U.C. Täuber, M.J. Howard, and H. Hinrichsen, Phys. Rev. Lett. 80, 2165 (1998);
- Y.Y. Goldschmidt, Phys. Rev. Lett. 81, 2178 (1998);
- Y.Y. Goldschmidt, H. Hinrichsen, M.J. Howard, and U.C. Täuber, Phys. Rev. E 59, 6381 (1999);
- [42] J.M. López and H.J. Jensen, Phys. Rev. Lett. 81, 1734 (1998).
- [43] T. Sams, K. Sneppen, M. H. Jensen, C. Ellegaard, B. E. Christensen, and U. T. Thrane, Phys. Rev. Lett. 79, 313 (1997).
- [44] U. Alon, M.R. Evans, H. Hinrichsen and D. Mukamel, Phys. Rev. Lett. 76, 2746 (1996);.
- [45] U. Alon, M.R. Evans, H. Hinrichsen and D. Mukamel, Phys. Rev. E 57, 4997 (1998).
- [46] H. Hinrichsen and G. Ódor, Phys. Rev. Lett. 82,1205 (1999); Phys. Rev. E 60, 3842 (1999).
- [48] S. Douady and A. Daerr, in Physics of Dry Granular Media, edited by H. J. Herrmann et al., (Kluwer Academic Publishers, New York, 1998), p.339.
- [49] A. Daerr and S. Douady, Nature 399, 241 (1999).
- [50] H. Hinrichsen, A. Jiménez-Dalmaroni, Y. Rozov, and E. Domany, preprint cond-mat/9908103, to appear in Phys. Rev. Lett.; preprint cond-mat/9909376, submitted to J. Stat. Phys.
- [51] J. P. Bouchaud and M. E. Cates, Granular Matter 1, 101 (1998).
- [52] R. Dickman and A. Yu. Tretyakov, Phys. Rev. E 52, 3218 (1995).
- [54] H. Hinrichsen and G. Ódor, Phys. Rev. E 58, 311 (1998); Comp. Phys. Comm. 121, 392 (1999).
- [55] S. Dippel, G. G. Batrouni, and D. E. Wolf, Phys. Rev. E 54, 6845 (1996).
- [56] R. Hilfer, T. Rage, and B. Virgin, Physica A 241, 105 (1997).
- [57] D. Mollison, J. Roy. Stat. Soc. B 39, 283 (1977).
- [58] E. V. Albano, J. Phys. A 27, L881 (1994).
- [59] H. Tephany, J. Nahmias, and J. A. M. S. Duarte, Physica A 242, 57 (1997).
- [60] J.-P. Bouchaud and A. Georges, Phys. Rep. 195, 127 (1990).
- [61] H. K. Janssen, K. Oerding, F. van Wijland, Eur. Phys. J. B 7, 137 (1999);
- H. Hinrichsen and M. Howard, Eur. Phys. J. B 7, 635 (1999).
- [62] M. J. Berridge, Nature 361, 315 (1993).
- [63] J. Keizer, Y.-X. Li, J. Rinzel, and S. Stojilkovic, Mol. Biol. Cell 6, 945 (1995).
- [64] J. Lechleiter and D. Clapham, Cell 69, 283 (1992).
- [65] L. F. Jaffe, Cell Calcium 14, 736 (1993); M. Falcke, "Inositol 1,4,5-trisphosphate Induced Calcium Waves'', in Transport and Structure in Biophysical and Chemical Phenomena (Springer Verlag, in press).
- [66] J. Keizer and G. D. Smith, Bioph. Chem. 72, 87 (1998).
- [67] M. Bär, M. Falcke, H. Levine, and L. Tsimring, "Discrete stochastic modeling of calcium channel dynamics'', submitted to Phys. Rev. Lett.
- [68] D. A. Huse and C. Henley, Phys. Rev. Lett. 54, 2708 (1985).
- [70] J. Kertész, V. K. Horváth, and F. Weber, Fractals 1, 67 (1992).
- [71] H. Chaté and P. Manneville, in New Trends in Pattern Forming Phenomena, edited P. Coullet and P. Huerre (Plenum press, New York, 1990).
- [72] P. Grassberger and K. Sundermeyer, Phys. Lett. B 77, 220 (1978).
- J. L. Cardy and R. L. Sugar, J. Phys. A 13, L423 (1980);
- H. K. Janssen, Z. Phys. B 42, 151 (1981).
- [73] H. K. Janssen, Phys. Rev. E 55, 6253 (1997).
- [74] A. G. Moreira and R. Dickman, Phys. Rev. E 54, 1 (1996);
- R. Dickman and A. G. Moreira, Phys. Rev. E 57, 5060 (1998).
- [75] R. Cafiero, A. Gabrielli, and M. A. Muńoz, Phys. Rev. E 57, 5060 (1998).
- [76] I. Jensen, Phys. Rev. Lett. 77, 4988 (1996).
Appendix
Publication Dates
-
Publication in this collection
17 Oct 2001 -
Date of issue
Mar 2000
History
-
Received
01 Nov 1999