Abstract
Proca's equations for two types of fields in a Dirac's æther with electric conductivity sigma are solved exactly. The Proca electromagnetic fields are assumed with cylindrical symmetry. The background is a static, curved spacetime whose spatial section is homogeneous and has the topology of either the three-sphere S³ or the projective three-space P³. Simple relations between the range of Proca field lambda, the Universe radius R, the limit of photon rest mass mgamma and the conductivity sigma are written down.
Dirac's æther; Proca Field; curved spacetime; three-sphere; projective three-space
Dirac's æther in curved spacetime
ALEXANDRE L. OLIVEIRA1 and ANTONIO F. F. TEIXEIRA2
1Universidade Federal do Rio de Janeiro, Departamento de Astronomia
Observatório do Valongo - 20080-090 Rio de Janeiro, RJ, Brazil
2 Centro Brasileiro de Pesquisas Físicas - 22290-180 Rio de Janeiro, RJ, Brazil
Manuscript received on August 11, 1999; accepted for publication on December 1, 1999;
presented by AFFONSO GUIDÃO GOMES
ABSTRACT
Proca's equations for two types of fields in a Dirac's æther with electric conductivity s are solved exactly. The Proca electromagnetic fields are assumed with cylindrical symmetry. The background is a static, curved spacetime whose spatial section is homogeneous and has the topology of either the three-sphere S 3 or the projective three-space P 3. Simple relations between the range of Proca field l, the Universe radius R, the limit of photon rest mass mg and the conductivity s are written down.
Key words: Dirac's æther, Proca Field, curved spacetime, three-sphere, projective three-space.
INTRODUCTION
The possibility of a nonzero electric conductivity s in cosmic scale (Dirac's æther) has been considered by several authors and in various contexts: Vigier (Vigier 1990), e.g., showed that introducing  in the vacuum is equivalent to attributing a nonzero mass
in the vacuum is equivalent to attributing a nonzero mass  to the photon. Further study of the relation between s and mg was performed by Kar, Sinha and Roy (Kar et al. 1993), who also discussed possible astrophysical consequences of having nonzero mg. More recently, Ahonen and Enqvist (Ahonen & Enqvist 1996) studied the electric conductivity in the hot plasma of the early universe.
to the photon. Further study of the relation between s and mg was performed by Kar, Sinha and Roy (Kar et al. 1993), who also discussed possible astrophysical consequences of having nonzero mg. More recently, Ahonen and Enqvist (Ahonen & Enqvist 1996) studied the electric conductivity in the hot plasma of the early universe.
In this paper we study the time evolution of an electromagnetic field with  ; in the background we assume a curved spacetime together with a constant conductivity
; in the background we assume a curved spacetime together with a constant conductivity  . In the next section we present the three existing classes of exact solutions for the field; they depend on the relative values of s, mg and the curvature of spacetime as given by a constant radius R. In the last section we describe in some detail a set of solutions in which the quantity E
. In the next section we present the three existing classes of exact solutions for the field; they depend on the relative values of s, mg and the curvature of spacetime as given by a constant radius R. In the last section we describe in some detail a set of solutions in which the quantity E
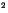 is homogeneous throughout the spacelike hypersurfaces
is homogeneous throughout the spacelike hypersurfaces  .
.
EQUATIONS AND SOLUTIONS
In the static elliptic spacetime we use the cylindrical Schrödinger coordinates  and write the line element
and write the line element
 (1)
(1)
where  is the characteristic radius of the three-geometry. We assume a nonstatic four-potential with cylindrical symmetry
is the characteristic radius of the three-geometry. We assume a nonstatic four-potential with cylindrical symmetry
 (2)
(2)
where  is a function to be determined from the field equations; clearly
is a function to be determined from the field equations; clearly  satisfies the Lorentz gauge,
satisfies the Lorentz gauge,  . The only surviving independent components of
. The only surviving independent components of  are then
are then
 (3)
(3)
where the overdot means the time  derivative. In the orthonormal basis the nonvanishing components of the E and B fields are
derivative. In the orthonormal basis the nonvanishing components of the E and B fields are
 (4)
(4)
Proca equations in a conducting medium are
 (5)
(5)
where  is the electric displacement conductivity,
is the electric displacement conductivity,  is the four-velocity of the observer, l is the range of the Proca field, and
is the four-velocity of the observer, l is the range of the Proca field, and  accounts for two different categories of field. For
accounts for two different categories of field. For  eq.(5) gives
eq.(5) gives
 (6)
(6)
where
 (7)
(7)
Three classes of solutions of (6) exist, depending on the relative values of the constants  (nonnegative) and
(nonnegative) and  (arbitrary); see Table I, where
(arbitrary); see Table I, where  and
and  are integration constants.
are integration constants.
Solutions in which the field energy is homogeneously distributed in three-space are of particular interest. From eqs.(4) we find that the quantity  is independent of
is independent of  only when
only when  , which implies that
, which implies that  , with
, with  . Three non-equivalent sets of solutions with
. Three non-equivalent sets of solutions with  are discussed in the next section, and constraining relations among the quantities
are discussed in the next section, and constraining relations among the quantities  in each set are given.
in each set are given.
DISCUSSION
As is seen from (4), in all solutions the E and B fields are mutually orthogonal and spatially inhomogeneous. The E field is purely azimuthal, vanishes on the  axis (the axis where
axis (the axis where  ), and is maximum along the circle
), and is maximum along the circle  . Oppositely, the B field is purely longitudinal, is maximum along the
. Oppositely, the B field is purely longitudinal, is maximum along the  axis and vanishes on the circle
axis and vanishes on the circle  . These expressions for the fields are globally possible whenever the topology of the underlying
. These expressions for the fields are globally possible whenever the topology of the underlying 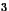 -space is either the simply connected
-space is either the simply connected  -sphere S 3 or the multiply connected real projective
-sphere S 3 or the multiply connected real projective 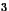 -space P 3. No other multiply connected
-space P 3. No other multiply connected 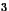 -space endowed with the elliptical geometry (e.g. the Poincaré dodecahedron) seems appropriate to globaly accomodate these forms of field.
-space endowed with the elliptical geometry (e.g. the Poincaré dodecahedron) seems appropriate to globaly accomodate these forms of field.
From Table I we immediately distinguish two static solutions: one is the trivial no-field solution E  B
B  , corresponding to
, corresponding to  ; the other is a pure magnetostatic field with E
; the other is a pure magnetostatic field with E  and
and  , and belongs to class
, and belongs to class  with
with  .
.
All non-static solutions are standing Proca waves. Most have exponential damping with increasing time. Nevertheless, in the class  , an exception deserves mentioning: when
, an exception deserves mentioning: when  , that is
, that is  and
and  in eq.(7), the potential
in eq.(7), the potential  and the Proca fields show an exponential growth as time increases. Three sets of non-static solutions with the quantity
and the Proca fields show an exponential growth as time increases. Three sets of non-static solutions with the quantity  independent on the location in three-space were encountered: see Table II. Sets a and b both have
independent on the location in three-space were encountered: see Table II. Sets a and b both have  (damping along the time), and both contain
(damping along the time), and both contain  ,
,  (a Maxwell field) as a special case. The set c has
(a Maxwell field) as a special case. The set c has  (increasing along the time). Sets b and c both contain the special case
(increasing along the time). Sets b and c both contain the special case  (vanishing conductivity).
(vanishing conductivity).
A few words seem worthwhile, concerning the physical values of the constants  and R. First recall that the mass mg and the range l share the quantum correspondence
and R. First recall that the mass mg and the range l share the quantum correspondence  , where
, where  J s is Planck's constant. Assuming
J s is Planck's constant. Assuming  l.y.
l.y.  m, then
m, then  kg, which is fifteen orders of magnitude smaller than the upper limit obtained by experimental techniques (Goldhaber & Nieto 1971); this amounts to saying that a Proca field with that value for the range l is presently indiscernible from a Maxwell field. From Table II, and still assuming
kg, which is fifteen orders of magnitude smaller than the upper limit obtained by experimental techniques (Goldhaber & Nieto 1971); this amounts to saying that a Proca field with that value for the range l is presently indiscernible from a Maxwell field. From Table II, and still assuming  m, one should have
m, one should have  /s for systems with E
/s for systems with E
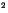 homogeneous over the
homogeneous over the 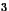 -space; this value for the conductivity coincides in order of magnitude with that of ref. (Kar et al. 1993), obtained in a different context. To conclude, if we consider the above values for the various constants in the damping harmonic class
-space; this value for the conductivity coincides in order of magnitude with that of ref. (Kar et al. 1993), obtained in a different context. To conclude, if we consider the above values for the various constants in the damping harmonic class 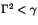 in Table I, then the resulting frequency would be
in Table I, then the resulting frequency would be 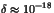 Hz; fields with such a slow variation would seem static.
Hz; fields with such a slow variation would seem static.
ACKNOWLEDGEMENTS
One of us (A.L.O.) wishes to thank Prof. A.O. Caride for calling attention to related work on finite-range theories, Dr. Hirokazu Hori for sending copies of his work on near-field optics and M.F. Carvalho for friendly encouragement and discussions on Dirac's æther.
Correspondence to: A. L. Oliveira
E-mail: alexandr@ov.ufrj.br
- AHONEN J & ENQVIST K. 1996. Electrical conductivity in the early universe. Phys Lett B 382: 40-44.
- GOLDHABER AS & NIETO MM. 1971. Terrestrial and Extraterrestrial Limits on The Photon Mass. Rev Mod Phys 43: 277-296.
- KAR G, SINHA M & ROY S. 1993. Maxwell Equations, Nonzero Photon Mass, and Conformal Metric Fluctuation. Int J Theor Phys 32: 593-607.
- VIGIER JP. 1990. Evidence For Nonzero Mass Photons Associated With a Vacuum-Induced Dissipative Red-Shift Mechanism. IEEE Transactions on Plasma Science 18: 64-72.
Publication Dates
-
Publication in this collection
07 Aug 2000 -
Date of issue
June 2000
History
-
Accepted
01 Dec 1999 -
Received
11 Aug 1999




