Abstracts
This paper assesses empirically the sign of the uncertainty-investment relation in Brazil within a quadratic adjustment cost model. It is shown that these variables are negatively related in the Brazilian economy. The implication is that investment can be enlarged with the adoption of a sustainable macroeconomic policy that rules out uncertainty-yielding shocks, such as a huge devaluation in domestic currency, or defaults in internal and external debts. The paper also proposes a method for estimating the quadratic adjustment cost model when the endogenous variable is I(2) and the forcing variables are I(1). Since capital stock is typically an I(2) variable, the econometric insight seems particularly suited for models of investment.
aggregate investment; quadratic adjustment cost; integrated variables; garch-constructed uncertainty
Este artigo avalia empiricamente o sinal da relação entre investimento e incerteza no Brasil, utilizando o arcabouço dos modelos com custo de ajustamento quadrático. O artigo mostra que essas variáveis são negativamente relacionadas na economia brasileira. A implicação é que o nível de investimento pode ser aumentado com a adoção de uma política macroeconômica sustentável capaz de evitar choques que geram incerteza, como grandes desvalorizações no câmbio ou moratórias nas dívidas interna e externa. Propõe, ainda, um método para estimar o modelo com custo de ajustamento quadrático quando a variável endógena é I(2) e as variáveis exógenas são I(1). Dado que o estoque de capital é tipicamente uma variável I(2), o procedimento econométrico parece particularmente apropriado para modelos de investimento.
Investment and uncertainty in a quadratic adjustment cost model: evidence from Brazil* * This paper was received in Mar. and approved in Aug. 2000. The author is grateful to Afonso Celso Pastore, Fabiana Rocha, Paulo Picchetti, Eustáquio Reis, the participants of the 1st USP/EPGE Macroeconomics Meeting, and two anonymous referees for their helpful comments. He holds himself responsible for the remaining errors.
Rodrigo M. Pereira*** * This paper was received in Mar. and approved in Aug. 2000. The author is grateful to Afonso Celso Pastore, Fabiana Rocha, Paulo Picchetti, Eustáquio Reis, the participants of the 1st USP/EPGE Macroeconomics Meeting, and two anonymous referees for their helpful comments. He holds himself responsible for the remaining errors.
Summary: 1. Introduction; 2. The neoclassical framework; 3. Quadratic adjustment cost models and the stochastic setting; 4. Estimation procedures with integrated variables; 5. Empirical results for investment in Brazil; 6. Conclusions.
Key words: aggregate investment; quadratic adjustment cost; integrated variables; garch-constructed uncertainty.
JEL codes: E22 and C22.
This paper assesses empirically the sign of the uncertainty-investment relation in Brazil within a quadratic adjustment cost model. It is shown that these variables are negatively related in the Brazilian economy. The implication is that investment can be enlarged with the adoption of a sustainable macroeconomic policy that rules out uncertainty-yielding shocks, such as a huge devaluation in domestic currency, or defaults in internal and external debts. The paper also proposes a method for estimating the quadratic adjustment cost model when the endogenous variable is I(2) and the forcing variables are I(1). Since capital stock is typically an I(2) variable, the econometric insight seems particularly suited for models of investment.
Este artigo avalia empiricamente o sinal da relação entre investimento e incerteza no Brasil, utilizando o arcabouço dos modelos com custo de ajustamento quadrático. O artigo mostra que essas variáveis são negativamente relacionadas na economia brasileira. A implicação é que o nível de investimento pode ser aumentado com a adoção de uma política macroeconômica sustentável capaz de evitar choques que geram incerteza, como grandes desvalorizações no câmbio ou moratórias nas dívidas interna e externa. Propõe, ainda, um método para estimar o modelo com custo de ajustamento quadrático quando a variável endógena é I(2) e as variáveis exógenas são I(1). Dado que o estoque de capital é tipicamente uma variável I(2), o procedimento econométrico parece particularmente apropriado para modelos de investimento.
1. Introduction
Investment theory is one of the most recurrent themes in modern macroeconomic research. Understanding the mechanisms that drive investment decision is an issue of great concern for policy prescriptions, considering its direct impact on growth and welfare. It has long been recognized that aggregate investment is affected by uncertainty. However, the direction of this effect still remains to puzzle economists.
In the literature that follows on Jorgenson's (1963, 1967) early models of investment, the sign of the investment-uncertainty relationship depends on assumptions about risk aversion, adjustment costs of capital stock, and market structure (Caballero, 1991). Abel (1983) finds that if a firm is risk-neutral, operates in a competitive market, and faces convex adjustment costs, then an increase in price uncertainty raises investment. The reason is that the profit function is convex in prices, which implies that the average profit tends to be higher with volatile prices, compared to fixed prices.
More recently, there has been a growing literature that focuses on the irreversibility of investment. The main idea is that the resale of capital stock involves large discounts. If firms cannot disinvest when market conditions change adversely that is, if the adjustment cost function is asymmetric , then it may be profitable to wait for new information and postpone the rise in capacity. A higher level of uncertainty tends to assign a larger value to this information. Hence, the option of waiting becomes more attractive. In this case uncertainty can hinder investment. Pindyck (1988) finds that it is plausible, from a theoretical point of view, that uncertainty and investment are negatively related. He argues that firms operating in highly volatile and uncertain markets should hold a lower capacity than firms operating in stable markets. Bertola and Caballero (1994) show that, in the presence of idiosyncratic uncertainty, irreversibility constraints at the microeconomic level are able to rationalize the smoothness and low volatility of aggregate investment series.
Besides these analytical studies, an empirical literature mostly directed to the UK and US economies has examined the investment-uncertainty relationship. These works are surveyed by Carruth and Henley (1999). Although a negative uncertainty effect is most frequently obtained, this empirical literature is far from solving the conflicts of theoretical works. Henley (1999) uses panel data techniques applied to UK industrial companies to show that the uncertainty effect depends on the firm type. Specifically, for less specialized firms, uncertainty tends to increase investment. Servén (1998) constructs several uncertainty measures based on developing countries pooled data and finds negative associations between the uncertainty measures and private investment.
This paper addresses the issue of the investment-uncertainty relationship to quadratic adjustment cost models, a popular framework used to examine the dynamic behavior of economic agents. The model provides theoretical support for an empirical assessment of how uncertainty affects investment. In this regard, the paper estimates a quadratic adjustment cost model for investment using Brazilian data. It has been long recognized that the way of estimating this kind of model varies according to the order of integration of the variables. Kennan (1979) proposes a two-step estimation procedure that uses a partial adjustment rule and the Euler equation to obtain consistent estimates of structural parameters. Yet, Kennan's procedure does not fit to deal with nonstationary variables. Dolado et alii (1991) present estimation strategies that allow for the presence of unit roots. They show that if all variables are integrated of order one (I(1)) or two (I(2)), it is possible to accurately estimate the parameters, improving the estimation method through the previous knowledge of the integration order. Cointegration techniques are used to superconsistently estimate the long-run structural parameters.
The only attempt to estimate the quadratic adjustment cost model for variables with different orders of integration is due to Engsted and Haldrup (1995). They show that, in a context of an I(2) endogenous variable and a mixture of I(1) and I(2) forcing or exogenous variables, not only long-run parameters, but also the adjustment cost parameter can be estimated superconsistently in a nonlinear cointegration regression. The approach, however, does not work if none of the forcing variables is I(2).
The second concern of this paper is to argue that Dolado's approach can be adapted to estimate models with an I(2) endogenous variable and I(1) forcing variables. It departs from the fact that a target for the I(2) stock variable implicitly gives a target for the I(1) flow variable. By assuming that the latter, instead of the former, is linearly related with the forcing variables, it is possible to obtain consistent estimates of the adjustment cost and the speed of adjustment parameters. This insight seems particularly suited for models of investment, since capital stock is usually I(2).
The form of obtaining a measure of uncertainty is another issue focused in the paper. Most of the empirical studies of uncertainty and investment use sample variability as a proxy for uncertainty (see Sérven, 1996, for a rich description of the existing literature). However, this proxy is not precise, provided that rational agents may partly predict fluctuations using information contained in their past behavior. We follow Sérven (1998), adopting an alternative measure of uncertainty, based on the estimation of a generalized conditional heteroskedastic (Garch) model.
The paper is organized as follows. Section 2 presents an overview of the neoclassical model of investment. Differently from the usual setting, we adopt the loss function approach, in which firms are assumed to minimize the present value of their future flow of losses. We use comparative static multipliers to analyze how investment and capital stock are affected in the long run by changes in demand conditions, interest rate and depreciation rate of capital. We introduce the quadratic adjustment cost model for investment in section 3. The use of a discrete time setup and of specific functional forms, as well as the hypothesis that agents form their expectations rationally, eases the link with the empirical work. Section 4 describes how Dolado's estimation procedure can be used with an I(2) endogenous variable and a set of I(1) forcing variables. The empirical evidence for Brazil is presented in section 5. The tests suggest that the Garch-constructed index of uncertainty is negatively related to investment. It is known that uncertainty sharply increases when agents perceive the nearness of an undesirable shock, such as a default in internal debt, a large devaluation of domestic currency, or an increase in trade barriers. Accordingly, the main policy implication is that investment can be strengthened through the avoidance of structural macroeconomic disequilibrium and, consequently, of large shocks. Finally, section 6 concludes the paper.
2. The Neoclassical Framework
The neoclassical theory has always been used to analyze investment behavior. Nevertheless, only since the early 1960's has the theme been discussed more seriously. Important contributions were made by Dale Jorgenson (1963 and 1967), who presented dynamic models in which firms choose time paths for labor and capital.
Although Jorgenson's optimization problem is treated in a dynamic setting, the absence of frictions like adjustment costs leads to straightforward solutions: at each point in time marginal products are equated to the ratio of input to output prices. Specifically, in the case of capital, marginal productivity must be equal to what Jorgenson defines as the user cost of capital.
As a natural extension of Jorgenson's model, subsequent work soon recognized that, unlike many other factor inputs, changes in capital typically involve additional expenditures. Some authors emphasize the consequences of internal adjustment costs, which are determined by technology. Eisner and Strotz (1963) and Lucas (1967) analyze the firm's maximum problem assuming the "fixity" of capital. The first two authors introduce an explicit adjustment cost function, while Lucas modifies the standard production function, allowing for the negative effect of investment in the form of output foregone. The standard example of internal adjustment costs is the acquisition of new machines, that may demand expensive installation procedures and time-consuming worker training sessions. Additionally, the effects of external adjustment costs related to market imperfections are sometimes relevant. The price of capital goods does not necessarily remain constant when the firm decides to increase its capital stock.
Thus, the basic idea is that firms cannot adjust their capital stock to a new desired level immediately and without cost. Although there is no consensus about the specification of the adjustment cost function, the convexity assumption is usually accepted. In this case, it means that costs increase with the size of adjustment. When a deterioration or an improvement of economic environment occurs, firms face a trade-off. If they change the capital stock to the new desired level, they incur adjustment costs. Otherwise, in the absence of adjustments, departures from current to desired levels of capital can be seen as another source of costs. Therefore, the capital level is chosen considering the adequate balance between adjustment costs and the costs of being out of the target level.
In this section we present a dynamic, continuous time model of investment that considers this intertemporal trade-off. To do so, we rely on optimal control techniques. However, instead of considering a firm that maximizes the present value of its future flow of profits, we use the loss function approach. The representative firm is assumed to minimize the present value of its future flow of losses (or, equivalently, to maximize the negative of this present value). Therefore, the optimization problem can be stated as:
subject to
where K is current capital, K* is the desired capital, r is the discount rate, and d is the depreciation rate of capital. The adjustment cost function, C(z), is assumed to satisfy the following conditions: C(0) = 0, C¢(0) = 0, and C¢¢(z) = positive constant. A(z) is a function that relates disequilibrium costs to the difference from current to desired levels of capital. We also suppose that A(z) is convex in K, in a way such that A(0) = 0, A¢(0) = 0, and A¢¢(z) = positive constant. In other words, the marginal cost of being out of the desired level increases with the value of |K-K*|. This function can be described, for instance, by a quadratic form with minimum at K*.
The target level of capital K* is assumed to vary with two forcing variables: an index for the demand conditions in the market where the firm sells its products (good proxies can be the value of sales or an index for physical production) and real interest rates. Formally, we have a function K* = f(Y,r), where Y represents the demand conditions and r the real interest rates, with partial derivatives fY > 0, fr < 0.
The firm chooses optimal paths for current capital stock and investment given the path of the desired capital stock. The current-value Hamiltonian function derived from the optimization problem is given by:
The costate variable q(t) represents the marginal value to the firm of capital in each point in time. Optimality conditions from (2) are:
Equation (4) states that the marginal cost of varying the capital stock should be equal to the firm's evaluation of capital marginal benefit, at each point in time. Equation (5) asserts that the gain of an additional unit of capital in terms of reducing disequilibrium costs (-A¢) must equal its opportunity cost. This consists of the value of forgone interest plus the value of capital depreciation (the higher the need of capital replacement, the lower the attractiveness of investment compared to its opportunity cost) minus eventual changes in the marginal value of capital. In other words, if q increases, the opportunity cost falls because the firm can obtain more by selling the capital. The right-hand side of equation (5) is Jorgenson's user cost of capital. Equation (6) is the transversality condition. Taking the derivative of (4) with respect to time and substituting in (5), we obtain the following expression for investment:
The model dynamics can be better analyzed through a phase diagram. We do this in (K,I) space using expressions (2) and (7). There is a positively sloped  = 0 locus and a negatively sloped
= 0 locus and a negatively sloped  = 0 locus described by I(t) = dK(t) and (d+r) C¢(I(t)) = -A¢(K(t)), respectively.
= 0 locus described by I(t) = dK(t) and (d+r) C¢(I(t)) = -A¢(K(t)), respectively.
Figure 1 shows that these two loci generate the saddle path SS', which is the only set of combinations of I and K that brings the economy to equilibrium E. Any point out of SS¢ does not satisfy optimality conditions (4), (5) and (6). An interesting feature of this model is that with a positive depreciation rate of capital the target level of capital stock, K*, will never be reached in the long run. The intuition behind this fact is easily attained. If the current level of capital is exactly the same as the desired level, then the marginal disequilibrium cost is zero (it is defined that A¢(0) = 0). In addition, the long run equilibrium requires that  = 0, which occurs whenever the marginal gain of capital related to the reduction of disequilibrium costs (-A¢) is equal to the marginal cost of investing multiplied by a constant term ((d+r)C¢). Thus, the only way of setting K = K* in the
= 0, which occurs whenever the marginal gain of capital related to the reduction of disequilibrium costs (-A¢) is equal to the marginal cost of investing multiplied by a constant term ((d+r)C¢). Thus, the only way of setting K = K* in the  = 0 locus is to have a zero level of investment (it is also defined that C¢(0) = 0). However, a positive depreciation rate of capital combined with no gross investment causes a decrease in capital stock. So, this cannot be a long run equilibrium. The steady-state level of capital stock equals the desired level only in the particular case of no depreciation, in which the
= 0 locus is to have a zero level of investment (it is also defined that C¢(0) = 0). However, a positive depreciation rate of capital combined with no gross investment causes a decrease in capital stock. So, this cannot be a long run equilibrium. The steady-state level of capital stock equals the desired level only in the particular case of no depreciation, in which the  = 0 locus is set in the horizontal K axis.
= 0 locus is set in the horizontal K axis.
Comparative static multipliers are useful tools to examine firms' capital accumulation behavior. The idea is to assess long-run effects of changes in demand conditions, real interest rate and depreciation rate over investment and capital stock. By totally differentiating expressions (2) and (7) in the steady-state, we obtain:
According to the assumptions of adjustment cost function, the sign of C¢ depends on the level of investment. More precisely, C' > 0 if and only if I > 0. The former inequality holds in this model because, with a positive depreciation rate, investment is always positive in steady-state. We can write expressions (8) and (9) in a matrix form and use Cramer's rule to determine the sign of the multipliers. Considering D = A''+ d(d+r) C'' > 0, these multipliers are:
The last multiplier in (10) has an ambiguous sign. As expected, demand conditions have a positive long-run effect on both investment and capital stock. In figure 1, an improvement of the demand conditions is represented by an upward shift of the  = 0 locus. Inasmuch as capital stock cannot adjust instantaneously, the investment level jumps, bearing firms to the new saddle path. From this point on, there is a smooth convergence to the new steady-state. Investment clearly overshoots. Intuitively, better demand conditions generate a higher desired level of capital. The current level, however, cannot be fully adjusted in the short run. Then the market value of the existing capital, q, rises, stimulating firms to invest more than replacement needs. Capital stock starts to grow while its value (and also investment) starts to decline. This movement continues until the steady-state is reached.
= 0 locus. Inasmuch as capital stock cannot adjust instantaneously, the investment level jumps, bearing firms to the new saddle path. From this point on, there is a smooth convergence to the new steady-state. Investment clearly overshoots. Intuitively, better demand conditions generate a higher desired level of capital. The current level, however, cannot be fully adjusted in the short run. Then the market value of the existing capital, q, rises, stimulating firms to invest more than replacement needs. Capital stock starts to grow while its value (and also investment) starts to decline. This movement continues until the steady-state is reached.
The second important result from comparative static is that an increase in the interest rate generates a decrease in investment and capital stock. Changes in interest rate have two effects, both acting in the same direction. First, the user cost of capital rises with the interest rate, reducing the attractiveness of investment. Graphically, there is a reduction in the steepness of  = 0 locus. Second, with higher interest rates, firms tend to reduce their desired levels of capital stock. The difference between current and desired levels diminishes, and, as a consequence, the marginal gain in terms of reduction of disequilibrium cost falls compared to the adjustment cost. This is represented by a downward movement of the
= 0 locus. Second, with higher interest rates, firms tend to reduce their desired levels of capital stock. The difference between current and desired levels diminishes, and, as a consequence, the marginal gain in terms of reduction of disequilibrium cost falls compared to the adjustment cost. This is represented by a downward movement of the  = 0 locus.
= 0 locus.
Finally, capital stock tends to fall when the depreciation rate increases. However, the effect on investment is ambiguous. On one side, capital is depreciating at a faster rate. So, investment needs to increase in order to satisfy these higher replacement requirements. On the other side, a higher depreciation rate means a greater user cost of capital, which implies a lower level of investment. The resulting impact on the level of investment depends on which of these two opposite effects prevails.
3. Quadratic Adjustment Cost Models and the Stochastic Setting
In the preceding section, the neoclassical model of investment was analyzed without specific assumptions about agents' expectations of future values of the forcing variables. The representative firm minimizes the present value of its loss stream facing a known future path of the desired level of capital, K*. In this section, instead, we suppose that firms can solely define the most likely path of K* based on their information set. The firm is assumed to use all available information, contained in past values of the relevant variables, to predict the future values based on rational expectations. This leads to a stochastic optimum problem that has a straightforward link with the empirical work. We also introduce specific functional forms for the adjustment cost and for the cost of being out of the desired level of capital. The idea is to employ quadratic functions in the model. As Sargent (1978 and 1987) soon pointed out, quadratic objective functionals have the advantage of generating linear decision rules that in many cases allow optimization to remain a tractable problem.
Similarly to the model of the last section, we suppose a representative firm that sets a target value K* for the capital stock at each point in time. The firm incurs a cost whenever the current capital stock differs from K*. Moreover, there are costs to adjust the current level of capital. We again put these two costs together in a loss function. Using a discrete time setup, the optimization problem becomes:
subject to
where 0 < q < 1 is the discount factor, 0 < d < 1 is the depreciation rate of capital, and a > 0 is the parameter that indicates the relative importance of adjustment to disequilibrium costs. The term Et is the expectations operator conditional on the information set available to the firm at time t. In the restriction for capital accumulation, we assume that investment becomes productive in the subsequent period of its installation. The firm minimizes the present value of its expected flow of losses. The first order condition is given by:
This expression is Euler equation that determines the optimal path for the capital stock. Supposing that the depreciation rate of capital is zero, for the sake of simplicity, and using in (13) the expectations operator conditional on the information set at time t, we have:
where f = [1+a-1+q-1] < 0 and B is an operator defined by B jEt xt = Et xt+j.1 1 Note that the B j operator differs from the widely used L j forward operator. While the latter shifts forward the variable and the information set (that is, L1Et xt = Et+1 xt+1), the former shifts forward the variable but keeps the information set unaltered. We can show that the characteristic polynomial of the preceding equation has real and distinct roots.2 2 Let the characteristic equation be represented by r 2+ t 1 r+ t 2 = 0, with t 1 = f and t 2 = 1/q. The roots are real and distinct if and only if | t 1| > 2q 1/2. This inequality holds as long as (1q 1/2) 2 > 0 for 0 < q < 1, and a 1 > 0. Therefore, (14) can be expressed as:
where  1+
1+ 2 = -f and
2 = -f and  1
1 2 = 1/q. These two equalities together assure that the roots
2 = 1/q. These two equalities together assure that the roots  1 and
1 and  2 are both positive. In addition, it can be seen that (
2 are both positive. In addition, it can be seen that ( 1-1)(
1-1)( 2-1) = -a-1 < 0, which implies one root lower and other higher than one. Solving (15) for the unstable root, say
2-1) = -a-1 < 0, which implies one root lower and other higher than one. Solving (15) for the unstable root, say  2, we obtain the motion equation for the capital stock:
2, we obtain the motion equation for the capital stock:
Current capital stock depends on its immediate past value, as well as on the present and expected future levels of the desired capital stock. A similar expression for investment can be obtained by multiplying both sides of (16) by (B 11), where B is the operator previously defined. This yields
where and It = DKt+1 and  =
=  . Thus, the current level of investment is influenced by its nearest past value and also by the present and expected future levels of the desired investment. However, these desired levels are not observable. In the literature of intertemporal quadratic adjustment cost models, the target of the stock variable is usually assumed to be linearly related with some strictly exogenous forcing variables (Kennan, 1979; Gregory et alii 1990; Dolado et alii 1991; Amano, 1995). We proceed in a slightly different manner, assuming that these forcing variables have a linear relation with the flow variable's target,
. Thus, the current level of investment is influenced by its nearest past value and also by the present and expected future levels of the desired investment. However, these desired levels are not observable. In the literature of intertemporal quadratic adjustment cost models, the target of the stock variable is usually assumed to be linearly related with some strictly exogenous forcing variables (Kennan, 1979; Gregory et alii 1990; Dolado et alii 1991; Amano, 1995). We proceed in a slightly different manner, assuming that these forcing variables have a linear relation with the flow variable's target,  .
.
While the usual assumption states that firms wish to operate with a higher capital stock whenever exogenous market conditions become favorable, our hypothesis goes further. The assumption that desired investment is related to these exogenous terms is just a consequence of our definition of  . If an exogenous term affects desired capital, it will also affect desired investment on the same direction. In the case of a good shock, for example, desired investment increases because the firm intends to reach a higher capital position in the short run and also because the firm faces higher replacement needs of capital in the long run (assuming a constant depreciation rate). The hypothesis of exogenous variables related to investment target is extremely convenient for the empirical implementation of the model, performed in the next two sections of the paper. By that means, we have:
. If an exogenous term affects desired capital, it will also affect desired investment on the same direction. In the case of a good shock, for example, desired investment increases because the firm intends to reach a higher capital position in the short run and also because the firm faces higher replacement needs of capital in the long run (assuming a constant depreciation rate). The hypothesis of exogenous variables related to investment target is extremely convenient for the empirical implementation of the model, performed in the next two sections of the paper. By that means, we have:
where Xt is an (n × 1) vector of observable forcing variables, b is an (n × 1) vector of parameters, and et is a white-noise disturbance that gives the idea that the information set available to the econometrician is smaller than the one available to the firm. Substituting (18) into (17), and using the fact that Et et = et and Et et+i = 0, "i > 0, we have:
where bj, j = 1,2,3,¼,n are the row elements of vector b', and xj,t are the column elements of vector Xt. Supposing that each of the n variables in vector Xt follows an AR(p) process given by r(j)(L)xj,t = mj,t, we use the Wiener-Kolmogorov prediction formula (see appendix AAppendix A ( We have to solve the prediction problem (1q)i Et xj,t+i. If xj,t follows the AR(p) process given by r(j)(L) xj,t = mj,t, the Wiener-Kolmogorov formula states that: ) to obtain:
Without loss of generality, (20) can be stated as:
where p(j)(L) are lag polynomials. Indeed, (21) is a dynamic demand equation that relates current investment to its lagged value and to current and lagged values of the forcing variables.
4. Estimation Procedures with Integrated Variables
The first proposals to estimate quadratic adjustment cost models are due to Sargent (1978) and Kennan (1979). These authors estimate dynamic labor demands using quadratic specifications. Meese (1980), expanded Sargent's model of labor demand to include capital. Unlike Sargent and Meese, who use full information maximum likelihood techniques, Kennan suggested a method based on the estimation of the Euler equation. Kennan's estimation strategy has the advantage of producing consistent estimates of parameters with relatively low computational costs.
None of these works, however, investigates how the nature of the variables affects the specification and estimation approach. Specifically, the order of integration of the forcing variables and its implications are not considered. It has been largely remarked that this procedure is not correct, provided that the hypothesis of stochastic trends absence is implicit in the conventional procedure of eliminating deterministic trends. Dolado et alii (1991) and Gregory et alii (1990) examine alternative estimation strategies that pre-test for the order of integration of the variables. They show that if series contain unit roots, Kennan's procedure should be modified. The reliance on the Euler equation, however, still holds. More recently, Amano (1995) and Amano & Wirjanto (1994) use the same technique suitable to nonstationary series to explain the dynamic behavior of Canadian labor demand and aggregate imports, respectively.
The estimation procedures suggested by Dolado et alii (1991) require that variables have the same order of integration. They must be integrated of order one (I(1)) or, in a slightly modified version of the strategy, of order two (I(2)). Engsted and Haldrup (1995) propose an estimation strategy appropriate for the case of an I(2) endogenous variable and a mixture of I(1) and I(2) forcing variables. In this section we show that when the endogenous variable is I(2) and all the forcing variables are I(1) it is possible to use Dolado's approach to consistently estimate the adjustment cost parameter and the speed of adjustment of the endogenous variable. We rely on the fact that a target stock variable implies a target flow variable. The assumption that the forcing variables are linearly related with the desired flow variable rather than with the desired stock variable allows us to estimate the adjustment cost and speed parameters of capital stock, using a series of investment. Since aggregate investment is typically I(1) implying that capital stock is I(2) , Dolado's procedure for I(1) variables can be used to estimate a model with an I(2) capital stock as the endogenous variable. The first step in the estimation strategy is to define a stochastic process for the forcing variables of vector Xt. For the sake of illustration, suppose that they follow random walk processes. Thus, we have:
where the vector mt has white noise terms as its elements, such that Et mt+i = 0, "i > 0. We are indeed assuming that r(j)(L) = 1L, "j. Taking account that (22) implies Et xj,t+i = xj,t, "i > 0, "j = 1,2,¼,n, and that  1qa1 = (1
1qa1 = (1 1)(1
1)(1 1q),3
3
This equality is obtained by substituting the smallest stable root on the characteristic polynomial, that is,
+
1f+q
-1 = 0.
expression (19) can be written as:
1q),3
3
This equality is obtained by substituting the smallest stable root on the characteristic polynomial, that is,
+
1f+q
-1 = 0.
expression (19) can be written as:
In this equation the forcing variables xj's are I(1), the white noise residual et is I(0), and the stable root  1 lies inside the unit circle. Investment is I(0) if and only if the forcing variables xj's are cointegrated and have b as a particular cointegrating combination. In this particular case the set of forcing variables should be treated as a single I(0) series in (18). If the forcing variables are noncointegrated (or even if they cointegrate but the linear combination used to explain
1 lies inside the unit circle. Investment is I(0) if and only if the forcing variables xj's are cointegrated and have b as a particular cointegrating combination. In this particular case the set of forcing variables should be treated as a single I(0) series in (18). If the forcing variables are noncointegrated (or even if they cointegrate but the linear combination used to explain  is not a cointegrating vector), then investment It must be I(1). Amano (1995) and Amano & Wirjanto (1994) are primarily concerned with this broader situation. Summing
is not a cointegrating vector), then investment It must be I(1). Amano (1995) and Amano & Wirjanto (1994) are primarily concerned with this broader situation. Summing  1Sbj xj,t 1 in both sides of (23) and rearranging the terms, we find:
1Sbj xj,t 1 in both sides of (23) and rearranging the terms, we find:
where nt = (1 1L)1[
1L)1[ 1q a 1et-
1q a 1et-  1
1 = 1bjmj,t]. The term nt clearly is I(0). With It being I(1), equation (24) asserts that there is a stationary linear combination of It and the xj's. In other words, investment and forcing variables cointegrate, with the cointegrating vector given by (1,b1,b2,¼,bn).
= 1bjmj,t]. The term nt clearly is I(0). With It being I(1), equation (24) asserts that there is a stationary linear combination of It and the xj's. In other words, investment and forcing variables cointegrate, with the cointegrating vector given by (1,b1,b2,¼,bn).
The variables to be estimated are the vector of parameters b, the parameter for the relative importance of disequilibrium to adjustment costs, a 1, and the speed of adjustment,  1. There is not a consensus about the capability of quadratic adjustment cost models to estimate the intertemporal discount factor, q. Gregory et alii (1990) show that it is difficult to obtain accurate estimates of this parameter because of identification problems. We begin our estimation procedure by checking the order of integration of the variables. Dickey-Fuller (1979) tests can be properly used to do so. If variables are I(1) we proceed to test for the presence of cointegration using, for example, the method suggested by Johansen (1988). We obtain a superconsistent estimate of vector b if the variables are actually cointegrated. The next step is to employ the Euler equation to obtain a consistent estimate of a1. Multiplying both sides of (13) by (B 11), with the depreciation rate of capital again assumed to be zero, and introducing the forecast error ht+1 = It+1Et It+1, the Euler equation becomes:
1. There is not a consensus about the capability of quadratic adjustment cost models to estimate the intertemporal discount factor, q. Gregory et alii (1990) show that it is difficult to obtain accurate estimates of this parameter because of identification problems. We begin our estimation procedure by checking the order of integration of the variables. Dickey-Fuller (1979) tests can be properly used to do so. If variables are I(1) we proceed to test for the presence of cointegration using, for example, the method suggested by Johansen (1988). We obtain a superconsistent estimate of vector b if the variables are actually cointegrated. The next step is to employ the Euler equation to obtain a consistent estimate of a1. Multiplying both sides of (13) by (B 11), with the depreciation rate of capital again assumed to be zero, and introducing the forecast error ht+1 = It+1Et It+1, the Euler equation becomes:
Substituting (18) into (25) and rearranging terms yields:
where
t+1 = ht+1a 1et and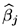 's are the superconsistent estimates of bj's. The series on the left-hand side is obtained through the standard practice of presetting a value for the discount factor q (see, for example, Gregory et alii 1990, and Amano, 1995). OLS applied to (26) does not yield a consistent estimate of a1. The reason is that the residual
's are the superconsistent estimates of bj's. The series on the left-hand side is obtained through the standard practice of presetting a value for the discount factor q (see, for example, Gregory et alii 1990, and Amano, 1995). OLS applied to (26) does not yield a consistent estimate of a1. The reason is that the residual 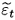 t+1 includes the term et, which is a component of nt, the deviation from long-run equilibrium. Hence, the residual and the regressor are correlated. In this case, the use of instrumental variables procedures is recommended. As Hansen and Sargent (1982) point out, the instruments do not necessarily need to be strictly exogenous with respect to the decision variable. Lags of DIt and Dxj,t are valid instruments for the estimation.
t+1 includes the term et, which is a component of nt, the deviation from long-run equilibrium. Hence, the residual and the regressor are correlated. In this case, the use of instrumental variables procedures is recommended. As Hansen and Sargent (1982) point out, the instruments do not necessarily need to be strictly exogenous with respect to the decision variable. Lags of DIt and Dxj,t are valid instruments for the estimation.
Once a consistent estimate of a1 is obtained, the last task is to estimate the parameter for the speed of adjustment of capital stock,  1. Expression (23) can be converted to an error correction specification given by:
1. Expression (23) can be converted to an error correction specification given by:
A consistent estimate of
1 is obtained by applying non-linear least squares estimation in (27) (Amano, 1995; Phillips & Loretan, 1991).5. Empirical Results for Investment in Brazil
The aim of this section is to estimate the quadratic adjustment cost model parameters for investment demand in the Brazilian economy. Our first task is to obtain reliable series for investment and capital stock in Brazil. Such kind of data set is typically very scarce, with sample spans that often are not large enough to permit statistical inferences. The detailed information regarding the series of aggregate investment and capital stock is in appendix B Appendix B .
Next, we need to define the forcing variables contained in vector Xt. We assume that the target level of investment is linearly related with four forcing variables. The first one is GDP, which serves as an index for demand conditions in economy. The second variable is the price of capital goods, frequently used in investment demand specifications. The series is obtained by dividing the index price for capital goods (named IPA-DI bens de produção) by the general price index (named IGP-DI). The third variable chosen is the real exchange rate. Our quarterly series is derived from the monthly average real exchange rate, in domestic currency per dollar. The exchange rate has two effects on investment. First, it is well known that imports respond for a large part of the capital goods market in Brazil. Thereby, the price of these goods should increase and investment should be hampered with a devaluation of domestic currency. Second, a higher exchange rate rises the competitiveness of the tradable sector, stimulating capital formation. The overall effect on aggregate investment depends on which of these two channels is most important.
Our latest forcing variable is uncertainty. The method used to construct a series of uncertainty deserves to be qualified. A great part of the literature uses sample variation (for example, of a price index) as a measure of uncertainty. The intuition is that when a variable becomes more volatile, it would be more difficult to make accurate predictions about its future values. In other words, uncertainty would increase. Nevertheless, this fact does not necessarily occur. Even sharp movements can be partly predicted from the past values of the variable. Sample variation cannot separate predictable from unpredictable innovations.
Sérven (1998) suggests a more refined measure of uncertainty. The idea is that the proxy for uncertainty should not be the variable's volatility, but rather the volatility of its unpredictable component. Following Sérven (1998), we use the generalized conditional heteroskedastic (Garch) model, first developed by Bollerslev (1986). Unlike conventional econometric models that assume a constant variance for the error term, in Garch specifications the conditional variance of the residual constitutes an Arma process. Using maximum likelihood techniques, it is possible to estimate simultaneously an AR process for the variable and an Arma process for the conditional variance of its unpredictable innovation. Uncertainty is assumed to be the fitted series of this conditional variance. We work with three variables: interest rate, real exchange rate, and price of capital goods. Some of these variables were already used in previous studies.4 4 The relative price of capital goods and the real exchange rate is also used in the panel data analysis of Servén (1998) to construct conditional variances through Garch(1,1) models. Provided that they affect the user cost of capital, the volatility of their innovations seems to be good proxies for uncertainty. We estimate Garch(1,1) models with the variables being described by AR(2) processes without constant nor trend (Schwartz criterion was used to choose the best specification for the AR equation).5 5 For each of the y j,t, j = 1,2,3 variables the Garch(1,1) employed is given by: y j,t = a 1 y j,t-1 + a 2 y j,t2 + u j,t h j,t = b 0 + b 1 ,t1 + c 1 h j, t1 where h j,t, j = 1,2,3 i s the variance of u j,t conditional on information available in period t.
The fitted series of conditional variances are presented in figure 2. Some interesting points should be emphasized. First, in the upper left-hand portion of the graph we can see a large increase in the uncertainty associated with interest rates in 1990Q1, the period of the Brazilian internal public debt default. Second, the uncertainty associated with the price of capital goods decreases persistently from the end of 1990 on. This tendency coincided with the Brazilian commercial openness and the resulting cheapness of capital goods. Once agents regarded reductions in trade barriers as being lasting, uncertainty related to the price of capital goods diminished. Finally, in the lower left-hand part of the graph we can see that the peak value of uncertainty about the real exchange rate occurred in 1983Q2, the period immediately after the domestic currency maxidevaluation of February 1983. Thus, the three series of estimated conditional variance seem to be suited for describing uncertainty. We take the average of these series as our measure of uncertainty.
Next, we pretest capital stock, investment, and the four forcing variables for their order of integration. Table 1 shows the results of augmented Dickey-Fuller tests. The null hypothesis of a unit root cannot be rejected at the 5% level of significance for all the variables in levels. Performing the test on the first differences of the variables, we can see that at the 5% level the null hypothesis is accepted only for the capital stock. These results suggest that investment and the forcing variables are I(1), while capital stock is I(2). This is not surprising since investment and the first difference of capital stock only differ by the depreciation rate (which makes investment slightly higher than the change in capital stock).
Figure 3 presents the six time-series. An inspection on these graphs reveals that there may be a structural break in 1994Q3, when the Real stabilization plan was implemented. This seems plausible especially for the exchange rate and uncertainty series. It is well known that the presence of structural breaks may bias Dickey-Fuller tests toward the nonrejection of the unit root. We performed Perron's test (Perron, 1989) to verify whether the results of table 1 still hold with a structural change. We used the more general version of the test, which posits the null hypothesis of a one-time jump in both the level and drift of a unit root process against the alternative of a one-time change in the slope of the trend and in the intercept of a stationary process. The results are presented in table 2. For all the variables the null hypothesis cannot be rejected even at the 10% level of significance. There is, by that means, strong evidence of the presence of stochastic trends in investment and in the four forcing variables.
Provided that the forcing processes and investment are I(1), we test if they cointegrate, using the Johansen methodology. The results are reported on table 3. The  -trace statistic tests the null hypothesis that there are r or less cointegrating vectors against the alternative of more than r cointegrating vectors. The
-trace statistic tests the null hypothesis that there are r or less cointegrating vectors against the alternative of more than r cointegrating vectors. The  -max statistic has the null hypothesis of r and the alternative of r+1 cointegrating vectors. The test is performed without drift term or constant in the cointegrating relation (indeed, we do not obtain much different results when these parameters are introduced). As shown on the first line of table 3, both statistics reject the null hypothesis of no cointegrating vector at the 1% significance level. In the second line, the two statistics point out that the null hypothesis (r = 1 for
-max statistic has the null hypothesis of r and the alternative of r+1 cointegrating vectors. The test is performed without drift term or constant in the cointegrating relation (indeed, we do not obtain much different results when these parameters are introduced). As shown on the first line of table 3, both statistics reject the null hypothesis of no cointegrating vector at the 1% significance level. In the second line, the two statistics point out that the null hypothesis (r = 1 for  -max and r £ 1 for
-max and r £ 1 for  -trace) cannot be rejected at the usual levels of significance. Thus, there is strong evidence that investment, GDP, real exchange rate, price of capital goods, and uncertainty cointegrate with only one cointegrating vector. The estimated long-run relation is given by:
-trace) cannot be rejected at the usual levels of significance. Thus, there is strong evidence that investment, GDP, real exchange rate, price of capital goods, and uncertainty cointegrate with only one cointegrating vector. The estimated long-run relation is given by:
I = 0.077 + GDP + 0.029 PCG + 0.425 ER - 0.055 UNC
The parameter for GDP has the expected sign. An improvement in demand conditions, which are proxied by GDP, generates increases in investment. Surprisingly, investment and the price of capital goods are positively related. One possible explanation for this unusual result is that a large portion of capital goods supply in Brazil comes from imports, such that changes in exchange rate impact the price of capital goods. In the nontradable sector, an increase in exchange rate yields increases in the prices of some inputs. In the tradable sector, however, besides this bad effect, there is a good effect given by the rise in competitiveness of firms' output. From this perspective, a devaluation of domestic currency works as an incentive to invest - as one can see by the estimated positive coefficient for exchange rate -, in spite of the resulting increase in the price of capital goods.
The most striking result in the estimated long-run relation is that uncertainty has a negative effect on investment. Researchers are far from a consensus on theoretical grounds about the sign of the investment-uncertainty relationship. Some authors emphasize that if profits are a convex function of the variable whose future behavior is uncertain (it is known, for instance, that the profit function is convex in prices), then investment increases with uncertainty (Abel, 1983; Caballero, 1991). The convexity ensures that average profits with fluctuation are at least as large as with stability. There is also a literature that points out the firm-specific nature of capital stock and its implications on the investment-uncertainty relationship. If capital is not easily reversible, highly uncertain environments may depress investment. The possibility of being caught with an unprofitable irreversible project diminishes the attractiveness of investment compared to the option of waiting for more information about future market conditions. Summing up, there are two channels through which uncertainty affects investment. The resulting impact is not straightforward. In spite of that, empirical observation can provide useful information about the sign of the overall effect (Sérven, 1998). The estimated long-run relation suggests that in the Brazilian economy the second channel tends to be more important. This finding is in line with Melo and Júnior (1998), who assess the sign of investment-uncertainty relation using a "naive" measure of uncertainty.
The superconsistent estimate of the cointegrating vector is used to obtain a series of the first term in the right-hand side of (26), which is the deviation from long-run equilibrium. Presetting a value for q and applying instrumental variables in (26), we obtain a consistent estimate of the adjustment parameter, a1. Table 4 presents the results for two different sets of instruments and four sensible values for the discount factor. The estimated value of a1 ranges between 0.1659 and 0.1026, which implies that the cost of adjusting capital stock is from six to 9.7 times more important than the cost of being out of the target level. However, all of these estimates have low significance levels, around 15%.
The last parameter to be estimated is the speed of adjustment of capital stock,
1. Nonlinear least squares estimation in (27) yields a consistent estimate of 1. We find
1. We find 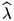 1 = 0.78 (with a t-statistic of 14.801), which is significantly different from zero at the 1% level. Fixing the discount factor q, a value for a1 can be univocally obtained from a1 = (1
1 = 0.78 (with a t-statistic of 14.801), which is significantly different from zero at the 1% level. Fixing the discount factor q, a value for a1 can be univocally obtained from a1 = (1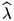 1)(1
1)(1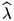 1q)/(
1q)/(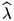 1q). Hence, if q = 0.9, a1 = 0.0965; if q = 0.85, a1 = 0.1153; and if q = 0.8, a1 = 0.1365. These values are close to the estimates of table 4, especially the estimates of the third line, performed with a larger set of instruments. This fact seems to reinforce the reliability of table 4 estimates, despite its low t-statistics.
1q). Hence, if q = 0.9, a1 = 0.0965; if q = 0.85, a1 = 0.1153; and if q = 0.8, a1 = 0.1365. These values are close to the estimates of table 4, especially the estimates of the third line, performed with a larger set of instruments. This fact seems to reinforce the reliability of table 4 estimates, despite its low t-statistics.
An insightful measure of the speed of capital stock adjustment is the median lag, which is obtained by solving  = 0.5 for t. The median lag gives the number of quarters needed by the firm to perform half of the adjustment towards the new desired level of capital stock. We find that it takes 2.74 quarters (or, equivalently, 8.22 months) for 50% of the adjustment to be completed in Brazil. In the literature on dynamic labor demand, the speed of employment adjustment is commonly defined through the median lag. This practice, however, is not much usual in investment studies. Despite the absence of international comparisons for the median lag of capital adjustment, it can be stated that the adjustment in Brazil is relatively fast. Goolsbee and Gross (1997) estimate the costs of adjusting capital using micro-level data of the US airline industry. Their results point to an extremely slow adjustment: it takes about one year for the US airline firms to adjust only 10% of the gap between current and desired levels of capital stock.
= 0.5 for t. The median lag gives the number of quarters needed by the firm to perform half of the adjustment towards the new desired level of capital stock. We find that it takes 2.74 quarters (or, equivalently, 8.22 months) for 50% of the adjustment to be completed in Brazil. In the literature on dynamic labor demand, the speed of employment adjustment is commonly defined through the median lag. This practice, however, is not much usual in investment studies. Despite the absence of international comparisons for the median lag of capital adjustment, it can be stated that the adjustment in Brazil is relatively fast. Goolsbee and Gross (1997) estimate the costs of adjusting capital using micro-level data of the US airline industry. Their results point to an extremely slow adjustment: it takes about one year for the US airline firms to adjust only 10% of the gap between current and desired levels of capital stock.
6. Conclusions
The idea that a sustainable growth inevitably requires large levels of investment is a consensus among economists. In Brazil, the unfavorable growth performance of the 1980's clearly coincides with a shortage in private investment. Thus, the investigation of the reasoning behind investment decision is highly relevant, especially in the Brazilian economy.
This paper has assessed the issue of how uncertainty affects capital accumulation. The sign of the relationship between investment and uncertainty is examined within the framework of quadratic adjustment cost models. Rather than using "naive" measures of uncertainty, such as sample variation, we construct a proxy based on the volatility of the innovations to three key variables: interest rate, price of capital goods, and exchange rate. Garch models are estimated in order to do so. The estimated long-run relation reveals that investment is negatively affected by uncertainty. We also find that investment is positively related with GDP, exchange rate, and price of capital goods. This latter positive association may be a consequence of the correlation between exchange rate and price of capital goods.
The finding that uncertainty hampers investment in Brazil leads to important policy recommendations. It is well known that high levels of uncertainty are essentially induced by structural unbalances in the macroeconomic policy. Thus, the government should carry out a policy with credible commitments about public debt and exchange rate path. In other words, the economy should be kept away from uncertainty-yielding defaults in public debt, or speculative attacks in domestic currency.
This paper also proposes a method for estimating quadratic adjustment cost models when the endogenous variable is I(2) and all the forcing variables are I(1). Indeed, the only modification in the available method for I(1) variables is to assume that the desired investment (which is a flow variable) rather than the desired capital (which is a stock variable) has a linear relationship with the forcing variables. By estimating the quadratic adjustment cost model for investment in Brazil, we have found that the adjustment cost of capital stock is from six to 9.7 times more important than its disequilibrium cost. A value for the median lag of the adjustment is also estimated. The obtained result suggests that in the Brazilian economy the half-way of capital adjustment comes about in 8.22 months. This value indicates that capital stock has a relatively quick adjustment in Brazil.
Eisner, R. & Strotz, R. The determinant of business investment. In: Commission on Money and Credit. Impacts of monetary policy. Englewood Cliffs, Prentice-Hall, 1963.
Enders, W. Applied econometric time series. John Wiley & Sons, 1995.
Engsted, T. & Haldrup, N. Estimating the LQAC model with I(2) variables. University of Aarhus, 1995. (Working Paper, 1996.)
Goolsbee & Gross. Estimating adjustment costs with data on heterogeneous capital goods. 1997. (NBER Working Paper Series, 6.342.)
Gregory, A.; Pagan, A. & Smith, G. Estimating linear quadratic models with integrated processes. In: Philips, Peter (ed.). Essays in honor of Rex Bergstrom. Cambridge, Blackwell Publishers, 1990.
Hansen, L.P. & Sargent, T. Instrumental variables procedures for estimating linear rational expectations models. Journal of Monetary Economics, 9, 1982.
Henley, A. Does uncertainty accelerate or retard investment? Panel data evidence. In: International Colloquium on Economic Dynamics and Economic Policy, 2. Proceedings. Brasília, 1999.
Johansen, S. Statistical analysis of cointegration vectors. Journal of Economic Dynamics and Control, 12, 1988.
Jorgenson, D. Capital theory and investment behavior. American Economic Review, 53(2), May 1963.
______. The theory of investment behavior. In: The determinants of investment behavior. New York, Columbia University Press, 1967.
Kennan, J. The estimation of partial adjustment models with rational expectations. Econometrica, 47, Nov. 1979.
Lucas, R. Adjustment costs and the theory of supply. Journal of Political Economy, 75(4), 1967.
Meese, R. Dynamic factor demand schedules for labor and capital under rational expectations. Journal of Econometrics, 14, 1980.
Melo, G. & Júnior, W. Determinantes do investimento privado no Brasil: 1970-1995. Rio de Janeiro, Ipea, 1998. (Texto para Discussão, 605.)
Perron. The great crash, the oil price shock and the unit root hypothesis. Econometrica, 57, 1989.
Phillips, P. & Loretan, M. Estimating long-run economic equilibria. Review of Economic Studies, 58, 1991.
Pindyck, R. Irreversible investment, capacity choice, and the value of the firm. American Economic Review, 78(5), Dec. 1988.
Sargent, T. Estimation of dynamic labor demand schedules under rational expectations. Journal of Political Economy, 86, 1978.
______. Macroeconomic theory. 2 ed. Academic Press, 1987.
Sérven, L. Irreversibility, uncertainty and private investment: analytical issues and some lessons for Africa. World Bank, 1996. mimeog.
______. Macroeconomic uncertainty and private investment in LDCs: an empirical investigation. World Bank, 1998. (Working Papers, 2.035.)
where s(L) is an MA polynomial that is related to the AR polynomial by r(j)(L) = [s(j)(L)]1 and [ ]+ is the annihilation operator. Omitting the forcing variable index, j, we have:
The last term in brackets is equal to:
Accordingly,
Using the fact that s(L)r(L) = 1 and s( 1q) = [r(
1q) = [r( 1q)]-1, we finally obtain
1q)]-1, we finally obtain
In this appendix we shed some light on the data obtaining method for aggregate investment and capital stock in Brazil. We depart from a fixed capital gross formation quarterly series, drawn from the Ipea-GAC (Instituto de Pesquisa Econômica Aplicada Grupo de Acompanhamento Conjuntural). Our sample is restricted to the period 1980Q1-1998Q4. Although we wish to investigate essentially private agents behavior, the disaggregated information about private investment is not available. The series of the gross formation of fixed capital comprises expenditures in public enterprises and public administration, and also private capital formation. As long as mechanisms that drive investment decision in private and public surroundings are not the same, such an aggregate series can distort results. One can argue, however, that the greatest part of these values (from 70% to 80%, according to the national accounts) refers to private investment.
The investment series does not provide all the information required to construct a series for capital stock. Actually, we need to preset an initial value, K0. In order to do so, we use Castelar and Matesco's (1989) estimates for the capital/product relation in Brazil. In 1979, this relation was 3.36. The initial value for the capital stock is assumed to be this number multiplied by the 1979 GDP value. Thereby, in subsequent periods capital stock is obtained by accumulating investment over K0. We also suppose a depreciation rate of capital of 1% per quarter. This corresponds to a depreciation rate of 4.06% per year, which is in line with current assumptions for this rate in Brazil.
*** Cornell University and Ipea.
- Abel, A. Optimal investment under uncertainty. American Economic Review, 73(1), Mar. 1983
- Amano, R. Empirical evidence on the cost of adjustment and dynamic labor demand Ottawa, Bank of Canada, 1995. (Working Paper, 95-3.)
- ______& Wirjanto, T. The dynamic behavior of Canadian imports and the linear-quadratic model: evidence based on the Euler equation Ottawa, Bank of Canada, 1994. (Working Paper, 94-6.)
- Bertola, G. & Caballero, R. Irreversibility and aggregate investment. Review of Economic Studies, 61, 1994.
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics, 31, 1986.
- Caballero, R. On the sign of the investment-uncertainty relationship. American Economic Review, 81(1), Mar. 1991.
- Carruth, Dickerson & Henley, A. What do we know about investment under uncertainty? Journal of Economic Surveys, 1999.
- Castelar, A. & Matesco, V. Relação capital/produto incremental: estimativas para o período 1948/87. Rio de Janeiro, Ipea, 1989. (Texto para Discussão, 163.)
- Dickey, D. & Fuller, W. Distribution of the estimator for autoregressive time series with a unit root. Journal of the American Statistical Association, 74, 1979.
- Dolado, J.; Galbraith, J. & Banerjee, A. Estimating intertemporal quadratic adjustment cost models with integrated series. International Economic Review, 32, Nov. 1991.
Appendix A
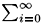 (
(
We have to solve the prediction problem 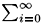 (
( 1q)i Et xj,t+i. If xj,t follows the AR(p) process given by r(j)(L) xj,t = mj,t, the Wiener-Kolmogorov formula states that:
1q)i Et xj,t+i. If xj,t follows the AR(p) process given by r(j)(L) xj,t = mj,t, the Wiener-Kolmogorov formula states that:
Appendix B
 +
+Publication Dates
-
Publication in this collection
16 Aug 2006 -
Date of issue
Apr 2001
History
-
Accepted
Aug 2000 -
Received
Mar 2000






































