Estudo da geometria da uréia por métodos ab initio e simulação computacional de líquidos

Studies of urea geometry by means of ab initio methods and computer simulations of liquids

urea; molecular geometry; Monte Carlo

Artigo

ESTUDO DA GEOMETRIA DA URÉIA POR MÉTODOS AB INITIO E SIMULAÇÃO COMPUTACIONAL DE LÍQUIDOS

José Jair Vianna Cirino

Departamento de Física, Universidade Federal de Juiz de Fora, 36036-330 Juiz de Fora - MG

Celso Aparecido Bertran*

Instituto de Química, Universidade Estadual de Campinas, 13083-970 Campinas - SP

*e-mail: [e-mail]

Recebido em 3/1/01; aceito em 12/9/01

STUDIES OF UREA GEOMETRY BY MEANS OF AB INITIO METHODS AND COMPUTER SIMULATIONS OF LIQUIDS. A study was carried out on the urea geometries using ab initio calculation and Monte Carlo computational simulation of liquids. The ab initio calculated results showed that urea has a non-planar conformation in the gas phase in which the hydrogen atoms are out of the plane formed by the heavy atoms. Free energies associated to the rotation of the amino groups of urea in water were obtained using the Monte Carlo method in which the thermodynamic perturbation theory is implemented. The magnitude of the free energy obtained from this simulation did not permit us to conclude that urea is non-planar in water.

Keywords: urea; molecular geometry; Monte Carlo.

INTRODUÇÃO

A uréia é uma substância que há muito tempo vem sendo estudada por possuir propriedades físico-químicas importantes, especialmente quando forma soluções aquosas de concentrações elevadas. Entre essas propriedades, podemos citar seu poder como desnaturante de proteínas¹, sua ação no aumento da solubilidade de hidrocarbonetos em água², a inibição da formação de agregados micelares³ e a formação de soluções quase ideais com a água⁴.

No campo da química computacional, diversos pesquisadores^5-8 investigaram propriedades termodinâmicas e estruturais das soluções aquosas de uréia por meio de simulação computacional, com a dinâmica molecular e o método de Monte Carlo. Nesses trabalhos a geometria utilizada para a uréia foi a obtida de experimentos de difração de raios X em estado sólido^9-13. Nessas condições a uréia e uma molécula totalmente planar devido aos efeitos do retículo cristalino e das ligações de hidrogênio entre os átomos de oxigênio do grupo carbonila de uma molécula e os átomos de hidrogênio dos grupos amino das outras moléculas de uréia vizinhas. Essas interações são responsáveis pela elevada energia da barreira de rotação de um grupo NH₂ em fase sólida, observada por Sklar¹³, de 125,8 kJ mol^-1e de 108,3 kJ mol^-1 obtida por Saito¹⁴. Em solução aquosa, a barreira rotacional experimental da uréia é de 47,2 kJ mol^-1.

No presente trabalho, investigamos a geometria da uréia tanto em fase gasosa quanto em fase condensada. Há uma forte evidência de que a uréia não é planar em fase gasosa, e pensamos que em fase condensada a geometria da uréia possa estar em uma configuração intermediária entre as geometrias do estado sólido e do estado gasoso. Para estudar as geometrias em fase gasosa utilizamos os programas Gaussian94¹⁷ e Gamess95¹⁸ , enquanto o estudo em fase condensada foi feito com o programa Diadorim²⁰.

METODOLOGIA

Métodos ab initio

Os cálculos ab initio da barreira de potencial foram realizados empregando-se os conjuntos de base 6-31G e 6-311G, em nível HF (Hartree-Fock) e MP2 (Møller-Plesset de 2^a ordem). Esses conjuntos de base são denominados "split valence", o que significa que há duas funções gaussianas para descrever separadamente a parte eletrônica interna e o nível de valência do átomo. O método MP2 é uma das maneiras de se introduzir uma correção na energia total de um sistema para compensar os efeitos da correlação eletrônica.

O conjunto de base 6-31G²⁰ é uma das mais usadas em cálculos ab initio. Nesse conjunto, são usadas 3 funções gaussianas para descrever a estrutura eletrônica dos átomos. A primeira delas é uma contração de 6 gaussianas primitivas e representa a estrutura eletrônica interna. A segunda função é obtida pela contração de 3 gaussianas primitivas, e a terceira é 1 função gaussiana não contraída. A segunda e terceira funções representam a camada de valência do átomo²¹. Por essa razão esse conjunto é denominado 6-31. As funções contraídas são obtidas por combinação linear das gaussianas primitivas. Esse conjunto de base é adequado para estudos de geometrias de moléculas²². O conjunto de base 6-311G²³ (ou MC-311G) tem como principal característica a otimização dos expoentes e coeficientes das gaussianas em nível MP2 para os átomos do primeiro período da tabela periódica para melhor descrição das camadas de valência. Nessa base a estrutura eletrônica interna é representada por uma contração de 6 gaussianas primitivas, e a camada de valência é desdobrada em três funções.

Simulação de líquidos

Em simulação computacional de líquidos o fator mais relevante é o emprego de um modelo matemático que descreva o sistema físico real de interesse da maneira mais realista possível. Os modelos usualmente empregados para a realização de simulações de líquidos são baseados em funções de energia potencial que dependem apenas das coordenadas das moléculas ou dos átomos, do sistema.

A descrição mais comum da energia potencial intermolecular em simulação computacional de Monte Carlo ou dinâmica molecular, é feita pela soma das interações de Coulomb e de Lennard-Jones. Além disso, é feita a aproximação da aditividade de pares, ou seja, a energia de interação entre dois sítios moleculares não é influenciada por um terceiro sítio. A energia de interação entre os sítios i e j localizados em duas moléculas distintas, e separados por distâncias r_ij é dada por,

em que e_kk e s_kk são os parâmetros de Lennard-Jones para um determinado sítio atômico k e q_k é a carga parcial desse sítio atômico. Os parâmetros cruzados e_ij e s_ij são obtidos pela regra de combinação geométrica: e_ij = (e_ie_j)^1/2e s_ij = (s_i s_j)^1/2. Mas, cabe enfatizar que esses parâmetros cruzados também podem ser obtidos pela aplicação da média aritmética²⁴.

A energia entre duas moléculas a e b (E_ab) é obtida pela soma sobre todos os sítios dessas moléculas,

Os parâmetros necessários para definir a Equação 1 podem ser obtidos por meio de métodos semi-empíricos ou ab initio, ou ainda de maneira empírica, fazendo-se ajustes de s, e e cargas de forma a reproduzir algumas propriedades termodinâmicas do líquido, tais como entalpia molar de vaporização (DH_vap), capacidade calorífica a pressão constante (Cp), compressibilidade isotérmica (k_T), coeficiente de expansão isobárica (a_P) e densidade (r).

Energia livre e teoria da perturbação termodinâmica

Energia livre é uma quantidade termodinâmica de suma importância na química e as simulações computacionais podem ser ferramentas poderosas para sua estimativa. O cálculo da energia livre é baseado na equação termodinâmica abaixo, no caso do ensemble NpT²⁵,

A função de partição Z é inacessível computacionalmente de forma que o cálculo direto de G é impraticável. Por outro lado, é possível calcular flutuações de G por meio da teoria da perturbação termodinâmica²⁶. A diferença de energia livre de Gibbs, DG, que acompanha a transformação entre um estado inicial A e um estado final B, pode ser escrita como²⁷,

Uma vez definidos os Hamiltonianos H_A e H_B, o método de Monte Carlo pode ser usado para fazer a média no segundo termo da Equação 5 para cada configuração. O termo á(exp(DH/k_BT)ñ _A indica a média estatística no ensemble de configurações do estado A, denominado estado de referência. Os valores de energia DH são calculados por meio do algoritmo de Metropolis²⁸. Os valores médios são calculados com o uso da Equação 6.

Estados intermediários entre A e B podem ser definidos, fazendo-se a função de potencial intermolecular depender de um parâmetro de acoplamento l, que toma valores discretos no intervalo [0,1], tal que,

A variação total de energia livre é obtida somando-se as contribuições de cada intervalo na variável l_i,

Como a energia livre é uma função de estado, DG_total não depende da escolha do parâmetro l_i. A dependência funcional de H(X) em l é obtida fazendo-se todos os termos do potencial de interação serem funções de l. Dessa forma, a função potencial varia durante a perturbação do sistema entre dois estados.

Então, define-se um novo parâmetro t que varia de acordo com a equação abaixo,

em que i, A e B são os estados de referência, inicial e final, respectivamente. O parâmetro t pode ser usado para causar a variação de cargas atômicas, dos parâmetros de potencial de Lennard-Jones, e também dos parâmetros geométricos de uma molécula, como ângulos e comprimentos de ligação e ângulos diedro.

Cálculos ab initio

Resultados experimentais de difração de nêutrons e raios X indicam que a geometria da uréia no estado sólido é totalmente planar, devido ao efeito do retículo cristalino e das ligações de hidrogênio entre os átomos de oxigênio das carbonilas e os átomos de hidrogênio dos grupos amino, como já foi mencionado anteriormente. Entretanto, trabalhos experimentais^29,30, nos quais a estrutura da uréia é investigada por meio de técnicas espectroscópicas, sugerem que a uréia pode apresentar estrutura não totalmente planar. Brown e col.²⁹ mediram o espectro de microondas da uréia em fase gasosa e baseados na análise desses espectros sugeriram uma estrutura piramidal para os grupos amino, provavelmente devido ao par eletrônico isolado no nitrogênio. King³⁰ realizou estudos espectroscópicos da uréia, também no estado gasoso, na região do infravermelho e concluiu que o grupo NH₂ apresenta-se numa conformação piramidal.

Alguns trabalhos teóricos sugerem que a uréia pode assumir uma geometria não planar no estado gasoso. Cálculos ab initio MP2/6-31G(d)³¹ predizem que a geometria de equilíbrio da uréia é não planar com o grupo amino em conformação piramidal com ângulo diedro HNCO de 137,9^o, e que a barreira rotacional da ligação C-NH₂ é de 30,9 kJ mol^-1.

A Figura 1 mostra a representação de um modelo para a molécula de uréia em sua geometria de equilíbrio, calculada no presente trabalho com a função de onda MP2/6-31G(d), em que os grupos NH₂ têm estrutura piramidal. Os ângulos diedro HNCO são de aproximadamente 13^o nos hidrogênios cis (H_c) e 150^o nos hidrogênios trans (H_t).

Tem sido relatado na literatura a necessidade do uso de conjuntos de base extensas com funções de polarização para descrever a hibridação do nitrogênio e as barreiras de inversão em aminas. Jasien e col.³² concluíram que a inclusão de funções de polarização nos átomos pesados em um conjunto de base "duplo-zeta" é essencial para reproduzir a barreira de potencial experimental da formamida. Boggs e Niu³³ mostraram que as funções de polarização são necessárias para a correta descrição do par isolado sobre o nitrogênio. Os conjuntos de base utilizados para os cálculos ab initio do presente trabalho foram escolhidos para atender a este requisito.

A barreira de potencial para a rotação de uma ligação CNH₂ da uréia foi calculada por meio do programa Gaussian94¹⁷ utilizando-se os conjuntos de base 6-31G(d), 6-31G(d,p) e MC-311G(d,p) em níveis de teoria HF e MP2. A barreira de potencial em torno da ligação C-NH₂ foi obtida por meio da variação do diedro HNCO em intervalos de 10^o_, entre 0^o e 180^o; e a cada mudança do ângulo HNCO foi permitido o relaxamento da molécula.

Na Figura 2 são mostradas as barreiras de potencial calculadas. Os cálculos em nível MP2 com as bases 6-31G(d) e 6-31G(d,p) mostraram resultados praticamente iguais para barreira de rotação. Observou-se o máximo na barreira em aproximadamente 22 kJ mol^-1 (MP2) e 26 kJ mol^-1 (HF), quando o grupo NH₂ é girado de 90^o.

Em cálculos preliminares realizados nesse trabalho, a rotação do grupo NH₂ foi feita de modo que o ângulo HNH fosse mantido fixo. Segundo esse procedimento três variáveis foram mantidas congeladas. A barreira rotacional obtida dessa maneira é mostrada na Figura 3. Nesse gráfico a geometria de mínima energia corresponde a uma torção de 5^o do grupo NH₂, e o máximo da barreira corresponde a 90^o de torção, com valor de 71 kJ mol^-1. Esses valores não estão em concordância com os encontrados em literatura. Portanto, é importante permitir que molécula relaxe a maior parte de suas variáveis durante a rotação. Esta observação esta em acordo com o que foi observado por Kontoyanni e Bowen³⁴.

As geometrias de equilíbrio da uréia em nível MP2 e HF são semelhantes entre si como mostra a Tabela 1, em que são listadas as distâncias de ligação, ângulos de ligação e ângulos diedro. E também são semelhantes à geometria obtida por Meier e Coussens³⁵ com ângulos diedro H_cNCO de 13^o e H_tNCO de 150^o.

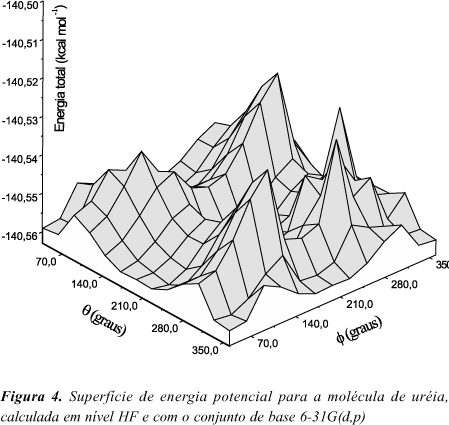
Também foi calculada, no presente trabalho, a superfície de potencial para a rotação simultânea dos dois grupos NH₂. Nesses cálculos um grupo NH₂ foi girado de 360^o, em etapas de 30^o, para cada rotação de 30^o do outro grupo NH₂. No total 68 cálculos foram realizados para a obtenção dos 169 pontos da superfície de potencial. O principal objetivo desses cálculos foi verificar se a energia mínima da barreira de potencial calculada era um ponto de mínimo global na superfície de potencial, a qual é mostrada na Figura 4.

O cálculo da superfície de potencial foi feito em nível HF devido aos bons resultados obtidos para a geometria de equilíbrio, comparados aos resultados em nível MP2 na Tabela 4. Por esta razão, e pelo fato do tempo de computação de um cálculo HF ser consideravelmente menor em relação a um cálculo MP2, consideramos mais adequado realizar cálculos HF para a superfície de potencial da uréia.

A superfície de potencial da Figura 4 mostra que a geometria de mínima energia, obtida nos cálculos da etapa anterior da barreira de potencial de rotação, corresponde de fato a um ponto de mínimo global da superfície de potencial da uréia. Todos os cálculos de otimização de geometria foram realizados sem consideração de simetria molecular para a uréia (C_2V), o que geralmente conduz a geometria da molécula a um mínimo global de energia. Caso fosse usada a condição de simetria seria então necessário recorrer à análise dos modos normais de vibração das moléculas com a geometria resultante da otimização³⁶. Outro aspecto dessa superfície é a ausência de simetria das barreiras de rotação dos grupos NH₂, fato que é explicado pela existência de um par eletrônico sobre o átomo de nitrogênio. A rotação de 180^o não restaura, portanto, a geometria inicial.

Portanto, a uréia parece ser realmente uma molécula não planar em fase gasosa. Entretanto esses cálculos nada predizem no caso da uréia estar inserida em um meio aquoso.

Cálculo da energia livre de Gibbs

Para avaliar a geometria da uréia em meio aquoso calculamos a variação de energia livre de Gibbs associada à rotação dos grupos NH₂ da uréia utilizando o método de Monte Carlo e teoria da perturbação termodinâmica³⁷, que estão implementados no programa DIADORIM¹⁹. O objetivo foi avaliar a contribuição energética do solvente para a rotação dos grupos amino da uréia.

Realizamos a rotação dos grupos amino por meio de um parâmetro geométrico de acoplamento (l) mantendo os demais parâmetros moleulares (r_ij, cargas, e, s) fixos. Com esse cálculo, ainda não explorado em literatura, esperávamos obter uma estimativa da geometria mais provável da uréia em meio aquoso. As simulações foram realizadas no ensemble NpT, a 298 K e 1 atm, com condições periódicas de contorno, convenção de imagem mínima, raio de corte esférico de 1,1 nm e amostragem preferencial próxima ao soluto. Esse valor de raio de corte é típico para simulação de líquidos em que o solvente considerado é a água. Nenhuma correção para as interações de curtas distâncias foi feita além do raio de corte uma vez que estudos prévios mostraram que a contribuição dessa correção é menor que 2% sobre a energia configuracional total do sistema^38,39.

Soluções aquosas infinitamente diluídas foram preparadas a partir de caixas cúbicas de simulação, previamente equilibradas, contendo 360 moléculas de água, em que as três mais próximas do centro da caixa foram substituídas por uma molécula de uréia, que será o soluto do sistema.

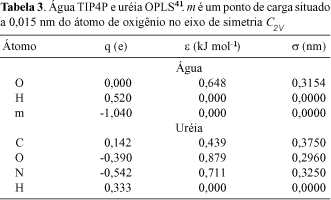
É necessário a retirada de três moléculas de água para acomodar uma de uréia devido à relação entre os volumes das moléculas. Os volumes moleculares foram calculados com o uso do programa GEPOL⁴⁰ e seus valores são 0,131nm³ para a água e 0,290nm³para a uréia. A Tabela 2 mostra os valores dos raios de van der Waals usados para calcular os volumes das moléculas e na Tabela 3 são descritos os modelos de uréia e água utilizados na simulação de energia livre. O modelo de uréia desse estudo não possui nenhum grau de liberdade interna.

Os grupos NH₂ da uréia foram girados em torno da ligação C-NH₂ de F=0^o a 90^o , sendo F o ângulo diedro HNCO. A rotação foi realizada de maneira anti-simétrica, ou seja, um grupo foi girado em um sentido enquanto o outro grupo foi girado no sentido oposto. Para converter a uréia da conformação planar até 90^o, fizemos o parâmetro de acoplamento l, da Equação 9, variar de 0 a 1. Com isso, a função potencial varia quando o parâmetro geométrico F vai do estado inicial (F=0^o) ao estado final (F=90^o), e a Equação 9 pode ser escrita do seguinte modo,

em que F_i (l_i) são estados intermediários.

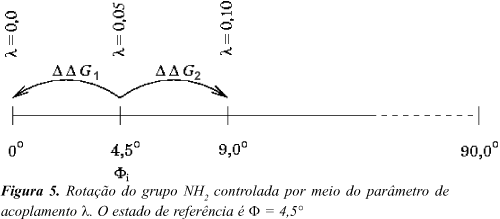
A conversão foi realizada em incrementos de DF_i = 4,5^o a partir da conformação planar e na Figura 5 está ilustrado um trecho da perturbação com os ângulos do estado de referência (F = 4,5^o) e dos estados perturbados (F = 0^o e F = 9^o). A variação da energia livre nesses passos é representada por DDG. A variação de energia livre da rotação de 0 a 9^o é dada pela soma de DDG em cada intervalo: DG = ¾ DDG₁ + DDG₂.

No total 20 simulações foram realizadas resultando em 20 incrementos de energia livre relativa, DDG, cujos resultados são mostrados na Tabela 4. DDG corresponde à variação de energia livre de cada passo da perturbação, como está ilustrado na Figura 5, e DG é a energia livre cumulativa. A partir dos dados dessa tabela pode-se construir um gráfico da variação de DG em função do ângulo de rotação dos grupos NH₂, como mostra a Figura 6. Esses resultados mostraram que a torção dos grupos NH₂, a partir de uma geometria inicial planar, é acompanhada de uma variação positiva de DG de aproximadamente 1,4 kJ mol^-1 quando os grupos amino são girados de 0 a 35^o.

Esse valor de energia livre é muito pequeno, comparado à energia da barreira de potencial em fase gasosa, por exemplo.

Portanto, pode-se afirmar que a rotação dos grupos NH₂ não é desfavorecida, energeticamente, em água. Mas esse resultado por si ainda não permite concluir que a uréia é de fato não totalmente planar em água. O resultado é apenas qualitativo, uma vez que o modelo da uréia apresenta limitações como a ausência de graus de liberdade internos de rotação e também não considera explicitamente os átomos de hidrogênio por meio dos seus parâmetros de Lennard-Jones.

Talvez essas sejam as principais razões para a pequena barreira de rotação obtida na simulação.

CONCLUSÃO

Os cálculos ab initio da barreira rotacional da uréia mostraram que a geometria de menor energia em fase gasosa não é totalmente planar, na qual os átomos de hidrogênio se localizam fora do plano formado pelos átomos pesados da molécula, formando uma estrutura piramidal com o átomo de nitrogênio. Porém, esse resultado é válido apenas para a fase gasosa e não leva em conta nenhum efeito do meio. Obtivemos uma estimativa da influência do meio através do cálculo de DG associado à rotação dos grupos amino da uréia em água. Esse cálculo fornece a influência de um meio discreto sobre a geometria da uréia. Os resultados mostraram que não se pode descartar a possibilidade de se considerar a uréia com geometria não planar em solução devido à pequena magnitude de DG. Ou seja, o solvente não impõe uma barreira energética significativa para a rotação dos grupos NH₂ da uréia em água.

AGRADECIMENTOS

CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico).

FAPEMIG (Fundação de Amparo à Pesquisa do Estado de Minas Gerais).

REFERÊNCIAS

• 1. Brandts, J. F.; Hunts, L. J.; J. Am. Chem. Soc. 1967, 89, 4826.
• 2. Wetlaufer, D. B.; Malik, S. K.; Stoller, L.; Coffin, R. I.; J. Am. Chem. Soc. 1964, 86, 508.
• 3. Shick, M. J.; J. Phys. Chem. 1964, 68, 3585.
• 4. Stokes, R. H.; Aus. J. Chem 1967, 20, 2087.
• 5. Kuharski, R. A.; Rossky, P. J.; J. Am. Chem. Soc 1984 106, 5786.
• 6. Nakanishi, K.; Chem. Soc. Rev. 1993, 177
• 7. Tanaka, H.; Touhara, H.; Nakanishi, K.; Watanabe, N.; J. Chem. Phys 1984, 80, 5170.
• 8. Tanaka, H.; Nakanishi, K.; Touhara, H.; J. Chem. Phys 1984, 82, 5184.
• 9. Swaminathan, S.; Craven, B. M.; McMullan, R. K.; Acta Cryst B 1984, B40, 300.
• 10. Andrew, M. R.; Hyndman, D.; Proc. Phys. Soc. A 1953, 66, 1187.
• 11. Waldron, R. D.; Badger, R. M.; J. Chem. Phys 1953, 66, 1187.
• 12. Warsham, J. E.; Levy, H. A.; Peterson, S. W.; Acta Cryst B 1957, 10, 319.
• 13. Sklar, N.; Senko, M. E.; Post, B.; Acta Cryst. B 1961, 14, 716.
• 14. Saito, Y.; Mashita, K.; Uno, T.; Spectrochim. Acta 1971, A27, 991.
• 15. Stilbs, P.; Forsen, S.; J. Phys. Chem 1971, 75, 1901.
• 16. Strassner, T.; J. Mol. Model 1996, 2, 217.
• 17. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Gill, P. M. W.; Johnson, B. G.; Robb, M. A.; J.R. Cheeseman, T. K.; Petersson, G. A.; Montgomery, J. A.; Raghavachari, K.; Al-Laham, M. A.; Zakrzewski, V. G.; Ortiz, J. V.; Foresman, J. B.; Cioslowski, J.; Stefanov, B. B.; Nanayakkara, A.; Challacombe, M.; Peng, C. Y.; Ayala, P. Y.; Chen, W.; Wong, M. W.; Andres, J. L.; Replogle, E. S.; Gomperts, R.; Martin, R. L.; Fox, D. J.; Binkley, J. S.; Defrees, D. J.; Baker, J.; Stewart, J. J. P.; Head-Gordon, M.; Gonzalez, C.; Pople, J. A.; Gaussian 94, Revision D.2, Gaussian Inc, 1995.
• 18. Schmidt, M. W.; Baldridge, K. K.; Boatz, J. A.; Elbert, S. T.; Gordon, M. S.; Jensen, J. H.; Koseki, S.; Matsunaga, N.; Nguyen, S. J. S.; Windus, T. L.; Dupuis, M.; Montgomery, J. A.; J. Comput. Chem. 1995, 14, 1347.
• 19. Freitas, L. C. G.; Programa Diadorim; Universidade Federal de São Carlos, Brasil, 1992.
• 20. Hehre, W. J.; Ditchfield, R.; Pople, J. A.; J. Chem. Phys 1972, 56, 2257.
• 21. Levine, I. N.; Quantum Chemistry, Prentice Hall: New York, 1991, p. 466.
• 22. Szabó, G. N.; Surján, P. R.; Ángyán, J. G.; Applied Quantum Chemistry; Reidel: Dordrecht, 1987, p. 197.
• 23. Krishnan, R.; Binkley, J. S.; Pople, J. A.; J. Chem. Phys 1980, 72, 650.
• 24. Allen, M. P. Tildesley, D. J.; Computer Simulation of Liquids, Oxford University Press: Oxford, 1987, p. 21.
• 25. Hill, T. L.; An Introduction to Statistical Thermodynamics, Dover: New York, 1986, p. 49.
• 26. Zwanzig, R. W.; J. Chem. Phys 1954, 22, 1420.
• 27. Barlette, V. E.; Tese de Doutorado, Universidade Federal de São Carlos, Brasil, 1996.
• 28. Metropolis, N.; Rosembluth, A. W.; Rosembluth, M. N.; Teller, A. H.; Teller, E.; J. Chem Phys 1953, 21, 1087.
• 29. Brown, R. D.; Godfrey, P. D.; Storey, J.; J. Mol. Spectrosc 1975, 58, 445.
• 30. King, S.; Spectrochim. Acta 1972, 28, 165.
• 31. Gobbi, A.; Frenking, G.; J. Am. Chem. Soc 1993, 115, 2362.
• 32. Jasien, P. G.; Stevens, W. J.; Kraus, M.; J. Mol. Struct. 1986, 139, 197.
• 33. Boggs, J. E.; Niu, Z.; J. Comput. Chem 1985, 6, 46.
• 34. Kontoyanni, M.; Bowen, J. P.; J. Comput. Chem. 1992, 13, 657.
• 35. Meier, R. J.; Coussens, B.; J. Mol. Struct. 1992, 25, 25.
• 36. Hehre, W. J.; Practical Strategies for Electronic Strucure Calculations, Wavefunction Inc.: California, 1995, p. 19.
• 37. Landau, L. D. Lifshitz, E.; Statistical Physics, Pergamon Press: New York, 1980, p. 243.
• 38. Newmann, M.; J. Chem. Phys 1985, 82, 5663.
• 39. Alper, H. E.; Levy, R. M.; J. Chem. Phys 1989, 91, 1242.
• 40. Pascual-Ahuir, J. L.; Silla, E.; Tunon, I.; GEPOL93 (GEometria POLihedro), Universidad de Valencia, Espanha, 1993.
• 41. Duffy, E. M.; Severance, D. L.; Jorgensen, W. L.; Isr. J. Chem. 1993, 33, 323.

Datas de Publicação

• Publicação nesta coleção
  07 Ago 2002
• Data do Fascículo
  Maio 2002

Histórico

• Aceito
  12 Set 2001
• Recebido
  03 Jan 2001