Resumo
The present article is devoted to Chemistry or Physics undergraduate students, given their difficulty to understand fundamental concepts and technical language used in atomic spectroscopy and quantum mechanics. An easy approach is shown in the treatment of the emission spectrum of the sodium atom without any involved calculations. In a previous article, the hydrogen spectrum was considered and the energy degeneracy of the angular momentum quantum number was observed. For the sodium spectrum, due to the valence electron penetration into internal shells, a breakdown of this degeneracy occurs and a dependence of this penetration on the angular momentum quantum number is observed. The eigenvalues are determined introducing the quantum defect correction (Rydberg correction) in the denominator of the Balmer equation, and the energy diagram is obtained. The intensity ratio for the observed doublets is explained by introducing new wave functions, containing the magnetic quantum number of the total angular momentum.
sodium; spectral series; eigenvalues
sodium; spectral series; eigenvalues
EDUCAÇÃO
Uma introdução à espectroscopia atômica. II - o espectro do sódio
An introduction to atomic spectroscopy. II - the sodium spectrum
Oswaldo Sala* * e-mail: oswsala@iq.usp.br
Departamento de Química Fundamental, Universidade de São Paulo, CP 26077, 05599-970 São Paulo SP, Brasil
ABSTRACT
The present article is devoted to Chemistry or Physics undergraduate students, given their difficulty to understand fundamental concepts and technical language used in atomic spectroscopy and quantum mechanics. An easy approach is shown in the treatment of the emission spectrum of the sodium atom without any involved calculations. In a previous article, the hydrogen spectrum was considered and the energy degeneracy of the angular momentum quantum number was observed. For the sodium spectrum, due to the valence electron penetration into internal shells, a breakdown of this degeneracy occurs and a dependence of this penetration on the angular momentum quantum number is observed. The eigenvalues are determined introducing the quantum defect correction (Rydberg correction) in the denominator of the Balmer equation, and the energy diagram is obtained. The intensity ratio for the observed doublets is explained by introducing new wave functions, containing the magnetic quantum number of the total angular momentum.
Keywords: sodium; spectral series; eigenvalues.
INTRODUÇÃO
Em artigo anterior1 foi examinado o espectro atômico do hidrogênio, considerando o modelo de órbitas circulares do elétron ao redor do núcleo. Foram obtidas as expressões para as séries espectrais e para os níveis de energia (autovalores), em função do número quântico principal n. Sommerfeld considerou o modelo de órbitas elípticas para este átomo, havendo neste modelo duas variáveis, a distância do elétron ao núcleo e o ângulo de seu raio vetor com o semi-eixo maior da elipse. Para órbitas circulares Bohr introduziu a quantização do momento angular mas para órbitas elípticas, além da quantização do momento angular, é necessário considerar a quantização do momento linear, pois na elipse o raio não é constante. Isto dá origem a dois números quânticos, o radial, nr, e o do momento angular, k (k=1, 2, ...), sendo o número quântico principal n definido como n = k+  .
.
Sommerfeld mostrou que o número quântico n é uma medida do eixo maior da elipse e k é uma medida do eixo menor; atualmente o número quântico k foi substituído pelo número quântico do momento angular  , que pode ter valores 0, 1, 2,...n. Foi definida uma nova função de onda, envolvendo n e
, que pode ter valores 0, 1, 2,...n. Foi definida uma nova função de onda, envolvendo n e  , e para um mesmo valor de n devem aparecer vários subníveis, com diferentes valores de
, e para um mesmo valor de n devem aparecer vários subníveis, com diferentes valores de  . No diagrama dos níveis de energia, para n=1 existirá somente um nível, com
. No diagrama dos níveis de energia, para n=1 existirá somente um nível, com  =0. Para n=2 comparecem dois níveis, com
=0. Para n=2 comparecem dois níveis, com  =0 e
=0 e  =1; para n=3 existem três níveis, para
=1; para n=3 existem três níveis, para  =0,
=0,  =1 e
=1 e  =2 etc. As transições devem obedecer as regras de seleção, sendo que para o número quântico n não há restrições (Dn = 0, 1, 2...) e para o número quântico
=2 etc. As transições devem obedecer as regras de seleção, sendo que para o número quântico n não há restrições (Dn = 0, 1, 2...) e para o número quântico  só pode haver variação por uma unidade (D
só pode haver variação por uma unidade (D = ±1).
= ±1).
Neste modelo de órbitas elípticas são obtidos, contudo, os mesmos valores de energia do modelo de órbitas circulares, ou seja, a energia não depende do número quântico do momento angular  , os autovalores para diferentes valores de
, os autovalores para diferentes valores de  e um mesmo valor de n são iguais; os estados para estas diferentes funções de onda são ditos degenerados. Como esperávamos resultado diferente para órbitas elípticas, poderíamos supor que este modelo não fosse correto. Para decidir esta questão convém examinar os espectros de emissão de metais alcalinos e consideraremos, como exemplo, o átomo de sódio.
e um mesmo valor de n são iguais; os estados para estas diferentes funções de onda são ditos degenerados. Como esperávamos resultado diferente para órbitas elípticas, poderíamos supor que este modelo não fosse correto. Para decidir esta questão convém examinar os espectros de emissão de metais alcalinos e consideraremos, como exemplo, o átomo de sódio.
ESPECTRO DE EMISSÃO DO SÓDIO
O número atômico do sódio é 11, havendo duas camadas eletrônicas completas, uma com dois e a outra com oito elétrons, com um total de dez elétrons que blindam a carga nuclear, ficando o elétron de valência submetido à carga +1, como no átomo de hidrogênio. Com estas considerações, seria esperado que o espectro do sódio fosse semelhante ao do hidrogênio.
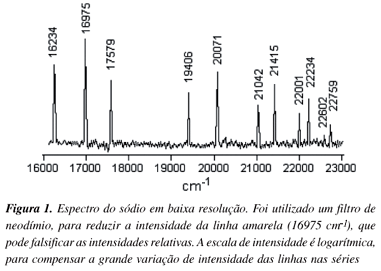
Examinando o espectro de emissão do átomo de sódio, mostrado na Figura 1, percebe-se que aparecem mais linhas que no espectro do hidrogênio. (Na obtenção deste espectro foi utilizada uma lâmpada de sódio do tipo empregado na iluminação em túneis; devido a grande intensidade da linha amarela 16956 cm-1, característica do espectro deste átomo foi usado um filtro de neodímio, que reduz drasticamente a intensidade desta linha. Como existe grande variação de intensidade das linhas consecutivas, o espectro está apresentado em escala logarítmica, tornando as intensidades mais comparáveis).
Pelo modelo de órbitas elípticas estas elipses teriam diferentes excentricidades, sendo mais excêntricas as órbitas com menor  , como mostra o esquema da Figura 2. Como conseqüência, a trajetória do elétron pode penetrar na camada completa, sendo esta penetração tanto maior quanto menor for o valor de
, como mostra o esquema da Figura 2. Como conseqüência, a trajetória do elétron pode penetrar na camada completa, sendo esta penetração tanto maior quanto menor for o valor de  . Elétrons com número quântico do momento angular
. Elétrons com número quântico do momento angular  = 0, 1, 2, 3... são conhecidos como elétrons s, p, d, f..., respectivamente.
= 0, 1, 2, 3... são conhecidos como elétrons s, p, d, f..., respectivamente.
Quanto mais o elétron penetra nas camadas fechadas, maior é o efeito da carga nuclear e, como conseqüência, maior será a energia pela qual ele está ligado ao átomo. Em relação à expressão para a série de Balmer, onde o valor de cada termo é dado por (R/n2), para os metais alcalinos deve haver um aumento da energia destes termos, o que pode ser obtido diminuindo o valor do denominador de uma quantidade proporcional ao número quântico  . Assim, o valor dos termos pode ser obtido de:
. Assim, o valor dos termos pode ser obtido de:
onde µl, denominado defeito quântico, é a correção (correção de Rydberg) a ser feita no número quântico principal n e cujo valor depende de  . O denominador não é mais um número quântico perfeito, tem valor fracionário, e é conhecido como número quântico principal efetivo. Este modelo é mais simples de ser tratado, para a finalidade deste artigo, que o da carga nuclear efetiva4.
. O denominador não é mais um número quântico perfeito, tem valor fracionário, e é conhecido como número quântico principal efetivo. Este modelo é mais simples de ser tratado, para a finalidade deste artigo, que o da carga nuclear efetiva4.
No espectro são observadas algumas séries de linhas, caracterizadas pela diminuição da intensidade e da distância entre as mesmas, seguindo uma seqüência uniforme. Assim, na Figura 1, a primeira, a quarta, a sexta, a oitava e a décima linha pertencem a uma série, enquanto que a terceira, a quinta, a sétima, a nona e a décima primeira linha pertencem a uma outra série.
As séries envolvem transições cujas energias são obtidas pela diferença entre dois termos definidos em (I), obedecendo a regra de seleção para o momento angular, D = ±1 , que fica implícita no valor de µl. Para o número quântico n não há restrição, podendo ocorrer transições entre valores de Dn = 0, ±1, ±2.... Ao contrário do que acontecia para o átomo de hidrogênio, agora pode haver transições entre termos com mesmo valor de n, mas com diferentes valores do número quântico do momento angular. Por exemplo, pode haver a transição 3µp® 3µs mas não pode haver transição entre termos com mesmo valor de
= ±1 , que fica implícita no valor de µl. Para o número quântico n não há restrição, podendo ocorrer transições entre valores de Dn = 0, ±1, ±2.... Ao contrário do que acontecia para o átomo de hidrogênio, agora pode haver transições entre termos com mesmo valor de n, mas com diferentes valores do número quântico do momento angular. Por exemplo, pode haver a transição 3µp® 3µs mas não pode haver transição entre termos com mesmo valor de  , como 3µp® 4µp.
, como 3µp® 4µp.
Haverá várias séries, de acordo com os valores de  envolvidos e as regras de seleção, isto é, transições entre elétrons s ® p, p ® d, p® s,.... Nas séries há um termo fixo (inicial) e um variável (final) e é este último que dá o nome às séries, que podem ser escritas:
envolvidos e as regras de seleção, isto é, transições entre elétrons s ® p, p ® d, p® s,.... Nas séries há um termo fixo (inicial) e um variável (final) e é este último que dá o nome às séries, que podem ser escritas:
vs= R  (n = 4, 5, 6,...) denominada série sharp
(n = 4, 5, 6,...) denominada série sharp
vp= R  (n = 3, 4, 5,...) denominada série principal
(n = 3, 4, 5,...) denominada série principal
vd= R  (n = 3, 4, 5, ...) denominada série diffuse
(n = 3, 4, 5, ...) denominada série diffuse
Conservamos o nome das séries em inglês para manter a nomenclatura s, p, d,...para os elétrons, que deriva da primeira letra do nome das séries.
Nestas séries o valor n=3 corresponde à camada do elétron de valência no estado fundamental.
No espectro atômico de hidrogênio, em alta resolução observa-se estrutura fina, correspondente às transições entre diferentes valores de
; esta estrutura foi explicada por Sommerfeld considerando correção relativística. Em resolução normal esta estrutura não é observada e pode-se considerar os termos dependentes somente do número quântico principal n, ou seja, degenerados em relação ao momento angular.No espectro mostrado na Figura 1 comparecem linhas características para duas das três séries e uma linha intensa (16975 cm-1) que, como veremos, é a única observada para a série principal nesta região. O primeiro passo neste estudo seria identificar cada série. Observando as expressões das séries nota-se que no limite, quando n ® ¥, as série sharp e diffuse tendem ao mesmo valor, R  . Pelo aspecto é fácil identificar no espectro estas duas séries, considerando o decréscimo das intensidades e do espaçamento entre as linhas de uma série (no sentido de menor para maior número de onda), além da convergência destas a um mesmo limite.
. Pelo aspecto é fácil identificar no espectro estas duas séries, considerando o decréscimo das intensidades e do espaçamento entre as linhas de uma série (no sentido de menor para maior número de onda), além da convergência destas a um mesmo limite.
As linhas de cada uma destas séries podem ser enumeradas tentativamente neste mesmo sentido, partindo de n = 3 ou 4 ou 5 para obter um gráfico, como será descrito. Como as linhas aparecem desdobradas pode-se, no momento, considerar nos dubletos somente as linhas mais intensas, que são as indicadas na Figura 1.
Para identificar as séries vamos considerar que a órbita para  = 3 (elétron d) é muito pouco penetrante e, em primeira aproximação, supor que µd = 0. Assim, a série diffuse seria escrita como equação de uma reta:
= 3 (elétron d) é muito pouco penetrante e, em primeira aproximação, supor que µd = 0. Assim, a série diffuse seria escrita como equação de uma reta:
onde A= R  , B = R e X = 1/n2.
, B = R e X = 1/n2.
Fazendo o gráfico do número de onda de uma destas duas séries, em função de 1/n2, partindo de um valor tentativo de n (a partir de 3), se o gráfico apresentar uma curvatura tenta-se outros valores iniciais de n. Se não obtivermos uma reta com estes novos valores, a série escolhida não é a diffuse. Pode-se fazer o mesmo procedimento com a outra série e para um determinado valor de n será obtida a reta esperada, confirmando ser esta a série diffuse. A regressão linear deste gráfico fornece como coeficiente angular o valor de R e como coeficiente linear o valor de R  . Conhecido R obtém-se o valor de
. Conhecido R obtém-se o valor de  e, conseqüentemente, o valor do defeito quântico µp.
e, conseqüentemente, o valor do defeito quântico µp.
CÁLCULO DOS DEFEITOS QUÂNTICOS
A Figura 3 mostra os gráficos dos números de onda da série diffuse em função de 1/n2 e a regressão linear, que fornece os valores de R (constante de Rydberg) e do coeficiente linear, que permitem calcular o valor de µp. Em (A) o gráfico é construído para n a partir de 3 e em (B) para n a partir de 4. Nota-se em (A) uma pequena curvatura (concavidade para baixo), enquanto que em (B) o gráfico é uma reta perfeita, além da boa concordância com o valor de R conhecido (já foi determinado para o átomo de hidrogênio1). O fato de n = 4 dar resultado correto é confirmado quando se observa o diagrama dos níveis de energia (Figura 4), onde é indicada a primeira transição no visível da série diffuse, que é a transição 4D®3P (a transição 3D®3P situa-se aproximadamente em 12200 cm-1, fora da região espectral analisada).
O dubleto da linha amarela, em 16980 e 16963 cm-1 (588,9 e 589,5 nm), usado para caracterização analítica do sódio, por sua intensidade deve ser atribuído à primeira transição da série principal, 3p®3s. Como já calculamos o valor de µp, podemos calcular o de µs, usando a expressão da série principal e o número de onda de uma destas duas linhas.
Conhecidos os valores dos defeitos quânticos podemos determinar os níveis de energia (autovalores) através da expressão (I).
As funções de onda dependem do número quântico principal n e do número quântico do momento angular  , como seria esperado para o modelo de órbitas elípticas. Assim, os autovalores são determinados por estes dois números quânticos. Para o hidrogênio, o elétron está submetido a um campo coulombiano e os estados são degenerados, as funções de onda para um mesmo valor de n e diferentes valores de
, como seria esperado para o modelo de órbitas elípticas. Assim, os autovalores são determinados por estes dois números quânticos. Para o hidrogênio, o elétron está submetido a um campo coulombiano e os estados são degenerados, as funções de onda para um mesmo valor de n e diferentes valores de  têm mesmo autovalor; para o sódio, devido à penetração das órbitas, o potencial que atua no elétron de valência varia durante sua trajetória. Fora das camadas fechadas a carga que atua sobre ele é +1, mas quando ele penetra na segunda camada, devido à blindagem da primeira camada, a carga efetiva que ele sentirá será +9 (=11-2). A degenerescência é rompida originando diferentes autovalores, como mostra o diagrama dos níveis de energia da ligação do elétron ao átomo (Figura 4), sendo estas energias calculadas com a equação (I). Os estados eletrônicos correspondentes estão representados pela notação espectral que será definida a seguir.
têm mesmo autovalor; para o sódio, devido à penetração das órbitas, o potencial que atua no elétron de valência varia durante sua trajetória. Fora das camadas fechadas a carga que atua sobre ele é +1, mas quando ele penetra na segunda camada, devido à blindagem da primeira camada, a carga efetiva que ele sentirá será +9 (=11-2). A degenerescência é rompida originando diferentes autovalores, como mostra o diagrama dos níveis de energia da ligação do elétron ao átomo (Figura 4), sendo estas energias calculadas com a equação (I). Os estados eletrônicos correspondentes estão representados pela notação espectral que será definida a seguir.
Examinando mais cuidadosamente o espectro verifica-se que é constituído por dubletos. Este desdobramento é devido ao acoplamento do momento angular do spin do elétron com o momento angular orbital (acoplamento spin-órbita5). Temos de introduzir mais um número quântico, associado ao momento angular de spin . O momento angular do spin é dado por pS=sh/2p, onde s é o número quântico do spin do elétron, sendo seu valor ½. Os vetores associados ao momento angular orbital e do spin são acoplados, dando como resultado o momento angular total j, obtido da soma vetorial dos vetores  e
e  onde estes vetores têm apenas as orientações definidas pela mecânica quântica. Esta soma vetorial, para s = ½ e
onde estes vetores têm apenas as orientações definidas pela mecânica quântica. Esta soma vetorial, para s = ½ e  = 0 resulta em j = ½; para s = ½ e
= 0 resulta em j = ½; para s = ½ e  =1 resulta em j = 1/2 e j = 3/2. Estas notações valem para um elétron, para o átomo deve-se considerar o momento resultante dos vários elétrons
=1 resulta em j = 1/2 e j = 3/2. Estas notações valem para um elétron, para o átomo deve-se considerar o momento resultante dos vários elétrons  e escrever a notação para os termos espectrais usando letras maiúsculas. Esta notação tem a forma 2S+1LJ, onde 2S+1 é denominada multiplicidade, L é o número quântico do momento angular orbital resultante (no caso de somente um elétron de valência tem o mesmo valor de
e escrever a notação para os termos espectrais usando letras maiúsculas. Esta notação tem a forma 2S+1LJ, onde 2S+1 é denominada multiplicidade, L é o número quântico do momento angular orbital resultante (no caso de somente um elétron de valência tem o mesmo valor de  ) e J é o número quântico do momento angular total, obtido pela soma vetorial quantizada de
) e J é o número quântico do momento angular total, obtido pela soma vetorial quantizada de  e
e  (no caso presente tem o mesmo valor deste momento para o elétron, pois só há 1 elétron de valência). Para o sódio a multiplicidade é 2, pois o spin resultante é o mesmo do elétron, ½. Os termos espectrais para os elétrons s ficam: n 2S1/2. Para elétrons p ficam n 2P1/2 e n 2P3/2; para elétrons d ficam n 2D3/2 e n 2D5/2. Os valores de J é que distinguem os componentes de um multipleto.
(no caso presente tem o mesmo valor deste momento para o elétron, pois só há 1 elétron de valência). Para o sódio a multiplicidade é 2, pois o spin resultante é o mesmo do elétron, ½. Os termos espectrais para os elétrons s ficam: n 2S1/2. Para elétrons p ficam n 2P1/2 e n 2P3/2; para elétrons d ficam n 2D3/2 e n 2D5/2. Os valores de J é que distinguem os componentes de um multipleto.
DIAGRAMA DOS NÍVEIS DE ENERGIA
O diagrama da Figura 4 mostra os valores da energia da ligação do elétron ao átomo (em cm-1), para os correspondentes termos espectrais, e as transições iniciais utilizadas em cada série na obtenção dos gráficos de nd em função de 1/n2. A segunda linha da série principal é a transição 42P1/2, 3/2®32S1/2, que se situa em 41450-11248 = 30202 cm-1 (=331 nm), no ultravioleta, sendo absorvida pelas paredes de vidro da lâmpada de sódio, ficando fora da região de observação do espectro. Isto explica porque só observamos uma única linha desta série. (Usando, como fonte da radiação, um arco elétrico com eletrodos de carvão embebido em sal de sódio, pode-se obter o espectro na região do ultravioleta).
Neste diagrama aparecem três colunas, uma para cada valor do número quântico do momento angular, diferentemente do diagrama para o hidrogênio1 onde só há uma coluna, contendo a variação do número quântico principal.
RAZÃO DE INTENSIDADES ENTRE OS COMPONENTES DOS DUBLETOS
Observando os dubletos nota-se que há uma relação de intensidade de 2:1 entre as duas linhas, como se observa na Figura 5 para os componentes em 22232 e 22249 cm-1 da série diffuse. O espectro foi obtido com maior resolução e sem uso de filtros, para não haver falsificação da intensidade. O espaçamento de 17 cm-1 entre as duas linhas é devido à diferença entre as energias dos níveis 3 2P1/2 e 3 2P3/2, que é o espaçamento medido em todos os dubletos, pois este termo é comum em todas as séries observadas. A separação entre os componentes do dubleto 2D3/2, 5/2 é muito pequena e seus níveis não são resolvidos.
A razão de intensidade 2:1 só pode ser explicada utilizando conceitos da mecânica quântica. Consideremos o que ocorre no espectro quando é aplicado na fonte de radiação um campo magnético intenso. O efeito observado constitui o conhecido Efeito Zeeman. Sem campo magnético observa-se a linha amarela como um dubleto (transição 3 2P1/2 e 3 2P3/2 para 3 2S1/2). Quando é aplicado o campo magnético estas linhas ficam desdobradas, uma em quatro componentes e a outra em seis componentes, como mostra o esquema da Figura 6.
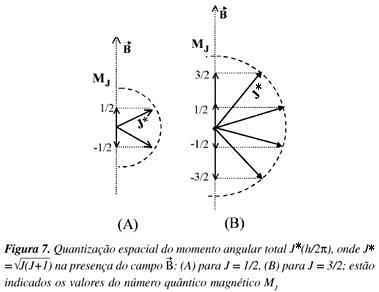
Para entender este desdobramento é necessário introduzir o número quântico magnético MJ, que resulta da projeção do momento angular total na direção do campo magnético, como no esquema da Figura 7. Na mecânica quântica o valor do momento angular total é dado por  (ou J*(h/2p) e não por J(h/2p). A aplicação do campo magnético causa orientações bem definidas do vetor deste momento angular em relação à direção do campo. Haverá uma quantização espacial, sendo a projeção de J* na direção do campo quantizada, adquirindo valores de MJ (número quântico magnético) J, J-1,..., -J. Na Figura 7(A) o esquema mostra para o número quântico J = 1/2 as projeções (MJ) sob ação do campo magnético, que ocorrem para o nível 3 2P1/2 ou 3 2S1/2; na Figura 7(B) o esquema mostra estas projeções para J=3/2, que ocorrem para o nível 3 2P3/2.
(ou J*(h/2p) e não por J(h/2p). A aplicação do campo magnético causa orientações bem definidas do vetor deste momento angular em relação à direção do campo. Haverá uma quantização espacial, sendo a projeção de J* na direção do campo quantizada, adquirindo valores de MJ (número quântico magnético) J, J-1,..., -J. Na Figura 7(A) o esquema mostra para o número quântico J = 1/2 as projeções (MJ) sob ação do campo magnético, que ocorrem para o nível 3 2P1/2 ou 3 2S1/2; na Figura 7(B) o esquema mostra estas projeções para J=3/2, que ocorrem para o nível 3 2P3/2.
Resumindo, o campo magnético causou o desdobramento de 2J+1 valores de MJ. Cada valor de MJ corresponde a uma diferente função de onda, cujos autovalores dependem do valor deste número quântico. Sem o campo não há este desdobramento, pois não existem as projeções e o autovalor dependerá somente de J* e não de MJ .
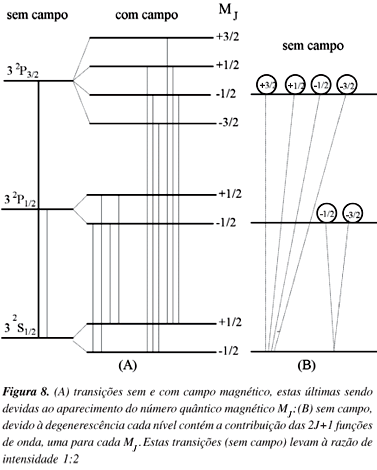
Na Figura 8(A) é mostrado, no efeito Zeeman, o aparecimento das 6 linhas para a transição 3 2P3/2®3 2S1/2 e das 4 linhas para a transição 3 2P1/2®3 2S1/2. Pela presença do campo foram criadas novas funções de onda (dependentes de MJ) e quando o campo é removido estas funções continuam a existir, embora se observe apenas um autovalor. As funções de onda são degeneradas, sendo o grau de degenerescência dado pelo número de valores possíveis de MJ, 2J+1. A aplicação do campo remove a degenerescência aparecendo níveis de energia diferentes, um para cada valor de MJ.
Foram criadas novas funções de onda, assim, mesmo sem campo devemos considerar, para um determinado nível, a presença das 2J+1 funções de onda, como é mostrado na Figura 8(B). Como as transições ocorrem entre estados, nota-se nesta Figura que para 3 2P3/2®3 2S1/2 existem quatro transições, envolvendo os diferentes valores de MJ, ao passo que para 3 2P1/2®3 2S1/2 só ocorrem duas transições. Portanto, a razão de intensidade entre os dois componentes do dubleto é de 4:2 ou 2:1, em concordância com o observado experimentalmente.
CONCLUSÃO
A penetração das órbitas rompe a degenerescência dos estados para diferentes valores do número quântico do momento angular e acarreta uma modificação na expressão da série de Balmer, pela introdução do "defeito quântico", que é função deste número quântico. Com a nova expressão para os autovalores é construído o diagrama dos níveis de energia. O aparecimento de dubletos é explicado pela presença do spin do elétron (e seu acoplamento com o momento angular) e novos números quânticos devem ser introduzidos na função de onda. A presença do número quântico magnético é evidenciada pelo efeito observado quando é aplicado um campo magnético (efeito Zeeman). A razão de intensidades, 2:1, entre as duas linhas dos dubletos decorre da presença destes números quânticos na função de onda, considerando que as transições são entre estados e não entre os autovalores, como pode parecer dos diagramas.
Recebido em 14/2/07; aceito em 18/5/07; publicado na web em 9/11/07
- 1. Sala, O. ; Quim. Nova 2007, 30, 1773.
- 2. Herzberg, G.; Atomic Spectra and Atomic Structure, 2nd ed., Dover Publications: NewYork 1944.
- 3. White, H. E.; Introduction to Atomic Spectra, 5th ed., McGraw-Hill, 1934.
- 4. Sala, O.; Araki, K.; Noda, L.K.; J. Chem. Educ 1999, 76, 1269.
- 5. Semat, H.; Introduction to Atomic Physics, Rinehart & Company, Inc.: New York, 1946.
Datas de Publicação
-
Publicação nesta coleção
21 Jan 2008 -
Data do Fascículo
2007
Histórico
-
Aceito
18 Maio 2007 -
Recebido
14 Fev 2007