Resumo
A maioria dos trabalhos sobre convergência de renda pressupõe que os países são unidades geográficas isoladas, não considerando os efeitos espaciais (dependência e heterogeneidade) subjacentes. Este artigo investiga a análise de convergência de renda entre países, incorporando o efeito de vizinhança proporcionado pela interação espacial, e, portanto, controlando-se para os efeitos espaciais, dependência espacial e heterogeneidade espacial observável e não observável. Para se conseguir isso, foi construído um modelo de convergência espacial local para 148 países no período quinquenal entre 1985 e 2005, em primeiras diferenças, usando a técnica da Regressão Ponderada Geograficamente. Os principais resultados revelam a existência de múltiplos equilíbrios quando considerada a análise de convergência local. Um grupo de países se aproxima de um equilíbrio particular em virtude da existência de atributos correlatos ou porque se encontrava em uma localização inicial correspondente àquele equilíbrio, fato em consonância com a convergência em clubes ou múltiplos equilíbrios. A diferença, todavia, repousa no fato de que os intervalos de convergência aqui definidos são consequência de como o crescimento de um país se processa, em termos de seu próprio ritmo condicionado às suas características socioeconômicas iniciais, relativamente ao crescimento de outros países e não em relação a si mesmo. Além disso, em contraste com os clubes de convergência, esses intervalos de convergência são definidos ex-post, levando em consideração a dinâmica de crescimento específica a cada país.
Palavras-Chave
Convergência de renda local; Heterogeneidade espacial; Regressão ponderada geograficamente
Abstract
The most studies on income convergence imply that countries are isolated geographic units, not considering the underlying spatial interaction (spatial dependence and heterogeneity). This paper investigates the analysis of income convergence among countries incorporating the neighborhood effect provided by the spatial interaction and, thereby, controlling for spatial dependence and spatial heterogeneity. To do so, a local spatial model was constructed over five-year period between 1985 and 2005 for 148 countries. Main findings reveal the existence of multiple equilibria considering the analysis of local convergence. A group of countries is approaching a particular equilibrium due to the existence of correlated attributes or because it was in an initial location corresponding that equilibrium, fact in line with the convergence clubs and multiple equilibria. The convergence intervals defined here result from how economic growth in a country progresses as for its pace, which is conditioned to its initial socioeconomic characteristics in relation to the growth of other countries and not in relation to its own growth trajectory. Furthermore, in contrast to convergence clubs, these convergence intervals are defined ex-post, taking into consideration the growth dynamics specific to each country.
Keywords
Local income convergence; Spatial heterogeneity; Geographically weighted regression
1. Introdução
A análise de convergência de renda passou nos últimos vinte anos por diversos desenvolvimentos teóricos e empíricos. Isto se deve ao fato de que a convergência de renda tem implicações relevantes sobre o processo de crescimento e desenvolvimento de regiões e a relação econômica entre elas, bem como sobre a atuação das políticas públicas nesse processo. Como relatado por Fagerberg e Godinho (2005)FAGERBERG, J.; GODINHO, M. Innovation and Catching-up.In: Fagerberg et al. (Eds) 2005., convergência de renda pode ser entendida como a tendência para uma redução das diferenças de renda no mundo como um todo.
A formalização dos modelos de análise de convergência tem sido direcionada em diferentes perspectivas teóricas, a saber, modelos neoclássicos iniciados por Solow (1956)SOLOW, R.M., A Contribution to the Theory of Economic Growth. Quarterly Journal of Econom ics, Vol. LXX, p. 65-94, 1956. e modelos de crescimento endógeno (Romer, 1986ROMER, P.M. Increasing returns and long-run growth. Journal of Political Economy . Vol. 94, n. 5 p. 1002-37, 1986.; Lucas, 1988LUCAS, R. E. On the Mechanics of Economic Development. Journal of Monetary Economics. Vol. 22, n. 1, p. 3-42, 1988.), além da abordagem de clubes de convergência (Quah, 1996QUAH, D. Empirics for economic growth and convergence. European Economic Review, Vol. 40, p. 1353-75, 1996.). Além disso, diversas estratégias econométricas têm sido adotadas, tais como análise cross section, séries de tempo e painel de dados. Portanto, essa variedade de modelos, ideias e resultados presentes na literatura são provas cabais da importância acadêmica dessa linha de pesquisa e sua notável evolução.
O trabalho seminal de Baumol (1986)BAUMOL, W. J. Productivity growth, convergence and welfare: what the long-run data show. American Economic Review. Vol. 76, p. 1072-1085, 1986. incentivou muitos estudos com o intuito de examinar a hipótese de convergência em nível internacional, como Barro (1991)BARRO, R. Economic growth in a cross section of countries. The Quarterly Journal of Economics, Vol. 106, Issue 2, p. 407-443, 1991., Mankiw et al. (1992)MANKIW, N.G. D.; ROMER, D.; WEIL, A. Contribution to the Empirics of Economic Growth. Quar terly Journal of Economics, vol.107 (2), pp.407-437, 1992., Barro e Sala-i-Martin (1992)BARRO, R.; SALA-I-MARTIN, X. Convergence. Journal of Political Economy, Vol. 100, n. 2, 1992., Sala-i-Martin (1996)SALA-I-MARTIN, X. The Classical Approach to Convergence Analysis. Economic Journal,Royal Economic Society, vol. 106(437), p. 1019-36, 1996., Rey e Montoury (1999)REY, S. J. MONTOURI, B. D. US regional income convergence: A spatial econometric perspective. Regional Studies, Vol. 33, n.2, p. 143-156, 1999., entre outros. Diante do considerável número de resultados, Islam (2003)______. What have we learnt from the convergence debate? Journal of Economic Surveys. Vol. 17, p. 309-362, 2003. faz uma retomada teórica e empírica da literatura de convergência, reexaminando seus diferentes conceitos, os resultados alcançados pelos diversos pesquisadores, mostrando a ligação existente entre o debate de crescimento econômico e a hipótese de convergência. Segundo o autor, a questão da convergência tornou-se cada vez mais importante na medida em que sua aceitação ou rejeição passou a ter implicação direta na validação do modelo de crescimento neoclássico ou das novas teorias de crescimento econômico. Dessa forma, apesar de a pesquisa sobre convergência não ter resolvido o debate de crescimento econômico inteiramente, ela tem sido fundamental para que tanto a vertente neoclássica quanto a nova teoria de crescimento se desenvolvessem e se adaptassem aos resultados encontrados.
Vale observar também a importância da utilização de ferramentas de econometria espacial nos estudos de convergência. A Nova Geografia Econômica (NGE) investiga as causas determinantes da concentração das atividades econômicas no espaço, utilizando a hipótese de retornos crescentes de escala (Fujita et al., 2002FUJITA, M.; KRUGMAN, P.; VENABLES, A. J. Economia Espacial: urbanização, prosperidade eco nômica e desenvolvimento humano no mundo. Editora Futura, São Paulo, 2002.). Entre os motivos que produzem aglomerações produtivas tão díspares entre si estão a localização das atividades de invenção e de inovação e suas inter-relações com os processos de crescimento econômico e de convergência inter-regionais. Um modelo de convergência composto por dados organizados em unidades espaciais deveria, por conseguinte, levar em consideração os efeitos espaciais (dependência e heterogeneidade) que poderiam resultar da interação espacial entre os agentes (Rey e Montouri, 1999REY, S. J. MONTOURI, B. D. US regional income convergence: A spatial econometric perspective. Regional Studies, Vol. 33, n.2, p. 143-156, 1999.). Todavia, como observado por Quah (1996)QUAH, D. Empirics for economic growth and convergence. European Economic Review, Vol. 40, p. 1353-75, 1996., a maioria dos trabalhos sobre convergência utilizou dados regionais, mas a grande parte dos trabalhos tratava as regiões como unidades isoladas, assumindo nenhuma interação espacial. Já Temple (1999)TEMPLE, J. The New Growth Evidence. Journal of Economic Literature, American Economic Association, vol. 37(1), p. 112-156, 1999. observa que é usual na literatura sobre crescimento estimar regressões para verificar o processo de convergência entre países, partindo do pressuposto de que os parâmetros são constantes entre as unidades geográficas. Todavia, é possível que os parâmetros variem de país para país de forma a tornar as estimativas convencionais de convergência inconsistentes, caso a heterogeneidade espacial não seja contemplada nas estimações (Temple, 2000______. Growth Regressions and What the Textbooks Don't Tell You. Bulletin of Economic Research, Wiley Blackwell, vol. 52(3), p. 181-205, 2000.).
Diante disso, procurando contribuir com a literatura vigente, o presente trabalho propõe a construção de modelos de convergência- β condicional local, controlando para a dependência espacial e a heterogeneidade espacial observável e não observável em nível mundial. Com modelos de convergência local são fornecidas informações sobre o coeficiente β para cada país. Com base nisso, é possível descobrir se cada país está convergindo ou não, assim como a sua velocidade de convergência e a meia-vida. Trata-se de um desenvolvimento da análise de convergência para contornar o problema da convergência de renda global: se o β global indicar convergência, isso não significa que todas as regiões amostradas estejam convergindo. Pode haver países que convergem, outros que divergem e outros para os quais a averiguação de convergência/divergência seja inconclusiva. A grande mensagem desse desenvolvimento, portanto, é a tentativa de se investigar mais a fundo a questão da convergência de renda entre os países em busca de resultados que não sejam apenas globais, mas que possam prover informação mais detalhada.
Nesse sentido, a proposta deste trabalho pode ser considerada inovadora, visto que desenvolve na literatura o modelo de convergência- β condicional espacial local, além de aplicar a metodologia de estimação econométrica local da regressão ponderada geograficamente (RPG), ainda pouco utilizada nos estudos empíricos. Como discorrido por Fotheringham et al.(2000)FOTHERINGHAM, A.S.;; BRUNSDON, C. CHARLTON, M.E. Quantitative Geography, London: Sage, 2000., o método RPG reconhece que é possível existir variações espaciais nas relações, que se refletem em diferentes coeficientes, um para cada região i. Dessa forma, esse instrumental metodológico torna possível a construção dos modelos de convergência- β condicional locais que possam controlar para os dois efeitos espaciais de tal sorte que tenha condições de acomodar a heterogeneidade espacial, relacionada à falta de estabilidade estrutural das relações, bem como a dependência espacial, vinculada à interação entre países.
Diante do exposto, este trabalho pretende investigar a hipótese de convergência condicional numa perspectiva espacial local. O indicador da variável dependente, a saber, o nível de renda por trabalhador, será o produto por trabalhador avaliado em nível mundial, variável indicada pela literatura macroeconômica como medida de crescimento econômico. A relação entre a taxa de crescimento do PIB por trabalhador mundial e o PIB por trabalhador inicial será testada a fim de se verificar a existência de um coeficiente negativo de β como previsto pela hipótese de convergência. Serão considerados 148 países no período quinquenal compreendido entre os anos 1985 e 2005. Serão adicionadas variáveis de controle relevantes relacionadas ao processo de crescimento, conforme sugerido pela literatura. A heterogeneidade espacial observável mundial será considerada nas estimações da taxa de crescimento do PIB por trabalhador por meio da metodologia de Regressão Ponderada Geograficamente (RPG). Já a heterogeneidade espacial não observável será controlada pela remoção dos efeitos fixos na estimação.
As evidências obtidas neste trabalho mostram que os efeitos não observados e os efeitos espaciais devem ser considerados na análise de convergência de renda. As evidências constatam a existência de múltiplos equilíbrios, quando considerada a análise de convergência local. Um grupo de países se aproxima de um equilíbrio particular em virtude da existência de atributos correlatos ou porque se encontrava em uma localização inicial correspondente àquele equilíbrio, fato em consonância com a convergência em clubes ou múltiplos regimes. A diferença, todavia, repousa no fato de que os intervalos de convergência aqui definidos são consequência de como o crescimento de um país se processa, em termos de seu próprio ritmo condicionado às suas características socioeconômicas iniciais, relativamente ao crescimento de outros países e não em relação a si mesmo.
Além desta seção introdutória, o presente trabalho está estruturado como segue. Na segunda seção é feita a revisão de literatura dos trabalhos de convergência de renda entre países. A terceira seção aborda o modelo teórico, enquanto na quarta seção é descrita a metodologia implementada. Já, na quinta seção, são discutidos os resultados e, por fim, as considerações finais do estudo são tecidas na sexta seção.
2. O Debate sobre convergência de renda entre países: Evidências empíricas
Na última década, a literatura econômica tem dedicado crescente atenção à investigação das causas do desenvolvimento econômico e às razões das disparidades de renda entre nações. Com relação à literatura de crescimento econômico, os trabalhos clássicos (Solow, 1956SOLOW, R.M., A Contribution to the Theory of Economic Growth. Quarterly Journal of Econom ics, Vol. LXX, p. 65-94, 1956.; Ramsey, 1929RAMSEY, F. A mathematical theory of savings. The Economic Journal, Vol. 38, p. 543-59, 1929.),1 1 Mais detalhes sobre os modelos em Romer (2006). apesar de identificarem a tecnologia como o fator determinante do crescimento econômico, adotam o pressuposto de que essa variável seja exógena. Buscando solucionar esse impasse, uma linha importante do mainstream iniciou um esforço para a incorporação de elementos da dimensão tecnológica nos modelos de crescimento econômico (Romer, 1990ROMER, P.M. Increasing returns and long-run growth. Journal of Political Economy . Vol. 94, n. 5 p. 1002-37, 1986.; Barro e Sala-i-Martin, 1997BARRO, R.; SALA-I-MARTIN, X. Technological Diffusion, Convergence and Growth. Journal of Economic Growth, Vol. 1, p. 1-26, 1997.).
Muitos trabalhos examinaram a natureza do processo de crescimento dentro do modelo neoclássico e fora dele, apontando para a convergência (Baumol, 1986BAUMOL, W. J. Productivity growth, convergence and welfare: what the long-run data show. American Economic Review. Vol. 76, p. 1072-1085, 1986., Barro, 1991BARRO, R. Economic growth in a cross section of countries. The Quarterly Journal of Economics, Vol. 106, Issue 2, p. 407-443, 1991.) ou para a persistência de diferenças na renda per capita entre países (ROMER, 1986ROMER, P.M. Increasing returns and long-run growth. Journal of Political Economy . Vol. 94, n. 5 p. 1002-37, 1986.; LUCAS, 1988LUCAS, R. E. On the Mechanics of Economic Development. Journal of Monetary Economics. Vol. 22, n. 1, p. 3-42, 1988.). Como consequência desses trabalhos, porém, a controvérsia e o debate acerca de como medir e interpretar a convergência e o crescimento dos países aumentou. A falta de convergência entre países foi utilizada como evidência contra o modelo neoclássico e a favor dos novos modelos de crescimento endógeno.
Uma questão que tem atraído considerável atenção ao trabalho empírico sobre convergência é se os países pobres tendem a crescer mais rápido que os países ricos. A partir do trabalho seminal de Baumol (1986)BAUMOL, W.J.; WOLFF, E.N. Productivity Growth, Convergence, and Welfare: Reply. American Economic Review, American Economic Association, vol. 78(5), p. 1155-59, 1988., que concluiu pela existência de convergência entre os países industrializados, vários outros estudos foram empreendidos. De Long (1988)DE LONG, J.B. Productivity Growth, Convergence, and Welfare: Comment. American Economic Review. American Economic Association, vol. 78(5), p. 1138-54, 1988. criticou o trabalho de Baumol ao discutir o problema de viés de seleção da amostra utilizada pelo autor que contava com dados de dezesseis países industrializados. Baumol e Wolff (1988)BAUMOL, W.J.; WOLFF, E.N. Productivity Growth, Convergence, and Welfare: Reply. American Economic Review, American Economic Association, vol. 78(5), p. 1155-59, 1988., ao considerar uma amostra de 72 países, não encontraram evidências de convergência.
Grier e Tullock (1989)GRIER, K.B.; TULLOCK, G. An Empirical Analysis of Cross-National Economic Growth, 1951-1980. Journal of Monetary Economics, Vol. 24, p. 259-276, 1989. provêem evidências que podem ser interpretadas como convergência condicional. De posse de uma amostra de 113 países, os autores obtiveram indícios de convergência somente para 24 países da OCDE. Barro (1991)BARRO, R. Economic growth in a cross section of countries. The Quarterly Journal of Economics, Vol. 106, Issue 2, p. 407-443, 1991., por sua vez, discute diversas variáveis que podem ser incluídas na análise de convergência entre países. Barro (1991)BARRO, R. Economic growth in a cross section of countries. The Quarterly Journal of Economics, Vol. 106, Issue 2, p. 407-443, 1991., Barro e Sala-i-Martin (1992)BARRO, R.; SALA-I-MARTIN, X. Convergence. Journal of Political Economy, Vol. 100, n. 2, 1992. e Mankiw et al. (1992)MANKIW, N.G. D.; ROMER, D.; WEIL, A. Contribution to the Empirics of Economic Growth. Quar terly Journal of Economics, vol.107 (2), pp.407-437, 1992. encontraram convergência condicional para a mesma amostra de 98 países no período de 1960 a 1985. Sala-i-Martin (1996)SALA-I-MARTIN, X. The Classical Approach to Convergence Analysis. Economic Journal,Royal Economic Society, vol. 106(437), p. 1019-36, 1996. obteve os mesmos resultados para os países e convergência absoluta no grupo de países da OCDE. Durlauf e Johnson (1995)DURLAUF, S.; JOHNSON, P. Multiple regimes and cross-country growth behaviour. Journal of Applied Econometrics. Vol. 10, n. 4, p. 365-384, 1995. tomam como ponto de partida o modelo de Solow ampliado proposto por Mankiw et al.(1992)MANKIW, N.G. D.; ROMER, D.; WEIL, A. Contribution to the Empirics of Economic Growth. Quar terly Journal of Economics, vol.107 (2), pp.407-437, 1992., mas, ao invés de testarem a forma tradicional de prever convergência, os autores, alternativamente, utilizam a regressão para identificar múltiplos regimes. Os autores contaram com uma amostra de 96 países entre os anos 1960 e 1985 e mostraram que a convergência é realmente mais forte dentro dos grupos de países.
Vários estudos utilizaram a metodologia de séries temporais para empreender a análise de convergência. Quah (1990)QUAH, D. International Patterns of Economic Growth: I. Persistence in Cross Country Disparities, Department of Economics, MIT, Cambridge, 1990., por exemplo, ao rejeitar a hipótese nula de presença de raiz unitária para 114 países no período entre os anos 1970 e 1985, interpretou o resultado como falta de convergência absoluta entre os países. Já a rejeição da hipótese nula de existência de raiz unitária na análise de Evans (1996)EVANS, P. Using Cross-country Variances to Evaluate Growth Theories. Journal of Economic Dynamics and Control, Vol. 20, p. 1027-1049, 1996. para 13 países desenvolvidos e Evans e Karras (1996)EVANS, P.; KARRAS, G. Convergence Revisited. Journal of Monetary Economics, Vol. 37, p. 249-265, 1996. para 56 países foi identificada como vestígio de convergência condicional.
Utilizando outra ferramenta econométrica, Islam (1995)ISLAM, N. Growth Empirics: a panel data approach. The Quarterly Journal of Economics. Vol. 110, n.4, p.1127-1170, 1995. incorpora modelos de painel de dados dinâmico na estimação de convergência de renda. O estudo contou com três amostras de 98, 75 e 22 países, e, em todas, a hipótese de convergência condicional foi confirmada. A introdução de dados em painel representa um avanço importante devido à possibilidade de realizar o controle para efeitos não observados, além de fornecer estimativas das diferenças existentes na produtividade entre os países.2 2 A abordagem de painel de dados tem sido aplicada por diversos autores como Caselli et al. (1996), Canova e Marcet (1999), De La Fuente (2002), entre outros. Tais estudos são em nível regional.
Lee et al. (1997)LEE, K.; PESARAN, M.H.; SMITH, R. Growth and convergence in a multi-country empirical stochastic Solow model. Journal Applied of Economics. Vol.12, p. 357-392, 1997., por sua vez, propõem a abordagem de painel de dados, considerando a heterogeneidade dos países por intermédio do estimador de Mínimos Quadrados por Variáveis Dummies para estudar convergência em 102 países no período de 1960 a 1989. Os resultados obtidos indicam que o crescimento da tecnologia foi muito maior nos 22 países da OCDE constantes na amostra (com uma pequena dispersão) quando comparado ao mundo como um todo. Como consequência, a dispersão global é crescente: os países estão divergindo, não convergindo.
A questão sobre convergência passou por considerável desenvolvimento teórico a partir dos modelos de crescimento endógeno que demonstraram a importância do capital humano e do progresso tecnológico para a análise. Não obstante isso, como discutido por Brasili et al. (2009)BRASILI C., BRUNO F., SAGUATTI A. A spatial econometric model for evaluating conditional β-convergence across EU regions, contributed paper presentato alla III World Conference of Spatial Econometrics, Barcelona, 2009., as intuições derivadas da Nova Geografia Econômica mostraram a importância da localização espacial das atividades econômicas para explicar sua trajetória de crescimento, na medida em que origina um mecanismo circular que perpetuaria o desenvolvimento desigual dos territórios, uma vez estabelecidas. Conforme crítica de Quah (1996)QUAH, D. Empirics for economic growth and convergence. European Economic Review, Vol. 40, p. 1353-75, 1996., os países ou regiões são tratados como "ilhas isoladas" na abordagem padrão quando, na verdade, as interações espaciais devidas aos spillovers geográficos deveriam ser levadas em consideração. Diante disso, por meio de técnicas de econometria espacial, é possível lidar com os principais problemas gerados pela dimensão espacial dos dados – dependência e heterogeneidade espaciais - o que poderia afetar a confiabilidade das estimativas cross country, se não devidamente modeladas.
O trabalho de De Long e Summers (1991)DE LONG, J.B.; Summers, L.H. Equipment Investment and Economic Growth, The Quarterly Journal of Economics, MIT Press, vol. 106(2), p. 445-502, 1991. foi o primeiro estudo a retomar explicitamente o assunto de localização e crescimento. No entanto, apesar de pressuporem que os resíduos das nações vizinhas estivessem correlacionados, os autores não encontraram evidências de correlação espacial para as amostras de 25 e 61 países para o crescimento da produtividade advinda do investimento em equipamentos. A partir do estudo de De Long e Summers (1991)DE LONG, J.B.; Summers, L.H. Equipment Investment and Economic Growth, The Quarterly Journal of Economics, MIT Press, vol. 106(2), p. 445-502, 1991., o interesse pela inclusão dos efeitos espaciais na análise de convergência e pela utilização adequada do instrumental econométrico espacial tem aumentado nos últimos anos,3 3 Uma revisão detalhada sobre os estudos que consideram os efeitos espaciais é encontrada em Abreu et al.(2005). mas, o foco desta aplicação tem sido os estudos regionais, por exemplo, Rey e Montouri (1999)REY, S. J. MONTOURI, B. D. US regional income convergence: A spatial econometric perspective. Regional Studies, Vol. 33, n.2, p. 143-156, 1999. para os Estados Unidos, Fingleton (1999)FINGLETON, B. Economic geography with spatial econometrics: a "third way" to analyse economic development and "equilibrium" with application to the EU regions. EUI Working Paper ECO, n. 99/21, 1999., López-Bazo et al. (1999)LÓPEZ-BAZO, E.; VAYÁ, A.M.; Suriñach, J. Regional economic dynamic and convergence in the European Union, Annals of Regional Science, Vol. 33, p. 343-70, 1999. e Arbia e Piras (2004)ARBIA, G.M.; PIRAS, G. Convergence in per-capita GDP across European regions using panel data models extended to spatial autocorrelation effects. ERSA conference papers, ERSA 04, p.524, European Regional Science Association, 2004. para a Europa, Magalhaes et al. (2000)MAGALHÃES, A. M.; HEWINGS, G. D.; AZZONI, C. Spatial Dependence and Regional Convergence in Brazil. In: Internacional Regional Science Meeting, Chicago. ANAIS DO INTERNACIONAL REGIONAL SCIENCE MEETING, 2000., Silveira Neto (2001)SILVEIRA NETO, R.M. Localização, Crescimento e Spillovers: Evidências para os Estados Brasileiros e Setores. In: XXIX ENCONTRO NACIONAL DE ECONOMIA. Salvador/BA, 2001. Anais do XXIX Encontro Nacional de Economia, 2001., Silveira Neto e Azzoni (2008)SILVEIRA NETO, R.M.; Azzoni, C.R. Non Spatial Public Policies and Regional Inequality in Brazil. In: RSAI WORLD CONGRESS 2008, São Paulo. Annals of RSAI World Congress 2008., Barreto e Almeida (2008)BARRETO, R. C. S.; ALMEIDA, E. S. Crescimento econômico e convergência de renda no Brasil: a contribuição do capital humano e da infra-estrutura. In: VI ENCONTRO NACIONAL DA AS SOCIAÇÃO BRASILEIRA DE ESTUDOS REGIONAIS E URBANOS - VI ENABER, 2008, Aracaju. Anais do VI ENABER, 2008. para estados brasileiros, entre outros. Em nível mundial, Moreno e Trehan (1997)MORENO, R.; TREHAN, B. Location and the Growth of Nations, Journal of Economic Growth, Springer, vol. 2(4), p. 399-418, 1997. aplicaram a metodologia econométrico-espacial para 93 países, usando dados em corte cruzado entre 1965 e 1989. Os autores concluem que a taxa de crescimento de um país está intimamente relacionada à taxa de crescimento das nações vizinhas.
Baseados em uma amostra de 98 países para diferentes períodos (1965-1975, 1975-1985 e 1985-1995),Ramírez e Loboguerrero (2002)RAMIREZ, M.T.; LOBOGUERRERO, A. Spatial Dependence and Economic Growth: Evidence from a Panel of Countries, Banco de la República, Colombia, 2002.constatam que as relações espaciais entre os países são relevantes. De acordo com os resultados obtidos a partir das diferentes amostras de dados em cross section utilizadas, as autoras concluem que a taxa de crescimento de um país é afetada pelo desempenho dos seus vizinhos. Portanto, os efeitos de spillovers entre países são importantes para o crescimento e a omissão da dependência espacial conduziria à má especificação do modelo.
Já Florax e Nijkamp (2005)FLORAX R.J.G.M.; NIJKAMP, P. Misspecification in linear spatial regression models. In: K. Kempf-Leonard (ed.), Encyclopedia of Social Measurement, San Diego: Academic Press, p. 695-707, 2005. utilizam a mesma base de dados de Mankiw et al. (1992)MANKIW, N.G. D.; ROMER, D.; WEIL, A. Contribution to the Empirics of Economic Growth. Quar terly Journal of Economics, vol.107 (2), pp.407-437, 1992.para 98 países no período compreendido entre os anos 1960 e 1985, e encontraram evidências de dependência espacial. A heterogeneidade espacial foi controlada no estudo por meio de regimes espaciais definidos de acordo com o nível de crescimento dos países. Para os países de crescimento rápido, a velocidade de convergência encontrada foi da ordem de 1,2%, enquanto os países de baixo crescimento convergem a uma taxa de 0,3%. A principal conclusão dos autores é a necessidade da utilização das técnicas de econometria espacial para as análises de convergência. Nessa mesma linha, os resultados do estudo de Behar (2008)BEHAR, A. Neighborhood growth effects: An annual panel data approach. Background paper, Resha ping Economic Geography, 2008., contemplando uma variedade de amostras de países4 4 A amostra máxima do estudo de Behar (2008)conta com 134 países. no período compreendido entre 1980 e 2004, revelam que há efeitos de vizinhança na forma de correlação entre as taxas de crescimento dos países e as de seus vizinhos. Os efeitos não observados foram tratados usando o método de primeiras diferenças.
Uma abordagem que também pode ser considerada inovadora trata-se das estimações de modelos de convergência local. Por meio de modelos de convergência local são fornecidas informações sobre o coeficiente β para cada região amostrada. Com base nisso, é possível descobrir se cada país está convergindo ou não, assim como a sua velocidade de convergência e a meia-vida. Nesse cenário, Durlauf et al. (2001)DURLAUF, S. N.; KOURTELLOS, A.; MINKIN, A. The Local Solow Growth Model. European Economic Review. Vol. 45, n. 4-6, pp. 928-940, 2001. aplicam o modelo de Solow local para uma amostra de 98 países no período de 1960 a 1985. Por local, os autores entendem o modelo de Solow aplicado a cada país, mas considerando a variação da função de produção agregada entre os países. Os autores assumem que essa variação pode ser indexada a uma variável índice escalar zi, específica a cada país. O achado do estudo é de que o modelo de Solow local se encaixa melhor aos países do que a abordagem tradicional global, pois foram encontradas evidências de substancial heterogeneidade de um país para outro.
Reunindo a definição de método de estimação local de convergência à análise econométrica espacial, Pace e Le Sage (2002)PACE, R.K.; LE SAGE, J.P. Omitted variables biases of OLS and spatial lag models. In: PÁEZ, A.;; LE GALLO, J. BULIUNG, R. AND DALL'ERBA, S. (eds.). Progress In Spatial Analysis: Theory and Computation, and Thematic Applications, Berlin:, Springer forthcoming, 2009. desenvolveram um método de estimação denominado Spatial Autoregressive Local Estimation(SALE), objetivando acomodar tanto a dependência quanto a heterogeneidade espaciais. O modelo proposto pelos autores produz estimativas usando n regressões, em que n representa o número de observações cross section da amostra. Este modelo autorregressivo espacial localmente linear foi aplicado para dados em nível municipal da eleição presidencial dos EUA de 1980. Uma extensão do modelo SALE aplicada à convergência de renda foi proposta por Ertur et al. (2004). Os autores elaboraram um modelo teórico capaz de acomodar, além dos efeitos espaciais, a variância não constante por meio do método bayesiano. Com dados para o período de 1980 a 1995, os autores estimaram convergência de renda de 138 regiões europeias, utilizando o método SALE em sua versão bayesiana. A conclusão do estudo foi de que somente 31 das 138 estimativas autorregressivas espaciais localmente lineares de β foram negativas e significantes e, portanto, consistentes com a inferência de convergência. As regiões em que ocorreu convergência remetem à Espanha, Portugal e sul da França.
Outro método de estimação local capaz de acomodar os dois efeitos espaciais é o instrumental metodológico da Regressão Ponderada Geograficamente (RPG).5 5 Tradução do inglês, geographically weighted regression (GWR). O estudo de Yildirim (2005)YILDIRIM, J. Regional Policy and Economic Convergence in Turkey: a Spatial Data Analysis. In: 18TH EUROPEAN ADVANCED STUDIES INSTITUTE IN REGIONAL SCIENCE. Kraków e Łódź, 2005. analisou o processo de convergência na Turquia no período de 1990 a 2001. Os resultados do estudo revelaram que o modelo de defasagem espacial, melhor especificado para o caso, sugere considerável variação na velocidade de convergência das províncias juntamente com uma instabilidade estrutural. Contudo, contrariamente às conclusões da análise β tradicional realizada, as províncias do Oriente e as do Sudeste atingiram velocidades mais altas de convergência quando variáveis de política regional são tomadas em conta na análise local. Nesse mesmo enfoque, Wei e Ye (2009)WEI, Y.H.D.; YE, X. Beyond Convergence: Space, Scale and Regional Inequality in China. Tijd schrift voor Economische en Sociale Geografie. Vol. 100, No. 1, pp. 59-80, 2009.examinaram o caso chinês de desigualdade de renda. De posse de taxas de crescimento do PIB per capita de 1990/1998 e de 1998/2004 e variáveis de controle para os mesmos períodos, os resultados da estimação de coeficientes locais por intermédio da metodologia RPG demonstraram melhorias sobre a análise convencional de regressão global.
Diante do exposto acerca da literatura sobre a questão de convergência, percebe-se a relevância da inclusão do espaço na regressão. Em que pese isso, os efeitos espaciais têm recebido pouca atenção na literatura e, por conseguinte, o instrumental econométrico-espacial tem sido pouco aplicado nos trabalhos empíricos sobre convergência em nível mundial. Com menor gama de aplicação prática, podem ser citados os modelos espaciais com respostas locais.
Dessa forma, este trabalho propõe-se à construção de modelos de convergência- β condicional local. Serão levados em consideração, particularmente, os problemas de má-especificação decorrentes de efeitos não observados, dependência espacial, e, em especial, da heterogeneidade espacial dos parâmetros, que considera as diferenças internacionais, e que foram pouco contempladas na literatura empírica existente até então.
Convém observar que o presente estudo se diferencia em relação à discussão sobre convergência de renda em nível mundial em quatro aspectos. Em primeiro lugar, é o primeiro trabalho na literatura econômica que faz o controle explícito da dependência espacial e da heterogeneidade espacial observável e não observável para a convergência de renda condicional entre países, concomitantemente. Em segundo lugar, a variável dependente utilizada neste trabalho é a taxa de crescimento do produto interno bruto (PIB) por trabalhador, medida da produtividade do trabalho indicada pela teoria macroeconômica como a medida de crescimento econômico (SOLOW, 1956SOLOW, R.M., A Contribution to the Theory of Economic Growth. Quarterly Journal of Econom ics, Vol. LXX, p. 65-94, 1956.), porém pouco utilizada nas aplicações empíricas realizadas até então.6 6 A maior parte dos estudos sobre convergência de renda utiliza a variável taxa de crescimento do PIB per capita. Em terceiro lugar, salienta-se que não foi encontrado em nenhum estudo anterior, quer seja cross-section, quer seja em painel de dados, tal tamanho amostral (148 países). Além disso, a análise é aplicada para um período consideravelmente recente (1985 a 2005), e a estimação local por meio da Regressão Ponderada Geograficamente, empreendida neste estudo, considera tanto os efeitos não observados quanto a heterogeneidade espacial observada entre os países simultaneamente.
3. A Hipótese de convergência local
A hipótese de convergência (absoluta ou condicional) especifica uma relação negativa entre o nível inicial de renda de uma economia e sua taxa de crescimento durante determinado período de tempo. Essa característica decorre da hipótese de retornos marginais decrescentes para o capital na função de produção do modelo de crescimento neoclássico de Solow (1956)SOLOW, R.M., A Contribution to the Theory of Economic Growth. Quarterly Journal of Econom ics, Vol. LXX, p. 65-94, 1956.. O modelo pode ser representado pela seguinte equação:
em que a variável dependente é a taxa de crescimento da renda por trabalhador para o país i no período t; ln(yi,t-1) é o nível inicial da renda por trabalhador para o país i e Xi denota um vetor de variáveis que controlam para o nível da renda por trabalhador do país i no seu estado estacionário. Por sua vez, θrefere-se a um vetor de coeficientes.
Neste trabalho, segue-se a estratégia proposta por Ertur e Koch (2007)ERTUR, C.; KOCH, W. Growth, Technological Interdependence and Spatial Externalities: Theory and Evidence. Journal of Applied Econometrics.Vol. 22, p. 1033-1062, 2007.7 7 O modelo detalhado e suas implicações empíricas podem ser visto em Ertur e Koch (2007). para testar a hipótese de convergência local que melhor descreve a dinâmica da renda por trabalhador entre os países. Com a inclusão do espaço na análise de convergência e a importância cada vez mais acentuada do progresso tecnológico como propulsor do crescimento econômico, o modelo de Solow espacialmente ampliado de Ertur e Koch (2007)ERTUR, C.; KOCH, W. Growth, Technological Interdependence and Spatial Externalities: Theory and Evidence. Journal of Applied Econometrics.Vol. 22, p. 1033-1062, 2007. insere-se na literatura teórica sobre convergência, por incluir em sua modelagem externalidades do capital físico, bem como externalidades espaciais do conhecimento (que envolve interdependência tecnológica entre os países). Entende-se por externalidades espaciais o conhecimento acumulado em um país que depende da tecnologia acumulada em outros países. Os autores partem de uma função Cobb-Douglas com retornos constantes, como no modelo de Solow:
Com as notações padrão, a saber, Y representa o produto, K é o nível de capital físico, L refere-se ao nível de trabalho e A é o nível agregado de tecnologia:
Como apontado pelos autores, a Equação (3.2b) supõe que alguma proporção do progresso tecnológico é exógena e idêntica em todos os países (Ωi(t)), além de depender do estoque de capital físico por trabalhador (Kiφ(t)), o qual é complementar ao estoque de conhecimento no país doméstico (Π Nj≠iAiywij(t)). De outra forma, cada unidade de investimento em capital não somente aumenta o estoque de capital físico, mas também eleva o nível de tecnologia para todas as firmas por meio dos spillovers do conhecimento, como descrito em Romer (1986)ROMER, P.M. Increasing returns and long-run growth. Journal of Political Economy . Vol. 94, n. 5 p. 1002-37, 1986.. A taxa de crescimento da tecnologia doméstica também depende do estoque de conhecimento em outros países que, por sua vez, afeta o progresso tecnológico do país vizinho. Daí a configuração de interdependência tecnológica entre os países. A intensidade desse efeito spillover é assumida ser relacionada a algum conceito de proximidade socioeconômica ou institucional, que é capturada pelo modelo por intermédio da proximidade geográfica exógena (Wij).
Linearizando a Equação (3.2b) e reescrevendo em notação matricial, após alguns arranjos algébricos, tem-se:
em que k refere-se ao capital por trabalhador.
Desenvolvendo a Equação (3.3),| Υ|<1 e reagrupando termos, é obtido para cada país i um nível tecnológico dado por:
Substituindo essa equação na função de produção (3.2a), denotada por trabalhador, obtém-se:
Com uiiwij(r) são os elementos da linha i e coluna j da matriz W de acordo com a ordem de vizinhança (r) de um determinado país8
8
Nesse caso, quanto mais próxima a ordem de vizinhança, maior o valor do parâmetro y portanto, maior a força de interdependência tecnológica.
, e yi(t) = Yi(t)/Li(t) corresponde ao nível de produto por trabalhador. . Os termos
. Os termos
Esse modelo implica heterogeneidade espacial nos parâmetros da função de produção. O modelo provê uma equação para o nível de renda de steady state para cada país expressa como:
A equação de steady state fornece as mesmas predições qualitativas do modelo de Solow básico sobre a influência das taxas de poupança e de crescimento populacional sobre a renda per capita de um país no estado estacionário. Quanto à equação de convergência condicional, o modelo também prevê retornos decrescentes do capital. Matematicamente é expressa como (Ertur e Koch, 2007ERTUR, C.; LE GALLO, J.; BAUMONT, C. The European Regional Convergence Process, 1980-1995: Do Spatial Regimes and Spatial Dependence Matter? International Regional Science Review. Vol. 29, n. 1, p. 3-34, 2006.):
Dessa forma, quando um país aumenta seu capital físico, a taxa de crescimento cai e converge a seu próprio estado estacionário. Todavia, um acréscimo no capital físico no país vizinho aumenta a produtividade das firmas no país doméstico por causa da interdependência tecnológica. A hipótese de convergência é verificada caso o coeficiente referente ao PIB inicial (lnyi(t-1)) seja negativo e estatisticamente significativo. Externalidades do capital físico e interdependência tecnológica, portanto, somente retardam o decréscimo da produtividade marginal do capital físico; como consequência, o resultado de convergência ainda se mantém no modelo. Por fim, a taxa de convergência do país doméstico também depende das taxas de crescimento dos países vizinhos ponderadas por suas velocidades de convergência e por termos friccionais.
4. Modelo de convergência- β condicional local com dependência espacial – RPG
A técnica de regressão linear estima um parâmetro β que relaciona as variáveis explicativas à variável dependente. Todavia, quando essa técnica é aplicada para dados espaciais, algumas questões concernentes à estabilidade desses parâmetros no espaço surgem. O termo heterogeneidade espacial dos parâmetros diz respeito às variações nas relações entre as variáveis ao longo do espaço. Essas diferentes relações são expressas por diferentes coeficientes das regressões. No caso extremo, há uma regressão para cada unidade espacial analisada. Existem algumas abordagens econométricas para incorporar essa heterogeneidade espacial no modelo. A metodologia conhecida por Regressão Ponderada Geograficamente (RPG), desenvolvida por Brundson, Fotheringham e Charlton (1996)BRUNSDON, C.; FOTHERINGHAM, A.S.; CHARLTON, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geographical Analysis. Vol. 28, n. 4, p. 281-298, 1996., é um dos exemplos. RPG é uma técnica que permite a modelagem das interações que variam no espaço por introduzir pesos baseados na distância para prover estimativas de βki para cada variável Xk e cada localização geográfica i(Chasco et al., 2007CHASCO, C.; GARCÍA, I.; VICÉNS, J. Modeling spatial variations in household disposable income with Geographically Weighted Regression. Munich Personal RePEc Archive. Universidad Au tónoma de Madrid, Spain, 2007.).
A ideia de atribuir pesos para cada observação a partir de um ponto de calibragem incorpora o conceito de que a importância relativa diminui com a distância do ponto analisado. Em outras palavras, subconjuntos de dados são criados em torno de determinadas pontos onde a influência das observações é reduzida à medida que se tornam mais distantes do ponto de calibragem (Fotheringham et al., 2002FOTHERINGHAM, A.S.;; BRUNSDON, C. CHARLTON, M.E. Quantitative Geography, London: Sage, 2000.). É patente que a metodologia RPG logra êxito em acomodar o efeito espacial representado pela heterogeneidade espacial extrema, manifestada nos coeficientes, tanto de intercepto quanto de inclinação.
Assim, a estimação do modelo de convergência- β condicional local terá a seguinte especificação econométrica:
em que TXCRESC refere-se à taxa de crescimento do PIB; (ui, vi) representam as coordenadas do ponto i no espaço, β(ui, vi) e χh(ui, vi) representam as estimativas locais da hipótese de convergência e das variáveis de controle, respectivamente.
A estimação de β(ui, vi) e χh(ui, vi) é feita por mínimos quadrados ponderados, em que os pesos modificam-se sob influência da proximidade com o ponto de regressão i, e são definidos pela função W(ui,vi) e pelo kernel espacial. A matriz W(ui,vi) representa os pesos wij baseados na distância entre a observação no ponto i e as demais observações da sub-amostra selecionada pela "janela móvel", e definidos pela função do kernel espacial. Há diversas maneiras de se definir a matriz de ponderação W(ui,vi), conforme a distância da observação j em relação ao ponto de regressão i(dij).9 9 Ver detalhes a respeito disso em Fotheringham et al. (2002).
Segundo Fotheringham et al. (2002)FOTHERINGHAM, A.S.;; BRUNSDON, C. CHARLTON, M.E. Quantitative Geography, London: Sage, 2000., a escolha ótima de largura de banda envolve um trade-off entre viés e variância: uma largura de banda muito pequena leva a uma variância grande nas estimativas locais; uma banda muito larga traz viés às estimativas locais. Os coeficientes locais estimados para uma variável explicativa podem ser avaliados por intermédio de um teste de significância de Monte Carlo: caso não haja uma variabilidade espacial significativa, a hipótese nula de estacionariedade espacial se sustenta.10 10 Para maiores detalhes técnicos sobre o teste de Monte Carlo, ver Fotheringham et al. (2002). Em resumo, ao possibilitar a estimação dos parâmetros considerando sua variabilidade espacial, a metodologia RPG soluciona uma importante fonte de má-especificação, qual seja, a omissão da heterogeneidade espacial11 11 O problema da omissão da heterogeneidade espacial nas regressões de convergência é abordado em Temple (1999; 2000). nos parâmetros em nível de país. Além disso, os efeitos de dependência espacial podem ser considerados localmente, caso uma avaliação dos resíduos do modelo RPG mostrem a presença de autocorrelação espacial.
Para lidar com o problema de diferenças de dimensões de dados para o caso dos 148 países considerados na amostra, um kernel adaptativo com uma forma bi-quadrado foi escolhido para estimar as regressões. A largura de banda foi escolhida levando em consideração os resultados para a minimização do critério de informação Akaike (AIC). Em termos quantitativos, a amostra de 148 países detém, em média, 93% da população mundial e 87% do PIB real por trabalhador no período em questão. Os dados macroeconômicos do presente estudo foram retirados da Penn World Table12 12 Dados disponíveis em: http://pwt.econ.upenn.edu/php_site/pwt63/pwt63_form.php. Todos os dados retirados da PWT, exceto dados de população e de poder de paridade de compra, estão a preços constantes de 2005. (PWT, versão 6.3), enquanto os indicadores sociais foram extraídos do Banco Mundial.13 13 Dados disponíveis em: http://databank.worldbank.org/ddp/home.do?Step=12&id=4&CNO=2. A variável dependente (TXCRESC) é o logaritmo natural da razão entre os valores do PIB real por trabalhador relativos a dois anos consecutivos. O PIB inicial (PIBt-1), variável que indica a existência de convergência, caso o parâmetro estimado seja negativo e estatisticamente significativo, é representado pelo logaritmo da variável PIB real por trabalhador referente ao quinquênio anterior.
Outras variáveis explicativas apontadas pela literatura em crescimento econômico como importantes para explicar o processo de convergência de renda foram incluídas: capital físico (S); NGS que consiste da adição do valor da taxa de depreciação e da tecnologia (g+δ = 0,05 anuais) aos valores das taxas de crescimento populacional (n); como proxy para capital humano (H), foi utilizada a taxa bruta de matrículas no ensino secundário; como medida de saúde, a expectativa de vida ao nascer (EXPVI); para medida de qualidade do governo, a proporção dos gastos do governo em relação ao PIB per capita (GOV). Além disso, foram utilizados o grau de abertura (OPEN) e o índice de poder de paridade de compra (PPC).
As variáveis dependente e explicativas levadas em consideração no modelo empírico estão detalhadas no Quadro 1.
5. Resultados e discussão
Com o intuito de remover os efeitos não observados, específicos às regiões e invariantes no tempo, o modelo foi estimado em primeiras diferenças (2005-1985). A fim de avaliar se o modelo de convergência condicional local (estimado por RPG) se ajusta melhor aos dados, o modelo linear clássico de coeficientes globais foi também estimado para que uma comparação entre esses dois modelos seja possível.
Os resultados do modelo global, bem como alguns critérios de ajuste do modelo, são apresentados na Tabela 1 para os dados transformados em diferenças (2005-1985).
Resultados do modelo de coeficientes globais estimados para a variável taxa de crescimento do PIB por trabalhador, 1985-2005 (em diferenças)
Os resultados do modelo global, em diferenças, confirmam a hipótese de convergência. O coeficiente referente ao PIB inicial é negativamente relacionado à taxa de crescimento do PIB por trabalhador, corroborando a predição de convergência dos modelos clássicos. Fator que se apresenta como propulsor do crescimento é o investimento em capital físico (S) por apresentar um coeficiente positivo. As demais variáveis consideradas neste estudo, citadas na literatura como importantes para determinar a taxa de crescimento do PIB por trabalhador, no entanto, não se mostraram significantes para os 148 países amostrados no período, em diferenças, de 1985 a 2005. Cabe notar que apenas 27% da variação na taxa de crescimento do PIB por trabalhador é explicada pelo modelo de coeficientes globais.
O modelo RPG ajusta-se melhor aos dados em relação ao modelo global, pois o valor do critério de informação de Akaike é menor para o modelo de convergência condicional local (AICRPG: -25,27 < AICglobal: -11,11). Dessa forma, uma regressão de convergência condicional para cada unidade espacial parece mais adequada. Outra questão que sugere que o modelo estimado por RPG é superior ao modelo global é o fato de que 42% da variação na taxa de crescimento do PIB por trabalhador ser explicada pelo modelo, ajuste bem acima dos 27% observados no modelo global. Para averiguar a pressuposição de melhor ajuste do modelo RPG em relação ao modelo de coeficientes globais, o teste ANOVA deve ser analisado. Por meio do valor da estatística F de 3,645, rejeita-se a hipótese nula de que o modelo RPG não melhora os resultados do modelo global.
Os resultados do teste de Monte-Carlo, por sua vez, indicam se os parâmetros estimados não exibem estabilidade espacial. Na Tabela 2são apresentados os resultados do teste. Observa-se que, considerando o nível de 5% de significância, apresenta variabilidade espacial somente a variável relativa ao PIB inicial.
A inclusão de variáveis dummies para representar os outliers superiores e inferiores de resíduos não afeta significativamente o modelo RPG, como pode ser observado ao se comparar a primeira e a segunda colunas da Tabela 2: é verificada a instabilidade espacial para o coeficiente do PIB inicial, considerando o nível de significância de 10%. Os coeficientes das demais variáveis permanecem não significativos. Os resíduos do modelo RPG foram analisados no tocante à autocorrelação espacial por meio da estatística I de Moran. Foram testadas diversas matrizes de ponderação espacial do tipo k-vizinhos mais próximos,14 14 Foram testadas matrizes de pesos espaciais baseados em um vizinho mais próximo até vinte vizinhos mais próximos (k=1,..., 20). as quais não indicaram presença de dependência espacial remanescente para o modelo de convergência local com dados em diferenças. Portanto, no caso dos 148 países analisados, apenas o PIB inicial possui resposta local. Com isso, é possível descobrir se cada país está convergindo ou não, assim como a sua velocidade de convergência e a meia-vida.
Isso pode ser esclarecido pela visualização dos mapas de taxa de convergência local (Figura 1) e de meia-vida local (Figura 2), obtidos por meio do parâmetro local estimado pelo modelo RPG para o PIB inicial. Na Figura 1 é apresentada a velocidade de convergência local para os países amostrados em um nível de significância de 5%, seguindo a distribuição de desvios-padrão. Quanto à escala de cores, quanto mais escuras, maior é a velocidade de convergência do país em questão.
Velocidade de convergência local para o período, em diferenças, 2005-1985, em 5% de significância.
Por intermédio da inspeção visual da Figura 1, percebe-se que para todo o continente americano, para os países africanos Cabo Verde, Gâmbia, Senegal e Serra Leoa e para Samoa e Tonga na Oceania, a averiguação do processo de convergência é inconclusiva para o período em questão. A natureza inconclusiva da análise para a América Latina pode ter sido em decorrência do período considerado neste trabalho. Segundo relatório do FMI, "o desempenho da economia latino-americana nas últimas duas décadas foi algo decepcionante". O estudo concluiu que as reformas estruturais e de estabilização ocorridas na década de 1990 estimularam o crescimento, mas não foram suficientes para superar problemas estruturais, incluindo a pobreza (IMF, 2005). Além disso, deve-se atentar para o fato de que a década de 1980 é conhecida como a "década perdida" para a América Latina. Cabe enfatizar que não foram encontrados coeficientes positivos referentes ao PIB inicial. Portanto, não há indícios de divergência, como pressuposto pelos modelos de crescimento endógeno, entre os 148 países amostrados.
Resultados interessantes referem-se aos países que reduziram a desigualdade econômica em relação às nações mais avançadas. Pode-se perceber que os países asiáticos foram os que obtiveram velocidade de convergência de, pelo menos, um (1) desvio-padrão acima da média, ou seja, as taxas de convergência alcançadas por esses países estiveram acima de 1,67% ao ano, demonstrando que nesses países o efeito catch up foi significativo para o período analisado. Ressalta-se ainda que nove países da sub-região do Oriente Médio (Arábia Saudita, Bahrein, Catar, Emirados Árabes Unidos, Irã, Iraque, Kuwait, Omã, Síria) estão nesse grupo. Pertencem a esse grupo também China e Índia.
Além dos países asiáticos, as nações africanas Nepal, Djibouti, Maurício e Etiópia e a Finlândia, um país situado no norte da Europa, obtiveram, também, uma expressiva taxa de convergência entre os anos 1985 e 2005. Para esse conjunto de países, a meia-vida verificada foi de 34 anos, em média. Isso significa dizer que em 34 anos a desigualdade observada entre esses países seria reduzida à metade. Cabe salientar que Irã e Emirados Árabes Unidos foram os países que cresceram às maiores taxas encontradas neste trabalho, 2,35% e 2,27% ao ano, respectivamente (meia-vida de, aproximadamente, 30 anos). Crescendo também acima da média, estão alguns países da Oceania e Europa assim como boa parte dos países da África. Exemplos de tais países são Austrália, Egito, Japão, Sudão, Suécia, Papua Nova Guiné, Quênia e Camarões. A taxa de convergência obtida por esses países situa-se entre 1,67% e 1,46% ao ano (1/2 desvio-padrão em relação à média).
De modo oposto, alguns países de sub-regiões da África, quais sejam, Central, Ocidental e Meridional e da Europa Ocidental e Meridional cresceram abaixo da velocidade média de convergência local estimada, entre 1,05% e 1,46% ao ano. Países que alcançaram os menores valores para a velocidade de convergência (entre 1,05% e 0,47% ao ano) são países da África Ocidental (exceto Níger); da região Norte da África constam dois países, Argélia e Marrocos, além de Namíbia (África Meridional) e Gabão e Guiné Equatorial (África Central). Convergindo a essa taxa estão também os países europeus Espanha, Islândia e Portugal.
Na Figura 2 são apresentados os resultados para a meia-vida local. O objetivo de se mapear a meia-vida local é compreender de maneira mais adequada o conceito de velocidade de convergência. Os intervalos foram definidos com base em desvios-padrão em relação à média da meia-vida local, a saber, 53 anos.
Como pode ser observado, Irã, Emirados Árabes Unidos, Catar, Kuwait, Omã e Bahrein, em menos de 32 anos, conseguem eliminar o hiato de desigualdade de renda em relação aos países mais ricos. Cabe salientar que são países do Oriente Médio que têm sua economia impulsionada pela produção de petróleo. Ainda com uma meia-vida menor que os 53 anos médios estimados neste trabalho, estão países da África Oriental e Norte da África, exceto Argélia, Marrocos e Tunísia, da Ásia e da Oceania, além de alguns países europeus.
Países com meia-vida entre 53 e 63 anos podem ser citados França, Inglaterra e Bélgica (Europa Ocidental), Chade, África Central e República Democrática do Congo (África Central), Botsuana e África do Sul (África Meridional) além de Zâmbia, Zimbábue (África Oriental) e Tunísia (Norte da África). Nesses países, mais de meio século seria necessário para reduzir pela metade a desigualdade de renda. Os países africanos como Gana, Costa do Marfim, Guiné, Libéria, entre outros e Portugal (Europa) obtiveram meia-vida acima de 74 anos, ou seja, nesses países a velocidade de convergência observada situou-se abaixo de 1% ao ano implicando, pelo menos, 74 anos para eliminar apenas a metade da lacuna inicial da renda por trabalhador em relação ao estado estacionário. Esse valor é o dobro da meia-vida de 35-45 anos tradicionalmente encontrada pelos modelos neoclássicos (Barro e Sala-i-Martin, 1992BARRO, R.; SALA-I-MARTIN, X. Convergence. Journal of Political Economy, Vol. 100, n. 2, 1992.; Mankiw et al., 1992MANKIW, N.G. D.; ROMER, D.; WEIL, A. Contribution to the Empirics of Economic Growth. Quar terly Journal of Economics, vol.107 (2), pp.407-437, 1992.).
6. Considerações finais
A heterogeneidade espacial pôde ser contemplada em sua forma extrema por intermédio da técnica de Regressão Ponderada Geograficamente (RPG). Após a estimação de um modelo de convergência local, percebe-se que um modelo de convergência global pode ser considerado falho: há diferenças significativas quando consideradas as respostas locais, específicas a cada país. A melhor especificação para representar a hipótese de convergência condicional para a amostra de 148 países no período de 1985 a 2005, em diferenças, é o modelo RPG sem correção para dependência espacial, pois não foi identificada a presença de autocorrelação espacial nos resíduos.
Os resultados do modelo RPG mostraram que houve variabilidade espacial nos parâmetros somente para o PIB do ano inicial. Portanto, condicionada às demais variáveis, a hipótese de convergência local foi confirmada, exceto para o continente americano e os países africanos Cabo Verde, Gâmbia, Senegal e Serra Leoa e para Samoa e Tonga na Oceania, onde a análise de convergência demonstrou-se inconclusiva para o período considerado neste trabalho. De posse dos coeficientes negativos estimados para o PIB inicial, tornou-se possível calcular a velocidade de convergência para cada país. Em média, a velocidade de convergência local encontrada neste trabalho foi de 1,46% ao ano, valor condizente com as estimativas neoclássicas de 1,4% - 1,8% ao ano (Barro e Sala-i-Martin, 1992BARRO, R.; SALA-I-MARTIN, X. Convergence. Journal of Political Economy, Vol. 100, n. 2, 1992.; Mankiw et al., 1992MANKIW, N.G. D.; ROMER, D.; WEIL, A. Contribution to the Empirics of Economic Growth. Quar terly Journal of Economics, vol.107 (2), pp.407-437, 1992.). A meia-vida local associada a esse valor é de 47 anos. Os países do Oriente Médio (Irã, Emirados Árabes Unidos, Catar, Kuwait, Omã e Bahrein) foram os que obtiveram as maiores taxas de convergência, entre 2,16% e 2,35% ao ano, implicando uma meia-vida abaixo de 32 anos. De modo oposto, países que alcançaram valores para a velocidade de convergência abaixo da média de 1,46% ao ano estão os países africanos (com exceção de Egito, Sudão, Etiópia, Quênia e Madagascar) além de Espanha, Islândia e Portugal na Europa. Para esse grupo de países, mais de meio século é necessário para eliminar metade da lacuna inicial da renda por trabalhador em relação ao estado estacionário.
Ressalta-se que, apesar de não ter sido detectada a dependência espacial nos resíduos no modelo global, o mapeamento dos resultados da velocidade de convergência local e da meia-vida local demonstrou certa concentração geográfica, isto é, países vizinhos estão convergindo a taxas similares e, por conseguinte, o tempo para eliminar metade do gap de desigualdade de renda tem sido semelhante.
Desde a confirmação da hipótese de convergência condicional para 98 países realizada por Mankiw et al. (1992)MANKIW, N.G. D.; ROMER, D.; WEIL, A. Contribution to the Empirics of Economic Growth. Quar terly Journal of Economics, vol.107 (2), pp.407-437, 1992. e Barro e Sala-i-Martin (1992)BARRO, R.; SALA-I-MARTIN, X. Convergence. Journal of Political Economy, Vol. 100, n. 2, 1992., com dados em cross section, uma vasta literatura se seguiu explorando essa questão com diferentes bases de dados e diversos métodos econométricos. Contudo, a principal conclusão de velocidade de convergência ao nível de, aproximadamente, 2% ao ano tem sido confirmada (Sala-i-Martin, 1995; Durlauf e Johnson, 1995DURLAUF, S.; JOHNSON, P. Multiple regimes and cross-country growth behaviour. Journal of Applied Econometrics. Vol. 10, n. 4, p. 365-384, 1995., Rivera-Batiz, 1993RIVERA-BATIZ, L. Convergence of Regional Income in China, UFP, Working Paper, 1993.). De acordo com Canova e Marcet (1999)CANOVA, F.; MARCET, A. The poor stay poor: non-convergence across countries and regions. CEPR Discussion Paper n. 1265, 1999., esses resultados suportam a visão de que, controlando para as características dos países (acumulação de capital físico e humano, tamanho do governo, inserção no mercado, distorções no mercado, entre outras), diferenças na renda desaparecerão vagarosamente.
Os resultados encontrados por este trabalho também validam a hipótese de convergência teorizada pela vertente neoclássica de crescimento econômico. Nas estimações realizadas, considerando os efeitos fixos em primeiras diferenças, e a heterogeneidade espacial extrema, foi encontrada velocidade de convergência de, em média, 1,5% ao ano. Mais interessante, porém, é a constatação de múltiplos equilíbrios quando considerada a análise de convergência local.
Um grupo de países se aproxima de um equilíbrio particular em virtude da existência de atributos correlatos ou porque se encontrava em uma localização inicial correspondente àquele equilíbrio. Portanto, os países aproximam-se um dos outros em termos de renda, fato em consonância com a convergência em clubes ou múltiplos equilíbrios (Durlauf e Johnson, 1995DURLAUF, S.; JOHNSON, P. Multiple regimes and cross-country growth behaviour. Journal of Applied Econometrics. Vol. 10, n. 4, p. 365-384, 1995.; Quah, 1996QUAH, D. Empirics for economic growth and convergence. European Economic Review, Vol. 40, p. 1353-75, 1996.).
Vale destacar que os intervalos de convergência aqui definidos são consequência de como o crescimento de um país se processa, em termos de seu próprio ritmo condicionado às suas características socioeconômicas iniciais, relativamente ao crescimento de outros países, e não em relação a si mesmo. Neste caso, as economias têm um grau de dependência de suas condições iniciais, criando uma resistência a permanecer em seu grupo, como no caso dos países africanos. Entretanto, de acordo com seu processo histórico, algumas economias realizam catch up, superando suas limitadas condições iniciais, e ingressam em um grupo de renda mais alta (caso dos países do Oriente Médio, dos "tigres asiáticos", da China e da Índia), ou mesmo são rebaixadas a um grupo mais pobre (como exemplos, Portugal, Espanha e Islândia). Dessa forma, a presença de intervalos de países convergentes a taxas similares, em faixas que variam entre 0,47% e 2,35% ao ano, reafirma a importância da integração regional para o crescimento econômico dos países em virtude da concentração geográfica referente à velocidade de convergência local.
-
♦
Os autores agradecem o apoio do Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) e da Fundação de Amparo à Pesquisa no Estado de Minas Gerais (FAPEMIG) durante a elaboração deste artigo.
-
1
Mais detalhes sobre os modelos em Romer (2006)ROMER, D. Advanced Macroeconomics. McGraw-Hill, 2006..
-
2
A abordagem de painel de dados tem sido aplicada por diversos autores como Caselli et al. (1996)CASELLI, F., ESQUIVEL, G., LEFORT, F. Reopening the Convergence Debate: A New Look at Cross-Country Growth Empirics, Journal of Economic Growth, 1, 3, p. 363-389, 1996., Canova e Marcet (1999)CANOVA, F.; MARCET, A. The poor stay poor: non-convergence across countries and regions. CEPR Discussion Paper n. 1265, 1999., De La Fuente (2002)DE LA FUENTE, A. On the sources of convergence: a close look at the Spanish regions. European Economic Review. Vol. 46, p. 569-599, 2002., entre outros. Tais estudos são em nível regional.
-
3
Uma revisão detalhada sobre os estudos que consideram os efeitos espaciais é encontrada em Abreu et al.(2005)ABREU, M.; de GROOT, H.L.F; FLORAX, R.J.G.M. Space and growth: a survey of empirical evidence and methods. Région et Développement, Vol. 21, p.12-43, 2005..
-
4
A amostra máxima do estudo de Behar (2008)BEHAR, A. Neighborhood growth effects: An annual panel data approach. Background paper, Resha ping Economic Geography, 2008.conta com 134 países.
-
5
Tradução do inglês, geographically weighted regression (GWR).
-
6
A maior parte dos estudos sobre convergência de renda utiliza a variável taxa de crescimento do PIB per capita.
-
7
O modelo detalhado e suas implicações empíricas podem ser visto em Ertur e Koch (2007)ERTUR, C.; KOCH, W. Growth, Technological Interdependence and Spatial Externalities: Theory and Evidence. Journal of Applied Econometrics.Vol. 22, p. 1033-1062, 2007..
-
8
Nesse caso, quanto mais próxima a ordem de vizinhança, maior o valor do parâmetro y portanto, maior a força de interdependência tecnológica.
-
9
Ver detalhes a respeito disso em Fotheringham et al. (2002)FOTHERINGHAM, A.S.;; BRUNSDON, C. CHARLTON, M.E. Quantitative Geography, London: Sage, 2000..
-
10
Para maiores detalhes técnicos sobre o teste de Monte Carlo, ver Fotheringham et al. (2002)FOTHERINGHAM, A.S.;; BRUNSDON, C. CHARLTON, M.E. Quantitative Geography, London: Sage, 2000..
-
11
O problema da omissão da heterogeneidade espacial nas regressões de convergência é abordado em Temple (1999TEMPLE, J. The New Growth Evidence. Journal of Economic Literature, American Economic Association, vol. 37(1), p. 112-156, 1999.; 2000______. Growth Regressions and What the Textbooks Don't Tell You. Bulletin of Economic Research, Wiley Blackwell, vol. 52(3), p. 181-205, 2000.).
-
12
Dados disponíveis em: http://pwt.econ.upenn.edu/php_site/pwt63/pwt63_form.php. Todos os dados retirados da PWT, exceto dados de população e de poder de paridade de compra, estão a preços constantes de 2005.
-
13
Dados disponíveis em: http://databank.worldbank.org/ddp/home.do?Step=12&id=4&CNO=2.
-
14
Foram testadas matrizes de pesos espaciais baseados em um vizinho mais próximo até vinte vizinhos mais próximos (k=1,..., 20).
Agradecimentos
Os autores gostariam de agradecer o suporte financeiro provido pelo Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Fundação de Amparo à Pesquisa do Estado de Minas Gerais (Fapemig) e à Universidade Federal de Juiz de Fora (UFJF).
Referências
- ABREU, M.; de GROOT, H.L.F; FLORAX, R.J.G.M. Space and growth: a survey of empirical evidence and methods. Région et Développement, Vol. 21, p.12-43, 2005.
- ARBIA, G.M.; PIRAS, G. Convergence in per-capita GDP across European regions using panel data models extended to spatial autocorrelation effects. ERSA conference papers, ERSA 04, p.524, European Regional Science Association, 2004.
- BARRETO, R. C. S.; ALMEIDA, E. S. Crescimento econômico e convergência de renda no Brasil: a contribuição do capital humano e da infra-estrutura. In: VI ENCONTRO NACIONAL DA AS SOCIAÇÃO BRASILEIRA DE ESTUDOS REGIONAIS E URBANOS - VI ENABER, 2008, Aracaju. Anais do VI ENABER, 2008.
- BARRO, R. Economic growth in a cross section of countries. The Quarterly Journal of Economics, Vol. 106, Issue 2, p. 407-443, 1991.
- BARRO, R.; SALA-I-MARTIN, X. Convergence. Journal of Political Economy, Vol. 100, n. 2, 1992.
- BARRO, R.; SALA-I-MARTIN, X. Technological Diffusion, Convergence and Growth. Journal of Economic Growth, Vol. 1, p. 1-26, 1997.
- BAUMOL, W. J. Productivity growth, convergence and welfare: what the long-run data show. American Economic Review Vol. 76, p. 1072-1085, 1986.
- BAUMOL, W.J.; WOLFF, E.N. Productivity Growth, Convergence, and Welfare: Reply. American Economic Review, American Economic Association, vol. 78(5), p. 1155-59, 1988.
- BEHAR, A. Neighborhood growth effects: An annual panel data approach Background paper, Resha ping Economic Geography, 2008.
- BRASILI C., BRUNO F., SAGUATTI A. A spatial econometric model for evaluating conditional β-convergence across EU regions, contributed paper presentato alla III World Conference of Spatial Econometrics, Barcelona, 2009.
- BRUNSDON, C.; FOTHERINGHAM, A.S.; CHARLTON, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geographical Analysis Vol. 28, n. 4, p. 281-298, 1996.
- CANOVA, F.; MARCET, A. The poor stay poor: non-convergence across countries and regions. CEPR Discussion Paper n. 1265, 1999.
- CASELLI, F., ESQUIVEL, G., LEFORT, F. Reopening the Convergence Debate: A New Look at Cross-Country Growth Empirics, Journal of Economic Growth, 1, 3, p. 363-389, 1996.
- CHASCO, C.; GARCÍA, I.; VICÉNS, J. Modeling spatial variations in household disposable income with Geographically Weighted Regression. Munich Personal RePEc Archive. Universidad Au tónoma de Madrid, Spain, 2007.
- DE LA FUENTE, A. On the sources of convergence: a close look at the Spanish regions. European Economic Review. Vol. 46, p. 569-599, 2002.
- DE LONG, J.B. Productivity Growth, Convergence, and Welfare: Comment. American Economic Review. American Economic Association, vol. 78(5), p. 1138-54, 1988.
- DE LONG, J.B.; Summers, L.H. Equipment Investment and Economic Growth, The Quarterly Journal of Economics, MIT Press, vol. 106(2), p. 445-502, 1991.
- DURLAUF, S.; JOHNSON, P. Multiple regimes and cross-country growth behaviour. Journal of Applied Econometrics Vol. 10, n. 4, p. 365-384, 1995.
- DURLAUF, S. N.; KOURTELLOS, A.; MINKIN, A. The Local Solow Growth Model. European Economic Review Vol. 45, n. 4-6, pp. 928-940, 2001.
- ERTUR, C.; LE GALLO, J.; BAUMONT, C. The European Regional Convergence Process, 1980-1995: Do Spatial Regimes and Spatial Dependence Matter? International Regional Science Review Vol. 29, n. 1, p. 3-34, 2006.
- ERTUR, C.; KOCH, W. Growth, Technological Interdependence and Spatial Externalities: Theory and Evidence. Journal of Applied Econometrics.Vol. 22, p. 1033-1062, 2007.
- EVANS, P. Using Cross-country Variances to Evaluate Growth Theories. Journal of Economic Dynamics and Control, Vol. 20, p. 1027-1049, 1996.
- EVANS, P.; KARRAS, G. Convergence Revisited. Journal of Monetary Economics, Vol. 37, p. 249-265, 1996.
- FAGERBERG, J.; GODINHO, M. Innovation and Catching-up.In: Fagerberg et al. (Eds) 2005.
- FINGLETON, B. Economic geography with spatial econometrics: a "third way" to analyse economic development and "equilibrium" with application to the EU regions EUI Working Paper ECO, n. 99/21, 1999.
- FLORAX R.J.G.M.; NIJKAMP, P. Misspecification in linear spatial regression models. In: K. Kempf-Leonard (ed.), Encyclopedia of Social Measurement, San Diego: Academic Press, p. 695-707, 2005.
- FOTHERINGHAM, A.S.;; BRUNSDON, C. CHARLTON, M.E. Quantitative Geography, London: Sage, 2000.
- FUJITA, M.; KRUGMAN, P.; VENABLES, A. J. Economia Espacial: urbanização, prosperidade eco nômica e desenvolvimento humano no mundo. Editora Futura, São Paulo, 2002.
- GRIER, K.B.; TULLOCK, G. An Empirical Analysis of Cross-National Economic Growth, 1951-1980. Journal of Monetary Economics, Vol. 24, p. 259-276, 1989.
- HESTON, A. SUMMERS, R.; ATEN, B. Penn World Table Version 6.3 Center for International Com parisons of Production, Income and Prices at the University of Pennsylvania, 2009.
- ISLAM, N. Growth Empirics: a panel data approach. The Quarterly Journal of Economics. Vol. 110, n.4, p.1127-1170, 1995.
- ______. What have we learnt from the convergence debate? Journal of Economic Surveys. Vol. 17, p. 309-362, 2003.
- LEE, K.; PESARAN, M.H.; SMITH, R. Growth and convergence in a multi-country empirical stochastic Solow model. Journal Applied of Economics Vol.12, p. 357-392, 1997.
- LÓPEZ-BAZO, E.; VAYÁ, A.M.; Suriñach, J. Regional economic dynamic and convergence in the European Union, Annals of Regional Science, Vol. 33, p. 343-70, 1999.
- LUCAS, R. E. On the Mechanics of Economic Development. Journal of Monetary Economics. Vol. 22, n. 1, p. 3-42, 1988.
- MAGALHÃES, A. M.; HEWINGS, G. D.; AZZONI, C. Spatial Dependence and Regional Convergence in Brazil. In: Internacional Regional Science Meeting, Chicago. ANAIS DO INTERNACIONAL REGIONAL SCIENCE MEETING, 2000.
- MANKIW, N.G. D.; ROMER, D.; WEIL, A. Contribution to the Empirics of Economic Growth. Quar terly Journal of Economics, vol.107 (2), pp.407-437, 1992.
- MANKIW, G. The Growth of Nations, Brookings Papers on Economic Activity, p. 275-326, 1995.
- MELICIANI V.; PERACCHI, F. Convergence in per-capita GDP across European regions: a reappraisal. Empirical Economics. Vol. 31, p.549-568, 2006.
- MORENO, R.; TREHAN, B. Location and the Growth of Nations, Journal of Economic Growth, Springer, vol. 2(4), p. 399-418, 1997.
- PACE, R.K.; LE SAGE, J.P. Omitted variables biases of OLS and spatial lag models. In: PÁEZ, A.;; LE GALLO, J. BULIUNG, R. AND DALL'ERBA, S. (eds.). Progress In Spatial Analysis: Theory and Computation, and Thematic Applications, Berlin:, Springer forthcoming, 2009.
- QUAH, D. International Patterns of Economic Growth: I. Persistence in Cross Country Disparities, Department of Economics, MIT, Cambridge, 1990.
- QUAH, D. Empirics for economic growth and convergence. European Economic Review, Vol. 40, p. 1353-75, 1996.
- RAMIREZ, M.T.; LOBOGUERRERO, A. Spatial Dependence and Economic Growth: Evidence from a Panel of Countries, Banco de la República, Colombia, 2002.
- RAMSEY, F. A mathematical theory of savings. The Economic Journal, Vol. 38, p. 543-59, 1929.
- REY, S. J. MONTOURI, B. D. US regional income convergence: A spatial econometric perspective. Regional Studies, Vol. 33, n.2, p. 143-156, 1999.
- RIVERA-BATIZ, L. Convergence of Regional Income in China, UFP, Working Paper, 1993.
- ROMER, D. Advanced Macroeconomics. McGraw-Hill, 2006.
- ROMER, P.M. Increasing returns and long-run growth. Journal of Political Economy . Vol. 94, n. 5 p. 1002-37, 1986.
- ______. Endogenous technological change . Journal of Political Economy. v. 98, n. 5, p. 71-102, 1990.
- SALA-I-MARTIN, X. The Classical Approach to Convergence Analysis. Economic Journal,Royal Economic Society, vol. 106(437), p. 1019-36, 1996.
- SILVEIRA NETO, R.M. Localização, Crescimento e Spillovers: Evidências para os Estados Brasileiros e Setores. In: XXIX ENCONTRO NACIONAL DE ECONOMIA. Salvador/BA, 2001. Anais do XXIX Encontro Nacional de Economia, 2001.
- SILVEIRA NETO, R.M.; Azzoni, C.R. Non Spatial Public Policies and Regional Inequality in Brazil. In: RSAI WORLD CONGRESS 2008, São Paulo. Annals of RSAI World Congress 2008.
- SOLOW, R.M., A Contribution to the Theory of Economic Growth. Quarterly Journal of Econom ics, Vol. LXX, p. 65-94, 1956.
- TEMPLE, J. The New Growth Evidence. Journal of Economic Literature, American Economic Association, vol. 37(1), p. 112-156, 1999.
- ______. Growth Regressions and What the Textbooks Don't Tell You. Bulletin of Economic Research, Wiley Blackwell, vol. 52(3), p. 181-205, 2000.
- WEI, Y.H.D.; YE, X. Beyond Convergence: Space, Scale and Regional Inequality in China. Tijd schrift voor Economische en Sociale Geografie Vol. 100, No. 1, pp. 59-80, 2009.
- YILDIRIM, J. Regional Policy and Economic Convergence in Turkey: a Spatial Data Analysis. In: 18TH EUROPEAN ADVANCED STUDIES INSTITUTE IN REGIONAL SCIENCE. Kraków e Łódź, 2005.
Datas de Publicação
-
Publicação nesta coleção
Apr-Jun 2015
Histórico
-
Recebido
14 Ago 2012 -
Aceito
03 Fev 2014











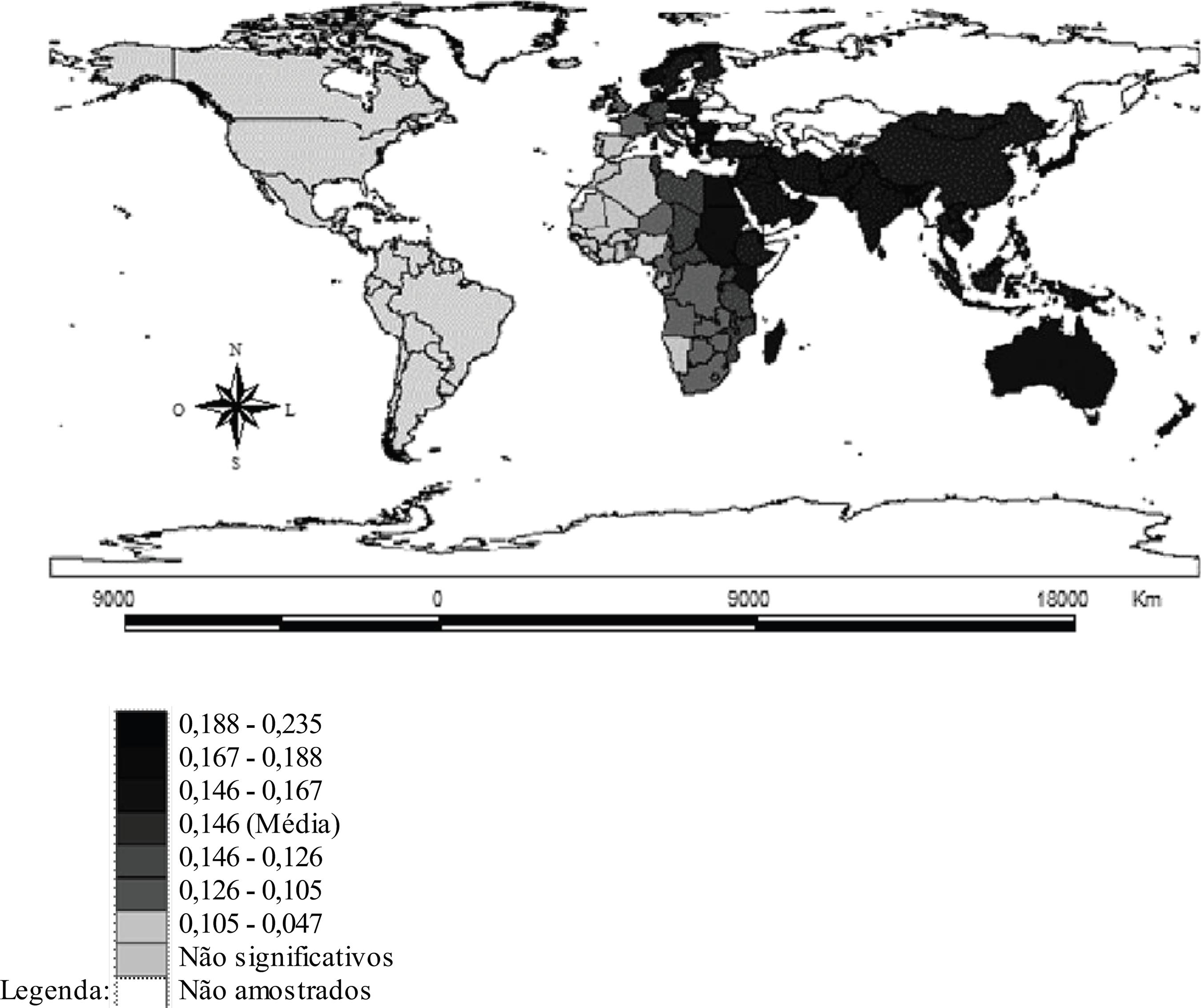 Nota: A distribuição dos valores segue desvios-padrão da média da velocidade de convergência. Fonte: Elaboração própria.
Nota: A distribuição dos valores segue desvios-padrão da média da velocidade de convergência. Fonte: Elaboração própria.
 Nota: A distribuição dos valores segue desvios-padrão da média da meia-vida local. Fonte: Elaboração própria.
Nota: A distribuição dos valores segue desvios-padrão da média da meia-vida local. Fonte: Elaboração própria.