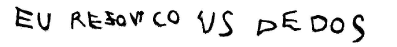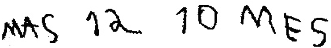A notação escrita na resolução de problemas por crianças pré-escolares

Written notation in problem solving by pre-school children

A Notação Escrita na Resolução de Problemas por Crianças Pré-Escolares ¹

Ana Coêlho Vieira Selva²

Ana Carolina Perrusi Brandão

Universidade Federal de Pernambuco

RESUMO - O estudo investigou como crianças de 4 a 6 anos resolvem problemas de subtração usando a notação escrita. Trinta crianças nas séries de Alfabetização, Jardim II e Jardim I foram solicitadas a resolverem quatro problemas (dois do tipo mudança e dois de comparação), envolvendo pares numéricos maiores e menores que dez. Os problemas foram inseridos em uma situação que buscou dar maior significado para o uso do registro no papel. Os protocolos das entrevistas com as crianças foram analisados a partir de dois eixos: a influência do registro no papel para o processo de resolução dos problemas e os tipos de registros produzidos. Observamos que o registro escrito foi utilizado para apoiar os cálculos realizados, possibilitar o acompanhamento do processo de raciocínio e favorecer o avanço no registro das operações matemáticas. Concluímos que resolver problemas no papel pode se constituir em uma alternativa interessante para a educação infantil.

Palavras-chave: notação escrita; resolução de problemas; educação infantil.

Written Notation in Problem Solving by Pre-School Children

ABSTRACT - This study analyses how children from 4 to 6 years use written notation in subtraction problem solving. Thirty children from kindergarten to first levels were asked to solve four problems (two of the kind change and two of comparison), which involved numerical sets greater and smaller than 10. These problems were in a context which intented to give more sense for use of written notation. The written notation was analysed from two perspectives: the effect of the written notation in the solving process and the types of notations produced by the children. We observed that written notation help children in doing their calculations, allow them to follow their process of thinking and improve the representation of mathematical operations. We concluded that solving problems using written notations could be an interesting alternative for Kindergarten.

Key words: written notation; numerical problem-solving; kindergarten.

Atualmente, observa-se um esforço das redes de ensino público e mais recentemente do próprio MEC, em explicitar claramente os princípios que deverão nortear o trabalho pedagógico a ser desenvolvido nas escolas de educação infantil³. No que se refere à área de matemática, é unânime a recomendação para que se aproveitem as situações do cotidiano escolar (os famosos momentos de distribuição do lanche ou do material, arrumação da sala, uso do calendário etc), bem como os jogos e brincadeiras infantis que envolvam contagens, comparação entre quantidades, medidas, relações espaciais, classificações etc. Defende-se uma proposta que explore as idéias intuitivas das crianças, sua linguagem própria encorajando-se o contato com uma gama de idéias e representações matemáticas relativas a números, medidas, geometria e noções rudimentares de estatística (Smole, 1996). O trabalho com resolução de problemas também tem sido constantemente indicado, reforçando-se a necessidade de estimular as crianças a formular hipóteses, desenvolver estratégias de solução, relacionando e aplicando os conhecimentos que possuem, interagindo com as demais crianças de seu grupo.

Diante destas propostas, a nossa intenção é compreender melhor como crianças pequenas lidam com problemas matemáticos e mais particularmente, como utilizam a notação escrita para resolver problemas. Esperamos com isso fornecer subsídios ao educador infantil para que possa formular problemas mais desafiadores, e saiba intervir, de modo mais consciente, nas situações-problema por ele criadas.

A resolução de problemas e a notação escrita

São poucos os estudos que analisam o uso da notação escrita em matemática. Hughes (1986) verificou que crianças de 3 a 5 anos de idade, ao serem solicitadas a representar por escrito conjuntos de objetos discretos, usavam notações idiossincráticas, pictográficas e simbólicas. Sinclair, Siegrist e Sinclair (1983) e Sinclair, Mello e Siegrist (1990) observaram seis diferentes notações escritas utilizadas por crianças de 4 a 6 anos para representar quantidades de objetos discretos e quantidades numéricas ditas verbalmente. As notações foram as seguintes: (1) representação global da quantidade sem relevância para o valor cardinal da série. Ex.IIIIIIIII para quatro bolas; (2) representação de alguma característica perceptual do objeto. Ex. o desenho de uma casa representando cinco casas; (3) representação de cada objeto por um símbolo gráfico não-numérico. Ex. 000 ou III para três bolas; (4) representação de cada objeto por um símbolo numérico. Exs. 1234 ou 4444 para quatro bolas; (5) representação do valor cardinal por um numeral. Ex. 5 para cinco lápis; (6) representação do valor cardinal com algum adicional para representar o tipo de objeto. Ex. 5 e o desenho de bolas para representar cinco bolas.

Zunino (1995) analisou as representações apresentadas por crianças de 1ª série ao resolver problemas e contas, no papel, bem como descreveu as estratégias utilizadas por elas na solução dos problemas. O estudo mostrou que as crianças têm idéias próprias sobre quais são os aspectos das operações que devem ser representados graficamente (por exemplo, se representam exclusivamente o resultado do problema ou os dados incluídos no enunciado). Revelou ainda que nenhuma criança utiliza, de forma exclusiva, a representação convencional, observando-se na mesma criança formas de representação originais e convencionais.

Higino (1990) analisou os erros produzidos por crianças a partir de um ditado e leitura de números. Tal análise demonstrou que seus registros não eram aleatórios, mas sim refletiam os princípios lógicos subjacentes ao sistema de numeração decimal.

Assim como o estudo de Higino (1990), outros trabalhos na área de notação escrita têm dado maior ênfase à observação de como os princípios lógico-matemáticos são representados na escrita da criança, não investigando de que forma sua representação escrita espontânea pode influenciar a compreensão de conceitos matemáticos. Tal distinção é importante porque enquanto na primeira perspectiva temos apenas o sujeito representando seu conhecimento através da escrita, na segunda perspectiva, considera-se uma relação dialética entre sujeito e representações escritas. Desta forma, a criança produz a notação escrita, mas sua produção também exerce influência sobre seu raciocínio.

O estudo de Meira (1991) se insere neste último enfoque. O autor analisou a resolução de problemas sobre o conceito de função linear a partir do manuseio de materiais oferecidos a pares de sujeitos da sétima série. Os sujeitos produziram notações escritas como apoio para o raciocínio desenvolvido. Estas representações escritas, por sua vez, favoreciam o surgimento de novas interpretações.

Selva (1993) também analisou as representações escritas de crianças de alfabetização, primeira e segundas séries ao resolverem de problemas de divisão. As crianças foram distribuídas em grupos com diferentes materiais (fichas, papel/lápis, sem material) para apoiar seus cálculos. Foi verificado que o desempenho das crianças era favorecido tanto no grupo que utilizava fichas, quanto no grupo com papel e lápis. Entretanto, analisando as estratégias utilizadas constatou-se que o grupo de crianças que utilizou o papel e o lápis apresentou estratégias mais sofisticadas de resolução. As crianças do grupo com fichas usaram basicamente a estratégia de modelagem.

O estudo de Meira (1991) e o de Selva (1993) indicam a importância de se aprofundar a análise do uso das representações escritas espontâneas, pois tal tipo de representação parece favorecer em muitos aspectos o desenvolvimento da compreensão dos conceitos matemáticos. Smole (1996) observa que as crianças de 6 anos ao resolverem o problemas de subtração têm como opção "primeira e natural" o desenho. A autora afirma ainda que: "a criança só não recorre ao desenho como linguagem para resolver problemas se a escola inibir essa manifestação ou se houver uma exigência precoce do uso dos sinais aritméticos" (p. 103).

Um estudo realizado por Selva e Brandão (1999) indicou, entretanto, que este tipo de representação não tem sido considerada na Educação Infantil. Em 40 horas de observação nas séries de Jardim II e Alfabetização, foi evidenciado que o estímulo ao registro no papel aparecia apenas para o trabalho de escrita convencional dos numerais, no caso do Jardim II, ou para formalização do algoritmo da adição e subtração, no caso da Alfabetização.

Selva e Brandão (1999) analisaram o desempenho de crianças na resolução de problemas de subtração do tipo mudança, envolvendo pares numéricos inferiores a 10. Em cada série, os sujeitos resolveram os mesmos problemas variando apenas o recurso disponível para auxiliá-los: o grupo 1 possuía fichas, o grupo 2 papel e lápis, o grupo 3 não teve material algum para ajudá-los, e o grupo 4 dispunha tanto de fichas, como de papel e lápis.

Os resultados encontrados foram interessantes, pois diferentemente dos estudos de Meira (1991) e Selva (1993), o uso de papel e lápis nos grupos 2 e 4 foi bastante reduzido em todas as séries. Foi observado ainda que nos poucos casos em que as crianças usavam o registro no papel, o faziam apenas para escrever os dados ou o resultado do problema. Poucas crianças, portanto, usavam o papel para desenvolver suas estratégias de solução para o problema apresentado. Tais constatações confirmam o que foi verificado nas observações em sala de aula, em que o papel e o lápis são introduzidos apenas no momento de formalização dos conhecimentos matemáticos, bem como parece explicar o fato das crianças não saberem o que fazer, ou como usar papel e lápis enquanto uma possibilidade de apoio para a resolução de problemas matemáticos.

Considerando a existência de poucos estudos investigando a resolução de problemas por crianças pré-escolares, bem como o que tem sido produzido em pesquisa na área de representação escrita, cabe levantar algumas questões a partir do estudo de Selva e Brandão (1999), citado anteriormente:

1. Por que tão poucas crianças pré-escolares utilizaram papel e lápis como um recurso auxiliar para a resolução dos problemas a elas propostos? Será que este comportamento reflete a não familiaridade com este instrumento no contexto da educação infantil? Ou trata-se de uma questão de impossibilidade de sua utilização por crianças menores de 6 anos?

2. Será que a utilização de pares numéricos inferiores a 10 fez com que as crianças não sentissem necessidade de recorrer a outros recursos, como papel e lápis?

3. Será que se alterando a situação experimental, solicitando-se explicitamente a criança que utilize o papel para desenvolver seu raciocínio, o pedido seria atendido?

4. E neste caso, de que maneira o papel seria utilizado pela criança?

5. Em relação à estrutura dos problemas, qual a influência que esta exerceria sobre o desempenho das crianças?

O presente estudo pretende, portanto, explorar as questões apresentadas acima. Iremos a seguir apresentar a metodologia empregada nesta pesquisa.

Método

Sujeitos

A pesquisa envolveu 30 crianças, freqüentando uma mesma Pré-escola da cidade do Recife, distribuídas igualmente nas séries de Jardim I (média de idade: 4 anos e 9 meses), Jardim II (média de idade: 5 anos e 8 meses) e Alfabetização (média de idade: 6 anos e 5 meses).

Material

Gravador, fitas cassete, papel e lápis, e folhas para anotações durante as entrevistas com os sujeitos.

Procedimento

A tarefa consistiu em quatro problemas de subtração organizados em um pequeno texto (Quadro 1), que pretendeu contextualizar os problemas propostos buscando promover um maior envolvimento da criança com a situação experimental. A tarefa envolveu ainda uma "situação de comunicação", ou seja, a criança foi solicitada a auxiliar "um menino de outra escola" que, supostamente, não conseguia resolver alguns problemas e que, posteriormente, as soluções encontradas seriam transmitidas ao tal menino fictício. Esta instrução buscou, portanto, dar um sentido maior ao uso de papel e de lápis na resolução dos problemas. Vale ressaltar que mesmo quando as crianças resolviam o problema por cálculo mental ou uso dos dedos, também era pedido que resolvessem no papel.

Abaixo, encontra-se transcrição da instrução:

"A professora de um menino chamado Paulinho que estuda em outra escola pediu pra ele resolver alguns problemas. Só que ele não está conseguindo. A professora disse que tem que resolver no papel. Será que você pode ajudar Paulinho a resolvê-los, fazendo aqui no papel?"

Os problemas propostos foram dos tipos mudança e comparação, envolvendo pares numéricos grandes (minuendo e subtraendo variando entre 10 e 13) e pequenos (minuendo e subtraendo menor do que 10). Tais problemas fazem parte do campo conceitual das estruturas aditivas (Vergnaud, 1982), sendo definidos da seguinte forma:

¾ Problemas de mudança: implicam uma ação direta que causa um aumento ou decréscimo de uma dada quantidade. Ex. Pedro comprou 8 bombons. Ele deu 5 bombons a Marcela. Com quantos bombons ele ficou?

¾ Problemas de comparação: implicam a comparação entre duas quantidades. Ex. Marcela comprou 12 chicletes e Pedro comprou 10 chicletes. Quantos chicletes Marcela comprou a mais do que Pedro?

Para uma melhor visualização do plano experimental apresentamos o esquema seguido nas três séries investigadas:

Os pares numéricos utilizados nos quatro problemas propostos apareceram sempre em uma mesma ordem (ou seja: 8 e 5, 12 e 10, 13 e 11, 7 e 3), sendo os tipos de problemas apresentados de forma intercalada, ora começando-se por um problema de mudança, ora por um de comparação. Desta forma, um mesmo par numérico era sempre apresentado, ora em um problema de comparação, ora em um problema de mudança.

Resultados

Os dados obtidos foram analisados quantitativa⁴ e qualitativamente, porém neste artigo optamos por dar ênfase à análise qualitativa dos protocolos com a transcrição das entrevistas feitas com as crianças. Os resultados quantitativos serão, portanto, apenas apresentados e brevemente comentados.

Como já era esperado as crianças da série de Alfabetização apresentaram um desempenho significativamente superior em relação às crianças do Jardim II e Jardim I (72,5%, 50% e 22,5% de acertos, respectivamente, [F_{(2, 27)} = 8,01, p < 0,002]). A variável tipo de problema também mostrou-se significativa, ou seja, problemas do tipo mudança foram mais fáceis de serem resolvidos que os problemas do tipo comparação (66,6% e 30% de acertos, respectivamente, [F_{(1, 27)} = 18,94, p < 0,000]). Um dado interessante, ainda que não tenha sido significativo, diz respeito a interação entre as variáveis Série e Tipo de Problema. As crianças da Alfabetização apresentaram desempenhos semelhantes na resolução de problemas de mudança e comparação (80% e 65 % de acertos, respectivamente) enquanto que para as crianças do Jardim II, os problemas de comparação não foram facilmente entendidos (75% de acerto em mudança e 25% de acertos em comparação). Já as crianças do Jardim I demonstraram dificuldades em ambos os tipos de problemas, principalmente nos problemas de comparação (45% de acertos nos problemas de mudança e nenhum acerto nos problemas de comparação). Apesar dos dados mostrarem que os problemas de comparação são realmente mais complexos, isto não implica que não possam ser apresentados para crianças pré-escolares. Em uma análise de livros didáticos dirigidos à Educação Infantil realizada por Brandão e Selva (1998), foi observado uma reduzida variedade em termos dos tipos de problemas de estrutura aditiva, constatando-se uma quase exclusividade de problemas de mudança e combinação.

Um outro dado interessante diz respeito à variável tamanho dos pares numéricos. Foi evidenciado que os problemas com pares numéricos pequenos foram significativamente mais fáceis de serem resolvidos que os problemas com pares numéricos maiores (56,6% e 40%, respectivamente, [F_{(1, 27)} = 13,64, p < 0,001]). A interação tipo de problema e tamanho também mostrou-se significativa [F_{(1, 27)} = 8,82, p < 0,006]. Enquanto o tamanho dos pares numéricos influenciou a resolução dos problemas de mudança (83,3% de acertos para pares pequenos e 50% de acertos para os grandes), nos problemas de comparação não se observaram diferenças significativas de acertos (30% de acertos para pares numéricos grandes e pequenos). Conclui-se, portanto, que problemas do tipo comparação, por serem mais complexos, trazem maior dificuldade, mesmo envolvendo pares numéricos com valores pequenos.

Passaremos agora para uma análise de natureza qualitativa, em que se buscou discutir quando e como as crianças usam o papel na resolução dos problemas.

Um primeiro aspecto que merece atenção é o fato de que a instrução dada, em que se pedia explicitamente para que a criança usasse o papel, não surtiu o efeito esperado. As crianças quase sempre tentavam, inicialmente, resolver os problemas através de estratégias mentais⁵, utilizando-se dos dedos para apoiar seus cálculos. Assim, o recurso do papel foi utilizado espontaneamente, ou seja, sem qualquer sugestão extra do examinador, em apenas 17,5% dos problemas na Alfabetização, em 12,5%, no Jardim II e em 17,5% no Jardim I.

Estes dados confirmam o estudo de Selva e Brandão (1999), mostrando que resolver problemas no papel não é algo familiar a crianças pré-escolares. No entanto, apesar da estranheza provocada pela solicitação do examinador, as crianças efetivamente conseguem fazer registros no papel bastante interessantes e articulados com os problemas propostos. Assim, crianças entre 4, 5 e 6 anos conseguem atender ao pedido do examinador e usar o papel, como se pode constatar no protocolo de Juliana (Jardim II):

Juliana responde corretamente e sem dificuldade ao problema do tipo mudança (8-5), ocorrendo o seguinte diálogo com o examinador (E). E - Então coloca aqui no papel como você fez pra resolver o problema, porque Paulinho vai querer saber, tá certo? Cr - Eu digo o que eu pensei? E - É, você coloca aí no papel como foi que você resolveu o probleminha. Cr - Não entendi... E - (Insiste) Cr - Eu coloco como? E - Como foi que você fez o probleminha? Cr - Eu fui resolvendo com os dedos... Posso colocar eu contei com os dedos? E - Pode sim. Cr - Escreve⁶:

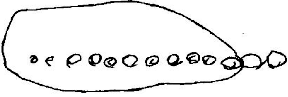
E - E se Paulinho não souber ler? Cr - (Faz o desenho abaixo):

Cr - Aqui nessa mão tem o cinco, se ele deu cinco a Marcela ele ficou com três (apontando para o desenho da outra mão).

É interessante notar que este diálogo ocorreu no primeiro problema, nos demais problemas propostos, Juliana não se mostra mais "relutante" ao papel. Este comportamento de familiarização com o papel ao longo da entrevista foi observado na maioria das crianças.

Analisaremos, agora, o uso de papel e lápis a partir de dois grandes eixos: (1) a influência do uso do papel no processo de resolução e (2) os tipos de registros feitos pelas crianças ao resolverem os problemas. Considerando o primeiro eixo, observamos que o uso do papel favoreceu na explicação da estratégia utilizada pela criança, bem como serviu de apoio para o desenvolvimento de estratégias em problemas com pares numéricos maiores que 10 ou nos problemas do tipo comparação, considerados mais difíceis. Vejamos alguns exemplos:

Protocolo de Gabriela (Alfabetização - Problema de mudança) E - Pedro comprou 8 bombons e deu 5 bombons para a irmã dele, Marcela. Com quantos bombons ele ficou? Cr - (Mostra oito dedinhos e baixa cinco dedos). É 3. E -... Faz agora aqui no papel .... Cr - (Desenha uma mão com cinco dedos e outra com três). E - Paulinho vai entender? Cr - (Escreve 1, 2, 3, 4, 5, 6, 7, 8 e depois 1, 2, 3). Agora ele vai saber que esta quantidade é a que ele ficou (apontando para o três).

No problema de comparação: E: Marcela comprou 7 pirulitos e Pedro comprou 3 pirulitos. Quantos pirulitos Marcela comprou a mais do Pedro? Cr - (Desenha os pirulitos em correspondência um-a-um). Quatro pirulitos a mais do que ele. Estou tapando aqui esses três e vendo esses aqui (apontando para os pirulitos que não estavam em correspodência).

Fica evidente que no problema de mudança Gabriela usa o papel apenas para mostrar a estratégia já explicada verbalmente, fazendo desenhos das mãos para demonstrar o que já havia realizado com os dedos. Por outro lado, nos problemas de comparação, o papel passa a ser necessário para o próprio desenvolvimento da estratégia.

O protocolo de Heitor (Alfabetização) é um exemplo da contribuição do uso do papel na solução de problemas com pares numéricos maiores que 10. Vejamos:

Heitor resolve rapidamente o problema de mudança que envolve o par 8 e 5, entretanto, quando se depara com o par 13 e 11 neste mesmo tipo de problema, ele recorre imediatamente ao papel e lápis.

E - Marcela comprou 13 chocolates e comeu 11. Com quantos chocolates ela ficou? Cr - 13? Deixa eu ver... Tô somando... (Desenha 13 bolinhas) um, dois, três, ..., doze, treze. (Apontando para primeira bolinha desenhada inicia uma contagem decrescente). Onze, dez, nove, ..., dois, um. (Circula as onze bolinhas contadas). Dois. E - Como foi que você descobriu ? Cr - É que eu arrodiei 11 "laranjas", eu tinha 13, arrodiei 11, ficou sobrando duas.

Pode-se observar neste caso a importância do registro no papel para a organização da estratégia da criança, possibilitando a adequada resolução do problema. Outro aspecto interessante evidenciado em alguns protocolos é que, após conseguir resolver um problema com o auxílio do papel, no problema seguinte a criança recorre imediatamente a este recurso, como pode ser visto no protocolo de Maria Eduarda (Alfabetização):

E - Marcela comprou 13 chocolates e comeu 11. Com quantos chocolates ela ficou? Cr - Sete. E - Como foi que você fez? Cr - (não responde). E - Tenta mostrar no papel como foi que você fez. Cr - (Desenha 13 chocolates e conta baixinho, olhando para os chocolates)... Um... E - Me explica como você está fazendo? Cr - (Conta os chocolates, apontando para cada um no papel.) Um, dois, três, quatro, cinco, seis, sete, oito, nove, dez, onze, sobrou dois.

No problema seguinte... E - Marcela comprou 7 pirulitos e Pedro comprou 3 pirulitos. Quantos pirulitos Marcela comprou a mais do que Pedro? Cr - (Desenha sete bolinhas e três bolinhas em correspondência um-a-um). Dá 4. E - Como você descobriu que era 4? Cr - Contando. Eu não contei esse não (os que estavam em correspondência), só precisei contar esses outros (circulando as quatro bolinhas).

Os exemplos citados acima mostram que o registro no papel pode servir como um recurso de apoio aos cálculos realizados pelas crianças. Assim, é preciso repensar a ênfase dada aos objetos concretos, que muitas vezes se apresentam como único recurso para as classes de educação infantil.

Um outro ponto importante em relação ao uso do papel é a possibilidade que este recurso oferece em termos de um refinamento nos registros feitos pelas crianças. A análise dos protocolos mostra que algumas delas vão percebendo a necessidade de serem mais claras nas informações prestadas a "Paulinho". Vejamos o protocolo de Ana Luísa (Alfabetização):

E - Pedro comprou 8 bombons e deu 5 bombons para a irmã dele, Marcela. Com quantos bombons ele ficou? Cr - (responde 3, levantando 8 dedos e separando 5). E - Faz aqui no papel pra Paulinho saber como você fez. Cr - (Desenha 3 dedinhos e 5 dedinhos). Fiz uma mão com 3 e uma mão com 5. Vou fazer outra que esta está feia! E - Paulinho vai entender? Cr - Não. Vou ter que fazer assim ... com número (Escreve no papel 1, 2, 3 e embaixo desses números, faz 4, 5, 6, 7, 8). Agora ele vai.

Vale ressaltar que esta reflexão que Ana Luísa faz só foi possível porque o papel permite que a criança possa desenvolver seu raciocínio sem perder o registro de todos os seus passos, possibilitando um comportamento metacognitivo de pensar sobre o próprio pensamento. Neste contexto, o uso deste recurso deve ser mais estimulado na Pré-escola, especialmente quando se constata que esta reflexão também pode ocorrer entre as crianças mais novas. Vejamos, por exemplo, o protocolo de Juliana (Jardim II):

No primeiro problema (8-5), citado na página 12, observamos que seu registro no papel corresponde a duas mãozinhas. No problema seguinte (12-10) de comparação, Juliana passa a escrever números acrescentando palavras para definir as relações entre eles. Cr - Eu acho que é 12. E - Tá jóia! Mas como foi que você pensou? Cr - Se Marcela comprou 10, ela tem menos e se ele comprou 12, ele ficou com mais. E - Então coloca aqui no papel pra Paulinho saber como foi que você fez. Cr - Escreve:

Este refinamento nos registros também pode ser observado no protocolo de Laís (Jardim I). Para tornar seu registro mais comunicativo Laís vai inserindo números, desenhos e palavras como pode ser visto a seguir:

E - Pedro comprou 8 bombons e deu 5 bombons para a irmã dele, Marcela. Com quantos bombons ele ficou? Cr - (Conta 8 dedos, baixa 5 e diz: 3). E - Faz no papel para Paulinho saber como você fez. Cr - Escreve:

E - Esse três... Cr - É o bombom que Pedro comprou. E - Paulinho vai entender? Cr - Vou fazer o bombom.

Cr - Três bombons (apontando para o número 3 e para os bombons desenhados). E - E agora, Paulinho vai entender? Cr - Escreve:

E - O que você fez? Cr - O "8" , a barraquinha (onde Pedro comprou os bombons) e a boneca (Marcela)...

E - Ok. Cr - Vou escrever "é três". Agora ele vai entender.

Neste protocolo podemos observar a busca de Laís por mais elementos que permitam a "Paulinho" uma melhor compreensão sobre o problema que ela resolveu. Neste sentido, ela vai acrescentando novos dados que enriquecem e ampliam seus registros.

Um outro aspecto a ser ressaltado é que a sugestão do entrevistador para que as crianças desenhem os dados do enunciado do problema nem sempre contribuiu para a solução do problema. Vejamos o caso de André (Alfabetização) em que os limites do uso do papel ficam bem claros: E - Marcela comprou 7 pirulitos e Pedro comprou 3 pirulitos. Quantos pirulitos Marcela comprou a mais do que Pedro? Cr - ... 7. E - Como você sabe? Cr - ... não sei, tu disse. E - ... Se você desenhar os pirulitos de Marcela e de Pedro, será que isso vai te ajudar? Cr - (Desenha sete pirulitos para Marcela e em seguida, os três pirulitos de Pedro). E - Quantos pirulitos Marcela tem a mais do que Pedro? Cr - os sete. A entrevistadora insiste diversas vezes, mas André não sabe o que fazer com o desenho...

Assim, ao que parece, quando a estrutura do problema não é compreendida pela criança, a pista dada pelo entrevistador solicitando o desenho dos dados não faz com que a criança resolva adequadamente o problema. Por outro lado, este mesmo registro pode ajudar quando a criança já dispõe de alguma estratégia de resolução e precisa de um "apoio" que facilite seu raciocínio, como pode ser visto no protocolo de Mirella (Jardim II). No problema de mudança (12-10), ela insiste que não sabe. Diante disso a entrevistadora sugere que ela desenhe os 12 bombons no papel, ocorrendo o seguinte diálogo: E - E aí? Quantos bombons você fez? Cr - 12 (conta até 12 apontando para as bolinhas que havia desenhado) E - Quantos bombons Pedro deu pra irmã dele? Cr - 10 (conta fazendo um tracinho para cada bolinha contada) E - E aí? Ele ficou com quantos? Cr - Não sei... 2! E - Como foi que você descobriu que era 2? Cr - Assim: eu contei assim (conta até 10), ele ficou com 2 e a irmã ficou com 10. E - Paulinho vai entender o que você fez aqui? Cr - Eu vou fazer o número 2.

Em relação ao segundo eixo de análise, ou seja, os registros feitos pelas crianças, foi possível organizá-los em cinco grupos: 1. Uso de desenhos; 2. Registro apenas dos dados do problema e/ou a resposta; 3. Registro de dados e/ou resposta acrescentando elementos tais como desenhos, palavras, marcas, buscando facilitar o entendimento da representação; 4. Registro da estratégia através de desenho e/ou texto escrito; 5. Tentativa de uso de sinais convencionais para representar a operação realizada. Vejamos alguns exemplos:

O uso do desenho pode ser visto no protocolo de Vinícius (Jardim I). Ao resolver o problema de comparação (7-3), Vinícius responde: "7, porque você disse". Solicitado a fazer no papel, ele diz: "vou fazer vários desenhos para ele (Paulinho) entender.

Cr - Fiz um tracinho, um sapato, uma bandeira, uma bota, folha de jardim, outra bota e uma batida.

Este tipo de registro em que a criança faz desenhos que não se relacionam ao enunciado do problema foi observado apenas entre algumas crianças do Jardim I.

O segundo tipo de registro pode ser observado no protocolo de Mariana (Jardim II). No problema de Comparação (7-3), Mariana escreve um dos dados do problema e completa sua resposta dizendo⁷: "Porque ele tinha 3 e pra ele ficar ... ficar como Marcela ele tinha que ficar com 4".

Vale ressaltar que Mariana complementa seu registro através da fala, o que, no entanto, nem sempre ocorreu com as demais crianças que apresentaram este tipo de registro. Registros dos dados e/ou resposta do problema foram freqüentes entre as crianças de Jardim I e II, sendo menos utilizados por crianças da Alfabetização.

O terceiro grupo de registro mencionado acima pode ser exemplificado a partir do registro de Beatriz (Jardim II) ao resolver corretamente o problema de mudança (12-10).

Cr - Eu coloquei aqui um menino com 12 e uma menina com 10, que ele deu pra menina, que ela não tinha nenhuma. Aí ele deu 10, aí sobrou 2, aí ele ficou com 2. E - aqui (aponta para o traço entre os números 12 e 2) é pra ele (Paulinho) saber que é 2.

O protocolo de Rafael (Alfabetização) é um outro exemplo desse grupo de registros. Rafael sente necessidade de incluir marcas para conseguir comunicar seu pensamento com clareza. Após resolver o problema de mudança (7-3) corretamente, escreve no papel:

E - O que você colocou aí no papel? Cr - Eu tinha 7, tirou 3, ficou com 4. E - E o que é isto que você colocou aí (apontando para os tracinhos no papel). Cr - Um tracinho pra não ficar setenta e três e pra não ficar trinta e quatro.

O quarto grupo de registro, encontrado apenas nas séries de Jardim II e Alfabetização, pode ser exemplificado a partir de Henrique (Jardim II), que preferiu escrever o seu raciocínio nos 4 problemas. Vejamos um exemplo no problema 8-5 (Comparação):

E - ...Quantos bombons Pedro comprou a mais do que Marcela? Cr - ... 3. E - Como foi que você descobriu? Cr - Porque Marcela pegou 5 e ele pegou 8, aí Marcela ficou com 5, aí ele pegou mais 3 que ficou com 8... porque 5 mais 3 faz 8 e então se ele tirasse 3, aí os dois ia ficar com a mesma coisa. E - Ok, entendi! Agora, você mostra no papel como você resolveu. Cr - Eu escrevo ou boto número? E - Pode colocar com quiser. Cr - Como é mais, é um traço ou é um vezes? E - Coloque como você souber. Então, Henrique opta por escrever a explicação que havia dado seguindo este procedimento nos demais problemas:

"5 mais 3 vira 8, se Pedro tem 8, tirando 3 fica 5"

Vale ressaltar que neste grupo também estão incluídos os registros da própria estratégia de resolução sem acompanhamento da escrita. Nestes casos, as crianças resolvem os problemas desenhando a sua estratégia, como fazem por exemplo: Heitor, Maria Eduarda e Ana Luiza, apresentados anteriormente.

Finalmente, em relação ao quinto grupo de registro, vale notar que nenhuma das crianças que usaram o papel no Jardim I utilizou sinais convencionais de adição, subtração ou igualdade. No Jardim II, apenas uma utilizou sinais convencionais em sua representação. Vejamos este caso:

No problema de Mudança (8-5), Dóris responde: Se comprou 8 bombons, aí deu 5, ficou com 3!" (mostrando 8 dedinhos e baixando 5). Em seguida vai espontaneamente para o papel e escreve:

Cr - Lá na minha casa tem um jogo de matemática...ai tem assim: 5 vezes 3?...aí dá 3, aí se deu 5 ficou com 3.

Nos demais problemas Dóris segue registrando os sinais que aprendeu no seu joguinho, embora não utilize tais sinais num contexto convencional.

Na Alfabetização foi observado um pequeno aumento no uso de sinais em relação ao Jardim II (quatro usaram sinais). O protocolo de Edson (Alfabetização) exemplifica este uso, que já é mais próximo da forma convencional de utilização de sinais em sentenças matemáticas. Vejamos o registro de Edson no problema (12-10) de mudança:

Cr - 10. Se botar 2 é 12. Ela deu 10, aí ficou com 2, então é 12.

Discussão

O estudo mostra que crianças pré-escolares são capazes de se interessar e refletir sobre problemas matemáticos, apesar de estarem inseridas numa situação um tanto distante de um contexto natural. O desempenho revelado nos dados quantitativos, bem como o que se observou na análise dos protocolos evidencia que crianças entre 4 e 6 anos já conseguem resolver problemas, explicando suas estratégias de solução e refletindo sobre elas.

O estudo também evidencia que saber ou não usar os sinais convencionais não é um conhecimento indispensável para que se possa introduzir o registro no papel nas atividades de resolução de problemas com crianças. Conforme foi visto na análise dos protocolos, o papel foi usado sem essa aprendizagem formal, trazendo contribuições para o trabalho com resolução de problemas ao servir de apoio para os cálculos realizados, possibilitar o acompanhamento do processo de raciocínio da criança e favorecer o avanço no registro das operações matemáticas. Desta forma, o presente estudo mostrou que resolver problemas no papel pode se constituir numa alternativa interessante para a educação infantil.

Devemos frisar, entretanto, que não basta abrir espaço para o uso de diferentes recursos na Educação Infantil (material concreto, papel e lápis, estratégias mentais). É fundamental também saber como usá-los de modo a propiciar uma maior reflexão por parte das crianças. Assim, em primeiro lugar, recomenda-se que a resolução de problemas esteja inserida em situações significativas (por exemplo, na produção de tabelas para o registro do peso das crianças ou do número de figurinhas de uma coleção, jogos de compra e venda etc.), fugindo-se do esquema mais comum de resolver continhas isoladamente. Ressalta-se ainda, a importância do professor conhecer os diversos tipos de problemas, estimular a interação entre as crianças, fazer perguntas, explorando as diferentes estratégias de solução que elas utilizam, seja através do cálculo mental, seja com o uso dos dedos ou materiais concretos, seja no papel, cabendo ao professor conhecer e utilizar as possibilidades que cada recurso oferece... Partindo destes princípios, o presente estudo espera ter fornecido algumas contribuições acerca da utilização de registros no papel para o trabalho de resolução de problemas na educação infantil.

Recebido em 13.10.1999

Primeira decisão editorial em 23.10.2000

Versão final em 22.12.2000

Aceito em 19.01.2001

• Brandăo, A.C.P. & Selva, A.C.V. (1998). A resoluçăo de problemas na pré escola: o caso dos livros didáticos de matemática Anais da 21Ş ANPEd, Caxambu, Minas Gerais.
• Higino, Z. M. (1990). A criança e a escrita numérica. Revista Brasileira de Estudos Pedagógicos, 71, 141-162.
• Hughes, M. (1986). Children and number Oxford: Basil Blackwell.
• Meira, L. (1991). Explorations of mathematical sense-making: an activity-oriented view of children's use and design of material displays Ph.D Dissertation, University of California-Berkeley.
• Selva, A.C.V. (1993). A influęncia de diferentes tipos de representaçăo na resoluçăo de problemas de divisăo Dissertaçăo de Mestrado, Universidade Federal de Pernambuco, Brasil.
• Selva, A.C.V. & Brandăo, A.C.P. (1999). Reflexőes sobre a aprendizagem de matemática na Pré-escola. Psicologia: Teoria e Pesquisa, 14, 67- 75.
• Sinclair, A., Mello, D. & Siegrist, F. (1990). A notaçăo numérica na criança. Em H. Sinclair (Org.), A produçăo de notaçőes na criança (pp. 71-96). Săo Paulo: Cortez.
• Sinclair, A., Siegrist, F. & Sinclair, H. (1983). Young children's ideas about the written number system. Em D. Rogers & J. Sloboda (Orgs.), The acquisition of symbolic skills (pp. 535-542). New York: Plenum Press.
• Smole, S.K.C. (1996). A matemática na educaçăo infantil - a teoria das inteligęncias múltiplas na prática escolar Porto Alegre: Artes Médicas.
• Vergnaud, G. (1982). A classification of cognitive tasks and operations of thougt invoved in addition and subtraction problems. Em T.P. Carpenter, J.M. Moser, T.A. Romberg (Orgs.), Addition and subtract: a cognitive perspective (pp. 39-59). New Jersey: LEA.
• Zunino, D.L. (1995). Problemas e contas: desafios diferentes. Em D.L. Zunino (Org.), A matemática na escola: aqui e agora (pp. 28-69). Porto Alegre: Artes Médicas.

3

Ver por exemplo, os documentos: Tecendo a Proposta Pedagógica - Prefeitura da Cidade do Recife (1996) e Referencial Curricular Nacional para a Educação Infantil, Brasília: MEC, 1998.

4

Foi conduzida uma MANOVA tendo a freqüência de acerto nos problemas como variável dependente e como variável independente (inter-sujeitos): a série; e variáveis independentes (intra-sujeitos): tipo de problema (mudança e comparação) e tamanho do par numérico (grande e pequeno).

5

Ainda que se reconheça uma tendência geral em resolver problemas "de cabeça", esperava-se que a solicitação de que "Paulinho precisava ver os problemas resolvidos no papel", gerasse um maior uso deste recurso.

6

Todos os registros feitos pelas crianças apresentados neste estudo foram reduzidos do original.

Datas de Publicação

• Publicação nesta coleção
  27 Nov 2001
• Data do Fascículo
  Dez 2000

Histórico

• Recebido
  13 Out 1999
• Aceito
  19 Jan 2001