Resumos
As ligas com memória de forma (Shape Memory Alloy - SMA) consistem em um grupo de materiais metálicos que possuem a habilidade de retornar a um formato ou tamanho previamente definido quando submetidas a um ciclo térmico adequado. Os efeitos de memória de forma ocorrem devido a mudanças na estrutura cristalina do material, dependentes da temperatura e da tensão ao qual está sujeito. A fase de Martensita, estado presente a baixas temperaturas, apresenta comportamento plástico, com maior facilidade para deformações permanentes. A fase de Austenita, que ocorre a altas temperaturas, apresenta comportamento elástico com alta rigidez. A mudança na estrutura cristalina do material não é um processo termodinamicamente reversível, apresentando, conseqüentemente, histerese. Portanto, a característica principal destes materiais é a habilidade de sofrer grandes deformações plásticas e, em seguida, recuperar sua forma original quando a carga é removida ou o material é aquecido. Assim, pode-se utilizar esse fenômeno para construir atuadores leves e silenciosos, como verdadeiros músculos metálicos. O desenvolvimento de atuadores com as SMAs apresenta grande atrativo para diversos campos da engenharia, principalmente na área de robótica, substituindo os atuadores convencionais de grande peso e ruidosos, como motores, válvula solenóides, etc. Entretanto, para o bom desempenho de atuadores SMA requer-se um complexo sistema de controle e resfriamento, reduzindo-se o tempo de resposta do atuador e minimizando-se os efeitos da histerese. Nesse trabalho, propõe-se um inovador sistema de resfriamento, baseado em pastilha termo-elétrica (efeito Seebeck-Peltier). Este método possui a vantagem de ser mais compacto e simples que outros métodos de resfriamento forçado. Um modelo matemático completo é também desenvolvido, e um protótipo experimental foi construído. Diversos experimentos foram utilizados para a validação do modelo e para a identificação de todos seus parâmetros. Em um próximo trabalho, um sistema de controle será desenvolvido e implementado no protótipo, baseado no modelo matemático ora proposto.
Modelagem; atuador com liga de memória de forma; resfriamento forçado com pastilhas termoelétricas; robótica
Shape Memory Alloys (SMA) consist of a group of metallic materials that demonstrate the ability to return to some previously defined shape when subjected to the appropriate thermal procedure. The shape memory effect occurs due to a temperature and stress dependent shift in the materials crystalline structure between two different phases. Martensite, the low temperature phase, is relatively soft whereas Austenite, the high temperature phase, is relatively hard. The change that occurs within SMAs crystalline structure is not a thermodynamically reversible process and results in temperature hysteresis. The key feature of these materials is the ability to undergo large plastic strains and subsequently recover these strains when a load is removed or the material is heated. Such property can be used to build silent and light actuators, similar to a mechanical muscular fiber. SMA actuators have several advantages in several engineering fields, mainly in robotics, replacing the conventional actuators like motors or solenoids. However, the good performance of the SMA actuator depends on a complex control and cooling systems, reducing the time constant and minimizing the effects of hysteresis. In the present paper, a novel cooling system is proposed, based on thermo-electric effect (Seebeck-Peltier effect). Such method has the advantage of reduced weight and requires a simpler control strategy compared to other forced cooling systems. A complete mathematical model of the actuator is also derived, and an experimental prototype was implemented. Several experiments were used to validate the model and to identify all parameters. In a next work, a control system will be developed and implemented in the prototype, based on the mathematical model here exposed.
Modeling; shape memory alloy actuator; thermoelectric tablet; robotics
AUTOMOÇÃO INDUSTRIAL
Modelagem e validação experimental de um atuador baseado em liga de memória de forma
Roberto RomanoI; Eduardo Aoun TannuriII
IInstituto de Pesquisas Tecnológicas do Estado de São Paulo, Departamento de Engenharia de Telecomunicações e Controle - Escola Politécnica USP, rromano@ipt.br
IIInstituto de Pesquisas Tecnológicas do Estado de São Paulo, Departamento de Engenharia Mecatrônica e Sistemas Mecânicos - Escola Politécnica USP, eduat@usp.br
RESUMO
As ligas com memória de forma (Shape Memory Alloy - SMA) consistem em um grupo de materiais metálicos que possuem a habilidade de retornar a um formato ou tamanho previamente definido quando submetidas a um ciclo térmico adequado. Os efeitos de memória de forma ocorrem devido a mudanças na estrutura cristalina do material, dependentes da temperatura e da tensão ao qual está sujeito. A fase de Martensita, estado presente a baixas temperaturas, apresenta comportamento plástico, com maior facilidade para deformações permanentes. A fase de Austenita, que ocorre a altas temperaturas, apresenta comportamento elástico com alta rigidez. A mudança na estrutura cristalina do material não é um processo termodinamicamente reversível, apresentando, conseqüentemente, histerese.
Portanto, a característica principal destes materiais é a habilidade de sofrer grandes deformações plásticas e, em seguida, recuperar sua forma original quando a carga é removida ou o material é aquecido. Assim, pode-se utilizar esse fenômeno para construir atuadores leves e silenciosos, como verdadeiros músculos metálicos. O desenvolvimento de atuadores com as SMAs apresenta grande atrativo para diversos campos da engenharia, principalmente na área de robótica, substituindo os atuadores convencionais de grande peso e ruidosos, como motores, válvula solenóides, etc. Entretanto, para o bom desempenho de atuadores SMA requer-se um complexo sistema de controle e resfriamento, reduzindo-se o tempo de resposta do atuador e minimizando-se os efeitos da histerese.
Nesse trabalho, propõe-se um inovador sistema de resfriamento, baseado em pastilha termo-elétrica (efeito Seebeck-Peltier). Este método possui a vantagem de ser mais compacto e simples que outros métodos de resfriamento forçado. Um modelo matemático completo é também desenvolvido, e um protótipo experimental foi construído. Diversos experimentos foram utilizados para a validação do modelo e para a identificação de todos seus parâmetros. Em um próximo trabalho, um sistema de controle será desenvolvido e implementado no protótipo, baseado no modelo matemático ora proposto.
Palavras-Chave: Modelagem, atuador com liga de memória de forma, resfriamento forçado com pastilhas termoelétricas, robótica.
ABSTRACT
Shape Memory Alloys (SMA) consist of a group of metallic materials that demonstrate the ability to return to some previously defined shape when subjected to the appropriate thermal procedure. The shape memory effect occurs due to a temperature and stress dependent shift in the materials crystalline structure between two different phases. Martensite, the low temperature phase, is relatively soft whereas Austenite, the high temperature phase, is relatively hard. The change that occurs within SMAs crystalline structure is not a thermodynamically reversible process and results in temperature hysteresis.
The key feature of these materials is the ability to undergo large plastic strains and subsequently recover these strains when a load is removed or the material is heated. Such property can be used to build silent and light actuators, similar to a mechanical muscular fiber. SMA actuators have several advantages in several engineering fields, mainly in robotics, replacing the conventional actuators like motors or solenoids. However, the good performance of the SMA actuator depends on a complex control and cooling systems, reducing the time constant and minimizing the effects of hysteresis.
In the present paper, a novel cooling system is proposed, based on thermo-electric effect (Seebeck-Peltier effect). Such method has the advantage of reduced weight and requires a simpler control strategy compared to other forced cooling systems.
A complete mathematical model of the actuator is also derived, and an experimental prototype was implemented. Several experiments were used to validate the model and to identify all parameters. In a next work, a control system will be developed and implemented in the prototype, based on the mathematical model here exposed.
Keywords: Modeling, shape memory alloy actuator, thermoelectric tablet, robotics.
1 INTRODUÇÃO
As ligas com memória de forma (Shape Memory Alloy - SMA) são ligas metálicas especiais que possuem a propriedade de serem termicamente ativas, retornando ao seu estado original quando aquecidas. Esta característica, conhecida como "efeito memória", ocorre para uma determinada temperatura e tensão, provocada por uma mudança na estrutura cristalina entre duas diferentes fases chamadas de martensita e austenita. Martensita é a fase de baixa temperatura (abaixo de 40 ºC), na qual o limite elástico do material é baixo, apresentando um comportamento plástico. A austenita é a fase de altas temperaturas (acima de 70 ºC), na qual a liga possui um comportamento tipicamente elástico. Aquecendo-se a SMA até uma determinada temperatura, ocorre uma mudança de fase na estrutura cristalina do material, ocorrendo assim uma contração. Como na fase fria ocorre um estiramento devido à carga aplicada e à alta plasticidade e no aquecimento ocorre a contração do material, pode-se utilizar esse fenômeno para construir atuadores leves e silenciosos, como verdadeiros músculos metálicos (Texas A&M Smart Lab, 2004).
O desenvolvimento de atuadores com as SMAs apresentam grandes atrativos para diversos campos da engenharia, principalmente na área de robótica, substituindo os atuadores convencionais de grande peso e ruidosos, como motores e válvula solenóides. Os atuadores baseados em SMA possuem a maior relação de carga útil por peso em relação aos atuadores convencionais. Entretanto, o desempenho dinâmico dos atuadores com SMA é ruim devido ao elevado tempo de resposta. Para a SMA operar rapidamente, deve-se aquecê-la para haver a contração e resfriá-la na recuperação. O aquecimento é um processo simples e rápido, podendo ser feito com a passagem de corrente elétrica pelo fio de SMA. Entretanto, o resfriamento é lento, o que limita o comportamento dinâmico dos atuadores SMA. Além disso, a mudança de fase é um processo não termodinamicamente reversível, apresentando histerese. Esta característica não linear exige, portanto, um complexo sistema de controle.
Diversas propostas em reduzir o tempo de resfriamento para aumentar a velocidade do atuador foram estudadas. Algumas utilizam métodos estáticos, como o atuador SMA resfriados continuamente, por meio de fluxo de ar constante (Tanaka;Yamada, 1991). De forma semelhante, já se relataram outras propostas, como imersão em água ou até mesmo dissipador de calor, com promissores resultados. Furuya e Shimada (1990) descreveram a aplicação de um radiador que, embora tenha diminuído em 10 vezes o tempo de resposta do atuador, elevou o consumo de potência em 20 vezes. Portanto é importante obter a melhor resposta com o menor consumo de energia para que o projeto utilizando as SMAs como atuadores não se torne inviável pelo consumo excessivo de energia. Golbert e Russel (1995) utilizam a condução de calor em um dissipador metálico móvel para promover o resfriamento do fio de SMA. Um sistema mecânico elaborado permite que o dissipador fique em contato apenas com o fio que deve ser resfriado, melhorando o desempenho dinâmico do sistema. O consumo de energia também é minimizado, já que o dissipador utilizado é passivo. Asada e Mascaro (2002) desenvolveram um atuador cujo resfriamento forçado é feito com circulação de água pelo fio de SMA. Um elaborado e complexo sistema de controle garante que a circulação de água só ocorra na fase de resfriamento, diferentemente do sistema de resfriamento a ar previamente mencionado. Como a troca de calor com a água circulante é mais eficiente do que com um dissipador metálico, há uma melhora na resposta dinâmica do atuador.
A fim de melhorar o desempenho dinâmico destes atuadores, mantendo-se a simplicidade construtiva e de controle e um baixo consumo de energia, será proposto um sistema de resfriamento forçado baseado em pastilha termoelétrica (efeito Seebeck-Peltier). Um modelo matemático completo foi desenvolvido para o atuador. Um protótipo experimental foi construído, a fim de se validar o modelo desenvolvido e se identificar todos os parâmetros necessários. O modelo matemático foi simulado numericamente e diversos experimentos realizados com o protótipo confirmam sua validade.
2 PRINCÍPIO DE FUNCIONAMENTO DA PASTILHA TERMOELÉTRICA
Segundo Danvic (2004), as pastilhas termoelétricas baseiam-se no efeito Seebek-Peltier. Há o aquecimento ou resfriamento quando uma corrente elétrica passa por dois condutores de diferentes tipos de materiais. Uma diferença de potencial elétrico (ddp) é aplicada aos pólos de dois materiais condutores de corrente elétrica com naturezas distintas, que ao serem unidos na extremidade, faz com que haja a circulação de uma corrente elétrica no circuito criando-se uma diferença de temperatura entre o ponto de união ("junta quente") e os pólos onde estão sendo aplicada a ddp ("junta fria"). Essa diferença de temperatura (efeito Seebek-Peltier) fará o calor se movimente de um lado para o outro.
Uma típica pastilha termoelétrica contém uma série de elementos semicondutores do tipo P e tipo N agrupados em pares que agirão como condutores de diferentes natureza. Esses elementos (P, N) são soldados entre duas placas cerâmicas, eletricamente em série e termicamente em paralelo. Quando uma corrente circula por um ou mais pares de elementos do tipo P para o tipo N, ocorre uma redução de temperatura da junta ("lado frio"), resultando uma absorção do calor do meio ambiente. Este calor é transferido pela pastilha sendo transportados pelos elétrons e enviados para o outro lado da pastilha ("lado quente"). O fenômeno ocorre quando uma carga muda de um material para outro, na junção, ela emite ou absorve essa diferença na energia causando o efeito Seebeck-Peltier.
3 MONTAGEM EXPERIMENTAL DO ATUADOR SMA REFRIGERADO COM PASTILHA TERMOELÉTRICA
Um protótipo experimental do atuador SMA refrigerado com pastilha termoelétrica foi construído, com a finalidade de se validar o modelo matemático exposto na seção seguinte, bem como testar as metodologias de controle que serão desenvolvidas em um trabalho futuro.
Na Figura 1 mostra-se como o atuador está interligado com o computador, permitindo que todos os comandos sejam feitos através do microcomputador, além da aquisição, registro e tratamento dos dados provenientes do atuador, bem como a execução das ações de controle.
Um esboço da montagem mecânica do atuador pesando aproximadamente 990g está mostrada na Figura 2. Nota-se em evidência o fio de SMA em contato com a pastilha termoelétrica, provendo assim a refrigeração forçada.
O fio de SMA está fixado em uma extremidade no suporte da estrutura, por intermédio de um conector elétrico (C1). Sua outra extremidade é fixada diretamente no eixo da polia (raio r1 = 0,45cm). Uma massa de 40g é utilizada como carga e está acoplada ao diâmetro externo da polia (raio r2 = 4,5cm) por meio de um fio comum.
Como a relação r2/r1 @ 10, o movimento da massa será amplificado por um fator 10 em relação ao deslocamento do fio de SMA, que sofrerá uma contração aproximada de 4 a 4,5% do seu comprimento útil (15cm), quando alimentado com a corrente elétrica. Isto, portanto, resulta um movimento da carga de aproximadamente 6cm, com uma rotação do eixo de 76º. O sistema de medida é feito por um potenciômetro ligado ao eixo da polia.
A polia está aterrada eletricamente ao potencial neutro da fonte de corrente.
O atrito é minimizado pela utilização de rolamentos para o apoio do eixo, além da seleção de um potenciômetro com rolamentos internos e baixo atrito.
Uma foto do atuador construído é mostrada na Figura 3, onde se pode-se ver a estrutura de alumínio responsável pela sustentação dos componentes mecânicos (polia, fio de SMA, rolamentos, potenciômetro de medida, transferidor, pastilha termoelétrica, carga de teste, fio de sustentação da carga e conectores elétricos).
3.1 Montagem da pastilha termoelétrica do atuador SMA
A pastilha termoelétrica utilizada no atuador em estudo é mostrada na Figura 4 Possui dimensão de 50x50 mm e sua área de dissipação foi ampliada com uma chapa de cobre de 2mm de espessura e de 50x150 mm, pois este é um ótimo condutor térmico. Além disso, o dissipador de calor montado no corpo da pastilha termoelétrica possui aletas de alumínio pintadas de preto e um ventilador montado sobre as mesmas, aumentando sua eficiência e evitando-se que o ar quente se propague por convecção para o fio de SMA e para o lado frio da pastilha termoelétrica. Para manter o ar quente que foi expelido do dissipador de calor fora do alcance das partes frias da pastilha termoelétrica, foi colocada uma placa isolante de isopor de 10mm de espessura, entre o dissipador de calor e a placa de cobre.
A pastilha termoelétrica é alimentada continuamente com 5V e uma corrente aproximada de 2A. Os testes mostraram que a mesma atinge, em alguns minutos, a temperatura de aproximadamente 15ºC, dispensando, portanto o controle de temperatura. O ventilador utilizado é alimentado independente com 12 V e uma corrente de aproximada de 0.1A. Assim, o consumo total da pastilha termoelétrica é de 11,2W.
Entre a placa de cobre e o fio de SMA foi fixada uma placa cerâmica de alumina com 1mm de espessura, que é um bom condutor térmico e um bom isolante elétrico, permitindo que o fio de SMA fique em contato direto sobre a pastilha termoelétrica sem provocar curto circuito.
O fio de SMA fica em contato com a placa de alumina com uma fina camada de pasta térmica de baixa resistência térmica comumente utilizada em componentes eletrônicos que trabalham com dissipador de calor. Utilizando-se essa técnica obtém-se uma melhora considerável na condução de calor entre fio e a pastilha termoelétrica, uma vez que se eliminam as bolhas de ar entre a placa cerâmica de alumina e o fio de SMA.
O sistema possui um circuito condicionador de sinais mostrado na Figura 5, contendo um amplificador de corrente constante que fornece a potência necessária para o aquecimento do fio de SMA e um circuito amplificador ligado ao potenciômetro de medida. Esses circuitos estão interligados a um microcomputador (Pentium 100MHz) com uma placa conversora com saídas digital/analógica (D/A) e entradas analógica/digital (A/D), fazendo a interface entre o atuador em estudo e o programa interno no microcomputador.
O modulo condicionador de sinais (amplificador de corrente e o amplificador do sinal do potenciômetro) foi projetado utilizando amplificadores operacionais e transistores bipolares.
O amplificador de corrente fornece uma corrente constante independente da variação da resistência do fio de SMA, ou variação dos contatos de conexões entre o gerador de corrente e o fio de SMA. Na Figura 6 mostra-se um diagrama em blocos do circuito condicionador. Esse circuito tem como características o baixo consumo e alta linearidade. Possui reguladores de tensões internas impedindo derivas nos sinais por flutuação de tensões ou derivas térmicas, além de possuir uma ótima imunidade a ruídos, uma vez que sua impedância de saída é baixa (50 W) e impedância de entrada não é muito alta (cerca 10KW ).
Nessa fase de desenvolvimento optou-se por esse tipo de tecnologia (utilizando amplificadores lineares) por ser simples, possuir uma boa linearidade e ser bastante robusto e confiável. De fato, drivers PWM (pulse width modulation) são mais eficientes em termos de dissipação de energia do que os baseados em amplificadores lineares, como o utilizado no presente trabalho. Entretanto, a escolha do driver não acarretaria uma mudança significativa em termos de desempenho dinâmico do atuador. Assim sendo, em face da simplicidade de desenvolvimento e do fato de que o objetivo do presente trabalho é avaliar e otimizar o desempenho dinâmico do atuador, optou-se, por ora, pela tecnologia de amplificadores lineares.
A placa conversora A/D e D/A foi obtida comercialmente podendo ser facilmente encontrados similares no mercado. A placa utilizada no sistema em estudo em especial possui uma resolução de 10 bits no conversor A/D onde o sinal de entrada corresponde de -5 a +5V (sinal amplificado do potenciômetro). Possui 8 bits no conversor D/A com uma variação no sinal de saída de -5 a +5V, sendo esse sinal correspondente de 0 a 1A no fio de SMA do atuador.
Essa placa possui ótima imunidade a ruídos e adicionalmente optou-se em utilizar cabos de interligação blindados aterrando-se apenas uma das pontas ao ponto comum do microcomputador, evitando-se com isso a circulação de corrente de terra, que poderia provocar ruídos indesejáveis.
O sistema de resfriamento (pastilha termoelétrica) e circuito condicionador de sinais é alimentado por uma fonte comum de microcomputador que oferece a robustez e regulação necessária para essa aplicação.
O conjunto completo (atuador, circuito amplificador de corrente e sinal do potenciômetro, fonte de alimentação e microcomputador com a placa A/D e D/A instalada internamente está mostrado na Figura 7.
O microcomputador possui um aplicativo desenvolvido em ambiente Matlab/Simulink, onde todos os dados e sinais serão processados. Esse software permite ao operador enviar sinais externos e receber os sinais provenientes dos sensores ligados ao atuador durante o processo de simulação.
4 MODELO MATEMÁTICO DO ATUADOR SMA REFRIGERADO POR PASTILHA TERMOELÉTRICA
O presente desenvolvimento do modelo matemático foi baseado nos trabalhos de Hirose, Ikuta e Tsukamoto (1991); Grant, Hayward e Lu (1997), Ashrafiuon e Elahinia (2002) e Holder, Solc e Vasina (2003). As equações básicas foram divididas em grupos conforme é mostrado na Figura 8.
O fio de SMA é percorrido por uma corrente elétrica sofrendo um aquecimento por efeito Joule e, em seguida, ocorre a transformação de fase com a posterior deformação do fio. No primeiro bloco serão analisadas as equações dos fenômenos térmicos do sistema e posteriormente os fenômenos envolvendo a transformação de fase e finalmente as deformações mecânicas ocorridas no fio de SMA.
As variáveis envolvidos na Figura 8 são: Ifio - corrente elétrica no fio da SMA (A), T - temperatura no fio da SMA (ºC), x - fração de martensita (0 a 100% ou 0 a 1), s - tensão mecânica no fio de SMA (N/m2), e- deformação (DL/L) -variação do comprimento / comprimento do fio.
4.1 Modelo térmico
O modelo térmico foi baseado na estrutura de montagem mostrada na Figura 9, onde o fio da SMA está em contato com a pastilha termoelétrica e entre o fio de SMA e a pastilha há uma fina camada de pasta térmica permitindo que a condução de calor entre o fio de SMA e a pastilha cerâmica seja eficiente.
Considerando várias simplificações e hipóteses (Grand; Hayward;Lu, 1997), e os conceitos básicos da termodinâmica, conservação de energia e transmissão de calor (Incropera, 1998) o modelo térmico pode ser expresso conforme mostra a equação (1):
Segundo catálogo técnico Dynalloy (2005), referente ao fio de SMA utilizado (Flexinol -FLX00870 0.008" 70 ºC) , este possui as seguintes especificações técnicas: m- massa por metro do fio (2.10 - 4 Kg/m), cp - calor específico do fio SMA (837 J/Kg.K), R-resistência elétrica do fio de SMA por metro ( 32W/m), A- área da seção transversal do fio ( 6,28.10 - 4 m2), d-diâmetro fio SMA (2.10 - 4m)
Além disso, considera-se a temperatura da pastilha na face fria (Tp) igual a 15ºC e a temperatura ambiente (Tamb ) igual a 20ºC.
Os parâmetros h e C são difíceis de serem estimados uma vez que dependem de muitas variáveis. Um cálculo aproximado de cada parâmetro, baseada na teoria mostrada em Incropera e Witt (1998) e Holman (1977), obtiveram-se: C = 0,4 W/ºC/m e h=6,55W/m2oC/m. Esses valores não são definitivos e serão melhorados no processo de identificação.
4.2 Modelo da transformação de fase
No aquecimento ocorre a transformação no fio da fase de Martensita (M) para Austenita (A). No resfriamento, ocorre a transformação no fio da fase de Austenita (A) para Martensita (M). As equações básicas que modelam esta transformação, em função da temperatura, são dadas em (2), obtidas do trabalho de Hirose, Ikuta e Tsukamoto (1991).
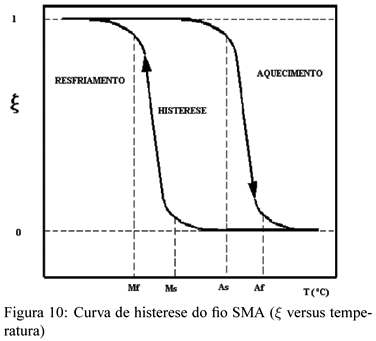
Onde: As e Af são as temperaturas inicial e final da transformação para austenita (ºC), Ms e Mf são as temperaturas inicial e final da transformação para martensita (ºC), x - fração de martensita, xm - maior fração de martensita durante o resfriamento (ou valor inicial durante o aquecimento), x A - valor inicial da fração durante o resfriamento. Os valores característicos para as fases de transformação são As = 68ºC, Af = 78ºC, Ms =52ºC e Mf = 42ºC. Entretanto, admitem-se variações de até 15ºC nestes valores, o que impõe a necessidade de um procedimento de identificação, exposto na próxima seção.
Segundo Holder; Solc; Vasina (2003) o aspecto do gráfico das fases de transformação é mostrado na Figura 10, onde verifica-se a histerese de fio de SMA.
4.3 Modelo das propriedades mecânicas
Na literatura científica, as propriedades mecânicas das ligas com memória de forma são obtidas com um modelo de camadas. Na fase de austenita, (temperatura alta), o fio de SMA torna-se elástico e, portanto, para x= 0, a relação entre tensão e deformação é dada na equação (3):
onde sA é a tensão na fase de austenita, EA é o módulo de elasticidade (módulo de Young) da austenita e e é a deformação.
O outro caso extremo, quando x = 1, equivale à fase da martensita (fria). Essa fase é plástica modelada segundo equação (4), cujo o gráfico característico é mostrado na Figura 11.
sendo EM o módulo de elasticidade da martensita, emyo limite elástico na fase da martensita e sm a tensão máxima do fio na fase de martensita.
Baseando-se nas equações anteriores obtém-se, para o caso intermediário (0 < x< 1), a relação entre tensão e deformação dada por pulse width modulation:
4.4 Modelo do sistema mecânico
O atuador proposto é composto por uma polia, na qual acoplam-se a carga deslocada e o fio de SMA, responsável pelo movimento.
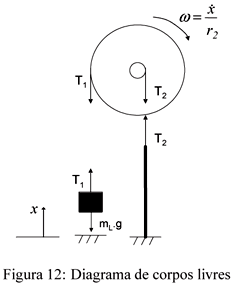
O diagrama de corpos livres da polia, da carga e do fio de SMA, apresentado na Figura 12, é utilizado para a dedução das equações do movimento. A posição da carga é dada pela coordenada x, orientada positivamente para cima. Na figura, T1 é a tração no fio que suporta a carga, T2 é a tração no fio de SMA, wg a velocidade de rotação da polia e r2 é o raio externo.
Assim, aplicando-se o Teorema do Momento Angular (TMA) para a polia obtém-se:
onde J é o momento de inércia da polia.
Sendo mL a massa da carga, a 2ª Lei de Newton aplicada para esta fornece:
Para estimar a tração no fio T2, considera-se a Figura 13 que apresenta o fio de SMA em seus três estados possíveis. Será feita uma analogia com uma mola linear a fim de se obter um modelo simplificado para a tração T2. Na fase de austenita pura, considera-se o comprimento inicial da "mola" l0 . Na fase de martensita pura, o fio atinge seu comprimento máximo lfio , que também corresponde à situação na qual a carga encontra-se na posição x=0. A diferença entre os comprimentos l0 e lfio é aproximadamente 4% do comprimento lfio, conforme visto anteriormente. Numa situação intermediária, a deformação Dl da "mola" em relação ao seu comprimento inicial l0 é dada por 4%.lfio x/n, onde n é a relação entre os raios da polia (n = r2 / r1 ).
Assim, a tração T2 será dada por T2 = K.Dl = K.( 0,04.lfio - x / n) na qual K é a rigidez equivalente do fio de SMA. Incluindo um coeficiente de amortecimento a equação do movimento do atuador fica:
sendo c o coeficiente de amortecimento equivalente (ajustado experimentalmente para c=100 N.s/m). A rigidez K pode ser obtida de forma aproximada, utilizando-se a formulação dada em (5). Assumindo-se deformações elásticas e sendo, Afio a área seccional do fio de SMA fica:
Assim, fazendo algumas manipulações algébricas com a equação (9) e a equação :T2 = K.Dl= K.( 0,04.lfio x/n), o coeficiente de rigidez equivalente fica:
Finalmente considerando-se que a tensão na martensita supera o seu limite elástico, e a mesma opera na fase plástica, onde a rigidez equivalente é muito inferior. Assim, faz-se uma simplificação na equação (10), retirando-se a parcela de rigidez proveniente da fase elástica da martensita (EM), resulta a aproximação:
5 IDENTIFICAÇÃO DE PARAMÊTROS
Nesta seção será exposto o procedimento experimental utilizado para se identificar os parâmetros do modelo desenvolvido.
Conforme já exposto, na equação térmica (1), os parâmetros a serem determinados são: C, h, Ms, Mf, As e Af. No modelo termo-mecânico os parâmetros a serem identificados são as temperaturas Ms, Mf, As e Af. Como já mencionado, os valores de catálogo podem sofrer variações de até ±15 ºC, o que requer portanto uma identificação para cada fio utilizado.
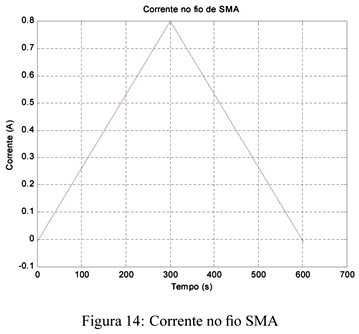
O processo de identificação de parâmetros foi realizado em malha aberta e o utilizando um ensaio em rampa. O programa de controle gera um sinal de comando sobre o fio em forma de rampa, conforme mostra a Figura 14.
O sinal obtido referente ao deslocamento real é mostrado na Figura 15.
Com os parâmetros originais calculados e fornecidos pelo fabricante do fio, foram traçados os gráficos da planta real juntamente ao resultado da simulação do modelo (Figura 16).
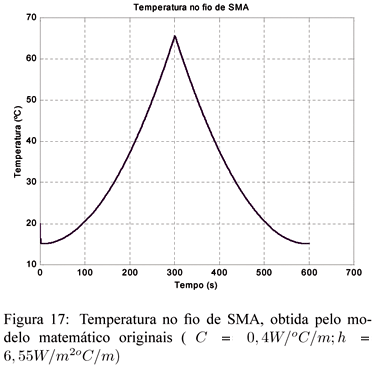
Pode-se concluir que o modelo térmico está mau ajustado, pois a temperatura não está atingindo as fases de transformação. Isto pode ser confirmado pela Figura 17, que mostra que a temperatura do fio obtida pelo modelo matemático atinge o valor máximo de 65ºC. O principal parâmetro que causa esta elevada dissipação é o coeficiente de conduçãoC.
Desenvolveu-se então um programa de otimização dos parâmetros baseado no algoritmo de Programação Quadrática Seqüencial (SQP), que minimiza a norma E dada por:
sendo  = ( h C Ms Mf As Af ) o vetor de parâmetros a serem estimados, ymedido a posição da carga medida no experimento, ysimulado a posição obtida pelo modelo matemático e T o tempo do ensaio (600s).
= ( h C Ms Mf As Af ) o vetor de parâmetros a serem estimados, ymedido a posição da carga medida no experimento, ysimulado a posição obtida pelo modelo matemático e T o tempo do ensaio (600s).
A variação dos parâmetros foi limitada. Assim, para as temperaturas, admitiu-se uma variação máxima de ±15ºC, valor dado no catálogo do fio. Para o coeficiente de condução térmica C, permitiu-se uma variação de ±0,2W/ºC/m em relação ao valor previamente estimado e para o coeficiente de convecção h permitiu-se uma variação de ±3W/m2 oC/m.
Obtiveram-se, assim, os seguintes valores para os parâmetros: C=0,2547W/ºC/m, h = 7 W/m2oC/m, Ms = 66ºC , Mf = 34.ºC As = 53ºC, Af = 93 ºC. Obteve-se, portanto, o gráfico da Figura 18.
Pode-se verificar que esses parâmetros estão bem mais adequados e os formatos das curvas estão bastante próximos, mostrando que o modelo obtido é semelhante ao caso real.
A verificação da temperatura no fio de SMA é mostrada na Figura 19. Nota-se que a temperatura máxima alcança aproximadamente 94 ºC, que é um valor aceitável pelas características físicas do fio de SMA.
6 VALIDAÇÃO EXPERIMENTAL DO MODELO
Após a identificação dos parâmetros, realizaram-se ensaios em degrau para validar o modelo matemático. No primeiro caso, aplicou-se uma entrada de corrente cíclica em degrau no fio de SMA com amplitude máxima de 0,8 A, conforme mostra a Figura 20(a) . A posição da carga é mostrada na Figura 20(b), onde confronta-se o resultado medido com o obtido pela simulação.
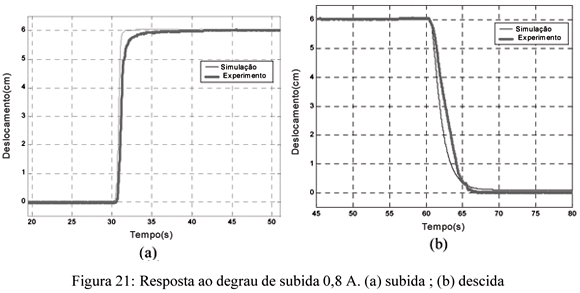
Detalhes da resposta na subida e na descida são mostradas na Figura 21 (a) e (b) respectivamente. Verifica-se que as respostas experimentais são muito bem reproduzidas pelo modelo de simulação durante a subida. O tempo de estabilização 5% é da ordem de 1,2s na simulação e 2,15s na medida experimental. Na descida, entretanto, verifica-se uma maior discrepância entre as curvas experimentais e teóricas. Isto pode ser explicado pelo fato que no resfriamento, o fenômeno térmico mais importante é a condução do calor do fio para a pastilha termoelétrica, fenômeno este muito complexo e que fora modelado segundo diversas hipóteses simplificadoras. Já no aquecimento, o fenômeno térmico mais importante é a geração de calor por efeito Joule (passagem de corrente), cuja modelagem é mais precisa.
A temperatura estimada na simulação está mostrada na Figura 22. Pode-se verificar que a temperatura máxima nessas condições é de aproximadamente 94ºC e acompanha o sinal de corrente injetado no fio de SMA.
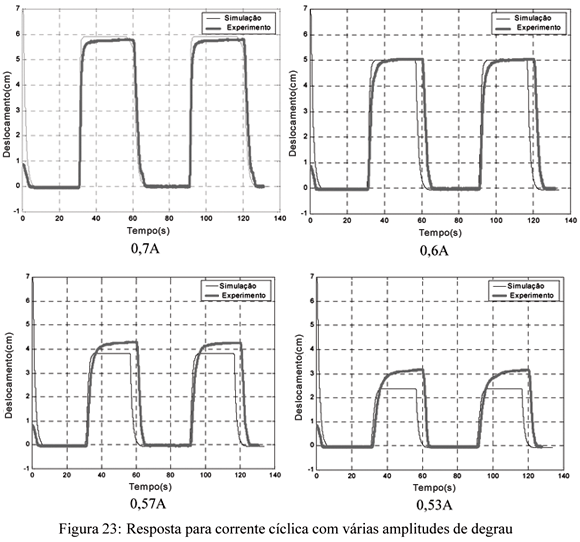
Os gráficos mostrados na Figura 23 mostram o comportamento da resposta do sistema para os vários níveis de corrente.
Nota-se que há uma maior discrepância entre a simulação e os valores experimentais conforme a corrente imposta ao fio é reduzida. Este efeito é novamente explicado pelo fato de que para correntes inferiores, o fenômeno de condução passa a ser mais importante em relação a geração de calor por efeito Joule.
Um sistema de controle adequado em malha fechada deverá corrigir as imperfeições obtidas em malha aberta.
7 CONCLUSÃO
Neste trabalho foi mostrado o princípio de funcionamento das ligas de memória de forma ("Shape Memory Alloy" - SMA). Foi também mostrado o funcionamento de pastilhas termoelétricas, e como as mesmas podem ser utilizadas como elemento de refrigeração de fios SMA.
Foi proposto um inovador sistema de atuador baseado em liga de memória de forma refrigerado com uma pastilha termoelétrica. Um protótipo completo foi construído, incluindo o sistema mecânico, eletrônico e um sistema de aquisição de dados e controle baseado em microcomputador.
Um modelo matemático simplificado foi desenvolvido, baseado nas teorias obtidas na literatura e nas especificações do fabricante do fio de SMA. O modelo e os parâmetros foram identificados e foram feitos ensaios práticos para validar esse modelo.
Esse modelo servirá de base para se projetar um controlador adequado para otimizar o funcionamento desse tipo de atuador, que possui como característica básica a existência de histerese.
Apesar das dificuldades em se fazer o controle, esse tipo de atuador pode ser utilizado em várias aplicações práticas, sendo uma boa alternativa em aplicações onde tamanho, peso e nível de ruído são relevantes.
Artigo submetido em 21/09/2005
1a. Revisão em 14/03/2006
2a. Revisão em 07/08/2006
3a. Revisão em 19/04/2007
Aceito sob recomendação do Editor Associado Prof. José Reinaldo Silva
- Asada, H.H. and S. Mascaro (2002). Wet Shape Memory Alloy Actuators, MIT Home Automation and Healthcare Consortium, Phase 3 Final Report, Boston, Estados Unidos.
- Ashrafiuon, H. and H.M. Elahinia (2002). Nonlinear Control of a Shape Memory Alloy Actuated Manipulator. ASME Journal of Vibration and Acoustics, Vol. 124 , pp.566-575.
- Danvic, (2004). Tecnologia em Efeito Peltier. Definição Efeito Peltier. Disponível em <http://www.efeitopeltier.com.br>. Acesso em 27 Nov 2004.
- Dynalloy, INC (2005). Flexinol - Wire Specifications (catálogo). Costa Mesa, Estados Unidos.
- Furuya, Y. and H. Shimada (1990). Shape Memory Actuator for Robotic Applications, Engineering Aspect of Shape Memory Alloys, Butterworth-Heinemann, Londres, pp 338-355.
- Gorbet, B.R. and A.R. Russel (1995). Improve the Response of SMA Actuators, IEEE International Conference on Robotic and Automation, Vol. 3, Maio, 2299-2303.
- Grant, D., V. Hayward and A. Lu (1997). Design and Comparison of High Strain Shape Memory Alloy Actuators, International Conference on Robotic and Automation, Albuquerque, New Mexico, 260-265.
- Hirose, S., K. Ikuta and M. Tsukamoto (1991). Mathematical Model and Experimental Verification of Shape Memory Alloy for Designing Micro Actuator, Proc. of the IEEE on Micro Electromechanical Systems, an Investigation of Microstructures, Sensors, Actuators, Machines, and Robots, pp.103-108.
- Holder, K. Solc, F. and Vasina, M., (2003). Shape Memory Alloy- Unconventional Actuators, International Conference on Industrial Technology ICIT, Maribor, Slovenia, pp. 190-193.
- Holman, P.J. (1977). Transferencia de Calor, México, CECSA. (em espanhol).
- Incropera, P. and D.P. Witt (1998). Fundamentos de Transferęncia de Calor e de Massa; 4Ş ed., Rio de Janeiro, LTC.
- Tanaka,Y. and A. Yamada (1991). A Rotary Actuator Using Shape Memory Alloy for a Robot, and Analysis of the Response with Load. IEEE/RSJ International Workshop on Intelligent Robots and Systems IROS '91, Osaka, Japăo, pp1163-1168.
- Texas A&M Smart Lab. (2004). Definition of Shape Memory Alloy. Disponível em <http://smart.tamu.edu/overview/smaintro/simple/definition.html>. Acesso em 18 out. 2004.
Datas de Publicação
-
Publicação nesta coleção
18 Abr 2008 -
Data do Fascículo
Mar 2008
Histórico
-
Recebido
21 Set 2005