Resumos
Os objetivos do presente estudo foram a formulação e a aplicação de um modelo matemático de localização de packing-houses para regiões representativas do Estado de São Paulo, de acordo com sete diferentes capacidades de processamento dessas plantas e com vistas à minimização dos custos de implantação, processamento e transporte da laranja. O modelo matemático proposto foi baseado na teoria da localização, e utilizou-se uma estrutura de programação inteira-mista. Para os fins da presente análise, adotaram-se como centros de oferta e de consumo e como potenciais centros de processamento os 40 Escritórios de Desenvolvimento Rural (EDRs) do Estado de São Paulo. Os principais parâmetros considerados no modelo incluem os custos de transporte e de processamento da laranja e custos de implantação de packing-houses de diferentes capacidades, bem como a oferta e demanda de cada EDR. Analisaram-se quatro cenários distintos, considerando a possibilidade de instalação de apenas uma planta processadora por região, a igualdade entre a oferta e a demanda e a inexistência de plantas processadoras. Os resultados evidenciaram a necessidade de economia de escala no processamento e o pequeno volume de transporte inter-regional. Em relação à localização das plantas, o modelo recomendou as áreas intermediárias e identificou áreas potenciais para futuras instalações.
laranja; programação inteira mista; localização de planta industrial
This study discusses the formulation and application of a mathematical location model. The model was used to determine the optimum locations for orange packing houses in the state of São Paulo, Brazil. The proposed model considers orange packing-houses of seven different capacities, seeking to minimize their implementation, processing, and transportation costs. It is based on the theory of location and makes use of a mixed-integer programming structure. For the purposes of the current analysis, 40 Rural Development Offices (EDR) in the state of São Paulo have been adopted as hubs of supply and consumption and as focal points for the installation of orange packing facilities. The main parameters considered in the model include the costs of orange processing/packing and transportation, the costs to implement different capacity orange packing-houses, and each EDR region’s orange supply and user demand. Four distinct scenarios were analyzed, each conditioned by a different mix of specific assumptions: a maximum of one facility per region, equality between supply and demand, and a lack of pre-existent facilities. Results have shown a low volume of inter-regional orange transport and economies of scale in packing-house operations. The model determined intermediate areas as the best packing-house locations and identified areas for future plant construction.
packing-houses; orange; mixed-integer programming; packing-houses; industrial plant location
Distribuição espacial de packing-houses de laranja no Estado de São Paulo: uma aplicação da teoria da localização
Simone Yuri RamosI; José Vicente Caixeta FilhoII
IEngenheira-Agrônoma e Mestra em Economia Aplicada pela Escola Superior de Agricultura "Luiz de Queiroz" ESALQ/USP. E-mail: simoneyramos@aol.com
IIProfessor Associado do Departamento de Economia, Administração e Sociologia ESALQ/USP. E-mail: jvcaixet@esalq.usp.br
RESUMO
Os objetivos do presente estudo foram a formulação e a aplicação de um modelo matemático de localização de packing-houses para regiões representativas do Estado de São Paulo, de acordo com sete diferentes capacidades de processamento dessas plantas e com vistas à minimização dos custos de implantação, processamento e transporte da laranja. O modelo matemático proposto foi baseado na teoria da localização, e utilizou-se uma estrutura de programação inteira-mista. Para os fins da presente análise, adotaram-se como centros de oferta e de consumo e como potenciais centros de processamento os 40 Escritórios de Desenvolvimento Rural (EDRs) do Estado de São Paulo. Os principais parâmetros considerados no modelo incluem os custos de transporte e de processamento da laranja e custos de implantação de packing-houses de diferentes capacidades, bem como a oferta e demanda de cada EDR. Analisaram-se quatro cenários distintos, considerando a possibilidade de instalação de apenas uma planta processadora por região, a igualdade entre a oferta e a demanda e a inexistência de plantas processadoras. Os resultados evidenciaram a necessidade de economia de escala no processamento e o pequeno volume de transporte inter-regional. Em relação à localização das plantas, o modelo recomendou as áreas intermediárias e identificou áreas potenciais para futuras instalações.
Palavras-chave: laranja, programação inteira mista, packing-houses e localização de planta industrial.
1. Introdução
A implantação da indústria de suco concentrado no Estado de São Paulo, iniciada em meados da década de 60, provocou uma profunda alteração na estrutura de comercialização de laranja, uma vez que esse segmento tornou-se o pólo dinâmico do sistema, direcionando a disponibilidade interna da fruta em razão de suas necessidades e demandas. O Estado de São Paulo acabou por consolidar-se como grande produtor e exportador de suco de laranja, satisfazendo, principalmente, as demandas norte-americana e européia. Na década de 80, os Estados Unidos, em virtude das freqüentes geadas na Flórida e da elevada demanda interna, transformaram-se no maior importador de suco de laranja concentrado brasileiro, absorvendo cerca de 47% das exportações. Nessa época, as altas cotações do suco de laranja no mercado internacional estimularam os citricultores brasileiros a realizar novos plantios, que ocorreram de forma acelerada e desordenada.
A recuperação dos pomares da Flórida, baseada no deslocamento da produção para áreas menos sujeitas a geadas e no adensamento do plantio, aliada ao crescimento da produção brasileira, geraram grande aumento na oferta internacional de laranja e de suco concentrado, levando à queda nas cotações internacionais desses produtos. Conseqüentemente, na década de 90 houve forte redução nos preços pagos aos produtores, em relação aos elevados valores observados no final da década de 80.
Nesse contexto, um dos grandes problemas para os citricultores paulistas passou a ser o excesso de oferta de laranja para processamento. Estatísticas da ABECITRUS evidenciam que durante a década de 90 houve crescimento de 2,62% na produção paulista, enquanto o processamento industrial cresceu a uma taxa de 2,14% ao ano. A solução para esse problema passa pela redução do crescimento da produção, pelo aumento das exportações de suco concentrado e pelo crescimento e fortalecimento do mercado interno de laranjas, que representa grande oportunidade para o sistema agroindustrial citrícola superar suas atuais dificuldades, já que se constitui num amplo mercado a ser explorado, capaz de consumir boa parcela da produção.
Nas últimas décadas, o mercado de laranja in natura ficou em segundo plano, em face do privilégio dado às exportações de suco concentrado. Para grande parte dos citricultores, esse mercado passou a ser considerado residual, visto como alternativa nos momentos em que o preço do suco concentrado sofria reduções significativas. Trata-se, portanto, de um setor que apresenta baixa profissionalização e cujo desenvolvimento tecnológico é bastante lento. Neves et al. (2001) salientaram que, no mercado de laranja in natura, existem deficiências relacionadas à padronização da fruta, à logística de distribuição, à falta de união e profissionalismo dos produtores, à ausência de marketing e à falta de foco nas vendas para o mercado interno. Para superar tais dificuldades, o sistema necessita de melhor estrutura, profissional e moderna, na qual a logística de distribuição assume papel fundamental, haja vista a grande participação dos custos associados à movimentação do produto no faturamento total do sistema (4%) e no valor do produto final (8 a 16%). Logo, a análise da distribuição espacial de packing-houses no Estado de São Paulo torna-se importante instrumento para a modernização e incremento competitivo do setor.
Dessa forma, o presente estudo objetivou propor e aplicar um modelo matemático de localização de packing-houses em regiões representativas do Estado de São Paulo, considerando-se as diferentes capacidades de processamento das empresas. A estratégia a ser incorporada no modelo proposto será baseada na minimização dos custos de implantação, processamento e transporte da laranja.
2. Metodologia
2.1. Teoria da Localização
O referencial teórico utilizado neste estudo foi a teoria da localização de plantas industriais, desenvolvida inicialmente por Alfred Weber (1909) e aprimorada através da evolução da programação matemática e dos avanços computacionais.
Segundo Saboya (2001), no modelo weberiano, a decisão locacional é função de três forças atrativas: o custo de transporte, o custo de mão-de-obra e as forças de aglomeração e de desaglomeração. Para Weber, o custo de transporte era a principal variável que afetava a localização das atividades industriais. Em seu modelo, o ponto de mínimo custo de transporte era obtido por meio do triângulo locacional, constituído, apenas, por três forças atrativas, a saber: um mercado consumidor e duas fontes de matéria-prima. Inicialmente, o equilíbrio dessas três forças determinava a localização da atividade industrial (o ponto de mínimo custo de transporte). A partir dessa primeira aproximação, eram consideradas as possíveis vantagens que outros locais podiam oferecer, tanto em temos de mão-de-obra mais barata quanto de economias de aglomeração, fatores que podiam promover o deslocamento da firma para uma nova região.
O efeito das outras forças de atração (mão-de-obra e aglomeração) sobre a localização da firma era analisado por meio das curvas isodapanas, definidas como o conjunto de pontos que tinham igual acréscimo de custo de transporte em relação àquele local onde esse custo era mínimo. Para análise da influência da mão-de-obra, Weber utilizou o conceito de isodapana crítica, que era obtida quando o acréscimo do custo de transporte se igualava à redução de custo proporcionada pela mão-de-obra mais barata. Lopes (1997) destacou que, se a localização inicial estivesse contida no interior da isodapana crítica, a mudança de localização não era interessante. No entanto, se a localização inicial estivesse situada externamente à isodapana crítica, a mudança tornava-se vantajosa.
Por fim, Weber considerou os fatores aglomerativos, uma vez que surgem economias resultantes da concentração de firmas em dado local. Para esta análise, o conceito de isodapana foi, mais uma vez, utilizado. No modelo weberiano, a interseção das isodapanas críticas era considerada a única área de aglomeração, onde as economias de custo eram capazes de contrabalançar os custos adicionais, em razão do afastamento das firmas em relação ao ponto de custo mínimo de transporte.
O surgimento da programação linear em meados da década de 40, em especial o modelo de transporte, proporcionou a introdução de situações mais complexas do que a inicialmente considerada por Weber. A partir de então, como destacou Lopes (1997), tornou-se possível adicionar ao modelo weberiano várias regiões de demanda, bem como de oferta de matéria-prima.
Lopes (1997) salientou que um grande avanço na modelagem de localização foi obtido a partir da utilização da programação inteira-mista, mais especificamente com a utilização de variáveis binárias no modelo. De acordo com essa concepção, tornou-se possível testar, para cada região, as diversas capacidades de processamento, procurando-se, assim, não só a localização que minimiza os custos de transporte, como também a melhor capacidade de processamento para a região. Conforme esse autor, a teoria da localização, em termos de programação, pode ser entendida como uma variação do modelo de transporte que, em conjunto com a programação inteira, constitui um ferramental bastante poderoso para determinação do melhor local para instalação de uma indústria.
A partir do advento da programação inteira-mista, surgiram alguns trabalhos cujo objetivo era a determinação de localizações ótimas. Dentre eles, pode-se mencionar, em termos nacionais, os realizados por Almeida (1981), Canziani (1991) e Lopes (1997). Nesses trabalhos, os autores consideraram economias de escala no transporte e no processamento.
Com relação à aplicações de modelos de localização ótima com o auxílio de programação inteira-mista, em contextos internacionais, podem ser destacados os trabalhos de Kilmer et al. (1983), Babcock et al. (1985), Brown et al. (1996), Durham et al. (1996) e Snyder et al. (1999). Alguns desses autores buscaram aprimorar os modelos de localização, eliminando algumas das considerações de modelos anteriores. Nesse sentido, Kilmer et al. utilizaram a programação dinâmica com o intuito de analisar os ajustamentos no curto prazo, os quais constituem uma das limitações dos modelos estáticos de localização que apresentam uma solução ótima somente para um equilíbrio de longo prazo. Durham et al. (1996) desenvolveram um modelo de programação não-linear para examinar a influência dos preços na alocação ótima das plantas.
2.2. Modelo Proposto
A partir do referencial teórico pesquisado, chegou-se à formulação de um modelo de programação inteira-mista, focado na otimização das localizações dos packing-houses de laranja no Estado de São Paulo. A estrutura genérica do modelo é apresentada a seguir:
a) Função objetivo
em que
Xij = quantidade de matéria-prima transportada da região produtora i aos packing-houses localizados no centro processador j;
Cij = custo de transporte da matéria-prima da região produtora i aos packing-houses localizados no centro processador j;
Hj = custo total de implantação e processamento dos packing-houses instalados na região processadora j;
Bjm = custo de transporte da laranja in natura dos packing-houses localizados no centro j ao mercado consumidor situado na região m; e
Yjm = quantidade de laranja in natura transportada dos packing-houses localizados no centro processador j para o mercado consumidor situado na região m.
b) Restrições
A capacidade de oferta de laranja da região i não deve exceder a capacidade de produção da própria região.
em que
 = quantidade total de laranja transportada da região de produção i para os packing-houses instalados nas diversas regiões j; e
= quantidade total de laranja transportada da região de produção i para os packing-houses instalados nas diversas regiões j; e
Si = quantidade total de laranja disponível na região produtora i.
Demanda por laranja pelos centros de processamento.
em que
 = quantidade de laranja recebida de todas as regiões produtoras i para atender à demanda total dos packing-houses de tamanho t, instalados no centro de processamento j; e
= quantidade de laranja recebida de todas as regiões produtoras i para atender à demanda total dos packing-houses de tamanho t, instalados no centro de processamento j; e
 = quantidade total de laranja demandada por todos os packing-houses de tamanho t instalados no centro processador j;
= quantidade total de laranja demandada por todos os packing-houses de tamanho t instalados no centro processador j;
 = variável binária (zero-um) associada à instalação ou não de um packing-house de tamanho t no centro de processamento j.
= variável binária (zero-um) associada à instalação ou não de um packing-house de tamanho t no centro de processamento j.
Oferta de laranja dos packing-house.
 = quantidade de laranja transportada, a partir dos packing-houses instalados nos centros de processamento j, que irá abastecer o mercado localizado na região m; e
= quantidade de laranja transportada, a partir dos packing-houses instalados nos centros de processamento j, que irá abastecer o mercado localizado na região m; e
 = quantidade de laranja recebida de todas as regiões produtoras i para atender à demanda total dos packing-houses instalados no centro de processamento j.
= quantidade de laranja recebida de todas as regiões produtoras i para atender à demanda total dos packing-houses instalados no centro de processamento j.
Demanda de laranja in natura pelo mercado consumidor
em que
 = quantidade de laranja transportada, dos diversos packing-houses instalados nos centros de processamento j, que irá abastecer o mercado localizado na região m;
= quantidade de laranja transportada, dos diversos packing-houses instalados nos centros de processamento j, que irá abastecer o mercado localizado na região m;
Dm = demanda por laranja in natura no mercado consumidor situado na região m.
Balanço entre a demanda dos centros de consumo e a oferta dos centros de processamento.
em que
 = demanda total dos diversos centros de consumo localizados nas regiões m; e
= demanda total dos diversos centros de consumo localizados nas regiões m; e
 = quantidade total de laranja ofertada por todos os packing-houses de tamanho t instalados no centro processador j.
= quantidade total de laranja ofertada por todos os packing-houses de tamanho t instalados no centro processador j.
Para contabilizar o custo total de implantação e processamento dos packing-houses a serem instalados em cada centro processador j ver a segunda parcela da função objetivo definida na equação (1) , foi inserida no modelo a seguinte equação:
em que
COj = custo operacional (implantação e processamento) dos packing-houses localizados na região processadora j.
O modelo proposto restringiu-se apenas ao mercado de laranja in natura, desconsiderando, portanto, a capacidade instalada das indústrias e o volume de laranja exportado, tanto para os demais estados brasileiros quanto para outros países.
Os limites superiores para i, j, m e t, adotados nas equações (1) a (7), foram: 40 (número de regiões produtoras), 40 (número de regiões processadoras, candidatas à localização de packing-houses), 40 (número de mercados consumidores) e 7 (número de tamanhos considerados para os packing-houses), respectivamente. Note-se, portanto, que as cidades-sede das 40 EDRs foram relacionadas como regiões produtoras, processadoras e consumidoras.
A estrutura matemática apresentada (expressões 1 a 6) foi codificada e processada através do sistema de otimização GAMS (Brooke et al., 1982).
2.3. Cenários
Foram analisados quatro cenários, nos quais se consideraram variações na oferta e na demanda dos EDRs, bem como restrições em relação ao número de packing-houses instalados por região. No cenário 1, considerou-se a não-existência (prévia) de packing-houses no Estado de São Paulo, uma vez que o intuito desta análise foi obter, para posterior comparação com a situação atual, o número, a localização dessas unidades de beneficiamento e as capacidades ótimas de processamento de cada região. No cenário 2, admitiu-se apenas a possibilidade de implantação de um packing-house por EDR, pois a finalidade, nesse caso, foi verificar se a disposição espacial das plantas sofreria alterações significativas ou se elas se distribuiriam pelas proximidades das regiões apontadas como ótimas pelo modelo de otimização proposto. No cenário 3, considerou-se a igualdade entre a oferta e a demanda por laranja de cada EDR, uma vez que esses valores são bastante distintos. Além disso, observou-se, por meio dos resultados obtidos nos cenários 1 e 2, que a quantidade de packing-houses suficientes para abastecer a demanda de laranja in natura no Estado de São Paulo era muito pequena, se comparada com a quantidade de plantas existentes atualmente. Portanto, o objetivo deste cenário foi verificar qual seria o número de unidades beneficiadoras caso o consumo de laranja in natura aumentasse, tornando-se igual ao da produção estadual. Por fim, no cenário 4, admitiu-se, para cada EDR, a igualdade entre a oferta e a demanda por laranja, bem como a possibilidade de instalação de apenas uma planta beneficiadora por região. A finalidade deste cenário foi avaliar situações semelhantes às descritas nos cenários 2 e 3.
2.4. Especificação dos dados
2.4.1. Subdivisão da área de estudo
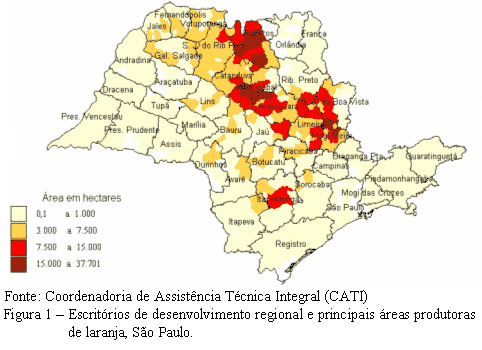
Com a finalidade de simplificar as análises relativas aos fluxos de oferta e de demanda de laranja, adotou-se, para fins do presente estudo, a divisão administrativa estabelecida pela Secretaria da Agricultura e do Abastecimento do Estado de São Paulo, de forma que os 40 escritórios de desenvolvimento rural (EDR) existentes foram considerados como centros de oferta e de consumo e como possíveis centros de processamento (Figura 1). Cada EDR foi representado por um único centróide, associado ao principal município da região, o qual serviu como referencial para obtenção dos custos de transporte e como referência para instalação das plantas processadoras, não significando, contudo, que essas plantas seriam, necessariamente, instaladas no centróide propriamente dito, mas sim distribuídas dentro do EDR.
2.4.2. Oferta e demanda de laranja
Adotou-se como oferta o valor da produção de cada EDR, ponderado pela parcela da produção paulista de laranja destinada ao mercado interno durante a década de 90 (22% em média), quando o excesso de oferta da fruta passou a se constituir num dos grandes problemas da citricultura paulista. A demanda por laranja in natura, em cada EDR, foi obtida ponderando-se o nível de consumo per capita médio nos anos de 1995/96 (12,8 kg/ano) pela população residente em cada região agrícola. Esse nível de consumo foi utilizado em razão de ser o valor mais recente obtido do Instituto Brasileiro de Geografia e Estatística (IBGE). Cabe ressaltar que a forma mais adequada de se medirem os valores de oferta e demanda de laranja para cada região seria a partir da estimativa das respectivas funções de oferta e demanda o que extrapola os objetivos deste estudo , de modo que os valores adotados para tais parâmetros podem ser considerados como simplificações de seus valores reais.
2.4.3. Localizações potenciais e capacidade de processamento dos packing-houses
Com o intuito de reduzir o tempo de processamento do modelo e o número de variáveis, assim como de evitar a necessidade de levantar dados muito mais detalhados, optou-se por uma análise baseada nas localizações associadas aos 40 EDRs do Estado de São Paulo e não nas relacionadas aos seus 624 municípios.
Quanto ao tamanho das plantas processadores de laranja, adotaram-se as sete diferentes capacidades de processamento mais comuns no Estado: 50 mil, 100 mil, 250 mil, 500 mil, 1 milhão, 2 milhões e 3 milhões de caixas por ano.
2.4.4. Custos de processamento, implantação e transporte
O custo de implantação foi calculado adicionando-se aos valores dos equipamentos, obtidos a partir de levantamento de campo, o valor da construção civil envolvida. Segundo esse levantamento de campo, packing-houses que processam até 250 mil caixas por ano ocupam uma área de, aproximadamente, mil metros quadrados. Já as plantas com capacidades superiores utilizam cerca de dois mil metros quadrados. Para cálculo do valor da construção civil, adotou-se, como referência, o valor de R$150,00 por metro quadrado construído. Os custos de processamento também foram obtidos através do levantamento de campo. Os valores de custo de transporte entre as 40 regiões de origem de matéria-prima, 40 possíveis regiões de processamento e 40 centros consumidores foram baseados em tabela de fretes rodoviários, em função da distância, fornecida por empresas do setor.
3. Resultados e Discussão
O custo mínimo de transporte, processamento e implantação de packing-houses, no cenário 1, foi equivalente a R$14.372.200. Para que a demanda por laranja no Estado de São Paulo fosse satisfeita, o modelo proposto sugeriu a implantação de 12 unidades de beneficiamento, as quais foram instaladas nos EDRs de Araraquara (1 unidade), Campinas (5 unidades), Dracena (1), Itapetininga (1), Limeira (1), Piracicaba (1), São José do Rio Preto (1) e São Paulo (1). Observou-se que o modelo sugeriu a instalação de plantas de maior porte (40.800 toneladas/ano), com a ressalva de que somente na região de Dracena a unidade implantada possuiria menor capacidade (2.040 toneladas/ano)1 1 Para maiores detalhes acerca dos resultados deste estudo, ver Ramos (2001). .
Comparando o número de unidades implantadas pelo modelo com os valores do levantamento realizado pelo FUNDECITRUS em 1998, constatou-se que a quantidade de plantas (cerca de 400) é muito superior ao número necessário para satisfazer a demanda interna do Estado. Entretanto, há que se considerar que São Paulo, além de ser um grande produtor de suco de laranja concentrado, é um exportador da fruta in natura para os demais estados da federação, fatores que não foram considerados no modelo proposto e que podem explicar a grande diferença observada entre os resultados obtidos e o número de plantas existentes atualmente no Estado.
No que tange à distribuição espacial das plantas processadoras, observou-se que o modelo priorizou a instalação de unidades em áreas mais próximas aos mercados consumidores, sobretudo no caso dos EDRs de Campinas e São Paulo, que, segundo a distribuição proposta, passaram a suprir cerca de 54% da demanda estadual. Tal comportamento difere significativamente da distribuição atual, mais voltada para a proximidade em relação aos principais centros produtores. Verificou-se, ainda, que regiões que apresentam proximidade em relação aos centros produtores e consumidores emergem como áreas potenciais para a instalação de packing-houses, como é o caso dos EDRs de Itapetininga, Limeira e Piracicaba.
Conforme os resultados, os oito centros de processamento atenderiam totalmente às demandas de todos os EDRs do Estado de São Paulo. Cabe salientar que as demandas dos EDRs seriam satisfeitas, em sua maioria, pelo fornecimento de somente um centro processador, exceção feita às regiões de Assis, Pindamonhangaba, Dracena, São Paulo, Campinas e Ribeirão Preto.
A análise dos custos marginais de transporte reflete as alterações que podem vir a ocorrer nos custos associados ao transporte de uma tonelada de matéria-prima da região de produção para a de processamento, caso haja a necessidade de alteração de alguma rota. De maneira geral, o acréscimo de uma mudança de rota é representado pela diferença entre o custo de transporte que se terá com a nova rota e o custo de transporte da rota que se encontra impossibilitada.
Com relação ao fornecimento de laranja dos centros de produção para os de processamento, observou-se que a principal região que poderia suprir a demanda dos EDRs de Campinas e Piracicaba, no caso de alguma eventualidade, seria a região de Limeira, já que o acréscimo no valor do custo de transporte, nesse caso, seria nulo. Isso se explica pelo fato de Limeira estar no mesmo raio de influência de Campinas e Piracicaba. No caso de São Paulo, as principais regiões fornecedoras seriam as de Bragança Paulista, Campinas e Mogi das Cruzes.
Já no cenário 2, verificou-se que o custo total de transporte, processamento e implantação de plantas processadoras seria o mesmo do cenário 1. No cenário 2, o número de plantas instaladas (12) permaneceu inalterado em relação ao do cenário 1. Contudo, devido à restrição de que cada região poderia abrigar somente uma unidade de beneficiamento, notou-se que foram implantados packing-houses em regiões próximas à região de Campinas, com a finalidade de suprir as áreas anteriormente cobertas pelo volume das cinco plantas existentes nesse EDR. Observou-se, ainda, que o transporte inter-regional seria pequeno. É importante salientar que a economia de escala no processamento também foi observada neste cenário, já que predominou a utilização de plantas de maior porte (11 com capacidade equivalente a 40.800 toneladas/ano e uma com capacidade igual a 2.040 toneladas/ano). Verificou-se, também, que prevaleceu a localização de unidades de beneficiamento em áreas intermediárias (próximas, ao mesmo tempo, dos centros de produção e de consumo).
O custo total de transporte, processamento e instalação de packing-houses, no cenário 3, seria equivalente a R$111.157.300,00. No cenário 4, esse valor seria igual a R$140.182.800,00. Observou-se, no cenário 3, que a laranja processada pelas 81 plantas instaladas pelo modelo seria oriunda de 39 EDRs. No cenário 4, o modelo evidenciou a instalação de uma unidade beneficiadora em cada um dos 40 EDRs do Estado de São Paulo. Verificou-se, também, que o transporte inter-regional, nos cenários 3 e 4, seria reduzido, de modo que a demanda dos centros processadores seria suprida, no máximo, a partir de quatro regiões produtoras.
Tanto no cenário 3 quanto no cenário 4, observou-se a predominância de unidades de beneficiamento com capacidades de processamento mais elevadas, o que poderia resultar em economias de escala no processamento. Quanto à localização das plantas, verificou-se, no cenário 3, que 40% das plantas seriam instaladas em regiões mais próximas aos centros consumidores, 32% em áreas intermediárias e 28% em áreas próximas aos maiores centros de produção. Observou-se, ainda, que seriam implantadas unidades na maior parte dos EDRs produtores de laranja, porém em menor número em relação à quantidade instalada nas proximidades dos maiores centros de consumo.
4. Conclusões
Os resultados fornecidos pelo modelo de otimização proposto sinalizam para a priorização da implantação de packing-houses de grande porte (de 500 mil a 1 milhão de caixas/ano), o que possibilitaria uma razoável economia de escala no processamento. Em relação à localização das plantas, o modelo deu preferência às áreas intermediárias. Contudo, verificou-se que as regiões que apresentam essa característica não fazem parte do "cinturão citrícola". Além disso, essas áreas são bem próximas dos centros de consumo mais expressivos do Estado, o que permite concluir que a solução sugerida pelo modelo de otimização enfatizou a proximidade em relação aos centros demandantes.
Um ponto importante refere-se ao transporte inter-regional, observado principalmente em centros de processamento que apresentam deficit de matéria-prima. Nos cenários 1 e 2, verificou-se que apenas 12 plantas seriam suficientes para processar o volume total de laranja demandado pelo Estado. Nos cenários 3 e 4, notou-se que haveria necessidade de se instalarem 81 e 103 packing-houses, respectivamente. Dessa forma, concluiu-se que o número de unidades beneficiadoras existentes atualmente no Estado (cerca de 400) é muito superior à sua real necessidade, quando se considera somente o mercado de laranja in natura.
Cabe também destacar que os modelos de localização podem ser considerados como importante instrumento de política pública, bem como um ferramental para a decisão empresarial, já que os resultados obtidos podem orientar os agentes em relação à instalação de futuras unidades de beneficiamento. Além disso, podem auxiliar na identificação de áreas potenciais, que ainda não foram exploradas, para o estabelecimento de firmas, assim como seu porte e sua capacidade de processamento ótima. Em suma, os modelos de localização são capazes de indicar a maneira mais eficaz de se estruturarem as atividades econômicas, fornecendo o número, o porte, a capacidade produtiva e a localização ótima das empresas, conferindo-lhes maior competitividade.
ASSOCIAÇÃO BRASILEIRA DOS EXPORTADORES DE CÍTRICOS ABECITRUS. Disponível em: http://www.abecitrus.com.br. (2000-2001).
- ALMEIDA, L. A. S. B. Viabilidade econômica e localização de unidades produtoras de farinha de milho para utilização em mistura com o no Estado de São Paulo Piracicaba, SP: ESALQ/USP, 1981. 159 f. Dissertação (Mestrado) Escola Superior de Agricultura "Luiz de Queiroz", Piracicaba.
- BABCOCK, M. W.; CRAMER, G. L.; NELSON, W. A. The impact of transportation rates on the location of the wheat flour milling industry. Agribusiness An International Journal, v.1, n.1, p.61-71, Spring 1985.
- BROOKE, A.; KENDRICK, D.; MEERAUS, A.G. A user's guide, Release 2.25. [S.l.]: The Scientific Press, 1992. 289 p.
- BROWN, E.; FATHI, Y.; SOWELL, R. Linear programming applied to a facility location problem. Applied Engineering in Agriculture, v.12, n.1, p.105-110, jan. 1996.
- CANZIANI, J. R. F. Simulação sobre a implantação da indústria de suco concentrado de laranja no Estado do Paraná Piracicaba, SP: ESALQ/USP, 1991. 111 f. Dissertação (Mestrado) Escola Superior de Agricultura "Luiz de Queiroz", Piracicaba.
- DURHAM, C. A.; SEXTON, R.J.; SONG, J.H. Spatial competition, uniform pricing and transportation efficiency in the California processing tomato industry. American Journal of Agricultural Economics, v.78, n.1, p.115-125, Feb. 1996.
- INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA IBGE. Pesquisa de Orçamentos Familiares 1995/96 São Paulo: IBGE, 1997.
- KILMER, R. L.; SPREEN, T.; TILLEY, D.S. A dynamic plant location model: the east Florida fresh citrus packing industry. American Journal of Agricultural Economics, v.46, n.1, p.94-108, 1964.
- LOPES, R. L. Suinocultura no estado de Goiás: aplicação de um modelo de localização Piracicaba, SP: ESALQ/USP, 1997. 95 f. Dissertação (Mestrado) Escola Superior de Agricultura "Luiz de Queiroz", Piracicaba.
- NEVES, E. M.; DRAGONE, D.; NEVES, M.F.; BOTEON, M. Conhecendo a citricultura: impactos alocativos, mercado, preços. Piracicaba, SP: ESALQ Departamento de Economia Administração e Sociologia, 2001. (disquete).
- RAMOS, S. Y. Avaliação da localização de packing-houses no Estado de São Paulo: o caso da laranja de mesa. Piracicaba, SP: ESALQ/USP, 2001. 132 f. Dissertação (Mestrado) Escola Superior de Agricultura "Luiz de Queiroz", Piracicaba.
- SABOYA, L. V. A dinâmica locacional da avicultura e suinocultura no Centro-Oeste brasileiro Piracicaba, SP: ESALQ/USP, 2001. Dissertação (Mestrado) Escola Superior de Agricultura "Luiz de Queiroz", Piracicaba.
- SÃO PAULO (Estado) – Secretaria de Agricultura e Abastecimento. Escritórios de Desenvolvimento Rural e Regionais Agrícolas. São Paulo: Instituto de Economia Agrícola. 2000. 16 p.
- SNYDER, S. A.; TYRRELL, L. E.; HAIGHT, R. G. An optimization approach to selecting research natural areas in national forests. Forest Science, v.45, n.3, p.458-468, 1999.
Datas de Publicação
-
Publicação nesta coleção
22 Nov 2005 -
Data do Fascículo
2002