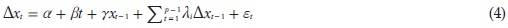Transmissão de preços e cointegração no mercado brasileiro de arroz

Transmissão de preços e cointegração no mercado brasileiro de arroz

Andréia Cristina de Oliveira Adami^I; Silvia Helena Galvão de Miranda^II

^IDoutora pela Esalq/USP. E-mail: [e-mail]

^IIProfessora Doutora da Esalq/USP. E-mail: [e-mail]

RESUMO

O objetivo do presente trabalho foi avaliar a dinâmica de formação de preços no mercado nacional de arroz em casca de modo a definir o processo de formação e intensidade do ajustamento (períodos em que se dá a transmissão de preços) entre os principais mercados produtores (RS e MT). O conhecimento das relações de preços entre os mercados importante para o desenvolvimento de contratos de comercialização (contratos a termo e de futuro) para o arroz e para a formulação (ou reformulação) de políticas públicas para o setor. Como instrumental metodológico utilizou-se da modelagem de sries temporais (Modelos de Autorregressão Vetorial com Correção de Erro (VEC)) e causalidade de Granger. O resultado do teste de causalidade de Granger apontou que os preços do RS são importantes para prever os preços de MT. O modelo de transferência estimado com correção de erro mostrou que, para cada 1% de aumento na taxa de crescimento dos preços no RS, a taxa de crescimento dos preços em MT registrará, em mdia, aumento contemporâneo de 0,44% e em torno de 0,17% com um período de defasagem.

Palavras-chave: transmissão de preços, arroz em casca, dominância de mercado.

ABSTRACT

The aim of this study is to evaluate the dynamics of pricing in the domestic market of paddy rice in order to define the process of prices formation and the adjustment intensity (periods in which the price transmission occurs) among the major producing markets (Rio Grande do Sul and Mato Grosso states). The knowledge of price ratios between markets is important for the development of trading contracts (fixed-term and future contracts) for rice and for the formulation (or reformulation) of public policies for the sector. As a methodological tool, we used the modeling of time series (Auto-Regression Models with Vector Error Correction - VEC) and Granger' causality. The Granger' causality test indicated that prices in the Rio Grande do Sul state are important to forecast prices in the Mato Grosso state. The model of transference estimated with an error correction term showed that for each 1% of increase in the growth rate for the RS prices, the growth rate of prices in MT will have, on average, a contemporaneous high of 0.44%, and around 0.17% in the following month.

Key-words: transmission of prices, paddy rice, market dominance.

Classificação JEL: Q19.

1. Introdução

A cadeia agroindustrial do arroz no Brasil tem passado por momentos de transformações importantes e redefinições de estratgias e objetivos, tanto em termos estruturais (produção e comercialização) como de políticas públicas (Política de Garantia de Preços Mínimos – PGPM). Em termos de políticas públicas, o surgimento de novos contratos de comercialização (Contratos de opção de venda públicos e Prêmio de Risco para contratos de opção de venda privados – Prop) pode prover uma relação mais sustentável entre política pública e o setor produtivo. O Prop, que um contrato privado, foi desenvolvido com o objetivo de melhorar o relacionamento entre os diversos agentes da cadeia produtiva e abrir caminho para o desenvolvimento de novos contratos privados de comercialização para o arroz.

O Brasil alcançou a autossuficiência na produção de arroz e parece inevitável quecontinuenarotado crescimento.Assim,a exportação de arroz comoalternativa para o escoamento do excedente de produção tem sido avaliada. Considere-se, ainda, que o equilíbrio do mercado de arroz no Brasil parece ter uma ligação intrínseca com o equilíbrio na região do Mercosul como um todo. Produtores e indústrias brasileiros no Uruguai e na Argentina usam da importação do Mercosul como forma de pressionar os valores no mercado brasileiro.

Com a perspectiva de aumento da oferta futura, surge a necessidade de se desenvolver estratgias de comercialização com foco numa melhor distribuição da oferta dentro e entre safras. Essa estratgia de comercialização deve ser definida com base nos principais produtores regionais, os quais podem servir de referência para a formatação de contratos, já que são líderes (dominantes) na formação e transmissão de preços.

Entre os principais estados produtores tem-se: Rio Grande do Sul, Santa Catarina, Mato Grosso, Maranhão e Pará. O estado de Santana Catarina possui participação (na produção brasileira) superior à de Mato Grosso, porm, pela proximidade e características do processo produtivo, considera-se a união de RS e SC como a principal região produtora do País.

Já o Pará e o Maranhão possuem participação menor e, devido à distância geográfica e diferenças no processo produtivo, não competem com o arroz produzido pelo Sul do Brasil.

A produção de Mato Grosso surgiu como opção de complementar o abastecimento das regiões Sul e Sudeste, competindo com o arroz do Sul (RS e SC). Nesse sentido, espera-se que o processo de formação de preços no estado de MT siga as condições de comercialização do RS, sendo, então, dois estados integrados no processo de formação de preços. A hipótese a ser testada, portanto, a de que o RS o estado formador de preços e que influencia na formação dos preços em MT. O processo e intensidade do ajustamento (períodos em que se dá a transmissão de preços) são objetos de estudo deste trabalho.

Na literatura disponível, para o mercado brasileiro de arroz em casca, não existem análises de cointegração e de dominância de mercado (causalidade), as quais podem auxiliar no entendimento das relações de formação e transmissão de preços entre os mercados regionais. A importância da análise de cointegração entre mercados deve-se ao fato da possibilidade de, sendo dois mercados integrados, haver influência de um mercado na formação de preços do outro.

A questão que surge: existe dominância entre os mercados produtores? Ou seja, em qual mercado se dá a formação de preços (dominante) e como os outros mercados (seguidores) são afetados por variações de preços no mercado dominante (transmissão de preços)? Visando fornecer base científica para melhor entender essas relações entre os mercados produtores de arroz em casca, o objetivo do presente trabalho foi avaliar a dinâmica de formação de preços no mercado nacional, de modo a definir o mercado dominante (formador de preços) e seus seguidores (transmissão de preços).

O conhecimento das relações de preços entre os mercados importante para que os agentes possam desenvolver contratos de comercialização (contratos a termo e de futuro) para o arroz e para a formulação (ou reformulação) de políticas públicas para o setor. Como instrumental metodológico utilizou-se da modelagem de sries temporais (Modelos de Autorregressão Vetorial com Correção de Erro – VEC) e causalidade de Granger.

2. Revisão de literatura

Vários estudos foram desenvolvidos para analisar relações de causalidade para produtos agrícolas. Quando há influência (causalidade) de um mercado sobre o outro, ocorre transmissão de preços entre esses dois mercados. Nesse caso, os preços no mercado dominante influenciam os preços no mercado seguidor e, há o que se convencionou chamar na teoria da comercialização, um sentido de causalidade entre os preços nos dois mercados. Muitos desses estudos fundamentaram-se nos testes de causalidade propostos por Granger (1969).

De acordo com a construção do teste de causalidade de Granger, uma relação de causalidade pode ser constatada se, e somente se, valores passados de uma determinada variável (X) ajudarem a prever os valores de uma outra variável (Y). O teste de causalidade, nesse caso, baseia-se na significância conjunta dos coeficientes associados aos valores defasados (passados) da variável explicativa.

Entre os estudos que utilizaram o teste de causalidade do tipo Granger pode-se citar Mafiloletti (2000), que estudou as relações entre os preços mensais da soja em grão, farelo e óleo nos diferentes níveis do mercado domstico (produtor, atacadista e consumidor) e, entre os preços do mercado interno e internacional; e Moraes (2002), que analisou a causalidade entre os preços da soja no mercado domstico e os do mercado internacional.

Para o mercado de arroz, o trabalho mais recente desenvolvido para avaliar a transmissão de preços no mercado o de Miranda et al. (2006). Os autores analisaram os coeficientes de correlação cruzada entre preços pagos ao produtor, no atacado e no varejo, levantados pela Companhia Nacional de Abastecimento (CONAB), para o período de 1995 a 2005. Foi verificada a existência de uma relação contemporânea entre os preços pagos ao produtor e os no atacado, tanto do produto do RS quanto do arroz de terras altas de MT. Verificou-se que o preço no atacado causa as variações nos preços do varejo. O sentido da causalidade encontrado foi do produtor para o varejo, ou seja, as variações de preços se iniciam no produtor e se transmitem ao varejo, tanto para o arroz agulhinha do RS quanto de MT. A transmissão de preços se dá do produtor para o varejo e do atacado para o varejo. Para o arroz gaúcho, essa transmissão ocorre, em parte, imediatamente, mas parte das variações se transmite ao longo do primeiro e segundo meses seguintes. No caso da causalidade entre o atacado do arroz de terras altas e o varejo do arroz agulhinha, e entre o produtor de MT e o varejo do arroz agulhinha, as variações ocorrem a partir do primeiro mês e tambm ao longo do segundo mês.

Estudos utilizando modelos de sries temporais para analisar transmissão de preços entre mercados agrícolas são freqüentes na literatura nacional e internacional. Alves (2002) analisou a transmissão de preços entre os mercados dos principais produtos do setor sucroalcooleiro paulista utilizando modelos do tipo VAR (Autorregressão Vetorial) com correção de erro (VEC).

Nos últimos anos, o mercado de arroz em casca tem passado por mudanças significativas, principalmente na participação dos principais estados produtores. O uso de modelos de sries temporais para estudar cointegração, integração entre os mercados produtores, e causalidade, para definir o sentido da influência na transmissão de preços entre os principais mercados produtores, pode sinalizar a existência de um mercado dominante na formação de preços do arroz o que, no futuro, pode ser útil na formatação de contratos de comercialização para o mercado (contratos a termo, contratos futuros e/ou opções).

3. Referencial teórico

O referencial teórico utilizado para analisar causalidade e transmissão de preços entre duas regiões produtoras de determinado bem (nesse caso o arroz em casca) está baseado em Barros (1987).

Considerando-se duas regiões separadas (X e Y) que produzem o bem (W), caso não haja comrcio entre as regiões, o preço em cada uma das regiões (Px e Py) será determinado pelas condições de oferta e demanda locais.

Na Figura 1 tem-se, à direita, as curvas normais de oferta e demanda do mercado Y. À esquerda, aparecem invertidas as curvas de oferta e demanda para o mercado X, pois as quantidades são medidas da direita para a esquerda. Em seguida, traçam-se as curvas de excesso de oferta para cada região (ESy e ESx) que relacionam diferentes níveis de preços e os respectivos montantes pelos quais as ofertas excedem as demandas regionais. Para representação gráfica, toma-se, para cada nível de preço, a diferença horizontal entre a curva de oferta e a curva de demanda em cada região.

Devido ao posicionamento das curvas de oferta e de demanda regionais, as curvas de excesso de oferta se cruzam em um dos lados da ordenada. Na Figura 1, isso se dá do lado direito, pois ao preço P* haverá um excesso de demanda (excesso de oferta negativo) em X. Esse excesso igual a Of.

Verifica-se que o comrcio tende a expandir a produção na região de preço menor e retrair a produção na região de preço maior. Portanto, a região Y expande a produção de Oe para Od. Do lado do consumo, na região X, onde o preço era maior, há um aumento do consumo do bem em questão, o contrário ocorre na região Y.

A partir desse modelo, pode-se considerar o custo de transporte (CT) por unidade entre as regiões X e Y. Como resultado da incorporação do custo de transporte tem-se:

• Com comrcio, a diferença de preços entre duas regiões tende a se reduzir, sendo o limite dado pelo custo de transferência (transporte).

• Quanto maior o custo de transferência entre as regiões, maior a diferença de preços que prevalecerá e menor a quantidade comercializada.

4. O mercado de arroz

4.1. Produção e Consumo

No final de 2007 e início de 2008 retoma-se, no cenário internacional, o polêmico debate sobre segurança alimentar, fomentado pela evolução crescente dos preços mundiais de alimentos, inclusive do arroz, e pelos estoques mundiais em patamares baixos.

O Quadro 1 mostra as condições de suprimento do mercado de arroz no Brasil. Verifica-se que a produção brasileira teve um aumento crescente em todo o período considerado. Já o consumo interno, desde a safra 2004/05, encontra-se estabilizado próximo de 13 milhões de toneladas. As importações, durante todo período, permaneceram acima de 700 mil toneladas, com exceção da safra de 2007/08. As exportações, por outro lado, at a safra 2003/04, participaram com volumes inferiores a 100 mil toneladas e passaram a ganhar fôlego a partir da temporada 2004/05. Com relação aos estoques de passagem, na safra 2008/09, estes estiveram próximos de 1 milhão de toneladas, volume mais baixo desde a temporada 1999/00.

O Brasil o 10º produtor mundial de arroz, com uma produção estimada, para a safra 2009/10, em 12 milhões de toneladas de arroz em casca. O País o maior consumidor ocidental do produto, com consumo estimado em aproximadamente 13 milhões de toneladas de arroz em casca em 2010 (CONAB, 2010b). A produção brasileira pouco significativa no mercado mundial, representando aproximadamente 2% da produção mundial de arroz, sendo predominantemente para consumo interno (Food and Agriculture Organization of United States – FAO, 2010).

A Tabela 1 apresenta a produção e a área colhida, discriminadas para os principais estados produtores de arroz em casca. Esses dados mostram que a região Sul do País a principal produtora de arroz. Aproximadamente 60% da produção nacional, em 2009, foi cultivada no Rio Grande do Sul e, somada à produção de Santa Catarina, atingiu 67% do volume do arroz em casca produzido no Brasil.

Em terceiro lugar está o estado de Mato Grosso, responsável pela produção de 6% do total nacional de 2010. Vale ressaltar que, de 2005 para 2006, houve redução de pouco mais de um terço na produção de arroz de Mato Grosso. Isso se deve ao fato de o arroz de sequeiro (chamado de terras altas em MT) ter que concorrer com outras culturas como soja e milho, o que não ocorre no RS, devido à dificuldade de adaptação de outras culturas em áreas alagadas – regiões conhecidas como várzea. Outro fator importante que o plantio do arroz em Mato Grosso tambm tido como um plantio para abertura de novas áreas agricultáveis (expansão da fronteira agrícola), ou seja, utilizado como primeiro plantio para preparar a nova terra para o cultivo de outras culturas como soja e algodão ou para recuperar áreas degradadas (DEL VILLAR et al., 2005).

No Rio Grande do Sul, produz-se o arroz longo-fino irrigado com uma produtividade mdia acima de 6.300 kg/ha. Em Santa Catarina, a produtividade mdia do arroz pode chegar alm de 7.000 kg/ha. Neste estado, o arroz longo-fino irrigado cultivado em pequenas áreas com alto grau de tecnologia.

Em Mato Grosso, a produtividade mdia do arroz ficou próxima de 3.000 kg/ha em 2010, sendo cultivado em terras altas. Apesar do desenvolvimento de variedades de arroz longo-fino, adaptadas ao Centro-Oeste, ainda há necessidade de avanços nesta área de pesquisa, segundo agentes do setor¹ , já que as variedades de melhor aceitação da indústria, nem sempre são as de maior facilidade de cultivo para os produtores, que podem preferir cultivares mais rústicas, principalmente quando seu objetivo a abertura de áreas.

No Brasil, 80% do arroz produzido são da classe longo-fino e os 20% restantes, da classe longo (CONAB, 2010b). Atualmente, o padrão de consumo do brasileiro a preferência pelo arroz longo-fino, mas há algumas dcadas, o arroz longo era o padrão vigente (FERREIRA et al., 2005). Este um dos elementos que distinguem a qualidade entre o produto do RS e SC do produto do Centro-Oeste. Esta última região ainda carece de variedades (longo-fino) mais adaptadas, que permitam concorrer com o produto do Sul do País. O arroz irrigado demanda grandes volumes de água e para produzir o arroz de sequeiro, que cultivado em Mato Grosso, utiliza-se de tecnologia desenvolvida para o cultivo em terras altas e que não depende da irrigação tradicional.

A colheita do arroz no Brasil está concentrada nos meses de março a junho e está distribuída de forma que os períodos de pico, ou seja, de maior volume colhido, se dá nos meses de março e abril, ao passo que o período de entressafra ocorre nos meses de agosto, setembro, outubro, novembro e dezembro (CONAB, 2010a) – Figura 2.

Devido à distribuição anual da oferta, a comercialização fica concentrada no período da safra, principalmente por parte dos produtores. A estratgia de comercialização mais comum, definida por produtores que preferem estocar seu produto, esperar maior preço para a entressafra, estocando o arroz em cooperativas. Em anos de oferta elevada, em que os preços não reagem, há forte pressão por intervenção governamental. O governo federal atua utilizando seus instrumentos (compras diretas e contratos de opção) atravs de apoio à comercialização.

5. Comercialização de arroz no Brasil

No Brasil, são poucos os contratos privados de comercialização para o arroz em casca. Geralmente, os produtores depositam seu produto em cooperativas para esperar a poca de entressafra para, então, negociar. Vendas antecipadas por meio de contratos a termo são raras. Assim, o que geralmente ocorre a venda à vista no período da colheita ou o depósito do produto em cooperativas para vendas futuras sem fixação de preços.

Dada essa característica do mercado, a comercialização do arroz fica dependente das políticas adotadas pelo governo, cuja principal ferramenta de intervenção a Política de Garantia de Preços Mínimos (PGPM). Por meio da PGPM, o governo fixa um preço mínimo para as safras.

Dos anos 1960 at meados dos anos 1990, a política de preços agrícolas (PGPM) consistiu na formação de estoques por parte do governo federal, que visava retirar o excesso de oferta em anos de safra abundante e reduzir o estoque em anos de escassez de produção. Os instrumentos de intervenção governamental nesse período eram as Aquisições do Governo Federal (AGF) e os Emprstimos do Governo Federal (EGF). Com a intensificação da abertura comercial e o agravamento da restrição fiscal, em meados dos anos 1990, o governo passou a adotar novos instrumentos de sustentação de preços de forma a apoiar a formação de estoques por parte da iniciativa privada (REZENDE, 2003).

A partir de 1996, passam a integrar a PGPM dois novos instrumentos de garantia de preços ao produtor que são respectivamente: o Prêmio de Escoamento de Produto (PEP) e os Contratos de Opções de Venda, no qual o governo o único lançador das opções. Em dezembro de 2004, o governo instituiu, por meio da lei 11.076, os contratos de Prêmio de Risco para Aquisição de Produto Agropecuário oriundo de Contrato Privado de Opção de Venda (Prop). Nesses contratos, o governo leiloa para indústrias e/ou cooperativas um prêmio, chamado prêmio de risco, para quem assumir o compromisso de lançar para o produtor rural os contratos de opção de venda (ADAMI, 2005).

Uma característica desses novos contratos de comercialização para o mercado de arroz em casca (PEP, Opção pública e Prop) o apoio para a distribuição da comercialização do produto dentro do ano safra. O PEP, que o prêmio para escoamento, tem como objetivo a redistribuição do produto entre regiões; já os contratos de Opção pública e o Prop são apoios para que o produtor possa armazenar seu produto na safra e vender na entressafra. Porm, em anos de oferta abundante e baixo preço, os produtores podem exercer seu direito de vender ao governo (exercer seus contratos de Opção pública), se esse volume não retornar para o mercado, esses contratos tornam-se uma AGF. Uma vantagem na utilização desses novos programas que o governo não precisa ter disponível o recurso para adquirir e manter em estoque parte da produção da safra, mas, apenas para subsidiar a diferença de preços. A formação de estoques fica por conta dos operadores privados.

A Tabela 2 resume as operações com a política de apoio à comercialização de arroz no Brasil a partir da adoção dos novos instrumentos de sustentação de preços.

At 1989, a estocagem de arroz no Rio Grande do Sul recebeu forte estímulo da PGPM via EGF que, era fortemente subsidiado. A partir dos anos 1990, a redução do papel da PGPM passou a viabilizar a estocagem privada nesse estado. Segundo Rezende (2003), devido ao fato de o arroz gaúcho ter maior participação de mercado, era a partir do preço mínimo que se formavam os preços nas regiões consumidoras.

A partir da safra 2004/05, o governo passou a utilizar, alm dos contratos de opção de venda públicos, os contratos privados (Prop) e, em 2006, pela primeira vez, o PEP. O Prop e o PEP – diferentemente dos contratos públicos que podem tornar-se uma AGF – são instrumentos de incentivo à armazenagem privada, com o governo atuando apenas atravs de subvenção econômica na diferença entre os preços de referência (preço mínimo e preço de exercício) e os preços de mercado (ADAMI, 2005).

As mudanças ocorridas na estrutura da PGPM e a atuação do governo ocorreram no sentido de incentivar a armazenagem privada e o relacionamento dos agentes da cadeia. Pois, o papel do preço mínimo não influenciar os preços de mercado, mas, sim, garantir um nível de preços minimamente remunerador ao produtor.

Adami et al. (2007) mediram os efeitos da PGPM sobre os preços no mercado gaúcho e concluíram que os formuladores de política não se influenciam pelo comportamento cíclico do preço de mercado, mas, atêm-se apenas ao nível mínimo de referência, que procuram assegurar. No curto prazo, porm, há um efeito da política sobre os preços de mercado. Em anos de oferta elevada, por exemplo, o preço mínimo serve como um piso ao mercado, assegurando aos produtores ao menos uma parte dos custos de produção. Nessas ocasiões verifica-se atuação mais acentuada pela Conab, por meio dos instrumentos de opções e AGF. Tudo isso se passa sem que as tendências de mercado sejam afetadas. Esse resultado sugere que o governo não tem como estratgia acompanhar os ciclos de mercado da cultura, mas, sim, assegurar um piso de rentabilidade ao setor.

Mesmo com a forte atuação do governo no mercado de arroz em casca, os preços têm registrado significativas variações em função das oscilações na oferta do produto. A Figura 3 mostra as mdias de preços para o Rio Grande do Sul (RS) e Mato Grosso (MT) e os respectivos preços mínimos fixados pelo governo para esses estados. Observa-se que, de maio/2005 at junho/2006, os preços de mercado, nas duas regiões, permaneceram abaixo do valor mínimo de referência. Apenas a partir de julho/2006 que voltam a se recuperar (superando o preço mínimo) sendo que, no RS, essa recuperação foi mais lenta, com os preços permanecendo abaixo do mínimo de referência at julho/2007. Em 2010, embora os preços tenham permanecido em patamares baixos, no primeiro semestre do ano, em mdia, não chegaram a romper a barreira do mínimo, para ambos os estados.

6. Procedimentos Economtricos

6.1. Dados

As sries de dados utilizadas foram: Preço mensal do arroz em casca do Rio Grande do Sul e de Mato Grosso, coletados pela Conab de agosto/1999 at junho/2010. As sries de preços foram consideradas em quilos e deflacionadas para preços de junho de 2010. O deflator utilizado foi o índice Geral de Preços – Disponibilidade Interna (IGP-DI) da Fundação Getúlio Vargas – FGV (2010).

Esses dois estados foram selecionados, considerando-se, primeiramente, a disponibilidade de dados. Embora o estado de Santa Catarina (SC) tenha participação maior que Mato Grosso, pela proximidade e características do processo produtivo, considera-se a união de RS e SC como a principal região produtora do País. Já os estados do Pará e Maranhão possuem participação menor e, devido à distância geográfica e diferenças do processo produtivo, não competem com o arroz produzido pelo Sul.

O software utilizado na modelagem do trabalho foi o Ratz na versão 6.0 (ENDERS, 1996).

6.2. Cointegração e modelo de correção de erro

O procedimento utilizado para avaliar relações de longo prazo entre as variáveis fundamenta-se nos testes de cointegração. Para proceder ao teste de cointegração necessário que as variáveis sejam não estacionárias e integradas de mesma ordem. Dessa forma, preciso realizar testes de raiz unitária nas sries de preços para definir a ordem de integração entre as variáveis (diferença do tipo xt - x(t-1) - valor da variável x observado no tempo t subtraído do valor da variável x observado no tempo (t-1)). Conforme definido por Engle e Granger (1987), uma srie sem componente determinístico, com representação ARMA (Autorregressivos e de Mdia Móvel), estacionária e invertível, após d diferenças, dita ser integrada de ordem d, denotada por xt ~ I(d) Assim, a ordem de integração diz respeito ao número de vezes em que uma srie precisa ser diferenciada para tornar-se estacionária.

Para avaliar a ordem de integração das sries, foi aplicado o teste de raiz unitária, utilizando-se a metodologia de Dickey-Fuller Aumentado – Dickey e Fuller (1979), Dickey e Fuller (1981), Fuller (1976). O processo gerador das sries de tempo estacionário se suas características não se alteram com o tempo. Assim, um processo gerador de dados xt será estacionário se possuir mdia e variância constantes ao longo do tempo e a covariância entre os valores da srie depender apenas da distância de tempo (t) que separa os dois valores e não dos tempos reais em que os valores da variável x são observados (GUJARATI, 2000).

O teste de hipótese realizado para testar a estacionariedade da srie foi baseado nas distribuições de Dickey e Fuller (1979), Dickey e Fuller (1981), Fuller (1976). Para averiguar a estacionariedade das sries temporais, utilizou-se o procedimento proposto por Enders (2004).

O primeiro teste de raiz unitária foi desenvolvido por Fuller (1976), considerando um processo autorregressivo de ordem um [AR(1)], conforme descrito a seguir – equação (1):

x_t = px_t-1 + ε_t(1)

Na equação (1) ε_tconsiderado ruído branco. A hipótese nula de que χ_t não estacionária. Assim, tem-se que: H0:ρ=1 contra HA : ρ <1 . O que equivale a testar: Δ y_t=(ρ-1)x_{t -1}+ε_t, a hipótese H0:ρ=1 contra HA :ρ<1 .

A aceitação da hipótese nula indica que o processo tem uma raiz unitária e, portanto, não estacionário. Para a realização deste teste de hipótese, utiliza-se como processo de estimação o mtodo dos Mínimos Quadrados Ordinários. No entanto, testes de raiz unitária e/ou estacionariedade não utilizam a distribuição padrão t de Student, mas os valores das distribuições denominadas x , as quais constam de Fuller (1976).

Considerando modelos que incorporam a presença de intercepto e tendência, têm-se respectivamente – equações (2) e (3):

χ_t= α + ρx_t-1 + ε_t(2)

E,

χ_t= α + βt +ρx_t-1 + ε_t(2)

A estatística utilizada no caso de modelos com intercepto denominada τ_µe, para se testar a presença de tendência, utiliza-se a estatísticaτ _τ. No entanto, possível testar de maneira conjunta a presença de um termo de intercepto e/ou tendência e de raiz unitária, cujos testes são denominado Φ se correspondem a um teste F. No caso do teste denominado Φ₁ , testa-se a hipótese de que (α,ρ) ≠ (0,1) contra a hipótese de que (α,β,ρ) ≠ (0,1) . No caso de Φ₂ , a hipótese nula de que (α,β,ρ) = (α,0,1) contra a hipótese alternativa de que (α,β,ρ) ≠ (α,0,1). Por fim, a estatísticaΦ3 testa a hipótese nula de que (α,β,ρ) = (α,0,1) contra hipótese alternativa de que (α,β,ρ) ≠ (α,0,1). Os valores críticos para estas distribuições estão tabulados em Dickey e Fuller (1981).

preciso definir a ordem do processo autorregressivo p (número de defasagens estatisticamente significativas) que descreve o comportamento da srie temporal – equação (4).

Em que, . Nesse caso, a presença de raiz unitária testada pela hipótese H0: c =0 . Este teste denominado de Teste de Dickey-Fuller Aumentado (ADF).

Para auxiliar a identificação da estacionariedade das sries e dos termos autorregressivos (número de defasagens) as funções de autocorrelação e autocorrelação parcial podem ser utilizadas. Para se determinar p – ordem do processo regressivo que descreve o comportamento da srie temporal –, alguns critrios como de Akaike (Akaike Information Criterion – AIC) e Schwarz (Schwartz Bayesian Criterion – SBC) tambm podem ser utilizados. Os critrios AIC e SBC são definidos como – equações (6) e (7):

AIC = TIn ^sqr h +2n (6)

SBC TIn (sqr ) (7)

Alm destes dois critrios, utiliza-se tambm a estatística Q de Ljung e Box (1978) para verificar a existência de autocorrelação serial. A estatística Q representada pela equação (8):

Nas equações (6), (7) e (8) n o número de parâmetros estimados, T o número de observações usáveis, sqr a soma do quadrado dos resíduos do modelo com defasagem p, r_k a autocorrelação para a defasagem k e s o número de defasagens a serem testadas.

A importância da análise de cointegração surge de seu uso em sries não estacionárias, pois, ao remover a tendência da srie (pela diferenciação) elementos de longo prazo entre as variáveis são eliminados. Se duas sries possuem uma relação de equilíbrio de longo prazo, mesmo que possuam tendências estocásticas, elas irão mover-se juntas no tempo e a diferença entre elas será estável. Para os casos de estimação de modelos do tipo VAR contendo variáveis não estacionárias, possível que haja combinações lineares estacionárias para variáveis integradas de mesma ordem, ou seja, relações de equilíbrio de longo prazo que devem ser incluídas no modelo para evitar erros de estimação. Portanto, pode-se utilizar a estabilidade de longo prazo dos comovimentos entre as sries para fins de modelagem e previsão. Esses comovimentos (cointegração) geram um Mecanismo de Correção de Erros (ECM) dos desvios aleatórios de curto prazo que precisa ser incluído no modelo. O novo modelo a ser estimado um modelo VAR com Correção de Erro ou VEC.

Considerem-se duas sries x_1t e x_2tnão estacionárias, isto , processos estocásticos com realização independente. Assim sendo, qualquer tentativa de prever seus valores futuros utilizando os valores passados das sries será sem significado – equações (9) e (10):

x_1t=x1_t-1+e_1t(9)

x_2t=x_2t-1+e_2t(10)

Contudo, se existir uma relação estável de longo prazo entre x_1te x_2t(as sries são integradas de mesma ordem e cointegradas), a diferença entre elas será estável. Essa diferença, que pode ser representada por: z_t = x_1t - x_2t, define uma combinação linear estacionária entre essas duas variáveis. Esse um exemplo simples de um sistema de cointegração em que a relação de cointegração definida por uma combinação linear estacionária e pode ser representada pelo vetor . Em notação matricial: z_t= β'X_t.

Neste caso, b conhecido como vetor de correção de erro ou vetor de cointegração e zt o mecanismo de correção de erro ou, modelo de correção de erro, que descreve a dinâmica da convergência das sries no longo prazo.

Formalmente, Engle e Granger (1987) consideraram um conjunto de variáveis econômicas (sistema) em equilíbrio de longo prazo quando – equação (11):

β₁χ_1t+β₂χ_2t +... + β_nχ_nt= 0 (11)

Na equação (11 )βeX_trepresentam os vetores (β₁ , β₂ ,..., β_n) e (χ₁, χ₂, ... ,χ_nt). O sistema está em equilíbrio de longo prazo quandoβ'χ0 . Os desvios do equilíbrio de longo prazo são chamados erros de equilíbrio e são representados como – equação 12:

e_t=β'χ(12)

Uma vez que são desvios de uma relação de equilíbrio de longo prazo e, portanto, de caráter temporário, e_t estacionário. Os componentes do vetor χ_t(χ₁, χ₂, ... ,χ_nt) são cointegrados de ordem b, d ou χ_t~ CI db (, ) se todos os componentes do vetor forem integrados de ordem d e, se existir um vetor β= (β₁, β₂,..., β_n) de forma que haja uma combinação linear β'X_t=β_tχ_1t +β₂x_2t+ ... +β_nx_ntintegrada de ordem (d-b) em que b>0, o que significa que a combinação linear resultante (z_t) tem ordem de integração menor do que as variáveis originais. Neste caso, o vetor b chamado de vetor de cointegração. No curto prazo, as variáveis cointegradas sofrem desvios da relação de longo prazo. Sem uma especificação dinâmica do modelo, não possível determinar de que maneira ocorrerá o ajuste. Este problema seria resolvido atravs da aplicação de um modelo de correção de erro, de forma que o desvio do período anterior seja corrigido (ENDERS, 2004).

Num sistema composto por mais de duas sries, integradas de mesma ordem, pode-se testar cointegração utilizando-se o mtodo proposto por Johansen (1988). Esse mtodo uma versão multivariada do mtodo de Engle e Granger para a detecção de cointegração para duas variáveis e consiste na utilização de estimadores de máxima verossimilhança para testar a presença e estimar vetores de cointegração. Este procedimento está centrado na relação existente entre o posto de uma matriz π e suas raízes características.

Considere o caso de n-variáveis – equação (13):

Nas equações (13), X _t-1e ε_tsão vetores (n x 1); A1 a matriz de parâmetros (n x n); r definido como (A_1-I) e I uma matriz identidade (n x n).

O posto deπigual ao número de vetores de cointegração. Supondo que π = 0 , não há combinações lineares de {X_u}, que sejam estacionárias e, portanto, as variáveis não são cointegradas.

Para conhecer o número de vetores de cointegração, verifica-se a significância das raízes características de π. O teste para verificar o número de raízes características que são não significativamente diferentes de zero realizado atravs de duas estatísticas – equações (14) e (15):

Nas equações (14) e (15) são os valores estimados das raízes características obtidas por meio da estimação da matriz π e T o número de observações.

Para a verificação do número de defasagens necessárias para o modelo multi-equacional pode-se utilizar o critrio AIC que consiste em – equação (16):

Na equação (16) a estimativa da matriz de variâncias/covariâncias do termo de erro e u o número de parâmetros considerados.

Determinados o número de vetores de cointegração e as defasagens do modelo pode-se estimá-lo incluindo-se na estimação o mecanismo de correção de erro. O modelo deve ser escolhido de acordo com os resultados dos testes de estacionariedade e do número de relações de cointegração encontradas. Se todas as n variáveis pertencentes ao vetor X_tsão estacionárias, o modelo VAR apropriado e não há necessidade de tomar as diferenças de X_t. Por outro lado, se todas as n variáveis pertencentes ao vetor X_tsão não estacionárias e não existe qualquer relação de cointegração (h=0, h o número de relações de cointegração que compõem o vetor z_t) entre elas, X_t, precisa ser diferenciado e, portanto, o modelo apropriado o VAR com as sries nas diferenças Δ X_t.

A equação (17) define algebricamente a especificação de um modelo VAR genrico:

X_t = θD + G₁X_t-1 + G₂X_t-2 + ... + G_pX_t-p+ ε_t (17)

Com:

θ = coeficiente das variáveis determinísticas D;

D = [d1 d2 ... df] variáveis determinísticas tais como: constantes, tendência temporal, dummies sazonais, dummies de intervenção (para outliers), dummies de quebra estrutural e regressores considerados fixos e não estocásticos; G_i= matriz nxn de coeficientes com elementos g_jk,i das variáveis defasadas X_t-i; ε_t= vetor de erros independentes no tempo mais correlacionados entre si, normal e identicamente distribuído com mdia zero e variância Λ t -ε_t~ N (0,Λ t) .

Se as variáveis são não estacionárias e existem 0 < h < n relações de cointegração entre elas, o modelo VAR precisa ser transformado em um modelo VEC – equação (18):

ΔX_t = θ + Γ₁ Δ X_t-1+ Γ₂ ΔX_t-2+ ... Γ_p-1 ΔX_t-p-1 + ΠX_t-1 + ε_t (18)

Na equação (18) ΔX_t = X_t - X_i-1,θo parâmetro referente a uma constante considerada no modelo e Π = αβ' , ou seja, uma matriz com (nxn) parâmetros que pode ser fatorada em dois produtos em que:

• β' um vetor de cointegração (h x n) que representa as h relações de cointegração e a existência das n sries estacionárias transformadas - z_t=β'X_t;

•α a matriz de parâmetros (parâmetros de ajustamento) que determinam a taxa pela qual os elementos de X_tse ajustam em resposta aos desvios defasados (Z_t-1) dadas as h relações de cointegração.

Para estimar os parâmetros θ, α, β e Γ , pode-se utilizar o mtodo FIML (Full information maximum likelihood) proposto por Hamilton (1994).

6.3. Causalidade de Granger

Para duas sries de tempo X_te Y_t, o teste de causalidade de Granger assume que a informação relevante para a predição das respectivas variáveis X e Y está contida apenas nas sries de tempo sobre essas duas variáveis. Portanto, uma srie de tempo estacionária X causa outra srie estacionária Y se melhores predições estatisticamente significantes de Y podem ser obtidas ao se incluir valores defasados de X aos valores defasados de Y. Assim, o teste envolve estimar as seguintes regressões dadas pelas equações (19) e (20):

X_t = Σ a_iY_t-1 +Σ b_iX_t-1 + u_1t (19)

Y_t = Σc_iY_t-i +Σ d_iX_t-1 + u_2t (20)

Nas equações (19) e (20) uitsão os ruídos que assumem-se não correlacionados. Pode-se distinguir quatro casos diferentes de causalidade de Granger:

1) Causalidade unilateral de Y para X: quando os coeficientes estimados em (19) para a variável defasada Y forem conjuntamente diferentes de zero (Σa_i ≠ 0) e quando o conjunto de coeficientes estimados em (20) para a variável X não for estatisticamente diferentes de zero (Σd_i ≠ 0) ;

2) Causalidade unilateral de X para Y: quando o conjunto dos defasados para a variável Y na equação (19) não for estatisticamente diferente de zero (Σa_i ≠ 0) e o conjunto de coeficientes defasados para a variável X em (20) for estatisticamente diferente de zero(Σd_i ≠ 0);

3) Bicausalidade ou simultaneidade: quando os conjuntos de coeficientes defasados de X e Y forem estatisticamente diferentes de zero em ambas as regressões;

4) Independência: quando, em ambas as regressões, os conjuntos de coeficientes defasados de X e Y não forem estatisticamente diferentes de zero.

7. Resultados e Discussão

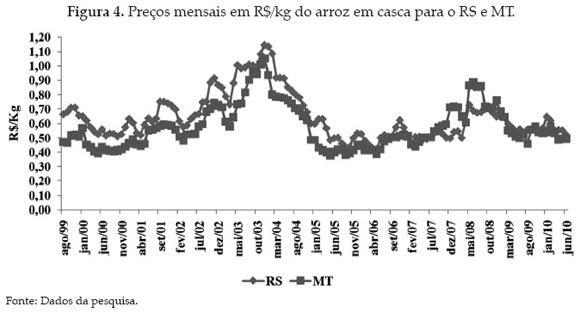
Na Figura 4 pode-se observar o comportamento das sries de preços reais do arroz em casca para o RS e MT de agosto de 1999 at junho de 2010. Observa-se que o mercado atingiu os maiores patamares de preços no final do ano de 2003. O pico de alta, nesse período, se deu em dezembro de 2003, quando os preços atingiram R$ 1,15 por quilo do grão no RS e R$ 1,05 por quilo em MT. A partir de janeiro de 2004, os preços passaram a cair, com piso (menor preço praticado no mercado) de R$ 0,44 para o RS e de R$ 0,40 em MT em outubro de 2005.

Na safra 2004/5, foram lançados os contratos de Prop e verifica-se, pela análise da Figura 4, que não houve mudança de nível ou na tendência de mercado, o que já havia sido constatado por Adami et. al (2007). Isso ocorre porque esses contratos, como a AGF e os contratos de Opção Pública, estão baseados no preço mínimo, política que teve início nos anos 1950.

No ano de 2008, verifica-se um novo período de alta, porm, o novo pico, se dá em outubro, com o quilo do arroz a R$ 0,72 no RS e a R$ 0,71 em MT, patamar inferior ao do pico observado em 2003. Já no novo ciclo de baixa, que ocorreu em 2005, os preços praticados ficaram próximos de R$ 0,50 por quilo nos dois estados e foram similares aos praticados no ciclo de baixa observado no ano de 2000 – Figura 4. Verifica-se, tambm, que as sries de preços das duas regiões parecem ter um comportamento muito semelhante ao longo do tempo o que pode ser um indicativo de que as sries sejam integradas.

Em se tratando de dados econômicos, trabalha-se com a transformação logarítmica das sries. Essa prática utilizada para estabilizar a variância dos dados, pois, uma das premissas do modelo que a variância constante ao longo do tempo. Outra vantagem de se trabalhar com a transformação logaritmica que a primeira diferença temporal do logartimo da srie refere-se à taxa de crescimento. Assim, obtêm-se de forma direta as variações ocorridas nas sries.

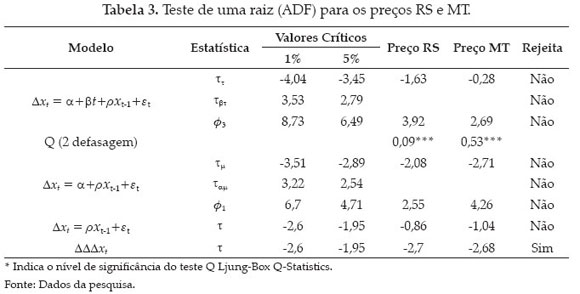
Para testar a estacionariedade da srie utilizou-se o teste Dickey-Fuller Aumentado. O número de defasagens foi determinado pelos critrios AIC e SBC e pela análise da função de autocorrelação e autocorrelação parcial. Nos dois casos, o número de defasagens foi de duas – p=2. Na tabela 2, são apresentados os resultados desse teste para os seguintes modelos:

Observa-se, de acordo com os resultados reportados na tabela 2, que as duas sries são integradas de mesma ordem, ou seja, I(1), e, portanto, possível aplicar o teste de cointegração nas variáveis.

O resultado do teste de cointegração de Engle e Granger (1987) mostrou que resíduo resultante da equação que considera as duas sries estacionário – valor estimado (-6,5) contra valor crítico para o teste ao nível de 1% de significância conforme Engle-Yoo (1987) (-4,07). Assim, existe uma relação de longo prazo entre os dois mercados e os preços num mercado devem influenciar a formação de preços no outro, o que pode ser confirmado por meio do teste de causalidade de Granger e da análise de correlação cruzada.

O resultado do teste de causalidade de Granger aponta que, para um nível de 1% de significância (valor estimado - 9,8), detecta-se que Mato Grosso sofre influência das condições de oferta no Rio Grande do Sul, ou seja, os preços do RS são variáveis importantes para a formação de preços em MT.

As estimativas de correlação cruzada constam da Figura 4. Observa-se que existe uma relação contemporânea muito forte entre os preços nos dois mercados e uma relação, tambm significativa, com defasagem de um período (um mês, no caso das sries analisadas). Esse resultado sugere que os preços no RS são importantes para explicar o comportamento dos preços em MT, constatação corroborada pelo resultado do teste de causalidade de Granger. O teste de causalidade de Granger indicou que os preços defasados do RS são importantes para explicar os preços de MT a um nível de significância inferior a 1%. Contudo, o contrário não ocorre, ou seja, uma relação de causalidade de Granger unidirecional, em que os preços do RS são importantes para prever o preço em MT.

Os resultados dos testes de raiz unitária e causalidade foram utilizados para definir um modelo e obter os parâmetros da transmissão de preços entre os dois mercados. O modelo de correção de erro obtido foi ajustado com as variáveis em logaritmo e nas diferenças a fim de resolver o problema de raiz unitária. A variável dependente o logaritmo neperiano do preço (tomada uma diferença) em MT (DLMT) e as variáveis explicativas: diferença do log do preço em MT com defasagem de um período (DLMT{1}), diferença do log do preço no RS (DLRS), diferença do log do preço no RS com um período de defasagem (DLRS{1}) e o resíduo da regressão (RES): .

Os valores dos coeficientes estimados constam da Tabela 3. O resultado mostra que se os preços no RS registraram um incremento de 1% (taxa de crescimento dos preços), esse aumento será transmitido para os preços no mercado em MT. A taxa de aumento dos preços em MT devido a 1% de aumento no RS será, em mdia, de 0,44% no período contemporâneo e em torno de 0,17% com um período de defasagem. Assim, um aumento na taxa de crescimento dos preços no mercado do RS percebido pelo mercado em MT no período contemporâneo e em menor magnitude num período posterior. Esse resultado de suma importância para a definição de políticas e estratgias de comercialização entre os dois mercados, pois, medidas de estímulo ou desestímulo de preços no mercado do RS certamente afetarão os preços no mercado de MT.

8. Conclusão

De 1999 at 2005, o estado de Mato Grosso foi o segundo maior produtor de arroz no Brasil, ficando atrás apenas do RS, maior produtor nacional. Nesse período, a produção mato-grossense foi muito importante para complementar o abastecimento do mercado interno. Contudo, a menor produtividade observada frente aos estados do RS e SC e a concorrência com a soja e o milho fizeram com que a produção de arroz em 2006 reduzisse cerca de um terço frente à produção de 2005.

Devido à importância na participação de mercado desses dois importantes produtores – RS e MT – no abastecimento interno de arroz, dúvidas quanto à relação que estes desempenham no papel de formação e transmissão de preços são levantadas pelos agentes comercializadores da cadeia produtiva, at mesmo com o enfoque de se desenhar contratos de comercialização para o produto e para as diferentes localidades. Assim, com o objetivo de saná-las, foram realizados testes de integração e dominância na formação de preços entre esses dois mercados.

Os resultados dos testes de raiz unitária mostraram que as sries de preços do RS e MT são integradas de ordem um – I (1). Assim, foi possível aplicar teste de cointegração de Engle Granger, que apontou para a existência de cointegração entre as sries de preços. Este resultado indica que as sries possuem uma relação econômica de equilíbrio de longo prazo, ou seja, trata-se de mercados integrados do ponto de vista da produção e comercialização do produto.

O resultado do teste de causalidade de Granger aponta que, para um nível de 1% de significância, os preços no mercado de Mato Grosso têm influência das condições de oferta no Rio Grande do Sul, ou seja, os preços do RS são variáveis importantes para a formação de preços em MT, confirmando a hipótese em estudo. Então, um modelo de transferência com correção de erro foi estimado para MT e a resposta quanto à magnitude do impacto dessa influência na formação de preços foi que: para cada 1% de aumento na taxa de crescimento dos preços no RS, a taxa de crescimento dos preços em MT terá, em mdia, um aumento 0,44% no período contemporâneo e em torno de 0,17% com um período de defasagem. Assim, um aumento na taxa de crescimento dos preços no mercado do RS sentido pelo mercado de MT no período contemporâneo e em menor magnitude num período posterior.

De posse desses resultados, os agentes de comercialização da cadeia poderão definir suas estratgias de comercialização entre os dois mercados com mais segurança e o desenvolvimento de contratos de comercialização (a termo, futuro e/ou opções) deverão considerar que medidas de estímulo ou desestímulo de preços no mercado do RS certamente afetarão os preços no mercado de MT.

9. Referências Bibliográficas

• ADAMI, A. C. O; BARROS, G. S.A. C; BACCHI, M. R. P. Política de garantia de preços para o arroz em casca do Rio Grande do Sul: curto ou longo prazo? In: XLV CONGRESSO DA SOCIEDADE BRASILEIRA DE ECONOMIA E SOCIOLOGIA RURAL, 2007, Londrina. Anais... Londrina: SOBER, 2007. 1 CD ROM.
• ADAMI, A.C.O. Contratos de opção: análise do potencial de sustentação de preços para o mercado de arroz. 2005. 117 p. Dissertação (Mestrado em Economia Aplicada) Escola Superior de Agricultura "Luiz de Queiroz", Universidade de São Paulo, Piracicaba, 2005.
• ALVES, L.R.A. Transmissão de preços entre produtos do setor sucroalcooleiro do Estado de São Paulo. 2002. 107 p. Dissertação (Mestrado em Economia Aplicada) Escola Superior de Agricultura "Luiz de Queiroz", Universidade de São Paulo, Piracicaba, 2002.
• BARROS, G.S.C. 1987. Economia da comercialização agrícola CEPEA/LES-ESALQ/ USP. Piracicaba/SP. 221p.
• BRASIL. Ministrio da Agricultura, Pecuária e Abastecimento -MAPA. Comercialização. Disponível em: <http:// www.agricultura.org.br>. Acesso em: 25 out. 2010a.
• BRASIL. Ministrio da Agricultura, Pecuária e Abastecimento MAPA. Estatísticas. Disponível em: <http:// www.agricultura.gov.br>. Acesso em: 25 mai. 2010b.
• COMPANHIA NACIONAL DE ABASTECIMENTO. Estoques públicos. Disponível em: <http//conab.gov.br>. Acesso em: 12 nov. 2010a.
• COMPANHIA NACIONAL DE ABASTECIMENTO. Indicadores agropecuários. Disponível em: <http//conab.gov.br>. Acesso em: 12 nov. 2010b.
• DEL VILLAR, P.M.; GAMEIRO, A.H.; FERREIRA, C.M.; BARATA, T.S.. Competitividade entre o arroz irrigado e o de terras altas no Brasil. In: FERREIRA, C.M.; SOUSA, I.S.F.; DEL VILLAR, P.M. (Ed.). Desenvolvimento tecnológico e dinâmica da produção do arroz de terras altas no Brasil. Santo Antônio de Goiás: Embrapa Arroz e Feijão, 2005. p.51-61.
• DIKEY, D.A.; FULLER, W.A. Distribution of the estimador for auto-regressive time series with a unit root. Journal of the American Statistical Association, Boston, v. 74, n. 366, p. 427-431, June, 1979.
• DIKEY, D.A.; FULLER, W.A. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica, Menasha, v. 49, n. 4, p. 1057-1072, July 1981.
• ENDERS, W. Applied econometric time series. New York: John Wiley& Sons, 2004, 2Ş ed., 466 p.
• ENDERS, W. RATS Handbook for econometric time series. New York: John Wiley& Sons, 1996. 204 p.
• ENGLE, R.F.; GRANGER, C.W.J. Co-integration and error correction representation, estimation and testing. Econometrica, Illinois, v. 52, n.2, p. 251276, 1987.
• FERREIRA, CARLOS MAGRI; SOUSA, IVAN SRGIO FREIRE DE; VILLAR, PATRICIO MNDEZ DEL. Desenvolvimento Tecnológico e Dinâmica de Produção do arroz de terras altas no Brasil. CEPEA/CIRAD/EMBRAPA. Santo Antônio de Goiás: Embrapa Arroz e Feijão. 2005. 118p.
• FOOD AND AGRICULTURAL ORGANIZATION OF UNITED STATES -FAO Statistical databases. Disponível em: <http://www.fao.org>. Acesso em: 19 mai. 2010.
• FULLER, W.A. Introduction to statistical time series. New York: John Wiley & Sons, 1976. 424 p.
• FUNDAÇÃO GETÚLIO VARGAS FGV. FGVdados Disponível em: <http:// www.portalibre.fgv.br>. Acesso em: 13 jul. 2010.
• GRANGER, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica, Menasha, v. 37, n. 3, p. 424-438, Aug. 1969.
• GUJARATI, D. N. Econometria Básica São Paulo: MAKRON Books, 2000. 846p.
• HAMILTON, J.D. Time series analysis New Jersey: Princeton University Press, 1994. 799p.
• JOHANSEN, S. Statistical analisys of cointegration vectors. Journal of Economics Dynamics and Control v.12, n.2/3, pg. 231-254, 1988.
• MAFIOLETTE, R. L. Formação de preços na cadeia agroindustrial da soja na década de 90 2000. 95 p. Dissertação (Mestrado em Economia Aplicada) Escola Superior de Agricultura "Luiz de Queiroz", Universidade de São Paulo, Piracicaba, 2000.
• MIRANDA, S.H.G.; SILVA, G.S.; FERREIRA, C.M. Indicadores da eficiência da comercialização do arroz de terras altas e irrigado no Brasil. In: 2ş. Congresso Brasileiro da Cadeia Produtiva do Arroz. VIII. Reunião Nacional de Pesquisa de Arroz Renapa, Brasília, DF, 26 a 28 de abril de 2006. Brasília, Maio de 2006. Anais.
• MORAES, M. Prêmio de exportação de soja brasileira 2002. 90 p. Dissertação (Mestrado em Economia Aplicada) Escola Superior de Agricultura "Luiz de Queiroz", Universidade de São Paulo, Piracicaba, 2002.
• REZENDE, G.C. Estado, macroeconomia e agricultura no Brasil Porto Alegre: UFRGS/ IPEA, 2003. 246 p.

1

Comunicação pessoal dos autores com agentes da cadeia arrozeira de Mato Grosso, durante viagem de levantamento de dados em 2006.

Datas de Publicação

• Publicação nesta coleção
  07 Jul 2011
• Data do Fascículo
  Mar 2011