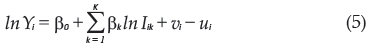Abstract
The objective of this study is to estimate the levels of technical efficiency of the small pineapple farmers of Santander, Colombia, using the stochastic frontier approach. In addition, this study attempts to determine whether the acreage and some of the socio-economic characteristics of farmers can influence the efficiency of their pineapple farms. By exploiting the information that was gathered in a survey of 194 pineapple farmers in the region, these farmers' technical efficiency was estimated using a Cobb-Douglas-type stochastic frontier model and a technical inefficiency model. The results suggest that acreage and the variables that are associated with the human capital, e.g., the level of schooling and the years of experience in agricultural activity, explain the levels of technical efficiency to a significant degree.
technical efficiency; stochastic frontier; Cobb-Douglas production function; pineapple
IAssistant Professor. Department of Economics, Universidad del Atlántico, Barranquilla, Colombia. E-mail: juantrujillo@mail.uniatlantico.edu.co
IIStudent of the Master in Applied Economics. Universidade Federal de Viçosa, Viçosa, Minas Gerais, Brazil. Scholarship granted by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (Capes). E-mail: wilman.pinedo@ufv.br
ABSTRACT
The objective of this study is to estimate the levels of technical efficiency of the small pineapple farmers of Santander, Colombia, using the stochastic frontier approach. In addition, this study attempts to determine whether the acreage and some of the socio-economic characteristics of farmers can influence the efficiency of their pineapple farms. By exploiting the information that was gathered in a survey of 194 pineapple farmers in the region, these farmers' technical efficiency was estimated using a Cobb-Douglas-type stochastic frontier model and a technical inefficiency model. The results suggest that acreage and the variables that are associated with the human capital, e.g., the level of schooling and the years of experience in agricultural activity, explain the levels of technical efficiency to a significant degree.
Key-words: technical efficiency, stochastic frontier, Cobb-Douglas production function, pineapple
JEL Classification: C21, Q12, Q16.
1. Introduction
Small-scale agriculture represents the smallest link in Colombia's agricultural chain. Within Colombian agricultural production, the small farmers (peasants, including both indigenous and African-American communities) constitute most of the domestic producers.1 1 . In this article, we use as synonyms the expressions "small farmers" and "small-scale farmers" as well as "small-scale agriculture" and "small-scale production". These small-scale farmers cultivate 7.2 acres on average; furthermore, they represent 87% of Colombian farmers, they contribute 41% of the agricultural gross domestic product, and they generate nearly 40% of the products that are considered basic food necessities in Colombia (MALDONADO et al., 2007). In spite of these records, it is curious that such issues as the measurement of the levels of technical efficiency and the determinants of the small farmers from Colombia have still not been explored.2 2 . The only exception is the study of Perdomo and Hueth (2011), which measures the technical efficiency for a sample of small coffee farmers in the Andean Region.
According to the figures of the Ministerio de Agricultura y Desarrollo Rural -MADR- (2012), Colombia possesses a harvested area of fruits that comprises approximately 750,085 acres. As for the pineapple, it reached a surface area of 27,951 acres, which ranks it as the sixth-most important fruit crop as determined by its sown area.3 3 . The five main fruit crops in Colombia are, in their order of importance, banana trees, avocadoes, mangoes, oranges and guavas (MADR, 2008). Pineapple (Ananas comosus) is a fruit that is native to southeastern Brazil and Paraguay (SAMSON, 1986). In 2010, the main pineapple-producing countries were the Philippines, Brazil, Costa Rica and Thailand, and their productions were 2,169,230, 2,120,030, 1,976,760 and 1,924,660 tons, respectively. In this regard, Colombia is ranked twelfth with a total of 398,010 tons (FAO, 2011). Based on Collins (1960), it is presumed that the pineapple was brought to Colombia by the Indians who spread it throughout Central and South America and reached the West Indies. From the commercial point of view, the main producing departments of this fruit in Columbia are Santander, where the predominant variety is Perolera, which is sold in the domestic market, and Valle del Cauca, where the Smooth Cayenne and Apple varieties prevail (graph 1); most of the production in the latter region is intended for export.
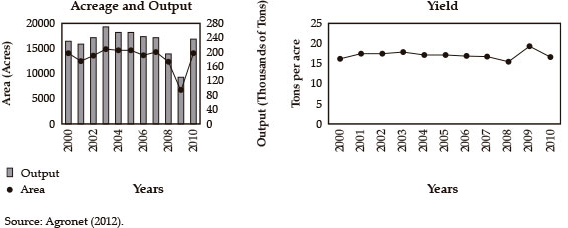
The Department of Santander maintains pineapple production during the whole year, and because it has a favorable altitude and climate, it positions itself as a leader in the country and has a continuous presence in the domestic market. The municipalities in which most of this activity is developed are Lebrija, Girón and Rionegro, and these regions have shares of 62.6%, 22.6% and 11.6% of the total production, respectively.4 4 . These percentages are obtained from the information contained in MADR and Gobernación de Santander (2010). However, in recent years there has been an unusual increase in acreage that is concomitant with a moderate fall in yield (see Appendix Appendix 1). Even when the gross output has followed the same trend as the acreage, the drop in the yield leads us to predict technical inefficiency problems in this crop. Thus, it is necessary to quantify the current levels of technical efficiency of the small pineapple farmers of Santander and to determine the causes of the deterioration in the productivity of acreage.
The objective of this research is to find the determinants of the technical efficiency of small pineapple farmers from the Department of Santander, Colombia. We should note that this agricultural activity is characterized by a highly rural life and the concentration of small-scale farmers, which is common in most of the fruit crops around the country.5 5 . According to MADR et al. (2006), 70% of those fruit farms that do not produce bananas for export belong to small and medium farmers. To accomplish our objective, we will econometrically estimate both a stochastic frontier production function and a technical inefficiency model. The basic idea is to provide relevant information about the impact of acreage and the socio-economic characteristics of this group of small farmers and how these factors influence their levels of technical efficiency.
This research is organized as follows: in Section 2, we present the theoretical foundations for the stochastic frontier production function and the technical efficiency as well as major empirical contributions. In Section 3, we present the methodology that is used to achieve the stochastic frontier function and the inefficiency model. The details of the econometric estimation are presented in Section 4. Finally, we present the conclusions of the study in Section 5.
2. Theoretical Foundations
The main motivation for measuring the technical efficiency of production processes is to formalize the responsiveness of the resulting yields to different inputs. The observed variations in this responsiveness are mainly due to differences in the technology that is used by firms, differences in the levels of efficiency of the production processes and differences in the context in which production takes place. Therefore, the economic efficiency is a function of the technical efficiency.
The methodology developed by Farrell (1957) represented a first step in the modeling of technical efficiency, as this research implies the existence of an efficient production-possibility frontier (PPF). This methodology assumes that the PPF represents the maximum possible output that can be achieved from a given set of productive factors. Technical inefficiency is calculated by the difference between the production levels of each firm and the peak level that is reached in the PPF. Thus, the technical efficiency can be calculated as a percentage of the most efficient production unit within the sample.
There are two alternative approaches for estimating this production function. Firstly, we have the non-parametric techniques, which are distinguished by their flexibility; they are less restrictive in the conditions that are applied to the reference technology and in the modeling of multi-product production processes. Secondly, there are parametric methods, which allow one to econometrically estimate a production function to make statistical inferences on the results that are obtained in the estimation. It should be noted that the application of these methods requires the dataset selected a functional form. With the latter method, Aigner et al. (1977) and Meeusen and van den Broeck (1977) introduce a stochastic production function in order to distinguish those errors that can be explained by productive inefficiencies from those errors that are derived from model misspecification. This discrimination involves defining both the functional form of the production function and the specific distribution of the error term.
Battese and Coelli (1995) present the main empirical reference regarding the determinants of technical efficiency in agriculture. The central conjecture these authors postulate is the joint estimation of a model that includes both the efficient frontier of agricultural production and the variables that influence the inefficiency of production. Indeed, Coelli and Battese (1996) show that Indian farmers with an older age, a larger farm and higher levels of education tend to be more efficient. Likewise, Tian and Wan (2000) find that education, the farm size and the adoption of multiple cropping systems have a positive effect on the efficiency of rice production in China. Similarly, in a sample of farmers in Central Luzon, the Philippines, Villano and Fleming (2006) find that variables such as age, education level, the proportion of adults in the household, and the generation of income from non-farm activities affect technical efficiency.
In contrast, in Nigeria, Amaza and Olayemi (2002) indicate that if education, technical assistance and the diversification of crops increase, higher levels of technical efficiency are achieved. In the same continent, Essilfie et al. (2011) estimate the technical efficiency of the maize crop at the farm level in Ghana. Their results show that differences in age, gender, years of schooling, family size and farmers' off-farm income affect technical efficiency.
In Latin America, there is little research on the estimation of the technical efficiency in agriculture using the stochastic frontier approach. It is worth highlighting the study of Benoit-Cattin and Moore (1996), which estimates the technical efficiency of a group of small coffee farmers in Guatemala. These authors conclude that both technical assistance and credit support contribute to sustaining Guatemalan coffee plantations. In Brazil, Conceição and Araújo (2000) estimate the technical efficiency of a sample of commercial farmers and find that experience is a key factor in explaining these farmers' technical efficiency. Additionally, the study of Richetti and Pereira (2003) examines the economic efficiency of the productive resources that are used in the cultivation of soybeans in the State of Mato Grosso do Sul. They show that technical inefficiency is linked to processes of technology transfers to farmers of this grain. In Chile, Santos et al. (2006) note that the size of a property, the distance between a property and the main road, the age of the household head and the membership in a group that transfers technology positively affects the technical efficiency. In a similar study that was conducted in the same country, Moreira et al. (2006) estimate a highly unbalanced panel dataset for a sample of small dairy farms in Southern Chile. Their findings are as follows: there is no agro-climatic effect, the presence of technical inefficiency is highly significant and technical efficiency is time-variant.
However, concerning pineapple production, there is a lack of studies on the technical efficiency of production that use the parametric approach. A noteworthy study is the study of Chen et al. (2001), in which the technical efficiency of 83 pineapple farms in China is estimated, with this result: labor is the most important factor in production. Similarly, Adinya et al. (2010) determine the inefficiency of pineapple production in Nigeria. Their results indicate that the farmers' levels of education positively influence the achievement of greater efficiency in production.
3. Methodology
The Department of Santander is located in the Central-Eastern Region of Colombia. This Department contributes approximately 7% to the nation's GDP, therefore, it is classified as the fourth department in the list of the country's economically important regions. The Department of Santander is the largest producer of Perolera pineapples in Colombia. Small pineapple farmers in this department produced 239,130 kilograms (kg) of this fruit in 2010, and as a result, they obtained an average yield of 15.4 tons per acre, which is slightly above the national average of 14.6 tons per acre (AGRONET, 2012). This similarity in performance reflects the high participation of this department in the country's aggregated pineapple production. In fact, on comparing the yield series for Colombia and Santander, we see the same drop in the recorded statistics of this variable over the period 2009-2010 (see Appendix 2 Appendix ).
The data for this study were obtained through a survey of 194 small pineapple farmers in the Department of Santander.6 6 . These 194 respondents represented 6.5% of the small pineapple farmers throughout the department in 2009. The stratified random sampling technique was adopted to select the following numbers of respondents in these three municipalities: 124 in Lebrija, 54 in Girón, and 16 in Rionegro. The data collection was carried out between January and April of 2011, and these data were obtained through direct questions to the producer that asked about his/her last harvest.
3.1. The theoretical stochastic frontier model7 7 . The theoretical derivation of the stochastic frontier model can be seen in more detail in both Kumbhakar and Lovell (2000) and Coelli et al. (2005).
Given a production function f(Ii,β), the formulation of the stochastic frontier model is as follows:
which vi is a two-sided symmetric, normally distributed idiosyncratic component [vi ~ N(0,σ2v)] and ui is a one-sided error that represents the technical inefficiency. It is assumed that the errors in vi are independent of ui, and the sum of these two terms is the random error εi. Stochastic frontier models differ in the statistical distribution that is assumed for the error term that corresponds to the technical inefficiency (ui). According to Aigner et al. (1977, p. 23), the error may have the following three types of distribution, as it is assumed that individual firms differ in their production practices for a given set of inputs; the exponential distribution, in which the ui are independently, exponentially distributed with variance σ2v; the half-normal distribution, in which the ui are independently N+(0, σ2v) distributed; lastly, the truncated normal distribution, in which the ui are independently N+(∝, σ2v) distributed with a truncation point at ∝.
From Equation (1), we can rewrite the stochastic frontier production model as follows:
which TE is the technical efficiency. Whenever the producer is on the efficient frontier of production, TE = 1. Otherwise, TE < 1 because TE a measure of the distance of the production level that is observed with respect to the frontier level of production. Thus, the measurement of technical efficiency can be summarized as follows:
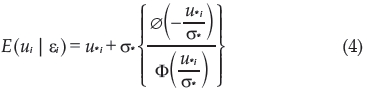
To estimate (3), it is necessary to calculate the error term ui, which is not observable. Following Kumbhakar (2000, p. 78), a general expression for the calculation of ui is:
which u*i and σ* depend on the distribution of ui, Φ(⋅) is the standard normal cumulative distribution function, and ∅(⋅) is the standard normal distribution function.
In the case of a half-normal distribution,
u*i = -εiσ2v /σ2
σ* = σuσv / σ
For an exponential distribution,
u*i = -εi - σ2v /σu
σ* = σv
Lastly, for a normal truncated distribution,
It should be noted that the stochastic frontier model is not the only method for modeling the technical efficiency. An alternative method would be Data Envelopment Analysis (DEA), which does not require the production function to be parameterized. This flexibility implies the assumption that unobserved factors do not affect production decisions. However, this assumption becomes an obstacle in the particular case of agriculture, in which the uncertainty that is caused by weather conditions greatly affects the chosen model. We use the stochastic frontier model to the extent that it allows us to control the errors and uncertainty from this type of factor (AIGNER et al., 1977; KUMBHAKAR and LOVELL, 2000).
3.1.1. Specifying the stochastic frontier model
The stochastic frontier model was initially estimated with a Translog functional specification. However, when we tested the hypothesis of the input interaction coefficients for the Translog model, the results indicated that the Cobb-Douglas (CD) functional form would best fit the data of the obtained sample. The stochastic frontier model CD is expressed as follows:
where Yi represents the yield of the ith small pineapple farmer, Ii are the inputs, and the β's are the parameters that must be estimated. To estimate the model of the stochastic production frontier (Equation 5), we used the STATA 12 command frontier. The model to be estimated has the following form:
which ln yieldi is the amount of pineapple that is produced in kilograms per acre; labori is the number of workers per day per acre; seedi is the number of seeds used per acre; defensivesi is the amount of chemicals that are used, and this term is computed by adding the amounts of fertilizers, fungicides, herbicides, insecticides and pesticides that are used in production (in liters per acre). Whereas the values of vi represent the occurrences that cannot be controlled by the farmer, the values of ui represent the technical inefficiency of the pineapple exploitation. The vector of coefficients (β) represents the parameters to be estimated.
The stochastic frontier model also estimates the variance parameters for certain errors, such as the total variance of the model's errors (σ2), which is represented in this way:
which σ2u is the variance of ui and σ2v is the variance of vi. The statistical significance of σ2 is an indicator of the quality of the fit and a test of the applied specification assumption for the distribution of those errors that are related to the technical inefficiency (ui). Second, the ratio between the standard deviation of the errors of the technical inefficiency (u) and the standard deviation of the model specification errors (v) is represented by (λ); this ratio is formally expressed as:
If λ approaches zero, then either σv is very large or σu is close to zero. Similarly, when σv is close to zero, λ becomes large and the one-sided error becomes the dominant source of random variation in the model. In addition, the parameter of the ratio of variances (γ), which relates the variability of ui to the total variability of the model's errors, is defined as follows:
This expression is a measure of the level of inefficiency of the stochastic frontier production model, and its outcome ranges between 0 and 1.
3.2. The empirical technical inefficiency model
The model of technical inefficiency of the production process is formalized as follows:
The term θ is a vector of the characteristics of small pineapple farmers that directly influence the technical efficiency of the production processes, and these characteristics are as follows: acreage, years of schooling, years of experience, technical assistance, access to credit and off-farm income. The term ϕi represents the errors of the model. The specification of the technical inefficiency model is as follows:
which σ2ui represents the variance of the estimated technical inefficiency for the ith farmer. We include the variable acreage to explain the potential obstacle that a great acreage poses to farmers who seek to increase their yield. To measure the levels of formal education, we incorporate the variable schooli, which is defined as the number of years of formal education of the farmer. However, because human capital is not exclusively accumulated through formal education, we also consider the variable expi, which indicates the number of years of experience that the farmer takes in the activity. Meanwhile, offfarmi represents a dummy variable that takes the value of 1 if the farmer receives off-farm income and the value of 0 otherwise. In the field of farm management, we include the dummy variable techi that takes the value of 1 if the farmer receives technical assistance and the value of 0 otherwise. Similarly, crediti is a dummy variable that takes the value of 1 if the farmer has access to credit and the value of 0 otherwise. The vector of coefficients (α) represents the parameters that must be estimated.
In addition, we determine the economic efficiency in the use of inputs by incorporating such variables as the marginal value product (MVP) and the marginal factor cost (MFC). The former variable is calculated by multiplying the marginal physical product (MPP) by the price of the product (p). Formally,
Thus,
The MFC of an input is the cost of an additional unit of a particular input. This datum is obtained from the input prices. Then, following Ingosi (2012, p. 22), the relative efficiency (R) of the use of an input is defined as the ratio between its MVP and MFC. If R is equal to unity, the input is being used efficiently. However, if R is greater than unity, the input is underused, and if it is less than unity, the input is overused. Equivalently, the optimal use of an input is attained when the MVP is equal to the MFC.
4. Results
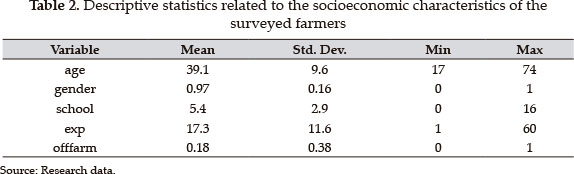
We divide the information that is obtained from the sample of farmers into these three categories: the production, the socio-economic characteristics of respondents, and the farm management. The result is summarized in Tables 1, 2 and 3.
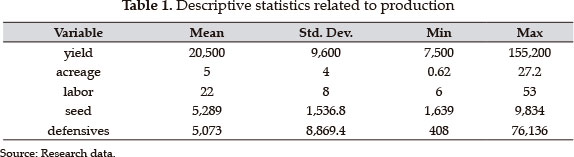
The typical pineapple farm had an average size of five acres and an average yield level of 20,500 kg per acre. The number of people who were involved in harvesting activities reached an average of 22 workers per day per acre. Furthermore, the average amount of seeds used per acre was 5,289, which agrees with the optimal requirements for planting in Colombia (MORALES and LÓPEZ, 2002). Moreover, we note that, on average, farmers use 5,073 liters of defensives per acre.
The socio-economic characteristics of farmers observed a mean age of approximately 39 years and average levels of schooling and experience of five and 17 years, respectively. Moreover, 97% of farmers are male and they dominate small-scale pineapple production in Santander. In addition, 18% of the surveyed farmers engaged in an off-farm income-earning activity. In the context of farm management, it appears that only 11% of farmers receive technical assistance and only 21% have access to credit.
Further analysis of the variables that are related to human capital shows that a low level of education is predominant in most of the farmers. Table 4 shows that 81% of the surveyed farmers have educational levels below eight years, which is the minimum required to complete a basic education. In addition, 78.4% of these farmers have between one and 25 years of experience in the pineapple industry.
The joint estimation of the CD stochastic frontier function (Equation 8) and the technical inefficiency model (Equation 13) is shown in Table 5. All of the estimated coefficients of the stochastic frontier function had a positive impact on yield, and they were all statistically significant. The estimates reported diseconomies of scale of 0.71, which indicates that the duplication of pineapple output per acre would require more than doubling the amount of labor, seeds and defensives. Nevertheless, the average value of technical efficiency that this sample of farmers attained is 76%.
It is evident from the measures of variance, namely, sigma squared (σ2) and lambda (λ), that the choice of an exponential distribution for the error ui was the best choice, as it ensured the robustness of the model. Furthermore, lambda (λ) indicates that variations in yield are mainly due to differences in the production practices of farmers and not random variations. Similarly, gamma (γ) measures the share of changes in the technical inefficiency with respect to the total variability of the model errors. Thus, the estimator of gamma (γ) indicates that 74% of the total variation in the pineapple yield is due to technical inefficiencies in the area under study.
In contrast, the null hypothesis that tests the technical efficiency of the sample of small pineapple farmers of Santander is rejected at a significance level of 1% (see Table 6). Because of this result, the technical inefficiency model highlights how the variables that are related to human capital (namely, the education level and years of experience) have a positive influence on the technical efficiency of this group of farmers. The estimator of the variable acreage was statistically significant at a 5% level, and its sign confirms that the acreage and technical efficiency are inversely related. The estimated coefficients for the variables school and exp were statistically significant at the 5% and 1% levels, respectively. The remaining variables had the expected sign but were not statistically significant.
Table 7 shows that few small pineapple farmers achieved outstanding levels of efficiency, and furthermore, only sixteen of them reached the highest class of technical efficiency. Nevertheless, only 25% of the group of farmers in the sample was below the average technical efficiency. Overall, the results highlight the existence of a wide distribution of the technical efficiency of farmers, and this distribution varies in a range between 0.11 and 0.95. It is remarkable that over half of the farmers were above the average technical efficiency. This situation reveals that technical efficiency can still be improved in the small-scale pineapple production of this department.
Figure 1 shows the technical efficiency according to the off-farm income, technical assistance, and credit access. As can be seen, farmers who receive off-farm income have a greater margin of efficiency compared to those who do not. Similarly, farmers who have access to credit and receive technical assistance reach higher levels of efficiency.
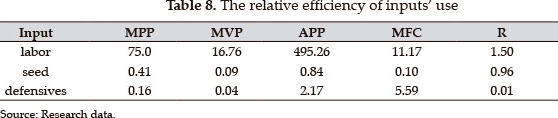
Table 8 presents the measures of MPP, MFC, and MVP and includes the average physical product (APP), which also contributes to measuring the efficiency of inputs' use.8 8 . The APP is calculated using the formula MPP/input-output elasticity (INGOSI, 2012, p. 21). As can be seen, labor has the highest MPP. Hence, an increase of one laborer per day is estimated to increase yield by 75 kg per acre. Similarly, an increase in defensives' application by an additional liter is estimated to increase the pineapple yield by 0.16 kg per acre. Furthermore, an increase of one unit of pineapple seeds is estimated to increase the total yield by 0.41 kg per acre. However, when we evaluate the efficiency of these inputs, we note that whereas seeds and defensives are overused, labor is underused. A careful examination of the result of seed suggests that the use of this input is close to its level of efficiency, which demonstrates that it meets the standards for the Colombian case. Finally, the APP was greater than the MPP for the whole set of inputs, which means that these farmers are operating in the second stage of short-run production.
5. Conclusions
In this study, we used the stochastic frontier approach to measure the technical efficiency and its determinants in a sample of 194 small Perolera pineapple farmers of Santander, Colombia. To conduct this measurement, we estimated a production frontier with a Cobb-Douglas functional form using inputs such as labor, the number of seeds, and the quantity of defensives. All of the estimated coefficients for inputs showed a positive influence on the pineapple yield, and all of them were statistically significant. Furthermore, the sum of the elasticities of the inputs reveals diseconomies of scale production on the order of 0.71. The results also show that this group of farmers has an average technical efficiency of 76%, which varies in the range of 11 to 95%. About one fourth of the sample is below the average estimated technical efficiency. In this respect, it is still possible for small-scale farmers to reallocate these inputs to improve their technical efficiency.
The variables used as the determinants of technical inefficiency indicate that an increase in acreage does not improve the technical efficiency of these small pineapple farmers. Moreover, the results show that this group of farmers still lacks the levels of education and experience that are sufficient to approach optimal levels of productive efficiency. Strictly speaking, only acreage, education, and experience were statistically significant. Nevertheless, variables such as off-farm income, technical assistance and access to credit did contribute positively to the levels of technical efficiency, but they were not statistically significant.
In addition, we considered a set of measures to assess the economic efficiency in the use of inputs, namely, the marginal physical product, the marginal value product, the average physical product, and the marginal factor cost. According to these results, the small pineapple farmers of Santander are operating in the second stage of production. In the case of seeds and defensives, the value of the marginal physical product is less than the corresponding marginal factor cost, but the opposite situation occurs in the case of labor. However, the use of seeds approaches its optimal level in Santander. Therefore, these farmers can further optimize production by increasing the use of labor and simultaneously reducing the use of defensives.
According to the evidence, the policy implications are clear. Given the high and positive correlation between the years of schooling and the technical efficiency, these farmers should be encouraged to improve their levels of education by becoming involved in rural extension programs such as continuing education centers for adults. Greater efforts must be made by government institutions with regard to providing technical assistance and promoting the training of small-scale farmers in new technologies that would help them boost their current levels of efficiency. If these efforts were made, small-scale farmers would be better prepared to take advantage of increases in acreage. Furthermore, access to credit is necessary to stimulate technological innovations that foster increases in crop yield.
Further studies on this subject should consider the acreage as a factor that causes technical inefficiency in the yield of fruit crops in Colombia. Another possibility would be to conduct studies of technical efficiency on this type of crop by using non-parametric methods such as the aforementioned Data Envelopment Analysis to compare the results that have been obtained to date.
6. References
Appendix
1. The pineapple output in the Department of Santander, 2000-2010
According to data from Agronet (2012), in the period from 2009 to 2010, whereas the total acreage increased from 6,854 to 14,188 acres, which represents a growth of 107%, the total yield fell from 19 to 17 tons per acre, which represents a decrease of 13%.
2. The pineapple output in Colombia, 2000-2010
According to figures from Agronet (2012), the pineapple acreage in Colombia increased from 19,743 acres in 2009 to 27,951 acres in 2010, which represents an increase of 42%. In contrast, the total yield increased from 16.6 tons per acre in 2009 to 15.8 tons per acre in 2010, which is equivalent to a decrease of 5%.
- ADINYA, I., AFU, S. and IJOMA, J. Economic meltdown and decline in pineapple production: Determinants of production inefficiency of Pineapple-Based Alley Cropping Practices in Cross River State, Nigeria. The Journal of Animal and Plant Sciences, v. 20, n. 2, p. 107-116, 2010.
- AGRONET, 2012. Reportes Estadísticos. Available at <http://www.agronet.gov.co/agronetweb1/Estadísticas/ReportesEstadísticos.aspx>. Diverse accesses. 2012.
- AIGNER, D., LOVELL, C.A. and SCHMIDT, P. Formulation and estimation of stochastic frontier production function models. Journal of Econometrics, v. 6, n. 1, p. 21-37, 1977.
- AMAZA, P. and OLAYEMI, J. Analysis of technical inefficiency in food crop production in Gombe State, Nigeria. Applied Economics Letters, v. 9, n.1, p. 51-54, 2002.
- BATTESE, G. and COELLI, T. A model for technical efficiency effects in a stochastic frontier production function for panel data. Empirical Economics, v. 20, p. 325-332, 1995.
- BENOIT-CATTIN, M. and MENDEZ, J. C. Determinación paramétrico-estocástica de la eficiencia técnica de la producción de café de los pequeños productores en Guatemala. Investigación agraria. Economía, n. 1, p. 117-138, 1996.
- CHEN, T., YANG, S. and PAN, T. A study on the technical efficiency of pineapple farms in Taiwan. Journal of Agricultural Research of China, v. 50, n. 3, p. 88-97, 2001.
- COELLI, T. and BATTESE, G. Identification of factors which influence the technical inefficiency of Indian farmers. Australian Journal of Agricultural Economics, v. 40, n. 2, p. 103-128, 1996.
- COELLI, T., RAO, D. S. P., O'DONNELL C. J. and BATTESE, G. E. An introduction to efficiency and productivity analysis New York, NY, USA: Springer, 2005. 331 p.
- COLLINS, J. L. The pineapple: botany, cultivation and utilization. London: Leonard Hill, 1960. 294 p.
- CONCEIÇÃO, J. C. P. R. and ARAÚJO, P. F. C. Fronteira de produção estocástica e eficiência técnica na agricultura. Revista de Economia e Sociologia Rural, v. 38, n. 1, p. 45-64, 2000.
- ESSILFIE, F. L., ASIAMAH, M. T. and NIMOH, F. Estimation of farm level technical efficiency in small scale maize production in the Mfantseman Municipality in the Central Region of Ghana: A stochastic frontier approach. Journal of Development and Agricultural Economics, v. 3, n. 14, p. 645-654, 26 nov. 2011.
- FAO, 2012. FAOSTAT-Agriculture Available at <http://faostat.fao.org/site/339/default.aspx >. Accessed: jul. 3. 2012.
- FARRELL, M. J. The measurement of productive efficiency. Journal of Royal Statistical Society, v. 120, n. 3, p. 253-290, 1957.
- INGOSI, A. Economic Evaluation of Factors Influencing Maize Yield: In north-rift region of Kenya. Saarbrücken, Germany: LAMBERT Academic Publishing, 2012. 68 p.
- KUMBHAKAR, S. C. and LOVELL, C. A. K. Stochastic Frontier Analysis Cambridge, UK: Cambridge University Press, 2000. 333 p.
- MALDONADO, J., MORENO, R. and VARAS, J. Impactos del TLC sobre agricultura familiar y políticas compensatorias: Caso Colombia. Bogotá: CEDE - Universidad de los Andes, FAO and BID, 2007.
- MEEUSEN, W. and van DEN BROECK, J. Efficiency estimation from Cobb-Douglas production functions with composed error. International Economic Review, v. 18, n. 2, p. 435-444, 1977.
- MINISTERIO DE AGRICULTURA Y DESARROLLO RURAL - MADR. Anuario de frutas y hortalizas de Colombia Bogotá, 2008. 80p.
- ______. Estadísticas sector agropecuario Bogotá, 2012. 37p.
- ______. et al. Plan frutícola y hortícola nacional. Bogotá, 2006. 80p.
- ______. and GOBERNACIÓN DE SANTANDER. Evaluaciones agropecuarias Santander 2009 Bucaramanga, 2010. 146p.
- MORALES, J. and LÓPEZ, J. Manejo integrado de la mosca de la piña en Santander Bucaramanga, Colombia: Corporación Colombiana de Investigación Agropecuaria (CORPOICA), Regional siete, 2001. 25p.
- MOREIRA, V., BRAVO-URETA, B., CARRILLO, B. and VÁZQUEZ, J. Technical efficiency measures for small dairy farms in southern Chile: A stochastic frontier analysis with unbalanced panel data. Archivos de Medicina Veterinaria, v. 38, n. 1, p. 25-32, 2006.
- PERDOMO, J. and HUETH, D. Funciones de producción, análisis de economías a escala y eficiencia técnica en el eje cafetero colombiano: una aproximación con frontera estocástica. Revista Colombiana de Estadística, v. 34, n. 2, p. 377-402, jun. 2011.
- RICHETTI, A. and PEREIRA, R. The soybean production frontier and economic efficiency in Mato Grosso do Sul, Brazil. Revista de Economia e Sociologia Rural, v. 41, n. 1, Brasília 2003, p. 45-64, jan./mar. 2000.
- SAMSON, J. A. Tropical Fruits 2nd ed. New York: Longman Scientific & Technical, 1986. 335p.
- SANTOS, J., FOSTER, W., ORTEGA, J. and RAMIREZ, E. Estudio de la eficiencia técnica de productores de papas en Chile: El rol del programa de transferencia tecnológica de INDAP. Economía Agraria, v. 10, p. 119-132, 2006.
- TIAN, W. and WAN, G. Technical efficiency and its determinants in China's grain production. Journal of Productivity Analysis, v. 13, n. 2, p. 159-174, 2000.
- VILLANO, R. and FLEMING, E. Technical inefficiency and production risk in rise farming: evidence from Central Luzon Philippines. Asian Economic Journal, v. 20, N. 1, p. 29-46, Mar. 2006.
Appendix
Measurement of the technical efficiency of small pineapple farmers in Santander, Colombia: a stochastic frontier approach
Publication Dates
-
Publication in this collection
25 Apr 2014 -
Date of issue
2013