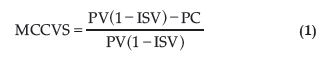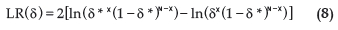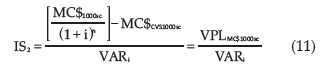Resumos
Em cada um dos elos da cadeia produtiva do agronegócio, encontrar estratégias viáveis para mitigação de riscos não é uma tarefa trivial. Usualmente são adotadas estratégias genéricas de redução do risco pela diversificação de culturas e/ou estratégias que objetivam a transferência ou diluição do risco por meio de seguros e contratos futuros. Este artigo tem por objetivo avaliar retornos e riscos de três estratégias de comercialização do milho: compra e venda simultânea, estocagem e venda a descoberto. A pesquisa é descritiva quanto ao seu objetivo, estudo de caso quanto à abordagem do problema e documental quanto ao procedimento de coleta de dados, com período de abrangência para as safras de 2003 a 2010. As métricas utilizadas foram o Value at Risk (VaR) e o índice de Sharpe modificado, que é uma variação do índice de Sharpe original. Os resultados apontam que os maiores retornos para a estocagem seriam obtidos durante as safras de inverno e para horizontes de tempos menores. Para a venda a descoberto, as médias dos retornos são próximas entre si para todos os horizontes de tempo. A compra e venda simultânea apresentou a melhor relação retorno/risco em relação às outras estratégias de comercialização.
Value-at-Risk (VaR); Índice de Sharpe; gestão de riscos; riscos no agronegócio
In each of the productive chain links, finding viable strategies for risk mitigation is not a trivial task. Usually, generic strategies are adopted to reduce risks, such as diversification of crops and/or strategies aiming at transferring or diluting risk through futures contracts and insurance. This article aims to evaluate three strategies for managing risks concerning the corn trading: simultaneous buying and selling, storage and short selling. Towards the methodological procedures, this study is descriptive regarding its goal and it is a case study regarding the approach of the problem. Literature and documents were used as procedures for data collection, with coverage for the period of crops from 2003 to 2010. The Value at Risk (VaR) and Sharpe Ratio Modified, which is a variation of the Sharpe Ratio, were used to evaluate commercialization strategies. The results show that the highest returns for the storage would be obtained during winter seasons and for shorter periods. For the short selling, the return averages are similar for all time horizons. The simultaneous buying and selling showed the best risk/return ratio.
Value-at-Risk (VaR); Sharpe Ratio; risk management; agribusiness risks
IEscola de Negócios da PUCPR. Professor Titular. E-mail: vilmar.moreira@pucpr.br
IIEscola de Negócios da PUCPR. Professor Titular. E-mail: alceu.souza@pucpr.br
IIIEscola de Negócios da PUCPR. Professor Titular. E-mail: luiz.duclos@pucpr.br
RESUMO
Em cada um dos elos da cadeia produtiva do agronegócio, encontrar estratégias viáveis para mitigação de riscos não é uma tarefa trivial. Usualmente são adotadas estratégias genéricas de redução do risco pela diversificação de culturas e/ou estratégias que objetivam a transferência ou diluição do risco por meio de seguros e contratos futuros. Este artigo tem por objetivo avaliar retornos e riscos de três estratégias de comercialização do milho: compra e venda simultânea, estocagem e venda a descoberto. A pesquisa é descritiva quanto ao seu objetivo, estudo de caso quanto à abordagem do problema e documental quanto ao procedimento de coleta de dados, com período de abrangência para as safras de 2003 a 2010. As métricas utilizadas foram o Value at Risk (VaR) e o índice de Sharpe modificado, que é uma variação do índice de Sharpe original. Os resultados apontam que os maiores retornos para a estocagem seriam obtidos durante as safras de inverno e para horizontes de tempos menores. Para a venda a descoberto, as médias dos retornos são próximas entre si para todos os horizontes de tempo. A compra e venda simultânea apresentou a melhor relação retorno/risco em relação às outras estratégias de comercialização.
Palavras-chave:Value-at-Risk (VaR), Índice de Sharpe, gestão de riscos, riscos no agronegócio.
ABSTRACT
In each of the productive chain links, finding viable strategies for risk mitigation is not a trivial task. Usually, generic strategies are adopted to reduce risks, such as diversification of crops and/or strategies aiming at transferring or diluting risk through futures contracts and insurance. This article aims to evaluate three strategies for managing risks concerning the corn trading: simultaneous buying and selling, storage and short selling. Towards the methodological procedures, this study is descriptive regarding its goal and it is a case study regarding the approach of the problem. Literature and documents were used as procedures for data collection, with coverage for the period of crops from 2003 to 2010. The Value at Risk (VaR) and Sharpe Ratio Modified, which is a variation of the Sharpe Ratio, were used to evaluate commercialization strategies. The results show that the highest returns for the storage would be obtained during winter seasons and for shorter periods. For the short selling, the return averages are similar for all time horizons. The simultaneous buying and selling showed the best risk/return ratio.
Key-words: Value-at-Risk (VaR), Sharpe Ratio, risk management, agribusiness risks.
Classificação JEL: G32, Q13.
1. Introdução
No agronegócio, algumas fontes de riscos, como instabilidade climática e ocorrência de doenças e pragas, são próprias das atividades do setor e influenciam a variação dos níveis de produção, caracterizando, assim, os riscos de produção. Outros tipos de riscos, como os de mercado, caracterizados por variação de preço, de oferta e demanda, ou os riscos institucionais, embora também estejam presentes no contexto empresarial, assumem importâncias e características marcantes no agronegócio. Para alguns tipos existem meios eficientes de proteção, disponibilizados pelo mercado ou pelo governo. Entretanto, para muitos tipos de riscos, o produtor se torna o tomador exclusivo. Devido à variedade dos tipos e origens dos riscos no agronegócio e às particularidades inerentes a cada tipo de produtor rural, não há uma estratégia gerencial única comum a todos os produtores (USDA, 2007; MOREIRA, 2009). Para o produtor, a administração dos riscos objetiva a determinação de combinações de ações que representam níveis diferentes de risco e de retorno (GOMES, 2000). Algumas estratégias visam a redução do risco, como a diversificação das atividades. Outras estratégias visam a transferência do risco, como contratos futuros e contratos de produção. Com relação aos riscos de mercado, as variações de preços de venda dos produtos, dos preços dos insumos necessários à produção e dos níveis de demanda, constituem as principais fontes destes tipos de riscos (MOREIRA, BARREIROS e PROTIL, 2011). Normalmente, tais variações não são facilmente previsíveis e ocorrem após o comprometimento do produtor com o nível de produção desejado, ou seja, após o investimento realizado para o plantio ou criação pecuária. As oscilações na oferta e demanda e na situação econômica nacional e internacional afetam a rentabilidade do produtor quando influenciam quedas significativas de preços de venda ou aumentos dos preços dos insumos. Algumas alternativas gerenciais para reagir a estes tipos de riscos incluem a utilização de informações de mercado como subsídios para o planejamento, a diversificação da produção e do mercado de vendas e a utilização de hedge por meio de contratos futuros e de opções (PINOCHET-CHATEAU et al., 2005; HARDAKER et al., 2007; USDA, 2007; MOREIRA et al., 2012).
No mercado de commodities agropecuárias, os agentes de comercialização desempenham um papel primordial no escoamento da produção. Normalmente, cerealistas e cooperativas são responsáveis pela intermediação entre o produtor rural e as indústrias de transformação internas ou internacionais. Estes agentes também estão expostos aos riscos inerentes à atividade agropecuária, sobretudo aos riscos de mercado. Estes riscos exercem grande influência nas estratégias de comercialização adotadas pelos agentes. Com a constante volatilidade dos preços de compra e venda do mercado, uma escolha inadequada da estratégia de comercialização pode gerar grandes prejuízos para a organização. O conhecimento das características dessas estratégias e dos instrumentos analíticos que auxiliam na escolha das melhores opções de comercialização permite aos agentes melhorar os retornos e reduzir os riscos envolvidos no processo (LEISSMANN, 2002).
Este artigo avalia as principais estratégias de comercialização do milho adotadas por uma cooperativa agroindustrial do Paraná. Por meio do cálculo do VaR (value-at-risk) e do índice de Sharpe modificado, foi possível ponderar o retorno pelo risco envolvido nas estratégias de compra e venda simultânea, estocagem e venda a descoberto. Com isso, foi possível definir qual estratégia é mais eficiente economicamente, em termos da relação retorno/risco, considerando períodos selecionados durante as safras de inverno e verão entre 2003 e 2010.
2. Revisão de literatura
Nesta seção é apresentada a revisão de literatura, considerando os principais conceitos envolvidos no embasamento teórico e metodológico do trabalho. São apresentadas considerações sobre estratégias de comercialização de commodities comumente utilizadas pelas cooperativas agroindustriais, junto aos riscos envolvidos, as definições e métodos de cálculo do VaR e o método de ponderação do retorno pelo risco por meio do cálculo do índice de Sharpe.
2.1.Estratégias de comercialização e os riscos envolvidos
Embora o aumento da produtividade seja um ponto de grande importância, isso pode não gerar tanto retorno se não houver a preocupação com o período de comercialização. Para o caso de commodities agropecuárias como o milho, por exemplo, a maioria dos produtores tem como alternativa para escoar a produção a intermediação de algum agente de comercialização, normalmente empresas cerealistas e cooperativas. Do ponto de vista das cooperativas, o período de comercialização envolve preocupações acerca da qualidade, disponibilidade e, sobretudo, rentabilidade do produto.
Entre as estratégias de comercialização mais comumente empregadas nas cooperativas pode-se citar a compra e venda simultânea (CVS), a estocagem (EST) e a venda a descoberto (VD). A CVS é literalmente a compra do produto e, simultaneamente, a sua venda, com os preços de compra e venda determinados pelo mercado. Por ser um procedimento de rápida transição, esta estratégia envolve menor risco para as cooperativas. Mas, como o mercado de commodities é muito volátil, o preço do produto pode oscilar e gerar prejuízos.
Na estratégia de estocagem, a cooperativa compra o produto e o estoca, aguardando uma eventual alta nos preços de venda. Seus riscos envolvem a queda na rentabilidade, calculada pela diferença entre o preço de venda e de compra, ocasionada por custos diversos, como o de armazenamento, e a possibilidade de baixa nos preços de venda. Assim, se os ganhos das vendas não forem superiores aos custos de armazenamento do produto, ou houver uma oscilação negativa nos preços, a cooperativa terá prejuízo.
Na estratégia de venda a descoberto, o produtor entrega o produto à cooperativa mediante um contrato de venda com preço a fixar. Nesse momento, a cooperativa possui um comprovante que permitirá faturar esses produtos em qualquer data futura. O risco por parte da cooperativa ocorre quando o produtor requerer seu pagamento. Neste momento o valor analisado é o preço de venda atual do produto no mercado. Se o preço for maior do que o preço que a cooperativa conseguiu obter à época da venda do produto, a cooperativa terá prejuízo. Caso contrário, a cooperativa terá ganho financeiro.
Muitas das decisões tomadas pelos produtores e agentes de comercialização, mesmo antes da colheita, são influenciadas pelo conhecimento de tendências de comportamento de preços em curto e médio prazo (RIBEIRO, SOSNOSKI e OLIVEIRA, 2010). A volatilidade associada aos preços das commodities agropecuárias, que configuram as principais fontes dos riscos de mercado, é associada a diversos fatores e se apresenta de forma inconstante ao longo do tempo. Há períodos de tempo em que o grau de volatilidade apresenta-se estável, enquanto que em outros períodos apresenta-se com altos graus de instabilidade. Esse comportamento dificulta a previsão de preços futuros. Alguns autores têm se dedicado à análise da volatilidade dos preços das commodities, tais como Gilbert e Morgan (2010), Martins e Martinelli (2010) e Irwin e Sanders (2011).
Em 2008, por exemplo, após um período de alta acentuada, houve queda brusca nos preços das commodities no mercado internacional, influenciando também os preços no mercado brasileiro. Segundo Gilbert e Morgan (2010), essa elevada variação, caracterizada por alta seguida de queda nos preços, foi ocasionada por fatores como o rápido crescimento econômico da China e outros países emergentes, décadas de baixo investimento na agricultura, baixos níveis dos estoques de alimentos, quebras de safras, especialmente na Austrália, depreciação do dólar norte-americano, aumento da produção destinada a biocombustíveis e especulação no mercado de futuros.
A escolha e adoção de estratégias alternativas de comercialização de commodities pelas cooperativas são influenciadas pelos riscos de mercado envolvidos. Nas cooperativas paranaenses, a maioria se limita à adoção das estratégias tradicionais abordadas neste trabalho, como a CVS, EST e VD. O potencial de ganho proporcionado pelo mercado de futuros e derivativos não é adequadamente aproveitado pelas cooperativas por diversos motivos, entre eles a falta de garantias e de opções de instrumentos nacionais voltados ao agronegócio na Bolsa de Mercadorias e Futuros (BM&F) (MOREIRA, 2009). Segundo Marques, Mello e Martines Filho (2006), os contratos agropecuários nas principais bolsas do mundo representam uma pequena parcela do total negociado. Ainda segundo os autores, esse pequeno volume é explicado, entre outros fatores, pela falta de conhecimento do uso de derivativos dentro do agronegócio, passado relativamente recente de intervenções governamentais no setor, e descapitalização do produtor que se vê obrigado a vender sua produção antecipadamente.
2.2.Value-at-risk
Uma ferramenta de avaliação e acompanhamento de risco financeiro e de mercado que se tornou bastante popular nos últimos anos é o value-at-risk (VaR). O VaR é uma medida de risco de fácil entendimento pelos usuários, gestores internos das empresas e também pelos investidores. Segundo Jorion (2006), o VaR mede o pior cenário possível de perdas esperadas, em um determinado horizonte de tempo e sobre condições normais de mercado, considerando um determinado nível de confiança. Por exemplo, se um banco considera que o VaR diário de seu portfólio de produtos é de US$ 35 milhões com um nível de confiança de 99%, então existe apenas uma chance em 100 de ocorrer uma perda maior que US$ 35 milhões em um dia, considerando condições normais de mercado. Este número resume a exposição do banco ao risco de mercado, com a probabilidade de ocorrência deste risco. Segundo o autor, em contraste com as demais ferramentas de avaliação de risco, o VaR fornece uma visão agregada dos riscos de mercado levando-se em conta alavancagem, correlação e demais situações.
O VaR resume, em um único número, a exposição total ao risco de uma carteira, empresa ou instituição financeira. De acordo com Odening e Hinrichs (2003), uma vantagem do VaR é que seu resultado é facilmente interpretável. Diferente de outros critérios de avaliação de risco, como dominância estocástica e equivalentes certos, que consideram a distribuição das perdas e ganhos de forma completa, o VaR pondera apenas uma parte da distribuição, uma porção da cauda esquerda, o que significa traduzir o risco como um efeito ruim. O cálculo do VaR permite a consideração conjunta de múltiplas fontes de riscos na análise, como por exemplo variações de preços, preços futuros, taxas de juros etc. Além disso, medidas temporais de volatilidade e análise de cenários são possíveis de serem implementadas com este enfoque (EISELE e KNOBLOCH, 2000).
Os métodos tradicionais empregados para o cálculo do VaR são os que utilizam os parâmetros de variância-covariância, conhecidos como métodos paramétricos, a simulação histórica e a simulação de Monte Carlo, que são os métodos não paramétricos. Um tratamento mais detalhado destes métodos pode ser encontrado em Jorion (2006) e em Eisele e Knobloch (2000). Embora alguns trabalhos critiquem o uso dos métodos paramétricos, em especial a técnica de estimação denominada delta-normal, por causa da exigência de normalidade dos dados, Sanders e Manfredo (2002) afirmam que os procedimentos não paramétricos de simulação tendem a apresentar maiores dificuldades de estimação e compreensão por parte dos gestores e não são facilmente adaptáveis a testes de confiabilidade do modelo. Segundo os autores, apesar dos pontos positivos e negativos de ambos os métodos (paramétricos e de simulação), verifica-se que os resultados alcançados estimam adequadamente as probabilidades de perdas quando são utilizados graus modestos de confiança, como 90% e 95%.
Um método alternativo de estimação do VaR é a teoria do valor extremo (extreme value theory) (ODENING e HINRICHS, 2003; GENÇAY, SELÇUK e ULUGÜLYAGCI, 2003; ARRAES e ROCHA, 2006), que avalia as situações mais extremas de ocorrência do VaR, tais como aquelas que ocorrem nas extremidades da curva de distribuição de probabilidade associada às perdas consideradas, possuindo níveis de significância menores que 1%. Essas situações são consideradas de "stress", em casos de perdas mais raras (SOUZA e SILVA, 1999).
Apesar de ter sido amplamente divulgado e desenvolvido para o mercado financeiro, sobretudo para avaliação de risco de derivativos, o VaR pode também ser aplicado na avaliação de outros tipos de riscos e em outros contextos, como no agronegócio, por exemplo. Viviani (2006) apresenta uma aplicação do VaR na determinação de estoques de reserva de vinho para proteger produtores franceses das flutuações de preços. Manfredo e Leuthold (1999, 2001), ao analisarem aplicações do VaR na agricultura, atestam a adequabilidade e potencial desta técnica como ferramenta de suporte à administração dos riscos no setor. Mas, segundo esses autores, a apresentação do desempenho das técnicas do VaR não tem sido rigorosamente testada em carteiras compostas de commodities agrícolas, sujeitas ao risco de mercado, e isso caracteriza uma oportunidade latente para estudos acadêmicos com grande potencial de aplicação prática na gestão.
3. Metodologia
Neste trabalho, o objetivo geral foi avaliar os retornos e riscos associados a estratégias adotadas por uma cooperativa agroindustrial paranaense para a comercialização do milho e definir qual a melhor estratégia considerando-se a relação retorno/risco. A estratégia que apresenta a melhor relação foi definida neste trabalho como sendo a estratégia mais eficiente economicamente. Assim, a pergunta de pesquisa que motivou e guiou a execução deste trabalho foi: "Qual é a estratégia de comercialização do milho que é mais eficiente economicamente considerando-se a relação retorno/risco?"
Este estudo pode ser classificado como uma pesquisa descritiva quanto ao seu objetivo e bibliográfico e documental quanto ao procedimento de coleta de dados. Na pesquisa descritiva, realiza-se o estudo, a análise, o registro e a interpretação dos fatos do mundo físico sem a interferência do pesquisador. Neste tipo de pesquisa, são realizadas a identificação e avaliação das características, fatores ou variáveis que se relacionam com o fenômeno ou processo (RICHARDSON, 2010). Uma pesquisa descritiva pode ser executada segundo várias abordagens, tais como estudos descritivos, pesquisa de opinião, pesquisa de motivação, levantamento e estudos de caso (SEVERINO, 2000). Neste trabalho, a abordagem do problema foi feita segundo os preceitos de um estudo de caso. O termo estudo de caso também é utilizado em variados contextos, abrangendo diferentes posturas epistemológicas, desde a geração de conhecimento mediante abordagem e critérios objetivos, funcionalistas, até a geração de conhecimento com abordagem e critérios interpretativos. Segundo Stake (2005), o estudo de caso visa a compreensão global de um caso ou de um fenômeno e não uma relação causal entre duas variáveis.
A escolha da cooperativa para aplicação do estudo de caso foi realizada levando-se em consideração os seguintes requisitos: a cooperativa deveria adotar estratégias variadas para comercialização de commodities agropecuárias; deveria possuir sistema de controles internos mediante acompanhamento de índices de desempenho financeiros e não financeiros; a cooperativa deveria, de preferência, estar situada em região não muito distante da base do pesquisador, dada a necessidade de constantes deslocamentos para a coleta de dados; a cooperativa deveria estar interessada em participar da pesquisa, dada a necessidade de fornecimento de dados. As características principais da cooperativa estudada, bem como as suas práticas quanto à gestão de riscos, foram levantadas por meio de entrevistas não estruturadas com o gerente administrativo e o responsável pela área comercial de commodities. Para o levantamento dos produtos comercializados e porte quanto ao faturamento e número de associados, foi feita uma análise de documentos institucionais. A série de dados referente aos preços de compra e venda do milho foi fornecida pela área comercial de commodities.
A cooperativa agroindustrial do estudo situa-se no Paraná e é considerada de médio porte, com faturamento anual acima de R$ 200 milhões e cerca de 3.200 associados, sendo 2.400 ativos. As principais atividades são o recebimento e repasse de insumos, secagem, armazenagem e comercialização de grãos e repasse de tecnologia. Os principais produtos comercializados pela cooperativa são soja, milho, trigo, feijão e boi de corte. Cerca de 60% da produção dos cooperados é entregue à cooperativa para comercialização. A produção destinada ao mercado externo (exportação) é de 40%. A composição do faturamento da cooperativa é a seguinte: 58% proveniente da venda de produtos agrícolas primários, 40%, da venda de insumos e 2%, da prestação de serviços.
A cooperativa executa uma administração de riscos baseada no acompanhamento de informações de mercado, sobretudo com base na Bolsa de Chicago (CME/CBOT), por meio de informações obtidas de corretores contratados. Também é feito o acompanhamento da oferta e demanda nacional e internacional. Raramente a cooperativa utiliza ferramentas de mitigação dos riscos de mercado, como derivativos, por exemplo.
As estratégias de comercialização consideradas na análise deste estudo e praticadas pela cooperativa estudada foram a compra e venda simultânea (CVS), a estocagem (EST) e a venda a descoberto (VD). O produto considerado foi o milho. Para a análise, foi utilizada a série histórica dos preços semanais de compra e venda, fornecida pela cooperativa, referente ao período compreendido entre a primeira semana de janeiro de 2003 e a segunda semana de dezembro de 2010. Para o cálculo dos retornos das estratégias, dos valores do VaR (risco das estratégias) e a ponderação dos retornos pelo risco por meio da análise do índice de Sharpe modificado, que é uma variação do índice de Sharpe original, foi seguida a metodologia proposta por Leismann (2002).
De acordo com Sanvicente (2012), a margem de contribuição é a diferença entre o preço de venda de um produto e o custo diretamente decorrente da "fabricação" e venda. Neste estudo, a margem de contribuição é a diferença entre o preço de venda líquido (preço de venda descontado dos custos de armazenagem e impostos) e o custo de aquisição somado aos encargos diretamente aplicáveis. Os retornos da estratégia de compra e venda simultânea, que é a estratégia considerada sem risco neste estudo, foram calculados por meio da margem de contribuição em base decimal, segundo a expressão seguinte:
em que PV é o preço de venda na data de análise, PC é o preço de compra e ISV é o imposto sobre vendas. Optou-se pelo cálculo em base decimal para que seja possível calcular as margens relativas a qualquer quantidade comercializada de sacas de milho.
Para a estratégia de estocagem, considerada de risco com relação a CVS, a margem de contribuição, também em base decimal, é dada pela expressão:
em que PC0 é o preço de compra na data analisada, PVn é o preço de venda n semanas após a compra, QbTE0n é a taxa de quebra técnica entre o período 0 e o período n, ISV é o imposto sobre vendas, AF = [(1 + i)n - 1] é a atualização financeira (custo financeiro decimal no período n entre a compra e a venda), i é a taxa de atualização financeira no período n.
Quanto à taxa de atualização financeira, existem várias taxas de juros relevantes no mercado, dependendo de o indivíduo ser um aplicador ou captador e da oferta e demanda de recursos financeiros. Optou-se pela atualização financeira calculada pela variação da rentabilidade da poupança por se tratar de um índice de referência possível para avaliação de custo de oportunidade e de fácil aceitação pela cooperativa estudada. A série de rentabilidade da poupança foi obtida junto ao Banco Central do Brasil.
Para a estratégia de venda a descoberto, também considerada de risco com relação a CVS, a margem de contribuição em base decimal foi calculada pela expressão:
em que PVo é o preço de venda na data analisada e PCn é o preço de compra n semanas a frente, e as demais variáveis são as mesmas descritas para a fórmula (2).
Na estratégia de venda a descoberto (VD), a exemplo da estocagem, os retornos também são calculados, como a margem de contribuição em percentual com relação à estratégia CVS, usando, nesse caso, as expressões (1) e (3). O preço de venda é o valor recebido pela cooperativa no momento da venda do milho. Esse momento ocorre antes de a cooperativa ter comprado o milho do produtor. Ou seja, o produtor deixa o milho depositado nas instalações da cooperativa ainda com preço a fixar e a cooperativa vende o produto a descoberto. Em um momento futuro, "n" semanas a partir da venda do milho a descoberto, o produtor cobra da cooperativa o preço do milho a valores correntes - sendo esse o preço de compra pago pela cooperativa. A diferença entre o preço obtido pela venda antecipada e o preço de compra pago pela cooperativa define o ganho obtido com essa estratégia. Esse ganho, comparado ao retorno que seria obtido se a cooperativa tivesse optado pela CVS, define o retorno líquido da estratégia VD.
É relevante destacar que, na análise das estratégias de comercialização do milho, adotadas pela cooperativa estudada, as margens de contribuição das estratégias consideradas alternativas, estocagem (EST) e venda a descoberto (VD), com relação à estratégia básica de compra e venda simultânea (CVS), foram feitas desconsiderando-se os impostos sobre vendas (ISV) e as taxas de quebra técnica (QbTE0n). Os impostos sobre vendas (3,65% referentes a 0,65% do PIS e 3% do Cofins) não são imputáveis à cooperativa na venda dos produtos dos cooperados e esta situação representa praticamente a totalidade do volume de comercialização do milho pela cooperativa. Os descontos de quebra técnica têm sido desconsiderados pelos agentes de comercialização por questões concorrenciais. Neste caso, as cooperativas também têm aderido a essa prática quando se trata de associados que deixam a safra estocada em suas instalações para faturamento futuro.
Como citado anteriormente, a estimativa dos riscos associados às estratégias de comercialização foi feita por meio do cálculo do VaR. A mensuração dos riscos através do VaR pode ser feita utilizando-se três métodos. Conforme apresentado por Jorion (2006), as abordagens sobre VaR podem ser classificadas em dois grupos: o primeiro baseia-se na avaliação local (local valuation), podendo ser mais bem exemplificada pelo método delta-normal. O segundo utiliza a avaliação plena (full valuation), que é implementada nos métodos Simulação Histórica e Monte Carlo Estruturado. Para a avaliação dos riscos das estratégias de comercialização (EST e VD), foi empregado o método delta-normal para o cálculo do VaR como função da volatilidade dos retornos. Uma das vantagens deste método é a sua facilidade computacional. Neste caso, quando a média dos retornos é diferente de zero, o VaR pode ser calculado pela fórmula (MORGAN-REUTERS, 1996):
VaR = V0 - V1(4)
em que, contextualizando para os dados deste estudo, V0 é a posição a preços de mercado de 1.000 sacas de milho e V1 = V0e-cσ+µ, em que e é o número de Euler (2,7128...), c é a constante para o número de desvios padrão para o nível de confiança desejado (considerado no modelo como 95% e, logo, c = 1,645), σ é o desvio padrão dos retornos logaritmizados da estratégia analisada e µ é a média dos retornos logaritmizados da estratégia analisada.
O exponencial do termo -cσ + µ mostra as perdas decimais a partir do nível de confiança desejado (representado pelo "c"), do desvio padrão dos retornos logaritmizados, representado pelo "σ", e da média dos retornos logaritmizados, representada pelo "∝". Assim, ao multiplicar esse valor pelo valor correspondente à posição assumida em determinado ativo (V0), obtém-se o valor, com dada confiança, que esse ativo poderá assumir. Dadas as características da fórmula, esse valor será inferior à posição inicial e a diferença entre essas duas posições mostra o potencial de perdas (JORION, 2006).
Inicialmente, para estimar os parâmetros e calcular o VaR usando essa metodologia, é necessário calcular as margens logaritmizadas, partindo-se das expressões (1), (2) e (3), segundo as expressões a seguir:
lnMCCVS = ln[PV0(1-ISV)] - ln(PC0) (5)
lnMCEST =
= ln[PVn(1-ISV)(1-QbTE0n)] - ln[PC0(1+AF)] (6)
lnMCVD =
= ln[PV0(1-ISV)+AF[PV0(1-ISV)]]-ln[PCn-QbTE0n(PCn)] (7)
Depois de calculadas as margens de contribuição decimais e logaritmizadas da estratégia sem risco (CVS) e das estratégias alternativas (EST e VD), foram realizados os cálculos necessários para a definição do VaR por meio da técnica delta-normal. Para tanto, inicialmente é necessário calcular a diferença entre (6) e (5), para o caso da estratégia de estocagem, e a diferença entre (7) e (5) para o caso da estratégia de venda a descoberto, em base monetária e para 1.000 sacas de milho. Isso foi feito para cada semana da série histórica considerada, definindo, assim, os retornos das estratégias alternativas em relação à estratégia CVS. Em seguida, calculando-se a média e o desvio padrão destas diferenças (dos retornos), é possível calcular o VaR segundo a expressão (4). Assim, foi calculado o VaR para cada semana da série histórica e, separadamente, para cada semana dos períodos das safras de verão e de inverno no período analisado. As safras de verão acontecem entre o início da quinta semana e o fim da 17ª semana do ano, enquanto que as safras de inverno acontecem entre o início da 27ª semana do ano e o fim da 39ª semana. No período do estudo (2003 a 2010), foram observadas oito safras de inverno e oito de verão, totalizando 104 semanas de análise para cada safra.
Para a consideração do valor do VaR delta-normal é necessário avaliar a adequação do modelo na previsão dos riscos. Para tanto, foi considerado o método proposto por Manfredo e Leithold (2001) para avaliação do número de violações do VaR e para avaliação do viés do modelo. No caso das violações, os autores avaliam o número de vezes que uma observação ultrapassa o valor do VaR calculado e verificam se esse número é significativamente diferente do esperado segundo o nível de significância adotado no modelo (5% neste estudo). Neste caso, por exemplo, em um modelo estimado com nível de confiança de 95% e com 500 observações, é esperado que ocorram em torno de 25 violações (5% do total de observações). Caso ocorra um número de violações que seja estatisticamente superior aos 25 previstos, o modelo estará subdimensionando o risco. Caso contrário, o modelo estará superdimensionando o risco. No caso de subdimensionamento do risco, o principal problema que pode ocorrer é a tomada de decisões tendo por base valores que seriam ultrapassados com frequência maior que a prevista. No caso de superdimensionamento, o problema é uma decisão de investimento deixar de ser tomada por ser considerada muito arriscada. Embora possa haver uma preferência por uma segurança maior por meio do superdimensionamento do risco, o modelo mais adequado é aquele que prevê o risco da forma mais precisa possível. Ou seja, que o número de violações ocorridas seja próximo ao número previsto, de preferência inferior. Para avaliação do número de violações, é aplicado um teste de razão de verossimilhança em que a hipótese nula é δ = δ*, sendo δ o nível de cobertura desejado (nível de significância adotado no modelo) e δ* = X/N, com X igual ao número de violações observadas e N, o tamanho da amostra. Neste teste, a razão de verossimilhança é dada pela expressão abaixo (que tem uma distribuição qui-quadrado com um grau de liberdade):
O LR(δ) é comparado ao valor qui-quadrado crítico e, se for maior que o valor tabelado, deve-se rejeitar a hipótese nula. Neste caso, é possível concluir que o modelo está gerando um número de violações diferente do esperado pelo nível de significância adotado no modelo do VaR e, assim, o modelo pode estar subestimando ou superestimando o risco.
Para o teste de viés do modelo, o procedimento é baseado um uma distribuição de probabilidade binomial, em que a expectativa do número de violações é N(1 - c), sendo N o número de observações e c, o nível de confiança do modelo na forma decimal (0,95, por exemplo). A variância da estimativa é Nc(1 - c) e o teste de viés é um teste Z que, em amostras grandes, é distribuído normalmente e é calculado conforme a expressão abaixo:
em que X = número de violações observadas. Se o Zc for significantemente positivo, o VaR subdimensiona os riscos de perdas. Caso contrário, se Zc for significantemente negativo, o VaR superdimensiona os riscos de perdas.
Após a definição dos retornos de cada estratégia de comercialização, dos valores do VaR para EST e VD e da avaliação do modelo, foi feita a ponderação do retorno com relação ao risco. Essa ponderação permitiu comparar as estratégias, definindo, assim, qual foi a mais viável em termos de retorno/risco. Para tanto, foi utilizado uma variação do índice de Sharpe.
O índice de Sharpe (IS) é similar ao coeficiente de variação. A diferença reside no fato de o retorno livre de risco ser subtraído do retorno do investimento (BAKER e GLOY, 2001). Este índice mede o retorno esperado por unidade de risco. Ou seja, considerando o retorno de um ativo acima da taxa de juros livre de risco (também considerado como o prêmio que o investidor recebe pelo risco assumido) dividido pelo desvio padrão (proxy para o risco), é possível avaliar a relação retorno/risco (ELTON et al., 2012).
Quanto ao emprego do índice de Sharpe conjugado com o VaR em estudos de riscos no contexto do agronegócio, Baker e Gloy (2001) apresentam uma avaliação de alguns critérios passíveis de serem usados para classificar estratégias de gerenciamento de riscos. Os autores sugerem o uso de softwares, como o @Risk e o AgRisk, para que os tomadores de decisão possam desenvolver rapidamente aproximações à distribuição cumulativa de lucros associados a um investimento. Esses autores avaliam o uso do VaR e do índice de Sharpe, afirmando que os dois critérios são extensamente usados pela comunidade financeira para avaliar tanto o risco quanto os lucros associados aos investimentos. O uso do VaR e do índice de Sharpe permitem classificar estratégias de administração de risco alternativas. Assim, uma classificação evidenciando os retornos e riscos envolvidos em cada opção, ordenando-as da melhor para a pior, permite uma tomada de decisão mais rápida e eficiente. Os autores concluem que a eficácia de cada critério está diretamente relacionada ao grau de aversão ao risco do tomador de decisão. Para decisores mais avessos ao risco e com maior acesso à alavancagem financeira, os critérios de classificação das estratégias se tornam mais úteis.
O Índice de Sharpe pode ser calculado pela fórmula:
em que E(Ri) é o retorno esperado do ativo i, Rf é a taxa livre de risco e σi é o desvio padrão dos retornos do ativo i. Assim, se o retorno esperado do ativo for maior que a taxa livre de risco, o índice será positivo, indicando que há um prêmio pelo risco assumido. Caso contrário, haverá um prêmio negativo pelo risco. Se o índice for maior que 1, o prêmio foi proporcionalmente maior que o risco assumido. Se o índice assumir valor entre 0 e 1, o prêmio foi proporcionalmente menor que o risco. Logo, quanto maior o IS, maior o retorno obtido por unidade risco assumido.
Para efetuar a ponderação do risco com relação ao retorno para cada estratégia de comercialização, foi utilizado o cálculo do índice de Sharpe modificado (IS2), proposto por Leissmann (2002). Este índice é uma variação do índice de Sharpe original, tendo a ponderação pelo valor do VaR e não pelo desvio padrão. Além disso, o retorno da estratégia de risco (EST ou VD) é o valor presente líquido da margem de contribuição da estratégia para 1.000 sacas de milho e o retorno considerado sem risco é a margem de contribuição da CVS, também para 1.000 sacas de milho. Assim, a fórmula usada para o cálculo foi:
Em que MC$1000sc é a margem de contribuição monetária da estratégia (MCEST ou MCVD) considerando 1.000 sacas de milho, obtido pela multiplicação do preço de venda na data de análise por 1.000 vezes a equação (2) ou (3), MC$CVS1000sc é a margem de contribuição monetária da estratégia de compra e venda simultânea, considerando 1.000 sacas de milho, obtido pela multiplicação do preço de venda na data de análise por 1.000 vezes a equação (1), i é a taxa de atualização financeira (taxa de juros decimal diária obtida através da taxa de remuneração da caderneta de poupança do período em análise), e n é o número de dias entre as datas analisadas (data de compra e venda).
Como é possível verificar na equação (11), o VaR é o divisor e, quanto maior este número, menor é a viabilidade da estratégia. O índice de Sharpe modificado (IS2) permite avaliar a relação entre o retorno líquido da estratégia de comercialização adotada e o risco associado. Esse índice fornece uma escala de preferência para as estratégias, tendo preferência a estratégia com maior IS2. Assim, o IS2 apresenta o retorno em unidades monetárias para cada unidade monetária de risco assumido. Além da escala de preferência para as estratégias, por meio do IS2 também é possível avaliar em quais períodos os retornos da estratégia adotada ultrapassaram o risco assumido. Na análise do índice, para verificar as situações em que houve viabilidade da estratégia adotada, é necessário levar em conta apenas os valores positivos. Estes valores, levando-se em consideração o retorno líquido com relação ao risco, são classificados em menos que proporcional se o índice estiver entre 0 e 1, proporcional se o índice for igual a 1, e mais que proporcional se o índice for maior que 1. Assim, nos momentos em que o IS2 foi negativo, houve perdas ao se optar pela estratégia alternativa (EST ou VD). Para IS2 positivo, mas abaixo de um, significa que o retorno alcançado não compensou os riscos. Somente quando o IS2 foi maior que 1 é que a estratégia foi eficiente economicamente em termos de retorno/risco.
A Figura 1 resume a metodologia aplicada nesse trabalho por meio da apresentação das etapas percorridas no estudo. Na etapa 1, foi feito o levantamento dos dados necessários para a construção do modelo de avaliação do risco das estratégias de comercialização. Este levantamento foi feito junto à cooperativa citada e por meio de entrevistas não estruturadas e análise documental. Como citado anteriormente, a série histórica de preços de compra e venda do milho foi fornecida pelo departamento comercial da cooperativa. Na etapa 2, foi realizado o cálculo dos retornos das estratégias de comercialização (CVS, EST e VD) segundo as equações 1, 2 e 3 e a metodologia apresentada por Leismann (2002) e fundamentada por Sanvicente (2012). Na etapa, 3 foi feita a estimação do risco associado a cada estratégia por meio do cálculo do VaR segundo a metodologia delta-normal, apresentada por Morgan-Reuters (1996), Manfredo e Leuthold (1999; 2001), Eisele e Knobloch (2000) e Jorion (2006). Na etapa 4, foi executada a validação do modelo de estimação do VaR por meio da avaliação do número de violações do VaR e do viés do modelo. Para tanto, foram utilizadas as equações 8 e 9, de acordo com o método proposto por Manfredo e Leithold (2001). Por fim, na etapa 5, foi feita a ponderação do retorno pelo risco por meio do cálculo do índice de Sharpe modificado, proposto por Leismann (2002) e fundamentado por Baker e Gloy (2001) e Elton et al. (2012).
4. Resultados e discussão
Nesta seção, são apresentados os retornos obtidos em cada estratégia de comercialização (CVS, EST e VD) a partir das semanas das safras de inverno e verão. Para as estratégias alternativas (EST e VD), foram considerados os horizontes de tempo (HT) de 1, 5, 10, 20, 30 e 40 semanas a partir de cada semana das safras. Também são apresentados os valores do VaR para cada HT, a análise da robustez do modelo (teste de violações) e o índice de Sharpe modificado (IS2), que serviu para a avaliação da eficiência econômica (retorno/risco) de cada estratégia para cada HT.
4.1.Retornos da estratégia de Compra e Venda Simultânea (CVS)
Na estratégia CVS, a cooperativa procura colocar no mercado, simultaneamente, volumes similares ao comprados. Isso se justifica pela possibilidade de reduzir riscos ou pela necessidade de recursos financeiros. A CVS apresenta baixo risco, pois não se assumem posições de investimento ou venda a descoberto. Embora existam riscos para fins de planejamento, por causa da variabilidade das margens ao longo do tempo, no momento da tomada de decisão não existe risco porque a margem é conhecida.
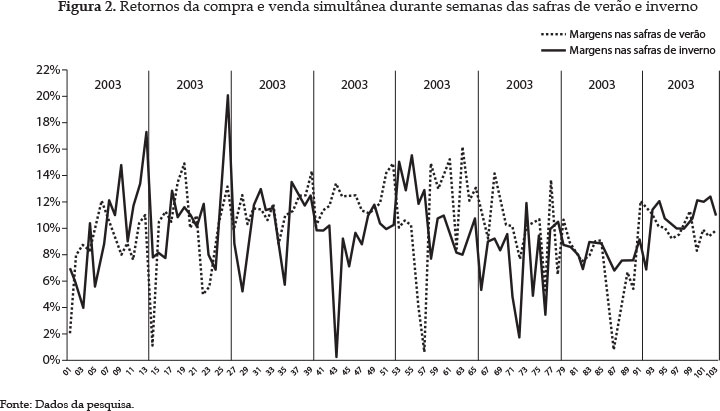
A estratégia de CVS do milho pela cooperativa estudada, no período de janeiro de 2003 a dezembro de 2010 (382 semanas de análise), apresentou retorno médio de 9,97% com desvio padrão de 3,31%. Neste estudo, a ênfase foi dada aos períodos durante as safras porque os produtores comercializam grande parte da produção durante as colheitas. A Figura 2 apresenta os retornos obtidos com a CVS durante os períodos das safras.
Os retornos médios para as safras de inverno e verão foram, respectivamente, de 10,07% e 9,69%. A figura ilustra a variabilidade dos retornos, que no caso da safra de inverno apresentou desvio padrão de 3,09% e, para a safra de verão, 2,97%. No caso da safra de inverno, o coeficiente de variação foi 30,65% e, para a safra de verão, 30,67%. Verifica-se que praticamente não há diferenças quanto ao grau relativo de variabilidade dos dados, medido pelo coeficiente de variação. Isso também se verifica na comparação dos períodos de safra com o período completo de análise, que apresentou coeficiente de variação de 33,20%. Isso denota que a variabilidade das margens é praticamente a mesma durante todas as semanas dos anos analisados. A Tabela 1 resume as estatísticas dos retornos da compra e venda simultânea.
Embora existam variações das margens nos períodos de safras de inverno e verão, é possível observar que as margens de contribuição nunca são negativas e são conhecidas no momento da compra e venda. Por ser conhecida a margem no momento da tomada de decisão, esta estratégia é considerada sem risco neste trabalho. As margens obtidas nas estratégias de EST e VD são comparadas às margens obtidas na CVS por meio da análise dos retornos líquidos. Os retornos são os prêmios obtidos por terem sido assumidas situações em que envolvem riscos de mercado (EST ou VD).
4.2.Retornos das estratégias alternativas (EST e VD)
A estratégia de estocagem (EST) é adotada quando a cooperativa decide vender a produção adquirida do produtor em um momento posterior ao da aquisição. Nesta situação, os retornos da estocagem são calculados como a margem de contribuição com relação à estratégia CVS usando-se as equações (1) e (2). O preço de aquisição é o que a cooperativa paga ao produtor no momento da compra e o preço de venda é aquele recebido no momento da venda, ocorrendo "n" períodos após a compra.
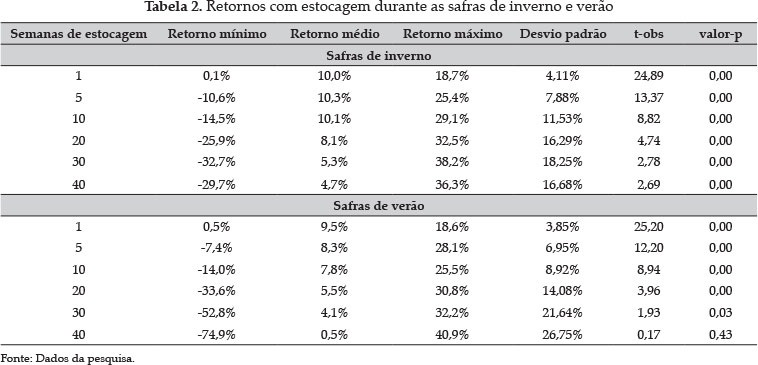
Na Tabela 2, são apresentados os retornos líquidos da estocagem para horizontes de tempo de 1, 5, 10, 20, 30 e 40 semanas a partir das semanas compreendidas entre os períodos das safras de inverno e verão durante o período analisado neste estudo. Na tabela também são apresentados os testes de hipóteses para as médias dos retornos iguais a zero.
Os maiores retornos para a estocagem seriam obtidos durante as safras de inverno e para horizontes de tempo menores. À medida que aumenta a quantidade de semanas de estocagem, as médias dos retornos diminuem e, ao mesmo tempo, a variabilidade dos retornos aumenta. Isso significa que os retornos são menos estáveis à medida que o período de estocagem aumenta. O teste de hipótese para retornos iguais a zero indicou que, com exceção da estocagem por 40 semanas durante as safras de verão, para os demais horizontes de tempo a média dos retornos é estatisticamente diferente de zero. Esses retornos representam os prêmios recebidos por se optar pela estratégia que envolve risco (EST) com relação à estratégia sem risco (CVS) - o risco significa a possibilidade de esses retornos serem negativos.
Na Tabela 3, são apresentados os retornos líquidos da VD para horizontes de tempo de 1, 5, 10, 20, 30 e 40 semanas a partir das semanas compreendidas entre os períodos das safras de inverno e verão. Também são apresentados os testes de hipóteses para médias iguais a zero. As diferenças entre as médias dos retornos para a VD podem ser consideradas pequenas para todos os horizontes de tempo, embora haja alta variabilidade, sobretudo para horizontes de tempo a partir de 10 semanas. O teste de hipótese para média dos retornos iguais a zero indica que, para todos os horizontes de tempo considerados na análise, a média é estatisticamente não nula. Os retornos representam os prêmios recebidos por se optar pela estratégia que envolve risco (VD) com relação à estratégia sem risco (CVS) - o risco significa a possibilidade de esses retornos serem negativos.
Segundo os testes estatísticos, o VaR calculado para a EST gerou violações estatisticamente iguais às previstas pelo nível de significância adotado no modelo do VaR (5%). O teste de viés não identificou subdimensionamento e nem superdimensionamento do risco. Para a VD, o número de violações do VaR foi estatisticamente superior ao previsto para horizontes de tempo de 20, 30 e 40 semanas e, nestes casos, o VaR calculado está subdimensionando os riscos. Mas, embora isso esteja acontecendo para alguns dos horizontes de tempo considerados no estudo, os resultados foram mantidos para fins de comparação.
É possível verificar que a estratégia de venda a descoberto do milho apresentou retornos crescentes e maiores que a estratégia de estocagem. Mas, para ambos os casos, é necessário avaliar se os retornos das estratégias podem ser considerados satisfatórios frente ao risco assumido ao adotá-las. Isso define a eficiência econômica da estratégia considerando-se a relação retorno/risco. Essa análise é apresentada na seção 4.4, logo após a apresentação das estimativas do VaR.
4.3.Estimativas do VaR para as estratégias alternativas (EST e Vd)
Como citado anteriormente, a estimativa do VaR para as estratégias de comercialização consideradas alternativas e de risco, com relação à CVS, foi feita utilizando-se o método delta-normal. Após o cálculo do VaR, foram feitos o teste de avaliação do modelo por meio da análise do número de violações e o teste de viés do modelo. A Tabela 4 apresenta o percentual de violações do VaR dos retornos da estocagem e da venda a descoberto, assim como os testes do número de violações e de viés.
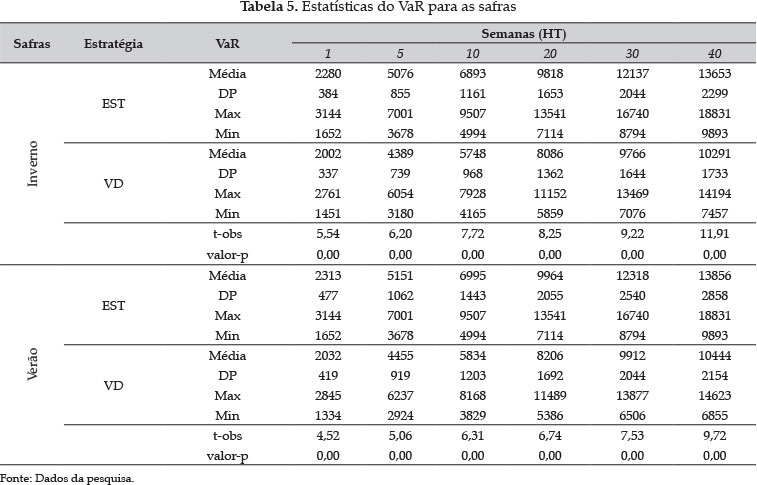
A Tabela 5 apresenta as estatísticas para os valores do VaR para os horizontes de tempo selecionados durante as safras. Também é apresentado o teste t para igualdade de médias, indicando que os valores médios do VaR das estratégias EST e VD são diferentes durante os horizontes de tempo nas safras de inverno e verão. No entanto, ao considerar a mesma estratégia (EST ou VD), é possível perceber que o risco (VaR) não difere significativamente entre as safras nos mesmos horizontes de tempo.
É importante ressaltar que os valores são referentes ao risco de se estocar 1.000 sacas de milho. Assim, por exemplo, considerando-se o período do estudo (2003 a 2010), ao se estocar o milho por uma semana, o potencial de perdas é de R$ 2.280 em média, durante a safra de inverno, e de R$ 2.313, em média, durante a safra de verão. Para o caso do inverno e estocagem por uma semana, por exemplo, isso significa que permanece a chance de 5% que as perdas superem R$ 2.280. Assim, é possível afirmar com 95% de confiança que as perdas atingirão no máximo R$ 2.280. A interpretação é análoga para os outros horizontes de tempo e para a estratégia VD.
Os valores médios do VaR representam um aumento do potencial de perdas à medida que a cooperativa opta em manter em estoque a produção adquirida por mais tempo, no caso da EST, ou tem que pagar a posição assumida ao produtor, no caso da estratégia VD. Além disso, também é possível verificar que o potencial de perdas é maior para a estratégia EST em todos os horizontes de tempo durante os dois tipos de safras. Entretanto, para avaliar qual é a melhor estratégia, é necessário ponderar o potencial de perdas (VaR) pelos retornos obtidos pelas estratégias EST e VD com relação à estratégia considerada sem risco, a CVS.
4.4.Análise retorno/risco
No caso da EST, os retornos desta estratégia foram economicamente eficientes em termos da análise retorno/risco, apresentando IS2 maior que 1, somente para 1, 5, 10 e 20 semanas de estocagem em 2003, cinco semanas de estocagem em 2006, e todos os períodos de estocagem em 2007. Mas, para cada ano citado, a eficiência não foi constatada durante todo o período da safra de inverno. Além disso, para os demais anos, essa estratégia não gerou retornos suficiente para compensar os riscos assumidos ou simplesmente foi inviável. Durante as safras de verão, a estratégia EST foi eficiente para uma e cinco semanas de estocagem em 2004 e 2005, apenas para cinco semanas de estocagem em 2006, 20 e 40 semanas de estocagem em 2007 e apenas 10 semanas de estocagem em 2008. E, novamente, para cada ano citado, a estratégia não foi eficiente durante todo o período da safra de verão.
Com relação ao IS2 da VD é possível constatar que a estratégia foi eficiente em um número menor de períodos se comparada à estratégia EST. É importante ressaltar que o modelo subdimensionou o risco para esta estratégia, de acordo com a análise das violações do VaR, o que implica que, se não houvesse o subdimensionamento, o índice seria ainda pior. Assim, é possível verificar que a estratégia VD é menos eficiente economicamente em termos de retorno/risco se comparada à estratégia EST. A Tabela 6 apresenta um resumo dos valores do IS2 para as estratégias EST e VD considerando-se os horizontes de tempo selecionados a partir das safras de inverno e verão. São apresentados os valores máximos e mínimos alcançados do IS2 e a quantidade de semanas em que o índice foi maior ou igual a 1. Nestas semanas, a estratégia alternativa, EST ou VD, foi economicamente eficiente em relação à estratégia sem risco (CVS).
A análise dos resultados do índice de Sharpe modificado evidencia que a estratégia EST apresentou viabilidade em um número maior de semanas quando comparada à estratégia VD. Além disso, a estocagem a partir de semanas da safra de inverno apresentou mais viabilidade do que a partir de semanas da safra de verão. Isso foi evidenciado pelo número de semanas com IS2 maior ou igual a 1 e pelos valores máximos do índice. A análise do IS2 indica que assumir o risco da estocagem ou da venda a descoberto não é vantajoso em termos de eficiência econômica (retorno/risco) em todos os períodos de tempo. Assim, é possível concluir que a estratégia de compra e venda simultânea foi a estratégia com melhor relação retorno/risco durante o período analisado neste estudo.
5. Conclusão
A fase de comercialização dos produtos é o momento em que o produtor coloca seu produto no mercado e, no caso do agronegócio, é comum os produtores acessarem o mercado consumidor via agentes de comercialização, como cooperativas agroindustriais e cerealistas. Essa situação é ainda mais evidente para o caso das commodities, que na sua maioria são destinadas à indústria de transformação ou alimentação animal.
Do ponto de vista dos agentes, é possível verificar que os riscos de mercado exercem grande influência em suas estratégias de comercialização. Isso porque, no mercado agropecuário, a volatilidade dos preços de venda e compra é uma realidade frequente e escolhas inadequadas quanto a estratégias de comercialização podem ocasionar perdas financeiras significativas. O conhecimento das características dessas estratégias e dos instrumentos analíticos que auxiliam na escolha das melhores opções de comercialização permite aos agentes melhorar os retornos e reduzir os riscos envolvidos no processo.
Neste trabalho, o objetivo geral foi o de avaliar os retornos e riscos associados a estratégias adotadas por uma cooperativa agroindustrial paranaense para a comercialização do milho e definir qual a melhor estratégia, considerando-se a relação retorno/risco. A estratégia que apresentou a melhor relação foi definida neste trabalho como sendo a estratégia mais eficiente economicamente. Por meio da consecução das etapas da pesquisa foi possível responder à pergunta de pesquisa proposta.
O estudo de caso foi realizado em uma cooperativa agroindustrial paranaense, caracterizada em detalhes na seção de metodologia. As estratégias de comercialização avaliadas e que são responsáveis pela totalidade da comercialização do milho pela cooperativa foram as estratégias de compra e venda simultânea, estocagem e venda a descoberto. Na estratégia da compra e venda simultânea, considerada sem risco, a cooperativa compra o milho e simultaneamente vende ao mercado. Nas estratégias alternativas, de estocagem e venda a descoberto, consideradas de risco, os momentos da compra e da venda são distintos e a volatilidade dos preços gera os riscos de mercado. Esses riscos são caracterizados pela ocorrência de retornos negativos das estratégias alternativas quando comparadas à estratégia sem risco.
Para avaliar os riscos envolvidos nas estratégias de comercialização, o método adotado foi o do cálculo do VaR por meio da técnica de estimação paramétrica conhecida como delta-normal. Após a avaliação dos riscos, foi feita a ponderação dos retornos, permitindo, assim, avaliar qual estratégia é mais eficiente economicamente em termos da relação retorno/risco. A ponderação foi feita por meio do índice de Sharpe modificado.
Os resultados evidenciam que os maiores retornos para a estratégia de estocagem seriam obtidos durante as safras de inverno e para horizontes de tempo menores. Ou seja, à medida que aumenta a quantidade de semanas de estocagem, as médias dos retornos diminuem. Também foi possível verificar que nestas situações a variabilidade aumentou. Isso significa que os retornos são menos estáveis à medida que o período de estocagem aumenta. Na estratégia de venda a descoberto, as diferenças entre as médias dos retornos não são significantes para todos os horizontes de tempo, embora haja alta variabilidade, sobretudo para horizontes de tempo a partir de 10 semanas. A estratégia de venda a descoberto do milho apresentou retornos crescentes e maiores que a estratégia de estocagem, embora menos estáveis, caracterizando maiores riscos.
Quanto aos riscos associados às estratégias alternativas, os valores médios do VaR evidenciam um aumento do potencial de perdas à medida que a cooperativa opta por manter em estoque a produção adquirida por mais tempo, no caso da estratégia de estocagem, ou tem que pagar a posição assumida ao produtor, no caso da estratégia de venda a descoberto. Também é possível verificar que o potencial de perdas é maior para a estratégia de estocagem em todos os horizontes de tempo durante os dois tipos de safras.
Ao se fazer a ponderação do retorno pelo risco, verificou-se que a estratégia de venda a descoberto é menos eficiente economicamente em termos de retorno/risco se comparada à estratégia de estocagem. Mas, considerando o período total de análise, os resultados do índice de Sharpe modificado evidenciam que assumir o risco da estocagem ou da venda a descoberto não seria sempre vantajoso em termos de retorno/risco. Os resultados do índice mostraram que, na maior parte do tempo, os retornos das estratégias alternativas foram proporcionalmente menores que o risco assumido ao não se optar pela estratégia sem risco. A estratégia de compra e venda simultânea foi a estratégia com melhor relação retorno/risco, sendo, portanto, a estratégia considerada mais eficiente economicamente. Estes resultados estão em conformidade com as conclusões apresentadas por Leismann (2002) em seu estudo sobre os retornos e riscos associados à comercialização do milho pelos agentes do agronegócio paranaense.
A revisão bibliográfica executada neste trabalho evidencia que esta área de estudo é promissora e desperta o interesse de vários pesquisadores estrangeiros. Entretanto, embora alguns autores tenham se dedicado ao estudo da gestão dos riscos no contexto cooperativista (ZEULI, 1999; MANFREDO e RICHARDS, 2007; MOREIRA, 2009; MOREIRA et al., 2012), foi possível verificar que, no Brasil, existem poucos estudos com enfoque específico na relação retorno/risco das estratégias de comercialização de commodities agrícolas. Além disso, conforme evidenciado por Moreira (2009), embora as cooperativas agroindustriais reconheçam a importância da análise de riscos, avaliando periodicamente os cenários de oferta e demanda e de tendências de preços para auxiliar no planejamento da produção, ferramentas quantitativas de análise e acompanhamento dos riscos financeiros e de mercado raramente são usadas. A utilização destas ferramentas pode contribuir com o aprimoramento dos cenários gerados.
A mensuração e acompanhamento dos riscos usando uma medida comum no mercado financeiro, o VaR, possibilita à cooperativa avaliar de forma objetiva os riscos envolvidos nas estratégias de comercialização de commodities e tem o potencial de melhorar o planejamento das práticas de comercialização, melhorando o retorno esperado em função dos riscos assumidos. Como desdobramento desta pesquisa, pretende-se executar a replicação do modelo, considerando-se um portfólio de commodities e o uso de outras técnicas de estimação do VaR.
6. Referências bibliográficas
- ARRAES, R. A. e ROCHA, A. S. Perdas extremas em mercados de risco. Revista Contabilidade e Finanças, v. 17, n. 42, p. 22-34, 2006.
- BAKER, G. T. e GLOY, B. A. A comparison of criteria for evaluating risk management strategies. Agricultural Finance Review, v. 61, n. 1, p. 38-56, 2001.
- EISELE, W. e KNOBLOCH, A. P. Value at Risk: Tool for Managing Trading Risks. FRENKEL, M., HOMMEL, U. e RUDOLF, M. (Eds.). Risk Management: challenge and opportunity. Berlin: Springer-Verlag, 2000.
- ELTON, E. J., GRUBER, M. J., BROWN, S. J. e GOETZMANN, W. N. Moderna teoria de carteiras e análise de investimentos Rio de Janeiro: Elsevier, 2012.
- GENÇAY, R., SELÇUK, F. e ULUGÜLYAGCI, A. High volatility, thick tails and extreme value theory in value-at-risk estimation. Insurance: Mathematics and Economics, v. 33, p. 337-356, 2003.
- GILBERT, C. L. e MORGAN, C. W. Food price volatility. Philosofical transactions of the royal society, v. 365, n. 1554, p. 3023-3034, 2010.
- GOMES, A. G. Administração de Riscos: Como proteger-se contra riscos na agricultura. In: Agrianual 2000: Anuário da Agricultura Brasileira. São Paulo: Instituto FNP, 2000.
- HARDAKER, J. B., HUIRME, R. B. M., ANDERSON, J. R. e LIEN, G. Coping with risk in agriculture CABI Publising, 2 ed., 2007.
- IRWIN, S. H. e SANDERS, D. R. Testing the masters hypothesis in commodity futures markets. Energy economics, v. 34, n. 1, p. 256-269, 2012.
- JORION, P. Value at Risk: The New Benchmark for Managing Financial Risk. McGraw-Hill, 3. ed., 2006.
- LEISMANN, E. L. Retornos e Riscos na Comercialização de Milho no Estado do Paraná: uma aplicação do modelo Value-at-Risk. Viçosa, 2002. 177 f. Tese (Doutorado em Economia Aplicada) - Programa de Pós Graduação em Economia Aplicada, Universidade Federal de Viçosa.
- MANFREDO, M. R. e LEUTHOLD, R. M. Value-at-Risk analysis: a review and the potential for agricultural applications. Rev. Agr. Econ., v. 21, p. 99-111, 1999.
- ______. Market risk measurement and the cattle feeding margin: an application of Value-at-Risk. Agribusiness, v. 17, n. 3, p. 333-353, 2001.
- MANFREDO, M. R. e RICHARDS, T. J. Cooperative Risk Management, Rationale, and Effectiveness: The Case of Dairy Cooperatives. Agricultural Finance Review, v. 67, n. 2, p. 311-340, 2007.
- MARQUES, P. V., MELLO, P. C. e MARTINES FILHO, J. G. Mercados Futuros e de Opções Agropecuárias Piracicaba, SP, Departamento de Economia, Administração e Sociologia da Esalq/USP, 2006, Série Didática no D-129.
- MARTINS, T. M. e MARTINELLI, D. P. Ciclos e previsão Cíclica dos Preços das Commodities: um modelo de indicador antecedente para a commodity açúcar. Revista de Administração, Contabilidade e Economia da FUNDACE - RACEF, v. 1, p. 1-12, 2010.
- MOREIRA, V. R. Gestão dos Riscos do Agronegócio no Contexto Cooperativista São Paulo, 2009. 205 f. Tese (Doutorado em Administração) - Escola de Administração de Empresas de São Paulo, Fundação Getulio Vargas.
- MOREIRA, V. R., BARREIROS, R. F. e PROTIL, R. M. Portfolio de produção agropecuária e gestão de riscos de mercado nas cooperativas do agronegócio paranaense. Revista de Administração - RAUSP, São Paulo-SP, v. 46, n. 4, p. 325-341, 2011.
- MOREIRA, V. R., SILVA, C. L., MORAES, E. A. e PROTIL, R. M. O Cooperativismo e a Gestão dos Riscos de Mercado: análise da fronteira de eficiência do agronegócio paranaense. Revista de Economia e Sociologia Rural - RESR, Piracicaba-SP, v. 50, n. 1, p. 51-68, 2012.
- MORGAN-REUTERS, J. P. Risk metrics - technical document 4. ed. New York, 1996.
- ODENING, M. e HINRICHS, J. Using Extreme Value Theory to Estimate Value-at-Risk. Agricultural Finance Review, v. 63, n. 1, p. 55-73, 2003.
- PINOCHET-CHATEAU, R. et al Changers in Risk Perception and Risk Management Strategies in New Zealand Dairy Farming International Food and Agribusiness Management Association: 2005 World Food and Agribusiness Congress, 2005. Disponível em: <www.ifama.org/conferences/2005Conference/Papers&Discussions/1157_Paper_Final.pdf>. Acesso em: 27 ago. 2008.
- RIBEIRO, C. O., SOSNOSKI, A. A. K. B. e OLIVEIRA, S. M. Um modelo hierárquico para previsão de preços de commodities agrícolas. Revista Produção Online, v. 10, n. 4, p. 719-733, 2010.
- RICHARDSON, R. H. Pesquisa social: métodos e técnicas. São Paulo: Atlas, 2010.
- SANDERS, D. R. e MANFREDO, M. R. The Role of Value-at-Risk in Purchasing: An Application to the Foodservice Industry. The Journal of Supply Chain Management: A Global Review of Purchasing and Supply, 2002.
- SANVICENTE, A. Z. e SANTOS, C. C. Orçamento na administração de empresas: planejamento e controle. 2. ed. São Paulo: Atlas, 2012.
- SEVERINO, A. J. Metodologia do trabalho científico São Paulo: Cortez, 2000.
- SOUZA, L. A. R. e SILVA, M. E. Teoria de Valores Extremos para Cálculo de VaR. Finance Lab Working Papers, Finance Lab, Insper Instituto de Ensino e Pesquisa, 1999.
- STAKE, R. Qualitative Case Studies. In: DENZIN, N. e LINCOLN, T. Handbook of Qualitative Research London: Sage, 2005.
- USDA. Risk management United States Department of Agriculture - 2007 Farm Bill Theme Papers. Disponível em: <http://www.usda.gov/documents/Farmbill07riskmgmtrev.pdf>. Acesso em: 27 ago. 2008.
- VIVIANI, J. Risk management of the agricultural income: the inter-Rhône reserve. British Food Journal, v. 108, n. 4, p. 290-305, 2006.
- ZEULI, K. A. New Risk-Management Strategies for Agricultural Cooperatives. American Journal of Agricultural Economics, v. 81, n. 5, p. 1234-1239, 1999.
Avaliação de retornos e riscos na comercialização de milho: estudo de caso usando value-at-risk
Datas de Publicação
-
Publicação nesta coleção
04 Set 2014 -
Data do Fascículo
Jun 2014