Resumos
Resumo
Com a intenção de compreender a dinâmica dos preços e as consequências de choques exógenos no mercado do boi gordo, a presente pesquisa buscou identificar se mudanças na estrutura da cadeia produtiva e no comportamento dos preços alteraram os centros formadores de preços do boi gordo no Brasil entre 2006 e 2017. Isso representa uma contribuição expressiva, uma vez que os estudos encontrados recentemente usavam formadores de preços de estudos defasados ou não consideravam os possíveis efeitos das quebras estruturais nas análises. Então, pretendeu-se testar a presença de quebras estruturais por meio do teste Chow e, conforme metodologia proposta por Asche et al. (2012), delimitar espacialmente o mercado do boi no Brasil pelo teste de cointegração de Johansen (1988, 1995) e identificar os centros formadores de preços pelo teste de exogeneidade fraca. O resultado do teste de quebra estrutural conjunta dividiu a série em três períodos distintos. No período I (início de 2006 a 2008), a região de São Paulo foi a que apresentou maior influência nos preços de outras regiões. Nos períodos II (2009 a 2013) e III (2014 a início de 2017), Mato Grosso do Sul passou a ser o estado com maior influência nos preços. Desse modo, comprovou-se que as modificações verificadas no agronegócio do boi e choques exógenos alteraram o mercado comum e o centro formador de preços no período analisado.
Palavras-chave:
centro formador de preços; quebra estrutural; diferenciais de preços
Abstract
Aiming to understand price dynamics and the consequences of exogenous shocks in the fat cattle market, the current study has as main goal to identify if structural changes in supply chain and in price dynamics led to changes in the Brazilian beef cattle central market between 2006 and 2017. Therefore, it was intended to test the presence of structural breaks through the Chow test and, according to methodology proposed by Asche et al. (2012), spatially delineate the beef market in Brazil by the Johansen cointegration test (1988, 1995) and identify the central market by the weak exogeneity test. According to the structural breaks test the series was divided into three smaller samples defined by Period I, II and III. In the Period I (early 2006 to 2008), São Paulo was the region that presented the deepest influence on prices comparing to other ones and it was identified as the central market. In the Period II (2009 to 2013) and III (2014 to early 2017), Mato Grosso do Sul became the central market. In conclusion, the results pointed out that the regional changes on beef cattle agribusiness changed the common economic market and the central market over the analyzed period.
Keywords:
central price market; market integration; structural breaks; price variations
1. INTRODUÇÃO
Atualmente, muitos são os estudos que examinam o comportamento dos preços nos mercados, pois além de ser um dos principais determinantes da demanda, também delimitam os lucros auferidos pelos agentes. Porém, a análise de preços apresenta certo grau de complexidade, pois, normalmente, não é apenas uma função de oferta e demanda, ou seja, muitos são os fatores determinantes, como, por exemplo, a estrutura do mercado, a concorrência do setor e as características de consumo do produto (elasticidade-preço e elasticidade-renda).
Segundo Zilli et al. (2008)Zilli, J. B., Silva, A. F., Campos, S. K., & Costa, J. S. (2008). Análise da cointegração e causalidade dos preços de boi gordo em diferentes praças nas regiões Sudeste e Centro-Oeste do Brasil. Revista de Economia Agrícola, 55(2), 105-119., os preços do boi gordo, regionalmente, são determinados pelas condições da oferta de animais para o abate, da demanda da carne bovina pelos consumidores finais e pela distância entre os elos da cadeia, ou seja, as relações entre produtores pecuaristas, indústria e consumidores finais. Segundo os autores, os agentes do mercado bovino no Brasil, ao operarem de forma integrada, necessitam de preços regionalizados e especificação por categorias de animais (boi magro, vaca, novilho, bezerros, boi gordo). Desse modo, as informações sobre o comportamento dos preços nas diversas regiões brasileiras e a possível relação temporal entre as praças produtoras podem auxiliar os pecuaristas a decidirem os melhores momentos de produção e venda de seus animais.
Shikida et al. (2016)Shikida, C., Paiva, G. L., & Junior, A. F. A. (2016). Análise de quebras estruturais na série do preço do boi gordo no Estado de São Paulo. Economia Aplicada, 20(2), 265-286. apontaram que o preço do boi gordo comporta-se diferentemente em cada praça de mercado, sugerindo que sua análise é uma rica fonte de estudo sobre a independência, custos de transação, bem como modelos de integração espacial. Porém, os autores alertaram que os comportamentos dos preços podem apresentar quebras estruturais. A respeito de quebras estruturais, Hansen (2001)Hansen, B. E. (2001). The new econometrics of structural change: dating breaks in U.S. labor productivity. The Journal of Economic Perspectives, 15(4), 117-128. apontou que estudos empíricos de séries temporais têm como hipótese a estacionariedade da série, ou seja, que os valores dos parâmetros sejam constantes ao longo do tempo (média, variância e tendência). Portanto, ignorar possíveis quebras estruturais em estudos de séries de tempo é um tanto quanto perigoso, pois as inferências sobre as relações econômicas podem ser viesadas, e as previsões imprecisas, levando então a conclusões equivocadas.
As quebras estruturais podem acontecer por forças externas, como o caso da crise financeira internacional de 2007/2008; mudanças na política econômica, por exemplo, o Plano Real em 1993-1994; pela instabilidade política e econômica do Brasil, iniciada em 2014; fenômenos naturais, como grandes secas e até mesmo alterações na estrutura do mercado em questão.
Desse modo, vale destacar que a pecuária bovina passou por diversas modificações nos últimos anos. A produção de animais elevou-se nos estados do Norte e Centro-Oeste, fazendo com que tais regiões se destacassem, a partir de meados de 2002, na produção de carne bovina. O estado do Mato Grosso, em 2002, além de se tornar o maior produtor, passou ter o maior número de abates no Brasil. Além disso, em 2004, o Pará ganhou destaque como nova fronteira de produção pecuária e, em 2015, apresentou o dobro da produção e o mesmo número de abate paulista.
Segundo Sachs & Pinatti (2007)Sachs, R. C. C., & Pinatti, E. (2007). Análise do comportamento dos preços do boi gordo e do boi magro na pecuária de corte paulista, no período de 1995 a 2006. Revista de Economia e Agronegócio, 5(3), 329-352., verificou-se um progresso tecnológico na cadeia produtiva do boi, principalmente na etapa de produção, que refletiu no aumento do volume produzido, na oferta de cabeças para o abate e, consequentemente, na elevação dos lucros do pecuarista. Ressalta-se que as mudanças na produção de carne bovina brasileira estão focadas no melhoramento genético animal, manejo correto de plantas forrageiras, permitindo melhor lotação de animais e a melhoria da eficiência alimentar, com maior ingestão de alimento no período da seca, resultando no aumento de carcaça e a consequente elevação do volume produzido (Organisation for Economic Co-opetation and Development, 2015Organisation for Economic Co-opetation and Development – OCDE, & Food and Agriculture Organization of United Nation – FAO. (2015). Agricultural outlook. Paris: OCDE.).
Quanto à indústria frigorífica, De Zen & Barros (2005)De Zen, S., & Barros, G. S. C. (2005). Formação de preços do boi, uma perspectiva histórica. Visão Agrícola, 3, 120-122. apontaram que, de modo geral, esta passou por uma forte evolução administrativa. Segundo os autores, o destaque brasileiro como exportador de carne levou essas empresas a ampliarem suas regiões de atuação, implantando novas unidades regionais, possibilitando compras eficientes, reduzindo a arbitragem regional dos preços.
Portanto, conclui-se que ao longo dos últimos anos a produção de bovinos de corte no Brasil apresentou mudanças, como a inovação tecnológica, o melhoramento genético e o consequente aumento de produtividade. Estes fatores, por sua vez, proporcionaram a conquista de novos mercados internacionais, a evolução da indústria frigorífica e a inserção dos novos polos de produção e abate, justificando a necessidade de um estudo que possa abordar as consequências dessas mudanças nas relações de preços entre as principais regiões produtoras de bovinos no Brasil.
Visto que a economia brasileira esteve suscetível a eventos capazes de proporcionar quebras estruturais nos últimos anos, e que o mercado do boi gordo apresentou mudanças espaciais e estruturais, é possível questionar se tais eventos foram capazes de alterar o comportamento dos preços entre as principais praças do boi gordo no Brasil e, consequentemente, modificar o centro formador de preços. A hipótese a ser testada nesse trabalho é que as modificações espaciais e estruturais verificadas no agronegócio do boi, que levaram aos novos polos de produção e de abatate de bovinos, como Mato Grosso e Mato Grosso do Sul, teriam alterado os centros formadores de preços e o mercado comum do boi gordo do Brasil nos últimos anos.
Assim sendo, o objetivo geral do estudo é verificar possíveis mudanças nos centros formadores de preço do boi gordo em consequência das dinâmicas nos comportamentos dos seus preços. Especificamente, pretende-se i) analisar se as mudanças no mercado bovino resultaram em quebras estruturais no modelo, ii) delimitar espacialmente o mercado do boi no Brasil; e iii) identificar os centros formadores de preços para cada período da quebra estrutural.
A análise do comportamento dos preços com a finalidade de identificar o mercado comum e o centro formador de preço é relevante, pois, conforme exposto por Asche et al. (2012)Asche, F., Gjoberg, O., & Guttormsen, A. G. (2012). Testing the central market hypothesis: a multivariate analysis of Tanzanian sorghum markets. Agricultural Economics, 1, 1-9., a detecção do mercado central pode melhorar a eficiência das assistências públicas ao setor, o que é essencial para os países em desenvolvimento. Dessa forma, os recursos direcionam-se apenas para um local que consequentemente é transmitido para os mercados secundários. Além disso, a identificação do centro formador de preços é a chave central para análise da integração espacial de um mercado. Assim, Pereira (2005)Pereira, L. R. R. (2005). Integração espacial no mercado do boi gordo (Tese de doutorado). Universidade Federal de Viçosa, Viçosa. ressalta que as políticas públicas voltadas para a melhoria no fluxo de comércio entre regiões seriam beneficiadas com as informações sobre o centro formador e a integração espacial do mercado, proporcionando o correto delineamento de políticas de desenvolvimento regional.
Vale destacar que o último estudo encontrado a analisar o centro formador de preços do boi gordo no Brasil foi o de Pereira (2005)Pereira, L. R. R. (2005). Integração espacial no mercado do boi gordo (Tese de doutorado). Universidade Federal de Viçosa, Viçosa.. Filgueiras et al. (2006)Filgueiras, G. C., Quieroz, J. C. B., Santos, R. B., Diniz, M. B., & Diniz, M. J. T. (2006). Causalidade de preço do mercado de carne de boi gordo para seis estados brasileiros, 1994 a 2003. In Congresso da Sociedade Brasileira de Economia e Sociologia Rural (Vol. 44). Brasília: SOBER. também testaram essa possível existência, porém abordaram apenas os estados de Minas Gerais, Mato Grosso do Sul, Paraná e São Paulo. Ressalta-se que estudos recentes definiram o centro formador de preços, respaldados em pesquisas elaboradas na década passada e nas características que um centro formador de preços deve ter: por exemplo, se destacar no consumo de carne bovina e sediar a bolsa de mercados futuros. Nesse caso, o estado de São Paulo foi a região mais utilizada como centro formador de preços dentre os principais estudos da integração espacial do boi no Brasil, sem nenhuma comprovação empírica que o confirmasse.
Portanto, ao longo dos últimos 21 anos, foram diversos os estudos que analisaram a integração espacial do boi gordo no Brasil, seja ela entre regiões ou até mesmo com os países vizinhos e, desse modo, foi possível notar diferentes períodos de análises e centros formadores de preços que levaram a distintos resultados, confirmando a importância da presente pesquisa em definir (e não tomar como dados) os centros formadores de preços, considerando possíveis quebras estruturais nas séries do modelo da integração espacial.
Por fim, vale destacar que não se verificaram na literatura, nacional e internacional, estudos empíricos de centros formadores que buscaram testar quebras estruturais nas séries, reforçando a contribuição do presente estudo para a literatura.
2. FUNDAMENTAÇÃO TEÓRICA
2.1. O mercado central
Conforme Balcombe et al. (2007)Balcombe, K., Bailey, A., & Brooks, J. (2007). Threshold effects in price transmission: the case of Brazilian wheat, maize and soya prices. American Journal of Agricultural Economics, 89(2), 308-323., na literatura econômica frequentemente se encontra uma relação entre os preços de bens similares em mercados espacialmente ou verticalmente separados como um conceito associado à Lei do Preço Único1 1 Quanto mais perfeito for um mercado, existirá forte tendência para que um mesmo preço seja pago pelo produto ao mesmo tempo e em todas as partes de um mercado (Marshall, 1980). Assim, na ausência dos custos de transação, os mercados regionais com o mesmo comércio apresentarão um único preço. (LPU) e como um sinal de concorrência e eficiência econômica.
Segundo Balcombe et al. (2007)Balcombe, K., Bailey, A., & Brooks, J. (2007). Threshold effects in price transmission: the case of Brazilian wheat, maize and soya prices. American Journal of Agricultural Economics, 89(2), 308-323., o mecanismo que mantém a relação da LPU é a arbitragem espacial. Portando, quando os preços de produtos homogêneos se diferenciarem em dois mercados, na ausência de custos de transporte, os arbitradores deslocarão parte do excesso de produção de um mercado para outro mais escasso, onde o preço do produto será mais elevado, e tal comportamento se manterá até que a LPU se estabeleça. Os autores destacaram que assimetria nos ajustamentos, baixa transmissão nos preços e desvios da LPU são justificadas pelo transporte ou custos de transação, protecionismo, barreiras de mercado ou por alguma outra forma de competição imperfeita.
Fackler & Goodwin (2001)Fackler, P. L., & Goodwin, B. K. (2001). Spatial price analysis. In B. L. Gardner & G. C. Rausser (Eds.), Handbook of agricultural economics (Vol. 1, Part B, chap. 1, pp. 972-1018). North-Holland: Elsevier. complementaram que os preços são utilizados para se investigar relações espaciais, e as técnicas de análise dinâmica de séries temporais são frequentemente empregadas para mensurar a integração espacial do mercado. Regressões de modelos dinâmicos tipicamente usam alguma versão do modelo de Vetores Autorregressivos,
sendo o vetor de preços, vetor de fatores exógenos que afetam os preços, a matriz de coeficientes e i vetor de erros representando os fatores exógenos.
Segundo Margarido (2012)Margarido, M. A. (2012). Análise da transmissão espacial de preços no mercado internacional de soja. Revista de Economia e Administração, São Paulo, 11(3), 281-303., o primeiro modelo a considerar os aspectos dinâmicos, até então não abordados nos modelos de integração espacial, foi o de Ravallion (1986)Ravallion, M. (1986). Testing market integration. American Journal of Agricultural Economics, 68(1), 102-109., sendo eles as expectativas na formação dos preços e os efeitos de integração de preços entre mercados
Conforme Mattos et al. (2010)Mattos, L. B. de; Lirio, V. S.; Lima, J. E. de; Campos, A. C. (2010) Uma aplicação de modelos TAR para o mercado de carne de frango no Brasil. EconomiA, 11(3), 537-557, esse aspecto dinâmico permite distinguir a integração de curto prazo, instantânea, e a de longo prazo, e desde então esses procedimentos de testes foram passando por sofisticações.
Os estudos empíricos sobre a integração espacial do boi gordo no Brasil confirmaram a existência de integração espacial em determinados períodos de tempo, principalmente entre as regiões do Sudeste e Centro Oeste, e a existência de um mercado central (De Zen, 1997De Zen, S. (1997). Integração entre os mercados de boi gordo e de carne bovina nas regiões centro-oeste e sudeste do Brasil (Dissertação de mestrado). Escola Superior de Agricultura “Luiz de Queiroz”, Piracicaba.; Pereira, 2005Pereira, L. R. R. (2005). Integração espacial no mercado do boi gordo (Tese de doutorado). Universidade Federal de Viçosa, Viçosa.; Gaio et al., 2005Gaio, L. E., Castro Júnior, L. G., & Oliveira, A. R. (2005). Causalidade e elasticidade na transmissão de preço do boi gordo entre regiões do Brasil e a Bolsa de Mercadorias & Futuros (BM&F). Organizações Rurais & Agroindustriais, 7(3), 282-297.; Cunha et al., 2010Cunha, D. A., Lima, J. E., & Braga, M. J. (2010). Integração espacial do mercado brasileiro de boi Gordo: uma análise de cointegração com Threshold. Análise Econômica, 28(53), 251-267.; Silva Neto et al., 2010Silva Neto, W. A., Fraga, G. J., & Marques, P. V. (2010). Eficiência de mercado: evidências empíricas para os preços spot e futuro de boi gordo. Revista de Economia, 36(3), 7-24.; Lafranco et al., 2015Lafranco, B. A., Ferraro, B., & Rostán, F. (2015). Beef Cattle in the MERCOSUR bloc: Integrated or Separate Markets? In Proceedings of the 29th International Conference of Agricultural Economists. USA: IAAE.; Soares & Lopes, 2015Soares, T. C., & Lopes, L. S. (2015). Quebras estruturais sistêmicas e efeito threshold na dinâmica dos preços do boi gordo: o caso das regiões Sudeste e Centro-Oeste. Revista de Economia e Sociologia Rural, 53(2), 343-360.). Desse modo, a estrutura de mercado do boi gordo comprovada empiricamente se aproxima da proposta por Ravallion (1986)Ravallion, M. (1986). Testing market integration. American Journal of Agricultural Economics, 68(1), 102-109., ao assumir a existência de um grupo de mercados locais2 2 Ravallion (1986) assume os mercados locais como aqueles secundários, os quais podem transacionar entre si. Porém, é na transação com o mercado central que se definirá a formação dos preços no mercado local. Dependendo do número de mercados locais e seus tamanhos, pode-se verificar a influência de diversos mercados locais no preço do central. (rural) e um único mercado central (urbano). Por mais que se estabeleça um comércio entre os mercados locais, será o comércio com o mercado central que dominará a formação de preços do mercado local.
Desse modo, Ravallion (1986)Ravallion, M. (1986). Testing market integration. American Journal of Agricultural Economics, 68(1), 102-109. aponta que a formação estática de preços entre N mercados, em que 1 é o mercado central, pode ser resumida pelo seguinte modelo,
em que (i = 1,..., N) é um vetor de outras influências sobre o mercado local. As funções (i = 1,..., N) podem ser apontadas como as soluções das condições apropriadas do equilíbrio de mercado, levando em conta as principais escolhas espaciais e os custos de ajustamento figurados pelos comerciantes quando decidem o que vender.
Combinadas as informações postuladas pelo autor, chega-se ao seguinte modelo para N mercados e T séries temporais de preços.
Sendo ruído branco, e os valores de a, b, e c fixos. Caso apresente valor nulo, o mercado será segmentado e o mercado central não influenciará preços do local. Se em t=0 o valor de for 1, verifica-se integração de curto prazo e, assim, mudanças no mercado central são imediatamente repassadas. Efeitos futuros serão observados por meio das variáveis defasadas, ou seja, para (j = 1,...,n). Caso o mercado se integre no curto prazo e existam efeitos defasados nos preços futuros, pode-se apontar uma integração com o mercado central dentro de um intervalo de tempo.
Na integração de longo prazo, o equilíbrio de longo prazo é aquele em que os preços são constantes ao longo do tempo, assume-se que ;e para todo t. Caso ocorra a integração de mercado, é necessário que . Desse modo, a restrição implica um processo de ajuste dos preços no curto prazo, consistente com o equilíbrio, em que um incremento no preço do mercado central é totalmente repassado aos preços locais. Portanto, aceitar as restrições de ajuste de curto prazo implica na integração de longo prazo, porém, o contrário não é verdadeiro.
A existência de características significantes de mercados locais pode indicar que a arbitragem é imperfeita para eliminar os diferenciais de preços. Então, uma integração forte pode ser formulada ao se considerar c=0. Portanto, mudanças nos preços locais são atribuídas a alterações no mercado central e por diferenças nos preços passados. As variáveis defasadas nos preços e características de mercado apontam para a possibilidade de os mercados não estarem em um equilíbrio integrado em determinado ponto do tempo, o que significa dizer que os mercados estariam em desequilíbrio em primeira instância.
Por fim, caso exista equilíbrio de longo prazo, Ravallion (1986)Ravallion, M. (1986). Testing market integration. American Journal of Agricultural Economics, 68(1), 102-109. ressalta que se pode aplicar métodos de estimação mais poderosos para testar o processo de integração, como, por exemplo, o modelo de correção de erro.
O estudo de Faminow & Benson (1990)Faminow, M. D., & Benson, B. L. (1990). Integration of Spatial Markets. American Journal of Agricultural Economics, 72(1), 49-62. apresentou um modelo com base na interdependência oligopolística, elaborado como um complemento aos pressupostos da LPU, revisando a forma estrutural da interdependência entre mercados. Por conseguinte, propuseram existência da interdependência oligopolística em mercados nos quais compradores e vendedores estão espacialmente separados e considera-se que os vendedores precificam seus produtos conforme seu concorrente mais próximo, mesmo em um mercado dominado por um grande número de produtores que comercializam produtos homogêneos, indicando concorrência perfeita.
Segundo os autores, essa teoria baseia-se nas hipóteses de que compradores e vendedores estão espacialmente dispersos e os custos intrarregionais são significantes. Desse modo, Faminow & Benson (1990)Faminow, M. D., & Benson, B. L. (1990). Integration of Spatial Markets. American Journal of Agricultural Economics, 72(1), 49-62. testam estatisticamente se os diferentes comportamentos dos preços em cada região seriam superiores, inferiores ou iguais ao custo de transferência do produto de uma região até outra. No estudo sobre a integração espacial, os produtos são considerados homogêneos, diferenciando-se apenas pela localização. Desse modo, com a finalidade de mensurar o grau de integração espacial entre as regiões, os autores utilizam testes estatísticos de interdependência entre preços para as diferentes localidades.
Conforme Goodwin & Schroeder (1991)Goodwin, B. K., & Schroeder, T. C. (1991). Cointegration tests and spatial price linkages in regional cattle markets. American Journal of Agricultural Economics, 73(2), 452-464., o modelo de interdependência oligopolística de Faminow & Benson (1990)Faminow, M. D., & Benson, B. L. (1990). Integration of Spatial Markets. American Journal of Agricultural Economics, 72(1), 49-62. e o da LPU são as duas teorias que sustentam os argumentos da integração entre mercados espacialmente separados. Desse modo, o modelo da presente pesquisa se sustenta nas teorias da LPU.
O trabalho de González-Rivera & Helfand (2001)González-Rivera, G., & Helfand, S. M. (2001). The extent, pattern, and degree of market integration: a multivariate approach for the brazilian rice market. American Journal of Agricultural Economics, 3(83), 576-592. foi um dos primeiros a identificar a existência do mercado comum nas pesquisas de integração espacial. Os autores objetivaram encontrar o único fator comum para um conjunto de localidades, o que implicou encontrar n-1 vetores de cointegração para n mercados. Assim, normalizando-se os n-1 vetores de cointegração em relação a um local específico, encontraram-se os pares de mercado para análise do modelo de integração.
González-Rivera & Helfand (2001)González-Rivera, G., & Helfand, S. M. (2001). The extent, pattern, and degree of market integration: a multivariate approach for the brazilian rice market. American Journal of Agricultural Economics, 3(83), 576-592., ao estimarem o fator comum, utilizaram a metodologia proposta por Gonzalo & Granger (1995)Gonzalo, J., & Granger, C. W. J. (1995). Estimation of Common LongMemory Components in Cointegrated Systems. Journal of Business & Economic Statistics, 13, 27-36., em que o fator comum seria associado às variáveis observadas e permitem a identificação da região que contribui para o comportamento de longo prazo dos preços. Então, buscou-se identificar o conjunto de localidades que se conectaram direta e indiretamente em um comércio contínuo.
Na determinação de quais regiões devam pertencer ao mesmo mercado, recomenda-se iniciar o estudo com o número máximo de localizações, n, e testar os n-1 fatores de cointegração, por meio dos testes de Johansen. Caso o número de vetores seja inferior a n-1, é necessário identificar quais localidades devem ser removidas do sistema (González-Rivera & Helfand, 2001González-Rivera, G., & Helfand, S. M. (2001). The extent, pattern, and degree of market integration: a multivariate approach for the brazilian rice market. American Journal of Agricultural Economics, 3(83), 576-592.).
O estudo de Asche et al. (2012)Asche, F., Gjoberg, O., & Guttormsen, A. G. (2012). Testing the central market hypothesis: a multivariate analysis of Tanzanian sorghum markets. Agricultural Economics, 1, 1-9. baseou-se na metodologia proposta por González-Rivera & Helfand (2001)González-Rivera, G., & Helfand, S. M. (2001). The extent, pattern, and degree of market integration: a multivariate approach for the brazilian rice market. American Journal of Agricultural Economics, 3(83), 576-592.. No entanto, os autores primeiramente estimaram um modelo bivariado entre o centro formador de preços e os demais mercados e depois o modelo multivariado, diferentemente do estudo anterior. Segundo Asche et al. (2012)Asche, F., Gjoberg, O., & Guttormsen, A. G. (2012). Testing the central market hypothesis: a multivariate analysis of Tanzanian sorghum markets. Agricultural Economics, 1, 1-9., quando mais de dois mercados são integrados, poderá existir, no máximo, um mercado central. Portanto, para evitar o problema de especificação do modelo frequentemente verificado nas análises de integração espacial, ao se estudar um grande número de mercados, os autores utilizaram o esquema de normalização de Johansen & Juselius (1994)Johansen, S., & Juselius, K. (1994). Identification of the long-run and the short-run structure: an application to the IS-LM model. Journal of Econometrics, 54, 159-178. para obter informações econômicas com o uso de testes bivariados. Conforme Asche et al. (2012)Asche, F., Gjoberg, O., & Guttormsen, A. G. (2012). Testing the central market hypothesis: a multivariate analysis of Tanzanian sorghum markets. Agricultural Economics, 1, 1-9., em um conjunto de n variáveis com n-1 vetores de cointegração, nenhum tipo de informação será perdida ao se normalizar um sistema, representado por relações bivariadas, para testar a integração entre dois mercados. Já para mercados que apresentam uma tendência estocástica comum, deverá ser realizada uma análise multivariada.
3. METODOLOGIA
3.1. O Modelo do Mercado Central
As análises dos centros formadores de preços normalmente são elaboradas conforme duas metodologias. A primeira busca, empiricamente, identificar o centro formador de preços do mercado para, assim, verificar como choques são transmitidos entre a região central e as secundárias (aquelas que recebem influência da formadora). A segunda não elenca uma região principal e considera a possibilidade de todas serem formadoras de preços. Porém, a segunda metodologia não é a mais apropriada, pois o agronegócio do boi apresenta regiões com expressivas produções de bovinos e abates, o que sugere a presença de um centro formador de preços. Desse modo, a presente pesquisa adotará a primeira metodologia.
O modelo em análise inicia-se com a relação exposta por Silva & Margarido (2009)Silva, J. R., & Margarido, M. A. (2009). Análise da transmissão espacial de preços no mercado de mandioca. Revista de Economia e Administração, São Paulo, 8(4), 464-484., e também encontrada em diversos estudos da integração espacial sustentados na LPU, em que os preços do produto em determinada região são função dos preços desse mesmo bem em outra região adicionado um termo de erro,
O parâmetro α comporta-se como o termo de erro por captar os desvios entre os preços. Logo, torna-se necessário que α~IID (µ, σ2) e E(,α) = 0. O coeficiente β apresentará valor igual a 1 sob a hipótese de integração perfeita entre os mercados, confirmando a Lei do Preço Único. O valor nulo de β evidencia que os mercados não apresentam relações nos preços dos produtos, em que ambas as regiões seriam autárquicas, ou seja, completamente fechadas. No caso em que β resulta em valores entre 0 e 1, algum tipo de restrição é imposta ao mercado, os preços apresentam algum tipo de relação não constante e os produtos seriam substitutos imperfeitos.
Conforme Asche et al. (2012)Asche, F., Gjoberg, O., & Guttormsen, A. G. (2012). Testing the central market hypothesis: a multivariate analysis of Tanzanian sorghum markets. Agricultural Economics, 1, 1-9., ao se estimar o modelo (6), verifica-se o problema da simultaneidade, que desaparece caso um preço seja exógeno. Na integração espacial entre mercados, isso só será possível se o mercado exógeno for assumido como o centro formador de preços (mercado central). Nesse caso, os preços seriam determinados pelas condições de oferta e demanda, que são exógenas aos sistemas de preços. Portanto, choques na oferta e demanda de outros mercados são corrigidos pelo comércio com o mercado central, sem influenciar seus preços, o que torna importante a identificação da exogeneidade de uma das variáveis no sistema. Além disso, os autores apontam que, ao escolher aleatoriamente os pares de mercado em análise, pode-se chegar a conclusões erradas, além de ser teoricamente impossível. Assim, utilizam a mesma metodologia de González-Rivera & Helfand (2001)González-Rivera, G., & Helfand, S. M. (2001). The extent, pattern, and degree of market integration: a multivariate approach for the brazilian rice market. American Journal of Agricultural Economics, 3(83), 576-592., baseada na de Gonzalo & Granger (1995)Gonzalo, J., & Granger, C. W. J. (1995). Estimation of Common LongMemory Components in Cointegrated Systems. Journal of Business & Economic Statistics, 13, 27-36., para identificar o mercado comum entre as regiões abordadas.
Segundo Asche et al. (2012)Asche, F., Gjoberg, O., & Guttormsen, A. G. (2012). Testing the central market hypothesis: a multivariate analysis of Tanzanian sorghum markets. Agricultural Economics, 1, 1-9., em um sistema de n regiões e r tendências estocásticas, deve-se ter no máximo r variáveis exógenas. Portanto, para que se considere um mercado como eficiente, deve-se encontrar n-1 vetores de cointegração e apenas uma tendência estocástica. Conforme exposto por Mattos et al. (2010)Mattos, L. B. de; Lirio, V. S.; Lima, J. E. de; Campos, A. C. (2010) Uma aplicação de modelos TAR para o mercado de carne de frango no Brasil. EconomiA, 11(3), 537-557, caso todos os preços praticados nos n mercados em análise pertençam ao mesmo mercado econômico, devem ser encontrados n-1 vetores de cointegração, o que significa que ambos apresentam uma tendência comum.
No entanto, caso se identifique um número de vetores de cointegração menor que n-1, deve-se excluir um a um cada mercado, de tal forma que o número de vetores não se altere, ou seja, retirar do modelo mercados que não apresentem a mesma tendência. Nesse caso, sugere-se excluir primeiramente aqueles com atributos próprios, ou seja, com características de comercialização ou produção diferenciadas e, em seguida, os mais distantes e menos relevantes.
3.2. Detalhamento dos testes
A análise proposta na pesquisa é dividida em duas etapas. A primeira consiste na identificação das quebras estruturais conjuntas do modelo, realizada por meio do teste de Chow. Espera-se nessa etapa verificar possíveis subamostras das séries de preços para as regiões em análise. A segunda compreende a identificação do centro formador de preços, realizada, primeiramente, pelo teste de raiz unitária Dikey-Fuller Aumentado (ADF), conforme metodologia exposta por Enders (2004)Enders, W. (2004). Applied econometric times series (p. 429). England: John Wiley & Sons. e, posteriormente, pelos testes de cointegração de Johansen (1988Johansen, S. (1988). Statistical analysis of cointegration vectors. Journal of Economic Dynamics & Control, 12(1), 231-254., 1995Johansen, S. (1995). Identifying restrictions of linear equations with applications to simultaneous equations and cointegration. Journal of Econometrics, 69, 111-132.) e o de exogeneidade fraca.
Conforme Hansen (2001)Hansen, B. E. (2001). The new econometrics of structural change: dating breaks in U.S. labor productivity. The Journal of Economic Perspectives, 15(4), 117-128., os estudos econométricos sobre mudanças estruturais aprimoraram os métodos de identificação de quebras estruturais em séries temporais, sendo que as mais importantes contribuições para essa literatura incluem: 1) testes que comprovam a existência de quebra estrutural; 2)estimativas da data da quebra estrutural; e, 3) testes que diferenciam um passeio aleatório e quebras nas tendências temporais.
Um dos testes mais famosos para identificação de quebra estrutural é o de Chow (1960)Chow, G. C. (1960). Tests of equality between sets of coefficients in two linear regressions. Econometrica, 28(3), 591-605., que se enquadra no primeiro grupo apontado. Segundo Hansen (2001)Hansen, B. E. (2001). The new econometrics of structural change: dating breaks in U.S. labor productivity. The Journal of Economic Perspectives, 15(4), 117-128., um dos seus principais procedimento metodológicos é a informação a priori que o pesquisador precisa dominar sobre o possível momento de quebra. Nesse caso, pode-se utilizar uma data de quebra arbitrária ou se elencar determinada data no ponto de inflexão do comportamento dos dados.
Segundo Cysne et al. (2009)Cysne, R. P.,, Issler, J. V., Lima, L. R. R. O, Hostalácio, H. (2009). Impacto do PIS e da COFINS na inflação: uma abordagem econométrica usando o teste de janela variável. Economia Aplicada, 13(2), 185-206., a necessidade de informações a priori consiste em um entrave à aplicação do teste Chow. Desse modo, uma possível solução foi inicialmente desenvolvida por Quandt (1960)Quandt, R. (1960). Tests of the hypothesis that a linear regression obeys two separate regimes. Journal of the American Statistical Association, 55(0), 324-330., e somente com os artigos de Andrews (1993)Andrews, D. W. K. (1993). Tests for parameter instability and structural change with unknown change point. Econometrica, 61(4), 821-856., Andrews (1994)Andrews, D. W. K. (1994). Optimal tests when a nuisance parameter is present only under the alternative. Econometrica, 62(6), 1383-1414. e Hansen (1997)Hansen, B. (1997). Approximate asymptotic p values for structural-change tests. Journal of Business & Economic Statistics, 15(0), 60-67. é que o problema se resolveu.
No segundo grupo de testes apontado, não se sabe o momento da quebra, e se estima essa data e seus respectivos intervalos de confiança. Hansen (2001)Hansen, B. E. (2001). The new econometrics of structural change: dating breaks in U.S. labor productivity. The Journal of Economic Perspectives, 15(4), 117-128. apontou que uma teoria de estimadores por mínimos quadrados foi desenvolvida em uma sequência de artigos propostos por Jushan Bai, escritos em coautoria e solo. Nesse caso, vale destacar o teste Bai-Perron apresentado em Bai & Perron (1998)Bai, J., & Perron, P. (1998). Estimating and testing linear models with multiple structural changes. Econometrica, 66, 47-78., em que é possível estimar múltiplas quebras estruturais de uma regressão linear.
Conforme Haywood & Randall (2008)Haywood, J., & Randall, J. (2008) Trending seasonal data with multiple structural breaks. NZ visitor arrivals and the minimal effects of 9/11. In: Research report 08/10. University of Wellington, Victoria, New Zealand, 26 p., o teste de Bai & Perron (1998Bai, J., & Perron, P. (1998). Estimating and testing linear models with multiple structural changes. Econometrica, 66, 47-78., 2003Bai, J., & Perron, P. (2003). Computation and analysis of multiple structural change models. Journal of Applied Econometrics, 18, 1-22.) é capaz de encontrar o ponto ótimo da quebra estrutural (). Essa posição ótima é determinada pela minimização da soma dos quadrados dos resíduos, sendo max. O número ótimo de quebras pode ser determinado, por exemplo, pelo menor valor de critérios, como, por exemplo, o de BIC (Schwarz, 1978Schwarz, G. (1978). Estimating the dimension of a model. Annals of Statistics, 6, 461-464.). Essa metodologia oferece duas formas de se estimar os pontos de quebra desconhecidos. Na primeira, o coeficiente de um dos componentes é fixo e o modelo apresenta uma mudança estrutural parcial e, na segunda, todos os parâmetros dos componentes apresentarão quebra e se terá um modelo de quebra estrutural pura.
Haywood & Randall (2008)Haywood, J., & Randall, J. (2008) Trending seasonal data with multiple structural breaks. NZ visitor arrivals and the minimal effects of 9/11. In: Research report 08/10. University of Wellington, Victoria, New Zealand, 26 p., ao verificarem que para séries de tempo sazonais com tendência as estimativas de Bai & Perron (1998Bai, J., & Perron, P. (1998). Estimating and testing linear models with multiple structural changes. Econometrica, 66, 47-78., 2003Bai, J., & Perron, P. (2003). Computation and analysis of multiple structural change models. Journal of Applied Econometrics, 18, 1-22.) deixam de ser satisfatórias, desenvolvem um modelo não paramétrico alternativo a tais características. Desse modo, os autores estimaram a tendência e os componentes sazonais separadamente, utilizando uma nova metodologia interativa inspirada no Método de decomposição do ciclo sazonal de Macaulay (Macaulay, 1931Macaulay, F. R. (1931). The Smoothing of Time Series. New York: National Bureau of Economic Research.), por exemplo, a técnica robusta STL de Cleveland et al. (1990)Cleveland, R. B., Cleveland, W. S., McRae, J. E., & Terpenning, I. (1990). STL: A seasonal-trend decomposition procedure based on loess. Journal of Official Statistics, 6, 3-73., realizada por médias ponderadas modernas.
Portanto, verifica-se que os testes de quebra estrutural evoluíram ao longo do tempo, aprimorando seus cálculos para os mais diversos tipos de séries. Assim, dentre todas as metodologias anteriormente abordadas, a apresente pesquisa optou pelo teste de Chow devido à sua capacidade de identificar quebras dada uma informação a priori, uma vez que, por meio de uma análise preliminar dos preços nas principias praças do boi gordo no Brasil, Rondônia, Tocantins, Goiás, Mato Grosso, Mato Grosso do Sul, Minas Gerais, São Paulo, Paraná e Rio Grande do Sul, para os anos de 2006 a 2017, foi possível verificar mudanças nos comportamentos das séries, indicando que os diferenciais de preços entre as praças modificam-se ao longo do tempo. Entre 2009 e 2014, os diferenciais de base foram menores que entre os anos de 2006 a 2008 e, no final da série, entre 2015 e início de 2017. Portanto, essas diferentes relações das séries ao longo do tempo sugerem modificações no comportamento dos preços no mercado do boi gordo em consequência de possíveis quebras estruturais que devem ser estatisticamente testadas.
Para a execução do teste de quebra estrutural (Chow), deve-se primeiramente dividir a série conforme uma possível mudança identificada. Para melhor compreensão do modelo, Gujarati (2006)Gujarati, D. (2006). Econometria Básica (4. ed., Tradução de Maria José Cyhlar Monteiro, 812 p.) Rio de Janeiro: Elsevier. utiliza o exemplo de apenas uma quebra estrutural com duas variáveis e as possíveis regressões,
sendo n o número de observações e ut os termos de erro de cada equação. Nesse caso, os parâmetros em análise são os referentes à Equação 6.
Se os valores dos parâmetros forem iguais nas Equações 7, 8 e 9 a hipótese de estacionaridade é mantida – parâmetros médios, variância e tendência constantes ao logo do tempo. Portanto, não existe uma quebra estrutural capaz de modificar os valores dos parâmetros. Caso contrário, deve-se utilizar o teste de Chow.
Estima-se a Equação 9 para se obter as Somas dos Quadrados dos Resíduos (SQR3), com graus de liberdade, sendo k o número de parâmetros estimados. Em seguida, estima-se as Equações 7 e 8, identificando as Somas dos Quadrados dos Resíduos e os graus de liberdade, que seriam, respectivamente, SQR1 e SQR2 e e .
Como os dois conjuntos são independentes, ao somar SQR1 e SQR2 encontra-se, como denominado por Gujarati (2006)Gujarati, D. (2006). Econometria Básica (4. ed., Tradução de Maria José Cyhlar Monteiro, 812 p.) Rio de Janeiro: Elsevier. , a soma dos quadrados dos resíduos sem restrições SQRSr, com graus de liberdade.
Segundo Gujarati (2006)Gujarati, D. (2006). Econometria Básica (4. ed., Tradução de Maria José Cyhlar Monteiro, 812 p.) Rio de Janeiro: Elsevier. , a ideia fundamental do teste de Chow é de que, se não há quebra estrutural no modelo, então a SQR3 e a SQRSr não deveriam ser estatisticamente diferentes. Desse modo, por meio da fórmula,
mostra que, sob a hipótese nula H0, as regressões (7) e (8) são estatisticamente iguais, ou seja, não há quebra estrutural no modelo, e a relação F segue a distribuição F com k e graus de liberdade do numerador e denominador, respectivamente.
Quanto aos procedimentos metodológicos realizados na segunda etapa do estudo, vale destacar que o teste de raiz unitária na presença de quebras estruturais pode ser viesado. Na literatura verificaram-se dois procedimentos metodológicos para a realização de testes de raiz unitária com quebra estrutural. No primeiro, estimam-se os termos determinísticos pelo método de Mínimos Quadrados Generalizados (GLS) sob a hipótese nula de raiz unitária para toda a série em questão, como, por exemplo, o estudo de Lanne & Lütkepohl (2002)Lanne, M., & Lütkepohl, H. (2002). Unit root tests for time series with level shifts: a comparison of different proposals. Economics Letters, 75, 109-114.. Portanto, nesse caso os testes do tipo Phillips-Perron não são recomendados. O segundo procedimento consiste em se realizar os testes de raiz unitária por métodos que estimam o termo determinístico por Mínimos Quadrados Ordinários para cada subperíodo da série identificado no teste de quebra estrutural, conforme aplicado por Soares & Lopes (2015)Soares, T. C., & Lopes, L. S. (2015). Quebras estruturais sistêmicas e efeito threshold na dinâmica dos preços do boi gordo: o caso das regiões Sudeste e Centro-Oeste. Revista de Economia e Sociologia Rural, 53(2), 343-360.. Portanto, a pesquisa adotou a segunda metodologia com a aplicação do teste ADF.
Por fim, em relação à condição de exogeneidade fraca, realizou-se o teste conforme procedimentos propostos por Johansen (1995)Johansen, S. (1995). Identifying restrictions of linear equations with applications to simultaneous equations and cointegration. Journal of Econometrics, 69, 111-132.. Desse modo, Johansen (1995)Johansen, S. (1995). Identifying restrictions of linear equations with applications to simultaneous equations and cointegration. Journal of Econometrics, 69, 111-132. apresentou a condição de exogeneidade fraca, por meio das análises estatísticas dos coeficientes de ajustamento α da matriz Π, ou seja, os que estabelecem os ajustamentos de curto e longo prazo. Portanto, dentre n diferentes variáveis para verificar se uma série i será fracamente exógena, basta testar a hipótese nula de que todos os coeficientes de ajustamento da i-ésima série sejam estatisticamente iguais a 0.
3.3. FONTE E NATUREZA DOS DADOS
Os dados da pesquisa foram disponibilizados pelo CEPEA-ESALQ, em valores diários em R$ a arroba, das regiões de Goiânia, Campo Grande, Cuiabá, Triângulo Mineiro, Noroeste Paranaense e Araçatuba, para o período de 24 de abril de 2006 a 28 de abril de 2017, totalizando 2.875 observações. Os preços foram corrigidos para abril de 2017 pelo Índice Geral de Preços Disponibilidade Interna, IGP-DI/FGV, para a análise comportamental (descritiva). Para a análise empírica, foram utilizadas as séries nominais, uma vez que, segundo Azevedo & Politi (2008)Azevedo, P. F., & Politi, R. B. (2008). Concorrência e estratégias de precificação no sistema agroindustrial do leite. Revista de Economia e Sociologia Rural – RESR, 46(3), 767-802., usar valores reais leva ao aumento da autocorrelação e reduz o poder explicativo do modelo. Além disso, em alguns dos trabalhos pesquisados não se identificaram tratamentos para a correção da inflação, como é o caso de Balcombe et al. (2007)Balcombe, K., Bailey, A., & Brooks, J. (2007). Threshold effects in price transmission: the case of Brazilian wheat, maize and soya prices. American Journal of Agricultural Economics, 89(2), 308-323., Azevedo & Politi (2008)Azevedo, P. F., & Politi, R. B. (2008). Concorrência e estratégias de precificação no sistema agroindustrial do leite. Revista de Economia e Sociologia Rural – RESR, 46(3), 767-802., Sousa & Campos (2008)Sousa, E. P., & Campos, A. C. (2008). Transmissão de preços no mercado brasileiro de soja. In Anais do 46º Congresso Brasileiro de Economia, Administração e Sociologia Rural. Brasília: SOBER. e Silva & Margarido (2009)Silva, J. R., & Margarido, M. A. (2009). Análise da transmissão espacial de preços no mercado de mandioca. Revista de Economia e Administração, São Paulo, 8(4), 464-484..
Portanto, a base de dados foi constituída por nove estados, que no estudo também foram denominados por regiões. Vale destacar que, devido à disponibilidade dos dados, não foi possível incluir o estado do Pará nas análises. Para os estados de Goiás, Mato Grosso do Sul, Mato Grosso, Minas Gerais, Paraná e São Paulo, os preços são aqueles correspondentes aos praticados em suas principais regiões produtoras respectivamente, Goiânia, Campo Grande, Cuiabá, Triângulo Mineiro, Noroeste Paranaense e Araçatuba, conforme metodologia de coleta do CEPEA-ESALQ.
Na análise empírica, as séries foram trabalhadas com seus valores em logaritmo natural (ln), pois, conforme apontado por Shikida et al. (2016)Shikida, C., Paiva, G. L., & Junior, A. F. A. (2016). Análise de quebras estruturais na série do preço do boi gordo no Estado de São Paulo. Economia Aplicada, 20(2), 265-286., esse procedimento é comum na literatura econômica geral e, em específico, aos estudos sobre os preços do boi gordo e, ainda, suavizam a variância da série. No presente estudo, foram escolhidos o período e as regiões de acordo com disponibilidade de dados para os mercados analisados e período de abrangência. Para a estimação dos modelos empíricos de identificação do centro formador de preços e da cointegração espacial na presença dos custos de transferências, utilizou-se o software Stata 12.0 da Statacorp LP.
RESULTADOS E DISCUSSÃO
Tendo em vista as modificações no agronegócio da carne bovina nos últimos anos, como a mudança regional do mercado, o surgimento de novos polos de produção e abate e a conquista de mercados internacionais, este trabalho buscou estudar as possíveis mudanças nos centros formadores de preço do boi gordo em consequência das dinâmicas nos comportamentos dos seus preços.
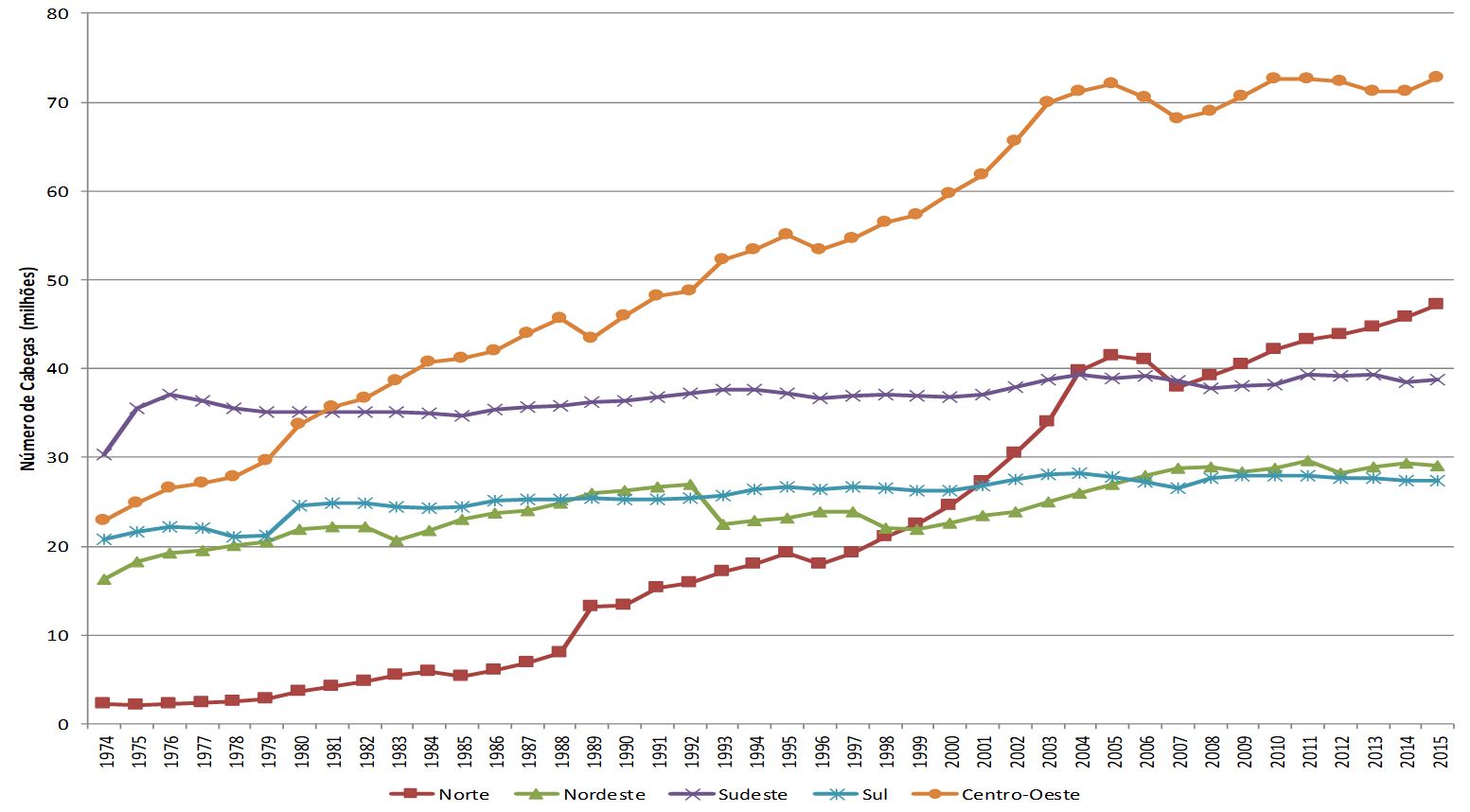
Para maior compreensão da evolução produção de bovinos ao longo do território brasileiro, bem como a inserção do Centro-Oeste e Norte como regiões de destaque, verifica-se no Gráfico 1 a evolução anual do efetivo de rebanho para cada Região em 41 anos.
No Gráfico 1 é possível observar que no início dos anos 1980 o Centro-Oeste desponta na produção de bovinos, momento em que as novas fronteiras agrícolas passam a ser exploradas. O Norte, no início dos anos 1970, apresentava a menor produção brasileira. No entanto, à medida que as terras locais foram exploradas, principalmente nos anos 1990, sua produção teve um expressivo crescimento. Com a elevação na produção, a Região tornou-se a segunda maior produtora de bovinos nos últimos anos, desbancando o Sul e Sudeste e mudando o cenário de produção. Portanto, estudos que analisaram centros formadores de preços em períodos anteriores a 2006, momento em que o Norte se firma como segundo maior produtor, não captaram essa mudança, sendo necessária e justificada uma reavaliação.
Assim, pressupõe-se uma modificação no estoque do boi gordo no Brasil no período em análise. Destaca-se, ainda, que o número de plantas frigoríficas também se modificou ao longo desse período, principalmente nos momentos em que o Centro-Oeste e o Norte despontaram-se na produção de animais para abate. Segundo De Zen & Barros (2005)De Zen, S., & Barros, G. S. C. (2005). Formação de preços do boi, uma perspectiva histórica. Visão Agrícola, 3, 120-122., na década de 1960 os frigoríficos concentravam-se regionalmente em uma única região, que apresentava grande peso na formação dos preços, o estado de São Paulo. No entanto, com a exploração da pecuária ao longo do território brasileiro, atualmente não se identifica apenas um único, mas sim diversos estados com elevada representatividade no número de abates brasileiro.
Conforme dados do IBGE (Instituto Brasileiro de Geografia e Estatística, 2016)Instituto Brasileiro de Geografia e Estatística – IBGE. (2016). Pesquisa trimestral do abate de animais. Rio de Janeiro: IBGE., os estados como Mato Grosso, Minas Gerais e Pará, além de serem os maiores ofertantes de boi, destacam-se também pela quantidade de animais abatidos, representando, respectivamente, 15%, 8% e 9% do total brasileiro em 2016. Além disso, esses estados elevaram seus resultados em 28% (valor médio) entre 2005 e 2016. Já o estado de São Paulo teve uma redução de 37%. Outros estados que também reduziram os seus abates foram Mato Grosso do Sul (queda de 14%) e Paraná (queda de 16%). Vale destacar que os estabelecimentos frigoríficos de São Paulo, bem como os do Rio Grande do Sul, passaram a abater animais com melhores padrões de qualidade, levando a melhores padrões de produção, quando comparados a outros estados.
A presente análise da produção de carne bovina, iniciada com o número de efetivo de rebanho por estado e finalizada com os valores de abate, permitiu concluir que os estados da região Centro-Oeste passaram a dominar tanto a criação de bovinos quanto a quantidade de abate, mostrando a importância da região para o agronegócio do boi, indícios de um novo polo de produção e, consequentemente, possíveis novos centros formadores de preços.
– Evolução dos números de efetivo de bovinos por Regiões brasileiras entre 1974 e 2015. Fonte: IBGE – Pesquisa Pecuária Municipal (Instituto Brasileiro de Geografia e Estatística, 2017Instituto Brasileiro de Geografia e Estatística – IBGE. (2017). Pesquisa pecuária municipal. Rio de Janeiro: IBGE.). Elaboração dos autores.
Vê-se a importância da análise do comportamento dos preços, que pode delimitar os lucros auferidos pelos agentes, auxiliar os pecuaristas nos seus momentos de decisão na produção e venda de animais, bem como apontar as relações entre mercados de diferentes regiões, indicando a existência do mercado comum e o centro formador de preços.
As análises de preços também podem proporcionar uma medida de eficiência de mercados futuros, como, por exemplo, os estudos de Abitante (2008)Abitante, K. G. (2008). Co-integração entre os mercados spot e futuro: evidências dos mercados de boi gordo e soja. Revista de Economia e Sociologia Rural – RESR, 46(1), 75-96. e Bressan & Lima (2002)Bressan, A. A., & Lima, J. E. (2002). Modelos de previsão de preços aplicados aos contratos futuros de boi gordo na BM&F. Nova Economia, 12(1), 117-140., em que o produtor pode utilizar o mercado futuro no intuito de descobrir os preços físicos futuros. Desse modo, Abitante (2008)Abitante, K. G. (2008). Co-integração entre os mercados spot e futuro: evidências dos mercados de boi gordo e soja. Revista de Economia e Sociologia Rural – RESR, 46(1), 75-96. identificou a cointegração de longo prazo entre os mercados futuros e spot do boi gordo, e que contratos futuros com determinados vencimentos podem auxiliar os produtores na determinação dos preços. Já Bressan & Lima (2002)Bressan, A. A., & Lima, J. E. (2002). Modelos de previsão de preços aplicados aos contratos futuros de boi gordo na BM&F. Nova Economia, 12(1), 117-140. apresentaram modelos que devem ser utilizados como ferramenta decisão de compra e venda de contratos futuros de boi gordo na então BM&F, em datas próximas ao vencimento.
Quanto aos estudos sobre a integração espacial envolvendo séries de preços, vale destacar o estudo de Cunha et al. (2010)Cunha, D. A., Lima, J. E., & Braga, M. J. (2010). Integração espacial do mercado brasileiro de boi Gordo: uma análise de cointegração com Threshold. Análise Econômica, 28(53), 251-267., no qual os autores estimaram um modelo com a presença dos custos de transferência com a metodologia de cointegração com threshold para os modelos Autorregressivos TAR e M-TAR, para o Sul, Sudeste e Centro-Oeste. Tendo o estado de São Paulo como o centro formador de preços, verificaram que Minas e Mato Grosso do Sul, por possivelmente estarem mais próximos do centro formador, apresentaram coeficiente mais elevados na transmissão de preços. O Rio Grande do Sul não se cointegra com São Paulo. Os custos de transferência foram significativos, uma vez que não existiram transferências para choques de baixas magnitudes entre Mato Grosso, Rio de Janeiro, Goiás, Santa Catarina e o centro formador, podendo-se afirmar que os ajustes seriam superiores aos ganhos. Os autores identificaram baixos valores para os threshold, o que indica os custos de transferências não geram grandes impedimentos à integração dos mercados.
Por fim, ainda é possível apontar os estudos que abordaram os comportamentos dos preços com o objetivo de se identificar possíveis assimetrias nas relações comerciais entre os agentes da cadeia produtiva do boi gordo, ou seja, pecuaristas, frigoríficos e supermercado como o de Urso (2007)Urso, F. S. P. (2007). A cadeia da carne bovina no Brasil: uma análise de poder de mercado e teoria da informação (Tese de doutorado). Fundação Getúlio Vargas, São Paulo.. Desse modo, a autora verificou a existência de poder de mercado dos frigoríficos na aquisição de boi gordo, poder de barganha dos supermercados junto aos frigoríficos e a existência assimetria de informação entre os participantes do mercado futuro de boi gordo da BM&F.
Portanto, dada essa riqueza de informações que as análises dos preços podem proporcionar, buscou-se primeiramente analisar seu comportamento entre as principais praças de comercialização do Brasil, ou seja, Rondônia, Tocantins, Goiás, Mato Grosso, Mato Grosso do Sul, Minas Gerais, São Paulo, Paraná e Rio Grande do Sul. Os resultados do Gráfico 2 ilustram as diferentes relações de preços do boi gordo nas distintas regiões do período de estudo.
– Preços reais do boi gordo entre as principais regiões produtoras de 2006 a 2017 Fonte: Resultados da pesquisa com dados fornecidos pelo CEPEA/ESALQ (Centro de Estudos Avançados em Economia Aplicada, 2017Centro de Estudos Avançados em Economia Aplicada – Cepea, Economia, Administração e Sociologia da Escola Superior de Agricultura “Luiz de Queiroz”. (2017) Dados diários preço do boi gordo. CEPEA).
A análise conjunta dos preços indicou mudanças nos comportamentos das séries, no que se refere aos diferenciais de preços entre as praças. Conforme se verifica no Gráfico 2, tanto no início quanto no final do conjunto de séries figurou maior dispersão dos dados. Desse modo, tal informação a priori indica a aplicação do teste Chow, com a finalidade de confirmar se tais mudanças dos diferenciais entre os preços foram consequências de choques exógenos, que por sua vez levaram a alguma quebra estrutural conjunta dos preços. Dado que tais comportamentos são observados em dois momentos distintos, sendo uma no início e outra ao final da série, a expectativa sobre o teste é de que o conjunto de dados apresente dois pontos de quebras estruturais.
Como os diferenciais de preços são menores entre os anos de 2009 e 2014, esses períodos foram utilizados como as possíveis datas de quebra. Desse modo, identificaram-se os possíveis fatores exógenos capazes de alterar o comportamento entre os preços em cada momento, ou seja, um fator para o ano de 2009 e outro para 2014.
Desse modo, 2009, além de ser um momento reflexos da crise de 2007/2008, foi o ano da fusão das empresas JBS e Bertin. Portanto, esse cenário de fusões e aquisições entre as grandes empresas pode levar ao amento da concentração do setor, distanciando o mercado da concorrência e, conforme apontado por Goodwin & Schroeder (1991)Goodwin, B. K., & Schroeder, T. C. (1991). Cointegration tests and spatial price linkages in regional cattle markets. American Journal of Agricultural Economics, 73(2), 452-464., em mercados mais concentrados os preços são mais estáveis e a cointegração espacial entre mercados pode aumentar.
Soares & Lopes (2015)Soares, T. C., & Lopes, L. S. (2015). Quebras estruturais sistêmicas e efeito threshold na dinâmica dos preços do boi gordo: o caso das regiões Sudeste e Centro-Oeste. Revista de Economia e Sociologia Rural, 53(2), 343-360., ao estudarem quebras estruturais pela abordagem proposta por Qu e Perron (2007)Qu, Z., & Perron, P. (2007). Estimating and testing structural changes in Multivariate regressions. Econometrica, 75(2), 459-502. no mercado do boi gordo entre o Sudeste e Centro-Oeste, identificaram uma quebra estrutural no início de 2007 e a justificaram como consequência da crise financeira internacional. No entanto, visto que o presente estudo aborda outras regiões e a importância dessas fusões, optou-se por manter o teste da quebra no início de 2009.
Quanto ao ano de 2014, esse teve seu início marcado por uma das maiores secas dos últimos períodos, proporcionando uma restrição na oferta de bovinos, principalmente nos estados das regiões Centro-Oeste e Sul, e o consequente aumento nos preços. Assim, a queda na produção reduz os excessos exportáveis que possibilitam a aplicação da LPU. Em suma, a possível causa para a redução dos diferenciais de preços, das praças em análise, iniciados em meados do ano 2009, foi o aumento da concentração do setor, e a justificativa para o aumento dos diferenciais iniciados em 2014 foi a redução no volume de produção em consequência da restrição hídrica.
Portanto, o teste de quebra estrutural foi realizado para confirmar estatisticamente se as mudanças proporcionadas pela fusão dos dois maiores frigoríficos em 2009 e o impacto climático vivenciado no final de 2013 e início de 2014 foram capazes de alterar o comportamento dos preços. O teste de Chow indicou uma quebra estrutural conjunta no início do ano de 2009 e outra início de 2014 (Tabela 1)
Conforme exposto na Tabela 1, as análises devem considerar três períodos: o período I, do início da série até a primeira quebra no início do ano de 2009 (nI=745), o período II, compreendido entre as duas quebras (nII=1262), e o período III, com início em janeiro de 2014 e fim em 28 de abril de 2017 (nIII=868). Com isso, as análises poderão captar as distintas relações entre os preços ao longo da série, ou seja, de valores mais correlacionados no período II (menores diferenciais de base) e menos correlacionados (maiores diferenciais de base) nos períodos I e III.
Verificou-se que mudanças estruturais da cadeia produtiva do boi gordo e eventos climáticos de alta intensidade foram capazes de alterar o comportamento dos preços dos produtos. Cabe então verificar se tais quebras também proporcionaram diferentes formas de organização de mercados e centros formadores de preços.
O estudo empírico sobre a identificação do mercado comum inicia-se com o teste de estacionariedade das séries, seguido pelo teste cointegração de Johansen, para identificação do mercado comum da carne bovina e o teste de exogeneidade fraca para detecção do centro formador de preços.
Segundo Enders (2004)Enders, W. (2004). Applied econometric times series (p. 429). England: John Wiley & Sons., três expressões são utilizadas para a aplicação do teste de raiz unitária; nesse caso, o Dickey-Fuller Aumentado. A diferença entre elas está na presença dos parâmetros determinísticos, intercepto e tendência. A primeira é definida como um passeio aleatório puro (τ), na segunda é adicionada o intercepto (τµ) e a terceira inclui o intercepto e tendência linear (ττ). Os resultados dos testes em suas três especificações são apresentados na Tabela 2.
A análise da Tabela 2 para o teste de raiz unitária de Dickey-Fuller Aumentado (ADF) apontou que as séries são não estacionárias em nível e estacionárias nas primeiras diferenças. Significa dizer que são integradas de ordem 1, ou seja, I(1).
Uma vez identificadas as estacionariedades das séries, cabe verificar a existência de mercado comum entre as principais regiões produtoras de boi gordo e se esse mercado se altera em cada período em análise. Assim como feito por González-Rivera & Helfand (2001)González-Rivera, G., & Helfand, S. M. (2001). The extent, pattern, and degree of market integration: a multivariate approach for the brazilian rice market. American Journal of Agricultural Economics, 3(83), 576-592., e posteriormente por Asche et al. (2012)Asche, F., Gjoberg, O., & Guttormsen, A. G. (2012). Testing the central market hypothesis: a multivariate analysis of Tanzanian sorghum markets. Agricultural Economics, 1, 1-9., Mattos et al. (2010)Mattos, L. B. de; Lirio, V. S.; Lima, J. E. de; Campos, A. C. (2010) Uma aplicação de modelos TAR para o mercado de carne de frango no Brasil. EconomiA, 11(3), 537-557 e Pereira (2005)Pereira, L. R. R. (2005). Integração espacial no mercado do boi gordo (Tese de doutorado). Universidade Federal de Viçosa, Viçosa., buscou-se encontrar o único fator comum para o conjunto de regiões, ou seja, os n-1 vetores de cointegração para os n=9 mercados em análise. São apresentados na Tabela 3 os resultados do teste de cointegração de Johansen, em suas aplicabilidades, Traço e λ máxima, para a identificação dos vetores de cointegração.
Os resultados da Tabela 3 apontam para o período I apenas três relações de cointegração, ano nível de 5% de significância na aplicabilidade Traço e 2 para λ máximo, para as nove regiões em análise. Já no período II, o teste Traço apontou sete relações de cointegracão e o de λ máximo oito. Visto que a literatura emprega mais o teste Traço, por exemplo, os estudos sobre os preços do boi gordo de Sachs & Pinatti (2007)Sachs, R. C. C., & Pinatti, E. (2007). Análise do comportamento dos preços do boi gordo e do boi magro na pecuária de corte paulista, no período de 1995 a 2006. Revista de Economia e Agronegócio, 5(3), 329-352., Campos et al. (2008)Campos, S. K., Silva, A. F., Costa, J. S., & Zilli, J. B. (2008). Análise da cointegração e causalidade dos preços de boi gordo em diferentes praças nas regiões Sudeste e Centro-oeste do Brasil. In Anais do XLVI Congresso da SOBER. Brasília: SOBER. Recuperado em 19 de abril de 2017, de https:// www.sober.org.br, Pitelli (2008)Pitelli, M. M. (2008) Testes de preços para a determinação do mercado relevante geográfico e de produto: uma aplicação empírica ao mercado brasileiro de compra de bovinos (Tese de Doutorado). Escola Superior de Agricultura Luiz de Queiroz, Piracicaba., Melo (2010)Melo, G. B. (2010). Integração entre os mercados de boi para abate na Argentina e no Brasil (Dissertação). Escola Superior de Agricultura Luiz de Queiroz, Piracicaba., Santos & Silva Neto (2012)Santos, H. D., & Silva Neto, A. S. N. (2012). Relação de longo prazo entre os preços do produtor e do varejo da carne bovina em Goiás. Goiânia: UFG/NEPEC/FACE. e Oliveira & Procópio (2016)Oliveira, D. B. O., & Procópio, D. P. (2016). Interdependência e formação dos preços de boi gordo nos estados de Mato Grosso, Mato Grosso do Sul e Goiás no período de 1980 a 2015. In Anais do 54° Congresso da SOBER - Sociedade Brasileira de Economia, Administração e Sociologia Rural. Brasília: SOBER., optou-se por considerar esse último resultado. Portanto, para o período I constatou-se que quatro regiões pertencem ao mercado comum, e no período II, oito, ou seja, apenas uma não pertenceu ao mercado comum.
Já no período III verificaram-se cinco relações de cointegração para as regiões em análise em ambas as aplicabilidades dos testes. Assim, para cada período verificou-se um determinado mercado comum, cabendo então identificar quais foram os respectivos estados. São apontados na Tabela 4 os resultados dos números de vetores de cointegração entre as regiões analisadas.
– Número de relações de cointegração entre as regiões analisadas conforme a aplicabilidade Traço
Objetivando encontrar as quatro regiões pertencentes ao mercado comum do período I, iniciaram-se os testes de exclusão das regiões possivelmente menos integradas, assim como feito por González-Rivera & Helfand (2001)González-Rivera, G., & Helfand, S. M. (2001). The extent, pattern, and degree of market integration: a multivariate approach for the brazilian rice market. American Journal of Agricultural Economics, 3(83), 576-592., e os demais estudos sobre mercado central. Nesse caso, a primeira exclusão foi o Rio Grande do Sul, por ser uma região com características de consumo e venda locais, que por sua vez não alterou o resultado do teste, indicando que o estado não pertence ao mercado comum. Posteriormente, optou-se por retirar o Paraná, por pertencer à mesma região, e os resultados também não se alteraram. O mesmo procedeu-se para os estados da região Norte, Tocantins e Rondônia. Então, pode-se inferir que no primeiro período os estados do Norte e Sul não pertencem ao mercado comum da série.
Por fim, buscou-se testar a relação de cointegração entre as regiões do Centro-Oeste e Sudeste e, dentre os cinco estados em análise, apenas a exclusão do Mato Grosso não alterou o número de três vetores de cointegração. Então, o resultado indicou que as regiões pertencentes ao mercado comum para o período I foram São Paulo, Minas Gerais, Goiás e Mato Grosso do Sul.
Como apenas uma região não pertenceu ao mercado comum do período II, uma vez que o número de vetores de cointegração foi 7, iniciou-se novamente a exclusão pelo estado do Rio Grande do Sul e a relação se manteve. Além disso, não foi possível retirar nenhum outro estado sem que o número de vetores reduzisse. Portanto, o mercado comum do período II foi composto pelos estados do Norte, Centro-Oeste, Sudeste e Paraná.
Em relação ao período III, a busca foi por seis regiões pertencentes ao mesmo mercado comum. Nesse caso, não foi possível retirar o Rio Grande do Sul do modelo sem que se alterasse o número de vetores de cointegração. Então, optou-se por excluir o Paraná, outro estado da região Sul, e nesse caso o número de vetores de cointegração se manteve. Posteriormente, optou-se em eliminar os estados do Norte, em que foi possível apenas retirar Tocantins sem alterar o resultado. Consequentemente, o primeiro indício foi que o Rio Grande do Sul e o Tocantins pertencem ao mesmo mercado comum. Dentre as cinco outras regiões (Mato Grosso, Mato Grosso do Sul, Goiás, São Paulo e Minas Gerais), optou-se por testar a exclusão de Goiás, por acreditar que Mato Grosso e Mato Grosso do Sul e São Paulo e Minas Gerais são pares de mercados que apresentam características mais próximas. Assim, verificou-se que a exclusão de Goiás não alterou o resultado do teste, e o mercado comum do período III foi composto por Mato Grosso, Mato Grosso do Sul, Minas Gerais, São Paulo, Rondônia e Rio Grande do Sul.
Os resultados do teste de cointegração indicaram que as quebras estruturais nas séries de preços do boi gordo afetaram a formação do mercado comum, uma vez que no período I foi formado por São Paulo, Mato Grosso do Sul, Goiás e Minas Gerais. No período II, o mercado comum se expandiu, abrangendo oito regiões e, por fim, no período III, o mercado comum se reduziu, sendo formado por seis regiões.
Ao se analisar os volumes de abates, conforme Pesquisa Trimestral do Abate de Animais - IBGE (Instituto Brasileiro de Geografia e Estatística, 2016Instituto Brasileiro de Geografia e Estatística – IBGE. (2016). Pesquisa trimestral do abate de animais. Rio de Janeiro: IBGE.), verificou-se que no Período II os volumes de abates apresentam tendência de crescimento, ou seja, período com os menores diferenciais nos preços. Nesse caso, sugere-se que, em momentos de queda no volume de abate, as regiões passam a seguir o próprio mercado, reduzindo o número de estados pertencentes ao mercado comum e, nos momentos de alta, as regiões seguem o centro formador de preços, confirmando o resultado dos tamanhos dos mercados comuns obtidos nas relações de cointegração.
Portanto pode-se concluir que, nos momentos em que os preços praticados nas praças são mais próximos, o mercado comum se expande, como foi o caso do Período II e, à medida que se distanciam, seu tamanho diminui, como no Período III e no Período I. Desse modo, os fatores exógenos, como a estrutura de mercado e restrição hídrica, interferem nessa dinâmica de preços e, consequentemente, no tamanho dos mercados comuns. Vale destacar que os resultados obtidos pelo modelo empírico estão em conformidade com a Lei do Preço Único.
Então, cabe identificar quais seriam os possíveis centros formadores de preços para os mercados comuns dos períodos I, II e III por meio do teste de Exogeneidade Fraca. Os resultados estão na Tabela 5.
– Teste de Exogeneidade Fraca para os estados pertencentes ao mercado comum dos períodos I e II
Conforme se observa na Tabela 5, a hipótese nula de que a região não é influenciada pelas demais no longo prazo foi rejeitada para apenas um estado em cada período em análise, em nível usual de significância estatística de 1%, indicando um único centro formador de preços para cada período. O período I foi o que apresentou a região fracamente exógena com maior probabilidade estatística, ou seja, com probabilidade 68% de São Paulo não ser influenciado pelas demais regiões do mercado comum do período I no longo prazo. Este resultado está de acordo com aqueles encontrados nos estudos de Pereira (2005)Pereira, L. R. R. (2005). Integração espacial no mercado do boi gordo (Tese de doutorado). Universidade Federal de Viçosa, Viçosa. e Filgueiras et al. (2006)Filgueiras, G. C., Quieroz, J. C. B., Santos, R. B., Diniz, M. B., & Diniz, M. J. T. (2006). Causalidade de preço do mercado de carne de boi gordo para seis estados brasileiros, 1994 a 2003. In Congresso da Sociedade Brasileira de Economia e Sociologia Rural (Vol. 44). Brasília: SOBER., de que São Paulo era centro formador de preços do mercado bovino de corte no Brasil, ou seja, estudos que contemplaram uma base de dados anterior ao Período I.
No entanto, para os períodos II e III, a única probabilidade estatisticamente significativa para exogeneidade fraca foi a do Mato Grosso do Sul, com 1,004% no Período II e 3,250% no Período III. Logo, essa estatística leva ao indício de que após a fusão entre Bertin e JBS e a crise financeira internacional, São Paulo deixa de ser um forte centro formador de preços e o mercado passa a ter uma nova referência, o Mato Grosso do Sul, porém com probabilidade estatística inferior.
Esses resultados se aproximam, mas trazem resultados mais robustos que os obtidos pela metodologia apontada por Mattos (2008)Mattos, L. B. (2008). Efeitos de custos de transação sobre a integração espacial de mercados regionais de carne de frango no Brasil (Tese de doutorado). Universidade Federal de Viçosa, Viçosa., que escolhe mercados com os maiores volumes de comercialização como os formadores de preços. São Paulo, ao se destacar como o segundo estado com maior abate de bovino entre os anos de 2005 e 2009, foi o centro formador de preços do Período I. No Período II, entre 2009 e 2014, Mato Grosso do Sul passa a ter o segundo maior volume abatido, perdendo apenas para Mato Grosso, sendo então o novo centro formador. No Período III, Mato Grosso do Sul mantém o segundo maior valor de cabeças abatidas e a posição centro formador de preços.
Portanto, ficou evidente que a indústria de abate de bovinos passou por mudanças estruturais, tornando-se mais oligopolizada em alguns estados e com maior concorrência em outros. Além disso, vale destacar a compra do frigorífico Bertin pela JBS e os incentivos do BNDES aos grandes frigoríficos em meados de 2009, que estimularam a primeira quebra estrutural conjunta do período em análise e, supostamente, ajudaram a explicar as mudanças do centro formador de preços e dos componentes do mercado comum.
Desse modo, Mato Grosso do Sul, região em que o grupo JBS apresentou uma das maiores fatias de mercado no período em análise (cerca de 34%), passou a ser o novo centro formador de preços e com o maior mercado comum no momento da elevação do abate (Período II). No entanto, a queda na oferta de bois e do abate, em consequência da seca de 2013/2014, diminuiu a capacidade do Mato Grosso do Sul em influenciar os preços das demais regiões produtoras, reduzindo o mercado comum e a integração. Portanto, pode-se concluir que choques estruturais no comportamento dos preços do boi gordo nas diferentes regiões em análise alteraram os integrantes do mercado comum e o centro formador.
Portanto, essa análise permitiu concluir que o mercado do boi gordo no Brasil sofreu mudança regional e estrutural, apresentando novos polos de produção e abate e, consequentemente, um novo centro formador de preços.
4. CONCLUSÕES
A presente pesquisa traz como inovação acadêmica a aplicação da metodologia do mercado comum juntamente do teste de quebra estrutural, pois se presume uma modificação no centro formador de preços em consequência dos diversos choques exógenos pelos quais a pecuária bovina passou nos últimos dez anos. Por exemplo, a crise financeira internacional de 2007/2008, fusão entre os frigoríficos Bertin e JBS, internacionalização das indústrias frigoríficas, restrição hídrica nos anos de 2013/2014 e até mesmo a crise política e econômica iniciada em 2014 no Brasil.
Assim, o estudo iniciou-se com a hipótese de que mudanças estruturais e espaciais na produção interferiram no mercado do boi gordo, modificando o mercado comum e o centro formador de preços. Desse modo, a presente pesquisa busca verificar possíveis mudanças nos centros formadores de preço do boi gordo em consequência das dinâmicas nos comportamentos dos seus preços. Os objetivos específicos da pesquisa foram testar a presença de quebras estruturais; delimitar espacialmente o mercado do boi no Brasil e identificar os centros formadores de preços. Com isso, pode auxiliar os tomadores de decisão públicos e privados de toda a cadeia produtiva.
Por meio do teste de quebra estrutural de Chow foi possível verificar duas quebras estruturais conjuntas, uma no início do ano de 2009 e outra no final de 2013, que dividiram a pesquisa em três distintos períodos: o Período I, do início da série até a primeira quebra no início do ano de 2009, o Período II, compreendido entre as duas quebras, e o Período III, com início em janeiro de 2014 e fim em 28 de abril de 2017.
Os resultados dos testes empíricos para o Período I apontaram São Paulo como o centro formador de preços e um mercado comum com apenas quatro regiões produtoras, sendo elas Mato Grosso do Sul, Minas Gerais, Goiás e São Paulo. O Período II apresentou mudanças nos resultados dos testes empíricos verificados. Mato Grosso do Sul tornou-se o novo centro formador de preços, e o mercado comum formou-se por esta região mais outras sete (Goiás, Rondônia, Tocantins, Mato Grosso, Paraná, São Paulo e Minas Gerais). Portanto, essa evidência indicou que uma mudança estrutural no mercado do boi gordo alterou o centro formador de preços.
Por fim, para o Período III, o mercado comum se reduziu, englobando Mato Grosso do Sul, Mato Grosso, Rondônia, Rio Grande do Sul, São Paulo e Minas Gerais, com Mato Grosso do Sul mantendo-se como o centro formador de preços. Nesse caso, novamente, um novo choque exógeno modificou o comportamento do mercado.
Assim, foi possível confirmar a hipótese central de que mudanças estruturais e espaciais na produção interferiram na integração espacial do boi gordo, modificando o mercado comum, o centro formador de preços. Visto que a identificação do mercado central melhora a eficiência das assistências públicas ao setor e direcionam as políticas públicas voltadas para a melhoria no fluxo de comércio entre regiões, pode-se concluir que os resultados encontrados são de grande relevância para a sociedade. Portanto, a identificação de um novo centro formador e diferentes mercados comuns auxilia a formulação de instrumentos de políticas públicas, pois nesse caso sinaliza-se um novo canal pelo qual se deve direcionar os recursos, para que assim a sociedade possa se beneficiar dos efeitos de transbordamentos para os mercados secundários, promovendo dessa maneira a alocação eficiente dos recursos escassos.
As principais limitações do trabalho estão inicialmente relacionadas à indisponibilidade de séries de preços de todos os estados brasileiros, em especial, o Pará. Outra limitação sustenta-se no fato de que a base de dados de alguns estados é formada pelos preços de apenas uma de suas principais praças, como é o caso do Mato Grosso do Sul e São Paulo. Como o mercado do boi gordo está em constante mudança e alterações regionais, e mudanças estruturais interferem no mercado comum, sugere-se a replicação desse estudo para os próximos anos, com a finalidade de se explorar o período atual pelo qual a pecuária está passando, bem como o comportamento dos preços de praças não abordadas.
-
1
Quanto mais perfeito for um mercado, existirá forte tendência para que um mesmo preço seja pago pelo produto ao mesmo tempo e em todas as partes de um mercado (Marshall, 1980Marshall, A. (2009) Principles of economics: unabridged eight edition. New York: Cosimo.). Assim, na ausência dos custos de transação, os mercados regionais com o mesmo comércio apresentarão um único preço.
-
2
Ravallion (1986)Ravallion, M. (1986). Testing market integration. American Journal of Agricultural Economics, 68(1), 102-109. assume os mercados locais como aqueles secundários, os quais podem transacionar entre si. Porém, é na transação com o mercado central que se definirá a formação dos preços no mercado local. Dependendo do número de mercados locais e seus tamanhos, pode-se verificar a influência de diversos mercados locais no preço do central.
-
Como citar: Pancera, A. Q. A. A., & Alves, A. F. (2020). Testando a hipótese do mercado central: uma análise dos preços do boi gordo na presença de quebras estruturais. Revista de Economia e Sociologia Rural, 58(4), e206751. https://doi.org/10.1590/1806-9479.2020.206751
-
JEL Classification: B23, C10, Q13 e L19
REFERÊNCIAS
- Abitante, K. G. (2008). Co-integração entre os mercados spot e futuro: evidências dos mercados de boi gordo e soja. Revista de Economia e Sociologia Rural – RESR, 46(1), 75-96.
- Andrews, D. W. K. (1993). Tests for parameter instability and structural change with unknown change point. Econometrica, 61(4), 821-856.
- Andrews, D. W. K. (1994). Optimal tests when a nuisance parameter is present only under the alternative. Econometrica, 62(6), 1383-1414.
- Asche, F., Gjoberg, O., & Guttormsen, A. G. (2012). Testing the central market hypothesis: a multivariate analysis of Tanzanian sorghum markets. Agricultural Economics, 1, 1-9.
- Azevedo, P. F., & Politi, R. B. (2008). Concorrência e estratégias de precificação no sistema agroindustrial do leite. Revista de Economia e Sociologia Rural – RESR, 46(3), 767-802.
- Bai, J., & Perron, P. (1998). Estimating and testing linear models with multiple structural changes. Econometrica, 66, 47-78.
- Bai, J., & Perron, P. (2003). Computation and analysis of multiple structural change models. Journal of Applied Econometrics, 18, 1-22.
- Balcombe, K., Bailey, A., & Brooks, J. (2007). Threshold effects in price transmission: the case of Brazilian wheat, maize and soya prices. American Journal of Agricultural Economics, 89(2), 308-323.
- Bressan, A. A., & Lima, J. E. (2002). Modelos de previsão de preços aplicados aos contratos futuros de boi gordo na BM&F. Nova Economia, 12(1), 117-140.
- Campos, S. K., Silva, A. F., Costa, J. S., & Zilli, J. B. (2008). Análise da cointegração e causalidade dos preços de boi gordo em diferentes praças nas regiões Sudeste e Centro-oeste do Brasil. In Anais do XLVI Congresso da SOBER Brasília: SOBER. Recuperado em 19 de abril de 2017, de https:// www.sober.org.br
- Centro de Estudos Avançados em Economia Aplicada – Cepea, Economia, Administração e Sociologia da Escola Superior de Agricultura “Luiz de Queiroz”. (2017) Dados diários preço do boi gordo CEPEA
- Chow, G. C. (1960). Tests of equality between sets of coefficients in two linear regressions. Econometrica, 28(3), 591-605.
- Cleveland, R. B., Cleveland, W. S., McRae, J. E., & Terpenning, I. (1990). STL: A seasonal-trend decomposition procedure based on loess. Journal of Official Statistics, 6, 3-73.
- Cunha, D. A., Lima, J. E., & Braga, M. J. (2010). Integração espacial do mercado brasileiro de boi Gordo: uma análise de cointegração com Threshold. Análise Econômica, 28(53), 251-267.
- Cysne, R. P.,, Issler, J. V., Lima, L. R. R. O, Hostalácio, H. (2009). Impacto do PIS e da COFINS na inflação: uma abordagem econométrica usando o teste de janela variável. Economia Aplicada, 13(2), 185-206.
- De Zen, S. (1997). Integração entre os mercados de boi gordo e de carne bovina nas regiões centro-oeste e sudeste do Brasil (Dissertação de mestrado). Escola Superior de Agricultura “Luiz de Queiroz”, Piracicaba.
- De Zen, S., & Barros, G. S. C. (2005). Formação de preços do boi, uma perspectiva histórica. Visão Agrícola, 3, 120-122.
- Enders, W. (2004). Applied econometric times series (p. 429). England: John Wiley & Sons.
- Fackler, P. L., & Goodwin, B. K. (2001). Spatial price analysis. In B. L. Gardner & G. C. Rausser (Eds.), Handbook of agricultural economics (Vol. 1, Part B, chap. 1, pp. 972-1018). North-Holland: Elsevier.
- Faminow, M. D., & Benson, B. L. (1990). Integration of Spatial Markets. American Journal of Agricultural Economics, 72(1), 49-62.
- Filgueiras, G. C., Quieroz, J. C. B., Santos, R. B., Diniz, M. B., & Diniz, M. J. T. (2006). Causalidade de preço do mercado de carne de boi gordo para seis estados brasileiros, 1994 a 2003. In Congresso da Sociedade Brasileira de Economia e Sociologia Rural (Vol. 44). Brasília: SOBER.
- Gaio, L. E., Castro Júnior, L. G., & Oliveira, A. R. (2005). Causalidade e elasticidade na transmissão de preço do boi gordo entre regiões do Brasil e a Bolsa de Mercadorias & Futuros (BM&F). Organizações Rurais & Agroindustriais, 7(3), 282-297.
- González-Rivera, G., & Helfand, S. M. (2001). The extent, pattern, and degree of market integration: a multivariate approach for the brazilian rice market. American Journal of Agricultural Economics, 3(83), 576-592.
- Gonzalo, J., & Granger, C. W. J. (1995). Estimation of Common LongMemory Components in Cointegrated Systems. Journal of Business & Economic Statistics, 13, 27-36.
- Goodwin, B. K., & Schroeder, T. C. (1991). Cointegration tests and spatial price linkages in regional cattle markets. American Journal of Agricultural Economics, 73(2), 452-464.
- Gujarati, D. (2006). Econometria Básica (4. ed., Tradução de Maria José Cyhlar Monteiro, 812 p.) Rio de Janeiro: Elsevier.
- Hansen, B. (1997). Approximate asymptotic p values for structural-change tests. Journal of Business & Economic Statistics, 15(0), 60-67.
- Hansen, B. E. (2001). The new econometrics of structural change: dating breaks in U.S. labor productivity. The Journal of Economic Perspectives, 15(4), 117-128.
- Haywood, J., & Randall, J. (2008) Trending seasonal data with multiple structural breaks. NZ visitor arrivals and the minimal effects of 9/11. In: Research report 08/10. University of Wellington, Victoria, New Zealand, 26 p.
- Instituto Brasileiro de Geografia e Estatística – IBGE. (2016). Pesquisa trimestral do abate de animais Rio de Janeiro: IBGE.
- Instituto Brasileiro de Geografia e Estatística – IBGE. (2017). Pesquisa pecuária municipal Rio de Janeiro: IBGE.
- Johansen, S. (1988). Statistical analysis of cointegration vectors. Journal of Economic Dynamics & Control, 12(1), 231-254.
- Johansen, S. (1995). Identifying restrictions of linear equations with applications to simultaneous equations and cointegration. Journal of Econometrics, 69, 111-132.
- Johansen, S., & Juselius, K. (1994). Identification of the long-run and the short-run structure: an application to the IS-LM model. Journal of Econometrics, 54, 159-178.
- Lafranco, B. A., Ferraro, B., & Rostán, F. (2015). Beef Cattle in the MERCOSUR bloc: Integrated or Separate Markets? In Proceedings of the 29th International Conference of Agricultural Economists USA: IAAE.
- Lanne, M., & Lütkepohl, H. (2002). Unit root tests for time series with level shifts: a comparison of different proposals. Economics Letters, 75, 109-114.
- Macaulay, F. R. (1931). The Smoothing of Time Series. New York: National Bureau of Economic Research.
- Margarido, M. A. (2012). Análise da transmissão espacial de preços no mercado internacional de soja. Revista de Economia e Administração, São Paulo, 11(3), 281-303.
- Marshall, A. (2009) Principles of economics: unabridged eight edition. New York: Cosimo.
- Mattos, L. B. (2008). Efeitos de custos de transação sobre a integração espacial de mercados regionais de carne de frango no Brasil (Tese de doutorado). Universidade Federal de Viçosa, Viçosa.
- Mattos, L. B. de; Lirio, V. S.; Lima, J. E. de; Campos, A. C. (2010) Uma aplicação de modelos TAR para o mercado de carne de frango no Brasil. EconomiA, 11(3), 537-557
- Melo, G. B. (2010). Integração entre os mercados de boi para abate na Argentina e no Brasil (Dissertação). Escola Superior de Agricultura Luiz de Queiroz, Piracicaba.
- Oliveira, D. B. O., & Procópio, D. P. (2016). Interdependência e formação dos preços de boi gordo nos estados de Mato Grosso, Mato Grosso do Sul e Goiás no período de 1980 a 2015. In Anais do 54° Congresso da SOBER - Sociedade Brasileira de Economia, Administração e Sociologia Rural Brasília: SOBER.
- Organisation for Economic Co-opetation and Development – OCDE, & Food and Agriculture Organization of United Nation – FAO. (2015). Agricultural outlook Paris: OCDE.
- Pereira, L. R. R. (2005). Integração espacial no mercado do boi gordo (Tese de doutorado). Universidade Federal de Viçosa, Viçosa.
- Pitelli, M. M. (2008) Testes de preços para a determinação do mercado relevante geográfico e de produto: uma aplicação empírica ao mercado brasileiro de compra de bovinos (Tese de Doutorado). Escola Superior de Agricultura Luiz de Queiroz, Piracicaba.
- Qu, Z., & Perron, P. (2007). Estimating and testing structural changes in Multivariate regressions. Econometrica, 75(2), 459-502.
- Quandt, R. (1960). Tests of the hypothesis that a linear regression obeys two separate regimes. Journal of the American Statistical Association, 55(0), 324-330.
- Ravallion, M. (1986). Testing market integration. American Journal of Agricultural Economics, 68(1), 102-109.
- Sachs, R. C. C., & Pinatti, E. (2007). Análise do comportamento dos preços do boi gordo e do boi magro na pecuária de corte paulista, no período de 1995 a 2006. Revista de Economia e Agronegócio, 5(3), 329-352.
- Santos, H. D., & Silva Neto, A. S. N. (2012). Relação de longo prazo entre os preços do produtor e do varejo da carne bovina em Goiás. Goiânia: UFG/NEPEC/FACE.
- Schwarz, G. (1978). Estimating the dimension of a model. Annals of Statistics, 6, 461-464.
- Shikida, C., Paiva, G. L., & Junior, A. F. A. (2016). Análise de quebras estruturais na série do preço do boi gordo no Estado de São Paulo. Economia Aplicada, 20(2), 265-286.
- Silva Neto, W. A., Fraga, G. J., & Marques, P. V. (2010). Eficiência de mercado: evidências empíricas para os preços spot e futuro de boi gordo. Revista de Economia, 36(3), 7-24.
- Silva, J. R., & Margarido, M. A. (2009). Análise da transmissão espacial de preços no mercado de mandioca. Revista de Economia e Administração, São Paulo, 8(4), 464-484.
- Soares, T. C., & Lopes, L. S. (2015). Quebras estruturais sistêmicas e efeito threshold na dinâmica dos preços do boi gordo: o caso das regiões Sudeste e Centro-Oeste. Revista de Economia e Sociologia Rural, 53(2), 343-360.
- Sousa, E. P., & Campos, A. C. (2008). Transmissão de preços no mercado brasileiro de soja. In Anais do 46º Congresso Brasileiro de Economia, Administração e Sociologia Rural Brasília: SOBER.
- Urso, F. S. P. (2007). A cadeia da carne bovina no Brasil: uma análise de poder de mercado e teoria da informação (Tese de doutorado). Fundação Getúlio Vargas, São Paulo.
- Zilli, J. B., Silva, A. F., Campos, S. K., & Costa, J. S. (2008). Análise da cointegração e causalidade dos preços de boi gordo em diferentes praças nas regiões Sudeste e Centro-Oeste do Brasil. Revista de Economia Agrícola, 55(2), 105-119.
Datas de Publicação
-
Publicação nesta coleção
24 Ago 2020 -
Data do Fascículo
2020
Histórico
-
Recebido
05 Jul 2018 -
Aceito
03 Nov 2019