ABSTRACT:
Intake is a multifactorial process that is influenced by animal type, environmental factors, and diet characteristics. Sheep, especially, have specific eating habits, with a greater selection of ingested feed compared to cattle. Thus, predictive equations for dry matter intake (DMI) must constantly be reviewed. The objective of this study was to combine different adjustment factors to develop one continuous adjustment factor for predicting the DMI of pregnant, dry, and lactating ewes. The equations evaluated for non-lactation ewes accounts for metabolic body weight and weight gain, and the equation for lactating ewes includes milk production and its fat content. The database used in this study was pooled from hair sheep ewes, two to four years old, with controlled feeding, during the pregnancy and lactating physiological phases. For the overall predictions (gestating and lactating ewes), the adjusted DMI prediction had greater accuracy but lower precision than the unadjusted DMI prediction. However, adjusting DMI increased the adequacy of the prediction as the mean square error of prediction difference (ΔMSEP) decreased (p = 0.0328). Similarly, for gestating ewes, the adjusted predicted DMI had a lower ΔMSEP than the unadjusted predicted DMI (p < 0.001). For lactating ewes, no difference was detected between the adjusted and unadjusted predicted DMI based on the ΔMSEP statistics (p = 0.3672), but the assumption that peak milk was 28 days (default) worsened the predictability of the adjusted predicted DMI as it had lower precision and accuracy. Adjustments for predicted DMI of dry and lactating ewes are necessary to increase adequacy and precision.
Keywords:
mathematical model; nutrition model; prediction; requirement; sheep
Introduction
The commercializing of sheep in the form of meat, leather, wool, and milk secure important market niches as well as delivering a product with high added value (FAO, 2018Food and Agriculture Organization of the United Nations [FAO]. 2018. FAOSTAT Data. FAO, Rome, Italy.). Thus, understanding and advancing sheep nutrition through research will help sheep to be more productive and competitive in the world market. The dry matter intake (DMI) of a ruminant is multifactorial, being influenced by animal type, environmental factors, and dietary characteristics (Pulina et al., 2013Pulina, G.; Avondo, M.; Molle, G.; Helena, A.; Francesconi, D.; Atzori, A.S.; Cannas, A. 2013. Models for estimating feed intake in small ruminants. Revista Brasileira de Zootecnia 42: 675-690. http://dx.doi.org/10.1590/S1516-35982013000900010
http://dx.doi.org/10.1590/S1516-35982013...
). Thus, understanding and better estimating the DMI is fundamental to improving various aspects of sheep production, including the supplementation of energy and nutrients needed by grazing animals, correct balancing of diets, supplementation and feed planning, as well as calculation of economic viability of a production system among other factors. Empirical equations (NRC, 2007National Research Council [NRC]. 2007. Nutrient Requirements of Small Ruminants. National Academies Press, Washington, DC, USA. https://doi.org/10.17226/11654
https://doi.org/10.17226/11654...
) and more complicated mathematical models (Cannas et al., 2004Cannas, A.; Tedeschi, L.O.; Fox, D.G.; Pell, A.N.; Van Soest, P.J. 2004. A mechanistic model for predicting the nutrient requirements and feed biological values for sheep. Journal of Animal Science 82: 149-169.; Pulina et al., 2013Pulina, G.; Avondo, M.; Molle, G.; Helena, A.; Francesconi, D.; Atzori, A.S.; Cannas, A. 2013. Models for estimating feed intake in small ruminants. Revista Brasileira de Zootecnia 42: 675-690. http://dx.doi.org/10.1590/S1516-35982013000900010
http://dx.doi.org/10.1590/S1516-35982013...
; Tedeschi and Fox, 2018Tedeschi, L.O.; Fox, D.G. 2018. The Ruminant Nutrition System: An Applied Model for Predicting Nutrient Requirements and Feed Utilization in Ruminants. 2ed. XanEdu, Ann Arbor, MIUSA.) were developed to calculate the DMI of sheep.
The majority of the equations for predicting DMI in sheep are usually made for confined animals and take into account metabolic weight or mature weight (MW) and average daily gain (ADG) for dry animals, as well as milk production for lactating animals. The existing DMI prediction equations, involving empirical or mathematical methods, include those developed and further modified by INRA (1988)Institut National de la Recherche Agronomique [INRA]. 1988. Feeding Cattle, Sheep and Goats = Alimentation des Bovins, Ovins et Caprins. INRA, Paris, France (in French).; CSIRO (1990)Commonwealth Scientific and Industrial Research [CSIRO]. 1990. Feeding Standards for Australian Livestock-Ruminants. CSIRO, Melbourne, Australia.; AFRC (1995)Agricultural and Food Research Council [AFRC]. 1995. Energy and Protein Requirements of Ruminants. CAB International, Wallingford, UK., Pulina et al. (1996)Pulina, G.; Bettati, T.; Serra, F.A.; Razio, O. 1996. Construction and validation of a software program for feeding sheep milk = Costruzione e validazione di un software per l'alimentazione degli ovini da latte. In: Proceedings National Congress of the Italian Society of Pathology and Breeding Of Sheep And Goats = Atti Congresso Nazionale Della Societa Italiana Di Patologia E Di Allevamento Degli Ovini E Dei Caprini 12: 11-14 (in Italian).; AFRC (1998)Agricultural and Food Research Council [AFRC]. 1998. The Nutrition of Goats. CAB International, Wallingford, UK.; Cannas et al. (2004)Cannas, A.; Tedeschi, L.O.; Fox, D.G.; Pell, A.N.; Van Soest, P.J. 2004. A mechanistic model for predicting the nutrient requirements and feed biological values for sheep. Journal of Animal Science 82: 149-169.; INRA (2007)Institut National de la Recherche Agronomique [INRA]. 2007. Feeding Cattle, Sheep and Goats: Animal Requirements: Food Values = Alimentation des Bovins, Ovins et Caprins: Besoins des Animaux: Valeurs des Aliments. INRA, Paris, France (in French).; NRC (2007)National Research Council [NRC]. 2007. Nutrient Requirements of Small Ruminants. National Academies Press, Washington, DC, USA. https://doi.org/10.17226/11654
https://doi.org/10.17226/11654...
; Cannas et al. (2010)Cannas, A.; Tedeschi, L.O.; Atzori, A.S.; Al, E. 2010. The development and evaluation of the Small Ruminant Nutrition System. p. 263-272. In: Sauvant, D.; Van Milgen, J.; Faverdin, P.; Al, E., eds. Modelling nutrient digestion and utilisation in farm animals. Wageningen Academic Publishers, Wageningen, The Netherlands.; Tedeschi et al. (2010)Tedeschi, L.O.; Nicholson, C.F.; Rich, E. 2010. Using system dynamics modelling approach to develop management tools for animal production with emphasis on small ruminants. Small Ruminant Research 98: 102-110. https://doi.org/10.1016/j.smallrumres.2011.03.026
https://doi.org/10.1016/j.smallrumres.20...
; Pulina et al. (2013)Pulina, G.; Avondo, M.; Molle, G.; Helena, A.; Francesconi, D.; Atzori, A.S.; Cannas, A. 2013. Models for estimating feed intake in small ruminants. Revista Brasileira de Zootecnia 42: 675-690. http://dx.doi.org/10.1590/S1516-35982013000900010
http://dx.doi.org/10.1590/S1516-35982013...
; Tedeschi and Fox (2018)Tedeschi, L.O.; Fox, D.G. 2018. The Ruminant Nutrition System: An Applied Model for Predicting Nutrient Requirements and Feed Utilization in Ruminants. 2ed. XanEdu, Ann Arbor, MIUSA.. For non-lactation ewes, the NRC (2007) took into account the MW of both the animal and the ADG. Similarly, the equation used by Cannas et al. (2004)Cannas, A.; Tedeschi, L.O.; Fox, D.G.; Pell, A.N.; Van Soest, P.J. 2004. A mechanistic model for predicting the nutrient requirements and feed biological values for sheep. Journal of Animal Science 82: 149-169.; Tedeschi and Fox (2018)Tedeschi, L.O.; Fox, D.G. 2018. The Ruminant Nutrition System: An Applied Model for Predicting Nutrient Requirements and Feed Utilization in Ruminants. 2ed. XanEdu, Ann Arbor, MIUSA. to calculate DMI using an animal's body weight (BW) and ADG. For lactating ewes, the NRC (2007) recommended the type of parturition, as well as the production and composition of milk. However, Cannas et al. (2004)Cannas, A.; Tedeschi, L.O.; Fox, D.G.; Pell, A.N.; Van Soest, P.J. 2004. A mechanistic model for predicting the nutrient requirements and feed biological values for sheep. Journal of Animal Science 82: 149-169. and Tedeschi and Fox (2018)Tedeschi, L.O.; Fox, D.G. 2018. The Ruminant Nutrition System: An Applied Model for Predicting Nutrient Requirements and Feed Utilization in Ruminants. 2ed. XanEdu, Ann Arbor, MIUSA. used the weight at birth of the lambs (i.e., litter), and the production and composition of the milk.
Although these equations are accurate, there is a constant need to change predictive equations and models to account for changes in an animal's behavior, feeding management, and dietary formulations. Recently, Pulina et al. (2013)Pulina, G.; Avondo, M.; Molle, G.; Helena, A.; Francesconi, D.; Atzori, A.S.; Cannas, A. 2013. Models for estimating feed intake in small ruminants. Revista Brasileira de Zootecnia 42: 675-690. http://dx.doi.org/10.1590/S1516-35982013000900010
http://dx.doi.org/10.1590/S1516-35982013...
discussed new considerations on the prediction of DMI for small ruminants, and Almeida et al. (2019)Almeida, A.K.; Tedeschi, L.O.; Resende, K.T.; Biagioli, B.; Cannas, A.; Teixeira, I.A.M.A. 2019. Prediction of voluntary dry matter intake in stall fed growing goats. Livestock Science 219: 1-9. https://doi.org/10.1016/j.livsci.2018.11.002
https://doi.org/10.1016/j.livsci.2018.11...
evaluated equations to predict the DMI for goats in tropical environments. Therefore, given the importance of sheep production around the world, the objective of this study was to combine different adjustment factors in developing a continuous adjustment factor for predicting the DMI of pregnancy, dry, and lactating ewes.
Materials and Methods
In this study, equations 1 to 3 were evaluated and newly adjusted as shown in equations 4 to 6.
Prediction of Dry Matter Intake
As pointed out above, many factors affect voluntary feed intake (VFI) by ruminants. This is especially true for small ruminants (Tedeschi and Fox, 2018Tedeschi, L.O.; Fox, D.G. 2018. The Ruminant Nutrition System: An Applied Model for Predicting Nutrient Requirements and Feed Utilization in Ruminants. 2ed. XanEdu, Ann Arbor, MIUSA.). Therefore, the prediction of DMI is complex, and in many instances, it resembles the quest for the holy grail. Pulina et al. (2013)Pulina, G.; Avondo, M.; Molle, G.; Helena, A.; Francesconi, D.; Atzori, A.S.; Cannas, A. 2013. Models for estimating feed intake in small ruminants. Revista Brasileira de Zootecnia 42: 675-690. http://dx.doi.org/10.1590/S1516-35982013000900010
http://dx.doi.org/10.1590/S1516-35982013...
provided an extensive discussion about predicting DMI for sheep and goats. The majority of DMI prediction equations are derived from confined and pellet-fed sheep. This is due to the ease and accuracy of collecting information. Measurements taken of animals in the pasture, with or without supplementation is complicated and involve many variables. However, the particular grazing behavior of the sheep may not be reflected in these equations.
The NRC (2007)National Research Council [NRC]. 2007. Nutrient Requirements of Small Ruminants. National Academies Press, Washington, DC, USA. https://doi.org/10.17226/11654
https://doi.org/10.17226/11654...
predictive equation takes into account the standard reference weight to compute the relative size of the animal in predicting DMI. When less than 2 tonnes of DM ha−1 of forage is available for consumption there is an adjustment to the predicted DMI. The NRC (2007)National Research Council [NRC]. 2007. Nutrient Requirements of Small Ruminants. National Academies Press, Washington, DC, USA. https://doi.org/10.17226/11654
https://doi.org/10.17226/11654...
adjusts the DMI for forage when digestibility is lower than 0.8 and when consuming legumes and the same model is used on both sheep and goats.
In developing the Ruminant Nutrition System (RNS) model, Tedeschi and Fox (2018)Tedeschi, L.O.; Fox, D.G. 2018. The Ruminant Nutrition System: An Applied Model for Predicting Nutrient Requirements and Feed Utilization in Ruminants. 2ed. XanEdu, Ann Arbor, MIUSA. adopted equation 1 for lactating ewes and equation 2 for gestating, non-lactating ewes. These equations were developed by Pulina et al. (1989)Pulina, G.; Serra, A.; Cannas, A.; Al., E. 1989. Determination and estimation of the energy value of milk from Sardinian breed sheep = Determinazione e stima del valore energetico di latte di pecore di razza Sarda. Atti della Società Italiana delle Scienze Veterinarie 43: 1867-1870 (in Italian).. The predicted DMI for lactating ewes uses fat-corrected milk (FCM) to ensure that ewes producing different amounts of milk and milk fat are compared based on the same net energy content of the milk. The NRC (2001)National Research Council [NRC]. 2001. Nutrient Requirements of Dairy Cattle. National Academies Press, Washington, DC, USA. https://doi.org/10.17226/9825
https://doi.org/10.17226/9825...
of dairy cattle uses fat content of 4 % as a standard value of milk fat. Dairy ewes compared to the meat and wool sheep show distinct milk production, lactation peak, and milk composition (protein and fat) (Dove and Kelman, 2015Dove, H.; Kelman, W.M. 2015. Comparison of the alkane-based herbage intakes and the liveweight gains of young sheep grazing forage oats, dual-purpose wheat or phalaris-based pasture. Animal Production Science 55: 1230-1240. https://doi.org/10.1071/AN15020
https://doi.org/10.1071/AN15020...
; Ferro et al., 2017Ferro, M.M.; Tedeschi, L.O.; Atzori, A.S. 2017. The comparison of the lactation and milk yield and composition of selected breeds of sheep and goats. Translational Animal Science 1: 498-506. https://doi.org/10.2527/tas2017.0056
https://doi.org/10.2527/tas2017.0056...
; Gonzalo et al., 1994Gonzalo, C.; Carriedo, J.A.; Baro, J.A. 1994. Factors influencing variation of test day milk yield, somatic cell count, fat, and protein in dairy sheep. Journal of Dairy Science 77:1537-1542. https://doi.org/10.3168/jds.S0022-0302(94)77094-6
https://doi.org/10.3168/jds.S0022-0302(9...
; Massouras et al., 2018Massouras, T.G.; Maragoudakis, S.; Hadjigeorgiou, I. 2018. Differences in sheep milk characteristics focusing on fatty acid profile between conventional and organic farming system. Archives of Dairy Research and Technology 2018: 1-12.; Nudda et al., 2002Nudda, A.; Bencini, R.; Mijatovic, S.; Pulina, G. 2002. The yield and composition of milk in sarda, awassi and merino sheep milked unilaterally at different frequencies. Jounal of Dairy Science 85: 2879-2884. https://doi.org/10.3168/jds.S0022-0302(02)74375-0
https://doi.org/10.3168/jds.S0022-0302(0...
; Park, 2007Park, Y.W. 2007. Rheological characteristics of goat and sheep milk. Small Ruminant Research 68: 73-87. https://doi.org/10.1016/j.smallrumres.2006.09.015
https://doi.org/10.1016/j.smallrumres.20...
). In contrast to dairy cattle, an exact value has not been stipulated for dairy sheep to use as a standard value for sheep milk, but predictive equations for DMI take into account milk composition to assess the energy content of the milk.
where ADG is the average daily gain, kg d−1; DMI the predicted dry matter intake, kg d−1; FBW the full (unshrunk) body weight, kg; FCM the fat-corrected milk, kg d−1; MkF the milk fat content, %; and MY the milk yield, kg d−1.
Equations 1 and 2 predict the average DMI, which is likely to be closer to the potential intake or the intake required to meet their energy and protein requirements for lactation, pregnancy, and growth. Ewes, however, like cows, decrease their DMI as they approach parturition with a slow increase in DMI after parturition (Tedeschi et al., 2013Tedeschi, L.O.; Fox, D.G.; Kononoff, P.J. 2013. A dynamic model to predict fat and protein fluxes and dry matter intake associated with body reserve changes in cattle. Journal of Dairy Science 96: 2448-2463. https://doi.org/10.3168/jds.2012-6070
https://doi.org/10.3168/jds.2012-6070...
). Therefore, adjustment factors should be incorporated to account for the parturition event of gestating and lactating ewes.
Dry Matter Intake Adjustments for dry and gestating ewes
Pulina et al. (1996)Pulina, G.; Bettati, T.; Serra, F.A.; Razio, O. 1996. Construction and validation of a software program for feeding sheep milk = Costruzione e validazione di un software per l'alimentazione degli ovini da latte. In: Proceedings National Congress of the Italian Society of Pathology and Breeding Of Sheep And Goats = Atti Congresso Nazionale Della Societa Italiana Di Patologia E Di Allevamento Degli Ovini E Dei Caprini 12: 11-14 (in Italian). provided discrete adjustment factors for the DMI of dry and pregnant ewes based on their days pregnant relative to lambing and expected lamb litter weight, i.e., combined lamb(s) birth weight(s). Such adjustments were adopted by Cannas et al. (2004)Cannas, A.; Tedeschi, L.O.; Fox, D.G.; Pell, A.N.; Van Soest, P.J. 2004. A mechanistic model for predicting the nutrient requirements and feed biological values for sheep. Journal of Animal Science 82: 149-169. in developing the Cornell Net Carbohydrate and Protein System for Sheep (CNCPS-Sheep) and subsequently incorporated in the Small Ruminant Nutrition System, SRNS (Tedeschi et al., 2010Tedeschi, L.O.; Nicholson, C.F.; Rich, E. 2010. Using system dynamics modelling approach to develop management tools for animal production with emphasis on small ruminants. Small Ruminant Research 98: 102-110. https://doi.org/10.1016/j.smallrumres.2011.03.026
https://doi.org/10.1016/j.smallrumres.20...
). In 2013, Pulina et al. (2013)Pulina, G.; Avondo, M.; Molle, G.; Helena, A.; Francesconi, D.; Atzori, A.S.; Cannas, A. 2013. Models for estimating feed intake in small ruminants. Revista Brasileira de Zootecnia 42: 675-690. http://dx.doi.org/10.1590/S1516-35982013000900010
http://dx.doi.org/10.1590/S1516-35982013...
listed similar discrete adjustments, but, unfortunately, the weekly assignment was incorrect. The original DMI adjustment for dry and pregnant ewes (Cannas et al., 2004Cannas, A.; Tedeschi, L.O.; Fox, D.G.; Pell, A.N.; Van Soest, P.J. 2004. A mechanistic model for predicting the nutrient requirements and feed biological values for sheep. Journal of Animal Science 82: 149-169.; Pulina et al., 2013Pulina, G.; Avondo, M.; Molle, G.; Helena, A.; Francesconi, D.; Atzori, A.S.; Cannas, A. 2013. Models for estimating feed intake in small ruminants. Revista Brasileira de Zootecnia 42: 675-690. http://dx.doi.org/10.1590/S1516-35982013000900010
http://dx.doi.org/10.1590/S1516-35982013...
) followed the guidelines of the Institut National de la Recherche Agronomique (INRA, 1988) to consider two weeks’ stepwise calculations for requirements and intake. Equation 4 has the proposed DMI adjustments (fDMI) depending on how far off the pregnant ewe is to lambing and its expected lamb litter weight.
where fDMI is the discrete adjustment factor for dry matter intake (DMI).
The discrete adjustment (Eq. 4), however, poses certain practical and physiological obstacles such as the discontinuity of the DMI adjustment and sudden changes in the DMI adjustment. Therefore, a continuous adjustment is necessary. We used an asymmetrical nonlinear function (Eq. 5) to convert these discrete adjustment factors into a continuous adjustment factor similar to that recommended by Tedeschi and Fox (2018Tedeschi, L.O.; Fox, D.G. 2018. The Ruminant Nutrition System: An Applied Model for Predicting Nutrient Requirements and Feed Utilization in Ruminants. 2ed. XanEdu, Ann Arbor, MIUSA., p. 255) to adjust DMI to the temperature for cattle.
where a, b, c, d, e, and f are parameters of the asymmetrical nonlinear function; ca a parameter for lactating ewe (default values are 0.52 and 0.71); Exp the exponential function; fDMI the adjustment factor for gestating ewe's potential dry matter intake; Ln the natural logarithmic function; and t is time (negative for pregnancy in which zero is at lambing) in days.
Figures 1A and B depict the discrete and continuous adjustment factor for gestating ewes (negative physiological days) for lamb litter weight, either less or more than 4 kg. The term 1/(1 + ca) in equation 5 provides the smallest adjustment factor and is dictated by the adjustment factor for lactating ewes (discussed in the next section).
Continuous adjustment of dry matter intake for gestating (negative days) and lactating (positive days) ewes with lamb litter with weight less than 4 kg (orange line and circles) or more than 4 kg (blue line and circles) for (A) Merino- and (B) Meat-type breeds. The circles indicate the discrete weekly adjustments for gestating ewes proposed by Pulina et al. (1996)Pulina, G.; Bettati, T.; Serra, F.A.; Razio, O. 1996. Construction and validation of a software program for feeding sheep milk = Costruzione e validazione di un software per l'alimentazione degli ovini da latte. In: Proceedings National Congress of the Italian Society of Pathology and Breeding Of Sheep And Goats = Atti Congresso Nazionale Della Societa Italiana Di Patologia E Di Allevamento Degli Ovini E Dei Caprini 12: 11-14 (in Italian). and Pulina et al. (2013)Pulina, G.; Avondo, M.; Molle, G.; Helena, A.; Francesconi, D.; Atzori, A.S.; Cannas, A. 2013. Models for estimating feed intake in small ruminants. Revista Brasileira de Zootecnia 42: 675-690. http://dx.doi.org/10.1590/S1516-35982013000900010
http://dx.doi.org/10.1590/S1516-35982013... . The continuous adjustment for lactating ewes is based on the Commonwealth Scientific and Industrial Research Organization (2007)Commonwealth Scientific And Industrial Research [CSIRO]. 2007. Nutrient Requirements of Domesticated Ruminants. CSIRO, Melbourne, Australia..
Dry Matter Intake Adjustments for Lactating Ewes
Based on the revision conducted by the Agricultural Research Council (ARC, 1980) suggesting that potential intake by cows and ewes consuming high-forage diets could be reduced by up to 60 % during lactation, the Commonwealth Scientific and Industrial Research Organization (CSIRO, 2007Commonwealth Scientific And Industrial Research [CSIRO]. 2007. Nutrient Requirements of Domesticated Ruminants. CSIRO, Melbourne, Australia.) proposed an adjustment factor that would have the same shape as that proposed by Wood (1967)Wood, P.D.P. 1967. Algebraic model of the lactation curve in cattle. Nature 5111: 164-165. to estimate lactation in dairy cows which means an incomplete Gamma distribution. Their adjustment factor varies from 1.0 to about 1.9 near the peak milk. Because we were only interested in the adjustment factor for post-lambing up to the peak milk, we slightly modified the CSIRO's (2007)Commonwealth Scientific And Industrial Research [CSIRO]. 2007. Nutrient Requirements of Domesticated Ruminants. CSIRO, Melbourne, Australia. equation by dividing their adjustment factor by the predicted adjustment factor at peak milk to yield one relative adjustment factor (Eq. 6). At lambing time, our adjustment yielded the lowest adjustment factor that is a function of sheep breed, and at peak milk, our adjustment factor would yield a value of 1.
where ca is a breed parameter that depends on the number of suckling lambs; cc the time at peak milk, days; Exp the exponential function; fDMI the adjustment factor for lactating ewes’ potential dry matter intake; and t is the days in milk (positive values after parturition), d.
The ca parameter in equation 6 depends on the number of suckling lambs and the breed. For Merino-type breeds, it is 0.52 for single or 0.71 for double lambs; and for the meat-type breed, it is 0.66 for single or 0.88 for double lambs. The cc parameter is assumed fixed at 28 days (peak of lactation), but it is likely that this value changes with different breeds, the plane of nutrition, and environmental and management conditions. Figure 1A depicts the continuous adjustment factor for lactating ewes assuming one or two suckling lambs for Merino-type breeds and Figure 1B shows the adjustment for meat-type breeds. As shown in Figure 1A, because the ca is either 0.52 (single lamb) or 0.71 (double lambs), the fDMI becomes 66 % or 59 % for lamb litter weight for less than 4 kg or more than 4 kg, respectively. Conversely, as shown in Figure 1B, because the ca is either 0.66 (single lamb) or 0.88 (double lambs), the fDMI becomes 60 % or 53 % for lamb litter weight for less than 4 kg or more than 4 kg, respectively. Therefore, based on the lactation continuous adjustment, meat-type breeds have a greater downturn in DMI near the parturition. The adjustment factor for gestating ewes, on the other hand, does not consider differences between breeds.
Animal data
The database used in this study was pooled from ewes, crossbreed of Santa Ines and Dorper, a hair sheep breed, two to four years old. The ewes were kept in paddocks, without forage, with feed supply twice a day, and daily control of offered and spare. The paddocks had a capacity of 7 ewes in 0.4 ha, with available shade and water all the time. Gestation and lactation occurred between Feb and Sept 2017, with a mean ambient temperature of 25.39 °C in Feb, 16.37 °C in July and 22.6 °C in Sept and annual precipitation of 230 mm. In these studies, ewes were fed ad libitum, with corn silage and concentrate (Table 1). The concentrate was adjusted in the final stage of gestation and lactation according to the recommendations of NRC (2007)National Research Council [NRC]. 2007. Nutrient Requirements of Small Ruminants. National Academies Press, Washington, DC, USA. https://doi.org/10.17226/11654
https://doi.org/10.17226/11654...
. During the period from 50 days of gestation to lambing, the animals had ADG of 0.171 kg d−1 and at 30 days of lactation the ADG was −0.150 kg d−1. The peak of milk production was reached at 40 days of lactation, with a production of 0.5 L d−1. Dairy production was evaluated at 20, 30, 40, 50 and 60 days after giving birth by the indirect method of the two weight measurements. Additional information about the animal is shown in Table 2.
Ingredients and chemical composition of experimental diets of ewes at the late gestation and lactation.
Model evaluation
The prediction evaluation was performed using the Model Evaluation System (MES; http://www.nutritionmodels.com/mes.html) software program (Tedeschi, 2006Tedeschi, L.O. 2006. Assessment of the adequacy of mathematical models. Agricultural System 89: 225-247. https://doi.org/10.1016/j.agsy.2005.11.004
https://doi.org/10.1016/j.agsy.2005.11.0...
) for all ewes (n = 61), non-lactating pregnant ewes (n = 33), as well as lactating ewes (n = 28). The following statistics were used to ensure precision and accuracy: coefficient of determination (r2), mean bias (MB), concordance correlation coefficient (CCC, varying from –1 to 1), bias correction factor (Cb, varies from 0 to 1) which indicates how far the regression line deviates from the slope of unity (45°), and the decomposition of the mean square error of prediction (MSEP). The ΔMSEP is the average difference between the predicted and actual DMI between two models. In our case, predicted DMI and adjusted predicted DMI. Next, a t-test was applied to verify if the ΔMSEP is different from zero (Tedeschi, 2006Tedeschi, L.O. 2006. Assessment of the adequacy of mathematical models. Agricultural System 89: 225-247. https://doi.org/10.1016/j.agsy.2005.11.004
https://doi.org/10.1016/j.agsy.2005.11.0...
). A simple optimization was also performed to identify the cc (peak milk in equation 6) that would minimize the MB between the predicted and actual DMI. As indicated above, the cc was assumed to be 28 days.
Results and Discussion
Table 3 shows the results of the prediction of DMI using equations 1 to 3 for the unadjusted predicted DMI and equations 5 and 6 for the adjusted predicted DMI. For the overall predictions (gestating and lactating ewes), the adjusted prediction had greater accuracy (higher Cb: 0.948 versus 0.762, and lower MSEP: 0.062 versus 0.073 kg2(d2)−1), but lower precision (0.667 versus 0.716) than the unadjusted prediction, respectively. The adjusted predicted DMI was more adequate than the unadjusted predicted DMI (p = 0.0328). Clearly, the adjustments for gestating (Eq. 5) had a decisive impact on the greater adequacy of adjusted versus unadjusted predicted DMI (Table 3). As shown in Table 3, the adjusted predicted DMI had greater adequacy statistics than the unadjusted predicted DMI (p < 0.001).
Adequacy statistics to compare observed dry matter intake (DMI) with unadjusted and adjusted predicted DMI1 1 p-value to simultaneously test if the intercept is equal to zero and the slope is equal to one (Tedeschi, 2006); .
In contrast, for lactating ewes, the assumption that peak milk was 28 days (default) worsened the predictability of the adjusted predicted DMI as it had lower precision (r2 of 0.58 versus 0.621), accuracy (Cb of 0.987 versus 0.998, and MSEP of 0.051 versus 0.043 kg2(d2)−1), respectively. No statistical difference compared to ΔMSEP (p = 0.3672) was found. When the peak milk was iteratively solved to reduce the difference between actual and predicted, a solution of 18.4 days was reached. The adequacy statistics for unadjusted and adjusted prediction DMI were similar, with no statistical difference (p = 0.6568). Interestingly, the measured peak milk was around 40 days, different from the optimized.
These findings suggested that adjustments for gestation had a greater impact on improving the predicted DMI than the adjustments for lactating ewes. In part, the lack of more data points for lactating ewes may have hindered our ability to improve the adjustment factor. Physiological status might be the most important homeorhetic mechanism (Tedeschi et al., 2013Tedeschi, L.O.; Fox, D.G.; Kononoff, P.J. 2013. A dynamic model to predict fat and protein fluxes and dry matter intake associated with body reserve changes in cattle. Journal of Dairy Science 96: 2448-2463. https://doi.org/10.3168/jds.2012-6070
https://doi.org/10.3168/jds.2012-6070...
; Tedeschi and Fox, 2018Tedeschi, L.O.; Fox, D.G. 2018. The Ruminant Nutrition System: An Applied Model for Predicting Nutrient Requirements and Feed Utilization in Ruminants. 2ed. XanEdu, Ann Arbor, MIUSA.) that alters the normal course of VFI of an animal, but it is certainly not the only one. Dietary (e.g., protein) and environmental factors (e.g., temperature) also affect VFI, but they behave more like homeostatic processes, i.e., short-term. For dairy cows, for instance, the adjustment factor for DMI is based on the ratio of metabolizable protein to net energy for lactation of the diet (INRA, 2018Institut National de la Recherche Agronomique [INRA]. 2018. Feeding System for Ruminants. INRA, Paris, France.); Hofmann (1989)Hofmann, R.R. 1989. Evolutionary steps of ecophysiological adaptation and diversification of ruminants: a comparative view of their digestive system. Oecologia 78: 443-457.; Van Soest (1994)Van Soest, P. 1994. Nutritional Ecology of the Ruminant. Cornell University Press, Ithaca, NY, USA.; Cannas et al. (2004)Cannas, A.; Tedeschi, L.O.; Fox, D.G.; Pell, A.N.; Van Soest, P.J. 2004. A mechanistic model for predicting the nutrient requirements and feed biological values for sheep. Journal of Animal Science 82: 149-169. affirmed that the ingestive behavior of small ruminants is different from large ruminants. The behavior differs as follows: a) small ruminants have higher DMI in relation to their metabolic weight because they have a higher rate of feed passage through the rumen; b) small ruminants have a higher energy requirement for maintenance; c) small ruminants have a heightened ability to select the food ingested, selecting plants or part of plants with higher nutrient content and lower fiber, facilitating the digestibility and absorption of nutrients; d) they spend more time selecting, chewing and ruminating a food to decrease the particle size and facilitate the passage of the same by the rumen; and e) because of the digestion capacity of small food particles, small ruminants make great use of the available energy of pelleted food or grain.
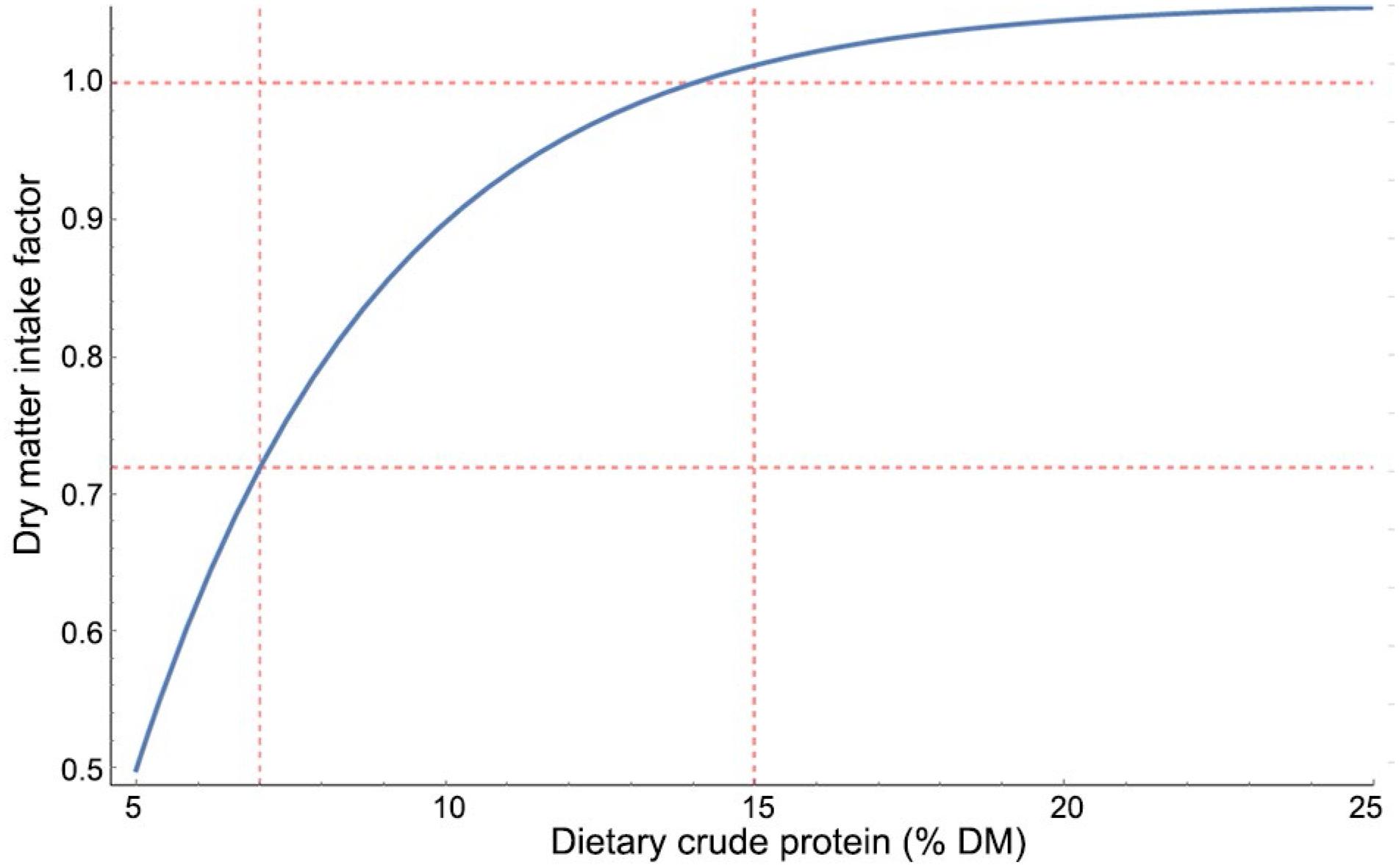
INRA (2018)Institut National de la Recherche Agronomique [INRA]. 2018. Feeding System for Ruminants. INRA, Paris, France. proposed an adjustment to DMI based on the dietary content of CP (Eq. 7) of goats. When diets contain less than 15 % CP (DM basis) they elicit a nonlinear reduction on intake, as shown in Figure 2. Accordingly, Van Soest (1994)Van Soest, P. 1994. Nutritional Ecology of the Ruminant. Cornell University Press, Ithaca, NY, USA. indicated that forage DMI is significantly reduced only when dietary crude protein is below 7 % (DM basis) at which, based on equation 7, DMI should be already reduced by 72 % (Figure 2). Assuming the CPfDMI (Eq. 7) holds for ewes, for our diets with CP of 11 % DM and 12 % DM, the CPfDMI would be 0.919 and 0.958, respectively, for gestating and lactating ewes. For gestating ewes, the CPfDMI would improve both unadjusted and adjusted predicted DMI considerably by raising the MB from −0.274 kg d−1 (1.576 – 1.85) to −0.124 kg d−1 (1.576 – 0.185 × 0.919) for unadjusted and from −0.232 kg d−1 (1.576 – 1.808) to −0.086 kg d−1 (1.576 – 0.1808 × 0.919) for adjusted predicted DMI (Table 3). For lactating ewes, however, the CPfDMI would worsen the predictions as it would further reduce the unadjusted and adjusted predicted DMI.
Continuous adjustment of dry matter intake for dietary crude protein content. Adapted from the Institut National de la Recherche Agronomique (2018)Institut National de la Recherche Agronomique [INRA]. 2018. Feeding System for Ruminants. INRA, Paris, France..
where CP is the dietary crude protein content, % DM; CPfDMI the adjustment factor for dry matter intake given the CP content; and Exp the exponential function.
In addition to the DMI factors modeled by Tedeschi and Fox (2018)Tedeschi, L.O.; Fox, D.G. 2018. The Ruminant Nutrition System: An Applied Model for Predicting Nutrient Requirements and Feed Utilization in Ruminants. 2ed. XanEdu, Ann Arbor, MIUSA., namely grazing-physical activity, temperature, mud, breed, body fat, and feed additives, small ruminants are also penalized by their relatively smaller rumen volume compared to their energy needs-digestive capacity (Tedeschi et al., 2019Almeida, A.K.; Tedeschi, L.O.; Resende, K.T.; Biagioli, B.; Cannas, A.; Teixeira, I.A.M.A. 2019. Prediction of voluntary dry matter intake in stall fed growing goats. Livestock Science 219: 1-9. https://doi.org/10.1016/j.livsci.2018.11.002
https://doi.org/10.1016/j.livsci.2018.11...
). The wet fermentative capacity in the rumen proportionally increases with body weight (Demment and Van Soest, 1985Demment, M.W.; Van Soest, P.J. 1985. A nutritional explanation for body-size patterns of ruminant and nonruminant herbivores. The American Naturalist 125: 641-672. https://doi.org/10.1086/284369
https://doi.org/10.1086/284369...
), indicating that small ruminants have less fermentative volume and contents per unit of energy required for maintenance and production. This is the reason that small ruminants must adopt the selective approach (Hofmann, 1989Hofmann, R.R. 1989. Evolutionary steps of ecophysiological adaptation and diversification of ruminants: a comparative view of their digestive system. Oecologia 78: 443-457.) when consuming feeds, and they do not have the option of consuming low digestible feeds. Thus, this selective process promotes a “distraction” to the small ruminant that forces them to spend time selecting the feed; thus, potentially reducing their potential intake within a time period. Small ruminants, mainly the selective ones, attempt to meet their VFI by selecting the most nutritious part (i.e., digestible) of the diet (e.g., forage), but it fails if the available time for such is shorter or if the relative intake is limited by the availability of the feed. This “adjustment factor” has not been modeled because there are too many confounding effects and a critical lack of data. It only lives in our conceptual, ideological understanding of grazing animal behavior. In reality, dietary digestibility and feed availability should provide sufficient information to model this “adjustment factor” that is more pertinent to grazing, extensive-type sheep production than confined scenarios.
Like the NRC (2001)National Research Council [NRC]. 2001. Nutrient Requirements of Dairy Cattle. National Academies Press, Washington, DC, USA. https://doi.org/10.17226/9825
https://doi.org/10.17226/9825...
, the CSIRO (2007)Commonwealth Scientific And Industrial Research [CSIRO]. 2007. Nutrient Requirements of Domesticated Ruminants. CSIRO, Melbourne, Australia. attempted to adjust DMI for herbage availability (weight) and sward structure (area). It indicated that when herbage availability is less than 2 t ha−1 (for sheep), the potential intake of feed is reduced progressively as it becomes more difficult for animals to achieve their satiety. Through the GrazFeed model, Freer (2002)Freer, M. 2002. The nutritional management of grazing sheep. p. 385. In: Freer, M.; Dove, H., eds. Sheep nutrition. CABI, Wallinford, UK. developed additional components to adjust the potential DMI of grazing sheep and we might be able to adapt some of those concepts to confined animals, particularly those consuming high-forage diets. Freer (2002)Freer, M. 2002. The nutritional management of grazing sheep. p. 385. In: Freer, M.; Dove, H., eds. Sheep nutrition. CABI, Wallinford, UK. indicated that the adjustment factor (0 to 1) is a function of the predicted relative rate of grazing (g h−1) and the predicted relative time spent grazing (h d−1) in which both were exponentially related to herbage (i.e., forage mass) availability (tonnes of DM ha−1). As shown in Figure 3, as time spent grazing (T) decreases with greater availability of herbage mass per area, the rate of eating increases and the relative availability also increases up to about a relative value of 1. Figure 2 and Figure 3 suggest that in addition to the physiological effects on VFI, many other factors can alter potential VFI up to a maximum that is likely dictated by physical constraints in the rumen and metabolic feedback signals (e.g., lipostatic, chemostatic, or thermostatic) (Tedeschi and Fox, 2018Tedeschi, L.O.; Fox, D.G. 2018. The Ruminant Nutrition System: An Applied Model for Predicting Nutrient Requirements and Feed Utilization in Ruminants. 2ed. XanEdu, Ann Arbor, MIUSA.). Because our animals (Table 2) were not grazing, these adjustments would not be a major determinant on intake, but additional adjustments are needed for grazing animals.
Relative availability of feed (F) and its main components (T = time spent eating and G = eating rate) versus herbage mass weight, assuming H = 0.8 and φ = 0.85. Adapted from Freer (2002)Freer, M. 2002. The nutritional management of grazing sheep. p. 385. In: Freer, M.; Dove, H., eds. Sheep nutrition. CABI, Wallinford, UK..
Furthermore, different factors affect nutritional requirements such as the environment and genetics. Salah et al. (2014)Salah, N.; Sauvant, D.; Archimède, H. 2014. Nutritional requirements of sheep, goats and cattle in warm climates: a meta-analysis. Animal 8: 1439-1447. https://doi.org/10.1017/S1751731114001153
https://doi.org/10.1017/S175173111400115...
studied, by meta-analysis, the influence of warm climates on nutritional requirements. However, a number of studies have focused on the determination of the requirement of a specific race, considering that there is a nutritional difference between them (Ji et al., 2015Ji, S.K.; Xu, G.S.; Diao, Q.Y.; Deng, K.D.; Jiang, C.G.; Tu, Y.; Zhang, N.F. 2015. Macromineral requirements of Dorper × thin-tailed Han crossbred female lambs. Journal of Integrative Agriculture 14: 1617-1626. https://doi.org/10.1016/S2095-3119(14)60901-1
https://doi.org/10.1016/S2095-3119(14)60...
; Pereira et al., 2017Pereira, E.S.; Lima, F.W.R.; Marcondes, M.I.; Rodrigues, J.P.P.; Campos, A.C.N.; Silva, L.P.; Bezerra, L.R.; Pereira, M.W.F.; Oliveira, R.L. 2017. Energy and protein requirements of Santa Ines lambs, a breed of hair sheep. Animal 11: 2165-2174. https://doi.org/10.1017/S1751731117001185
https://doi.org/10.1017/S175173111700118...
, 2016Pereira, E.S.; Carmo, A.B.R.; Costa, M.R.G.F.; Medeiros, A.N.; Oliveira, R.L.; Pinto, A.P.; Carneiro, M.S.S.; Lima, F.W.R.; Campos, A.C.N.; Gomes, S.P. 2016. Mineral requirements of hair sheep in tropical climates. Journal of Animal Physiology and Animal Nutrition 100: 1090-1096. https://doi.org/10.1111/jpn.12483
https://doi.org/10.1111/jpn.12483...
; Rodrigues et al., 2016Rodrigues, R.T.S.; Chizzotti, M.L.; Martins, S.R.; Silva, I.F.; Queiroz, M.A.Á.; Silva, T.S.; Busato, K.C.; Silva, A.M.A. 2016. Energy and protein requirements of non-descript breed hair lambs of different sex classes in the semiarid region of Brazil. Tropical Animal Health and Production 48: 87-94. https://doi.org/10.1007/s11250-015-0924-2
https://doi.org/10.1007/s11250-015-0924-...
). Certain researchers have worked on the effect of maternal nutritional requirement on progeny; these studies are called fetal programming, and are not usually studied in prediction equations (Campion et al., 2016Campion, F.P.; McGovern, F.M.; Lott, S.; Fahey, A.G.; Creighton, P.; Boland, T.M. 2016. Comparison of energy rationing systems for late gestation ewes: impacts on ewe and lamb performance. Journal of Animal Science 94: 3441-3456. https://doi.org/10.2527/jas.2016-0522
https://doi.org/10.2527/jas.2016-0522...
; Hoffman et al., 2018Hoffman, F.; Boretto, E.; Vitale, S.; Gonzalez, V.; Vidal, G.; Pardo, M.F.; Flores, M.F.; Garcia, F.; Bagnis, G.; Queiroz, O.C.M.; Rabaglino, M.B. 2018. Maternal nutritional restriction during late gestation impairs development of the reproductive organs in both male and female lambs. Theriogenology 108: 331-338. https://doi.org/10.1016/j.theriogenology.2017.12.023
https://doi.org/10.1016/j.theriogenology...
; McGovern et al., 2015McGovern, F.M.; Campion, F.P.; Sweeney, T.; Fair, S.; Lott, S.; Boland, T.M. 2015. Altering ewe nutrition in late gestation. II. The impact on fetal development and offspring performance. Journal of Animal Science 93: 4873-4882. https://doi.org/10.2527/jas.2015-9020
https://doi.org/10.2527/jas.2015-9020...
; Peine et al., 2018Peine, J.L.; Jia, G.; Van Emon, M.L.; Neville, T.L.; Kirsch, J.D.; Hammer, C.J.; O’Rourke, S.T.; Reynolds, L.P.; Caton, J.S. 2018. Effects of maternal nutrition and rumen-protected arginine supplementation on ewe performance and postnatal lamb growth and internal organ mass. Journal of Animal Science 96: 3471-3481. https://doi.org/10.1093/jas/sky221
https://doi.org/10.1093/jas/sky221...
; Roca Fraga et al., 2018Roca Fraga, F.J.; Lagisz, M.; Nakagawa, S.; Lopez-Villalobos, N.; Blair, H.T.; Kenyon, P.R. 2018. Meta-analysis of lamb birth weight as influenced by pregnancy nutrition of multiparous ewes. Journal of Animal Science 96: 1962-1977. https://doi.org/10.1093/jas/sky072
https://doi.org/10.1093/jas/sky072...
). Further investigation is warranted if the adjustments proposed in equations 5 and 6 would still apply to different levels of the plane of nutrition of gestating ewes. In summary, the adjustments made to the equations of non-lactation ewe were positive when accuracy is increased. The equations of lactating ewes are adequate for the actual results observed.
Acknowledgments
The São Paulo Research Foundation (FAPESP, process 2017/23861-2) and Texas A&M University for financial support.
References
- Agricultural and Food Research Council [AFRC]. 1998. The Nutrition of Goats. CAB International, Wallingford, UK.
- Agricultural and Food Research Council [AFRC]. 1995. Energy and Protein Requirements of Ruminants. CAB International, Wallingford, UK.
- Agricultural Research Council [ARC]. 1980. The Nutrient Requirements of Ruminant Livestock. Agricultural Research Council, Slough, UK.
- Almeida, A.K.; Tedeschi, L.O.; Resende, K.T.; Biagioli, B.; Cannas, A.; Teixeira, I.A.M.A. 2019. Prediction of voluntary dry matter intake in stall fed growing goats. Livestock Science 219: 1-9. https://doi.org/10.1016/j.livsci.2018.11.002
» https://doi.org/10.1016/j.livsci.2018.11.002 - Campion, F.P.; McGovern, F.M.; Lott, S.; Fahey, A.G.; Creighton, P.; Boland, T.M. 2016. Comparison of energy rationing systems for late gestation ewes: impacts on ewe and lamb performance. Journal of Animal Science 94: 3441-3456. https://doi.org/10.2527/jas.2016-0522
» https://doi.org/10.2527/jas.2016-0522 - Cannas, A.; Tedeschi, L.O.; Atzori, A.S.; Al, E. 2010. The development and evaluation of the Small Ruminant Nutrition System. p. 263-272. In: Sauvant, D.; Van Milgen, J.; Faverdin, P.; Al, E., eds. Modelling nutrient digestion and utilisation in farm animals. Wageningen Academic Publishers, Wageningen, The Netherlands.
- Cannas, A.; Tedeschi, L.O.; Fox, D.G.; Pell, A.N.; Van Soest, P.J. 2004. A mechanistic model for predicting the nutrient requirements and feed biological values for sheep. Journal of Animal Science 82: 149-169.
- Commonwealth Scientific and Industrial Research [CSIRO]. 1990. Feeding Standards for Australian Livestock-Ruminants. CSIRO, Melbourne, Australia.
- Commonwealth Scientific And Industrial Research [CSIRO]. 2007. Nutrient Requirements of Domesticated Ruminants. CSIRO, Melbourne, Australia.
- Demment, M.W.; Van Soest, P.J. 1985. A nutritional explanation for body-size patterns of ruminant and nonruminant herbivores. The American Naturalist 125: 641-672. https://doi.org/10.1086/284369
» https://doi.org/10.1086/284369 - Dove, H.; Kelman, W.M. 2015. Comparison of the alkane-based herbage intakes and the liveweight gains of young sheep grazing forage oats, dual-purpose wheat or phalaris-based pasture. Animal Production Science 55: 1230-1240. https://doi.org/10.1071/AN15020
» https://doi.org/10.1071/AN15020 - Food and Agriculture Organization of the United Nations [FAO]. 2018. FAOSTAT Data. FAO, Rome, Italy.
- Ferro, M.M.; Tedeschi, L.O.; Atzori, A.S. 2017. The comparison of the lactation and milk yield and composition of selected breeds of sheep and goats. Translational Animal Science 1: 498-506. https://doi.org/10.2527/tas2017.0056
» https://doi.org/10.2527/tas2017.0056 - Freer, M. 2002. The nutritional management of grazing sheep. p. 385. In: Freer, M.; Dove, H., eds. Sheep nutrition. CABI, Wallinford, UK.
- Gonzalo, C.; Carriedo, J.A.; Baro, J.A. 1994. Factors influencing variation of test day milk yield, somatic cell count, fat, and protein in dairy sheep. Journal of Dairy Science 77:1537-1542. https://doi.org/10.3168/jds.S0022-0302(94)77094-6
» https://doi.org/10.3168/jds.S0022-0302(94)77094-6 - Hoffman, F.; Boretto, E.; Vitale, S.; Gonzalez, V.; Vidal, G.; Pardo, M.F.; Flores, M.F.; Garcia, F.; Bagnis, G.; Queiroz, O.C.M.; Rabaglino, M.B. 2018. Maternal nutritional restriction during late gestation impairs development of the reproductive organs in both male and female lambs. Theriogenology 108: 331-338. https://doi.org/10.1016/j.theriogenology.2017.12.023
» https://doi.org/10.1016/j.theriogenology.2017.12.023 - Hofmann, R.R. 1989. Evolutionary steps of ecophysiological adaptation and diversification of ruminants: a comparative view of their digestive system. Oecologia 78: 443-457.
- Institut National de la Recherche Agronomique [INRA]. 2018. Feeding System for Ruminants. INRA, Paris, France.
- Institut National de la Recherche Agronomique [INRA]. 2007. Feeding Cattle, Sheep and Goats: Animal Requirements: Food Values = Alimentation des Bovins, Ovins et Caprins: Besoins des Animaux: Valeurs des Aliments. INRA, Paris, France (in French).
- Institut National de la Recherche Agronomique [INRA]. 1988. Feeding Cattle, Sheep and Goats = Alimentation des Bovins, Ovins et Caprins. INRA, Paris, France (in French).
- Ji, S.K.; Xu, G.S.; Diao, Q.Y.; Deng, K.D.; Jiang, C.G.; Tu, Y.; Zhang, N.F. 2015. Macromineral requirements of Dorper × thin-tailed Han crossbred female lambs. Journal of Integrative Agriculture 14: 1617-1626. https://doi.org/10.1016/S2095-3119(14)60901-1
» https://doi.org/10.1016/S2095-3119(14)60901-1 - Massouras, T.G.; Maragoudakis, S.; Hadjigeorgiou, I. 2018. Differences in sheep milk characteristics focusing on fatty acid profile between conventional and organic farming system. Archives of Dairy Research and Technology 2018: 1-12.
- McGovern, F.M.; Campion, F.P.; Sweeney, T.; Fair, S.; Lott, S.; Boland, T.M. 2015. Altering ewe nutrition in late gestation. II. The impact on fetal development and offspring performance. Journal of Animal Science 93: 4873-4882. https://doi.org/10.2527/jas.2015-9020
» https://doi.org/10.2527/jas.2015-9020 - National Research Council [NRC]. 2001. Nutrient Requirements of Dairy Cattle. National Academies Press, Washington, DC, USA. https://doi.org/10.17226/9825
» https://doi.org/10.17226/9825 - National Research Council [NRC]. 2007. Nutrient Requirements of Small Ruminants. National Academies Press, Washington, DC, USA. https://doi.org/10.17226/11654
» https://doi.org/10.17226/11654 - Nudda, A.; Bencini, R.; Mijatovic, S.; Pulina, G. 2002. The yield and composition of milk in sarda, awassi and merino sheep milked unilaterally at different frequencies. Jounal of Dairy Science 85: 2879-2884. https://doi.org/10.3168/jds.S0022-0302(02)74375-0
» https://doi.org/10.3168/jds.S0022-0302(02)74375-0 - Park, Y.W. 2007. Rheological characteristics of goat and sheep milk. Small Ruminant Research 68: 73-87. https://doi.org/10.1016/j.smallrumres.2006.09.015
» https://doi.org/10.1016/j.smallrumres.2006.09.015 - Peine, J.L.; Jia, G.; Van Emon, M.L.; Neville, T.L.; Kirsch, J.D.; Hammer, C.J.; O’Rourke, S.T.; Reynolds, L.P.; Caton, J.S. 2018. Effects of maternal nutrition and rumen-protected arginine supplementation on ewe performance and postnatal lamb growth and internal organ mass. Journal of Animal Science 96: 3471-3481. https://doi.org/10.1093/jas/sky221
» https://doi.org/10.1093/jas/sky221 - Pereira, E.S.; Carmo, A.B.R.; Costa, M.R.G.F.; Medeiros, A.N.; Oliveira, R.L.; Pinto, A.P.; Carneiro, M.S.S.; Lima, F.W.R.; Campos, A.C.N.; Gomes, S.P. 2016. Mineral requirements of hair sheep in tropical climates. Journal of Animal Physiology and Animal Nutrition 100: 1090-1096. https://doi.org/10.1111/jpn.12483
» https://doi.org/10.1111/jpn.12483 - Pereira, E.S.; Lima, F.W.R.; Marcondes, M.I.; Rodrigues, J.P.P.; Campos, A.C.N.; Silva, L.P.; Bezerra, L.R.; Pereira, M.W.F.; Oliveira, R.L. 2017. Energy and protein requirements of Santa Ines lambs, a breed of hair sheep. Animal 11: 2165-2174. https://doi.org/10.1017/S1751731117001185
» https://doi.org/10.1017/S1751731117001185 - Pulina, G.; Avondo, M.; Molle, G.; Helena, A.; Francesconi, D.; Atzori, A.S.; Cannas, A. 2013. Models for estimating feed intake in small ruminants. Revista Brasileira de Zootecnia 42: 675-690. http://dx.doi.org/10.1590/S1516-35982013000900010
» http://dx.doi.org/10.1590/S1516-35982013000900010 - Pulina, G.; Bettati, T.; Serra, F.A.; Razio, O. 1996. Construction and validation of a software program for feeding sheep milk = Costruzione e validazione di un software per l'alimentazione degli ovini da latte. In: Proceedings National Congress of the Italian Society of Pathology and Breeding Of Sheep And Goats = Atti Congresso Nazionale Della Societa Italiana Di Patologia E Di Allevamento Degli Ovini E Dei Caprini 12: 11-14 (in Italian).
- Pulina, G.; Serra, A.; Cannas, A.; Al., E. 1989. Determination and estimation of the energy value of milk from Sardinian breed sheep = Determinazione e stima del valore energetico di latte di pecore di razza Sarda. Atti della Società Italiana delle Scienze Veterinarie 43: 1867-1870 (in Italian).
- Roca Fraga, F.J.; Lagisz, M.; Nakagawa, S.; Lopez-Villalobos, N.; Blair, H.T.; Kenyon, P.R. 2018. Meta-analysis of lamb birth weight as influenced by pregnancy nutrition of multiparous ewes. Journal of Animal Science 96: 1962-1977. https://doi.org/10.1093/jas/sky072
» https://doi.org/10.1093/jas/sky072 - Rodrigues, R.T.S.; Chizzotti, M.L.; Martins, S.R.; Silva, I.F.; Queiroz, M.A.Á.; Silva, T.S.; Busato, K.C.; Silva, A.M.A. 2016. Energy and protein requirements of non-descript breed hair lambs of different sex classes in the semiarid region of Brazil. Tropical Animal Health and Production 48: 87-94. https://doi.org/10.1007/s11250-015-0924-2
» https://doi.org/10.1007/s11250-015-0924-2 - Salah, N.; Sauvant, D.; Archimède, H. 2014. Nutritional requirements of sheep, goats and cattle in warm climates: a meta-analysis. Animal 8: 1439-1447. https://doi.org/10.1017/S1751731114001153
» https://doi.org/10.1017/S1751731114001153 - Tedeschi, L.O. 2006. Assessment of the adequacy of mathematical models. Agricultural System 89: 225-247. https://doi.org/10.1016/j.agsy.2005.11.004
» https://doi.org/10.1016/j.agsy.2005.11.004 - Tedeschi, L.O.; Fox, D.G. 2018. The Ruminant Nutrition System: An Applied Model for Predicting Nutrient Requirements and Feed Utilization in Ruminants. 2ed. XanEdu, Ann Arbor, MIUSA.
- Tedeschi, L.O.; Fox, D.G.; Kononoff, P.J. 2013. A dynamic model to predict fat and protein fluxes and dry matter intake associated with body reserve changes in cattle. Journal of Dairy Science 96: 2448-2463. https://doi.org/10.3168/jds.2012-6070
» https://doi.org/10.3168/jds.2012-6070 - Tedeschi, L.O. 2019. ASN-ASAS symposium: future of data analytics in nutrition: Mathematical modeling in ruminant nutrition: approaches and paradigms, extant models, and thoughts for upcoming predictive analytics. Journal of Animal Science 97: 1921-1944. https://doi.org/10.1093/jas/skz092
» https://doi.org/10.1093/jas/skz092 - Tedeschi, L.O.; Nicholson, C.F.; Rich, E. 2010. Using system dynamics modelling approach to develop management tools for animal production with emphasis on small ruminants. Small Ruminant Research 98: 102-110. https://doi.org/10.1016/j.smallrumres.2011.03.026
» https://doi.org/10.1016/j.smallrumres.2011.03.026 - Van Soest, P. 1994. Nutritional Ecology of the Ruminant. Cornell University Press, Ithaca, NY, USA.
- Wood, P.D.P. 1967. Algebraic model of the lactation curve in cattle. Nature 5111: 164-165.
Edited by
Publication Dates
-
Publication in this collection
17 Apr 2020 -
Date of issue
2021
History
-
Received
28 Mar 2019 -
Accepted
06 Sept 2019