Resumos
Nas últimas décadas tem-se estudado a cinética da reação de cura de resinas epóxi por meio de técnicas analíticas como por exemplo a calorimetria exploratória diferencial. O uso desta técnica permite utilizar vários métodos de estudo da cinética de cura, divididos em: métodos dinâmicos e isotérmicos, e cada pesquisador escolhe o que melhor se adapta às suas necessidades. O presente trabalho tem como objetivo orientar na escolha de qual método deve ser utilizado, em função dos sistemas poliméricos em estudo, bem como sumarizar os principais métodos utilizados, auxiliando, dessa forma, no estudo da cinética de cura de resinas epóxi.
Cinética de cura; resina epóxi; métodos dinâmicos; métodos isotérmicos; DSC
The cure reaction kinetics of epoxy resins has been the object of many studies during the last decades. The cure process parameters can be obtained by using isothermal and dynamic differential scanning calorimetry analysis (DSC). The choice of the most suitable method depends on the requirements established by the researcher regarding the extent of the reaction. The main objective of the present work is to provide guidelines for the most appropriate method to be used in cure kinetics studies of epoxy matrix systems.
Cure kinetics; isothermal and dynamic methods; DSC; epoxy resin
NORMAS E MÉTODOS
Métodos de estudo da cinética de cura de resinas epóxi
Michelle L. Costa, Mirabel C. Rezende e Luiz C. Pardini
RESUMO: Nas últimas décadas tem-se estudado a cinética da reação de cura de resinas epóxi por meio de técnicas analíticas como por exemplo a calorimetria exploratória diferencial. O uso desta técnica permite utilizar vários métodos de estudo da cinética de cura, divididos em: métodos dinâmicos e isotérmicos, e cada pesquisador escolhe o que melhor se adapta às suas necessidades. O presente trabalho tem como objetivo orientar na escolha de qual método deve ser utilizado, em função dos sistemas poliméricos em estudo, bem como sumarizar os principais métodos utilizados, auxiliando, dessa forma, no estudo da cinética de cura de resinas epóxi.
Palavras-chave: Cinética de cura, resina epóxi, métodos dinâmicos, métodos isotérmicos, DSC.
Study methods of the cure reaction kinetics of epoxy resins
ABSTRACT: The cure reaction kinetics of epoxy resins has been the object of many studies during the last decades. The cure process parameters can be obtained by using isothermal and dynamic differential scanning calorimetry analysis (DSC). The choice of the most suitable method depends on the requirements established by the researcher regarding the extent of the reaction. The main objective of the present work is to provide guidelines for the most appropriate method to be used in cure kinetics studies of epoxy matrix systems.
Keywords: Cure kinetics, isothermal and dynamic methods, DSC, epoxy resin.
Introdução
Praticamente todos os materiais homogêneos isotrópicos podem apresentar limitações quanto às suas propriedades mecânicas. Entretanto, a combinação adequada de materiais permite que as propriedades intrínsecas de cada componente contribuam na obtenção de novos materiais, porém com características ajustadas e melhoradas para a aplicação final[1,2].
Como exemplo, pode-se citar os compósitos. Os compósitos são materiais de engenharia constituídos de um ou mais tipos de reforço, com orientação definida ou não, dispersos em uma matriz que tanto pode ser cerâmica, metálica ou polimérica. Os compósitos poliméricos avançados, por sua vez, são obtidos geralmente pela utilização de fibras contínuas pré-impregnadas com uma matriz termorrígida ou termoplástica.
O processamento desses materiais é considerado como tecnologia de ponta, devido às características dos produtos obtídos, como boas propriedades mecânicas aliadas à baixa massa específica. No caso em que a matriz é termorrígida, o entendimento do mecanismo e o conhecimento da taxa de cura da mesma são necessários, para que seja compreendida a relação existente entre o processamento, a morfologia, as propriedades e a durabilidade do termorrígido puro e, por conseqüência, do compósito final[3,4].
Cinética de cura
A cura de uma resina termorrígida é um processo bastante complexo que pode ser definido como a mudança nas propriedades químicas e físicas de uma determinada formulação resina/endurecedor.
Estas mudanças ocorrem irreversivelmente, por intermédio de reação química, usualmente acompanhada pela ação de calor e sob condições variadas de pressão e vácuo[3,4]. A gelificação e a vitrificação são os dois fenômenos macroscópicos mais importantes que ocorrem durante a cura de sistemas termorrígidos[5].
A gelificação corresponde à formação incipiente de uma rede de peso molecular infinito, onde a viscosidade à taxa de cisalhamento tendendo a zero também torna-se infinita, dando origem ao comportamento viscoelástico do fluido. O sistema passa de um líquido viscoso à um gel elástico[6]. Após a gelificação, o processo de cura continua mais lentamente, porque a mobilidade do sistema fica mais restrita devido ao aumento da densidade de ligações cruzadas. Esse aumento do número de ligações cruzadas provoca um acréscimo na temperatura de transição vítrea e nas propriedades mecânicas do material[7].
A vitrificação é a formação de um sólido vítreo a partir de um monômero, ou seja, é o processo no qual a reação química é resfriada durante o ciclo de cura, sendo que a resina não atinge o estado de cura total[5].
Como mencionado anteriormente, o mecanismo de cura das resinas epóxi é um dos mais estudados, e a técnica mais utilizada no estudo do comportamento cinético destas resinas é a calorimetria exploratória diferencial (DSC). Por meio desta técnica pode-se observar perfis de cura de sistemas reagentes, temperatura de transição vítrea e a determinação das melhores condições de preparação de compósitos[8].
O comportamento cinético da reação de cura ocorre concomitantemente às alterações em seu comportamento reológico, sendo comum denominar o fenômeno de comportamento reocinético[3].
Por ser uma reação exotérmica, inicialmente esse comportamento é caracterizado pelo predomínio de uma queda na viscosidade, devido ao aumento da temperatura interna da formulação. Logo após, tem início o aumento do seu peso molecular, ou seja, inicia-se a reticulação, provocando um aumento na viscosidade[7].
Portanto, o conhecimento do comportamento reocinético é de suma importância no estabelecimento de ciclos de cura destinados ao processamento de compósitos, pois a partir dele é que se determina o ciclo térmico e as etapas do processo de cura onde é mais adequado aplicar a pressão para a moldagem[9].
Nas curvas de DSC, a taxa de geração de calor exibe um pico máximo ou um mínimo, dependendo de como os termopares são alocados no aparelho, quando registrada em função do tempo, e a taxa de reação, que é proporcional à taxa de geração de calor, também exibe uma máxima ou uma mínima, e decresce em função do tempo. Por meio do DSC pode-se obter dois tipos de varreduras: as dinâmicas (fluxo de calor em função da temperatura) e as isotérmicas (fluxo de calor em função do tempo). Deve-se considerar, então, que o fluxo de calor exibido em relação à linha base do instrumento é proporcional à taxa de reação, também denominada de conversão, da / dt[10].
Todo estudo cinético inicia-se com a equação básica que relaciona a taxa de conversão da/dt à temperatura constante, com a concentração de um dos reagentes f(a) por meio da constante de velocidade k do sistema, como descrito pela equação 1[10]:
O mecanismo de reação de cura de termorrígidos obedece duas categorias gerais: a de ordem n ou a autocatalítica. De um modo geral, a cura não é limitada necessariamente apenas por uma única reação química. Assim, a cinética química pode obedecer a uma ou ambas ordens de reação simultaneamente, dependendo da região de estudo escolhida no gráfico isotérmico[10].
Para sistemas termorrígidos que obedecem a cinética de cura de ordem n, a taxa de conversão é função da concentração do reagente que é consumido no decorrer da equação 2:
onde a é a concentração fracionária dos reagentes consumidos no tempo t, a também é chamado de grau de conversão, e n é a ordem da reação.
As reações de cura autocatalíticas são caracterizadas por apresentarem um máximo na taxa de reação entre 30 a 40% da reação total de cura, obtida pela varredura isotérmica. A taxa depende das concentrações de moléculas formadas no início da reação, que a aceleram, agindo portanto, como autocatalisadores[10-12]. Nesse caso, tem-se a equação 3:
onde m é ordem da reação e (m + n) é a ordem total da reação.
Como a força motriz da reação de cura da maioria das resinas termorrígidas é a temperatura, pode-se considerar que esta ocorre segundo a equação de Arrhenius (4)[3]:
onde:
k = constante de velocidade da reação na temperatu-ra T (s-1);
E = energia de ativação (J/mol);
R = constante dos gases (8,314 J/K.mol);
T = temperatura absoluta (K), e
A = fator pré-exponencial ou de freqüência (s-1).
Portanto, a velocidade da reação aumenta exponencialmente com o aumento da temperatura.
Na prática, o curso das reações de cura da maioria dos sistemas termorrígidos pode ser adequadamente descrito em termos desses modelos cinéticos simples. Assim, pode-se concluir que as reações químicas de cura são basicamente controladas pela taxa de cura[10].
Um dos sistemas termorrígidos mais estudados por técnicas termoanalíticas é a reação entre os grupos epóxi e amina, utilizando-se, por exemplo, os reagentes: digilicidil éter do bisfenol-A e o m-fenilenodiamina (mPDA).
Dependendo das entidades químicas envolvidas na reação epóxi-amina esta pode ser representada tanto pela ordem de reação n quanto pela autocatalítica[10].
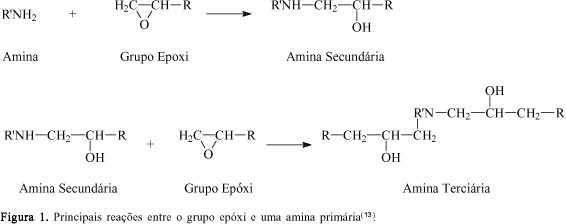
Shechter[13] mostrou que a química de cura de resinas epóxi com endurecedores amínicos, ou seja, a reação entre um grupo epóxi e uma amina primária leva à formação de duas principais reações, descritas na Figura 1. Shechter[13] observou, também, que grupos hidroxilas gerados durante a reação ou provenientes da adição de solventes ou outros catalisadores, ou pela presença de impurezas e até mesmo de umidade, aceleram significantemente a reação entre o glicidil éter e a amina. No entanto, em todos os casos os grupos hidroxila se comportam somente como catalisadores da reação e não como consumidores de grupos epóxi em competição com o grupamento amina. Dusek e Bleha[14,15] confirmaram os resultados anteriormente obtidos por Shechter[13], quando a amina está presente em excesso ou em quantidades estequiométricas. Geralmente, quando o grupo epóxi está em excesso existe a formação de uma reação secundária onde as hidroxilas são incorporadas ao anel epóxi[14].
Byrne[16] concluiu que a conversão, tanto da amina primária em secundária, como a conversão da amina secundária em terciária, ocorre ao acaso, isto é, as taxas de reação são indistingüíveis entre si. Pode-se dizer, portanto, que como tais reações ocorrem simultaneamente somente uma delas pode ser detectada e, por este fato, observa-se somente um único pico na curva de DSC.
Na área de compósitos estruturais, a técnica de DSC tem sido muito utilizada para a determinação de transições vítreas, ponto de fusão e no estudo da cinética de polimerização da matriz impregnante das fibras de reforço[17-20]. Este ponto é fundamental no processamento de pré-impregnados, pois é a cinética de cura que vai delinear o ciclo de cura a ser utilizado, ou seja, quais são as rampas de temperatura e os patamares isotérmicos a serem utilizados na fabricação do compósito.
O estudo da cinética de cura de resinas epóxi pode ser realizado via métodos dinâmicos e isotérmicos [17-20]. Estes dois métodos podem ser divididos segundo o diagrama mostrado na Figura 2.
Métodos Dinâmicos
O método dinâmico oferece resultados rápidos e aproximados do estudo da cinética de cura da reação e, subdivide-se em dois: o método de Borchardt e Daniels e o método ASTM-E-698[1720].
Método de Borchardt e Daniels
O método de Borchardt e Daniels permite calcular a energia de ativação, E, o fator pré-exponencial, A, o calor de reação, DH, a ordem de reação, n, e a constante de velocidade de reação, k, obtidos de uma única varredura dinâmica de DSC[21-24].
A técnica foi originalmente descrita por Borchardt e Daniels para soluções e foi subseqüentemente refinada por outros pesquisadores, como por exemplo Barret[24]. O método assume que a reação obedece a equação 5:
onde: da/dt é a taxa de reação (s-1); a é a taxa de conversão (adimensional); k(T) é a constante de velocidade da reação na temperatura T (s-1); e n é a ordem da reação (adimensional).
Portanto, o método assume que a reação obedece a cinética de ordem n e que a constante de velocidade k(T), depende da temperatura seguindo a equação de Arrhenius (4).
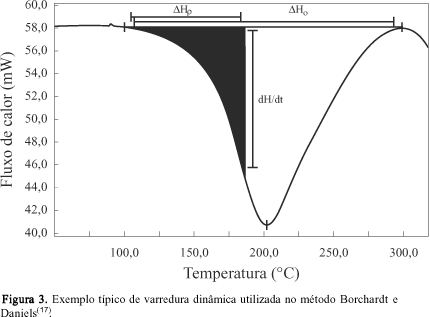
A curva de DSC, mostrada na Figura 3, é utilizada para medir os parâmetros básicos da/dt e a requeridos para resolver a equação. O método assume que o calor envolvido em um intervalo de tempo de segundos é diretamente proporcional ao número de moles reagidos durante aquele intervalo de tempo[17]. A taxa de reação é obtida pela divisão do termo dH/dT (calor de reação), a uma temperatura T, pela entalpia total DH0 (equação 6):
onde DH0é a entalpia experimental correspondente a área total do pico ou a entalpia teórica encontrada na literatura[5,10,17].
A taxa de conversão, a, é obtida pela razão da área parcial da curva, ou seja, DHp, a uma dada temperatura T , pela área total do pico, DH0 (equação 7).
Método ASTM-E-698
Esse método requer um mínimo de três varreduras dinâmicas obtidas por DSC a taxas de aquecimento diferentes. As taxas de aquecimento utilizadas estão geralmente na faixa de 1°C/min a 20°C/min. Considerando-se a relação linear entre a temperatura e o logaritmo da taxa de aquecimento, os parâmetros cinéticos E, A e k, podem ser obtidos[17]. Os cálculos são feitos assumindo três considerações :
1. o máximo do pico representa o ponto de conversão constante para cada taxa de aquecimento;
2. a constante de velocidade de reação depende da temperatura e obedece a equação de Arrhenius; e
3. a reação é de primeira ordem.
O método ASTM é baseado nos cálculos de Ozawa e Kissinger[25-27] e a reação obedece a equação 8:
A integração desta equação gera a equação 9:
onde: a é a taxa de reação;
Tpé a temperatura de pico,
b é a taxa de aquecimento; e
P(E/RT) é a função definida por Doyle[28, 29].
A função de Doyle corresponde a equação 10:
Assim, aplicando-se logaritmo na equação 9 e substituindo-se a função de Doyle, obtêm-se a equação 11:
Com essa equação é possível conhecer os valores de energia de ativação e o fator pré-exponencial[30,31].
Método Isotérmico
Utilizando-se o método isotérmico é possível avaliar dois tipos de reação: o de ordem n e o de ordem autocatalítica[32, 33].
Como a constante de velocidade da reação é função da temperatura, os cálculos dos parâmetros cinéticos necessitam de no mínimo três isotermas a temperaturas diferentes. Uma varredura dinâmica deve ser obtida para se verificar quais as temperaturas mais adequadas em que devem ser obtidas as isotermas, além de fornecer o valor do calor de reação total, DH0 , necessário nos cálculos. O ensaio deve ser feito com taxa de aquecimento entre 5 e 10°C/min. As temperaturas das isotermas são selecionadas com intervalos de 10 a 20°C entre as temperaturas inicial de cura e correspondente ao pico[10,17].
O modelo de ordem n assume que a reação segue a equação 12[33-35]:
onde a é a taxa de reação ou taxa de conversão em um dado tempo t.
Linearizando esta equação, obtém-se a equação 13:
Portanto, o coeficiente angular da reta será n e o coeficiente linear o log k.
O modelo autocatalítico considera ordens de reação independentes: m e n, como mostrado na equação 14:
Os dois parâmetros da/dt e a necessários para os cálculos são obtidos das isotermas de DSC. A taxa de reação é calculada pela divisão de dH/dt, a um tempo t, pela entalpia total, DH0,que é obtida da varredura dinâmica da amostra, obedecendo, portanto, a equação 6[33-40].
O valor de a é determinado pela medida do calor de reação parcial no tempo t, DHp dividido pelo calor total da reação isotérmica, DHiso, conforme mostram a Figura 4 e a equação 15.
Finalmente, com um mínimo de três isotermas obtêm-se os parâmetros cinéticos E e A de um gráfico de Arrhenius.
Escolha do método a ser utilizado
Como mencionado anteriormente, a reação entre epóxi-amina é bastante peculiar pois pode obedecer tanto uma cinética de ordem n como a autocatalítica[10]. Cabe ao estudioso verificar qual ordem de reação representa melhor o sistema analisado. Entretanto, existem parâmetros de grande valia que podem orientar na escolha do método a ser utilizado.
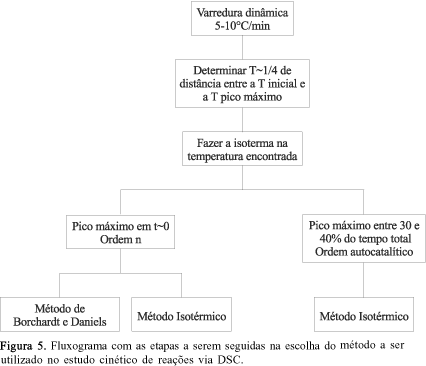
O fluxograma da Figura 5 mostra quais os passos que devem ser seguidos na escolha do método. Inicialmente, deve-se obter uma varredura dinâmica a uma taxa de aquecimento entre 5 e 10°C/min, determinar a temperatura próxima a um quarto da distância entre a temperatura inicial de cura e a temperatura correspondente ao pico máximo e, finalmente, efetuar uma isoterma nessa temperatura determinada[10,17,4143].
Se o pico máximo da isoterma estiver próximo a t= 0, como exemplificado na Figura 6 , o sistema obedece cinética de ordem n e pode ser estudado por Borchardt e Daniels ou pelo método isotérmico. Caso o pico máximo se forme entre 30 e 40% do tempo total da análise, como mostra a Figura 7, o sistema é autocatalítico e deve ser estudado exclusivamente pelo método isotérmico[10,17,33,42,43].
Conclusões
No estudo de cinética de cura existem dois métodos que podem ser utilizados: os métodos dinâmicos e o método isotérmico. Os métodos dinâmicos oferecem um rápido e aproximado estudo do comportamento cinético da reação em estudo. Por outro lado, limitam-se a um único tipo de reação, as de ordem n. Já o método isotérmico possui maior simplicidade na interpretação dos dados e maior aplicabilidade, descrevendo dois tipos de reação: as de ordem n e as autocatalíticas. Por não fazer aproximações nos cálculos, o método isotérmico representa com maior precisão a realidade cinética, entretanto, é um método mais demorado que os dinâmicos, uma vez que necessita de no mínimo três varreduras isotérmicas para se obter os resultados cinéticos.
O método de Borchardt e Daniels é bastante atrativo, pois necessita de uma única varredura dinâmica descrevendo uma cinética de cura de ordem n[11]. Porém, foi verificado em estudos que nesse método os valores de energia de ativação e o fator pré-exponencial aumentam com a taxa de aquecimento utilizado no experimento[11]. Além disso, tais valores são superestimados quando comparados com os valores de E e A obtidos pelo método isotérmico[11].
O método de Osawa é recomendado quando se observa linhas bases irregulares nas curvas de DSC, isotermas múltiplas ou a existência da influência do solvente na cura[11].
Agradecimentos
Os autores agradecem ao CNPq e à FAPESP pelo suporte financeiro e a Divisão de Sistemas Bélicos do IAE/CTA pelo auxílio nas análises térmicas.
Recebido:09/11/98
Aprovado:08/02/99
Michelle L. Costa, Departamento de Física/Instituto Tecnológico de Aeronáutica/Centro Técnico Aeroespacial, São José dos Campos ¾ SP/Tel: (012) 347-6434 ¾ Fax: (012) 347-6405, e-mail: leali@uol.com.br; Mirabel C. Rezende, Luiz C. Pardini, Divisão de Materiais/Instituto de Aeronáutica e Espaço/Centro Técnico Aeroespacial, São José dos Campos ¾ SP/ Tel: (012) 347-6420/6437 ¾ Fax: (012) 347-6405, e-mail: mirabelrezende@hotmail.com
- 1. Offringa, A.R. - Industrial Reporting, Composites: part A, p.329 (1996).
- 2. Newas, G.M. "Polymer matrix composites, in structure and properties of composites". v.13 . In: Chou, T.W. Material Science and Techonology Series. VCH Publishers, USA (1993).
- 3. Gilham, J.K. "Curing". In: Encyclopedia of Polymer Science and Engineering. 2.ed. [S.l.: s. n.], v. 4, (1986).
- 4. Loos, A. C. and Springer, G. S. "Curing of graphite/epoxy composites" Washington: NASA, (AFWAL - TR - 83 ž 4040), (1983).
- 5. Lee, H. and Neville, K. "Handbook of Epoxy Resin" McGraw-Hill, Plenum Press, USA (1967).
- 6. Manson, J.A . and Sperling, L.N. "Polymer blends and composites" Plenum Press, New York (1976).
- 7. Pardini,L.C. "Comportamento dinâmico mecânico e fratura de materiais compostos epóxi/elastômero/fibra de carbono". Tese de Mestrado, Universidade Federal de São Carlos, Brasil (1990).
- 8. Costa, M.L. "Estabelecimento de parâmetros de processamento de compósitos estruturais via análises térmica e viscosimétrica" Tese de Mestrado, Instituto Tecnológico de Aeronáutica, Brasil (1998).
- 9. Morales, A . R. " Morfologia e propriedades dinâmicas e mecânicas de resina epóxi/elastômero reativo". Tese de Mestrado, Universidade Federal de São Carlos, Brasil (1989).
- 10. Prime, R. B. "Thermosets, in thermal characterization of polymeric materials" Academic Press, cap. 5., p. 435-569, USA (1981).
- 11. Costa, M.L., Pardini, L.C., Rezende, M.C. "Cinética de cura de resinas epóxi no processamento de compósiots estruturais", in: Anais do 4o Congresso Brasileiro de Polímeros, Salvador ž BA, set/out, (1997).
- 12. Costa, M.L., Pardini, L.C., Rezende, M.C. "Cinética de cura de Formulações epóxi/diluente para compósitos estruturais", in: Anais do I Congresso Brasileiro de Análise Térmica e Calorimétrica, Poços de Caldas - SP, (1998).
- 13. Shechter, L. , Wynstra, J., Kurkjv, R.P. Ind. Eng. Chem., v. 48, p.94-97, (1956).
- 14. Dusek, K. and Bleha, M. Journal Sci. Poly. Chem., v.151, p. 2393-2400, (1977).
- 15. Dusek, K and Ilasky, M. Colloid Polymer Science, v.25, p.605, (1980).
- 16. Byrne, C. A ., Hagnauer, G. L., Schneider, N. S., Lenz, R. W. Polymer Composites, v.1, p.71-76, (1980).
- 17. Jang, W. A review of DSC kinetic methods. Du Pont Instruments.(1981).
- 18. Sichina, W.J. Du Pont Application Brief no TA93, Autocatalyzed Epoxy Cure Predictions Using Isothermal DSC Kinetics (1989).
- 19. Sichina, W.J. Du Pont Application Brief no TA98. Considerations in modeling of kinetics by thermal analysis, (1989).
- 20. Fair, P.G. and Gill, P.S. Du Pont Application Brief no TA91.Epoxy Prepreg Cure Predictions Using Borchardt and Daniels DSC Kinetics, (1989).
- 21. Borchardt, H.J. And Daniels, F.J. American Chemical Society, v.79, p.41, (1956).
- 22. Miranda, M.I.G., Tomedi, C., Bica, I.D., Samios, D. Polymer, v.38, p. 1017-1022, (1997).
- 23. Miranda, M.I.G. E Samios, D. European Polymer Journal, v.33, p.325-329, (1997).
- 24. Barret, K.E. Journal Appl. Polymer Science, v.3, p. 1617, (1970).
- 25. Ozawa, T. Bull. Chem. Soc. Jpn., v.38, p. 1881, (1965).
- 26. Ozawa, T. Journal Thermal Anal., v.2, p.301, (1970).
- 27. Kissinger, H.E. Analytical Chemistry, vol.29, p.1702, (1957).
- 28. Doyle, C.E. Anal. Chem, v.33, p.77, (1961).
- 29. Doyle, C.E. Nature, vol.207, p.290, (1965).
- 30. Rogers, R.N. and Smith, L.C. Analytical Chemistry, vol.39, p.1336, (1967).
- 31. Duswalt, A.A. Thermochimal Acta, vol.8, p.57, (1974).
- 32. Berglund, L.A . SAMPE Journal, v.27, n. 2, p. 27-37, Mar./Apr. , (1991).
- 33. Nam, J. And Seferis J.C. Journal of Applied Polymer Science, v. 50, p.1555-1564, (1993).
- 34. White, S.R. And Mather, P.T. Composite Polymers, v.4, n. 6, p.403-422, (1991).
- 35. Stutz, H., Mertes, J., Neubecker, K. Journal of Polymer Science: Part A: Polymer Chemistry, v.31, p.1879-1889, (1993).
- 36. Sykora, V., Spacek, V., Dobas, I. Journal of Applied Polymer Science, v.54, p.1463-1467, (1994).
- 37. Richardson, M.J. Polymer Testing, v.4, p.101, (1984).
- 38. Barton, J.M. Polymer, v.21, p.41-59, (1976).
- 39. Sourour, S. And Kamal, M . R. Thermochimica Acta, v.14, p.41-59, (1976).
- 40. Galy, J., Sabra, A . Pascault, J. P. Polymer Engineering and Science, v.26, p.1514-1523, (1986).
-
41The Perkin - Elmer Corporation. Operating Instruction for the DSC 7 Isothermal Kinetics Software Kit. N539-0266, version 3.0. USA, (1994).
-
42The Perkin - Elmer Corporation Perkin-Elmer Thermal Analysis Newsletter no 50, Nowalk, C.T. (1994).
-
43The Perkin - Elmer Corporation Perkin-Elmer Thermal Analysis Newsletter no 56, Nowalk, C.T. (1994).
Datas de Publicação
-
Publicação nesta coleção
24 Jun 2010 -
Data do Fascículo
Jun 1999
Histórico
-
Aceito
08 Fev 1999 -
Recebido
09 Nov 1998