Abstract
Aqueous two-phase systems (ATPSs) have found wide application in the separation of biological molecules such as amino acids, peptides and proteins. Most of the research in this area has been dedicated to experimental determination and less effort has been devoted to the proper thermodynamic modeling of these systems. This work presents a new model for ATPS that accounts for solvation effects between polymer and water molecules, which are commonly reported to be responsible for phase separation. The model uses the Flory-Huggins equation as a starting point and modifies the combinatorial term by considering the presence of a hydration shell. The modified equation parameters were fit to a number of isotherms of poly(ethylene glycol) - dextran systems, and the results obtained are reported herein. These results show that the adopted modification leads to remarkable improvements in the performance of the model.
Thermodynamic; liquid-liquid equilibrium; excess Gibbs energy; aqueous two-phase systems
A SOLVATION-BASED THERMODYNAMIC MODEL FOR AQUEOUS TWO-PHASE SYSTEMS
P.A Pessôa Filho and R.S.Mohamed* * To whom correspondence should be addressed
Universidade Estadual de Campinas, Faculdade de Engenharia Química,
Cx. P. 6066, CEP 13083-970, Phone +55 (19) 3788-3932,
Fax +55 (19) 3788-3922, Campinas - SP, Brazil
E-mail mohamed@feq.unicamp.br
(Received: May 15, 2001 ; Accepted: November 1, 2001)
Abstract - Aqueous two-phase systems (ATPSs) have found wide application in the separation of biological molecules such as amino acids, peptides and proteins. Most of the research in this area has been dedicated to experimental determination and less effort has been devoted to the proper thermodynamic modeling of these systems. This work presents a new model for ATPS that accounts for solvation effects between polymer and water molecules, which are commonly reported to be responsible for phase separation. The model uses the Flory-Huggins equation as a starting point and modifies the combinatorial term by considering the presence of a hydration shell. The modified equation parameters were fit to a number of isotherms of poly(ethylene glycol) - dextran systems, and the results obtained are reported herein. These results show that the adopted modification leads to remarkable improvements in the performance of the model.
Keywords: Thermodynamic, liquid-liquid equilibrium, excess Gibbs energy, aqueous two-phase systems.
INTRODUCTION
Aqueous two-phase systems, hereafter called ATPSs, are formed when either two polymers or a polymer and a salt are added to water at concentrations in a specific range. Not all polymers nor all salts induce this phase separation. Among the pairs for which phase separation occurs are poly(ethylene glycol) (PEG) and dextran (the most extensively studied system), poly(vinyl alcohol) (PVA) and dextran, PVA and PEG, PEG and ammonium sulfate, and PEG and sodium sulfate.
The main features of ATPSs include the fact that both phases are water-rich (usually more than 85% w/w in water) and have similar densities and low interfacial tensions (Albertsson, 1986).
Since the pioneering work of Albertsoon in the mid-1950's, it has been established that biological solutes added to these systems tend to partition unevenly between the phases (Albertsson, 1986). This fact, along with the features cited above, makes ATPS a convenient environment for the separation of complex mixtures of biomaterials. In fact, the main interest in studying these systems lies in their application as a separation technique in biomaterial-containing systems (Fisher and Sutherland, 1989). A wide variety of applications that included the separation of whey proteins (Alves et al., 2000), alkaline xylanase (Bim and Franco, 2000) and cell particles (Morré and Morré, 2000), just to name a few, has been suggested.
A necessary, but often neglected, condition for the proper design of any separation equipment is the existence of a reliable thermodynamic model. Research on ATPSs and their applications has concentrated on the gathering of experimental data, with less effort being devoted to the proper thermodynamic modeling of these systems. Excess Gibbs free energy models that have been employed to describe nonideality in ATPSs range from classical ones, such as those based on the virial series, to purely empirical ones (Cabezas, 1996). Of those models widely used, some employ the Flory-Huggins equation due to reasonable accuracy and simple mathematical structure.
Some authors (Diamond and Hsu, 1992; Sargantanis and Karim, 1997; and Hino and Prausnitz, 1998, among others) used the classic formulation in modeling ATPSs; however, the quantitative results are not so good, and some authors make use of the equation only for qualitative analyses (Johansson et al., 1998). Furthermore, Holtzer (1992,1994) pointed out that the use of the Flory-Huggins equation in its original form to model aqueous solutions of polymers constitutes an oversimplification of the real situation.
This work is part of a broad research project currently in progress and aimed at the thermodynamic modeling of the partitioning of biomolecules in ATPSs. The paper presented here deals with phase equilibrium calculations in the formation of ATPSs. Specifically, the aim of this work is to modify the Flory-Huggins model in order to account for the solvation of polymer molecules in aqueous solutions, i. e., to account for the fact that water molecules may bond to some sites on the polymer molecule, leading to the formation of a hydration shell around each one. As a result of this improved description of the physics in these systems, the quantitative representation of the model is expected to be enhanced.
THEORETICAL DEVELOPMENT
There is wide agreement in the literature that polymer molecules in water solution may undergo solvation. Experimental evidence to support this is given, for instance, by Kjellander and Florin (1981), who concluded that the solubility of PEG in water is due to the bonding of water molecules to the oxygen atoms in the PEG molecules. Further evidence of the existence of solvation in this system can be found in Goldstein (1984), Karsltröm (1985), Bordi, Cametti and di Biasio (1988), Yu and Nishiumi (1992) and Yu et al. (1993).
The hydration shell is the basis of the excluded volume theory of Guan et al. (1993a), used to explain phase separation in ATPSs. The theory, however, can only be used to fit the binodal curve and is not able to describe phase equilibrium. Guan et al. (1993b) tried to overcome this shortcoming by creating a mixed model that couples the expression previously developed for the binodial curve with a virial expansion. The fact that the model for the binodal curve (1993a) can be successfully used to describe salt-polymer systems can be attributed more to the convenient mathematical form of the equation, than to a correct description of the physics involved. Moreover, the coupling of this model with the virial equation can be achieved only on an approximate basis and does not constitute an excess Gibbs energy model on its own. The model presented in this work is an extension of these studies and modifies the entropic term of the Flory-Huggins equation by assuming that all polymer molecules are surrounded by a fixed number of water molecules; this number is not assumed to be a function of concentration. The development follows Hildebrand's approach (Flory, 1953) to the Flory-Huggins equation, which does not make use of the lattice structure to obtain the final expression.
The Flory-Huggins equation belongs to the general class of lattice models, whose common feature is that the behavior of the liquid mixture is modeled as a crystalline solid (Prausnitz et al., 1999), i. e., the molecules are assumed to remain in a specific position instead of moving freely as in the gas state. Despite all the cumbersome mathematical steps that must be followed to obtain it, the final Flory-Huggins expression for the Gibbs free energy of mixing is simple. It consists of two terms. The first one is the entropy of mixing, which is reckoned by accounting for molecule sizes, regardless of any molecular interaction (Flory, 1942):
wherein S is the entropy, fi is the volumetric fraction, ni is the amount of substance and R is the ideal gas constant. The second term is the enthalpy of mixing, known as Scatchard-Hildebrand's equation (Flory, 1953):
in which H is the enthalpy, T is the absolute temperature, Vi is the volume per amount of substance and cij is the interaction parameter, which is obtained through fitting experimental equilibrium data (either liquid-vapor or liquid-liquid). Equations (1) and (2) apply to binary systems and their extension to systems with more than two components is straightforward.
The expressions above show the classic expression of the Flory-Huggins model. The basis of the development presented here centers on the assumption that each polymer molecule is bonded to a defined number of water molecules and thus is a molecule of higher volume per amount of substance. Consequently this polymer molecule is less free to translate than if it were not bonded, for it is always accompanied by a specific number of water molecules.
Therefore, the total free volume available for the polymers is:
wherein ki is the number of water molecules bonded to each molecule of polymer i, Vfi is the free volume and vf is the fraction of the molar volume that corresponds to the free volume; this fraction is supposed to be independent of the compound considered. The subscript s stands for the solvent (water).
As to the water itself, the volume per amount of substance will not be altered. However, the total free volume available for its molecules will be less than if there were no hydration because some molecules will be bonded to the polymer molecules, and therefore,
The total free volume is insensitive to solvation, and thus,
Using these definitions, the entropy of mixing is written as
One should note that the number of moles of water is changed because only the nonbonded water molecules are to be distributed in the remaining free volume. It can also be observed that some inconsistency is introduced in the limit when the amount of water approaches zero. This situation, however, is never encountered in ATPSs for which the model is applied since both phases are always water-rich (usually more than 85% w/w). Equation (6) is similar to that of Glueckauf (1955) for the modeling of aqueous electrolyte solutions.
For the sake of simplicity, the following apparent quantities are defined:
a) amount of substance:
 = nj for the polymers
= nj for the polymers
 = ns -
= ns - niki for the water.
niki for the water.
b) volume per amount of substance:
 = Vi + kiVs for the polymers
= Vi + kiVs for the polymers
 = Vs , for the solvent.
= Vs , for the solvent.
An apparent volumetric fraction is defined for all components regardless of their condition:
The entropic term can then be written as
The enthalpic term remains the same. Solvation is believed to cause a strong deviation in the random distribution, but not to affect the interactions among molecules. For this reason, in many developments in which the Flory-Huggins equation is modified to allow for hydrogen bonding, the enthalpic term remains unchanged (Kretschmer and Wiebe, 1954). Therefore, the Scatchard-Hildebrand (Flory, 1953) term is maintained in this development:
As polymers have a molecular weight much higher than that of water, the use of molar fractions is inconvenient due to the very small mole fractions of polymer that results, which may thereby hinder numerical methods used in finding the minimum value for the Gibbs free energy in phase equilibrium calculations. In order to rewrite the expressions so that mass fractions can be used, we define the specific apparent volumes as
 = Vmi + kiVms
= Vmi + kiVms for the polymers
for the polymers
 = Vms for the water
= Vms for the water
in which M is the mass per amount of substance. The expression for the effective mass (m) is also defined as
 = mj for the polymers
= mj for the polymers
 = ms -
= ms - miki
miki for the water.
for the water.
The apparent volume fraction is rewritten as
The model presented above (eqs. (8) through (10)) can now be applied to calculate tie lines in systems formed of two polymers and water. The equilibrium compositions are those that lead to a minimum Gibbs free energy. This is the necessary and sufficient condition to assure that equilibrium is attained. It is not necessary to calculate activities and activity coefficients if phase equilibrium is calculated by this method. However, activities may be calculated to check whether the necessary (but not sufficient) condition of equilibrium (the equality of activities) is satisfied. Besides, the calculation of activities can provide some useful information on the behavior of the system.
When calculating the activities, one needs to obtain the derivative of the enthalpic and entropic terms with respect to the amount of substance of the compounds:
in which ai is the activity, G is the Gibbs energy and P is the pressure. The enthalpic term is that found in the original Flory-Huggins model. The entropic term, however, is quite different; the general expression for its derivative is
The derivative,  /¶ni, almost always has the same value that it would have if
/¶ni, almost always has the same value that it would have if  were replaced by nj (1 if i=j, and 0 otherwise). The only exception is the situation in which j is the solvent and i is a polymer; in this case, one obtains
were replaced by nj (1 if i=j, and 0 otherwise). The only exception is the situation in which j is the solvent and i is a polymer; in this case, one obtains
The derivative,  /¶ni , requires more care, since each possible combination of i and j leads to different results as shown below.
/¶ni , requires more care, since each possible combination of i and j leads to different results as shown below.
a) when both i and j represent the same polymer, we have
b) i and j represent different polymers:
c) j represents a polymer and i the solvent:
d) i represents a polymer and j the solvent:
e) both i and j represent the solvent:
RESULTS AND DISCUSSION
The parameters of the model developed were fit to a series of 73 PEG-dextran systems. The hydration number (k) was first regarded as an interaction parameter, and its value, along with the usual interaction parameters of the Flory-Huggins equation, was obtained by minimization of the following objective function:
wherein z is the mass fraction, r is the number of experimental points and c is the total number of solutes (water is not counted as one of them). The calculated compositions are those obtained by a flash calculation using the composition of the middle point on the tie line as the feed.
Phase equilibrium, as mentioned above, was calculated by minimizing the Gibbs free energy of the system. In order to assess the performance and the improvement of the correlation obtained with the model developed, the results obtained are compared to those found using the UNIQUAC equation (Abrams and Prausnitz, 1975) and the original Flory-Huggins equation. An optimal set of parameters was obtained for different PEG-dextran systems at different temperatures. A mean value of the hydration number was subsequently calculated for a given size of polymer molecule. The other parameters were obtained by keeping this hydration number constant.
As an example of the analysis carried out for each of the systems considered, the results for systems containing PEG 3400 are presented. Similar results were obtained for other systems. In Table 1, the values of the objective function, defined in eq. (19), are shown for the particular set of optimal parameters.
It is clear from these results that the number of adjustable parameters has little influence on the quality of the modeling. The UNIQUAC equation has six adjustable parameters, while the Flory-Huggins has three; nevertheless, the performance of the latter is slightly better. Thus, the number of adjustable parameters can not be associated with the better performance of a specific model.
When obtaining the parameters, the hydration number for dextran was set at zero, as the optimal value obtained was always insignificant (less than 1.0) and has no influence on the performance of the model. Therefore, in this specific situation only one adjustable parameter is added to the model, the hydration number for the PEG molecule which is given in the Table 2.
Even though the hydration number, ki, should, in principle, be regarded at least as an integer number since it is the number of water molecules bonded to each PEG molecule, noninteger values were accepted as well, since they are adjustable parameters representing an average hydration number. It must also be recalled also that the polymer molecules themselves show some variation in number of constituent units.
The mean value of ki obtained from Table 2 is 100.7. If one considers the number of oxygen atoms in this PEG molecule (an average of 77), this means that each oxygen atom will be bonded to at least one water molecule and one in every three oxygen atoms will be bonded to two water molecules. The optimization procedure was conducted again keeping the value for ki constant at 100.7, and the results obtained are shown in Table 3.
It can be seen that keeping the value of kPEG constant at this average value had a very slight effect on the results. Therefore, once ki values for different polymers are obtained, they can be applied to all other ATPSs involving these particular sets of polymers. In other words, ki can in fact now be regarded as a characteristic value of the molecule itself rather than just an adjustable parameter.
The tie-line slope (TLS) is defined for a pair of compositions in equilibrium as
In some cases the value of the TLS is a characteristic of the system at the given temperature, which means that the tie lines are parallel. This fact was pointed out by Zaslavsky (1995), who even uses the TLS as an index of the reliability of equilibrium data. This was observed for many of the systems studied and is closely approximated for the tie lines obtained with this model, as can be seen in Table 4.
The behavior of the modified equation can be analyzed with the help of Figures 1 and 2 for the PEG 3400 - dextran T40 and PEG 3400 - dextran T70 systems at 22oC, respectively. There is always a good correlation between the equilibrium compositions, even close to the critical point.
As seen previously, the hydration number can be regarded as a characteristic value for each polymer. In order to allow for extrapolations, the hydration number for PEG was correlated as a function of the molecular weight of the polymer and the following correlation was obtained:
The above correlation was used to predict the hydration number for PEG molecules with molecular weights that do not fall within the data used to establish the correlation. The model was subsequently applied for the prediction of equilibrium compositions in 23 ATPS containing these polymers. Some of the results obtained are presented in Table 5 (experimental data from Grobmann et al., 1995), where the modified model is compared with the original Flory-Huggins equation. It is seen that the modified model not only shows a better performance, but also can be used to model systems which the Flory-Huggins equation is not able to fit. The tie lines for the PEG35000 and dextran 500 system at 4°C are depicted in Figure 3.
The data bank used to generate equation (21) comprised systems containing PEG with molecular weights up to 20000. As can be seen in Table 5 and Figure 3, the model provides good predictions of equilibrium compositions in ATPS systems containing PEG with molecular weights both within in the range tested in this study but also outside it.
CONCLUSIONS
It was possible to incorporate the effect of hydration of polymer molecules in aqueous solutions into the Flory-Huggins model of excess Gibbs free energy in a simple way. Once the parameters had been fit to experimental equilibrium data, the model predicted that dextran molecules were practically free of hydration water, while PEG molecules were strongly bonded to water molecules. Once a characteristic hydration number is obtained for a specific polymer, it can be used for this polymer in all ATPSs containing it. A remarkable improvement was achieved by using the proposed model to correlate equilibrium data: the new model shows a better correlation of equilibrium compositions in ATPSs containing polymers. The model was also able to provide good consistent representation of phase equilibrium. It was possible to correlate the hydration number and to use the model in a predictive way with equally good results.
ACKNOWLEDGMENT
Financial support from FAPESP to PAPF and from the CNPq to RSM is gratefully acknowledged.
NOMENCLATURE
Latin Letters
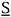
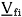
Greek Letters
Acronyms
- Abrams, D. S. and Prausnitz, J. M., Statistical Thermodynamics of Liquid Mixtures: a New Expression for the Excess Gibbs Free Energy of Partly or Completely Miscible Systems, AIChE J., 21, 116 (1975).
- Albertsson, P.-A., Partition of Cell Particles and Macromolecules, 3rd ed., Wiley, New York (1986).
- Alves, J. G. L. F., Chumpitaz, L. D. A., da Silva, L. H. M., Franco, T. T. and Meirelles, A. J. A., Partitioning of Whey Proteins, Bovine Serum Albumin and Porcine Insulin in Aqueous Two-Phase Systems, J. Chromatogr. B, 743, 235-240 (2000).
- Bim, M. A. and Franco, T. T., Extraction in Aqueous Two-Phase Systems of Alkaline Xylanase Produced by Bacillus pumilus and its Application in Kraft Pulp Bleaching, J. Chromatogr. B, 743, 349-356 (2000).
- Bordi, F., Cametti, C. and di Biasio, A., Electrical Conductivity Behavior of Poly(ethylene oxide) in Aqueous Electrolyte Solutions, J. Phys. Chem., 92, 4772-4777 (1988).
- Cabezas, H., Theory of Phase Formation in Aqueous Two-Phase Systems, J. Chromatogr. B, 680, 3-30 (1996).
- Diamond, A. D. and Hsu, J. T., Fundamental Studies of Biomolecule Partitioning in Aqueous Two-Phase Systems, 34, 1000-1014 (1989).
- Diamond, A. D. and Hsu, J. T., Correlation of Polymer Partitioning in Aqueous Two-Phase Systems, AIChE Symposium Series, 88, 105-111 (1992).
- Fisher, D. and Sutherland, I. A., Separations Using Aqueous Phase Systems, New York, Plenum Press (1989).
- Flory, P. J., Thermodynamics of High Polymer Solutions, J. Chem. Phys., 10, 51-61, (1942).
- Flory, P. J., Principles of Polymer Chemistry, Ithaca, Cornell University Press (1953).
- Glueckauf, E., The Influence of Ionic Hydration on Activity Coefficients in Concentrated Electrolyte Solutions, Trans. Faraday Soc., 51, 1235-1244 (1955).
- Goldstein, R. E., On the Theory of Lower Critical Solution Points in Hydrogen-Bonded Mixtures, J. Chem. Phys, 80, 5340-5341 (1984).
- Grobmann, C., Tintinger, R., Zhu, J. and Maurer, G., Aqueous Two-Phase Systems of Poly(ethylene glycol) and Dextran - Experimental Results and Modeling of Thermodynamic Properties, Fluid Phase Equilibria, 106, 111-138 (1995).
- Guan, Y., Lilley, T. H. and Treffry, T. E., A New Excluded Volume Theory and its Application to the Coexistence Curves of Aqueous Two-Phase Systems, Macromolecules, 26, 3971-3979 (1993a).
- Guan, Y., Lilley, T. H. and Treffry, T. E., Theory of Phase Equilibria for Multicomponent Aqueous Solutions: Applications to Aqueous Polymer Two-Phase Systems, Chem. Soc. Faraday Trans., 89, 4283-4298 (1993b).
- Hino, T. and Prausnitz, J. M., Lattice Thermodynamics for Aqueous Salt-Polymer Two-Phase Systems, Journal of Applied Polymer Science, 68, 2007-2017 (1998).
- Holtzer, A., The Use of Flory-Huggins Theory in Interpreting Partitioning of Solutes Between Organic Liquids and Water, Biopolymers, 32, 711-715 (1992).
- Holtzer, A., Does Flory-Huggins Theory Help in Interpreting Solute Partitioning Experiments Biopolymers, 34, 315-320 (1994).
- Johansson, H.-O., Karlström, G., Tjerneld, F. and Haynes, C. A., Driving Forces for Phase Separation and Partitioning in Aqueous Two-Phase Systems, J. Chromatogr. B, 711, 3-17 (1998).
- Karlström, G., A New Model for Upper and Lower Critical Solution Temperature in Poly(ethylene oxide) Solutions, J. Phys. Chem., 89, 4962-4964 (1985).
- Kjellander, R. and Florin, E., Water Structure and Changes in Thermal Stability of the System Poly(ethylene oxide)-Water, J. Chem. Soc. Faraday Trans. I, 77, 2053-2077 (1981).
- Kretschmer, C. B. and Wiebe, R., Thermodynamics of Alcohol-Hydrocarbon Mixtures, J. Chem. Phys., 22, 1697-1701 (1954).
- Morré, , D. M. and Morré, D. J., Aqueous Two Phase Partitioning Applied to the Isolation of Plasma Membranes and Golgi Apparatus from Cultured Mammalian Cells, J. Chromatogr. B, 743, 377-388 (2000).
- Prausnitz, J. M., Lichtenthaler, R. N. and Azevedo, E. G., Molecular Thermodynamics of Fluid-Phase Equilibria, 3rd ed., Prentice-Hall, Englewood Cliffs (1999).
- Sargantanis, I. G. and Karim, M. N., Prediction of Aqueous Two-Phase Equilibrium Using the Flory-Huggins Model, Ind. Eng. Chem. Res., 36, 204-211 (1997).
- Yu, M. and Nishiumi, H., Theory of Phase Separation in Mixtures With Lower Critical Solution Temperature, J. Phys. Chem., 96, 842-845 (1992).
- Yu, M., Nishiumi, H. and Arons, J. S., Thermodynamics of Phase Separation in Aqueous Solutions of Polymers, Fluid Phase Equilibria, 83, 357-364 (1993).
- Zaslavsky, B. Y., Aqueous Two-Phase Partitioning, Marcel Dekker, New York (1995).
Publication Dates
-
Publication in this collection
17 Apr 2002 -
Date of issue
Dec 2001
History
-
Accepted
01 Nov 2001 -
Received
15 May 2001






























