Abstract
Growth and product formation by a selected variant of Aspergillus oryzae showing high alpha-amylase production was studied in continuous cultivations carried out at six different specific growth rates, using glucose as the growth-limiting nutrient. The analysis of the steady-state data revealed that the variant and wild-type strains were similar with respect to glucose uptake system and stoichiometric coefficients. However, the variant was capable of maintaining an enzyme production as high as 40 FAUgDW-1h-1 at a dilution rate of 0.2 h-1, while the wild-type strain reached a maximum specific alpha-amylase production rate of 17 FAUgDW-1h-1 at a dilution rate of 0.1 h-1. Using a morphologically structured model originally proposed for the wild-type strain, it was possible to describe enzyme production, biomass formation and glucose consumption after modification of a few parameters to adjust the model to the characteristics of the selected variant.
Aspergillus oryzae; alpha-amylase; continuous cultivations; morphologically structured model
a05v19n1
GROWTH AND ENZYME PRODUCTION DURING CONTINUOUS CULTURES OF A HIGH AMYLASE-PRODUCING VARIANT OF Aspergillus Oryzae
T.C.Zangirolami1* * To whom correspondence should be addressed , M.Carlsen2, J.Nielsen2 and S.B.Jørgensen3
1Departamento de Engenharia Química, Universidade Federal de São Carlos, Rodovia Washington Luiz, km 235,
CEP 13.565-905, Phone: (16) 260-8264, Fax: (16) 260-8266, São Carlos - SP, Brazil.
E-mail: teresacz@power.ufscar.br.
2Center for Process Biotechnology, CPB, Department of Biotechnology, Building 223, Technical University of
Denmark, Lyngby, DK-2800, Phone: (45) 45252600, Fax: (45) 45884922, Denmark.
3Computer Aided Process Engineering Center, CAPEC, Department of Chemical Engineering, Building 229, Technical
University of Denmark, Lyngby, DK-2800, Phone: (45) 45252800, Fax: (45) 45882258, Denmark.
(Received: March 23, 2001 ; Accepted: November 22, 2001
Abstract - Growth and product formation by a selected variant of Aspergillus oryzae showing high a-amylase production was studied in continuous cultivations carried out at six different specific growth rates, using glucose as the growth-limiting nutrient. The analysis of the steady-state data revealed that the variant and wild-type strains were similar with respect to glucose uptake system and stoichiometric coefficients. However, the variant was capable of maintaining an enzyme production as high as 40 FAUgDW-1h-1 at a dilution rate of 0.2 h-1, while the wild-type strain reached a maximum specific a-amylase production rate of 17 FAUgDW-1h-1 at a dilution rate of 0.1 h-1. Using a morphologically structured model originally proposed for the wild-type strain, it was possible to describe enzyme production, biomass formation and glucose consumption after modification of a few parameters to adjust the model to the characteristics of the selected variant.
Keywords: Aspergillus oryzae, a-amylase, continuous cultivations, morphologically structured model.
INTRODUCTION
Since ancient times, filamentous fungi have been well known in many Asian countries for the starch and cellulose degrading enzymes they naturally secrete. With the development of more effective cultivation techniques and continuous screening for high-producing strains, the large-scale industrial production of enzymes in submerged cultures became an increasingly attractive business (Fogarty, 1994). Aspergillus oryzae plays a major role in the production of many commercial enzymes, such as a-amylase, glucoamylase, lipase and protease, among others (Archer and Wood, 1995; Harvey and McNeil, 1994; Oxenbøll, 1994).
With the development of molecular biology and gene-cloning technology for fungi, there has been considerable commercial interest in exploiting the Aspergilli as hosts for the production of fungal and mammalian proteins (Harvey and McNeil, 1994). Aspergilli are capable of carrying out efficient post-translational modifications and have the ability to secrete large amounts of correctly folded enzymes into the extracellular medium. Furthermore, A. oryzae and A. niger are well-characterized industrial microorganisms, which have obtained GRAS (Generally Regarded As Safe) status from the FDA and WFO (Fogarty, 1994; Oxenbøll, 1994).
In spite of its industrial importance, only recently studies have been conducted to elucidate the mechanisms behind enzyme production, growth and substrate uptake in Aspergillus oryzae. Carlsen et al. (1996) performed a physiological study of the a-amylase-producing wild-type strain of A. oryzae (A1560), using continuous cultivations in well-controlled bioreactors. The results indicated that enzyme production was closely connected to the growth of the fungus, while enzyme synthesis was tightly regulated by the concentration of glucose in the cultivation medium, resulting in lower a-amylase activity for increasing specific growth rates due to glucose repression. Based on the results described in Carlsen et al. (1996) and on the quantification of A. oryzae morphology, Agger et al. (1998) proposed a morphologically structured model, containing three morphological compartments, glucose concentration and a-amylase activity as model states. The model predicted fairly well biomass formation, enzyme production and glucose uptake in batch, fed-batch and continuous cultivations.
Several morphologically structured models (Paul and Thomas, 1996; Zangirolami et al., 1997; Agger et al., 1998) have focused on the description of variables such as concentrations of glucose, biomass and metabolic products, which are difficult to measure on-line. On the other hand, relevant, real-time information is available on the composition of exhaust gas and on the measurement of dissolved oxygen concentration. By incorporating the oxygen and carbon dioxide fractions in the exhaust gas as well as the dissolved oxygen concentration as model states, morphologically structured models can be applied as process models, either for control purposes or for on-line estimation of other process variables.
The present work describes the steady-state results obtained in glucose-limited continuous cultivations of a high a-amylase-producing variant, which was isolated from continuous cultures of the A. oryzae wild-type strain. The morphologically structured model proposed by Agger et al. (1998) was modified and successfully employed to describe growth, enzyme production and glucose uptake of the isolated variant as a function of the specific growth rate. The model was further expanded in order to include the fractions of carbon dioxide and oxygen in the exhaust gas as well as the dissolved oxygen concentration in the liquid phase.
MATERIAL AND METHODS
Microorganism
A morphological variant of Aspergillus oryzae A1560 donated by Novo Nordisk A/S (Bagsværd, Denmark) was used in the experiments. As described by Zangirolami et al. (2000), the high a-amylase-producing variant arose spontaneously during chemostat experiments carried out with the wild type at a dilution rate of 0.1 h-1. The selection was completed after 200-300 hours of continuous cultivation, when the culture population was dominated by the morphological variant.
Medium Composition
The composition of the inlet feed medium used during inoculum cultivation and continuous cultures was as follows (in g.l-1): glucose, 4.0; (NH4)2SO4, 2.5; MgSO4·7H2O, 1.0; NaCl, 1.0; CaCl2·2H2O, 0.1; KH2PO4, 0.75; 1 ml.l-1 of tracer solution and 20.0 ml.l-1 of anti-foam SB2121, from Schill and Seilacher (Germany). The composition of the tracer solution was as follows (in g.l-1): ZnSO4·7H2O, 14.3; CuSO4·7H2O, 2.5; CuSO4·5H2O, 2.5; NiCl2·6H2O, 0.5 and FeSO4·7H2O, 13.8. All reactants were purchased from Sigma.
Inoculum Preparation and Starting up of Chemostats
All continuous cultures were started by transferring aseptically 400 g of cultivation medium from a chemostat conducted at a dilution rate of 0.1 h-1, where the population consisted of the high a-amylase-producing, fast-growing variant (Zangirolami et al., 2000), to the bioreactor filled with 1100 g of continuous culture medium. Following inoculation, the cultivations were operated at a dilution rate of 0.1 h-1 for at least 5 residence times in order to assure that the a-amylase activity at steady state was comparable to the level reached in previous experiments. Then the dilution rate was increased or decreased from the reference dilution rate (0.1 h-1) to the desired value.
Experimental Setup
The experimental setup consisted of a B. Braun Biotech (Germany) bioreactor, load cells for activation of the harvest pump as well as a mass flow controller for regulation of air flow rate and an acoustic gas analyzer for measurement of oxygen and carbon dioxide concentrations in the exhaust gas (Zangirolami, 1998). The Shiva software, developed and implemented in cooperation with BIA, Ljubljana (Slovenia) was employed for continuous monitoring of the cultivation process and for on-line data acquisition (Podgornik et al., 1994).
All experiments were carried out at a constant load of 1500 g for dilution rates ranging from 0.06 to 0.2 h-1. The culture was agitated at 700 rpm, the air flow rate was 0.75 l.min-1 and the temperature was maintained at 30 oC. The pH was regulated at 6.0±0.03 using 2 M NaOH.
Determination of Biomass Concentration
Weighed samples of culture medium (approx. 20 g) were filtered on Whatman filter paper (Maidstone, UK) with a pore size of 70 mm and washed with the same volume of NaCl 0.9% (wt./vol.). The harvested cells were then dried to constant weight at 105 oC for 24 to 48 h to determine the dry weight content of the medium (expressed as g DW.kg-1, i.e., gram of dry biomass per kg of medium).
Determination of a-Amylase Activity
The extracellular a-amylase activity (in units of FAU.ml-1) was determined by a modified Boehringer Mannhein method. One FAU is the amount of a-amylase which at 37 oC hydrolyses 5.26 g of starch per hour (Carlsen et al., 1996). The method is based on an enzymatic colorimetric test with EPS (4,6-ethylidene(G7)-p-nitrophenyl(G1)-a,D-maltoheptaoside) as the main substrate which is cleaved by a-amylase (Zangirolami, 1998). The method was implemented in a Cobas-Mira automatic analyzer from Roche (France). The a-amylase standard was donated by Novo Nordisk, Denmark (Fungamyl, batch no. AFN015192-3).
Determination of Glucose Concentration
The glucose concentration was determined enzymatically using glucose dehydrogenase -Glucose GDH assay from Roche (Zangirolami, 1998). The detection limit is 1 mg.l-1 of glucose. The method was implemented in a Cobas-Mira automatic analyzer from Roche.
Determination of the Hypha Active Fraction
Characterization of the microscopic morphology was carried out using an image analysis system, which consisted of a Quantimet Q600 image analyzer (work station) from Leica, Cambridge Ltd. (United Kingdom), connected to a Nikon (Japan) optihot-2 microscope and a video camera (Spohr, 1997).
The fraction of the active region was measured using a combination of fluorescence microscopy and automated image analysis, as described in Agger et al. (1998). The 3,3-dihexyloxocarbocyanine (DiOC6) and Calcofluor White (CFW) fluorescent probes were employed for simultaneous staining of organelles inside the cells (mitochondria) and the cell wall, respectively. The samples for morphological analysis were taken from the culture medium at various cultivation times, immediately mixed with the fluorescent probes and examined in the image analysis system. The fraction of active region was calculated as the ratio between the area stained by DiOC6 and the area stained by CFW.
Model Description
The morphologically structured model proposed by Agger et al. (1998) is based on a division of the hyphal elements into three different regions, as illustrated in Figure 1:
1) active region: responsible for the uptake of substrate and growth of the hyphal element. It contains practically all of the organelles and cytoplasm. a-Amylase synthesis is assumed to occur only in the active region;
2) hyphal apex: where building of a new cell wall and extension takes place;
3) hyphal region: constitutes the degenerated part of the hyphal elements, which are inactive, vacuolated and devoid of any organelles
(a) Metamorphosis Reactions and Kinetic Expressions
Two metamorphosis reactions are considered in the model: generation of a new extension zone from the active region during branching [Eq. (1)] and differentiation of an active cell to a hyphal cell [Eq. (2)]. The kinetics of branching is given in Eq. (3) as the rate of formation of new extension zones. Agger et al. (1998) assumed that branching is initiated when the average active mass of a hyphal element exceeds a certain level, given as (xa/cn)0, where cn is the concentration of hyphal elements in the reactor. Once initiated, the rate of branching is assumed to be proportional to the concentration of active cells but it is also assumed to be inhibited at very low glucose concentrations. The parameter k1 is the specific rate of branching and the parameter "a" represents the number of tips per unit mass of the extension zones. The rate of differentiation, given in Eq. (4) as the rate of formation of hyphal cells, is assumed to be proportional to the concentration of active cells by Agger et al. (1998). The growth rate of the active region is described in Eq. (5) as being equal to the growth rate of each tip multiplied by the concentration of tips, given as axe. The first part of the expression in Eq. (5) describes how tip extension rate varies with the substrate concentration according to a Monod expression (Agger et al., 1998). The second part of the expression in Eq. (5) is based on the assumption that the rate of tip extension will increase in a saturation type fashion with respect to the mass of the active part of the hypha. The growth rate of total biomass is given in Eq. (6). The specific rate of a-amylase production is related to the active region and it is modeled by the kinetic expression in Eq. (7). According to Agger et al. (1998) this expression is based on findings supporting that a-amylase production is repressed by glucose. The catabolite repression is modeled by an exponential decrease in the specific rate of a-amylase production when the glucose concentration exceeds a certain threshold value, srep. On the other hand, a constitutive level of a-amylase production was found during growth at high glucose concentrations, which is included in the model by the parameter kc.
The rates of oxygen consumption (rO) and carbon dioxide formation (rC) were described by the simple linear models in Eqs. (8) and (9) (Nielsen and Villadsen, 1994).
Metamorphosis Reactions
Generation of extension zone:
Differentiation:
Kinetic Expressions
Branching:
Differentiation:
Growth of active region:
Specific growth rate of total biomass:
Specific rate of a-amylase production:
Specific rate of oxygen uptake:
Specific rate of CO2 production:
(b) Mass Balances
The mass balances for all model states in a bioreactor with sterile feed are set up in Eqs. (10) to (15).
Morphological states:
Glucose:
a-Amylase:
Dissolved O2 concentration:
O2 fraction:
O2 fraction:
(c) Simulation and Parameter Estimation
The algebraic and differential equations composing the model were implemented in Matlab 4.2c and simulated for steady-state conditions. The parameters used in Eqs. (3) to (5) are related to the microscopic morphology of the A. oryzae, which was quantified by automated image analysis. Equations (16) to (20) were set up by Agger et al. (1998) to show the relationships between the specific branching frequency (k1), the initiation parameter for branching [(xa/cn)0], the maximal tip extension rate (K3) and their counterparts (kbran, l0, ktip,max and K1) determined using automated image analysis. The parameter a, describing the number of tips per unit mass of the extension zone, was determined approximating the volume of a tip with that of one-half of a sphere with a diameter equal to that of the hypha, as given in Eq. (20). The hyphal diameter, d, is calculated according to Eq. (21). The hyphal density (r), the hyphal water content (w) and the average fraction of active cells in the hyphal elements (f) were determined experimentally during batch experiments with the wild type (Agger et al., 1998).
From the original set of model parameters used by Agger et al. (1998), only five were modified in order to adapt the model to the morphological and physiological characteristics of the high enzyme-producing variant. All model parameters used in the simulations are given in Table 1. Zangirolami et al. (2000) showed that the variant is more sparsely ramified than the wild type. In order to continue growing at high specific growth rates, the variant must compensate the lower branching frequency by a faster tip extension rate. Thus, the value for ktip,max in Eq. (18) was determined as 120 for the variant by scaling up the original value by a factor of 2.5, which is the ratio between the hyphal growth unit length of the variant (325 mm) and of the wild type (130 mm) (Zangirolami et al., 2000).
In order to fit the model to the high enzyme production in the variant, three parameters in the expression for the specific rate of amylase production [Eq. (7)] were modified. The rate constant, kp1, was scaled from the original value (32) to 58. The scaling factor corresponds to the ratio between the specific amylase production rates of the variant (31 FAUgDW-1h-1) and of the wild type (17 FAUgDW-1h-1) at a dilution rate of 0.1 h-1 (Zangirolami et al., 2000). The new value of kp2 was obtained by fitting the model to the experimental data representing the specific rate of amylase production as a function of the specific growth rate. Experimental evidence indicated that a-amylase synthesis in the variant was less repressed by glucose, i.e., repression occurred at a higher residual glucose concentration. For this reason parameter srep was increased from 0.0095 (wild type) to 0.014.
RESULTS AND DISCUSSION
An overview of the results for all continuous cultures is presented in Table 2.
The reproducibility between the experiments carried out at the same specific growth rates was rather satisfactory. Observation of the results listed in Table 2 for dilution rates 0.06, 0.1, 0.15 and 0.175 h-1 shows that the deviation from the average is less than 10 % in a group of experiments carried out at the same specific growth rate for all measured variables.
Carbon and Generalized Degree of Reduction Balances
Carbon and generalized degree of reduction balances are effective means to verify the reliability and consistency of the experimental data as well as to assure that the major metabolic products have been identified (Nielsen and Villadsen, 1994)._In Table 3 the flux of carbon in C-mmol.h-1 and the flux of electrons in mk .h-1 at different dilution rates are shown together with the recovery calculated in percent of the influx.
The recovery of carbon was always 97% or higher for all specific growth rates. It is interesting to note that more than 95% of the inlet carbon was converted into biomass and carbon dioxide, while only approximately 3% were effectively used for enzyme production.
A very satisfactory recovery is also observed for the generalized degree of reduction balance.
Both Table 2 and Figure 2 show clearly that carbon dioxide production and oxygen consumption increased linearly with the dilution rate, as it was expected for a strictly aerobic organism like A. oryzae. The high values found for the recovery in carbon and reduction degree balances indeed confirm that no byproducts were generated during the experiments.
Determination of Stoichiometric Coefficients
Using Eqs. (8) and (9) and the steady-state data representing the specific rates of oxygen consumption and carbon dioxide formation from Table 2, the values for yield and maintenance coefficients were estimated by linear regression, as illustrated in Figure 2. The stoichiometric coefficients for glucose uptake were also estimated in Figure 2, considering rs =  m + ms.
m + ms.
The estimated stoichiometric coefficients, gsx, gcx, gox, mo, mc and ms, are listed in Table 4. The values agree fairly well with those estimated by Carlsen et al. (1996) for the wild type.
Determination of the Gas-Liquid Mass Transfer Coefficient for Oxygen
The value of the mass transfer coefficient for oxygen was determined employing Eq. (13) at steady state and experimental data for oxygen uptake rate (OUR) and dissolved oxygen concentration (CO2) listed in Table 2. The value of CO2* was estimated using Henry's law. According to the results included in Figure 2, a value of 100 ± 3 h-1 was estimated for kLa as the best fit of the experimental data for dilution rates 0.1 to 0.175 h-1.
The apparently low kLa value for a laboratory bioreactor, with a low-viscosity medium, was mainly a consequence of the small impeller diameter. According to Badino Jr. (1997), power input (Pg) is a function of impeller diameter (Di), as indicated in the empirical correlation [Eq. (22)].
The power input without aeration (P0), in Eq. (23), is also a function of impeller diameter.
The values for Di (0.048 m), DT (0.13 m) and the type of impeller (Rushton disc with 6 blades) were obtained from Zangirolami (1998). Replacing them together with the values for N (11.67 rps), Qgas (0.0000125 m3/s) and NP (5, for Rushton disc with 6 blades) in Eqs. (22) and (23), the power input, Pg, was estimated as 1.34 W. Badino Jr. (1997) also proposed an expression [Eq. (24)] to correlate the mass transfer coefficient with the power input. For a medium volume (V) of 0.0015 m3, a kLa value of 64 h-1 was estimated.
The Morphological Regions for the Variant
The increase in the fraction of the active region for increasing specific growth rates is illustrated in Figure 3. The values for the wild type and for the variant are similar and both are well predicted by the model. The simulated values for the fractions of extension and hyphal regions are also included in Figure 3.
Enzyme Production and Biomass Formation
Both experimental and simulated steady-state results showing the trends in the a-amylase activity, in the a-amylase specific production rate as well as in the concentrations of biomass and residual glucose for different dilution rates are displayed in Figure 4.
As expected, enzyme activity decreases for specific growth rates higher than 0.05 h-1 due to glucose repression. As long as glucose repression is moderate (0.05 < D < 0.2 h-1), the specific rate of a-amylase production increased with the specific growth rate. But, according to the simulated profile, for higher specific growth rates, a-amylase synthesis is strongly repressed by residual glucose concentrations higher than 10 mgl-1 and the enzyme-specific productivity decreases rapidly. For low specific growth rates (D < 0.04 h-1), glucose supply was consumed mainly for maintenance requirements and the predicted biomass concentration remained below 1.8 gDW per kg of medium. For specific growth rates higher than 0.5 h-1, according to the simulated values, the biomass concentration increased slightly with the specific growth rate up to the specific growth rate of 0.37 h-1. At this value, the maximum specific growth for the morphological variant is reached (Zangirolami et al., 2000), causing the washout of the biomass.
The results for the modeling of the gas phase are summarized in Figure 5. The carbon dioxide fraction in the exhaust gas increased proportionally to the specific growth rate until washout of the biomass took place. In Figures 4 and 5, the model predictions showed a good agreement with the experimental data for all dilution rates studied.
CONCLUSION
The steady-state results obtained in continuous cultures carried out at different dilution rates showed that the wild type and the variant are similar with respect to the glucose uptake kinetics, the stoichiometric coefficients and the active fraction of the growing hypha. However, the morphological variant showed a better performance in terms of enzyme production.
Based on carbon balances of steady-state cultures, a recovery of over 97 % was obtained in all experiments.
The morphologically structured model proposed by Agger et al. (1998) was successfully adapted to match the morphological characteristics of the variant and its high enzyme productivity. In addition, the model was extended to describe carbon dioxide formation, oxygen uptake and dissolved oxygen concentration at steady-state conditions. The modified model provided a good description of the steady-state results for the variant.
NOMENCLATURE
constant (tips.(gDW extension zone)-1)
concentration of hyphal elements (kg-1)
concentration of dissolved oxygen at saturation (mol.m-3)
dilution rate (h-1)
specific branching frequency (tips.(gDW active)-1.h-1)
rate constant (h-1)
mo
ms
ngas
p
Qgas
rps
Vgas
yCO2
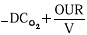 (mole O2.m-3.h-1)
(mole O2.m-3.h-1)Greek Letters
a
- Agger, T., Spohr, A.B., Carlsen, M. and Nielsen, J., Growth and Product Formation of Aspergillus oryzae during Submerged Cultivations: Verification of a Morphologically Structured Model Using Fluorescent Probes". Biotechnology and Bioengineering, 57, 321 (1998).
- Archer, D.B. and Wood, D.A., The Growing Fungus. Chapman & Hall, London (1995).
- Badino Jr., A.C., Reologia, Consumo de Potęncia e Transferęncia de Oxigęnio em Cultivos Descontínuos de Aspergillus awamori NRRL 3112. Ph.D. Dissertation, Escola Politécnica, Universidade de Săo Paulo (1997).
- Carlile, J.M. and Watkinson, S.C., The Fungi. Academic Press, London (1994).
- Carlsen, M., Nielsen, J. and Villadsen, J., Growth and a-Amylase Production by Aspergillus oryzae during Continuous Cultivations. Journal of Biotechnology, 45, 81 (1996).
- Fogarty, W.M., Biotechnology Handbooks 7: Aspergillus Plenum Press, New York (1994).
- Harvey, L.M. and McNeil, B., Biotechnology Handbooks 7: Aspergillus Plenum Press, New York (1994).
- Müller, C., Morphology and Protein Secretion of Aspergillus oryzae M.Sc. Thesis, Department of Biotechnology, Technical University of Denmark (1997).
- Nielsen, J. and Villadsen, J., Bioreaction Engineering Principles. Plenum Press, New York (1994).
- Oxenbřll, K., Aspergillus Enzymes and Industrial Uses, FEMS Symposium no. 69, The Genus Aspergillus: From Taxonomy and Genetics to Industrial Application. Plenum Press, New York (1994).
- Paul, G.C. and Thomas, C.R., A Structured Model for Hyphal Differentiation and Penicillin Production Using Penicillium chrysogenum Biotechnology and Bioengineering, 51, 558 (1996).
- Perry, R.H. and Green, D., Perry's Chemical Engineers' Handbook, 6th. edition. McGraw-Hill International (1984).
- Podgornik, A., Stravs, R., Koselj, P. and Raspor, P., Bioprocess Monitoring, Control and Data Management: Software SHIVA. Prehrambeno-tehnol. Biotehnol. Reviews, 32, 181 (1994).
- Spohr, A., Correlation between Protein Secretion and Morphology in Aspergillus oryzae Ph.D. Dissertation, Department of Biotechnology, Technical University of Denmark (1997).
- Zangirolami, T.C., Johansen, C.L., Nielsen, J. and Jřrgensen, S.B., Simulation of Penicillin Production in Fed-batch Cultivations Using a Morphologically Structured Model. Biotechnology and Bioengineering, 56, 593 (1997).
- Zangirolami, T.C., Modeling of Growth and Product Formation in Submerged Cultures of Industrially Important Filamentous Fungi. Ph.D. Dissertation, Department of Chemical Engineering, Technical University of Denmark (1998).
- Zangirolami, T.C., Carlsen, M., Nielsen, J. and Jřrgensen, S.B., Selection and Characterization of a High a-Amylase-producing Variant in Glucose-limited Continuous Cultures of Aspergillus oryzae. Mycological Research, 104, 1241 (2000).
Publication Dates
-
Publication in this collection
13 May 2002 -
Date of issue
Mar 2002
History
-
Accepted
22 Nov 2001 -
Received
23 Mar 2001




































