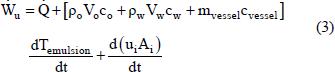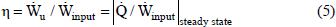Abstract
The aim of this study was to investigate the interfacial energy involved in the production of water-in-oil (W/O) emulsions composed of water and a Brazilian heavy crude oil. For such purpose an experimental set-up was developed to measure the different energy terms involved in the emulsification process. W/O emulsions containing different water volume fractions (0.1, 0.25 and 0.4) were prepared in a batch calorimeter by using a high-shear rotating homogenizer at two distinct rotation speeds (14000 and 22000 rpm). The results showed that the energy dissipated as heat represented around 80% of the energy transferred to the emulsion, while around 20% contributed to the internal energy. Only a very small fraction of the energy (0.02 - 0.06%) was stored in the water-oil interface. The results demonstrated that the high energy dissipation contributes to the kinetic stability of the W/O emulsions.
Emulsion; Interfacial energy; Energy balance; Droplet size
INTRODUCTION
During the production and processing of crude oil, the presence of water is very common because water is naturally present in the oil reservoir, caused by the oil recovery method (e.g., water injection in the reservoir) (Fan et al., 2009Fan, Y., Simon, S. and Sjöblom, J., Chemical destabilization of crude oil emulsions: Effect of nonionic surfactants as emulsion inhibitors. Energy & Fuels, 23, 4575-4583 (2009).) and/or from water injection in the production pipeline for friction reduction purposes (Bannwart, 2001Bannwart, A. C., Modeling aspects of oil – water core – annular flows. Journal of Petroleum Science and Engineering, 32, 127-143 (2001).). The turbulent shear associated with fluid flow within a pump, gas lift system and pipeline flow may cause the formation of water-in-oil (W/O) emulsions (Bhardwaj and Hartland, 1994Bhardwaj, A. and Hartland, S., Dynamics of emulsification and demulsification of water in crude oil emulsions. Industrial & Engineering Chemistry Research, 33, 1271-1279 (1994).; Peña et al., 2005Peña, A. A., Hirasaki, G. J. and Miller, C. A., Chemically induced destabilization of water-incrude oil emulsions. Industrial & Engineering Chemistry Research, 44, 1139-1149 (2005).). These emulsions remain stable for a long period of time, due the presence of natural emulsifying agents in the oil phase. Crude oils, especially heavy oils, contain significant amounts of asphaltenes (high molecular weight components), naphthenic acids and resins that act as natural emulsifiers because of their surface activity and capacity to produce viscoelastic layers around the droplets (Djuve et al., 2001Djuve, J., Yang, X., Fjellanger, I. J., Sjöblom, J. and Pelizzetti, E., Chemical destabilization of crude oil based emulsions and asphaltene stabilized emulsions. Colloid & Polymer Science, 279, 232- 239 (2001).; Sjöblom et al., 2003Sjöblom, J., Aske, N., Auflem, I. H., Brandal, Ø., Havre, T. E., Sæther, Ø., Westvik, A., Johnsen, E. E. and Kallevik, H., Our current understanding of water-in-crude oil emulsions. Recent characterization techniques and high pressure performance. Advances in Colloid and Interface Science, 100- 102, 399-473 (2003).; Wang et al., 2011Wang, W., Gong, J. and Angeli, P., Investigation on heavy crude-water two phase flow and related flow characteristics. International Journal of Multiphase Flow, 37, 1156-1164 (2011).).
The presence of water in crude oils is undesirable because it determines the commercial value of the oil (Peña et al., 2005Peña, A. A., Hirasaki, G. J. and Miller, C. A., Chemically induced destabilization of water-incrude oil emulsions. Industrial & Engineering Chemistry Research, 44, 1139-1149 (2005).) and can cause several problems, such as the corrosion and fouling of some equipment (Al-Sabagh et al., 2011Al-Sabagh, A. M., Kandile, N. G., El-Ghazawy, R. A. and Noor El-Din, M. R., Synthesis and evaluation of some new demulsifiers based on bisphenols for treating water-in-crude oil emulsions. Egyptian Journal of Petroleum, 20, 67-77 (2011).). In addition, the viscosity of W/O emulsions is much higher than the viscosity of the heavy oil alone, with a typically non-Newtonian behavior, mainly for higher water volume fractions and lower temperatures (Farah et al., 2005Farah, M. A., Oliveira, R. C., Caldas, J. N. and Rajagopal, K., Viscosity of water-in-oil emulsions: Variation with temperature and water volume fraction. Journal of Petroleum Science and Engineering, 48, 169-184 (2005).). Thus, the water must be removed to a level of less than 1% using processes called demulsification or dehydration (Rondón et al., 2006Rondón, M., Bouriat, P., Lachaise, J. and Salager, J. - L., Breaking of water-in-crude oil emulsions. 1. Physicochemical phenomenology of demulsifier action. Energy & Fuels, 20, 1600-1604 (2006).), which contribute to increase the production costs. Moreover, this step of demulsification is not always easily accomplished due to the high stability of these W/O emulsions.
Considering that emulsion formation is an inevitable process during the production and processing of heavy oils, the understanding of the energy balance involved in the production of water-in-oil emulsions can be important to define strategies to destabilize these emulsions. During emulsion formation, the water-oil interface is first deformed and broken up into many droplets under the action of external forces (McClements, 2005McClements, D. J., Food Emulsions – Principles, Practices and Techniques. CRC Press, Boca Raton (2005).). The force necessary to deform and disrupt a droplet should be larger than the interfacial force, which is characterized by the Young-Laplace equation (2σ/R) (where σ is the interfacial tension and R the radius of the droplet). This condition can be achieved by increasing the amount of energy supplied during emulsification through shear stresses in laminar flow, or pressure/velocity fluctuations in turbulent flow (Walstra, 1993Walstra, P., Principles of emulsion formation. Chemical Engineering Science, 48, 333-349 (1993).). However, it has been reported that only a small fraction of the energy input is spent in the increase of free energy of the interface (Walstra, 1993Walstra, P., Principles of emulsion formation. Chemical Engineering Science, 48, 333-349 (1993).; Lemenand et al., 2003Lemenand, T., Della Valle, D., Zellouf, Y. and Peerhossaini, H., Droplets formation in turbulent mixing of two immiscible fluids in a new type of static mixer. International Journal of Multiphase Flow, 29, 813-840 (2003).; Zhang et al., 2012Zhang, J., Xu, S. and Li, W., High shear mixers: A review of typical applications and studies on power draw, flow pattern, energy dissipation and transfer properties. Chemical Engineering and Processing, 57-58, 25-41 (2012).). In the literature such findings were only qualitatively obtained and, to our knowledge, there are no studies that have measured the fraction of energy input that is accumulated at the interface.
The objective of this study was to investigate the interfacial energy and the energy balance involved in the production of water-in-heavy crude oil emulsions through a quantitative study. An experimental set-up was developed in order to measure the terms of the energy balance during the emulsion generation. Determination of the interfacial energy was based on the droplet size distribution obtained by optical microscopy and the interfacial properties.
EXPERIMENTAL SECTION
Material
The materials used to prepare the water-in-oil (W/O) emulsions were a 17°API crude heavy oil and distilled water. Before emulsion preparation, the oil was dehydrated during 8 hours using a rotary evaporator (Buchi rotavapor model R-215, Buchi, Switzerland) in order to remove 13.9% water naturally present in the crude oil. After dehydration, the light compounds (organic phase) were separated from the water and re-mixed with the oil. Table 1 shows the properties of the dehydrated oil and the methods used to obtain these values.
Experimental Apparatus
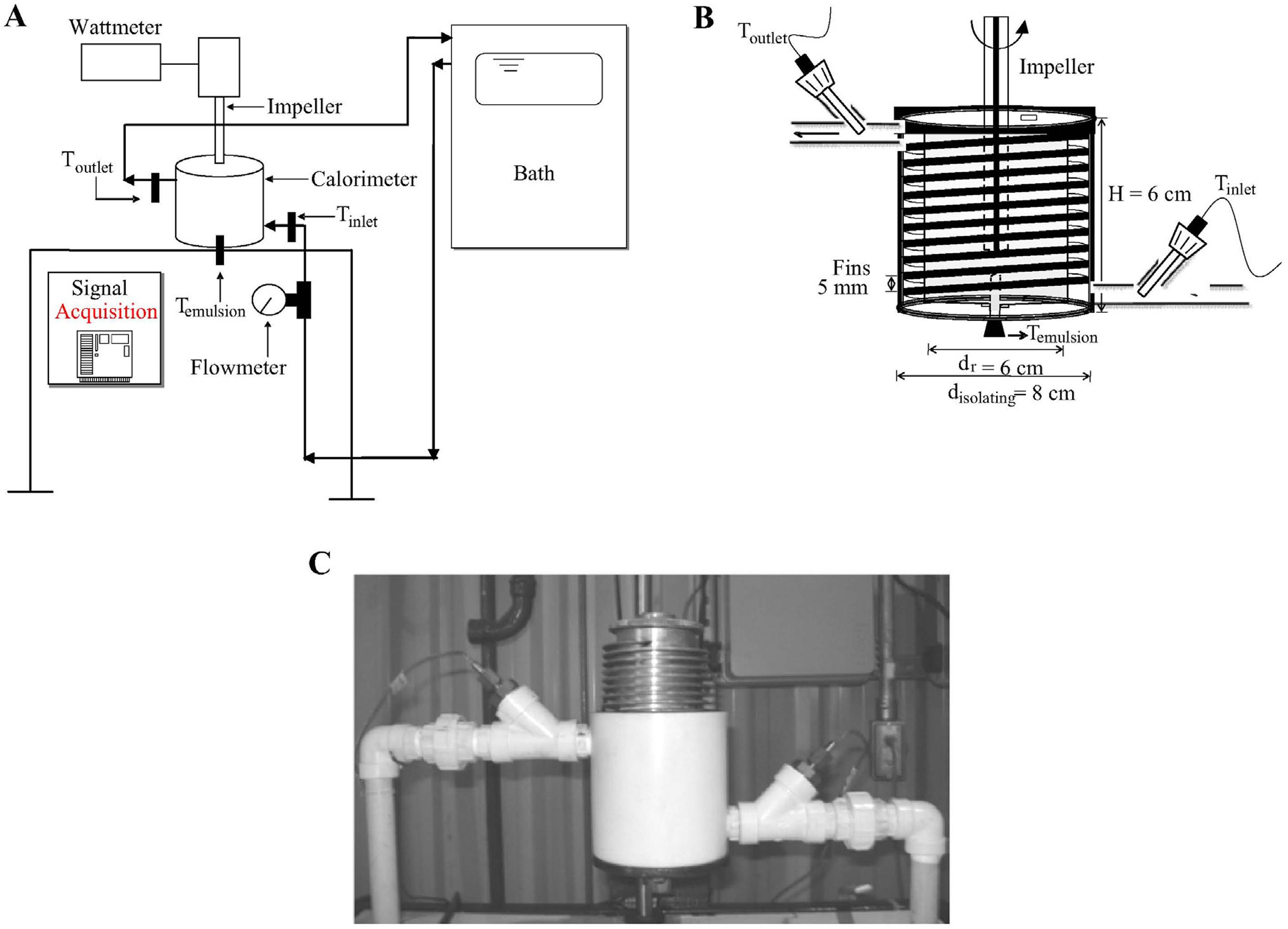
An especially designed calorimeter was built to determine the relative terms of the energy balance of the emulsification process. The schematic view of the experimental apparatus, including the control system, is shown in Figure 1A. This apparatus was composed of a hermetically closed aluminum vessel of 100 cm3 capacity (thermal conductivity ~ 250 W/m.K) with helical fins 1 mm in thickness with 5 mm pitch machined in its external surface to allow the cooling by a water jacket (Figure 1B). The vessel was placed into a cylindrical 1 cm thick Teflon box (thermal conductivity ~ 0.3 W/m.K) (Figure 1C), with cover of the same material to get good insulation. In addition, the connections of the calorimeter had rubber sealing rings to prevent heat exchange with the environment. The impeller of a homogenizer (Ultra Turrax T18 Basic, IKA, Germany) was inserted into the vessel to disperse the fluids (Figure 1A). The impeller was of the rotor stator type and the rotor and stator diameters were 19 mm and 12.7 mm, respectively.
A) Schematic view of the experimental set-up, B) aluminum vessel and C) calorimeter. Tinlet and Toutlet are the inlet and outlet temperatures of the cooling jacket, Temulsion is the internal temperature of the vessel, dr is the aluminum vessel diameter and disolating is the Teflon box diameter.
The cooling water was supplied by a centrifugal pump installed between the thermostatic bath and the calorimeter. The water flow rate was controlled by valves and measured with a Coriolis mass flowmeter. To reduce the uncertainty in the cooling heat transfer, the water mass flow rate in the jacket was set to 0.3 L/min for all the experiments. Inlet (Tinlet) and outlet (Toutlet) temperatures of the cooling jacket and the internal temperature of the vessel (Temulsion) were recorded by resistance temperature detectors (Pt100) 15 cm in length and 0.5 cm in diameter. A true rms wattmeter (model ET-4080, Minipa, Brazil) was used to measure the electrical power input to the homogenizer. The software LabView Signal Express (National Instruments, USA) was used for the data acquisition.
Experiments
Preliminary studies using single-phase fluids (glycerine and crude oil) were done in order to validate the constructed system. The viscosity of these fluids at 25°C was 1000 mPa.s and 2250 mPa.s, respectively. The single-phase fluids were stirred in the Ultra Turrax at 14000 and 22000 rpm and different temperatures (15, 25, 35 and 45 °C). In a second step, emulsions were prepared using different water volume fractions (0.1, 0.25 and 0.4) and rotation speeds (14000 - 22000 rpm). The total volume of the emulsion was 90 cm3. Each run lasted approximately 12 min and the cooling water was fixed at 25 °C. The experiments were carried out in duplicate to ensure repeatability.
Immediately after emulsion preparation, six fractions of each emulsion were poured onto microscope slides, covered with glass cover slips and observed using a Coleman model NT200 optical microscope (Coleman, Brazil). The microscopic images of the emulsions were analyzed using the image processing software Image Tool and the droplet diameters were determined. For this, about 400-800 droplets were measured individually for each sample. The size of the droplets was determined as the volume-surface mean diameter (d32) (Equation (1)).
where ni is the number of droplets with diameter di.
The specific interfacial area of the emulsions (Ai/V) was calculated using Equation (2).
where V is the volume and α is the water volume fraction.
The rheological measurements on emulsions were carried out at 25 °C in triplicate using a Haake RheoStress 1 rheometer (Haake, Germany). A parallel plate 30 mm in diameter and a gap of 1 mm was used to evaluate the emulsions. Flow curves were obtained for shear rate values ranging from 0 to 150 s-1. The data obtained were fitted to the power law model (τ=k. ẏn) , where τ is the shear stress, ẏ is the shear rate, k is the consistency index and n is the flow behavior index.
Instantaneous Energy Balance
Considering the scheme of Figure 2, the following general equation for the energy balance can be formulated (Delhaye, 1974Delhaye, J. M., Jump conditions and entropy sources in two-phase systems. Local instant formulation. International Journal of Multiphase Flow, 1, 395- 409 (1974).).
Schematic view of the emulsion generation experiment. H is the height of the vessel, dr is the vessel diameter, Tw is the temperature of the water jacket, Tbath is the temperature of the water in the bath, Ẇu is the power transferred to the emulsion by the impeller and
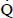 is the rate of heat transfer from the vessel.
is the rate of heat transfer from the vessel.
where Ẇu is the power transferred to the emulsion by the impeller (W), 3), V is the phase volume (m3), c is the specific heat (J/kg.°C), m is the mass (kg), Temulsion is the emulsion temperature (°C), ui is the specific energy per unit of interfacial area (J/m2), Ai is the total interfacial area of the emulsion (m2) and t is the time (s). The subscripts o, w and vessel represent oil phase, water phase and aluminum vessel, respectively.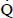 is the rate of heat transfer from the vessel (W), ρ is the density of the phase (kg/m
is the rate of heat transfer from the vessel (W), ρ is the density of the phase (kg/m
Thermal resistance inside the vessel was neglected due to the strong internal convection caused by the impeller. In addition, as aluminum is a very effective heat conductor, the temperature of the vessel wall (Tw) can be considered to be the same as that of the emulsions (Temulsion). In the steady state, Equation (3) becomes:
Thus, if the electric power input (Ẇinput) is known, then the internal losses of the homogenizer are Ẇlosses = Ẇinput - Equation (5).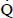 and the efficiency (η) can be calculated using
and the efficiency (η) can be calculated using
The specific interfacial energy of the emulsions can be related to the interfacial tension according to Equation (6) (Adamson and Gast, 1997Adamson, A. W. and Gast, A. P., Physical Chemistry of Surfaces. Wiley, New York (1997).).
where σ is the interfacial tension (N/m) and Ti is the interface temperature (°C). The first term of this expression (σ) represents the mechanical effect, while the second one Equations (2) and (6). expresses the thermal effect. Considering the water droplets of the emulsions as spheres, the interfacial energy can be obtained from the combination between
expresses the thermal effect. Considering the water droplets of the emulsions as spheres, the interfacial energy can be obtained from the combination between
RESULTS
Calorimetric Analysis
The experimental apparatus was first evaluated using pure glycerine and crude oil as single-phase fluids. The heat transfer (outlet - Tinlet)) and the electric power input (Ẇinput) were measured during the stirring using the data obtained through the temperature detectors and the wattmeter, respectively. Figure 3 shows the typical behavior of input with time obtained using glycerine as singlephase fluid, rotation of 14000 rpm and temperature of 25 °C. If the power transferred to the emulsion (Ẇu ) is equal to the heat transfer (Q) in the steady state (Equation (4)), the difference between the two curves at 12 min corresponds to the losses in the motor (Ẇlosses), as shown in Figure 3.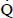 = ṁc(T
= ṁc(T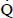 and Ẇ
and Ẇ
Typical time evolutions of the electrical power input (Winput) and heat transfer (Q) for singlephase fluids obtained using glycerine, rotation of 14000 rpm and temperature of 25 °C.
Table 2 shows the mean values of the terms of the energy balance in the steady state for the singlephase fluids (glycerine and crude oil). These tests using single-phase fluids showed that the Ẇlosses were mainly affected by the rotation speed, and the mean motor efficiency (η) was 48.3% ± 5.3% and tended to decrease with the reduction of temperature. The experimental uncertainties (δẆlosses) were lower than 7.6%. Both parameters (Ẇlosses and η) were very influenced by the process conditions (rotation speed and temperature), but η was not affected by the type of fluid. Thus, these results indicated that this is an effective way to measure the losses in the motor of the homogenizer.
Electrical power input (Winput), heat transfer (Q) and internal losses of the homogenizer (Ẇlosses) at the steady state, as well as experimental uncertainty (δẆlosses) and motor efficiency (η) for single-phase fluids homogenized at different rotation speeds and temperatures.
Effect of Emulsification Time
Figure 4 shows the typical time evolutions of temperature, power input and cooling heat transfer for a water-in-heavy oil (W/O) emulsion with a water fraction of 0.1 produced at 14000 rpm. In the beginning of the test (t = 0), all temperatures were approximately 25 °C (Figure 4A), i.e., the same temperature as the water bath. During the emulsification process, the emulsion temperature continuously increased, which resulted in an increase of the outlet temperature of the water jacket. At the same time, the increase of emulsion temperature promoted a reduction of the power input (Figure 4B). Figure 4C shows the typical behavior of electric power input as a function of the viscosity obtained using a glycerine solution, which indicated that these parameters were directly related. Thus, the increase of emulsion temperature caused a reduction in its viscosity and, consequently, a decrease in the electrical power input. The other emulsions showed the same behavior of time evolution.
Typical time evolutions of A) temperatures and B) power input and heat transfer obtained using an emulsion with water fraction of 0.1 and produced at 14000 rpm. Tinlet and Toutlet are the inlet and outlet temperatures of the cooling jacket and Temulsion is the internal temperature of the vessel. C) Behavior of the viscosity and electrical power input as a function of temperature, obtained using glycerine.
These results indicated that the steady state was achieved at approximately 5 min of homogenization. Thus, all experiments were performed until 12 min, assuring that the steady state was achieved.
Characterization of W/O Emulsions
The W/O emulsions produced after 12 min of homogenization were characterized by optical microscopy and rheological measurements. The droplet sizes of the produced emulsions were obtained through image analysis of the micrographs obtained from optical microscopy. The microstructures of W/O emulsions showed spherical water droplets (sphericity ~1) evenly dispersed in a continuous oily phase (Figure 5). Even for the water fraction of 0.4, flocculation was not observed.
Typical microstructure of the water-incrude heavy oil emulsions obtained using an emulsion with water fraction of 0.25 and produced at 14000 rpm. Scale bar = 100 μm.
Figure 6 shows the droplet size distribution and the droplet mean diameter (d32) of the W/O emulsions. In general, the histograms showed a log-normal distribution with the peak between 10 and 30 μm for experiments at 14000 rpm and around 20 μm for tests at 22000 rpm. At 14000 rpm (Figure 6A) the polydispersity (PDI) was higher than at 22000 rpm (Figure 6B). The evaluation of droplet diameters showed that d32 decreased with increasing rotation speed and with decreasing water volume fraction.
Droplet size distribution, mean droplet diameter (d32) and polydispersity (PDI) of the W/O emulsions prepared at A) 14000 rpm and B) 22000 rpm. Water volume fraction: (___) 0.1, (...) 0.25 and (_ _) 0.4.
Figure 7 shows the rheological properties of the W/O emulsions. The emulsions containing lower water volume fraction (0.1 and 0.25) behaved like Newtonian fluids, while those with 0.4 water fraction showed a shear-thinning behavior.
Flow curves of W/O emulsions produced at A) 14000 rpm and B) 22000 rpm. Water volume fractions of emulsions: (◇) 0 (pure oil), (○) 0.1, (∆) 0.25 and (□) 0.4.
The values of the flow behavior index (n) obtained from the fit of flow curves to the rheological model and the apparent viscosity at 100 s-1 are shown in Table 3. The results for the flow behavior index confirmed the pseudoplasticity of the emulsions containing higher water volume fraction (n < 1). In addition, the increase of the water volume fraction led to the increase of emulsion viscosity (Table 3). Emulsions produced at different rotation speeds were more similar, indicating that this variable had little influence on the rheological properties of the emulsions.
Flow behavior index (n), viscosity at 100 s-1 (η100s-1) and coefficient of determination (R2) for the different emulsions.
Energy Balance
The energy balance terms of the emulsification process at the steady state were obtained using Equations (4) and (5) and the values are summarized in Table 4. The results showed that the power input (Ẇinput) and heat transfer (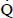 ) increased as the rotation speed was increased and were quite similar for distinct water volume fractions of the emulsions. The energy efficiency of the motor of the emulsifying device was around 50% for all the experimental conditions and had a tendency to decrease with increasing rotation speed.
) increased as the rotation speed was increased and were quite similar for distinct water volume fractions of the emulsions. The energy efficiency of the motor of the emulsifying device was around 50% for all the experimental conditions and had a tendency to decrease with increasing rotation speed.
The integration of the energy balance equation between 0 and 12 min led to the results of energy density for the emulsification process (Wu/V), heat transferred from the vessel (Q/V) and internal energy (U/V), as shown in Table 5. It can be observed that the energy necessary to produce the emulsion was between 438.7 and 828.6 J/cm3 and tended to increase with increasing rotation speed. Moreover, the increase in rotation speed and water content caused an increase in internal energy. However, about 80% of the total energy required to produce the emulsions was dissipated into heat (Q/Wu) and such energy dissipation was higher for higher rotation speed and lower water volume fraction (Table 5).
The energy stored at the interface has a much lower magnitude and can not be accurately determined from integration of Equation (3). Thus, this term should be calculated using Equation (7).
Determination of the Interfacial Energy
Table 6 shows the interfacial area per unit volume obtained from Equation (2) and the interfacial energy per unit volume (uiAi/V) obtained from Equation (7). The interfacial area per unit volume clearly increased with increasing agitation speed and water volume fraction, as expected. The specific interfacial energy ranged from 0.09 to 0.26 J/cm3 and tended to increase as the water volume fraction was increased for emulsions prepared at 14000 rpm. Nevertheless, the interfacial energy of the emulsions produced at 22000 rpm was almost equal and similar to those containing 0.25 and 0.4 water fraction at 14000 rpm.
Specific interfacial area (Ai/V), specific interfacial energy (uiAi/V) and fraction of energy used to produce the interface (uiAi/Wu)
Compared to the total energy per unit volume provided to the emulsion (uiAi/Wu), the interfacial energy represents a very small fraction (Table 6). This parameter tended to increase with the increase of water volume fraction for emulsions prepared at 14000 rpm, while the values for emulsions prepared at 22000 rpm were very similar.
DISCUSSION
Rotor-stator devices, such as the Ultra-Turrax, are widely used to produce W/O and O/W emulsions with medium to high viscosity (McClements, 2005McClements, D. J., Food Emulsions – Principles, Practices and Techniques. CRC Press, Boca Raton (2005).). In this type of device, the droplets are mainly produced by mechanical impingement against the wall due to high fluid acceleration and by shear stress in the gap between the rotor and stator (Jafari et al., 2008Jafari, S. M., Assadpoor, E., He, Y. and Bhandari, B., Re-coalescence of emulsion droplets during highenergy emulsification. Food Hydrocolloids, 22, 1191-1202 (2008).). In the present work, an Ultra-Turrax was used to produce water-in-heavy crude oil emulsions. The emulsions produced at different rotation speeds (14000 and 22000 rpm) and water volume fractions (0.1, 0.25 and 0.4) were highly stable and did not show phase separation. Emulsions produced at 14000 rpm showed a greater polydispersity than at 22000 rpm (Figure 6), which may be related to the non-uniformity of shear distribution within the emulsion due to the high viscosity of the continuous phase. On the other hand, the higher rotation velocity promoted the decrease of d32 (Figure 6), validating a well-known trend for emulsions (Gingras et al., 2005Gingras, J.-P., Tanguy, P. A., Mariotti, S. and Chaverot, P., Effect of process parameters on bitumen emulsions. Chemical Engineering and Processing: Process Intensification, 44, 979-986 (2005).; Darine et al., 2011Darine, S., Christophe, V. and Gholamreza, D., Emulsification properties of proteins extracted from beef lungs in the presence of xanthan gum using a continuous rotor/stator system. LWT – Food Science and Technology, 44, 1179-1188 (2011).). The rotation speed showed little influence on the viscosity of the emulsions (Table 3). With regard to the water volume fraction, the increase of this parameter led to bigger d32 (Figure 6). This fact could be attributed to the increase of the emulsion viscosity (Table 3) (Jafari et al., 2008Jafari, S. M., Assadpoor, E., He, Y. and Bhandari, B., Re-coalescence of emulsion droplets during highenergy emulsification. Food Hydrocolloids, 22, 1191-1202 (2008).), which difficults droplet disruption, or to an insufficient amount of emulsifier to completely cover the interface of the droplets, resulting in their coalescence (Guo and Mu, 2011Guo, Q. and Mu, T. H., Emulsifying properties of sweet potato protein: Effect of protein concentration and oil volume fraction. Food Hydrocolloids, 25, 98-106 (2011).). The increase of water volume fraction also led to the increase of shear-thinning behavior and viscosity (Table 3), which can be attributed to the greater interaction between water droplets in the emulsion (Paso et al., 2009Paso, K., Silset, A., Sørland, G., Gonçalves, M. A. L. and Sjöblom, J., Characterization of the formation, flowability, and resolution of Brazilian crude oil emulsions. Energy & Fuels, 23, 471-480 (2009).). Compared to the pure oil (Table 1), the viscosity of the emulsions was significantly higher (Table 3), especially for water volume fractions above 0.25. An increase of the viscosity with water volume fraction was also observed by Farah et al. (2005)Farah, M. A., Oliveira, R. C., Caldas, J. N. and Rajagopal, K., Viscosity of water-in-oil emulsions: Variation with temperature and water volume fraction. Journal of Petroleum Science and Engineering, 48, 169-184 (2005). for W/O emulsions.
The energy balance of the emulsifying process at the steady state showed that the Ultra Turrax efficiency was around 50% (Table 4), i.e., only approximately half of the power supplied to the device was transferred to the fluid. Tests carried out with single-phase fluids (glycerine and crude oil) also provided the same average efficiency (Table 2). This efficiency depends on the homogenizer used to produce the emulsions and the conditions of the emulsification process. Abismail et al. (1999)Abismaïl, B., Canselier, J. P., Wilhelm, A. M., Delmas, H. and Gourdon, C., Emulsification by ultrasound: Drop size distribution and stability. Ultrasonics Sonochemistry, 6, 75-83 (1999). verified an efficiency of ~40% (electrical power of 130 W and energy transferred to the liquid of 53 W) for ultrasound and ~70% (electrical power of 170 W and energy transferred to the liquid of 120 W) for mechanical agitation. Thus, the energy input required to produce an emulsion containing droplets of a given size depends on the energy efficiency of the homogenizer used (McClements, 2005McClements, D. J., Food Emulsions – Principles, Practices and Techniques. CRC Press, Boca Raton (2005).; Jafari et al., 2008Jafari, S. M., Assadpoor, E., He, Y. and Bhandari, B., Re-coalescence of emulsion droplets during highenergy emulsification. Food Hydrocolloids, 22, 1191-1202 (2008).).
The energy density for the emulsification process (Wu/V) was between 438.7 and 828.6 J/cm3 (Table 5). Comparisons between the energy density for different devices have been discussed in the literature (Walstra and Smulders, 1998Walstra, P. and Smulders, P. E. A., Emulsion Formation. In: Binks,
B. P., (Eds). Modern Aspects of Emulsion Science. The Royal Society of
Chemistry, Cambridge (1998).; Schubert et al., 2003Schubert, H., Ax, K. and Behrend, O., Product engineering of
dispersed systems. Trends in Food Science & Technology, 14, 9-16
(2003).; Schultz et al., 2004Schultz, S., Wagner, G., Urban, K. and Ulrich, J., High-pressure
homogenization as a process for emulsion formation. Chemical Engineering &
Technology, 27, 361-368 (2004).). In general, these authors verified that energy densities between 1 and 100 J/cm3 are needed to produce O/W emulsions using rotor stator devices. In the present work, the energy employed for emulsion generation was much higher than in other works, probably because of the higher viscosity of the continuous phase of the W/O emulsions when compared to O/W emulsions. Figure 7A shows the relation between energy density and mean droplet diameter, which demonstrated that the increase of the energy employed led to a reduction of the droplet diameter. The same tendency was verified by other authors (Walstra and Smulders, 1998Walstra, P. and Smulders, P. E. A., Emulsion Formation. In: Binks,
B. P., (Eds). Modern Aspects of Emulsion Science. The Royal Society of
Chemistry, Cambridge (1998).; Schubert et al., 2003Schubert, H., Ax, K. and Behrend, O., Product engineering of
dispersed systems. Trends in Food Science & Technology, 14, 9-16
(2003).; Schultz et al., 2004Schultz, S., Wagner, G., Urban, K. and Ulrich, J., High-pressure
homogenization as a process for emulsion formation. Chemical Engineering &
Technology, 27, 361-368 (2004).). Although the energy required to disperse two immiscible fluids is very high, most of the energy employed in the emulsification process (~80%) was dissipated into heat (Table 5). The reason for this inefficiency is because, in addition to the energy necessary to increase the interfacial area (=σ1∆A), the disruption of droplets requires the generation of a very high pressure difference, which should be large enough to overcome the Young-Laplace interfacial force McClements, 2005McClements, D. J., Food Emulsions – Principles, Practices and
Techniques. CRC Press, Boca Raton (2005).). For the rotor-stator device, these pressure differences are provided to the system through high shear rates, which result in large amount of energy dissipation due to the friction losses (McClements, 2005McClements, D. J., Food Emulsions – Principles, Practices and
Techniques. CRC Press, Boca Raton (2005).). (
(
In the energy balance (Table 5), the internal energy represented around 20% of the energy employed in the emulsification process and tended to increase with the increase of rotation speed (Table 5), which was caused by the higher shear applied by the impeller to the emulsion. Just a very small portion of the energy used to produce the emulsions was expended in the creation of interfacial area (Table 6). At 14000 rpm, the specific interfacial energy was higher for emulsions with higher water volume fraction. In this case, small droplets had larger specific interfacial energies than the large ones due to their greater total interfacial area (Aoki, 2011Aoki, K., Size-distribution of droplets in emulsions by statistical mechanics calculation. Journal of Colloid and Interface Science, 360, 256-261 (2011).). However, with the exception of the emulsion with 0.1 water volume fraction produced at 14000 rpm, the other systems showed higher and very similar specific interfacial energy. The percentage of interfacial energy in relation to the total energy employed in the emulsification process (uiAi/Wu) was between 0.019 and 0.061%. In general, studies in literature estimate that this fraction is lower than 0.1% (McClements, 2005McClements, D. J., Food Emulsions – Principles, Practices and Techniques. CRC Press, Boca Raton (2005).; Walstra, 1993Walstra, P., Principles of emulsion formation. Chemical Engineering Science, 48, 333-349 (1993).), which is in agreement with the results obtained here. The relation between the fractions of energy used to produce the interface and the mean droplet diameter can be observed in Figure 8B. In this case, uiAi/Wu was higher for emulsions with larger d32. Thus, emulsions in which a lower amount of energy is transferred to the interfacial area, i.e., when the energy dissipation was higher, showed smaller water droplets and tended to be more stable. This result can be explained by the kinetic stability of the emulsions. Despite the fact that the emulsions exist in a thermodynamically unstable state, they can remain kinetically stable for a long period of time (McClements, 2005McClements, D. J., Food Emulsions – Principles, Practices and Techniques. CRC Press, Boca Raton (2005).). The increase of energy dissipation during the homogenization process can mean that higher energy was provided to the emulsion and was probably sufficient to promote a higher kinetic stability and the process was more irreversible.
Relation between mean droplet diameter (d32) and A) total energy density (Wu/V) and B) fraction of energy used to produce the interface (uiAi/Wu) for different water volume fractions: (◆) 0.1, (□) 0.25and (∆) 0.4.
CONCLUSIONS
In this study the different terms of the energy balance during the generation of a water-in-oil emulsion were measured in order to determine the interfacial energy involved in this process. The measured terms include: impeller work, heat transfer and internal energy. The interfacial energy was very small and could only be determined from drop size information (d32) and interfacial tension data. The stirring method provided high energy dissipation in the vessel. From the energy provided to the emulsion, about 80% was converted into heat, and just 20% caused a change in internal energy. This energy partition is due to the highly dissipative nature of the method used for emulsion generation. Less than 0.1% of the energy transferred to the emulsion was stored in the wateroil interface and the decrease of this fraction led to emulsions with smaller water droplets, i.e., the increase of energy dissipation produced more kinetically stable emulsions.
NOMENCLATURE
Greek Symbols
ACKNOWLEDGEMENTS
The authors are grateful to PETROBRAS S.A. and FINEP, Brazil, for the financial support to this study. We also acknowledge the grants conceded by CAPES and CNPq, Brazil.
REFERENCES
- Abismaïl, B., Canselier, J. P., Wilhelm, A. M., Delmas, H. and Gourdon, C., Emulsification by ultrasound: Drop size distribution and stability. Ultrasonics Sonochemistry, 6, 75-83 (1999).
- Adamson, A. W. and Gast, A. P., Physical Chemistry of Surfaces. Wiley, New York (1997).
- Al-Sabagh, A. M., Kandile, N. G., El-Ghazawy, R. A. and Noor El-Din, M. R., Synthesis and evaluation of some new demulsifiers based on bisphenols for treating water-in-crude oil emulsions. Egyptian Journal of Petroleum, 20, 67-77 (2011).
- Aoki, K., Size-distribution of droplets in emulsions by statistical mechanics calculation. Journal of Colloid and Interface Science, 360, 256-261 (2011).
- Bannwart, A. C., Modeling aspects of oil – water core – annular flows. Journal of Petroleum Science and Engineering, 32, 127-143 (2001).
- Bhardwaj, A. and Hartland, S., Dynamics of emulsification and demulsification of water in crude oil emulsions. Industrial & Engineering Chemistry Research, 33, 1271-1279 (1994).
- Darine, S., Christophe, V. and Gholamreza, D., Emulsification properties of proteins extracted from beef lungs in the presence of xanthan gum using a continuous rotor/stator system. LWT – Food Science and Technology, 44, 1179-1188 (2011).
- Delhaye, J. M., Jump conditions and entropy sources in two-phase systems. Local instant formulation. International Journal of Multiphase Flow, 1, 395- 409 (1974).
- Djuve, J., Yang, X., Fjellanger, I. J., Sjöblom, J. and Pelizzetti, E., Chemical destabilization of crude oil based emulsions and asphaltene stabilized emulsions. Colloid & Polymer Science, 279, 232- 239 (2001).
- Fan, Y., Simon, S. and Sjöblom, J., Chemical destabilization of crude oil emulsions: Effect of nonionic surfactants as emulsion inhibitors. Energy & Fuels, 23, 4575-4583 (2009).
- Farah, M. A., Oliveira, R. C., Caldas, J. N. and Rajagopal, K., Viscosity of water-in-oil emulsions: Variation with temperature and water volume fraction. Journal of Petroleum Science and Engineering, 48, 169-184 (2005).
- Gingras, J.-P., Tanguy, P. A., Mariotti, S. and Chaverot, P., Effect of process parameters on bitumen emulsions. Chemical Engineering and Processing: Process Intensification, 44, 979-986 (2005).
- Guo, Q. and Mu, T. H., Emulsifying properties of sweet potato protein: Effect of protein concentration and oil volume fraction. Food Hydrocolloids, 25, 98-106 (2011).
- Jafari, S. M., Assadpoor, E., He, Y. and Bhandari, B., Re-coalescence of emulsion droplets during highenergy emulsification. Food Hydrocolloids, 22, 1191-1202 (2008).
- Lemenand, T., Della Valle, D., Zellouf, Y. and Peerhossaini, H., Droplets formation in turbulent mixing of two immiscible fluids in a new type of static mixer. International Journal of Multiphase Flow, 29, 813-840 (2003).
- McClements, D. J., Food Emulsions – Principles, Practices and Techniques. CRC Press, Boca Raton (2005).
- Paso, K., Silset, A., Sørland, G., Gonçalves, M. A. L. and Sjöblom, J., Characterization of the formation, flowability, and resolution of Brazilian crude oil emulsions. Energy & Fuels, 23, 471-480 (2009).
- Peña, A. A., Hirasaki, G. J. and Miller, C. A., Chemically induced destabilization of water-incrude oil emulsions. Industrial & Engineering Chemistry Research, 44, 1139-1149 (2005).
- Rondón, M., Bouriat, P., Lachaise, J. and Salager, J. - L., Breaking of water-in-crude oil emulsions. 1. Physicochemical phenomenology of demulsifier action. Energy & Fuels, 20, 1600-1604 (2006).
- Santos, R. G., Mohamed, R. S., Bannwart, A. C. and Loh, W., Contact angle measurements and wetting behavior of inner surfaces of pipelines exposed to heavy crude oil and water. Journal of Petroleum Science and Engineering, 51, 9-16 (2006).
- Schubert, H., Ax, K. and Behrend, O., Product engineering of dispersed systems. Trends in Food Science & Technology, 14, 9-16 (2003).
- Schultz, S., Wagner, G., Urban, K. and Ulrich, J., High-pressure homogenization as a process for emulsion formation. Chemical Engineering & Technology, 27, 361-368 (2004).
- Sjöblom, J., Aske, N., Auflem, I. H., Brandal, Ø., Havre, T. E., Sæther, Ø., Westvik, A., Johnsen, E. E. and Kallevik, H., Our current understanding of water-in-crude oil emulsions. Recent characterization techniques and high pressure performance. Advances in Colloid and Interface Science, 100- 102, 399-473 (2003).
- Walstra, P. and Smulders, P. E. A., Emulsion Formation. In: Binks, B. P., (Eds). Modern Aspects of Emulsion Science. The Royal Society of Chemistry, Cambridge (1998).
- Walstra, P., Principles of emulsion formation. Chemical Engineering Science, 48, 333-349 (1993).
- Wang, W., Gong, J. and Angeli, P., Investigation on heavy crude-water two phase flow and related flow characteristics. International Journal of Multiphase Flow, 37, 1156-1164 (2011).
- Zhang, J., Xu, S. and Li, W., High shear mixers: A review of typical applications and studies on power draw, flow pattern, energy dissipation and transfer properties. Chemical Engineering and Processing, 57-58, 25-41 (2012).
Publication Dates
-
Publication in this collection
Jan-Mar 2015
History
-
Received
09 May 2013 -
Reviewed
26 June 2013 -
Accepted
18 Dec 2013