Using the Newcomb-Benford Law as a Deviation Identification Method in Continuous Auditing Environments: A Proposal for Detecting Deviations over Time^*

ABSTRACT

This paper used the Newcomb-Benford Law (NB Law) to analyze 210,899 contracts issued by sixty management units in two states in the Brazilian Northeast in 2010. In this article we seek to address the following question: What proposal emerges from the need to identify financial deviations over time in terms of NB Law compliance in continuous auditing scenarios? To this end, the goal of the paper is to analyze this compliance with the aim of identifying deviations over time. The analysis focuses on first significant digit distribution. Graphical analysis of observed frequencies and time series of relative discrepancies reveals the formation of typical patterns of divergences from Public Tenders Law (Federal Law n. 8.666/93). From the results obtained, we conclude that time series analysis of NB Law compliance can improve the accuracy of sampling procedures in continuous auditing.

Keywords
Newcomb-Benford Law; first digit; time series analysis; continuous auditing; public spending

RESUMO

O presente trabalho utilizou a Lei de Newcomb-Benford (NB-Lei) para analisar 210.899 valores de notas de empenho emitidas por sessenta unidades gestoras pertencentes a dois estados do Nordeste brasileiro, no ano de 2010. A questão investigada neste artigo é a seguinte: Que proposta emerge da necessidade de identificação de desvios no tempo em relação à análise de conformidade da NB-Lei, no ambiente de auditoria contínua? O objetivo da pesquisa é analisar a conformidade da NB-Lei em um ambiente de auditoria contínua, como uma proposta de identificação de desvios no tempo. A análise realizada tem foco na distribuição do primeiro dígito significativo. Foi constatada, em razão da análise gráfica das frequências observadas e séries diárias das discrepâncias relativas, a formação de padrões típicos de possíveis fugas à Lei de Licitações (Lei Federal n. 8.666/93). A partir dos resultados obtidos, conclui-se que a realização de uma análise temporal de conformidade com a NB-Lei agrega maior precisão aos procedimentos de amostragem, em ambiente de auditoria contínua.

Palavras-chave
Lei de Newcomb-Benford; primeiro dígito; análise temporal; auditoria contínua; gasto público

1 INTRODUCTION

The essence of the Newcomb-Benford Law (NB Law) was discovered by Simon Newcomb in 1881, when he noticed the fact that books containing logarithmic tables, in various libraries, presented evidence of greater wear in their first pages. Since the initial pages of these books contained the values of logarithms of numbers that began with lower digits (digits 1, 2, and 3, for example), Newcomb concluded that people looked for values of logarithms that began with lower digits much more than those that began with higher digits (digits 7, 8, and 9, for example). Newcomb (1881), in his article titled Note on the Frequency of Use of the Different Digits in Natural Numbers, concluded that “the law of the probability of the occurrence of numbers is such that all the mantissas of their logarithms are equally probable”. Also along this line of work, Benford (1938) laid out the same conclusions as Newcomb, presenting more than 20,000 results of adjustments using the Law, in various databases from different branches of research.

In the context of studies regarding financial deviations, the NB Law pattern has been used as an auditing procedure, applied to analyzing the conformity of a set of financial data by detecting deviations in relation to the expected pattern of occurrence for the digits of an analyzed position. In this regard, previously studies conducted by Carslaw (1988), Nigrini (1996), Nigrini and Mittermaier (1997), Watrin, Struffert, and Ullmann (2008), among others, stand out.

Auditing procedures can be understood as techniques applied by an auditor in order to evaluate the legitimacy of the processes and rules of an entity from the public or private sector. According to Mills (1994), auditing consists of carrying out an evaluation, officially recognized and systematized by those interested, in order to ensure that an applicable system, program, product, service, or process, present all of the characteristics, criteria, and parameters required. According to Attie (1998, p.25), auditing can be seen as an accounting specialty focused on testing the efficiency and effectiveness of implanted asset controls, with the aim of expressing an opinion regarding a particular set of information given over for analysis.

Auditing procedures, in general, are supported in various topics of statistical inference, among which punctual and interval estimations for proportions and statistical hypothesis tests stand out. The most widely used statistical tests in analyzing the compliance of a data set with the NB Law include the Z-test and the χ²-test. However, some authors claim that the Z-test and the χ²-test present a problem when significantly large samples are used, defined as the “excess power” problem (Nigrini & Mittermaier, 1997; Nigrini, 2000; Krakar & Žgela, 2009). This sensitivity of the tests to large sample sizes can be understood when small deviations from NB Law patterns are marked as being statistically significant, even when they are considered irrelevant in terms of auditing analysis. Suh, Headrick, and Minaburo (2011) used Monte Carlo simulations and identified the problem in large samples. Additionally, these authors propose a regression procedure based on inferences via bootstrapping, with the aim of identifying unusual patterns in financial data, using the first two significant digits.

This paper aims to analyze Newcomb-Bedford Law compliance in continuous auditing scenarios, as a proposal for identifying deviations over time. For this, analyses were carried out regarding the NB Law pattern in first significant digit distribution in 210,899 contracts issued by 60 management units in two states in the Brazilian Northeast in 2010. In a first analysis, nine graphs were constructed with the frequency results observed and their respective confidence interval to apply the Z statistic to the digits 1 to 9, showing visually the effect of sample size when using the Z-test. In the following analysis, a proposal was presented for analyzing the NB Law digit pattern of over time, using time series of relative discrepancies.

The question that guides this paper is the following: What proposal emerges from the need to identify deviations over time, in relation to analyzing Newcomb-Bedford Law compliance, in continuous auditing scenarios? With this aim, the use of a measure of relative percentage variation is proposed, which is indicated by relative discrepancy. Such a measure becomes an alternative to the Z and chi-squared tests, which assume independence, which cannot be guaranteed in time series data.

This study is warranted for the following reasons: (i) the importance of monitoring the occurrence of standard deviations from the NB Law to identify indications of irregularities; (ii) the importance of implanting simultaneous controls in computerized auditing environments; (iii) to support auditing teams in selecting the data that will compose their analysis sample, proposing methodologies based on the NB Law.

Besides this introduction, this paper is organized in the following way: section 2 describes the theoretical framework by presenting continuous auditing and then the Newcomb-Bedford Law, with a discussion of papers related to the topic of study and some statistical inference techniques widely used in frequency of digits analyses based on the NB Law; section 3 discusses the methodology used in this study; then, in section 4, the results are presented from the empirical analyses carried out, and finally, section 5 contains the paper’s final remarks.

2 THEORETICAL FRAMEWORK

2.1 Continuous Auditing

There are various definitions for auditing. In a wider context, it can be understood as an evaluation that is officially recognized and systematized by those interested, with the aim of ensuring that the system, program, service, or process audited has all of the characteristics, criteria, and parameters required (Costa, 2012).

For Arens, Elder, and Beasley (2004), continuous auditing (CA) would work as a system of computerized accounting, in which auditors can execute tests over the year, in order to identify significant or uncommon transactions, as well as determining whether any alteration has been carried out in this computerized system of control.

Continuous auditing is characterized as producing simultaneous results, or in short time periods, after the occurrence of the relevant event being controlled, making it possible for the auditor to detect the occurrence of an event that is outside the norms or outside the controls. Therefore, continuous auditing processes depend on the existence of computerized systems of control and data stored in electronic format (Vasarhelyi & Halper, 1991).

The execution of this simultaneous control, to be carried out in a continuous auditing process, involves timeliness as its best feature when compared to the traditional a posteriori auditing model (Costa, Santos, & Travassos, 2012). For Lima and Vieira (2002), simultaneous control is carried out in parallel with the controlled events, it thus being considered the most effective, given the possibility of stopping the effects of any irregular activity that might be detected. Murcia, Souza, and Borba (2008) highlight, however, that the cost of its implantation would only be economically viable via the use of automated execution.

The implementation of automated auditing routines has become a reality, especially in the area of risk analysis for granting credit, carried out by credit card companies. To this end, Costa et al. (2012) emphasize the relevance of carrying out automatic tests to verify the fulfillment of bidding limits in public spending contracts, to verify the fiscal good standing of goods and service suppliers, and to monitor deviations in spending behavior in relation to forecasted values.

This study seeks to contribute to the literature by highlighting the importance of using these techniques in public sector audits via an application in which accounting metrics methods were used focused on analyzing NB Law compliance in a continuous auditing environment, with the additional aim of identifying deviations over time, based on the interdisciplinary methodology used by Nigrini (1996), Carslaw (1988), Krakar and Žgela (2009), and Žgela (2011).

2.2 The Newcomb-Benford Law

Pioneering studies regarding the NB Law were developed by Newcomb (1881) and Benford (1938), in which the authors showed that the probabilities of occurrence of numbers beginning with lower digits are higher than the probabilities of occurrence of numbers beginning with higher digits. In the context of the Theory of Probabilities, authors such as Hill (1995, 1996), Pinkham (1961), and Raimi (1969) showed that the NB Law applies in data of a numerical nature that present invariance with regards to scale and that arise in a random nature. Thus, data on financial flows have received considerable attention in the literature as apt for applications using the NB Law.

An initial study regarding the Newcomb-Benford Law in a context applied to social sciences was carried out by Varian (1972). In this paper, the author observes aspects of the law in public planning financial data and concludes favorably regarding the use of the NB Law in helping to detect financial irregularities.

The study conducted by Carslaw (1988) analyzes the financial statements of 220 companies in New Zealand. The author observed, in analyzing the second position digits, that the digit zero presented excessive occurrences relative to what is established by the NB Law, while the digit 9 presented a lower frequency than the value proposed in the Law. The author explains this fact in the tendency for rounding up to occur (for example, 3 is used instead of 2.9; 5 is used instead of 4.9), which may be associated with possible number management strategies aimed at achieving financial goals, for example. A similar study was proposed by Thomas (1989), in which the author studies NB Law patterns in US companies’ profit informations.

In the study from Nigrini (1999), the author shows evidence of the NB Law pattern in the exponential growth of a variable over time. The author considers a mutual fund growing at a rate of 10% a year. Supposing that the fund’s resources start at an initial level of 100 million, the first significant digit of the total value of resources is 1 and will only change when the total value of the fund’s resources reaches the amount of 200 million. This change in the first significant position (from 1 to 2) will only occur if there is a 100 million increase in the fund’s resources. Given that the growth rate is 10% a year, 10 years are needed for this to happen. If the change in the first digit was from 5 to 6 (changing the resources from 500 million to 600 million), given the same growth rate, this timeframe would be only 2 years. For a change from 900 million to 1 billion, at the same rate of growth, the time needed would be 1 year and 1 month. This behavior is characteristic of the NB Law pattern.

In a study involving taxpayers in the United States, Nigrini (1996) showed evidence of the NB Law pattern in financial information in tax returns declarations. Other authors, such as Huxley (1999), Ashcroft, Bae, and Norvell (2002), Kumar and Bhattacharya (2002), and Posch (2004), also used the NB Law pattern in their studies as a tool for supporting auditing processes.

The reduction in the probabilities of occurrence of the digits 1 to 9 as first significant digits was initially obtained by Beford (1938), and widely used and perfected by Hill (1995). The probability P (d) of digit d occurring as the first significant digit is obtained by the equation

Using equation (1), the probabilities of occurrences for the first digit are shown in Table 1. The probabilities listed in Table 1 are obtained by the equation p_ei, i = 1, …, 9 of the NB Law, considering the digits from 1 to 9 in the first significant position. As can be observed, the probabilities associated with the digits 1 to 5 are greater than with the digits 6 to 9, which would contradict common sense that the occurrences of the digits are associated with equiprobable events. The NB Law reinforces that this behavior does not in fact prevail.

Table 1
Probability of Occurrence of the First Significant Digit

I	Pei
1	0.301030
2	0.176091
3	0.124939
4	0.096910
5	0.079181
6	0.066947
7	0.057992
8	0.051153
9	0.045757

• Source: Prepared by the authors

In an application for Brazil, Santos, Ribeiro, Lagioia, Alves, and Araújo (2009) evaluated use of the NB Law in the area of tax auditing for the Tax on Services of Any Nature (ISS). For this, the authors analyzed records of tax invoices issued by an advertising company between 2002 and 2005. The results obtained showed the existence of possible deviations regarding the issuing and bookkeeping of the tax invoices of the company concerned, which were confirmed by the results of an inspection.

Some studies apply the NB Law in contracts resulting from state public spending, which was confirmed in the study from Santos, Diniz, and Corrar (2005). The authors applied the accounting metrics computerized auditing model using the NB Law together with the Z-test and the χ²-test in a sample formed of approximately 104 thousand contracts, with usefulness being found in the analysis in terms of it determining the standard spending behavior practiced by public administrators. The results obtained showed indications of overbilling and breaking up of expenses, with the aim of bypassing the limit established by Federal Law n. 8.666 (Public Tenders Law, 1993) for public sector acquisitions.

Another paper which presents the application of the NB Law in contracts was carried out by Ribeiro, Montenegro, Santos, and Galvão (2005), who reproduced the accounting metrics model created by Nigrini (2000), also used by Santos, Diniz, and Ribeiro (2003) in the context of accounting auditing to analyze the contracts of 20 municipalities in the state of Paraíba.

In 2010, Diniz, Corrar, and Slomski investigated whether non-random elements of human behavior could be determinants in the modification of expense values in municipal legal reporting. The authors opted to select 225,421 contracts from 40 investigated municipalities, in accordance with volumes of resources managed, dividing the sample into large and small municipalities (Diniz et al., 2010).

Another study which applies the NB Law pattern in contracts was conducted by Costa (2012), who developed and applied an accounting metrics model for detecting financial deviations based on the NB Law to analyze 335,830 contracts issued in the 2010 financial year by 60 Management Units (MUs) in three Brazilian states. Based on this study, the author presented a NB Law proposal to the Courts of Auditors. In 2012, Costa et al. analyzed compliance in public spending by federal bodies and applied the NB Law to 134,281 contracts issued by 20 MUs in two Brazilian states for the first and second digits (Costa, Santos & Travassos, 2012).

Costa, Silva, Travassos, and Santos (2013) analyzed NB Law compliance in a continuous auditing environment, in 210,899 contracts issued by 60 Management Units (MUs) in two states in the Brazilian Northeast during 2010. Costa, Travassos, Soeiro, and Santos (2013) used accounting metrics in detecting the occurrence of significant deviations in the distribution of the first digit in state public spending, in relation to the standard distribution defined in the NB Law, in 109,888 contracts issued by 20 MUs in two states in the Northeast, ten MUs in each state.

2.3 Statistical Inference in Frequencies of Digits Analyses

Some statistical tests have been used in studies with an emphasis on financial deviation detection analyses, such as those from Carslaw (1988) and Nigrini (1996), among others. Among the tests used, the Z-test and χ ²-test stand out.

In the context of the NB Law, the Z-test can be used for inferences regarding the frequencies of the digits 0 to 9, when individually observed for the first significant digits in a set of numerical information. The corresponding test statistic is given by

in which PE_i = p_ei xn, PO_i = p_oi xn, n being the sample size, p_ei the expected probabilities, and p_oi the frequencies observed. Thus, at a level of significance of α = 0.05, H _{0 A} (the null hypothesis being tested) is rejected when Z < - Z_critical or if Z > Z_critical. For a level of significance of α = 0.05, the hypothesis of inexistence of significant deviations (H _{0 A} ) will be rejected when Z < -1.96 or Z > 1.96.

Using the Z statistic given in equation (2), margins of tolerance [ Ic_poi ] can be obtained for the frequencies observed (p_oi, i = 1, 2, …, 9), in line with the NB Law, expressed as follows:

Using the χ²-test, the interest of analysis lies in investigating whether the frequencies of the digits in a particular position (for example, the frequencies of the digits 1 to 9 in the first significant position) follow the patterns established by the NB Law. To carry out the χ²-test, the following test statistic is used:

in which PO_i = p_oi xn and PE_i = p_ei xn are the absolute frequencies observed and expected for digit i = 1, …, 9 in the first significant position, and n represents the sample size. Thus, at a level of significance of α = 0.05, H _{0 B} (the hypothesis of global adjustment of frequencies in accordance with the NB Law) is rejected when the statistic χ² > 15.507.

As observed by some authors, the Z-test and the χ²-test present a problem when significantly large samples are used, leading to tests with very low error rates, and thus with considerably high powers (Nigrini & Mittermaier, 1997; Krakar & Žgela, 2009; Suh et al., 2011). This fact is known in the literature as “excess of power”. According to Nigrini and Mittermaier (1997), the Z-test rejects the null hypothesis in samples of more than 100,000 elements in size, even when the differences between the frequencies observed and the NB Law probabilities are considered as immaterial from the auditing point of view. According to Krakar and Žgela (2009), the χ²-test also presents this same problem in samples of more the 10,000 elements in size.

This paper proposes the use of a measure of relative percentage variation, which is defined as relative discrepancy, in a time series analysis of frequencies observed for the digits 1 to 9 in the first significant position. Such a measure was also used by Žgela (2011) in a study regarding percentage variations occurring between 2001 and 2011 in the DAX index in the German capital market. However, the analyses were carried out using accumulated information for the whole period (at the end of 2011). Using relative discrepancies, it is possible to construct time series without there being the problem of “excess power”, as highlighted in Nigrini and Mittermaier (1997), Nigrini (2000), and Krakar and Žgela (2009). There is a notable advantage in using relative discrepancy time series compared to the proposal analyzed in Suh et al., (2011): the study proposed by these authors, although it follows a robust simulation strategy, is computationally more exhaustive, which can create difficulties for its implementation in large databases. However, the use of it in a future study is suggested, which could compare the two methodologies.

In this paper, the studies were conducted using data on contracts issued by 60 management units, divided between two states in the Brazilian northeast, in 2010. Thus, the use of the Z and χ² tests can lead to unreliable results, given that these tests assume the use of independent samples. Moreover, the use of these tests in quite large samples tends to lead to the problem of “excess power”. This can be observed when a fixed level of significance α is used, and the sample size increases indefinitely. In this case, it is noted that the confidence intervals for the proportions observed tend to be close to zero in length.

Another important aspect of a practical nature is the fact that in two samples with large differences in sizes (n ₁ >> n ₂), a comparison between the confidence intervals constructed with the use of the Z statistic would tend to be uninformative, given that in this case the relative chance of finding information that is non-compliant with the NB Law in an n ₂ sized sample is greater than it is for an n₁ sized sample.

3 METHODOLOGICAL PROCEDURES

The methodology used in this study consisted of carrying out two empirical analyses regarding the relative frequencies of the digits 1 to 9 observed in the first significant position in a set of contracts issued by 60 MUs in two states in the Brazilian northeast (states S1 and S2). In the analyses, 30 MUs are considered per state, based on data related to 2010. In a first study, for each state, the information on the observed proportions was grouped by digit into each MU from states S1 and S2. The information was totaled for the end of 2010; that is, the quantities in contracts issued over the whole of 2010 were accumulated for each management unit in each one of states S1 and S2. At this point, the intention is to show how the NB Law pattern is observed more in the MUs that issued the greatest number of contracts in 2010. Subsequently, the time series of relative discrepancies in observed frequencies were evaluated relative to the respective probabilities expected by the NB Law. The series were constructed with the data grouped by state and analyzed by significant digit.

In the focus of this study, relative discrepancies are defined as the ratios of the differences between the frequencies of digits observed (calculated from the data) and the respective probabilities expected by the NB Law [ (p_oi - p_ei ), i = 1, ..., 9 ], over the respective expected probabilities (Cribari & Silva, 2011). For example, considering the digit 1 in the first significant position, the expression of discrepancy relative to the probability expected by the NB Law (given by p_e1 ≈ 0.301), in period t, is calculated using the following expression:

in which p _o1 (t) denotes the relative frequency of the digit 1 in the first significant position in the t^th period of time. With regards to the analysis results, these suggest that the use of time series information regarding the frequencies of digits observed allows for the periods when the greatest deviations are formed to be identified, as well as making it possible to carry out a more detailed study regarding management units that present specific deviation patterns, adding information to sampling procedures in continuous auditing environments.

4 RESULTS ANALYSIS

For the first analysis, the relative frequencies of each digit (1 to 9) were calculated, organizing the contracts issued in 2010 by management unit (MUs 1 to 30 in each state) and by state (states S1 and S2). The aim of this study lies in evaluating, in a general way, the behavior of the frequencies of the digits 1 to 9 in the first significant position as the number of contracts issued increases.

Based on accepting the hypothesis that the NB Law is a mathematical law that governs the natural distribution of the digits that compose numbers, the occurrence of deviations in the distribution of digits, with regards to complying with the frequencies predicted in the aforementioned Law, would show evidence of human interference (Diniz et al., 2010). Thus, the deviations marked as a result of the analyses would be indications of human interference in the natural behavior of numbers, with this interference, in turn, being a possible indication of the occurrence of errors or frauds.

In the context of this analysis, focused on determining the compliance deviations observed for each digit, it is emphasized that positive relative discrepancies will signal a set of information that is more relevant to an auditing sampling process which aims to collect contract values that are non-compliant with the NB Law (Costa et al., 2012).

To explain this fact, suppose that x contract values are added to a set of contract values complying with the NB Law, the former starting with each one of the digits 1 to 8, thus totaling 8x additions (x in each digit). In this case, in an analysis carried out solely for the digit 9, it would not be possible to locate the contracts added, while in an analysis for the digits 1 to 8 this would be possible. Even though the quantities added to the digits are the same (x for each digit), the chances of finding a non-compliant element inserted would be greater in a sample formed of elements starting with the digit 8. This occurs because the proportion of contracts altered in the group of values beginning with the digit 8 would have a superior value to the respective proportions related to the other digits (Costa, 2012).

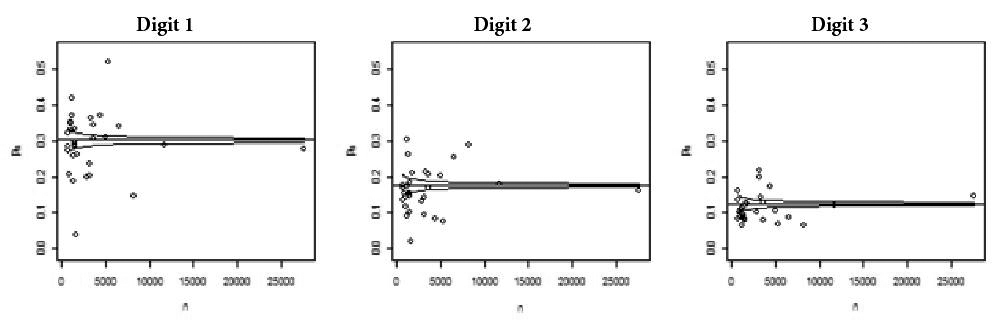
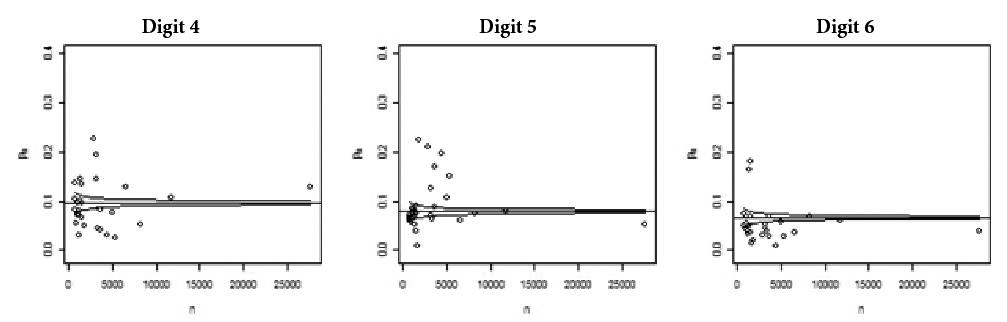
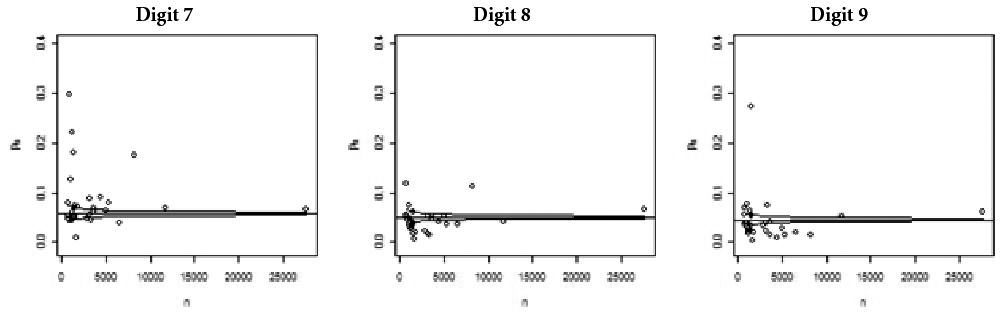
Figures 1 to 6 contain the graphs of observed relative frequencies (frequencies for the first significant position on the y axis) against the number of contracts issued by each MU in 2010 (x axis). The numbers of contracts recorded on the horizontal axis (x axis) were obtained directly from the historic databases for each MU in the corresponding year of analysis. Figures 1 to 3 refer to state S1 and figures 4 to 6 refer to state S2. In each graph, the margins of confidence are also shown for each frequency observed (limits of tolerance for NB Law compliance). The confidence intervals were constructed as described in expression (3) in section 2.3, this being α = 0.05 (that is, the degree of coverage considered is 95%). As can be observed, in all of the figures, as the number of contracts (n) increases, there is a tendency towards NB Law compliance. This fact was highlighted most in MUs 1 and 2 in state S1, with 27,691 and 11,809 contracts each, respectively, and for MUs 3 and 12 in state S2, with 21,796 and 11,006 contracts.

In general terms, in both states a greater spread of observed frequencies around the expected frequencies (established by the NB Law) is noted, when the number of contracts is lower than 5,000. Also in the context of this analysis, one fact to be observed is that graphs such as those in Figures 1 to 6 allow a general and comparative analysis to be carried out regarding all of the digits, signaling the MUs that present the greatest deviations from the NB Law via observed frequencies that are very far from the established confidence bands.

However, when structured as thus, this analysis does not allow for the period over the course of 2010 to be analyzed. Additionally, given the significantly high number of contracts, with α being fixed, the confidence intervals for the observed proportions tend to be close to zero in length. This is due to the fact that, at a fixed nominal level (fixed α value), the power of the Z-test tends towards a value close to 1 as the sample size increases indefinitely. These confidence intervals would show the “excess power” effect cited by Nigrini and Mittermaier (1997) and Krakar and Žgela (2009).

Figure 1
Graphs of observed frequencies for state S1 at the end of 2010 for the digits 1, 2, and 3

Figure 2
Graphs of observed frequencies for state S1 at the end of 2010 for the digits 4, 5, and 6

Figure 3
Graphs of observed frequencies for state S1 at the end of 2010 for the digits 7, 8, and 9

Figure 4
Graphs of observed frequencies for state S2 at the end of 2010 for the digits 1, 2, and 3

Figure 5
Graphs of observed frequencies for state S2 at the end of 2010 for the digits 4, 5, and 6

Figure 6
Graphs of observed frequencies for state S2 at the end of 2010 for the digits 7, 8, and 9

In the following analysis, the use of time series of relative discrepancies is proposed, as defined in expression (5) in section 3. This analysis aims to observe the behaviors of deviations from the NB Law probabilities over the course of 2010, and not only at the end of this period. As discussed in sections 2.3 and 3, the use of relative discrepancies allows time analyses to be carried out, which would not be adequate with the use of Z statistic values, since the Z-test assumes the use of independent samples. Moreover, there is a loss in comparative aspects in analyses of samples with big differences in size.

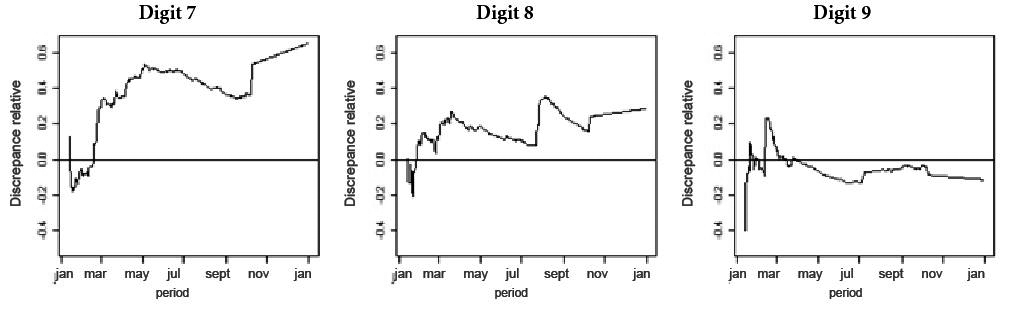
Figures 7 to 9 contain the time series graphs of relative discrepancies for the digits from 1 to 9 in the period from 01/17/2010 to 12/31/2010, considering the total values of contracts issued by the management units from state S2. It is worth noting that in all of the analyses, the choice of starting date for the time series fulfilled a minimum number n = 100 contracts. The pattern of deviations observed in Figure 7, with excessive occurrence of the digit 7 and absence of the digits 6, 8, and 9, was already identified by Costa et al. (2012), Costa (2012), and Costa, Travassos et al. (2013) in an analysis carried out regarding the behavior of public spending, with it being interpreted by the authors that the exemption limit for public tender processes (set out in Federal Law n. 8.666/93) probably influence the behavior of public spending.

The deviations suggest, given that the limit to spending on purchases and services not involving engineering is up to R$ 8,000.00, the occurrence of a possible displacement of the values starting with the digits 6, 8, and 9 to the digit ‘7’, in values lower than the legal limit established, thus avoiding the need to carry out bidding processes.

Figure 7
Time series graphs of relative discrepancies for state S2 in the period from 01/17/2010 to 12/31/2010 for digits 1, 2, and 3

Figure 8
Time series graphs of relative discrepancies for state S2 in the period from 01/17/2010 to 12/31/2010 for digits 4, 5, and 6

Figure 9
Time series graphs of relative discrepancies for state S2 in the period from 01/17/2010 to 12/31/2010 for digits 7, 8, and 9

Observing Figures 10 to 12, related to state S1 in the period from 01/31/2010 to 12/31/2010, it is noted once more that the pattern of deviations observed for the digits 6, 7, 8, and 9 also suggest the bidding limit having a possible influence over state S1’s spending, given that deviations due to the absence of the digits 6 and 9 were observed, accompanied by a deviation due to an excess in the digit 7. The digit 8, although it presented a deviation due to excess after 01/27/2010, showed evidence of the influence of bidding limits, given that 1,279 contracts out of the 5,878 contracts beginning with the digit 8 are equal in value to the bidding limit of up to R$ 8,000.00; that is, 21.76% of the total.

Figure 10
Time series graphs of relative discrepancies for state S1 in the period from 01/13/2010 to 12/31/2010 for the digits 1, 2, and 3

Figure 11
Time series graphs of relative discrepancies for state S1 in the period from 01/13/2010 to 12/31/2010 for the digits 4, 5, and 6

Figure 12
Time series graphs of relative discrepancies for state S1 in the period from 01/13/2010 to 12/31/2010 for the digits 7, 8, and 9

Figure 13 presents the time series graph of relative discrepancies observed for the digit 8, removing 1,279 contracts from the sample with values equal to the bidding limit (R$ 8,000.00), within the same period considered in figures 7 to 9. As can be observed, in contrast with the graph for the digit 8 in Figure 12, there is a change in the behavior of the time series (before typically rising, and after typically falling). Thus, it is concluded that the excesses of the digit 8 were caused principally by the great number of contracts issued with values equal to this limit (R$ 8,000.00) over the whole of 2010.

Figure 13
Graph of relative discrepancies observed for the digit 8 in the first significant position, considering all of the MUs from state S1 in the period from 01/31/2010 to 12/31/2010.

With a particular focus in the second analysis, two management units in state S2 (MUs 8 and 15) were identified as presenting positive variations over the financial period analyzed, which were mostly compensated for by the end of 2010. Figure 14 presents the time series graph of relative discrepancies observed for the digit 2 in the first significant position for the contract values reported by MU 15 in state S2 in 2010.

Observing Figure 14, a rising behavior for relative discrepancy is noted from the beginning of January until the end of June 2010, reaching its maximum positive deviation of 87% on 07/25/2010. Despite the occurrence of this expressive deviation in the first semester, it is seen that in the following semester there was an inverse behavior, with a gradual reduction in deviations until reaching a level of 23.5% at the end of the financial period. In the case of MU 15, the frequency observed for the digit 2 was 0.217 for 2010, a value outside the confidence interval with 95% coverage (Ic = [0.161, 0.190]). Thus, the two-tailed Z-test rejects the null hypothesis that the frequency observed for the digit 2 is equal to the probability established by the NB Law (≈ 0,176) at a level of significance of α = 0.05.

Figure 14
Graph of relative discrepancies observed for the digit 2 in the first significant position, considering MU 15 from state S2 in the period from 01/31/2010 to 12/31/2010.

Figure 15 shows the graph of relative discrepancies corresponding to the digit 7, considering the financial information on MU 8 from state S2. As can be observed, in the period between the end of May and the beginning of June the relative discrepancy values presented a rapid and significant increase, reaching their maximum point on 06/16/2010, with a positive deviation of 68.63%. From this point on, a reduction in the deviations is seen until the close of the 2010 financial year, with a relative discrepancy of 7.41%. Unlike MU 15, in the case of MU 8 the frequency observed for the digit 7 at the end of 2010 was 0.062, a value within the confidence interval with 95% coverage (Ic = [0.049, 0.066])

Figure 15
Graph of relative discrepancies observed for the digit 7 in the first significant position, considering MU 8 from state S2 in the period from 01/31/2010 to 12/31/2010.

The previous two examples show that carrying out a time series analysis such as that proposed in this study both allows for peaks in deviations occurring in the period analyzed to be identified, as well as making it possible to determine with greater precision the elements of interest in forming the sample to be audited. On the other hand, based on the positive relative discrepancy values, it is possible to estimate the probability of detecting the elements in excess. Taking, for example, the observed deviation calculation for the digit 7 in time period t, based on the expression /, the quantity / represents the relative chance of finding contracts that caused deviations due to excess in the set of contract values beginning with the digit 7. In the case of MU 8 in the previous analysis, as can be seen in Figure 15, at the beginning of June the relative discrepancy reached the value of 0.68, which means that the relative chance of finding contract values in excess, relative to the NB Law, in the set of contract values beginning with the digit 7, is close to 40.47%.

From the result above, it is seen that the use of relative discrepancies, unlike the Z and χ² tests, which become more rigorous when the number of elements analyzed increases, impairing NB Law compliance analyses, reflects the proportion of deviations observed, independent of sample size.

5 FINAL REMARKS

This paper analyzed NB Law compliance as a proposal for identifying deviations over time in continuous auditing environments, using 210,899 contracts issued by 60 MUs in two states in the Brazilian Northeast in 2010. These contracts were analyzed for the distribution of the first significant digit, at the end and over the course of that year.

Based on monitoring in a computerized environment, using graphical analysis of observed frequencies and time series of relative discrepancies (see Figures 1 to 12), the formation of typical patterns of possible irregularities or digressions from Public Tenders Law (Federal Law n. 8.666/93) was verified. This law grants coercive powers to external controlling bodies in relation to investigated irregularities in processing public spending. Figures 1 to 12 show possible features of public spending being broken up into lower values or ones equal to the spending limit, which is a practice used to bypass carrying out public tender processes, as well as to allocate public spending to a favorite supplier, as discussed in studies from Costa et al. (2012) and Costa (2012).

In using relative discrepancies over time, it was also identified that MU 8 from state S2 presented the occurrence of significant deviations over the period (Dr = 68.63%), in contrast with the deviation observed at the end of the period (of only 7.41%), even causing the non-rejection of the null hypothesis (H_0A) for the analyzed digit 7. Similarly, it was shown in this paper that NB Law compliance analyses, carried out using relative discrepancies, also allow to identify the risk of finding elements with excessive occurrence to be found for the digits analyzed, independent of sample size, unlike what is observed with the Z and χ² tests, which become more rigorous when the number of elements analyzed increases. Thus, implanting simultaneous controls in computerized auditing environments was found to be relevant, as well as their promptness and greater effectiveness, given that they are carried out over the course of or shortly after an occurrence. This short timeframe not only means a greater chance of success, but also the possibility of stopping the effects of any irregular activity that might be detected (Costa et al., 2012; Costa, 2012).

It was shown, in section 4, that a continuous auditing environment based on the methodological approach involving the NB Law contributes in helping auditing teams construct pathways, due to greater effectiveness over the course of or shortly after the occurrence of events to be inspected; that is, time and volume limits for processing information are extended. Thus, convinced the analyst, when selecting the data that will compose their samples for analysis, he suggests to the auditor the relevant points to be observed regarding deviations in public spending patterns, directly contributing to the planning of their audits.

It is clear that this article, in light of the results observed from carrying out a time series analysis of NB Law compliance, both makes it possible to identify peaks in deviations occurring in the period analyzed, as well as allowing for elements to be more precisely identified which are of interest when forming samples for applying this approach in continuous auditing environments.

REFERENCES

• Arens, A. A.; Elder, R. J., & Beasley, M. S. (2004). Auditing and Assurance Services (10th ed.). Upper Saddle River: Prentice Hall.
• Ashcroft, P., Bae, B., & Norvell, J. (2002). Application of digital analysis in the audit. Today's CPA, (5), 31-35. Retrieved from http://www.csub.edu/~bbae/publication/digital%20analysis%20in%20audit.todays%20cp a%202002.pdf
  » http://www.csub.edu/~bbae/publication/digital%20analysis%20in%20audit.todays%20cp a%202002.pdf
• Attie, W. (1998). Auditoria, conceitos e aplicações (3a ed.). São Paulo: Atlas.
• Benford, F. (1938). The law of anomalous numbers. Proceedings of the American Philosophical Society, 78(4), 551-572.
• Carslaw, C. A. P. N. (1988, April). Anomolies in income numbers: evidence of goal oriented behavior. The Accounting Review, 2(63), 321-327.
• Costa, J. I. F. (2012). Desenvolvimento de metodologias contabilométricas aplicadas à auditoria contábil digital: uma proposta de análise da lei de Newcomb-Benford para os Tribunais de Contas Master’s Degree, Universidade Federal de Pernambuco, Recife, PE, Brasil.
• Costa, J. I. F., Santos, J., & Travassos., S. K. M (2012). Análise de conformidade nos gastos públicos dos entes federativos: estudo de caso de uma aplicação da Lei de Newcomb-Benford para o primeiro e segundo dígito em dois estados brasileiros. Revista Contabilidade &. Finanças, 23(60), 187-198.
• Costa, J. I. F., Silva, W. B., Travassos, S. K. M., & Santos, J. (2013) Análise de Conformidade da Lei de Newcomb-Benford no Ambiente de Auditoria Contínua: Uma Proposta de Identificação de Desvios no Tempo. In Anais do 37º Encontro Nacional da Associação Nacional de Pós-Graduação e Pesquisa em Administração, Rio de Janeiro, RJ, Brasil.
• Costa, J. I. F., Travassos, S. K. M., Soeiro, T. M., & Santos, J. S. (2013). Statistical analysis in detection of deviation occurrence in the distribution of first significant digit of state public spending in relation to the standard distribution defined in Newcomb-Benford's law. In 10ª Conferência Internacional sobre Sistemas de Informação e Gestão de Tecnologia, São Paulo, SP, Brasil.
• Cribari-Neto, F., & Silva, W. B. (2011). A new heteroskedasticity-consistent covariance matrix estimator for the linear regression model. AStA Advances in Statistical Analysis, 95(2), 129-146.
• Diniz, J. A., Corrar, L. J., & Slomski, V. (2010). Análise digital: uma abordagem cognitiva na detecção de não conformidade em prestações de contas municipais. Anais do 10º Congresso USP de Controladoria e Contabilidade, São Paulo, SP, Brasil.
• Hill, T. P. (1995). Base-invariance implies Benford’s law. Proceedings of the American Mathematical Society, 123(3), 887-895.
• Hill, T. P. (1996). A Statistical derivation of the significant-digital law. Statistical Science, 10(4), 354-363.
• Huxley, S. J. (1999). Why Benford's law works and how to do digit analysis on spreadsheets. Proceedings of the Annual International Conference of the Decision Sciences Institute, Athens, Greece.
• Krakar, Z., & Žgela, M. (2009). Application of Benford's law in payment systems auditing. Journal of Information and Organizational Sciences, 33(1), 39-51.
• Kumar, K., & Bhattacharya, S. (2002). Benford’s law and its application in financial fraud detection. The Advances in Financial Planning and Forecasting, 11, 57-70.
• Lei n. 8.666, de 21 de junho de 1993 (1993). Regulamenta o art. 37, inciso XXI, da Constituição Federal, institui normas para licitações e contratos da administração pública, e dá outras providências. Brasília. Retrieved from http://www.planalto.gov.br/ccivil_03/Leis/L8666cons.htm
  » http://www.planalto.gov.br/ccivil_03/Leis/L8666cons.htm
• Lima, A. L. P., & Vieira, S. S. C. (2002). Auditoria e controle, Caderno 1, n. 1.
• Mills, A. C. (1994). A auditoria da qualidade: uma ferramenta para avaliação constante e sistemática da manutenção da qualidade (5a ed.). São Paulo: Makron Books.
• Murcia, F. D., Souza, F. C., & Borba, J. A. (2008). Continuous audit: a literature review. Revista Organizações em Contexto (online), 4(7), 1-17.
• Newcomb, S. (1881). Note on the frequency of use of the different digits in natural numbers. American Journal of Mathematics, 4(1), 39-40.
• Nigrini, M. J. (1996). A taxpayer compliance application of Benford’s law. The American Taxation Association 1, 72-91.
• Nigrini, M. J. (1999). I´ve got your number. Journal of Accountancy, 187(5), 79-83.
• Nigrini, M. J. (2000). Digital Analysis Using Benford’s Law: Tests& Statistics for Auditors Vancouver: Global Audit Publications.
• Nigrini, M. J., & Mittermaier, L. J. (1997). The use of Benford’s Law as an aid in analytical procedures. Auditing, 16(2), 52-68.
• Pinkham, R. S. (1961). On the distribution of first significant digits. Annals of Mathematical Statistics, 32(4), 1223-1230.
• Posch, P. N. (2004). Ziffernanalyse in der Fälschungsaufspürung. Benford’s Gesetz und Steuererklärungen in Theorie und Praxis. Unpublished manuscript Retrieved from http://www.posch.net/paper/posch_faelschungenbenford.pdf
  » http://www.posch.net/paper/posch_faelschungenbenford.pdf
• Raimi, R. (1969). The peculiar distribution of first significant digits. Scientific American, 221(6), 109-120.
• Ribeiro, J. C., Montenegro, G. B., Santos, J., & Galvão, K. S. (2005). Aplicação da Lei de Newcomb-Benford na Auditoria. Caso notas de empenho dos Municípios do Estado da Paraíba. In Anais do 5º Congresso USP de Controladoria e Contabilidade, São Paulo, SP, Brasil.
• Santos, J., Diniz, J. A., & Ribeiro, . F., Filho (2003). A Lei de Newcomb-Benford: uma aplicação para determinar o DNA-equivalente das despesas no setor público. In Anais do 3º Congresso USP de Controladoria e Contabilidade, São Paulo, SP, Brasil.
• Santos, J., Diniz, J. A., & Corrar, L. J. (2005). O foco é a Teoria Amostral nos campos da auditoria contábil tradicional e da auditoria digital: testando a Lei de Newcomb- Benford para o primeiro dígito nas contas públicas. Brazilian Business Review, 2(1), 71-89.
• Santos, J., Ribeiro Filho, J. F.; Lagioia, U., Alves Filho, B. F. A., & Araújo, I. J. C. (2009). Aplicações da lei de Newcomb-Benford na auditoria tributária do Imposto sobre Serviços de Qualquer Natureza (ISS). Revista Contabilidade & Finanças, 20(49), 79-94.
• Suh, I. S., Headrick, T. C, & Minaburo, S. (2011). An Effective and Efficient Analytic Technique: A Bootstrap Regression Procedure and Benford's Law. Journal of Forensic & Investigative Accounting, 3(3), 25-45.
• Thomas, J. K. (1989). Unusual patterns in reported earnings. The Accounting Review 64(4), 773-787.
• Varian, H. R. (1972). Benford's Law. The American Statistician, 26(3), 65-66.
• Vasarhelyi, M. A., & Halper, F.B. (1991). The continuous audit of online systems. Auditing : A Journal of Practice and Theory, 10(1), 110-125.
• Watrin, C., Struffert, R., & Ullmann, R. (2008). Benford’s Law: an instrument for selecting tax audit targets? Review of Managerial Science, 2(3), 219-237.
• Žgela, M. (2011). Application of Benford’s law in analysis of DAX percentage changes. Cybernetics and Information Technologies, 11(4), 2011.

• *Article presented at the XXXVII ANPAD Conference, Rio de Janeiro, RJ, Brazil, 2013.

Publication Dates

• Publication in this collection
  Apr 2017

History

• Received
  21 Oct 2015
• Accepted
  08 Nov 2015