Abstract
This study used real data from a Brazilian financial institution on transactions involving Consumer Direct Credit (CDC), granted to clients residing in the Distrito Federal (DF), to construct credit scoring models via Logistic Regression and Geographically Weighted Logistic Regression (GWLR) techniques. The aims were: to verify whether the factors that influence credit risk differ according to the borrower’s geographic location; to compare the set of models estimated via GWLR with the global model estimated via Logistic Regression, in terms of predictive power and financial losses for the institution; and to verify the viability of using the GWLR technique to develop credit scoring models. The metrics used to compare the models developed via the two techniques were the AICc informational criterion, the accuracy of the models, the percentage of false positives, the sum of the value of false positive debt, and the expected monetary value of portfolio default compared with the monetary value of defaults observed. The models estimated for each region in the DF were distinct in their variables and coefficients (parameters), with it being concluded that credit risk was influenced differently in each region in the study. The Logistic Regression and GWLR methodologies presented very close results, in terms of predictive power and financial losses for the institution, and the study demonstrated viability in using the GWLR technique to develop credit scoring models for the target population in the study.
Keywords:
credit risk; geographically weighted logistic regression; credit scoring
Resumo
Este estudo utilizou dados reais de uma instituição financeira nacional referentes a operações de Crédito Direto ao Consumidor (CDC), concedidas a clientes domiciliados no Distrito Federal (DF), para a construção de modelos de credit scoring utilizando as técnicas Regressão Logística e Regressão Logística Geograficamente Ponderada [Geographically Weighted Logistic Regression] (GWLR). Os objetivos foram: verificar se os fatores que influenciam o risco de crédito diferem de acordo com a localização geográfica do tomador; comparar o conjunto de modelos estimados via GWLR frente ao modelo global estimado via Regressão Logística, em termos de capacidade de previsão e perdas financeiras para a instituição; e verificar a viabilidade da utilização da técnica GWLR para desenvolver modelos de credit scoring. As métricas utilizadas para comparar os modelos desenvolvidos por meio das duas técnicas foram o critério informacional AICc, a acurácia dos modelos, o percentual de falsos positivos, a soma do valor da dívida dos falsos positivos e o valor monetário esperado de inadimplência da carteira frente ao valor monetário de inadimplência observado. Os modelos estimados para cada região do DF se mostraram distintos em suas variáveis e coeficientes (parâmetros), concluindo-se que o risco de crédito foi influenciado de maneira distinta em cada região do estudo. As metodologias Regressão Logística e GWLR apresentaram resultados bem próximos, em termos de capacidade de previsão e perdas financeiras para a instituição, e o estudo demonstrou a viabilidade da utilização da técnica GWLR para desenvolver modelos de credit scoring para o público-alvo do estudo.
Palavras-chave:
risco de crédito; regressão logística geograficamente ponderada; credit scoring
1. INTRODUCTION
The main activity of commercial banks is financial intermediation, which consists of raising financial resources and lending them to third parties under pre-established conditions, such as payment period, installment value, and interest rate (Hand & Henley, 1997Hand, D. J.; Henley, W. E. (1997). Statistical classification methods in consumer credit scoring: a review. Journal of the Royal Statistical Society: Series A (Statistics in Society), 160(3), 523-541.). As it involves expectation of future receipt, all credit granted is exposed to risks.
The topic “risk management” drew attention in the financial sector after the publishing of the Basel accords, which is a set of documents that serve as a basis for regulation and monitoring of the sector. Advances in technology and computing, together with the development of quantitative methods, have contributed in creating different tools for measuring risk, bringing significant gains in the financial management of institutions.
Credit risk can be defined as the possibility of financial losses occurring, associated with borrowers or counterparties not fulfilling their respective obligations in the agreed terms, with the devaluation of loan contracts because of a deterioration in borrowers’ risk classifications, with reductions in earnings or remunerations, with advantages conceded in renegotiations, and with recovery costs (Brazilian Central Bank [BACEN], 2009Banco Central do Brasil (2009). Resolução CMN nº 3.721, de 30/04/2009. Retrieved from http://www.bcb.gov.br
http://www.bcb.gov.br...
). It is one of the main risks that financial institutions are exposed to.
The models used to measure risk when granting credit are called credit scoring models. Due to them involving lower costs and greater agility, objectivity, and predictive power in credit granting decisions, credit scoring models have become popular and are widely used by the financial sector (Hand & Henley, 1997Hand, D. J.; Henley, W. E. (1997). Statistical classification methods in consumer credit scoring: a review. Journal of the Royal Statistical Society: Series A (Statistics in Society), 160(3), 523-541.).
Lessmann, Baesens, Seow, and Thomas (2015Lessmann, S.; Baesens, B.; Seow, H. V.; Thomas, L. C. (2015). Benchmarking state-of-the-art classification algorithms for credit scoring: An update of research. European Journal of Operational Research, 247(1), 124-136.) carried out a comprehensive study on the classification methodologies used for developing credit scoring models and indicated logistic regression as being the standard methodology in the financial sector.
Logistic regression is a multivariate analysis technique that aims to explain the relationship between a random binary dependent variable and a set of independent predictive variables (Hosmer & Lemeshow, 2000Hosmer, D. W.; Lemeshow, S. (2000). Applied logistic regression. Hoboken, NJ: John Wiley & Sons.).
Financial institutions use various credit scoring models, which are applied when evaluating different types of clients or credit operations to be contracted. The predictive variables that compose each model can be different, with the aim of improving predictions for the target population.
Geographical location (space) and its relationship with credit risk is the topic of some published studies. Among the most recent, Stine (2011Stine, R. (2011). Spatial temporal models for retail credit. In Proceedings of the Credit Scoring and Credit Control Conference, Edinburgh, UK.) analyzes the evolution of defaults on real estate loans in US counties between 1993 and 2010, contemplating pre- and post- subprime crisis periods, and finding evidence of a spatial correlation between default rates in these counties.
Fernandes and Artes (2015Fernandes, G. B.; Artes, R. (2016). Spatial dependence in credit risk and its improvement in credit scoring. European Journal of Operational Research, 249(2), 517-524.) used the Ordinary Kriging methodology to create a variable that reflects spatial risk and applied the Logistic Regression technique to verify the existence of a spatial correlation in defaults on loans taken out by small and medium sized enterprises (SMEs), using data from the SERASA credit bureau. The authors developed models with and without the spatial risk variable and confirmed that the inclusion of this variable improves credit scoring model performance.
The Geographically Weighted Regression (GWR) technique, proposed by Brunsdon, Fotheringham, and Charlton (1996Brunsdon, C.; Fotheringham, A. S.; Charlton, M. E. (1996). Geographically weighted regression: a method for exploring spatial nonstationarity. Geographical Analysis, 28(4), 281-298.), is used to model spatially heterogeneous (non-stationary) processes; that is, processes that vary (whether in mean, median, variance, etc.) from region to region. The basic idea of GWR is to adjust a regression model to each region in the data set using geographical location of the other observations to weight the parameter estimates. Application of the GWR technique can be observed in different areas of research, such as Geography (See et al., 2015See, L.; Schepaschenko, D.; Lesiv, M.; McCallum, I.; Fritz, S.; Comber, A.; Obersteiner, M. (2015). Building a hybrid land cover map with crowdsourcing and geographically weighted regression. ISPRS Journal of Photogrammetry and Remote Sensing, 103, 48-56.), Health (Gilbert & Chakraborty, 2011Gilbert, A.; Chakraborty, J. (2011). Using geographically weighted regression for environmental justice analysis: Cumulative cancer risks from air toxics in Florida. Social Science Research, 40(1), 273-286.), and Economics (Huang & Leung, 2002Huang, Y.; Leung, Y. (2002). Analysing regional industrialisation in Jiangsu province using geographically weighted regression. Journal of Geographical Systems, 4(2), 233-249.).
Atkinson, German, Sear, and Clark (2003Atkinson, P. M.; German, S. E.; Sear, D. A.; Clark, M. J. (2003). Exploring the relations between riverbank erosion and geomorphological controls using geographically weighted logistic regression. Geographical Analysis, 35(1), 58-82.) used Geographically Weighted Logistic Regression (GWLR) in their study to analyze the dependency of geographical location in the relationship between erosion and geomorphologic controls in a region of Wales. The dummy variable used in this study was the presence or absence of erosion in the areas studied. Applying the GWLR technique resulted in the estimation of models with different parameters (distinct models) for each area studied, revealing the need to adopt different practices to avoid erosion, depending on the region.
This article used data related to transactions involving Consumer Direct Credit (CDC), granted by a Brazilian financial institution to clients residing in the Distrito Federal (DF). The aims were as follows: to verify whether the factors that influence credit risk differ according to borrowers’ geographical locations; to compare the set of models estimated via GWLR with the global model estimated via Logistic Regression, in terms of predictive power and financial losses for the institution; and to verify the viability of using the GWLR technique to develop credit scoring models.
Although the central idea in this article of verifying whether space influences credit risk is similar to that of Stine (2011Stine, R. (2011). Spatial temporal models for retail credit. In Proceedings of the Credit Scoring and Credit Control Conference, Edinburgh, UK.) and Fernandes and Artes (2015Fernandes, G. B.; Artes, R. (2016). Spatial dependence in credit risk and its improvement in credit scoring. European Journal of Operational Research, 249(2), 517-524.), the target population and methodology used are different, with no studies being found in the literature that used the GWLR technique for the development of credit scoring models.
One advantage of applying the GWLR technique in relation to the others lies in estimating a model for each region in the study, allowing these models to be distinct in their variables and parameters (Atkinson et al., 2003Atkinson, P. M.; German, S. E.; Sear, D. A.; Clark, M. J. (2003). Exploring the relations between riverbank erosion and geomorphological controls using geographically weighted logistic regression. Geographical Analysis, 35(1), 58-82.), whereas a global model, represented by only one formula, may not represent local variations adequately. In relation to credit, different study regions can involve different risks, and if this phenomenon is observed, models that consider local characteristics can better differentiate the credit risk for borrowers residing there and generate financial gains for the institution.
Another difference from other studies on this topic and an advantage in the GWLR technique involves the use of different samples in developing each local model, giving greater weight to borrowers who are closer geographically, and not using distant information that is outside the radius defined by the weighting function.
Questions regarding endogeneity are not addressed in this study and could be raised by researchers in future papers.
In addition to this introduction, the second section of the article presents the geographically weighted logistic regression methodology and the process for developing the models, the thirds shows the results obtained, and the fourth sets out the conclusion.
2. METHODOLOGY
The flowchart presented in Figure 1 details all of the stages carried out in the process of developing the models in this study.
2.1. Database
The data related to this study refer to transactions involving Consumer Direct Credit (CDC) granted by a Brazilian financial institution to clients residing in the Distrito Federal (DF). These transactions are paid in installments over periods between 0 and 36 months and have a maximum contract value of R$30,000.00.
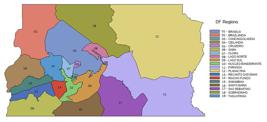
The territorial division of the DF used in this study was composed of 19 regions, shown in Figure 2.
The sample included all loans granted between December 2013 and September 2014, involving 10 rounds of borrowing and a total of 22,132 different loan contracts. Payment performance on these loans was monitored in the twelve months subsequent to the contract agreement date and those that exceeded 90 days in arrears in any of these months were labeled as being in default (Y=1). Due to loan arrears performance involving different moments in time, this database is classified as being of the panel data type.
The predictive variables selected to compose the models were: Age, Income, Level of Education, Borrower’s Time of Relationship with the Institution, Loan Contract Period, SELIC, Unemployment Rate, and Inflation (IPCA). These variables refer to the time credit is taken out (a single point in time), thus involving cross-sectional type data.
The latitude and longitude geographical coordinates for the regions used in the study and needed to apply the GWLR technique were obtained from the IBGE website, and refer to the central point in each region and are equal for borrowers residing in the same region.
The database was subdivided into model development and validation samples according to the date a transaction was contracted, with the development sample composed of the first five rounds (December 2013 to April 2014) and totaling 10,944 records. The validation database is composed of the final five rounds (May to September 2014), totaling 11,188 records.
The data manipulation, as well the univariate, bivariate, and spatial indicator calculations, along with those for developing the global model via logistic regression analysis, were carried out using the SAS software. The GWLR models were developed using the GWR4 software.
2.2. Spatial indicators
Moran’s I (Moran, 1950Moran, P. A. (1950). Notes on continuous stochastic phenomena. Biometrika, 37(1/2), 17-23.) is one of the most widely used global indicators for verifying the existence of spatial correlation. Global indicators present a single measure of spatial tendency for the whole region being studied, they allow the hypothesis of the existence of spatial dependency between regions to be tested in accordance with the variable of interest, and are used in exploratory analysis of data. The formula is given by:
in which n is the number of regions being studied, xi and xj are the values of the variable of interest in regions i and j, and wij are the spatial proximity matrix elements, which can be calculated in different ways, such as via the presence or absence of a frontier between the regions or by the Euclidian distance between them. The Moran index is restricted to the interval [-1,1], in which values close to -1 indicate negative spatial correlation, values close to 1 indicate positive spatial correlation, and a value equal to 0 indicates the absence of spatial correlation or spatial independence with relation to the variable tested.
Whereas the global indicators assume that all of the regions studied can be represented by a single value, the local indicators of spatial association (LISA), developed by Anselin (1995Anselin, L. (1995). Local indicators of spatial association - LISA. Geographical Analysis, 27(2), 93-115.), are used to verify the existence of spatial correlation within the geographical units studied and look for regional differences (peculiarities). The presence of areas with significant local indices is an indication of spatial (non-stationary) homogeneity.
The Moran Local Index formula is given by:
The database used in applying the Moran Global and Local Indices was the total database of records (without subdivision of samples) and the variable tested was the regional default rate, calculated via the following formula:
In this study the Moran Global Index was used to verify the existence of spatial correlation in the default rate between the regions in the DF. The Moran Local Index was used to verify the existence of regions with different default rates in relation to the others. The existence of significant regions (the confidence level used for the Moran Local Index was 95%) may indicate that the regression models developed for these regions are different in relation to the models for the other regions in the study, which may warrant applying the GWLR to this target population.
2.3. Geographically Weighted Regression
According to Fotheringham, Brunsdon, and Charlton (2002)Fotheringham, A. S.; Brunsdon, C.; Charlton, M. (2002). Geographically weighted regression: the analysis of spatially varying relationships. Chichester: John Wiley & Sons., given a basic linear regression model, the equivalent expression for the GWR is given by:
It is noted from the expression above that the model parameters represented by the function βk (ui, vi ) vary according to the values (ui, vi ), which represent the latitude and longitude geographical coordinates for observation (region) i, resulting in a different model for each region in the study. The assumptions of the classical linear regression model remain in place for GWR.
The matrix form for estimating the GWR parameters is given by:
in which
W(ui, vi ) is a diagonal matrix and different for each point i of coordinates (ui, vi ), containing the weights wij in its main diagonal, obtained via the weighting functions, or kernel. The substitution of all the weights wij for the value 1 equates to the identity matrix, which, substituted in (5), turns it back into the classical linear regression model.
The two main weighting functions found in the literature are the Normal or Gaussian function and the Bisquare function. The formulas for both functions are presented in Table 1.
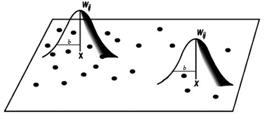
It is noted from Table 1 that there are two types of expressions for each one of the Gaussian and Bisquare functions, which differ in the method of choosing the b (bandwidth) parameter to be used (whether fixed or variable). The dij parameter contained in the weighting functions represents the distance from point i to point j, the b parameter is the fixed bandwidth (smoothing parameter), and the bi(k) parameter represents the adaptive bandwidth, with the letter k representing the number of neighbors closest to point i.
The bandwidth parameter controls the variance in the weighting function; for this reason, in situations in which the data are not equally distributed between regions, use of the bandwidth adaptive is recommended. Figure 3 illustrates the bandwidth in the weighting function and Figures 4 and 5 exemplify the use of fixed or adaptive bandwidths.
When developing a model via GWR using the fixed bandwidth, it should be specified by its value in unit of distance; however, in using the adaptive bandwidth, a k (fixed) number of closest neighbors to be used in the models should be defined, and based on this quantity k, the value of the bandwidth varies between the regions being studied.
2.4. Geographically Weighted Logistic Regression
When the response variable is binary, GWR should be applied via Geographically Weighted Logistic Regression (GWLR), in which the formula for obtaining the probability of the event of interest occurring is given by:
or still, in the form:
in which π(xj ) is the probability of the j th client defaulting and the function βk (ui,vi ) represents the parameters (coefficients) of the k variables in the model, which vary according to the region i of latitude and longitude coordinates (ui, vi ).
The GWLR parameters are estimated via the maximum vraisemblance method and the GWLR vraisemblance function is represented by the following expression:
By applying the natural logarithm transformation (ln) and developing the formula, we obtain:
The W(ui, vi ) matrix described in (6) features weights wij (calculated via the weighting functions shown in Table 1) and is used to geographically weight the observations in the estimation of each set of parameters βk (ui, vi ). That is, this matrix is responsible for assigning a higher weight to the geographically closest observations to region i in the estimation of its parameters, and assigning a lower or zero weight (depending on the weighting function chosen) for the most distant observations from region i in question in the estimation of its parameters βk (ui, vi ). The W(ui, vi ) matrix also varies according to the location of each borrower and composes the likelihood function in the following way:
Similar to the logistic regression model, after differentiating (11) in function of β(ui, vi ) and equating to zero, the model parameters are estimated using interactive numerical methods, such as the interactively reweighted least squares (IRLS) method. It should be noted that this maximization procedure is carried out for each one of the functions related to each region i in the study.
Initially, four different models were developed using each one of the weighting functions presented in Table 1. The best model based on AICc was selected for comparison with the global model and to compare between the local models (the models generated for each region in the DF) in terms of significance of the variables that composed the final formula and estimations of the coefficients of the variables.
2.5. Comparison Between the Models
The metrics used to compare the models developed via GWLR and Logistic Regression were: the AICc informational criteria (Hurvich, Simonoff, & Tsai, 1998Hurvich, C. M.; Simonoff, J. S.; Tsai, C. L. (1998). Smoothing parameter selection in nonparametric regression using an improved Akaike information criterion. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 60(2), 271-293.), the accuracy of the models, the percentage of false positives, the sum of the value of false positive debt, and the expected monetary value of portfolio defaults compared with the monetary value of defaults observed.
The accuracy of the models and percentage of false positives were obtained via the confusion matrix, given by:
According to Table 2, there are two types of error that a classifying model can commit: rejecting good clients (False Negative - FN), or approving bad clients (False Positive - FP). The latter, also known as a Type II Error, is considered to be the worst of the two errors, since these clients would be approved and could generate financial losses for the institution. Thus, the FP percentage was one of the metrics used to compare the models.
The sum of the outstanding balance of all borrowers classified as FP was measured to verify the monetary value that would enter into default due to classification error in the model.
The accuracy of the model is calculated using the proportion of TP and TN in relation to the total, as in the following formula:
The expected monetary value of portfolio defaults was calculated using the expected discrete distributions formula, given by:
in which n is the total number of borrowers in a portfolio, xi is the outstanding balance on the credit transaction for borrower i, and P(Yi = 1) is the probability of borrower i defaulting, resulting in the credit scoring models. This value was compared with the value of the sum of defaulting client debts, with the aim of verifying which model comes closest to the real default value.
3. RESULTS
3.1. Univariate and Bivariate Analyses
The results on general default rates and those by region are shown in Tables 3 and 4 and the spatial distribution of default rates is found in Figure 6.
As shown in Table 3, the general default rate in the DF was 27.66%; thus, it can be observed in Table 4 that only seven regions (Lago Sul, Cruzeiro, Brasília, Guará, Lago Norte, Taguatinga, and Núcleo Bandeirante) have lower default rates than the general average. It is also noted that the Lago Sul region presented the lowest default rate of the regions studied, followed by the Cruzeiro and Brasilia regions. As can be observed in Figure 6, the three regions are located in the center of the Distrito Federal.
Also by analyzing Figure 6, it is noted that the greater the distance from the central point in the DF, the more default rates increase (represented by the darkest areas on the map). The Santa Maria, Recanto das Emas, and Paranoá regions stand out in negative terms by presenting the worst default rates.
The frequencies were calculated, along with the mean, median, maximum, minimum, and quartiles statistics for the candidate variables for composing the models, and as there were no inconsistencies, missing values, or outliers, no variable was removed in this stage of the study.
The bivariate analysis consisted of calculating the cross frequency between the predictive variables and the response variable, with the aim of identifying the variables that differentiate credit risk among the target population in the study. The variables were categorized based on relative Risk (14), and using this categorization, dummy variables were created to compose the models.
All attributes of the rate of unemployment and inflation variables presented similar levels of credit risk, and for this reason, they were excluded from the study. The categories for the other variables are found in Table 5.
It is observed in Table 5 that borrowers with higher Formal Incomes presented a lower credit risk. It is also observed that the higher the borrower’s Level of Education, the lower the risk, with PhDs presenting a much higher relative risk than the rest. The results also indicated that the older the borrower and the shorter the loan period, the lower the credit risks. With relation to the borrower’s time of relationship with the institution, those with shorter times presented a greater credit risk.
The SELIC rate is the basic interest rate in the Brazilian economy. An increase in the SELIC makes it more expensive for financial institutions to raise funds, which consequently makes credit transactions more expensive. Higher interest rates in credit transactions reduce the purchasing power of borrowers, and because of this, it is expected that the higher the SELIC rate, the greater defaults and credit risk will be. However, as observed in Table 5, the results obtained were the opposite from expected, with lower relative risk (greater credit risk) for SELIC values below 10.00%, and lower credit risk for values above 10.00%. However, even in light of the results presented, the decision was made to maintain the SELIC rate variable in the study due to it being the only remaining macroeconomic variable. Subsequent studies using a more comprehensive target population should be conducted to better assess this variable.
Based on this categorization, dummy variables were created to be used for composing the regression models.
3.2. Spatial Indicators
The next stage in the study involved applying the Moran Global and Local Indices with the aim of verifying the existence of a spatial correlation between the default rate variable and the individual regions in the study population.
The Moral Global Index presented a value of 0.05, indicating an almost null spatial dependency.
Figure 7 presents the Moran dispersion map in which the regions colored in red tones present positive spatial dependency, whereas the regions colored in blue tones present negative spatial dependency. The “Low-Low” type regions presented the lowest default rates, followed by the “Low-High”, “High-Low”, and “High-High” regions. These results can be considered as spatial clusters of the default rate variable. This information could be used by the financial institution to define the target population in loan recovery campaigns, in which obtaining payment from clients residing in the “High-High” regions should be the initial focus of activities, with the aim of improving the company’s financial results.
The results found for the Moran Local Index, using a 95% level of significance, are presented in the Moran Map in Figure 8.
The Moran Map indicates the existence of local correlations in some regions that are significantly different from the others, revealing indications of spatial heterogeneity. The significant regions in the local index and which are labeled in Figure 8 are Brasilia and Cruzeiro (Low-Low), Lago Sul (Low-High), and Candangolândia (High-Low). According to Fotheringham et al. (2002Fotheringham, A. S.; Brunsdon, C.; Charlton, M. (2002). Geographically weighted regression: the analysis of spatially varying relationships. Chichester: John Wiley & Sons.), the existence of significant values for the Moran Local Index warrants applying the GWLR technique.
3.3. Global Model via Logistic Regression
The global model was developed using the development sample, containing 10,944 records.
The variables used in developing the model were all of the dummies created based on the categorizations presented in Table 5. Using the stepwise variable selection method, the variables with p-values under 0.10 (10% level of significance) and which were selected to compose the final logistic regression model (global model) are presented in Table 6.
The SELIC variable was not significant and was not selected to compose the final global regression model. One possible explanation for this fact is the use of a short loan contract period, leading to few distinct values for this variable.
Moreover, the coefficients for the Formal Income variable were inverted, in which the best income bands (d_income1 and d_income2) obtained worse coefficients with relation to the worst band (d_income4, the coefficient for which is zero). This result can be explained by the variable’s behavior, with inversions of relative risk in its value ranges when categorized granularly. Another possible explanation is that the categorization was carried out based on total records and the model was developed using the development database, which covers a smaller number of records.
The nomenclature for the dummy variables respects the nomenclature for the categories shown in Table 5. For example, the dummy d_age1 represents the age category “> 55 years old” and is the best category of this variable with relation to credit risk, and the dummy d_education4 represents clients in the category “Incomplete College Degree or lower level of education”, with this being the worst category for the Level of Education variable with relation to credit risk.
Response variable Y involves the occurrence of defaults (Y=1) as the event of interest, with the probability resulting from the logistic regression models and via GLWR referring to the probability of this event occurring; that is, of the client defaulting. Thus, it can be noted in Table 6 that all of the global regression coefficients, except for the Formal Income variable, are coherent, since the best categories for each variable with relation to credit risk presented lower coefficients in relation to the higher risk categories for the same variable; that is, the presence of the best categories for each variable reduces the probability of a client defaulting. This analysis is called congruence analysis; it is important for verifying whether there are inversions in the coefficients and whether categorization of the variables was carried out correctly.
The value found for the AICc informational criterion of the global model was 12,098.29, with this value being used for comparison with the models estimated via GWLR, the results from which are presented below.
3.4. Local Models via Geographically Weighted Logistic Regression (GWLR)
As described in the methodology, four models using the GWLR were developed, one for each weighting function shown in Table 1. The predictive variables used were those selected by the logistic regression model, shown in Table 6.
The best model using GWLR, following the AICc criterion, was the Adaptive Gaussian model, with a value of 2,022 closest neighbors to estimate the adaptive bandwidths.
Table 7 contains the descriptive statistics of the coefficients estimated by the GWLR model, in which it is noted that the averages for the coefficients were very close to the coefficients for the global model presented in Table 6.
Table 8 contains the final formula of the models estimated via Adaptive Gaussian GWLR for the 19 regions in the DF.
It is noted in Table 8 that the Intercept was significant for all the regions in the Distrito Federal and varied from -1.3922 to -1.2005, indicating a regional difference between the values estimated.
With relation to the borrower’s age, the variables d_age1 and d_age5 were significant for all of the regions in the Distrito Federal, whereas the variables d_age2 and d_age4 were not significant for some regions, indicating that the borrower’s age influences risk differently, depending on the region studied.
The d_education4 variable was also significant for all of the regions in the Distrito Federal, presenting a small variation in coefficients between the regions.
With relation to the borrower’s Time of Relationship with the institution, the variables d_time_rel1 and d_time_rel4 were significant for all of the regions in the Distrito Federal, whereas the d_time_rel2 variable was not significant for the Cruzeiro region.
With relation to the borrower’s Income, the d_income1 variable was significant for all of the regions in the Distrito Federal, whereas the d_income2 variable was significant only for the regions of Candangolândia, Gama, Núcleo Bandeirante, Recanto das Emas, Riacho Fundo, Samambaia, Santa Maria, and Taguatinga, indicating that the borrower’s Income also influences credit risk differently between the regions.
The variables d_pd_contract1 and d_pd_contract2, which represent the Loan Contract Period, were significant for all of the regions in the Distrito Federal.
3.5. Comparison Between the Models
The comparison between the Logistic Regression model and the GWLR Adaptive Gaussian model was made using the following metrics: International AICc Criterion, Accuracy, Percentage of False Positives, Sum of Value of False Positive Debt, and Expected Monetary Value of Defaults in the portfolio compared with the monetary value of defaults observed.
Except for the AICc informational criterion, calculated when developing the model, the other metrics were calculated based on the validation database, composed of 11,188 records.
Table 9 shows the descriptive statistics for the scores obtained by both the models selected in the validation sample.
The means for the model scores were very close, with a difference only in the third decimal place; however, the model using GWLR presented a greater range of scores. The use of few predictive variables meant that the scores produced by the models did not present values greater than 0.585 and 0.639.
To calculate the confusion matrix, a cut-off point had to be defined in terms of score, so that borrowers could be classified as good or bad (0 or 1). This cut-off point was defined based on the shortest distance between Sensitivity and Specificity and its value was 0.30.
It can be noted in Table 10 that the models presented very close results with regards to client classification.
Table 11 contains all of the metrics used for comparison between the models, in which a small difference is noted between the values of the indicators in the two models.
In Table 11, all of the values obtained for the metrics of the two models were also very close, with the model using GWLR being the one with the best (lowest) AICc informational criterion and best (highest) Accuracy, which indicates a better percentage of hits and lower percentage of False Positives. The model using LR was slightly higher in the metrics Sum of the Value of False Positives - this metric can be considered as an estimate of the monetary value that would be granted and enter into default, resulting in financial loss for the institution - and Expected Value of Defaults, since the sum of the value of debt of all of the contracts in default (Y=1) in the validation database of the model was R$ 12,026,290.09, and the value that comes closest is the value from the model using LR.
4. CONCLUSION
In this article, real data were used from a Brazilian financial institution on transactions involving Consumer Direct Credit, granted to clients residing in 19 regions in the Distrito Federal, to develop credit scoring models using two different methodologies: Logistic Regression and Geographically Pondered Logistic Regression.
The Logistic Regression methodology is quite widespread in the financial sector, and is used in this study to develop a global credit scoring model for the whole Distrito Federal.
The Geographically Weighted Logistic Regression methodology is quite rare and uses the borrower’s geographical location to weight observations when developing different models for each region studied.
The indicators used for comparison between the models developed via the two methodologies were very close, and based on the results obtained, the methodologies can be considered as similar in terms of their power to predict financial losses for the institution.
The study demonstrated that some variables were significant for all of the regions, whereas others were significant only for particular regions, concluding that credit risk is influenced by different factors, depending on the region studied.
It was also observed that all of the regression models developed using GWLR (regional models) presented different values for the coefficients (parameters) of the variables, showing that the weights (importance) of the variables varied from region to region.
The results demonstrated the viability of applying the GWLR methodology for developing credit scoring models for the target population in this study. The formulas obtained are applicable only to this population, however, it is believed that this methodology could be extended to other credit transactions and spatial levels (e.g. neighborhoods, municipalities, federal units).
Due to great advances in computing and technology occurring in recent decades, institutions granting credit have robust credit risk evaluation systems, which makes the implantation and use of a set of models estimated via GWLR viable.
With relation to the limitations of the study, the use of few predictive variables meant that the models presented low ranges of scores.
Categorization of the Formal Income variable was carried out so that the classes were monotonic with relation to relative risk; however, the values of their coefficients were inverted. Studies considering another categorization or target population should be carried out to verify the relevance of this variable for credit risk.
For future study topics, it is suggested that: the GWLR methodology is applied to develop credit scoring models for other target populations (for example, different credit transactions or geographical regions); comparisons are carried out with other methodologies (such as Support Vector Machines or Boosting); other predictive variables are used; the GWLR methodology is applied to develop models in other areas of a financial institution, such as strategy and marketing; or other functions are used, such as the Log Binomial, to develop geographically weighted models.
REFERENCES
- Anselin, L. (1995). Local indicators of spatial association - LISA. Geographical Analysis, 27(2), 93-115.
- Atkinson, P. M.; German, S. E.; Sear, D. A.; Clark, M. J. (2003). Exploring the relations between riverbank erosion and geomorphological controls using geographically weighted logistic regression. Geographical Analysis, 35(1), 58-82.
- Banco Central do Brasil (2009). Resolução CMN nº 3.721, de 30/04/2009. Retrieved from http://www.bcb.gov.br
» http://www.bcb.gov.br - Brunsdon, C.; Fotheringham, A. S.; Charlton, M. E. (1996). Geographically weighted regression: a method for exploring spatial nonstationarity. Geographical Analysis, 28(4), 281-298.
- Crook, J. N.; Edelman, D. B.; Thomas, L. C. (2007). Recent developments in consumer credit risk assessment. European Journal of Operational Research, 183(3), 1447-1465.
- Fernandes, G. B.; Artes, R. (2016). Spatial dependence in credit risk and its improvement in credit scoring. European Journal of Operational Research, 249(2), 517-524.
- Fotheringham, A. S.; Brunsdon, C.; Charlton, M. (2002). Geographically weighted regression: the analysis of spatially varying relationships Chichester: John Wiley & Sons.
- Gilbert, A.; Chakraborty, J. (2011). Using geographically weighted regression for environmental justice analysis: Cumulative cancer risks from air toxics in Florida. Social Science Research, 40(1), 273-286.
- Hand, D. J.; Henley, W. E. (1997). Statistical classification methods in consumer credit scoring: a review. Journal of the Royal Statistical Society: Series A (Statistics in Society), 160(3), 523-541.
- Hosmer, D. W.; Lemeshow, S. (2000). Applied logistic regression Hoboken, NJ: John Wiley & Sons.
- Huang, Y.; Leung, Y. (2002). Analysing regional industrialisation in Jiangsu province using geographically weighted regression. Journal of Geographical Systems, 4(2), 233-249.
- Hurvich, C. M.; Simonoff, J. S.; Tsai, C. L. (1998). Smoothing parameter selection in nonparametric regression using an improved Akaike information criterion. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 60(2), 271-293.
- Lessmann, S.; Baesens, B.; Seow, H. V.; Thomas, L. C. (2015). Benchmarking state-of-the-art classification algorithms for credit scoring: An update of research. European Journal of Operational Research, 247(1), 124-136.
- Moran, P. A. (1950). Notes on continuous stochastic phenomena. Biometrika, 37(1/2), 17-23.
- See, L.; Schepaschenko, D.; Lesiv, M.; McCallum, I.; Fritz, S.; Comber, A.; Obersteiner, M. (2015). Building a hybrid land cover map with crowdsourcing and geographically weighted regression. ISPRS Journal of Photogrammetry and Remote Sensing, 103, 48-56.
- Stine, R. (2011). Spatial temporal models for retail credit. In Proceedings of the Credit Scoring and Credit Control Conference, Edinburgh, UK.
-
*
*Paper presented at the XL ANDAP Congress, Costa do Sauípe, BA, Brazil, September 2016.
Publication Dates
-
Publication in this collection
Apr 2017
History
-
Received
11 May 2016 -
Accepted
10 Nov 2016








 Source: Prepared by the authors.
Source: Prepared by the authors.
 Source: Prepared by the authors.
Source: Prepared by the authors.
 Source: Adapted from
Source: Adapted from  Source: Adapted from
Source: Adapted from  Source: Adapted from
Source: Adapted from 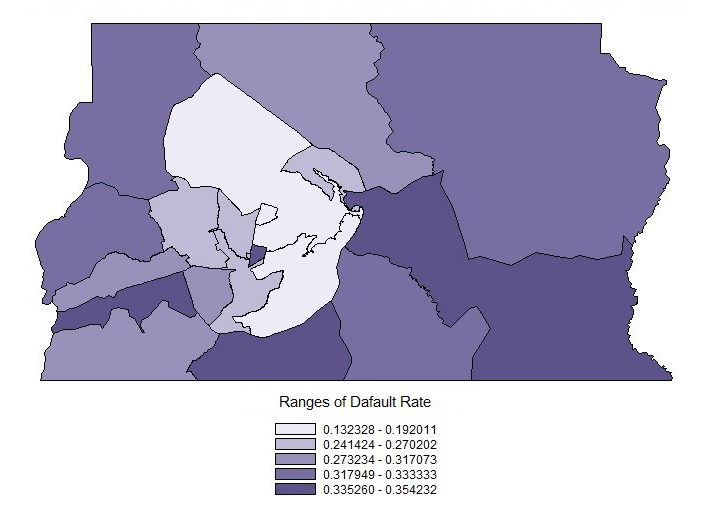 Source: Prepared by the authors.
Source: Prepared by the authors.
 Source:
Source:  Source: Prepared by the authors.
Source: Prepared by the authors.