Resumo
No Brasil, o documento normativo NBR 7190 (ABNT, 1997ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projeto de estruturas de madeira. Rio de Janeiro, 1997.) estabelece os métodos de ensaio para obtenção das propriedades físico-mecânicas da madeira. Na impossibilidade da determinação dos resultados experimentais, a norma estabelece relações entre propriedades. Porém as relações entre as propriedades de rigidez apresentadas foram determinadas com base no antigo referencial normativo MB-26:1940 (NBR 6230), que considerava outro modelo de cálculo e não ao utilizado pela norma brasileira. Nesse contexto, este trabalho objetivou investigar a equivalência entre os módulos de elasticidade na flexão (EM), compressão (Ec0) e tração (Et0) paralela às fibras de dez espécies de madeiras tropicais, assim como de estabelecer correlações adequadas entre tais propriedades em caso de não equivalência. Os resultados da ANOVA acusaram que Ec0 e Et0 são estatisticamente equivalentes, o mesmo não ocorreu entre EM e 0,90∙Ec0, implicando a determinação do coeficiente ótimo de 0,98 pelo método dos mínimos quadrados. Tal coeficiente mostrou ser 8,89% superior ao apresentado pela norma brasileira.
Palavras-chave:
Relações entre propriedades; Madeiras tropicais; Rigidez; Teoria de vigas
Abstract
In Brazil, the Brazilian Standard NBR 7190 (ABNT, 1997ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projeto de estruturas de madeira. Rio de Janeiro, 1997.) establishes testing methods to obtaining the physical and mechanical properties wood. With the impossibility of determining the experimental results, the Brazilian Code establishes relations among the properties. However, the relations between the stiffness properties are based on the older normative standard MB-26: 1940 (Brazilian Standard NBR 6230), which condisidered another calculation model rather than the one used by the Brazilian standard. This research aimed to investigate the equivalence between the conventional modulus of elasticity in static bending tests (EM), with compression parallel to the fibres (Ec0) and tension parallel to the fibres (Et0) of ten species of tropical wood, as well as to establish relations between these properties, in case they are not equivalent. The ANOVA results showed that Ec0 and Et0 were statistically equivalent, and the relation between EM and 0.90∙Ec0 was not statistically equivalent, implying the determination of an ideal coefficient equal to 0.98 by the least squares method. This coefficient was 8.89% higher than the Brazilian standard.
Keywords:
Relations between properties; Hardwood; Stiffness; Beams theory
Introdução
A madeira, material natural renovável e de fácil obtenção, é a matéria-prima mais antiga adotada em construções. Devido à sua ampla disponibilidade na natureza e relativa facilidade de manuseio, tem sido usada pela humanidade ao longo da história, atendendo atividades humanas habituais, como superar obstáculos, transporte, moradias, entre outros (CHRISTOFORO et al., 2013aCHRISTOFORO, A. L. et al. Characterization of tropical wood species for use in civil constructions. Journal of Civil Engineering Research, v. 3, n. 3, p. 98-103, 2013a.; ARAUJO et al., 2016ARAUJO, V. A. et al. Classification of wooden housing building systems. BioResources, v. 11, n. 3, p. 7889-7901, 2016.; WIERUSZEWSKI; MAZELA, 2017WIERUSZEWSKI, M.; MAZELA, B. Cross Laminated Timber (CLT) as an alternative form of construction wood. Drvna industrija, v. 68, n. 4, p. 359-367, 2017.; ALMEIDA et al., 2018aALMEIDA, T. H. et al. Effect of service temperature on shear strength of Pinus wood for roof structures. Acta Scientiarum. Technology, v. 40, p. 2-6, 2018a.).
Juntamente com o aço e o concreto armado, a madeira é atualmente um dos três materiais estruturais utilizados na construção de grandes estruturas. No que diz respeito à resistência à compressão, a madeira apresenta valor semelhante ao concreto e ambos os materiais possuem resistência inferior ao aço; no entanto, a madeira possui baixa densidade quando comparada a esses outros materiais estruturais, resultando em uma excelente relação entre resistência e densidade (RAMAGE et al., 2017RAMAGE, M. H. et al. The wood from the tress: The use of timber in construction. Renewable and Sustainable Energy Reviews, v. 68, p. 333-359, 2017.). Segundo Calil Jr. e Dias (1997)CALIL Jr., C.; DIAS, A. A. Utilização da madeira em construções rurais. Revista Brasileira de Engenharia Agrícola e Ambiental, Campina Grande, v. 1, p. 71-77, 1997., essa relação é aproximadamente três vezes maior que para o aço e dez vezes maior que para o concreto, o que evidencia a madeira como um material estrutural eficiente, sendo de uso inteligente em estruturas nas quais uma alta proporção das cargas a ser resistida é seu peso próprio, como em estruturas de cobertura, algumas pontes e edifícios altos (RAMAGE et al., 2017RAMAGE, M. H. et al. The wood from the tress: The use of timber in construction. Renewable and Sustainable Energy Reviews, v. 68, p. 333-359, 2017.).
Para a maioria dos países da América do Norte e Europa, casas de madeira são a solução habitacional mais comum, econômica e prática (ARAUJO et al., 2016ARAUJO, V. A. et al. Classification of wooden housing building systems. BioResources, v. 11, n. 3, p. 7889-7901, 2016.). No Reino Unido aproximadamente 29% das novas residências são em madeira, na Escócia esse percentual é na ordem de 83%, na Inglaterra 23%, e na Irlanda do Norte 17% (ARAUJO et al., 2018ARAUJO, V.A. et al. Difficulties of wooden housing production sector in Brazil. Wood Material Science & Engineering, p. 1-10, 2018.). Na Áustria, construções em wood frame representam cerca de 40% do total de edificações unifamiliares (HURMEKOSKI; JONSSON; NORD, 2015HURMEKOSKI, E.; JONSSON, R.; NORD, T. Context, drivers, and future potential for wood-frame multi-story construction in Europe. Technological Forecasting & Social Change, v. 99, p. 181-196, 2015.), no Japão 45%, na Nova Zelândia tem-se 85%, chegando aos impressionantes 90% na América do Norte (MAHAPATRA; GUSTAVSSON; HEMSTRÖM, 2012MAHAPATRA, K.; GUSTAVSSON, L.; HEMSTRÖM, K. Multi-storey wood-frame buildings in Germany, Sweden and the UK. Construction Innovation, v. 12, p. 62-85, 2012.).
Com 8.715 espécies do total de 60.065 de árvores registradas em todo o mundo, o Brasil é o país com maior diversidade de espécies do planeta (BEECH et al., 2017BEECH, E. et al. GlobalTreeSearch: the first complete global database of tree species and country distributions. Journal of Sustainable Foresty, v. 36, p. 454-489, 2017.). Apesar de ter uma área de cobertura florestal nativa de 60,7% do território nacional, e do evidente potencial florestal, o aproveitamento dos recursos naturais madeireiros é insignificante, em função do potencial que representa (VIDAL et al., 2015VIDAL, J. M. et al. Preservação de madeiras no Brasil: histórico, cenário atual e tendências. Ciência Florestal, Santa Maria, v. 25, n. 1, p. 257-271, 2015.). Têm-se, como exemplo, as construções em madeira que ainda sofrem alguns preconceitos devido a questões culturais remanescentes desde a colonização, a escassez de mão de obra qualificada e o desconhecimento das espécies e suas propriedades. Tais fatores induzem o uso inadequado da madeira, com construções com baixa vida útil e que sucumbem às vantagens deste material (PEDRESCHI; GOMES; MENDES, 2005PEDRESCHI, R.; GOMES, F. C.; MENDES, L. M. Avaliação do desempenho da madeira na habitação utilizando abordagens de sistemas. Cerne, Lavras, v. 11, n. 3, p. 283-293, jul./set. 2005.).
Para a utilização racional da madeira nas mais diversas finalidades, torna-se necessário o conhecimento de suas propriedades físicas, químicas, mecânicas e anatômicas (ALMEIDA et al., 2014ALMEIDA, D. H. et al. Tenacidade da madeira como função da densidade aparente. Revista Árvore, Viçosa, v. 38, n. 1, p. 203-207, 2014., 2018b). Dentre as propriedades requisitadas para o dimensionamento de uma estrutura, destaca-se o módulo de elasticidade. Em um projeto de vigas, assim como outros elementos estruturais, o conhecimento dos módulos de elasticidade longitudinal (E) e transversal (G) é de suma importância (CHRISTOFORO et al., 2013bCHRISTOFORO, A. L. et al. Metodologia para o cálculo dos módulos de elasticidade longitudinal e transversal em vigas de madeira de dimensões estruturais. Ciência Rural, Santa Maria, v. 43, n. 4, p. 610-615, 2013b.).
No Brasil, a Associação Brasileira de Normas Técnicas (ABNT) através do seu documento normativo n. 7.190 de 1997 (ABNT, 1997ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projeto de estruturas de madeira. Rio de Janeiro, 1997.), intitulado de “Projeto de Estruturas de Madeira”, estabelece as premissas e os métodos de cálculo para dimensionamento das estruturas em madeira, assim como os métodos de ensaios para caracterização completa das propriedades de resistência e rigidez da madeira.
Para a obtenção das propriedades das espécies de madeira, a norma exige procedimentos realizados em laboratórios especializados e com equipamentos de alto custo (DIAS e LAHR, 2004DIAS, F. M.; LAHR, F. A. R. Estimativa de propriedades de resistência e rigidez da madeira através da densidade aparente. Scientia Florestalis, Piracicaba, v. 65, p. 102-113, jun. 2004.). Considerando a impossibilidade da obtenção dessas propriedades via experimentação, a norma brasileira propõe algumas relações entre propriedades mecânicas.
Dentre tais relações, a NBR 7.190 (Item 6.3.4 (ABNT, 1997ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projeto de estruturas de madeira. Rio de Janeiro, 1997.)) estabelece que o valor médio do módulo de elasticidade na compressão paralela às fibras (Ec0) assume o mesmo valor do módulo de elasticidade na tração paralela às fibras (Et0) [Ec0 = Et0], sem fazer distinção entre folhosas e coníferas. Para as folhosas, que são usualmente utilizadas em projetos estruturais devido a sua alta resistência, o mesmo referencial normativo permite, na impossibilidade do ensaio de compressão simples, a determinação do Ec0 por meio do ensaio de flexão estática, considerando que o módulo de elasticidade convencional na flexão (EM) é igual a 0,90 (90%) do módulo de elasticidade na compressão paralela às fibras [EM = 0,90∙Ec0].
Segundo a norma brasileira, para obtenção das propriedades de resistência e rigidez da madeira na flexão, os corpos de prova devem possuir as dimensões 5 cm × 5 cm × 115 cm, respeitando-se a relação entre o vão do ensaio de flexão (L) e a altura da seção (h) igual a 21. Tal relação, obtida por Lahr (1983)LAHR, F. A. R. Sobre a determinação de propriedades de elasticidade da madeira. São Carlos, 1983. 221 f. Tese (Doutorado em Engenharia de Estruturas) - Escola de Engenharia, Universidade de São Paulo, São Carlos, 1983., utiliza-se do ensaio de flexão estática a três pontos em peças de madeira serrada. Os valores do módulo de elasticidade obtidos com o auxílio da Equação 1, que contabiliza apenas a existência dos momentos fletores (sendo δ o deslocamento no ponto médio, F o carregamento aplicado no meio do vão, L o vão entre os apoios, EM o módulo de elasticidade na flexão e I o momento de inércia da seção transversal), apresentam ser equivalentes (convergentes) para relações L/h≥21, e distintos para relações inferiores. Esse resultado garante que os esforços cisalhantes presentes no ensaio de flexão possam ser desprezados na determinação dos deslocamentos, validando o modelo de cálculo (teoria de vigas de Euller Bernoulli) utilizado pela norma brasileira NBR 7190 (ABNT, 1997ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projeto de estruturas de madeira. Rio de Janeiro, 1997.) e por outros documentos normativos para a determinação do módulo de elasticidade na flexão (ZANGIÁCOMO; CHRISTOFORO; LAHR, 2014ZANGIÁCOMO, A. L.; CHRISTOFORO, A. L.; LAHR, F. A. R. Módulo de elasticidade aparente em vigas roliças estruturais de madeira Pinus elliottii. Ambiente Construído, Porto Alegre, v. 14, n. 1, p. 7-13, jan./mar. 2014.).
A NBR 7190 (ABNT, 1997ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projeto de estruturas de madeira. Rio de Janeiro, 1997.) substituiu e cancelou o antigo documento normativo MB-26:1940 (NBR 6230), o qual preconizava que os corpos de prova destinados à obtenção das propriedades de resistência e rigidez da madeira na flexão deveriam ter dimensões de 2 cm × 2 cm × 30 cm, implicando a relação L/h<21. Os resultados obtidos conforme a metodologia de ensaio proposta pela MB-26:1940 (NBR 6230) condicionaram a relação de equivalência entre o módulo de elasticidade na flexão e o módulo de elasticidade na compressão paralela às fibras (EM = 0,90∙Ec0), atualmente presente na NBR 7190 (Item 6.3.4 (ABNT, 1997ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projeto de estruturas de madeira. Rio de Janeiro, 1997.)). Com a mudança das dimensões dos corpos de prova pela NBR 7190 (ABNT, 1997ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projeto de estruturas de madeira. Rio de Janeiro, 1997.), implicando a relação L/h≥21, fazem-se necessários novos estudos sobre a relação de equivalência entre tais propriedades.
Notadamente, tais propriedades são de extrema importância para o dimensionamento estrutural. Considerando as dificuldades associadas à caracterização completa de madeiras, juntamente com a possibilidade de relações entre propriedades, esta pesquisa objetiva investigar as relações entre os módulos de elasticidade na flexão, compressão e tração paralela às fibras das madeiras folhosas, com resultados em potencial para serem incorporados nas normas brasileiras, em especial na NBR 7190 (ABNT, 1997ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projeto de estruturas de madeira. Rio de Janeiro, 1997.), atualmente em revisão.
Materiais e métodos
As madeiras de cambará rosa (Erisma sp.), cedro (Cedrella sp.), copaíba (Copaiba resinifera), canafístula (Cassia ferruginea), oiticica amarela (Clarisia racemosa), angelim araroba (Vataireopsis aroroba), louro verde (Ocotea sp.), guaiçara (Luetzelburgia sp.), cedroarana (Cedrelinga cateniformis) e maçaranduba (Manilkara sp.) foram devidamente estocadas e ensaiadas nas dependências do Laboratório de Madeiras e de Estruturas de Madeira (LaMEM) pertencente ao Departamento de Engenharia de Estruturas (SET), da Escola de Engenharia de São Carlos (EESC), da Universidade de São Paulo (USP), responsável por conduzir os ensaios experimentais com o rigor requerido pela norma brasileira.
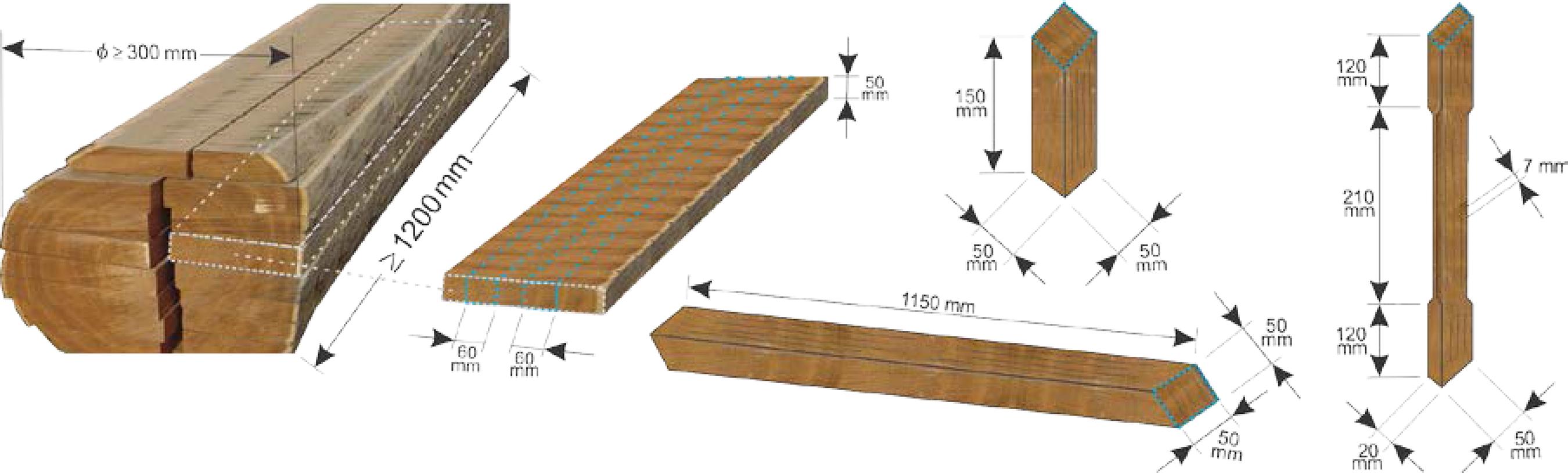
Para tanto, as 10 espécies pesquisadas foram ensaiadas com a umidade de equilíbrio de 12%, como estabelecido na NBR 7190 (p. 47, Anexo B, (ABNT, 1997ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projeto de estruturas de madeira. Rio de Janeiro, 1997.)), com experimentos conforme premissas e métodos de ensaio e de cálculo deste documento normativo. A Figura 1 esquematiza a forma de extração e dimensões dos corpos de prova, conforme preconiza essa norma.
Esquema de extração e dimensões dos corpos de prova para os ensaios dos módulos de elasticidade na flexão, compressão e tração paralela às fibras
As espécies de madeiras foram categorizadas em classes de resistência para o grupo das folhosas de acordo com o valor característico (Equação 2) obtido do ensaio de compressão paralela às fibras (NBR 7190, 1997ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projeto de estruturas de madeira. Rio de Janeiro, 1997.).
Da Equação 2, os resultados foram colocados em ordem crescente (f1≤f2≤f3...≤fn), desprezando-se o maior valor da resistência em caso de número de corpos de prova ímpar, não se tomando para fc0,k valor de resistência inferior a f1 e nem inferior a 0,70 do valor médio das resistências. A Tabela 1 apresenta os resultados dos valores característicos e os respectivos enquadramentos das espécies nas classes de resistência da norma brasileira.
Para cada espécie de madeira foram fabricados 12 corpos de prova para cada um dos ensaios: compressão (Figura 2a), visando a determinação dos valores do Ec0, tração (Figura 2b) para a obtenção dos valores do Et0, e flexão estática para a determinação dos valores do EM (Figura 3a), resultando no total de 360 determinações experimentais.
(a) Ensaio de resistência à compressão paralela às fibras; (b) ensaio de tração paralela às fibras; e (c) Corpo de prova após o ensaio de tração paralela às fibras
Por meio dos ensaios descritos, utilizando-se das Equações 3 a 5, foram determinados para cada amostra os valores das propriedades de rigidez (Ec0, Et0 e EM).
Das Equações 3 a 5, σ50% e σ10% são as tensões normais no corpo de prova, respectivamente para 50% e 10% da resistência estimada; ε50% e ε10% são as deformações específicas, respectivamente, para 50% e 10% da resistência estimada; L corresponde ao vão do ensaio de flexão, F50% e F10% denotam as cargas correspondentes a 50% e 10% da carga máxima estimada; ν50% e ν10% referem-se aos deslocamentos no meio do vão correspondentes a 10% e 50% da carga máxima estimada; enquanto b e h correspondem, respectivamente, à largura e à altura da seção transversal do corpo de prova de flexão.
Inicialmente, a análise de variância (ANOVA), ao nível de 5% de significância, foi utilizada na verificação das relações entre Et0 e Ec0 (Ec0 = Et0) e entre EM e Ec0 (EM = 0,90∙Ec0) propostas pela norma brasileira NBR 7.190 (ABNT, 1997ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projeto de estruturas de madeira. Rio de Janeiro, 1997.). Acusada equivalência entre as médias (P-valor maior ou igual a 5% - hipótese nula), isso implica a boa precisão fornecida pelas relações estabelecidas pela norma brasileira, e em caso contrário (P-valor < 5% - hipótese alternativa) novos coeficientes devem ser determinados.
No caso da não equivalência estatística entre as relações, utilizou-se do método dos mínimos quadrados (Equação 6 e 7), possibilitando determinar o coeficiente ótimo (λ) das relações entre os módulos de elasticidade (Ec0 = λ·Et0 e EM = λ·Ec0), com o auxílio do método de Newton com aproximação quadrática (Equação 8), ficando a convergência para solução ótima independente da escolha da estimativa inicial λ0 do método iterativo.
Resultados e discussão
A Tabela 2 apresenta os valores médios (x), mínimos (Mín), máximos (Máx) e os coeficientes de variação (Cv), das propriedades de rigidez (Ec0, Et0 e EM) obtidos experimentalmente para cada uma das espécies investigadas.
Para a madeira de cambará os valores de Ec0 (12.578 MPa), Et0 (12.636 MPa) e EM (12.530 MPa), determinados neste estudo, são próximos aos apresentados por Morales et al. (2018)MORALES, E. A. M. et al. Evaluation of the number of load cycles to determine some wood stiffness properties. Current Journal of Applied Science and Technology, v. 29, n. 1, p. 1-7, 2018. [Ec0 (12.708 MPa), Et0 (12.509 MPa) e EM (11.564 MPa)], por Lahr et al. (2016)LAHR, F. A. R. et al. Full Characterization of Erisma uncinatum warm wood specie. International Journal of Materials Engineering, v. 6, n. 5, p. 147-150, 2016. [Ec0 (12.967 MPa), Et0 (12.764 MPa) e EM (12.376 MPa)], por Moreira et al. (2017)MOREIRA, A. P. et al. Toughness and impact strength in dynamic bending of wood as a function of the modulus of elasticity and the strength in compression to the grain. International Journal of Materials Engineering, v. 7, n. 4, p. 61-67, 2017. [Ec0 (12.967 MPa)] e por Icimoto et al. (2015)ICIMOTO, F. H. et al. Influence of specimen orientation on determination of elasticity in static bending. Maderas. Ciencia y Tecnología, v. 17, n. 5, p. 229-238, 2015. [EM (12.150,50 MPa)]. Considerando a mesma espécie, valores superiores de Ec0 foram determinados por Almeida et al. (2018b)ALMEIDA, A. S. et al. Evaluation of Stiffness in compression perpendicular to grain of Brazilian tropical wood species. Current Journal of Applied Science and Technology, v. 28, n. 5, p. 1-7, 2018b., em torno de 13.000 MPa, com variações de 11.000 MPa a 15.000 MPa, e por Ferro et al. (2015)FERRO, F. S. et al.. Influência da posição dos instrumentos de medida na determinação do módulo de elasticidade da madeira na compressão paralela às fibras (Ec0). Revista Árvore, Viçosa, v. 39, n. 4, p. 743-749, 2015. (13.867,50 MPa). Para esta propriedade a norma brasileira apresenta valor inferior [Ec0 (9.067 MPa)]. Valores inferiores também foram determinados por Grobério e Lahr (2002)GROBÉRIO, M. P.; LAHR, F. A. R. Indicações para o emprego da madeira de espécies tropicais do Brasil. Revista Madeira: arquitetura e engenharia, v. 3, n. 8, 2002. [Ec0 (8.782,8 MPa), Et0 (9.172,3 MPa) e EM (8.841,9 MPa)] e por Araújo (2007)ARAUJO, H. J. B. Relações funcionais entre propriedades físicas e mecânicas de madeiras tropicais brasileiras. Floresta, Curitiba, v. 37, n. 3, set/dez. 2007. para o EM (10.787 MPa).
Dias e Lahr (2004)DIAS, F. M.; LAHR, F. A. R. Estimativa de propriedades de resistência e rigidez da madeira através da densidade aparente. Scientia Florestalis, Piracicaba, v. 65, p. 102-113, jun. 2004. determinaram para a madeira de cedro valores médios de 8.358 MPa, 9.851 MPa e 8.866 MPa, correspondentes respectivamente a Ec0, Et0 e EM. Tais valores são próximos aos obtidos no presente estudo [Ec0 (8.270 MPa), Et0 (9.523 MPa) e EM (8.717 MPa)], assim como os valores de Ec0 apresentados por Moreira et al. (2017)MOREIRA, A. P. et al. Toughness and impact strength in dynamic bending of wood as a function of the modulus of elasticity and the strength in compression to the grain. International Journal of Materials Engineering, v. 7, n. 4, p. 61-67, 2017. (8.354 MPa) e pela norma brasileira (8.058 MPa). Para a mesma espécie, valores superiores de Ec0 foram determinados nos estudos de Ferro et al. (2015)FERRO, F. S. et al.. Influência da posição dos instrumentos de medida na determinação do módulo de elasticidade da madeira na compressão paralela às fibras (Ec0). Revista Árvore, Viçosa, v. 39, n. 4, p. 743-749, 2015. (11.368 MPa) e Almeida et al. (2018b)ALMEIDA, A. S. et al. Evaluation of Stiffness in compression perpendicular to grain of Brazilian tropical wood species. Current Journal of Applied Science and Technology, v. 28, n. 5, p. 1-7, 2018b. (13.000 MPa), sendo que neste os valores variaram de 11.000 MPa a 14.500 MPa.
A madeira de cedroarana apresentou valor do EM correspondente a 10.119 MPa, com variações de 8.404 MPa a 12.324 MPa. Gonçalez e Gonçalves (2001)GONÇALEZ, J. C.; GONÇALVES, D. M. Valorização de duas espécies de madeira Cedrelinga catenaeformis e Enterolobium shomburgkii para a indústria madereira. Brasil Florestal, v. 70, p. 69-74, jun. 2001. determinaram valor médio de EM igual a 11.500 MPa, contemplado na faixa de valores obtidos neste estudo. O EM, assim como os demais valores das propriedades de rigidez obtidos [Ec0 (10.394 MPa), Et0 (10.967 MPa)], foram condizentes aos determinados por Grobério e Lahr (2002)GROBÉRIO, M. P.; LAHR, F. A. R. Indicações para o emprego da madeira de espécies tropicais do Brasil. Revista Madeira: arquitetura e engenharia, v. 3, n. 8, 2002. [Ec0 (10.252,4 MPa), Et0 (10.969,7 MPa) e EM (10.032,4 MPa)]. Para a mesma espécie, o resultado obtido do Ec0 (10.394 MPa) diverge do encontrado por Moreira et al. (2017)MOREIRA, A. P. et al. Toughness and impact strength in dynamic bending of wood as a function of the modulus of elasticity and the strength in compression to the grain. International Journal of Materials Engineering, v. 7, n. 4, p. 61-67, 2017. (8.962 MPa).
Em relação aos valores das propriedades de rigidez da madeira de canafístula [Ec0 (14.175 MPa), Et0 (13.665 MPa) e EM (14.326 MPa)], resultados próximos foram determinados por Dias e Lahr (2004)DIAS, F. M.; LAHR, F. A. R. Estimativa de propriedades de resistência e rigidez da madeira através da densidade aparente. Scientia Florestalis, Piracicaba, v. 65, p. 102-113, jun. 2004. [Ec0 (14.613 MPa), Et0 (14.087 MPa) e EM (14.769 MPa)] e também pela norma brasileira [Ec0 (14.613 MPa)]. No que diz respeito ao Et0, o valor determinado neste estudo mostrou-se inferior ao encontrado por Faria et al. (2012)FARIA, O. B. et al. Influence of wood moisture content on modulus of elasticity on tension parallel to the grain of Brazilian species. European International Journal of Science and Technology. v. 1, n. 2, p. 11-22, 2012. (15.281,7 MPa). Lahr et al. (2017)LAHR, F. A. R. et al. Shear and longitudinal modulus of elasticity in wood: relations based on static bending tests. Acta Scientiarum. Technology, v. 39, n.4, p. 433-437, oct./dec. 2017., em estudo sobre relações entre o módulo de elasticidade longitudinal e transversal da madeira, determinaram, para a espécie de canafístula, os valores de 14.288 MPa e 14.466 MPa correspondentes respectivamente aos módulos de elasticidade na flexão ensaiados no plano longitudinal-radial [EM(LR)] e no plano longitudinal-transversal [EM(LT)], considerando para tanto ensaios de flexão a quatro pontos. Tais valores de EM são próximos ao determinado neste estudo.
Os valores das propriedades de rigidez da madeira de angelim araroba, determinados no presente estudo [Ec0 (12.714 MPa), Et0 (12.371 MPa) e EM (12.633 MPa)], mostraram-se próximos aos valores encontrados por Grobério e Lahr (2002)GROBÉRIO, M. P.; LAHR, F. A. R. Indicações para o emprego da madeira de espécies tropicais do Brasil. Revista Madeira: arquitetura e engenharia, v. 3, n. 8, 2002. [Ec0 (12.525,4 MPa), Et0 (11.885,4 MPa) e EM (11.943,3 MPa)] e por Dias e Lahr (2004)DIAS, F. M.; LAHR, F. A. R. Estimativa de propriedades de resistência e rigidez da madeira através da densidade aparente. Scientia Florestalis, Piracicaba, v. 65, p. 102-113, jun. 2004. [Ec0 (12.587 MPa), Et0 (11.661 MPa) e EM (11.457 MPa)]. No que diz respeito ao Ec0, o valor determinado é próximo ao apresentado pela norma brasileira (12.876 MPa).
Em relação a madeira de copaíba, os valores de Ec0 (12.662 MPa), Et0 (13.188 MPa) e EM (12.617 MPa), determinados neste estudo, foram próximos aos encontrados por Araújo (2007)ARAUJO, H. J. B. Relações funcionais entre propriedades físicas e mecânicas de madeiras tropicais brasileiras. Floresta, Curitiba, v. 37, n. 3, set/dez. 2007. [EM (12.062 MPa)], por Jesus, Logsdon e Finger (2015)JESUS, J. M. H.; LOGSDON, N. B.; FINGER, Z. Classes de resistência de algumas madeiras de Mato Grosso. Engineering and Science, v. 1, n. 3, 2015. [Ec0 (12.143 MPa)], por Aquino et al. (2018)AQUINO, V. B. M. et al. Physical and mechanical characterization of Copaifera sp. wood specie. International Journal of Materials Engineering, v. 8, n. 3, p. 55-58, 2018. [Ec0 (12.845 MPa), Et0 (13.382 MPa) e EM (12.440 MPa)] e inferiores aos obtidos por Dias e Lahr (2004)DIAS, F. M.; LAHR, F. A. R. Estimativa de propriedades de resistência e rigidez da madeira através da densidade aparente. Scientia Florestalis, Piracicaba, v. 65, p. 102-113, jun. 2004. [Ec0 (14.012 MPa), Et0 (14.627 MPa) e EM (13.572 MPa)]. Quanto ao Et0, o valor determinado, com variações de 10.591 MPa a 15.482 MPa, foi superior ao encontrado por Faria et al. (2012)FARIA, O. B. et al. Influence of wood moisture content on modulus of elasticity on tension parallel to the grain of Brazilian species. European International Journal of Science and Technology. v. 1, n. 2, p. 11-22, 2012. (11.957,7 MPa).
Para a madeira de louro verde, os valores de Ec0 (14.649 MPa), Et0 (14.026 MPa) e EM (15.178 MPa), determinados neste estudo, foram superiores aos encontrados por Dias e Lahr (2004)DIAS, F. M.; LAHR, F. A. R. Estimativa de propriedades de resistência e rigidez da madeira através da densidade aparente. Scientia Florestalis, Piracicaba, v. 65, p. 102-113, jun. 2004. [Ec0 (13.536 MPa), Et0 (12.851 MPa) e EM (13.556 MPa)] e por Araújo (2007)ARAUJO, H. J. B. Relações funcionais entre propriedades físicas e mecânicas de madeiras tropicais brasileiras. Floresta, Curitiba, v. 37, n. 3, set/dez. 2007. [EM (14.024 MPa)]. No que diz respeito ao Ec0, a norma brasileira apresenta valor próximo (14.185 MPa).
Em relação às propriedades de rigidez da madeira de oiticica amarela, o Ec0 apresentou valor de 14.277 MPa, com mínimo e máximo correspondentes respectivamente a 11.994 MPa e 16.889 MPa. Para a mesma propriedade, Jesus et al. (2015)JESUS, J. M. H.; LOGSDON, N. B.; FINGER, Z. Classes de resistência de algumas madeiras de Mato Grosso. Engineering and Science, v. 1, n. 3, 2015. determinaram valor superior (17.512 MPa), enquanto a norma brasileira apresenta valor próximo (14.719 MPa). No que diz respeito ao EM, o valor determinado (14.057 MPa) mostrou-se próximo ao definido por Dias e Lahr (2004)DIAS, F. M.; LAHR, F. A. R. Estimativa de propriedades de resistência e rigidez da madeira através da densidade aparente. Scientia Florestalis, Piracicaba, v. 65, p. 102-113, jun. 2004. (14.491 MPa) e superior ao encontrado por Araújo (2007)ARAUJO, H. J. B. Relações funcionais entre propriedades físicas e mecânicas de madeiras tropicais brasileiras. Floresta, Curitiba, v. 37, n. 3, set/dez. 2007. (12.160 MPa). O resultado do Et0 (14.235 MPa) foi condizente ao valor de 14.675 MPa apresentado por Dias e Lahr (2004)DIAS, F. M.; LAHR, F. A. R. Estimativa de propriedades de resistência e rigidez da madeira através da densidade aparente. Scientia Florestalis, Piracicaba, v. 65, p. 102-113, jun. 2004..
Os valores das propriedades de rigidez para a madeira de Guaiçara, obtidos no presente estudo [Ec0 (15.148 MPa), Et0 (16.055 MPa) e EM (15.132 MPa)], mostraram-se próximos aos encontrados por Grobério e Lahr (2002)GROBÉRIO, M. P.; LAHR, F. A. R. Indicações para o emprego da madeira de espécies tropicais do Brasil. Revista Madeira: arquitetura e engenharia, v. 3, n. 8, 2002. para Ec0 (15.301,7 MPa), Et0 (16.304,7 MPa) e EM (15.126,4 MPa) e por Moreira et al. (2017)MOREIRA, A. P. et al. Toughness and impact strength in dynamic bending of wood as a function of the modulus of elasticity and the strength in compression to the grain. International Journal of Materials Engineering, v. 7, n. 4, p. 61-67, 2017. para Ec0 (15.301 MPa). Para a mesma espécie, valores inferiores foram apresentados por Dias e Lahr (2004)DIAS, F. M.; LAHR, F. A. R. Estimativa de propriedades de resistência e rigidez da madeira através da densidade aparente. Scientia Florestalis, Piracicaba, v. 65, p. 102-113, jun. 2004. [Ec0 (14.027 MPa), Et0 (14.946 MPa) e EM (13.866 MPa)] e pela norma brasileira [Ec0 (14.624 MPa)].
Para a madeira de maçaranduba, os valores determinados neste estudo [Ec0 (21.681 MPa), Et0 (20.933 MPa) e EM (19.934 MPa)] mostraram-se próximos aos determinados por Dias e Lahr (2004)DIAS, F. M.; LAHR, F. A. R. Estimativa de propriedades de resistência e rigidez da madeira através da densidade aparente. Scientia Florestalis, Piracicaba, v. 65, p. 102-113, jun. 2004. [Ec0 (21.900 MPa), Et0 (20.267 MPa e EM (18.184 MPa)]. Para a mesma espécie, a norma brasileira apresenta valor próximo de Ec0 (22.733 MPa), enquanto valores inferiores de propriedades de rigidez foram determinados por Faria et al. (2012)FARIA, O. B. et al. Influence of wood moisture content on modulus of elasticity on tension parallel to the grain of Brazilian species. European International Journal of Science and Technology. v. 1, n. 2, p. 11-22, 2012. (17.755 MPa) e por Jesus et al. (2015)JESUS, J. M. H.; LOGSDON, N. B.; FINGER, Z. Classes de resistência de algumas madeiras de Mato Grosso. Engineering and Science, v. 1, n. 3, 2015. (18.620 MPa), para Et0 e Ec0, respectivamente.
As comparações das propriedades apresentadas na Tabela 2 com os valores determinados na literatura validam os resultados obtidos neste trabalho. Ressalta-se, contudo, que pequenas dispersões nos resultados podem ser justificadas, em partes, pela forma como os ensaios experimentais são executados, pelo modelo de cálculo adotado para determinação dos resultados e pela variabilidade intrínseca do material.
Nas Tabelas 3 e 4 são apresentados os resultados da ANOVA das relações Ec0 = Et0 e EM = 0,90∙Ec0, respectivamente.
Da Tabela 3, verifica-se que a média dos grupos Ec0 e Et0 são estatisticamente equivalentes (P-valor ≥ 0,05), o que implica a boa precisão da equação proposta pela norma brasileira. Por outro lado, a ANOVA acusou diferença significativa nas médias entre EM e 0,90∙Ec0 (P-valor < 0,05 - Tabela 4), o que implica que o coeficiente de 0,90 da equação EM = 0,90∙Ec0 não se apresenta como estimativa precisa na obtenção do módulo de elasticidade na flexão estática.
Constatada a não equivalência entre EM e 0,90∙Ec0, o método dos mínimos quadrados (Equação 7 e 8) foi utilizado para a determinação do coeficiente ótimo (λ) da relação entre EM e Ec0 (EM = λ·Ec0). A Tabela 5 apresenta o resultado de λ considerando cada espécie individualmente e o conjunto de todas as espécies estudadas.
Resultado do coeficiente ótimo (λ) da relação entre EM e Ec0 para cada espécie e para o conjunto de todas as espécies estudadas
O coeficiente ótimo obtido para o conjunto envolvendo todas as espécies apresentado na Tabela 5 corresponde a 0,98, sendo 8,89% superior ao atual valor de 0,90 apresentado pela normativa brasileira. A Equação 9 apresenta a relação de equivalência entre o EM e Ec0 obtida neste estudo.
Conclusão
Este estudo contribui para ampliar o conhecimento quanto à relação entre propriedades de rigidez das madeiras folhosas, subsidiando a tomada de decisão sobre os parâmetros normativos a serem adotados. Considerando os resultados obtidos, pôde-se concluir:
-
a ANOVA acusou equivalência estatística entre Ec0 e Et0, evidenciando a boa precisão da equação . Cabe ressaltar que esta conclusão é pertinente apenas para as madeiras folhosas, haja vista que a equação entre Ec0 e Et0 prescrita pela norma brasileira não faz distinção entre folhosas e coníferas;
-
pela ANOVA, a média dos grupos EM e 0,90∙Ec0 apresentaram diferença significativa, implicando que o coeficiente 0,90 da equação não conduz a obtenção do EM;
-
o valor do coeficiente ótimo (λ) obtido no presente estudo para a relação entre EM e Ec0 corresponde a 0,98, sendo 8,89% superior ao estabelecido pela NBR 7190 (Item 6.3.4 (ABNT, 1997ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projeto de estruturas de madeira. Rio de Janeiro, 1997.));
-
nas verificações do estado limite de utilização de projetos de estrutura de madeira, a adoção dos valores de Ec0 determinados a partir de EM, por meio da Equação 9, conduzem a deslocamentos verticais maiores em relação aos calculados adotando-se os valores de Ec0 obtidos pela equação . Desse modo, o emprego da equação conduz a elementos estruturais de maior inércia, e, portanto, a favor da segurança; e
-
para a revisão desta normativa, sugere-se o ajuste do coeficiente da equação conforme apresentado na Equação 9, com o intuito de assegurar projetos estruturais mais precisos, visto a importância do módulo de elasticidade no dimensionamento de estruturas de madeira.
-
ErrataNo artigo "Relações entre propriedades de rigidez para distintas solicitações mecânicas visando projetos de estruturas de madeira", com número de DOI: <http://dx.doi.org/10.1590/s1678-86212020000200385>, publicado no periódico Ambiente Construído, 20(2):25-35.Nas páginas 25 e 35:Onde se lia:"Rodrigo Peixoto Guerra"Leia-se:"Rodrigo Guerra Peixoto"Na página 271 e nas páginas pares:Onde se lia:"GUERRA, R. P."Leia-se:"PEIXOTO, R. G."
Referências
- ALMEIDA, A. S. et al Evaluation of Stiffness in compression perpendicular to grain of Brazilian tropical wood species. Current Journal of Applied Science and Technology, v. 28, n. 5, p. 1-7, 2018b.
- ALMEIDA, D. H. et al Tenacidade da madeira como função da densidade aparente. Revista Árvore, Viçosa, v. 38, n. 1, p. 203-207, 2014.
- ALMEIDA, T. H. et al Effect of service temperature on shear strength of Pinus wood for roof structures. Acta Scientiarum. Technology, v. 40, p. 2-6, 2018a.
- AQUINO, V. B. M. et al Physical and mechanical characterization of Copaifera sp. wood specie. International Journal of Materials Engineering, v. 8, n. 3, p. 55-58, 2018.
- ARAUJO, H. J. B. Relações funcionais entre propriedades físicas e mecânicas de madeiras tropicais brasileiras. Floresta, Curitiba, v. 37, n. 3, set/dez. 2007.
- ARAUJO, V. A. et al Classification of wooden housing building systems. BioResources, v. 11, n. 3, p. 7889-7901, 2016.
- ARAUJO, V.A. et al Difficulties of wooden housing production sector in Brazil. Wood Material Science & Engineering, p. 1-10, 2018.
- ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. MB-26 (NBR 6230): ensaios físicos e mecânicos de madeira. Rio de Janeiro, 1940.
- ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7190: projeto de estruturas de madeira. Rio de Janeiro, 1997.
- BEECH, E. et al GlobalTreeSearch: the first complete global database of tree species and country distributions. Journal of Sustainable Foresty, v. 36, p. 454-489, 2017.
- CALIL Jr., C.; DIAS, A. A. Utilização da madeira em construções rurais. Revista Brasileira de Engenharia Agrícola e Ambiental, Campina Grande, v. 1, p. 71-77, 1997.
- CHRISTOFORO, A. L. et al Characterization of tropical wood species for use in civil constructions. Journal of Civil Engineering Research, v. 3, n. 3, p. 98-103, 2013a.
- CHRISTOFORO, A. L. et al Metodologia para o cálculo dos módulos de elasticidade longitudinal e transversal em vigas de madeira de dimensões estruturais. Ciência Rural, Santa Maria, v. 43, n. 4, p. 610-615, 2013b.
- DIAS, F. M.; LAHR, F. A. R. Estimativa de propriedades de resistência e rigidez da madeira através da densidade aparente. Scientia Florestalis, Piracicaba, v. 65, p. 102-113, jun. 2004.
- FARIA, O. B. et al Influence of wood moisture content on modulus of elasticity on tension parallel to the grain of Brazilian species. European International Journal of Science and Technology. v. 1, n. 2, p. 11-22, 2012.
- FERRO, F. S. et al. Influência da posição dos instrumentos de medida na determinação do módulo de elasticidade da madeira na compressão paralela às fibras (Ec0). Revista Árvore, Viçosa, v. 39, n. 4, p. 743-749, 2015.
- GONÇALEZ, J. C.; GONÇALVES, D. M. Valorização de duas espécies de madeira Cedrelinga catenaeformis e Enterolobium shomburgkii para a indústria madereira. Brasil Florestal, v. 70, p. 69-74, jun. 2001.
- GROBÉRIO, M. P.; LAHR, F. A. R. Indicações para o emprego da madeira de espécies tropicais do Brasil. Revista Madeira: arquitetura e engenharia, v. 3, n. 8, 2002.
- HURMEKOSKI, E.; JONSSON, R.; NORD, T. Context, drivers, and future potential for wood-frame multi-story construction in Europe. Technological Forecasting & Social Change, v. 99, p. 181-196, 2015.
- ICIMOTO, F. H. et al Influence of specimen orientation on determination of elasticity in static bending. Maderas. Ciencia y Tecnología, v. 17, n. 5, p. 229-238, 2015.
- JESUS, J. M. H.; LOGSDON, N. B.; FINGER, Z. Classes de resistência de algumas madeiras de Mato Grosso. Engineering and Science, v. 1, n. 3, 2015.
- LAHR, F. A. R. et al Full Characterization of Erisma uncinatum warm wood specie. International Journal of Materials Engineering, v. 6, n. 5, p. 147-150, 2016.
- LAHR, F. A. R. et al Shear and longitudinal modulus of elasticity in wood: relations based on static bending tests. Acta Scientiarum. Technology, v. 39, n.4, p. 433-437, oct./dec. 2017.
- LAHR, F. A. R. Sobre a determinação de propriedades de elasticidade da madeira São Carlos, 1983. 221 f. Tese (Doutorado em Engenharia de Estruturas) - Escola de Engenharia, Universidade de São Paulo, São Carlos, 1983.
- MAHAPATRA, K.; GUSTAVSSON, L.; HEMSTRÖM, K. Multi-storey wood-frame buildings in Germany, Sweden and the UK. Construction Innovation, v. 12, p. 62-85, 2012.
- MORALES, E. A. M. et al Evaluation of the number of load cycles to determine some wood stiffness properties. Current Journal of Applied Science and Technology, v. 29, n. 1, p. 1-7, 2018.
- MOREIRA, A. P. et al Toughness and impact strength in dynamic bending of wood as a function of the modulus of elasticity and the strength in compression to the grain. International Journal of Materials Engineering, v. 7, n. 4, p. 61-67, 2017.
- PEDRESCHI, R.; GOMES, F. C.; MENDES, L. M. Avaliação do desempenho da madeira na habitação utilizando abordagens de sistemas. Cerne, Lavras, v. 11, n. 3, p. 283-293, jul./set. 2005.
- RAMAGE, M. H. et al The wood from the tress: The use of timber in construction. Renewable and Sustainable Energy Reviews, v. 68, p. 333-359, 2017.
- VIDAL, J. M. et al Preservação de madeiras no Brasil: histórico, cenário atual e tendências. Ciência Florestal, Santa Maria, v. 25, n. 1, p. 257-271, 2015.
- WIERUSZEWSKI, M.; MAZELA, B. Cross Laminated Timber (CLT) as an alternative form of construction wood. Drvna industrija, v. 68, n. 4, p. 359-367, 2017.
- ZANGIÁCOMO, A. L.; CHRISTOFORO, A. L.; LAHR, F. A. R. Módulo de elasticidade aparente em vigas roliças estruturais de madeira Pinus elliottii Ambiente Construído, Porto Alegre, v. 14, n. 1, p. 7-13, jan./mar. 2014.
Datas de Publicação
-
Publicação nesta coleção
08 Maio 2020 -
Data do Fascículo
Apr-Jun 2020
Histórico
-
Recebido
26 Fev 2019 -
Aceito
07 Ago 2019