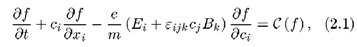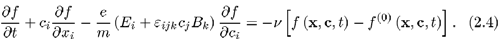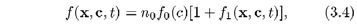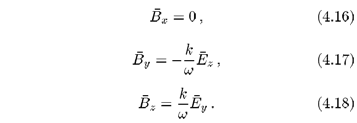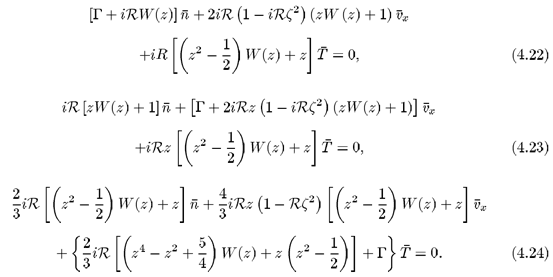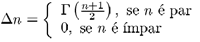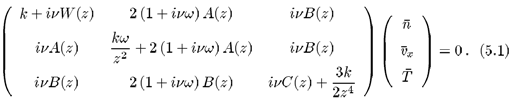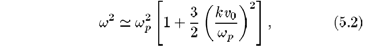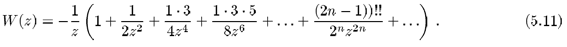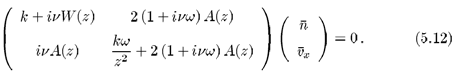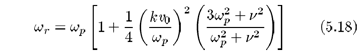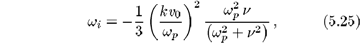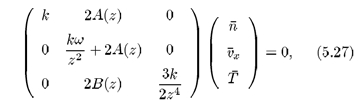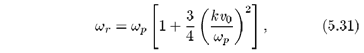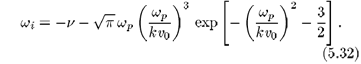Propagação de ondas longitudinais eletrostáticas em plasmas

Propagation of electrostatic longitudinal waves in plasmas

Propagação de ondas longitudinais eletrostáticas em plasmas

Propagation of electrostatic longitudinal waves in plasmas

Alcione Silva Fernandes^* e Wilson Marques Junior^‡

Departamento de Física, Setor de Ciências Exatas,

Universidade Federal do Paraná, Caixa Postal 19044, 81.531-990, Curitiba, Brasil

Recebido em 01/03/2001. Aceito em 20/04/2001

Neste artigo apresentamos uma descrição cinética com base no modelo BGK com o objetivo de estudar a propagação de ondas longitudinais num plasma colisional e isotrópico. Somente o movimento dos elétrons é considerado e as colisões entre os elétrons e os íons são descritas através de um termo de relaxação. Obtemos uma relação de dispersão que depende da freqüência de colisão bem como do fator de amortecimento de Landau.

In this paper a kinetic description based on the BGK model is developed to study the propagation of longitudinal waves in a collisional and isotropic plasma. Only electron motions are considered and the collisions between electrons and ions are represented by a relaxation term. We obtain a dispersion relation which depends on the collision frequency and on the Landau damping.

I Introdução

O termo plasma foi introduzido na Física por Tonks e Langmuir[1] para designar um sistema formado por partículas carregadas em movimento e que interagem entre si através de forças eletromagnéticas.

O plasma é considerado o quarto estado da matéria, podendo ser obtido da seguinte forma: aquecendo um sólido obtemos um líquido, aquecendo o líquido obtemos um gás e, finalmente, aquecendo o gás obtemos o plasma.

A importância do estudo de sistemas no estado de plasma torna-se evidente ao considerarmos que 99 % do universo conhecido encontra-se no estado de plasma.

Um plasma pode ser caracterizado por dois parâmetros: a densidade de número de partículas n (número de partículas por unidade de volume) e a temperatura T do plasma. Valores típicos destes parâmetros cobrem várias ordens de grandeza. Por exemplo, para plasmas utilizados em fusão termonuclear temos n 10²² m^-3 e T 10⁸ K; para a ionosfera, que é a camada de plasma que envolve o nosso planeta, temos n 10¹² m^-3 e T 10² K[2].

Atualmente plasmas são produzidos em laboratório com o objetivo de estudar suas propriedades fundamentais e também para futuras aplicações tecnológicas. Assim, por exemplo, são objeto de pesquisa: o gerador magneto-hidrodinâmico, que converte energia cinética de um plasma em energia elétrica bem como o processo inverso, em que energia elétrica é transformada em energia cinética de um plasma com a perspectiva de utilizá-lo na propulsão de foguetes[3].

As separações de cargas que ocorrem em plasmas originam forças restauradoras que criam modos coletivos de oscilação com freqüências próximas da freqüência de plasma. Estas oscilações longitudinais de carga foram descritas primeiramente por Tonks e Langmuir[1].

Vlasov[4] abordou o problema da propagação de ondas longitudinais em plasmas sob o ponto de vista da teoria cinética, com base numa equação de Boltzmann não-colisional, tendo obtido uma relação de dispersão para o caso em que a velocidade térmica dos elétrons é muito menor que a velocidade de fase da onda. Esta condição equivale a considerar a propagação no limite de comprimentos de onda muito maiores que o comprimento de Debye.

Landau[5] mostrou que, mesmo na ausência de colisões entre as partículas constituintes do plasma, as ondas longitudinais que se propagam são atenuadas. Esta atenuação é conhecida na literatura como amortecimento de Landau. Segundo Bohm e Gross[6] há um mecanismo ressonante de transferência de energia da onda que se propaga para os elétrons térmicos do plasma que se movimentam com velocidades próximas da velocidade de fase da onda. A importância do amortecimento de Landau se estende além da física de plasmas e se aplica aos campos mais diversos; em biologia, por exemplo, é empregado no estudo da luz emitida por vaga-lumes[7] e nas descargas periódicas de marca-passos utilizados no controle de batimentos cardíacos[8].

Do ponto de vista da teoria cinética de gases e com base na equação de Boltzmann, a abordagem matemática dos fenômenos que ocorrem em gases é sempre complexa desde que ela envolve a solução de uma equação íntegro-diferencial. Para contornar esta dificuldade Bathnagar, Gross e Krook[9] apresentaram um método de solução, conhecido na literatura como método BGK, no qual o operador colisional da equação de Boltzmann é substituido por um termo de relaxação mais simples; este termo contém um parâmetro que representa a freqüência das colisões binárias entre as partículas constituintes do gás de modo que o seu inverso representa o intervalo de tempo entre duas colisões sucessivas de uma partícula do gás. Bathnagar, Gross e Krook, dentre outros resultados, obtiveram relações de dispersão para a propagação de ondas longitudinais eletrostáticas com pequenas amplitudes num plasma homogêneo e isotrópico, que dependem da freqüência de colisão. O cálculo desenvolvido, baseado numa teoria cinética com cinco campos escalares (densidade de número de partículas, velocidade hidrodinâmica e temperatura), é extenso e os resultados são bastante gerais abrangendo tanto gases ionizados quanto gases neutros.

Neste artigo mostramos que as relações de dispersão para ondas longitudinais eletrostáticas em plasmas, apresentadas em[9], podem ser obtidas de uma maneira simples através de uma teoria cinética com base no modelo BGK para a equação de Boltzmann, com cinco campos escalares acoplados às equações de Maxwell. Obtemos uma matriz que contém os parâmetros do plasma e da onda que se propaga sendo que o cálculo do determinante desta matriz permite determinar as relações de dispersão. A abordagem adequada da função de dispersão de plasma, como sugerido por Landau[5], conduz a um segundo modo de amortecimento da onda representado pelo fator de amortecimento de Landau. Assim, nossos resultados englobam dois mecanismos fundamentais de amortecimento para a onda que se propaga: o amortecimento colisional e o amortecimento de Landau.

II Modelo BGK para a Equação de Boltzmann

Na descrição da propagação de ondas longitudinais trataremos o plasma como sendo constituido de elétrons e uma única espécie de íons. Para ondas com altas freqüências podemos considerar os íons em repouso de modo que a função de distribuição para os íons é invariável na posição e no tempo. O estado do plasma será então descrito por uma função de distribuição para os elétrons f(x, c, t) tal que f(x, c, t) dc fornece, no instante t, o número de elétrons com velocidades entre c e c + dc, em torno do ponto x. A função de distribuição para os elétrons satisfaz a equação de Boltzmann

onde

e é a carga fundamental,

m a massa do elétron,

E

_i(

x,

t) é o campo elétrico e

B

_i(

x,

t) a indução magnética associados às distribuições de cargas e correntes no plasma;

(

f ) denota o termo colisional da equação de Boltzmann.

Do ponto de vista matemático, a solução da equação de Boltzmann é complexa devido à dificuldade na determinação do termo colisional (f ). Para contorna-la utilizaremos o modelo BGK para a equação de Boltzmann[9], com o termo colisional dado por

onde n é a freqüência de colisão entre elétrons e íons, considerada constante, e

é a função de distribuição de equilíbrio local para os elétrons. Na equação (2.3)

n(

x,

t) e

T(

x,

t) representam, respectivamente, a densidade de número de elétrons e a temperatura do plasma,

C

_i(

x,

t)=

c

_i-

v

_i (

x,

t) é a velocidade peculiar dos elétrons,

v

_i(

x,

t) é a velocidade hidrodinâmica dos elétrons e

k

_B é a constante de Boltzmann.

Com a equação (2.2) a equação de Boltzmann (2.1) pode ser escrita como

O campo elétrico

E

_i(

x,

t) e a indução magnética

B

_i(

x,

t) obedecem às equações de Maxwell que, no Sistema Internacional de Unidades, são escritas como

com as densidades volumétrica de cargas e superficial de correntes dadas, respectivamente, por

onde o índice a denota elétrons ou íons.

III Campos Básicos e Linearizações

Caracterizamos o estado macroscópico do plasma pelos campos de densidade de número de elétrons n(x, t), velocidade hidrodinâmica dos elétrons v_i(x, t) e temperatura do plasma T(x, t), definidos por

Para estados próximos do equilíbrio a função de distribuição para os elétrons pode ser escrita como

onde

n

₀ é a densidade de número de elétrons no equilíbrio,

é a função de distribuição Maxwelliana global e

f

₁(

x,

c,

t) é uma perturbação de primeira ordem para

f

₀(

c).

Substituindo a equação (3.4) nas equações (3.1) a (3.3) obtemos os campos básicos linearizados, dados por

onde

v

₀ = (2

k

_B

T

₀/

m)

^1/2 é a velocidade térmica dos elétrons e as perturbações de primeira ordem para os campos básicos são

com o parâmetro b

₀ = 1/

.

A função de distribuição de equilíbrio local (2.3) linearizada, através das equações (3.6) a (3.8), resulta

A equação cinética (2.4) linearizada, através das equações (3.4) e (3.12), é dada por

e as perturbações do campo elétrico

_i(

x,

t) e da indução magnética

_i(

x,

t), nulas no equilíbrio, satisfazem as equações de Maxwell (2.5) linearizadas

A determinação dos campos básicos (3.6) a (3.8) requer o conhecimento da função f₁(x, c, t) a qual pode ser obtida da solução das equações (3.13) e (3.14). Para isso necessitamos de um modelo para as perturbações, o qual será introduzido na seção seguinte.

IV Soluções para Ondas Harmônicas Planas com Pequenas Amplitudes

Iremos considerar que as perturbações se propagam no plasma como ondas planas com pequenas amplitudes, número de onda k e freqüência angular w. Assim,

Com as equações (4.1) a (4.6), a equação cinética (3.14) pode ser escrita como

Para as equações de Maxwell (3.14), temos

Eliminando

_j das equações (4.10) e (4.11), obtemos

Sem perda de generalidade iremos considerar o eixo dos x como sendo a direção de propagação; neste caso, as componentes para o campo elétrico são dadas por

Por outro lado, das equações (4.9) e (4.10) obtemos as correspondentes componentes da indução magnética

As equações (4.13) e (4.16) representam as componentes do campo elétrico e da indução magnética para a propagação de ondas longitudinais eletrostáticas; as demais componentes representam ondas eletromagnéticas transversais.

Eliminando as componentes do campo elétrico na equação (4.7), através das equações (4.13) a (4.15), obtemos

Introduzindo as quantidades adimensionais

onde

c = (1/m

₀e

₀)

^1/2 é a velocidade da luz no vácuo e w

_p = (

n

₀

e

²/e

₀

m)

^1/2 é a freqüência de plasma para os elétrons, a equação (4.19) pode ser escrita como

Substituindo as equações (4.1) a (4.3), (4.6) e (4.21) nas equações (3.9) a (3.11) e realizando as integrações nas velocidades, obtemos o seguinte sistema de equações para as amplitudes das perturbações:

Ao realizarmos as integrações introduzimos a função

onde

t =

c

_x/

v

₀ e a fórmula de recorrência

onde

e G(

n) é a função gama.

A função de dispersão de plasma W(z) está relacionada à equação (4.25) por

É importante observar que as integrações das equações (3.9) a (3.11) nas componentes das velocidades c_y e c_z, onde ]₁ (c) é dada pela equação (4.21), resultam nulas; assim, as componentes (4.14) e (4.15) do campo elétrico e as componentes (4.17) e (4.18) da indução magnética não contribuem para o sistema de equações (4.22) a (4.24) o qual representa, portanto, a propagação de ondas longitudinais eletrostáticas.

O sistema de equações (4.22) a (4.24) pode ser escrito na forma matricial Mx = 0, ou

onde

O sistema de equações (4.28) admite solução não trivial se det[M] = 0. Com esta condição podemos obter as relações de dispersão para a propagação de ondas longitudinais eletrostáticas no plasma, da qual trataremos na próxima seção.

V Propagação de Ondas Planas Longitudinais Eletrostáticas

As relações de dispersão w = w(k) ou k = k(w) para ondas longitudinais eletrostáticas podem ser obtidas pela resolução do sistema de equações (4.28)

Na equação (5.1) introduzimos grandezas adimensionais com a freqüência angular w e a freqüência de colisão n em unidades da freqüência de plasma w_p e o número de onda k em unidades de w_p/v₀ de modo que z = i(n - i w)/k. Antes de resolvermos a equação (5.1) são necessárias algumas considerações sobre a função de dispersão de plasma W(z), definida pela equação (4.27), a qual apresenta singularidades para valores de z no eixo real t (t^* = z). De modo geral esta integral deve ser calculada numericamente e seus resultados são apresentados por Fried e Conte[10].

Para ondas que se propagam com velocidade de fase muito maior que a velocidade térmica dos elétrons num plasma não-colisional podemos expandir o integrando da equação (4.27) em potências de k c_x/w. Vlasov[4] tomou o valor principal de Cauchy da integral e ignorou o polo. De modo análogo, Bohm e Gross[6] não consideraram a contribuição à integral das partículas com velocidades na vizinhança do polo. O resultado obtido, aproximado até a ordem de (k v₀/w_p)², é dado por

e denominado de relação de dispersão de Bohm-Gross, a qual é válida para a propagação de ondas com l

l

_D onde l

_D=(e

₀

k

_B

T/

n

₀

e

²)

^1/2 é o comprimento de Debye.

Landau[5] mostrou que o fato de considerarmos o polo para t^* = z na integração da equação (4.27) conduz a uma profunda modificação na relação de dispersão (5.2), a qual não é prevista pela teoria de fluidos. Ela introduz o fenômeno conhecido na literatura como amortecimento de Landau, que consiste na atenuação da amplitude da onda que se propaga embora as colisões dos constituintes do plasma não sejam consideradas. O resultado obtido por Landau para a parte imaginária da freqüência angular é

sendo | w

_i/w

_p|

1 desde que |

k

v

₀/w

_p|

1. A validade desta equação foi verificada experimentalmente por Derfler e Simonen[11].

Iremos considerar que o plasma experimenta uma pertubação sinusoidal com número de onda real k e freqüência angular complexa w = w_r + i w_i. Para ondas temporalmente amortecidas temos w_i < 0 de modo que a parte imaginária de z, z_i = (n- | w_i|)/k, será positiva se n > | w_i| ou negativa se n < | w_i| . O primeiro caso, no qual predomina a freqüência de colisão sobre a freqüência de amortecimento, denominaremos de amortecimento colisional e no segundo, no qual predomina a freqüência de amortecimento sobre a freqüência de colisão, denominaremos de amortecimento de Landau.

Para analisarmos a integração da equação (4.27) ao longo do eixo real t, consideraremos as três situações possíveis para a parte imaginária de z. Para z_i > 0, que corresponde ao amortecimento colisional, W(z) é uma função analítica no primeiro quadrante do plano complexo t. Para z_i = 0, há um polo para t = w_r/k no eixo real t e W(z) não é uma função analítica para este ponto.

Para continuarmos W(z) analíticamente para o quarto quadrante do plano complexo t, onde z_i < 0 e que corresponde ao amortecimento de Landau, consideremos as integrais de Plemelj[12] para a integração com polos em x = x₀ ± e, próximos do eixo real x,

onde o primeiro termo do lado direito representa o valor principal de Cauchy para a integral e o segundo termo representa as contribuições dos polos acima (+e) ou abaixo (-e) do eixo x. A equação (5.4) exibe a descontinuidade de f(x) através do eixo real x com um salto igual a -2pi f(x₀).

Os três casos para a integração da equação (4.27) podem resumidos no contorno C, prescrito originalmente por Landau[5] e mostrado na Fig. 1, tal que

de modo que

A Fig. 1.a exibe o contorno C para a integração da equação (5.6) enquanto que para as equações (5.7) e (5.8) o contorno C é deformado de modo a passar sob o polo, como mostrado nas Figs 1.b e 1.c.

Consideraremos o caso em que a velocidade de fase w_r/k para a propagação da onda é muito maior que a velocidade térmica v₀ dos elétrons de modo que a velocidade de fase da onda é igual à velocidade de um pequeno número de elétrons localizados na cauda da distribuição maxwelliana.

Se t |z| podemos expandir o integrando da equação (5.5) em potências de t/z e obtemos

a qual é válida para qualquer valor da freqüência de colisão. Na equação (5.9)

a = 0 para

z

_i > 0,

a = 1 para

z

_i = 0 e

a = 2 para

z

_i < 0.

Integrando a equação (5.9), resulta

Trataremos, em seguida, de cada um dos casos mencionados.

V.1 Amortecimento Colisional

Com n > | w_i| e w_r/k v₀ 1 a equação (5.6) é escrita, através da equação (5.10) com a = 0, como

Com o objetivo de comparar as soluções para o sistema de equações (5.1) vamos considerar inicialmente a propagação de ondas longitudinais eletrostáticas num plasma isotérmico. Em seguida trataremos da solução para o caso geral.

V.1.1 Propagação em um Plasma Isotérmico

Para um plasma mantido à temperatura constante temos, da equação (5.1):

A solução não trivial para o sistema de equações (5.12) é obtida igualando-se a zero o determinante dos coeficientes, o que resulta

Na equação (5.13) o termo independente de

W(

z) é da ordem de

k

³ e o coeficiente de

W(

z) é da ordem de

k

²; substituindo

W(

z) da equação (5.11) até o termo da ordem de

k

⁵, obtemos

Reintroduzindo as grandezas usuais e mantendo os termos até a ordem de (k v₀/w_p)², temos

onde fizemos w = w

_p no coeficiente de

k

v

₀/w

_p.

A equação (5.15) é a relação de dispersão, aproximada até a ordem de (kv₀/w_p)², para um plasma colisional isotérmico.

Consideremos alguns casos particulares. Se a freqüência de colisão for muito menor que a freqüência de plasma, obtemos

que é a relação de dispersão de Bohm-Gross (5.2), válida para a propagação de ondas longitudinais num plasma rarefeito com velocidades de fase muito maiores que a velocidade térmica dos elétrons.

Se a freqüência de colisão for muito maior que a freqüência de plasma, a equação (5.15) se reduz a

que é o resultado obtido anteriormente por Thomson e Thomson[13] utilizando a equação de transferência de Maxwell.

As partes real e imaginária da freqüência angular são dadas, através da equação (5.15), por

e

onde verificamos que |w

_i|/ n

1.

Da equação (5.19) concluimos que a máxima atenuação para ondas longitudinais que se propagam num plasma isotérmico ocorre quando a freqüência de colisão coincide com a freqüência de plasma, isto é

A atenuação das ondas que se propagam é pequena; por exemplo, para kv₀/w_p = 1/10 verificamos que (w_i )_max/w_p é menor que um por cento.

V.1.2 Propagação em um Plasma Térmico

Para um plasma que apresenta flutuações na temperatura a solução não trivial é obtida igualando a zero o determinante dos coeficientes do sistema de equações (5.1). Com o mesmo argumento que utilizamos para obter a equação (5.14) substituimos a função de dispersão de plasma (5.11) até o termo de ordem de k⁹ e obtemos:

Reitroduzindo as unidades originais para as freqüências w e n e para o número de onda k, aproximando até o termo de ordem (k v₀/w_p)², obtemos a relação de dispersão

onde substituimos w por w

_p no coeficiente de (

k

v

₀/w

_p)

².

Para n w_p a equação (5.22) se reduz a

No regime de baixas pressões, com n w_p, a equação (5.22) se reduz à relação de dispersão de Bohm-Gross (5.16).

As parte real e imaginária da freqüência angular são dadas, através da equação (5.22), por

e

onde verificamos que |w

_i|

n.

Da equação (5.25) concluimos que a máxima atenuação da onda ocorre quando a freqüência de colisão é igual à freqüência de plasma, isto é

que é igual a 2/3 da máxima atenuação para o caso isotérmico, dada pela equação (5.20).

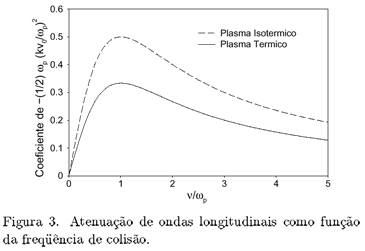
O gráfico da Fig. 2 exibe as variações dos coeficientes de 3 w_p (kv₀/ w_p)²/4, como funções de n/w_p, para a parte real das freqüências dadas pelas equações (5.18) e (5.24); o valor 1 para este coeficiente corresponde à relação de dispersão de Bohm-Gross (5.16). As variações para a parte imaginária w_i, das equações (5.19) e (5.25), são mostradas no gráfico da Fig. 3.

5.2 Amortecimento de Landau

Consideraremos o caso em que a freqüência de colisão é menor que a freqüência de amortecimento (n < |w_i|) e as ondas são fracamente atenuadas (|(n + w_i)/w_r| 1); assim, o polo t^*=z está localizado abaixo e próximo do eixo real t, no quarto quadrante do plano complexo t. Seguindo a prescrição de Landau[5], o contorno C para a integração da equação (5.5) coincide com o eixo real t sendo deformado para passar abaixo do polo t = w_r/k de modo que a função de dispersão de plasma é dada pela equação (5.7).

Desprezando os termos que envolvem produtos do número de onda k com a freqüência de colisão n, desde que k n 1, podemos escrever a equação (5.1) como

e, das equações (5.7) e (5.11), temos para a função de dispersão de plasma

Igualando a zero o determinante dos coeficientes da equação (5.27) e com A(z) dado pela equação (4.29), temos

Substituindo a equação (5.28) na equação anterior e reintroduzindo as unidades usuais, obtemos a relação de dispersão

onde tomamos w = w_p no segundo membro exceto no expoente onde usamos a relação de dispersão (5.16).

Da equação (5.30) obtemos para a parte real da freqüência

que é equivalente à relação de dispersão de Bohm-Gross (5.16); para a parte imaginária da freqüência, obtemos

Os dois termos do lado direito da equação (5.32) representam os diferentes mecanismos de atenuação para a onda que se propaga. O primeiro deles representa a atenuação devida às colisões entre os elétrons e os íons constituintes do plasma. O segundo termo representa um mecanismo ressonante para a transferência de energia da onda que se propaga para os elétrons que se movimentam com velocidades próximas da velocidade de fase da onda. Este termo, denominado fator de amortecimento de Landau, é essencialmente o resultado (5.3) exceto que Landau empregou w = w_p no termo exponencial, de modo que seu resultado é exp(3/2) 4,48 maior que o resultado mais preciso dado pela equação (5.32)[14].

VI Conclusões

Nosso objetivo neste artigo foi obter, através do modelo BGK para a equação de Boltzmann acoplada às equações de Maxwell, as relações de dispersão para ondas eletrostáticas longitudinais apresentadas nos trabalhos clássicos de Landau[5] e de Bathnagar, Gross e Krook[9], de uma maneira simples e consistente. O resultado obtido mostra que a onda que se propaga é atenuada por colisões entre elétrons e íons bem como por um mecanismo de transferência de energia da onda para os elétrons que se movimentam com velocidades próximas da velocidade de fase da onda.

Desta forma, este artigo constitui uma excelente aplicacão para os alunos iniciados em teoria cinética de gases e eletromagnetismo, no nível dos cursos de graduação, bem como aos interessados no estudo de física de plasmas.

Agradecimentos

Os autores agradecem as sugestões do Professor Gilberto Medeiros Kremer e o apoio do Professor Márcio Henrique Franco Bettega na obtenção de artigo de referência.

^†e-mail:[e-mail]

• [1] L. Tonks e I. Langmuir, Phys. Rev., 33, 195 (1929).
• [2] S. Ichimaru, Basic Principles of Plasma Physics, A Statiscal Approach, 2nd ed. W. A. Benjamin, Reading, Massachusetts (1973).
• [3] J. A. Bittencourt, Fundamentals of Plasma Physics, 2nd ed., co-edition Fapesp, São José dos Campos, São Paulo (1995).
• [4] A. Vlasov, J. Phys. (USSR), 9, 25 (1945).
• [5] L. Landau, J.Phys. (USSR), 10, 25 (1946).
• [6] D. Bohm e E. P. Gross, Phys. Rev., 75, 1851 (1949).
• [7] J. Buck, Q. Rev. Biol., 63, 256 (1988).
• [8] T. A. Winfree, The Geometry of Biological Time, Springer, New York (1980).
• [9] P. L. Bathnagar, E. P. Gross e M. Krook, Phys. Rev., 94, 511 (1954).
• [10] B. D. Fried e S. D. Conte, The Plasma Dispersion Function, Academic Press, New York (1961).
• [11] H. Derfler e T. C. Simonen, J. App. Phys., 17, 5014 (1967).
• [12] D. R. Nicholson: Introduction to Plasma Theory, Krieger Publishing Company, Florida (1992).
• [13] J.J. Thomson and G.P. Thomson, Conduction of Eletricity Through Gases, Cambridge University Press, Cambridge, Vol. 2, (1933).
• [14] J. D. Jackson, Nucl. Energy, Part C, 1, 171 (1960).

Datas de Publicação

• Publicação nesta coleção
  20 Maio 2011
• Data do Fascículo
  Jun 2001

Histórico

• Aceito
  20 Abr 2001
• Recebido
  01 Mar 2001